Abstract
Precise soil moisture prediction is important for water management and logistics of on-farm operations. However, soil moisture is affected by various soil, crop, and meteorological factors, and it is difficult to establish ideal mathematical models for moisture prediction. We investigated various machine learning techniques for predicting soil moisture in the Red River Valley of the North (RRVN). Specifically, the evaluated machine learning techniques included classification and regression trees (CART), random forest regression (RFR), boosted regression trees (BRT), multiple linear regression (MLR), support vector regression (SVR), and artificial neural networks (ANN). The objective of this study was to determine the effectiveness of these machine learning techniques and evaluate the importance of predictor variables. The RFR and BRT algorithms performed the best, with mean absolute errors (MAE) of <0.040 m3 m−3 and root mean square errors (RMSE) of 0.045 and 0.048 m3 m−3, respectively. Similarly, RFR, SVR, and BRT showed high correlations (r2 of 0.72, 0.65 and 0.67 respectively) between predicted and measured soil moisture. The CART, RFR, and BRT models showed that soil moisture at nearby weather stations had the highest relative influence on moisture prediction, followed by 4-day cumulative rainfall and PET, subsequently followed by bulk density and Ksat.
1. Introduction
Soil moisture has a strong influence on the distribution of water between various components of the hydrological cycle in agricultural fields. It helps in understanding the hydrology and climatic conditions that have high spatial and temporal variability. Precise measurement and/or prediction of soil moisture provides insights into expected infiltration and runoff generation during rainfall events and the management of water for agricultural purposes [1]. In agricultural fields, soil moisture affects key farm activities from crop selection to timing of tilling, planting, fertilizer application, and harvesting due to infiltration, evaporation, runoff, heat, and gas fluxes [2,3]. Soil moisture prediction across large spatial scales is difficult due to the heterogeneity in soil texture, crop type, and crop residue cover. Point measurements that include gravimetric methods and in-situ electromagnetic sensors are accurate but have limited spatial extent and require significant time and labor [4]. Remote sensing tools have been used recently to predict surface soil moisture, but efficiency and models applicable to multiple landscapes are still under study [5].
In practice, farmers typically rely on heuristic approaches with weather station data (e.g., rainfall, evapotranspiration, temperature) to predict (or extrapolate) conditions in their crop fields. More accurate and optimal computational approaches need to explicitly consider various factors such as crop type, soil texture, saturated hydraulic conductivity, and residue content affecting the soil moisture in these crop fields.
Soil moisture is often predicted using information collected from nearby weather stations and variables from soil and crops using one of three empirical, regression, and machine learning methods [6]. These methods include forecasting models such as empirical formulas [7], water balance approach, dynamic soil water models [8], time series models [9], and neural network models [10]. Statistical models include regression techniques to develop geospatial functions from in-situ measurements of target and predictor variables. The advantage of traditional models is that they are typically fast to derive and do not require many inputs [11]. However, the disadvantage of traditional models is the need for an abundance of ground measurements that could be time-consuming and expensive. Moreover, traditional modeling approaches follow strict statistical assumptions and data requirements that frequently utilize linear and additive modeling approaches that are not consistent with natural processes [12].
Recently, the use of machine learning techniques has gained attention because they can overcome some of the limitations of traditional and physics-based models. Ali et al. (2015) [11] suggested machine learning models provide the benefit to understand and estimate complex non-linear mapping of the data distributed without any prior knowledge. In addition to that, this also helps to combine various sources that are poorly defined and have unknown probability functions. However, machine learning algorithms provide no information on how they have established relationships between different variables and require a large number of data points used for training. The machine learning technique is rapidly growing in predictive modeling to identify complex data structures that are often non-linear, and generating accurate predictive models [13,14]. Machine learning models have greater power for resolving and establishing complex relations (nonlinear, nonmonotonic, multimodal relationships common with landscape and ecological applications) as they are not restricted to traditional assumptions about data characteristics. There are numerous machine learning algorithms, such as classification and regression trees (CART), random forest regression (RFR) [15], support vector regression (SVR) [16,17], multiple linear regression modeling, boosted regression tree (BRT), artificial neural networks (ANN) [18], etc. that are used for predictions. In the hydrology domain, neural networks [19], vector machines [20], and polynomial regression [21] have been applied in soil moisture prediction using historical soil moisture datasets.
For example, Matei et al. (2017) [22] used different machine learning models (SVR, NN, LR, RFR, etc.) for real-time soil moisture prediction in the Transylvanian Depression in Romania. They used data (soil temperature, air temperature, precipitation) from a nearby weather station and crop and soil information from nearby agricultural fields. Machine learning-based models (e.g., an RFR) achieve better performance when compared with the physics-based Richards equation model in predicting soil matric potential in the root zone [23]. Yoon et al. (2011) [24] used ANN to model the water table dynamics of various agricultural systems. The random forest model was found to be superior to the ANN model when predicting lake water levels with fewer parameters and less training time [25]. Alternatively, Gill et al. (2006) [1] used SVM to predict soil moisture using meteorological data, field data, and crop data. The SVM employs structural risk minimization instead of the traditional risk minimization, which formulates quadratic optimization to ensure a global optimum. The SVM model is sparse and not affected by dimensionality. Support vector regression is less prone to overfitting the regression function and will generate precise predictions because it uses the generalization error bound (ɛ)-insensitive loss function and structural risk optimization [26].
There are research gaps for using these machine learning methods in landscapes with frigid soil classifications, underlain by very poorly drained geological material, and having a diversity of production agriculture crop species. The research presented here aids in filling in these gaps. The goal of this study was to determine the performance of the abovementioned machine learning models for predicting soil moisture in crop fields throughout the Red River Valley of the North by using weather station observations and field characteristics of nearby areas under crop management. The objectives of this study were to (i) investigate the effectiveness of different machine learning tools in soil moisture prediction, and (ii) determine the important predictor variables affecting field soil moisture content using machine learning tools.
2. Methods
2.1. Study Site and Weather Station
This study was conducted along the Red River Valley of the North (RRVN) in North Dakota and Minnesota (Figure 1). The RRVN is a glaciolacustrine lakebed formed by ancient Lake Agassiz, which existed for more than 4000 years. The topography is minimal (1 m per 5 km), and Mollisols and Vertisols are the dominant soil orders, with soil texture ranging from clay to loamy sand. The parent material for RRVN is poorly drained and consists of gray, slickensided, flat clays of Brenna/Argusville formation that are overlain by the tan-buff, laminated silty clays of the Sherack formation. The major crops cultivated in this area includes corn, soybean, wheat, sugarbeet, barley, canola, and potato. The annual mean temperature is 4 °C, and temperatures typically vary from −16 °C to 29 °C, whereas 30-year mean annual rainfall and snowfall are 60 cm and 125 cm, respectively [27]. Summers are long and warm, winters are frigid, snowy, and windy, and the skies are partly cloudy year-round.
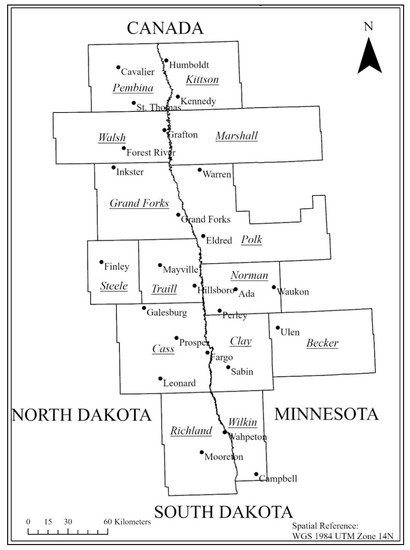
Figure 1.
Map showing counties of North Dakota and Minnesota and weather stations in study area around Red River Valley. Black dots in map represent weather stations, and county names are in italics and underlined.
There are 117 weather stations in the North Dakota Agricultural Weather Network (NDAWN) in North Dakota (83), Minnesota (28) and Montana (6), which report 32 weather parameters (e.g., air temperature, rainfall, wind direction, soil moisture). Our study area covered a total of 25 weather stations, of which 15 are located across eight counties in North Dakota and 10 across seven counties in Minnesota (Figure 1). Weather station data and measurements from nearby agricultural fields of the study area were collected during the cropping season from June to September 2019. Soil moisture was measured around the weather stations and in nearby crop fields in 16-day intervals. The distance between crop fields and the weather stations was measured in meters. The distance measures were classified into six different classes (0–100 m, 100–200 m, 200–400 m, 400–800 m, 800–1200 m and 1200–2000 m). The crop fields under study were within the range of 2000 m from the nearest weather station for the entire study area in the RRVN.
2.2. Soil Moisture Measurement
Soil moisture from each field and weather station was measured using the gravimetric method. Soil samples were collected from fields using Uhland cores. Composite soil samples were collected from 3 different locations in individual fields using sampling cores of dimensions 6 cm × 8 cm at 0 to 6 cm depth, and GPS coordinates were recorded. Wet soil samples collected from the fields were weighed and then oven-dried at 105 °C for 48 h. Gravimetric water content was determined using soil sample dry weight and the amount of water lost during drying. Volumetric water content (VWC) of soil was calculated by multiplying gravimetric water content (m3 m−3) by bulk density (g cm−3) [28].
2.3. Crop Types in Study Area
This study covered all types of crops grown in this area, such as soybean (24 plots), wheat (18 plots), corn (16 plots), sugarbeet (6 plots), dry beans (5 plots), oats (2 plots), barley (1 plot), potato (1 plot), canola (1 plot), and alfalfa (1 plot). Soil samples for measurements of bulk density and moisture content were collected after the germination of the crops starting from the first week of June 2019. Soil samples were collected in 16-day intervals, and growth stages of each crop were recorded using the standards developed by the United States Department of Agriculture [29].
2.4. Residue Cover, Soil Texture, and Saturated Hydraulic Conductivity
Antecedent characteristics such as residue cover, soil texture, and saturated hydraulic conductivity (Ksat) were determined for each location from where soil samples were collected. Residue cover was determined using the rope method along 8 transects per sample site (i.e., residue presence at 100 points along 15 m oriented 45° to plant rows) [30]. Crop residues were then pooled and classified as percentages in 3 different categories (<10%, 20–30%, and 50–60% residue cover) for analysis. Soil texture for this experiment was determined for each soil sample using the pipette method described by Gee and Bauder (1986) [31]. Ksat (inch hr−1) was estimated using Rosetta neural network pedotransfer function in Hydrus-1D that uses input data on sand, silt, clay percent, bulk density (g cm−3), and water content at 33 and 1500 kPa suctions (cm3 cm−3) [32,33]. Pressure plate apparatus were used to determine water content at 33 and 1500 kPa suctions [34].
2.5. Rainfall and Potential Evapotranspiration
Rainfall and potential evapotranspiration data recorded by each weather station were downloaded from the North Dakota Agricultural Weather Network (NDAWN) (https://ndawn.ndsu.nodak.edu/, accessed on 1 October 2020). Rainfall was measured hourly at a 1-meter height above soil surface using TE525 tipping bucket rain gauges (Texas Electronics TR-525I, Dallas, TX, USA) at each NDAWN weather station. Each gauge measures rainfall in 0.254-mm increments. Potential evapotranspiration (PET) is the estimate of the maximum daily crop water loss when water is readily available. It is calculated with the Penman equation [35] that use soil radiation, dew point temperature, and wind speed and air temperature. The 4-day cumulative rainfall measure showed higher correlation (r = 0.8) with field soil moisture in a study conducted in 3 European countries [36]. In this study, we used 4-day cumulative rainfall and PET to predict soil moisture. The 4-day cumulative rainfall and PET were calculated by adding up the preceding 4 days of values for rainfall and PET in mm.
2.6. Machine Learning Algorithms
2.6.1. Classification and Regression Trees (CART)
CART is a tree-based regression model and rule-based procedure that creates a binary tree using binary recursive partitioning (BRP) to yield the maximum reduction in the variability of the response variable [37]. The BRP is a nonparametric nonlinear technique that splits the data into subsets based on available independent factors, which means it divides nodes into yes/no answers as predictor values. Regression trees are generated for continuous data and classification trees for categorical data [38].
Suppose input variables are x1, x2, …. xn and output variable is y for training dataset in the space D with n input variables and m input samples. Let D = {(x11, x12, …. x1n, y1), (x21, x22, …. x2n, y1), (xm1, xm2, …. xmn, ym)}. The CART model splits D into a certain number of subspaces using BRP. Each recursive process attempts to select several splitting variables and splitting points from the current space S (parent node) to divide the space into two inhomogeneous subspaces S1 and S2. Every subspace has an estimated value ŷ determined by fitting using the least square method; the optimal splitting variable j and splitting point s are finally selected to ensure that the binary division has the minimum residual variance [39].
2.6.2. Random Forest Regression (RFR)
Random forest regression was developed by Breiman (2001) [40] and is relatively simple to train, tune, and apply. This technique is developed as average over the many individual decision tree-based models that are built on the bootstrapped training sample. Each training sample considers a small group of predictor variables at every split that maintains decorrelation among the variables and splits [41]. The RFR improves predictive accuracy by generating large numbers of decision trees that classify a case using each tree in the new forest and deciding a final predicted outcome by combining the results across all the trees. Each tree is built using a deterministic algorithm by selecting a random set of variables and a random sample from the training dataset (i.e., the calibration dataset). The RFR uses 3 parameters, (1) the number of regression trees grown based on the bootstrap sample of the observation (e.g., hundreds or thousands of trees), (2) the number of different predictors tested at each node (e.g., one third of the total number of variables) and (3) the minimal size of the terminal nodes of the trees (e.g., 1).
2.6.3. Boosted Regression Trees (BRT)
Friedman (2002) [42] defined BRT as a decision tree model that is improved by the gradient boosting algorithm, which constructs an additive regression model that fits in chronological order based on a simple base learner function to current pseudo-residuals at each iteration. The pseudo-residuals are defined as the slope of the loss function that is being minimized. Due to the use of pseudo-residuals, simple base learner function, and iteration at each level, this model has performed better compared to other machine learning models [43,44]. Due to their ability to perform better with complicated data, BRT models are popular and attractive among data scientists [45]. However, the data used for training sets are compiled from different sources, making the model susceptible to certain types of inconsistencies [40,41].
The BRT helps in partitioning influences of the independent (predictor) variables on the dependent variable (soil moisture for this study). This combination of regression trees with the boosting algorithm has been used by ecologists to explore the relationship between ecological processes and predictors [46]. The BRT handles predictor variables with different data types, distributions, and completeness (i.e., level of missing values) [47]. The fitting of the BRT model is controlled by different factors, such as the learning rate that determines the contribution of each tree to the growing model, the tree complexity that controls the level of interactions in BRT, the bagging fractions that set the proportion of observations used in selecting variables, and the cross validation that specifies the number of times to randomly divide the data for model fitting and validation [48].
2.6.4. Multiple Linear Regression (MLR)
Multiple linear regression is an extension of simple linear regression used to predict an outcome variable based on multiple distinct predictor variables. With ‘n’ number of predictor variables (x), the predictions of y are expressed by the following equation.
y = b0 + b1X1 + b2X2……… bnxn
The b values are called the regression weights (beta coefficients). The measures of association between the predictor variable and the outcome ‘bi’ can be interpreted as the average effect on y of a unit increase in xi, holding all other predictors constant.
2.6.5. Support Vector Regression (SVR)
Support vector regression uses a support vector machine (SVM) to solve regression problems [49,50]. SVM learning simplifies a maximal margin classifier to map the input variables into a high dimensional space using a fixed mapping kernel function. To overcome local minima problems created due to the use of few parameters while tuning the training dataset, SVR uses a radial basis kernel function by constructing the hyperplanes that can be used for regression. Yang et al. (2009) [51] found radial basis functions powerful because they are simple and reliable and deal with complex dimensional space and margin separation factors.
The SVR involves the use of a subset of data points that are based on a predefined error margin to fit a regression model between dependent variable and explanatory variables. Those subsets of data points are called support vectors. Let us suppose, there are given samples X = {} and corresponding target values Y = {y1, y2, ……, yi}, yi ∈ R. The goal of SVR is to find the function f(x) that has at most standard deviation from the obtained target yi for all training data and is meanwhile as flat as possible.
2.6.6. Artificial Neural Network (ANN)
Artificial neural networks are a powerful computing tool constructed through many simple interconnected elements called neurons with unique capability of recognizing underlying relationships with input and output events. An ANN consist of input, hidden, and output layers arranged in a discrete manner [52]. A collection of neurons arranged in the dimensional array is called a layer, where each layer includes 1 or more individual nodes. The number of input variables necessary for predicting the desired output variables determines the number of input nodes. The complexity of modeling is dependent upon the optimum number of hidden nodes and hidden layers (i.e., larger numbers of hidden layers result in a larger, more complex model) [53].
These ANN models mimic human learning ability by learning from a training dataset. They are robust to noisy data and a powerful tool to approximate multivariate non-linear relations among the variables [54]. ANN is a powerful tool that can approximate all types of non-linear mapping. These models have been used for input-output correlations of non-linear processes in water resources and hydrology [55].
2.7. Machine Learning Procedures
The machine learning procedures were performed using the R environment software [56]. The caTools R package was used to handle training and testing of the dataset, and the Metrics package was used to calculate RMSE and MAE for all models.
Karatzolou et al. (2004) [57] suggested the use of the kernlab R-package along with eps-regression SVM type, radial kernel, cost value of 1, gamma value of 0.04167, and epsilon value of 0.1 to execute the SVR function for analysis. Liaw and Wiener (2015) [58] have used the randomForest R-package to implement a random forest regression model, and as values for ntree, mtry, and nodesize, used 1000, 4 and 1, respectively.
The BRT algorithm was implemented using the gbm R package and CART algorithm using the rpart R package. Similarly, the neuralnet package [59] was used for the ANN algorithm, which depends on two other packages, grid and MASS [60]. The metrics R package is used in supervised machine learning, and it implements metrics for regression, classification, and information retrieval problems. The iml R-package is used for predictor variable importance and accumulated local effects plots. The above-mentioned R packages were used to execute the respective machine learning models for this study to predict field soil moisture.
The entire dataset was divided 70–30%, with 70% of the data used as a training set and 30% used for testing (i.e., validation). The testing set was used to evaluate final trained models. All training sets had samples from all 7 sampling dates throughout the study period.
2.8. Statistical Analysis
2.8.1. Model Performance
The model was developed based on the training dataset, and the performance of the model was evaluated based on the testing dataset, also known as validation. Mean absolute error (MAE), root mean square error (RMSE), and coefficient of determination (r2) were used as tools to measure the performance of different models, and were determined as follows:
where N, y, ŷ, denotes the number of observations, measured values, predicted values, and mean of measured values, respectively. Scatter plots and box plots were used to show relationships between the observed and predicted soil moisture for different machine learning models.
The soil moisture (VWC) of a crop field was set as the dependent variable, whereas predictor variables were VWC of the weather station, bulk density, and Ksat of crop field and weather station, crop type, distance from crop field to weather station, sand, silt, and clay percentages in crop field soil, residue cover, 4-day cumulative rainfall, and PET.
2.8.2. Variable Importance
Each predictor variable has an impact on the model generated by the machine learning algorithm; the statistical significance can be measured using the variable importance. RFR algorithms calculate variable importance internally in the form of increases in the RMSE, whereas BRT determines variable importance as a percentage. On the other hand, the CART model derives the variable importance as the relative contribution of the predictor variable to field soil moisture.
Loss of mean absolute error (MAE) can characterize the influence of the predictor variable in the generated model and shows the level of effect if not considered in the prediction model. This loss of MAE was implemented using the iml R-package and showed 5th and 95th percentiles of the loss of MAE due to the particular model.
2.8.3. Effect of Predictor Variables
Apley and Zhu (2020) [61] and Greenwell (2017) [62] have proposed the concept of accumulated local effects (ALE) plots to establish relationships between the predictor variables and generated output. ALE plots are used to study the relationship between the outcome of machine learning models and predictor variables. Machine learning algorithms can use many variables in prediction models, but few variables have huge impacts when compared to others. In this study, the top 4 predictor variables were selected based on variable importance, and ALE plots were created using the iml R-package. ALE plots construct unbiased plots even when the variables under study are correlated [59]. ALE values in the plot showed the effect of a variable on the outcome at certain values when compared to the average prediction, and center values indicate the mean effect as zero. Molnar (2019) [63] gave an example of ALE estimate of-2; when variable interest had a value of 3, then it could be understood that the prediction was lowered by 2 compared to the average prediction.
3. Results and Discussion
3.1. Model Performance
Machine learning algorithms tested for performance based on the MAE, RMSE, and r2 are presented in Table 1. The best performance was observed under the RFR and BRT models and had MAE values of less than 4%. The RMSE of the predicted soil moisture used five different machine learning algorithm ranges from 0.045 to 0.085 m3 m−3. The RFR model outperformed the other models based on the lowest RMSE value of 0.045 m3 m−3 and higher r2 value of 0.72. After RFR model, SVR and BRT performed well based on the RMSE (0.050 m3 m−3, 0.048 m3 m−3), MAE (0.039 m3 m−3, 0.037 m3 m−3) and r2 (0.65, 0.67) values, respectively.

Table 1.
Comparison of the machine learning algorithms for soil moisture prediction using coefficient of determination (r2), root mean squared error (RMSE), and mean absolute error (MAE). Algorithms included classification and regression trees (CART), multiple linear regression (MLR), random forest regression (RFR), support vector regression (SVR), boosted regression trees (BRT), and artificial neural networks (ANN).
The soil moisture estimates from different models for testing phase are shown in Figure 2. The RFR, BRT, and SVR models performed reasonably well in capturing the soil moisture prediction in the scatter plot diagrams. The RFR model could capture the extremes (low and high values) in soil moisture content depicted by most of the sample points lying on and around the bisector line. There were few sample points that were positioned far away from the bisector line representing poor estimates (too high or too low). The soil moisture estimates for the BRT and SVR models showed they can depict soil moisture prediction with slope values of 0.69 and 0.65, respectively. However, MLR and ANN models showed poorer performance (0.58, 0.53) in terms of spread along the bisector line for the test data.
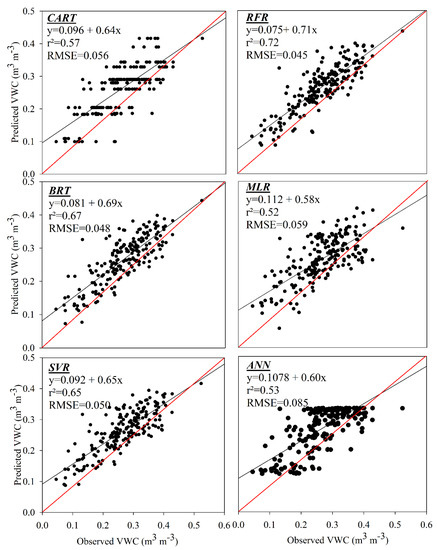
Figure 2.
Scatter plots showing observed versus predicted volumetric water content (m3 m−3) during the testing phase along with regression coefficient (r2) and root mean square error (RMSE) for 6 different machine learning models. Algorithms included classification and regression trees (CART), multiple linear regression (MLR), random forest regression (RFR), support vector regression (SVR), boosted regression trees (BRT), and artificial neural networks (ANN).
Box plots depicting the median and percentiles (5th, 25th, 75th and 95th) of the testing dataset for both the measured and predicted soil moisture are shown in Figure 3. The solid horizontal line inside each box shows the median value; boxes represent the 25th and 75th percentile (interquartile range) values, whereas the whiskers extend from 5th to 95th percentile values. The dashed line inside each box represents the mean of the measured data for the testing phase. The RFR model, compared to other machine learning algorithm, showed that the mean of the measured soil moisture was represented by the median of the estimated soil moisture. The RFR model used contributions from all of the soil and climate variables (Figure 4), thereby yielding better predictions compared to the other models. The distribution of the soil moisture data for this study was better related by when using random forest trees compared to other models. RFR followed by SVR and BRT models were able to capture the relationship between the soil moisture in each field with VWC as recorded for each pertinent weather station, rainfall, PET, crop, and soil factors with lower RMSE and MAE.
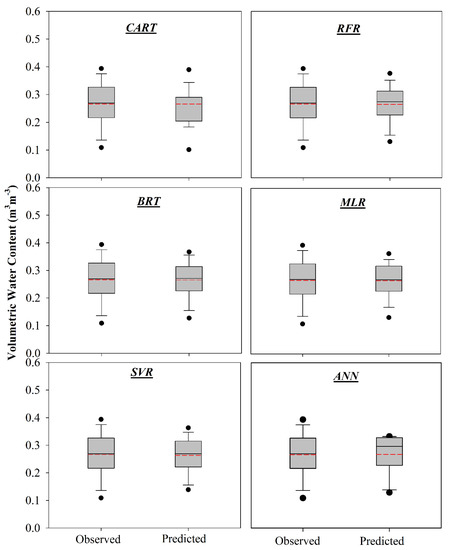
Figure 3.
Box plots depicting the spread of observed and predicted soil moisture (m3 m−3) during the testing phase for 6 different machine learning models. The box shows the interquartile range (25th–75th percentile). The whiskers extend from 5th to 95th percentile values. The solid line inside the box shows the median value (50th percentile) and the dashed line represents the mean value of the observed soil moisture during testing phase. Algorithms included classification and regression trees (CART), multiple linear regression (MLR), random forest regression (RFR), support vector regression (SVR), boosted regression trees (BRT), and artificial neural networks (ANN).
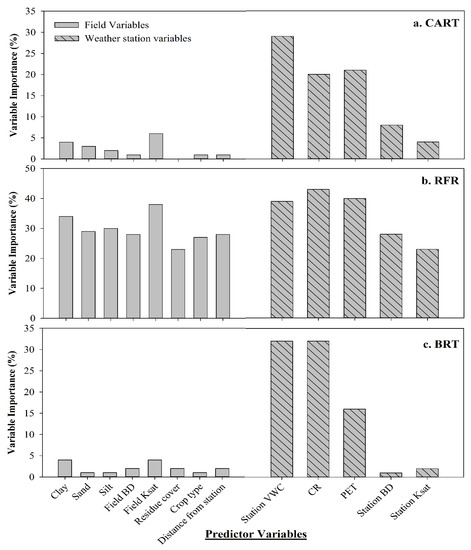
Figure 4.
Variable importance for 3 tree-based model types: (a). classification and regression trees (CART), calculated as the relative influence (%); (b). random forest regression (RFR), calculated as the increase in mean squared error (MSE) (%); and (c). boosted regression trees (BRT), calculated as the relative influence (%). Out of 13 predictor variables, the first 8 represent field, and remaining 5 represent station variables. As the calculation of variable importance differs among CART, RFR and BRT, only the ranking of the variables can be compared, not the absolute values.
The RMSE, r2 and MAE values for the six different machine learning models showed RFR, SVR, and BRT had RMSE of less than 0.05 m3 m−3 and satisfactory r2 values (0.65–0.67), whereas the remaining three models had RMSE higher than 0.05 m3 m−3 and r2 values lower than 0.60. This showed RFR as the best model compared to the other machine learning models due to powerful averaging capacity of all the random trees generated by the model based on the number of parameters used to predict soil moisture [22]. The results for scatter (Figure 2) and box plots (Figure 3) indicated that the difference in soil moisture estimates could be due to the cumulative effect of soil and crop types and change in micro-climate variables (i.e., rainfall and PET). The scatter plot for the CART model showed strange trendlines because it followed only one tree and not the combinations; these data were categorized based on the sampling dates where they were highly correlated. The multiple number of trees addressed the issue similarly to the RFR model. Similarly, in the artificial neural network (ANN) the categorical data for texture, crop type was created the upper limit of moisture value. The relatively high accuracy of RFR and BRT models is consistent with other studies that find ensemble decision-based regression models perform better than many other machine learning models [64], particularly in terrain and soil spatial predictions [65,66,67,68,69]. The scatter plots and box plots showed that CART, MLR, and ANN models did not capture the extreme values in the prediction of soil moisture as well as the RFR, BRT, and SVR models. Results showed that machine learning models such as the RFR, BRT, and SVR outperformed the ANN, MLR, and CART models, possibly due to the carefully selected parameter optimization algorithms used to train the models. Superiority of RFR and SVR over other models has also been reported in various studies [1,70,71,72,73,74]. The SVR model provides an appropriate choice of kernels that allow non-separable data in original space to become separable in the feature space. This subsequently helps to obtain non-linear algorithms from algorithms previously restricted to handling linearly separable datasets [75,76]. Similar results for SVR model performance over other machine learning models was also observed by Karandish and Simunek (2016) [75] in soil water content predictions under water stress conditions; Pal and Mather (2003) [77] for land cover classification; and Gill et al. (2006) [1] for soil moisture prediction in Southwestern Oklahoma. The CART model performed better than the MLR with the formation of a binary tree using binary recursive partitioning that yields the maximum reduction in the variability of the response variable [37]. Successful soil moisture estimation using the CART model has also been reported by Han et al. (2018) [78] in China.
3.2. Importance of Predictor Variables
The importance of predictor variables was determined for the three tree-based machine learning models. The variable importance for the CART, RFR, and BRT models was separated based on the weather station variables (5) and crop field variables (8) (Figure 4). The CART and BRT models measure variable importance (as a percentage) by the relative contribution of each variable to the output (crop field soil moisture). However, the RFR measures variable importance based on the percent increase in root mean square error (RMSE) after removing a particular variable and compared with the previous value. The higher the percent increase in RMSE, the more important the variable was for soil moisture prediction.
All three models showed soil moisture at each weather station to have a high relative influence on the moisture prediction for nearby fields. This was followed by the 4-day cumulative rainfall and PET as the next most important variables. For the CART model, the weather station VWC, 4-day cumulative rainfall, and 4-day PET had 29%, 20%, and 21% relative importance, respectively, in predicting field soil moisture, followed by the weather station’s bulk density (8%), the crop field’s Ksat (6%), and the weather station’s Ksat (4%). Similarly, the BRT model showed that the weather station VWC, 4-day cumulative rainfall, and 4-day PET had the highest influence at 32%, 32%, and 16%, respectively. This was followed by the crop field’s clay content and Ksat, which both contributed 4%. Among the CART and BRT models, the weather station VWC, rainfall, and PET were the dominant variables for predicting nearby crop field soil moisture. For the RFR model, the 4-day cumulative rainfall, 4-day PET, weather station VWC, and crop field’s Ksat had 43%, 40%, 39%, and 38% increases in RMSE, respectively, when they were left out of the model, indicating their relative importance. The soil sand, silt, and clay contents had 29%, 30%, and 34% increases in RMSE, respectively, while the remaining variables ranged from 23% to 28%.
Another way to evaluate variable importance is by the loss of MAE, which is presented in Figure 5. Similar to the previous measures of variable importance, all models showed weather station VWC, 4-day cumulative rainfall, and PET as the variables with highest importance, followed by the silt and clay content from the crop fields. The range of loss in MAE was highest in the RFR model (1.6–2.5) as compared to the other models (1.2–1.6).
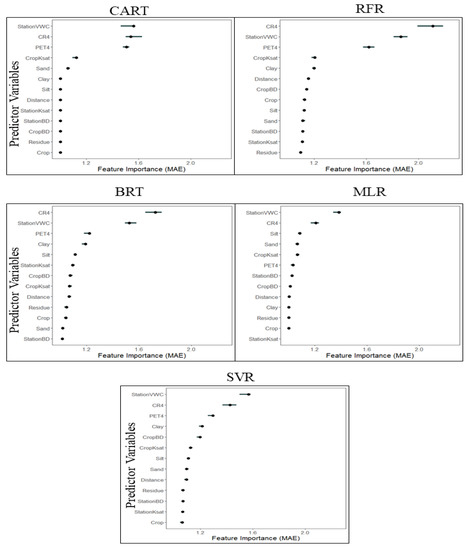
Figure 5.
Feature importance of predictor variables for 5 different machine learning model based on the loss of mean absolute error (MAE) along with 5th to 95th percentile values. Algorithms included classification and regression trees (CART), multiple linear regression (MLR), random forest regression (RFR), support vector regression (SVR), and boosted regression trees (BRT).
These findings are in accordance with Araya et al. (2020) [69], where precipitation was one of the top four important variables for moisture prediction in a grassland catchment area of California, and with Revermann et al. (2016) [79], where precipitation-related variables had the high influence on the soil moisture. This is expected since rainfall and evapotranspiration have a direct influence on the soil moisture [80,81,82]. Our study also revealed that Ksat of both the nearby crop field and at the weather stations were the next most influential variables for predicting soil moisture. This is due to Ksat being a governing property for water flows in the soil [83] and its well-known high spatial variability [84]. Additionally, soil particle sizes in the crop fields are an important variable since these govern pore sizes and their ability to retain water in the field [85,86]. Other variables in this study (i.e., residue cover, crop type, and distance from station) showed little influence on the ability to accurately predict soil moisture by these machine learning models, which corroborates studies by Aarya et al. (2020) [69], Kravchenko et al. (2011) [87], and McIsaac et al. (2010) [88].
3.3. Accumulated Local Effect of Predictor Variables
The ALEs of predictor variables on predicting soil moisture with the various machine learning algorithms were evaluated graphically (Figure 6). The variables previously determined to have a high relative influence (i.e., importance) were graphed; these included the weather station’s VWC, 4-day cumulative rainfall, 4-day cumulative PET, and Ksat. The ALE plots show that predicted soil moisture generally increased with higher values of weather station VWC. The CART model showed stationary ALE values except for a sharp increase at 0.25 m3 m−3 in the weather station VWC. This sharp increase in ALE was likely due to the single tree structure of the CART model. In contrast, the RFR model (an ensemble of thousands of trees) showed a gradual sigmoidal increase in ALE values with increasing station VWC values. This same general trend was observed in the BRT and SVR models.
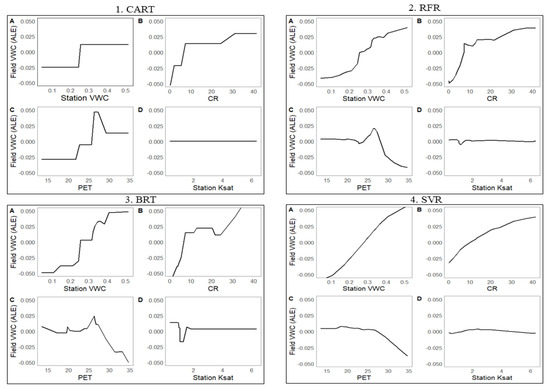
Figure 6.
Accumulated local effect plots for (A) Station VWC, (B) 4-day cumulative rainfall (CR), (C) 4-day cumulative potential evapotranspiration (PET) and (D) weather station saturated hydraulic conductivity (Station Ksat) under 4 machine algorithms 1. Classification and regression trees (CART), 2. Random forest regression (RFR), 3. Boosted regression trees (BRT), and 4. Support vector regression (SVR) for model training datasets.
The ALE for predicting the crop field VWC also increased with the 4-day cumulative rainfall (Figure 6). All four models showed a similar trend with the steepness of the ALE slope tending to dissipate with higher weather station VWC and a tendency for the ALE to flatten between 10–25 mm of cumulative rainfall. For the 4-day cumulative PET, the ALE was generally stationary until 23 mm of PET, after which the ALE decreased as the PET increased. The only exceptions were slight irregularities in the ALE near 25 mm of PET. This showed that cumulative PET less than 23 mm had no effect on the moisture prediction, whereas above that (23 mm), it had an inverse effect on the predicted soil moisture. In this study, the ALE plots showed that station Ksat had minimal effect on the predicted soil moisture. Although there was a slight decrease in predicted soil moisture between 1.5–1.7-inch h−1 in the RFR and BRT models, the other models showed only stationary AEL values at zero.
Overall, the cumulative rainfall, PET, and weather station VWC were the most important predictor variables for soil moisture prediction in nearby crop fields, which also contained dynamic local effects. For instance, there were particular points for each of the predictor variables (i.e., 0.25 m3 m−3 for the weather station VWC, 10 mm for the cumulative rainfall, and 23 mm for PET) that led to large changes in crop field soil moisture prediction accuracy. In Aarya et al. (2020) [69], similar dynamics were observed among predictor variables (topography, curvature, and flow accumulation) on soil moisture estimates using ALE plots for a BRT model. Similarly, other studies have shown the significant effect of cumulative rainfall and PET on predicting soil moisture—for example, Entekhabi and Rodriguez-Iturbe (1994) [89], Pan et al. (2003) [90], and Brocca et al. (2013) [36].
4. Conclusions
Machine learning algorithms can be used effectively in predicting field soil moisture. These algorithms are based on different principles (regression trees, kernels, and regression) and result in different levels of effectiveness in prediction. Successful soil moisture prediction involves establishing the effect of each variable on the output (variable importance). The RFR, BRT, and SVR predictions performed better than the remaining algorithms based on high correlations and low RMSE and MAE during model validation using an independently derived dataset. The weather station variables (station soil moisture, 4-day cumulative rainfall, and PET) were relatively more influential than the soil and crop variables for predicting field soil moisture in the nearby plots.
In summary, the following conclusions can be drawn from this study:
- RFR, BET, and SVR outperformed other models in soil moisture prediction based on the r2, RMSE, and MAE values.
- RFR showed the highest r2 (0.72), and lowest MAE (0.034 m3 m−3) and RMSE (0.045 m3 m−3).
- RFR, CART, and BRT showed that weather station soil moisture, 4-day cumulative rainfall, and PET had a strong influence compared to soil and crop factors on predicting soil moisture in nearby crop fields.
This study will be useful for further investigations into incorporating large weather stations, soil, and crop information to predict soil moisture in agricultural fields. The selection of key variables and proper machine learning models will help in improving accurate soil moisture prediction.
Author Contributions
Conceptualization, U.A. and A.L.M.D.; Methodology, U.A., A.L.M.D. and P.G.O.; Software, U.A.; Validation, U.A., A.L.M.D. and P.G.O.; Formal Analysis, U.A.; Investigation, U.A. and A.L.M.D.; Resources, A.L.M.D. and P.G.O.; Data Curation, U.A.; Writing—Original Draft Preparation, U.A.; Writing—Review and Editing, A.L.M.D. and P.G.O.; Visualization, U.A.; Supervision, A.L.M.D.; Project Administration, A.L.M.D.; Funding Acquisition, U.A. and A.L.M.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the North Dakota Agricultural Experiment Station, USDA-NRCS-CIG 69-3A75-17-282, and USDA-NIFA Hatch project 1005366. North Dakota Water Resources Research Institute provided support for graduate student stipend.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not Applicable.
Data Availability Statement
Data is contained within the present article.
Acknowledgments
The authors thank Nathan Derby, Zachery Leinter, and Megan Ostrand for help in collecting soil samples from weather stations around the Red River Valley and Sudha GC Upadhaya for assistance in writing machine learning codes in R-language.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gill, M.K.; Asefa, T.; Kemblowski, M.W.; McKee, M. Soil moisture prediction using support vector machines. J. Am. Water Resour. Assoc. 2006, 42, 1033–1046. [Google Scholar] [CrossRef]
- Amani, M.; Salehi, B.; Mahdavi, S.; Masjedi, A.; Dehnavi, S. Temperature-Vegetation-soil Moisture Dryness Index (TVMDI). Remote Sens. Environ. 2017, 197, 1–14. [Google Scholar] [CrossRef]
- Hamman, B.; Egil, D.B.; Koning, G. Seed vigor, soilborne pathogens, pre-emergent growth, and soybean seeding emergence. Crop Sci. 2002, 42, 451–457. [Google Scholar] [CrossRef]
- Laguardia, G.; Niemeyer, S. On the comparison between the LISFLOOD modelled and the ERS/SCAT derived soil moisture estimates. Hydrol. Earth Syst. Sci. 2008, 12, 1339–1351. [Google Scholar] [CrossRef] [Green Version]
- Zeng, Y.; Su, Z.; Van der Velde, R.; Wang, L.; Xu, K.; Wang, X.; Wen, J. Blending satellite observed, model simulated, and in situ measured soil moisture over Tibetan Plateau. Remote Sens. 2016, 8, 268. [Google Scholar] [CrossRef] [Green Version]
- Cai, Y.; Zheng, W.; Zhang, X.; Zhangzhong, L.; Xue, X. Research on soil moisture prediction model based on deep learning. PLoS ONE 2019, 14, 0214508. [Google Scholar] [CrossRef]
- Sanuade, O.A.; Hassan, A.M.; Akanji, A.O.; Olaojo, A.A.; Oladunjoye, M.A.; Abdulraheem, A. New empirical equation to estimate the soil moisture content based on thermal properties using machine learning techniques. Arab. J. Geosci. 2020, 13, 377. [Google Scholar] [CrossRef]
- Zhou, L. Study on estimation of soil-water content by using Soil-Water Dynamics Model. Water Sav. Irrig. 2007, 3, 10–13. [Google Scholar]
- Zhang, H.X.; Yang, J.; Fang, X.Y.; Fang, J.; Feng, C. Application of time series analysis in soil moisture forecast. Res. Soil Water Conserv. 2008, 15, 82–84. [Google Scholar]
- Huang, C.; Li, L.; Ren, S.; Zhou, Z. Research of soil moisture content forecast model based on genetic algorithm BP neural network. In Proceedings of the International Conference on Computer and Computing Technologies in Agriculture, Beijing, China, 22–25 October 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 309–316. [Google Scholar]
- Ali, I.; Greifeneder, F.; Stamenkovic, J.; Neumann, M.; Notarnicola, C. Review of machine learning approaches for biomass and soil moisture retrievals from remote sensing data. Remote Sens. 2015, 7, 16398–16421. [Google Scholar] [CrossRef] [Green Version]
- Clapcott, J.; Goodwin, E.; Snelder, T. Predictive Models of Benthic Macro-Invertebrate Metrics; Cawthron Report No. 2301; Cawthron Institute: Nelson, New Zealand, 2013; p. 35. [Google Scholar]
- Olden, J.D.; Lawler, J.J.; Poff, N.L. Machine learning methods without tears: A primer for ecologists. Q. Rev. Biol. 2008, 83, 171–193. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Naghibi, S.A.; Pourghasemi, H.R.; Dixon, B. GIS-based groundwater potential mapping using boosted regression tree, classification and regression tree, and random forest machine learning models in Iran. Environ. Monit. Assess. 2016, 188, 44. [Google Scholar] [CrossRef] [PubMed]
- Liaw, A.; Wiener, M. Classification and regression by RandomForest. R News 2002, 2, 18–22. [Google Scholar]
- Zaman, B.; McKee, M.; Neale, C.M.U. Fusion of remotely sensed data for soil moisture estimation using relevance vector and support vector machines. Int. J. Remote Sens. 2012, 33, 6516–6552. [Google Scholar] [CrossRef]
- Zaman, B.; Mckee, M. Spatio-temporal prediction of root zone soil moisture using multivariate relevance vector machines. Open J. Mod. Hydrol. 2014, 4, 80–90. [Google Scholar] [CrossRef] [Green Version]
- Hassan-Esfahani, L.; Torres-Rua, A.; Jensen, A.; McKee, M. Assessment of surface soil moisture using high-resolution multi-spectral imagery and artificial neural networks. Remote Sens. 2015, 7, 2627–2646. [Google Scholar] [CrossRef] [Green Version]
- Qiao, X.; Yang, F.; Xu, X. The prediction method of soil moisture content based on multiple regression and RBF neural network. In Proceedings of the 15th International Conference on Ground Penetrating Radar (GPR), Brussels, Belgium, 30 June–4 July 2014; pp. 140–143. [Google Scholar]
- Kashif Gill, M.; Kemblowski, M.W.; McKee, M. Soil moisture data assimilation using support vector machines and ensemble Kalman filter. J. Am. Water Resour. Assoc. 2007, 43, 1004–1015. [Google Scholar] [CrossRef]
- Gorthi, S.; Dou, H. Prediction models for the estimation of soil moisture content. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference 54808, Washington, DC, USA, 28–31 August 2011; pp. 945–953. [Google Scholar]
- Matei, O.; Rusu, T.; Petrovan, A.; Mihuţ, G. A data mining system for real time soil moisture prediction. Procedia Eng. 2017, 181, 837–844. [Google Scholar] [CrossRef]
- Gumiere, S.J.; Camporese, M.; Botto, A.; Lafond, J.A.; Paniconi, C.; Gallichand, J.; Rousseau, A.N. Machine Learning vs. Physics-Based Modeling for Real-Time Irrigation Management. Front. Water 2020, 2, 8. [Google Scholar] [CrossRef] [Green Version]
- Yoon, H.; Jun, S.C.; Hyun, Y.; Bae, G.O.; Lee, K.K. A comparative study of artificial neural networks and support vector machines for predicting groundwater levels in a coastal aquifer. J. Hydrol. 2011, 396, 128–138. [Google Scholar] [CrossRef]
- Li, B.; Yang, G.; Wan, R.; Dai, X.; Zhang, Y. Comparison of random forests and other statistical methods for the prediction of lake water level: A case study of the Poyang Lake in China. Hydrol. Res. 2016, 47 (Suppl. 1), 69–83. [Google Scholar] [CrossRef] [Green Version]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 2000. [Google Scholar] [CrossRef]
- NOAA/NCEI. National Oceanic and Atmospheric Administration/National Centers for Environmental Information. 2020. Available online: https://www.ncdc.noaa.gov/ (accessed on 15 July 2020).
- Reynolds, S.G. The gravimetric method of soil moisture determination Part I: A study of equipment, and methodological problems. J. Hydrol. 1970, 11, 258–273. [Google Scholar] [CrossRef]
- USDA. United States Department of Agriculture, International Production Assessment Division. Metadata for Crops at Different Growth Stage. 2020. Available online: https://ipad.fas.usda.gov/cropexplorer/description.aspx?legendid=312 (accessed on 8 May 2020).
- Daigh, A.L.M.; DeJong-Hughes, J.; Gatchell, D.H.; Derby, N.E.; Alghamdi, R.; Leitner, Z.R.; Wick, A.; Acharya, U. Crop and soil responses to on-farm conservation tillage practices in the Upper Midwest. Agric. Environ. Lett. 2019, 4, 190012. [Google Scholar] [CrossRef] [Green Version]
- Gee, G.W.; Bauder, J.W. Particle Size Analysis. In Methods of Soil Analysis, Part A, 2nd ed.; Klute, A., Ed.; American Society of Agronomy: Madison, WI, USA, 1986; Volume 9, pp. 383–411. [Google Scholar]
- Schaap, M.G.; Leij, F.J.; van Genuchten, M.T. Rosetta: A computer program for estimating soil hydraulic parameters with hierarchical pedotransfer functions. J. Hydrol. 2001, 251, 163–176. [Google Scholar] [CrossRef]
- Simunek, J.; Sejna, M.; Saito, H.; Sakai, M.; van Genuchten, M.T. The HYDRUS-1D Software Package for Simulating the One-Dimensional Movement of Water, Heat, and Multiple Solutes in Variably-Saturated Media; Version 4.0.; Department of Environmental Sciences, University of California: Riverside, CA, USA, 2008. [Google Scholar]
- Richards, L.A. Porous plate apparatus for measuring moisture retention and transmission by soil. Soil Sci. 1948, 66, 105–110. [Google Scholar] [CrossRef]
- Penman, H.L. Natural evaporation from open water, bare soil and grass. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1948, 193, 120–145. [Google Scholar]
- Brocca, L.; Moramarco, T.; Melone, F.; Wagner, W. A new method for rainfall estimation through soil moisture observations. Geophys. Res. Lett. 2013, 40, 853–858. [Google Scholar] [CrossRef]
- Stewart, J.R. Applications of Classification and Regression Tree Methods in Roadway Safety Studies. In Transportation Research Record 1542, TRB; National Research Council: Washington, DC, USA, 1996; pp. 1–5. [Google Scholar]
- Samadi, M.; Jabbari, E.; Azamathulla, H.M. Assessment of M5 model tree and classification and regression trees for prediction of scour depth below free overfall spillways. Neural Comput. Appl. 2014, 24, 357–366. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. CART. Classification and Regression Trees; Wadsworth and Brooks/Cole: Monterey, CA, USA, 1984. [Google Scholar]
- Breiman, L. Random Forest. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: New York, NY, USA, 2013. [Google Scholar]
- Friedman, J.H. Stochastic gradient boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Elith, J.; Leathwick, J.R.; Hastie, T. A working guide to boosted regression trees. J. Anim. Ecol. 2008, 77, 802–813. [Google Scholar] [CrossRef] [PubMed]
- Natekin, A.; Knoll, A. Gradient boosting machines, a tutorial. Front. Neurorobot. 2013, 7, 21. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Zhang, W.; Yuan, S.; Hu, N.; Lou, Y.; Wang, S. Predicting soil fauna effect on plant litter decomposition by using boosted regression trees. Soil Biol. Biochem. 2015, 82, 81–86. [Google Scholar] [CrossRef]
- Moisen, G.G.; Freeman, E.A.; Blackard, J.A.; Frescino, T.S.; Zimmermann, N.E.; Edwards, T.C. Predicting tree species presence and basal area in Utah: A comparison of stochastic gradient boosting, generalized additive models, and tree-based methods. Ecol. Model. 2006, 199, 176–187. [Google Scholar] [CrossRef]
- De’Ath, G. Boosted trees for ecological modeling and prediction. Ecology 2007, 88, 243–251. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V.N. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Drucker, H.; Burges, C.J.; Kaufman, L.; Smola, A.; Vapnik, V. Support vector regression machines. Adv. Neural Inf. Process. Syst. 1997, 9, 155–161. [Google Scholar]
- Yang, H.; Huang, K.; King, I.; Lyu, M.R. Localized support vector regression for time series prediction. Neurocomputing 2009, 72, 2659–2669. [Google Scholar] [CrossRef]
- Priddy, K.L.; Keller, P.E. Artificial Neural Networks: An Introduction; SPIE Press: Bellingham, WA, USA, 2005; Volume 68. [Google Scholar]
- Grimes, D.I.F.; Coppola, E.; Verdecchia, M.; Visconti, G. A neural network approach to real-time rainfall estimation for Africa using satellite data. J. Hydrometeorol. 2003, 4, 1119–1133. [Google Scholar] [CrossRef]
- Twarakavi, N.K.; Misra, D.; Bandopadhyay, S. Prediction of arsenic in bedrock derived stream sediments at a gold mine site under conditions of sparse data. Nat. Resour. Res. 2006, 15, 15–26. [Google Scholar] [CrossRef]
- Ahmad, S.; Simonovic, S.P. An artificial neural network model for generating hydrograph from hydro-meteorological parameters. J. Hydrol. 2005, 315, 236–251. [Google Scholar] [CrossRef]
- R Development Core Team. R: A Language and Environment for Statistical Computing. 2020. Available online: https://www.r-project.org/ (accessed on 1 October 2020).
- Karatzoglou, A.; Smola, A.; Hornik, K.; Zeileis, A. Kernlab: An S4 Package for Kernel Methods in R (version 0.9-25). J. Stat. Softw. 2004, 11, 1–20. Available online: http://www.jstatsoft.org/v11/i09/ (accessed on 1 October 2020). [CrossRef] [Green Version]
- Liaw, A.; Wiener, M. RandomForest: Breiman and Cutler’s Random Forests for Classification and Regression; R Package Version 4; CRAN R package, 2015. pp. 6–10. Available online: https://cran.r-project.org/web/packages/randomForest/randomForest.pdf (accessed on 15 September 2021).
- Gunther, F.; Fritsch, S. Neuralnet: Training of neural networks. R J. 2010, 2, 30–38. [Google Scholar] [CrossRef] [Green Version]
- Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S (Statistics and Computing); Springer: New York, NY, USA, 2002. [Google Scholar]
- Apley, D.W.; Zhu, J. Visualizing the effects of predictor variables in black box supervised learning models. J. R. Stat. Soc. B. 2020, 82, 1059–1086. [Google Scholar] [CrossRef]
- Greenwell, B.M. An R Package for Constructing Partial Dependence Plots. R J. 2017, 9, 421. [Google Scholar] [CrossRef] [Green Version]
- Molnar, C. Interpretable Machine Learning: A Guide for Making Black Box Models Explainable. 2019. Available online: https://christophm.github.io/interpretable-ml-book/ (accessed on 10 January 2020).
- Caruana, R.; Niculescu-Mizil, A. An empirical comparison of supervised learning algorithms. In Proceedings of the 23rd international conference on Machine learning, Pittsburgh, PA, USA, 25–29 June 2006; pp. 161–168. [Google Scholar]
- Hengl, T.; Mendes de Jesus, J.; Heuvelink, G.B.; Ruiperez Gonzalez, M.; Kilibarda, M.; Blagotić, A.; Shangguan, W.; Wright, M.N.; Geng, X.; Bauer-Marschallinger, B.; et al. SoilGrids250m: Global gridded soil information based on machine learning. PLoS ONE 2017, 12, e0169748. [Google Scholar]
- Nussbaum, M.; Spiess, K.; Baltensweiler, A.; Grob, U.; Keller, A.; Greiner, L.; Schaepman, M.E.; Papritz, A. Evaluation of digital soil mapping approaches with large sets of environmental covariates. Soil 2018, 4, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Keskin, H.; Grunwald, S.; Harris, W.G. Digital mapping of soil carbon fractions with machine learning. Geoderma 2019, 339, 40–58. [Google Scholar] [CrossRef]
- Szabo, B.; Szatmári, G.; Takács, K.; Laborczi, A.; Makó, A.; Rajkai, K.; Pásztor, L. Mapping soil hydraulic properties using random-forest-based pedotransfer functions and geostatistics. Hydrol. Earth Syst. Sci. 2019, 23, 2615–2635. [Google Scholar] [CrossRef] [Green Version]
- Araya, S.N.; Fryjoff-Hung, A.; Anderson, A.; Viers, J.H.; Ghezzehei, T.A. Advances in Soil Moisture Retrieval from Multispectral Remote Sensing Using Unmanned Aircraft Systems and Machine Learning Techniques. Hydrol. Earth Syst. Sci. 2020, 1–33. [Google Scholar] [CrossRef]
- Kalra, A.; Ahmad, S. Using oceanic–atmospheric oscillations for long lead time streamflow forecasting. Water Resour. Res. 2009, 45, W03413. [Google Scholar] [CrossRef]
- Dibike, Y.B.; Velickov, S.; Solomatine, D.; Abbott, M.B. Model induction with support vector machines: Introduction and application. J. Comput. Civ. Eng. 2001, 15, 208–216. [Google Scholar] [CrossRef]
- Asefa, T.; Kemblowski, M.; McKee, M.; Khalil, A. Multi-time scale stream flow predictions: The support vector machines approach. J. Hydrol. 2006, 318, 7–16. [Google Scholar] [CrossRef]
- Liong, S.Y.; Sivapragasam, C. Flood stage forecasting with support vector machines 1. J. Am. Water Resour. As. 2002, 38, 173–186. [Google Scholar] [CrossRef]
- Achieng, K.O. Modelling of soil moisture retention curve using machine learning techniques: Artificial and deep neural networks vs. support vector regression models. Comput. Geosci. 2019, 133, 104320. [Google Scholar] [CrossRef]
- Karandish, F.; Simunek, J. A comparison of numerical and machine-learning modeling of soil water content with limited input data. J. Hydrol. 2016, 543, 892–909. [Google Scholar] [CrossRef] [Green Version]
- Bray, M.; Han, D. Identification of support vector machines for runoff modeling. J. Hydrol. 2004, 6, 265–280. [Google Scholar]
- Pal, M.; Mather, P.M. Support Vector Classifiers for Land Cover Classification. Map India 2003, Image processing and interpretation. 2003. Available online: http://www.gisdevelopment.net/technology/rs/pdf/23.pdf (accessed on 1 October 2020).
- Han, J.; Mao, K.; Xu, T.; Guo, J.; Zuo, Z.; Gao, C. A soil moisture estimation framework based on the CART algorithm and its application in China. J. Hydrol. 2018, 563, 65–75. [Google Scholar] [CrossRef]
- Revermann, R.; Finckh, M.; Stellmes, M.; Strohbach, B.J.; Frantz, D.; Oldeland, J. Linking land surface phenology and vegetation-plot databases to model terrestrial plant α-diversity of the Okavango Basin. Remote Sens. 2016, 8, 370. [Google Scholar] [CrossRef] [Green Version]
- Brocca, L.; Morbidelli, R.; Melone, F.; Moramarco, T. Soil moisture spatial variability in experimental areas of Central Italy. J. Hydrol. 2007, 333, 356–373. [Google Scholar] [CrossRef]
- Cosh, M.H.; Stedinger, J.R.; Brutsaert, W. Variability of surface soil moisture at the watershed scale. Water Resour. Res. 2004, 40, W12513. [Google Scholar] [CrossRef]
- Ziadat, F.M.; Taimeh, A.Y. Effect of rainfall intensity, slope, land use and antecedent soil moisture on soil erosion in an arid Environment. Land Degrad. Dev. 2013, 24, 582–590. [Google Scholar] [CrossRef]
- Zhang, R. Determination of soil sorptivity and hydraulic conductivity from the disk infiltrometer. Soil Sci. Soc. Am. J. 1997, 61, 1024–1030. [Google Scholar] [CrossRef]
- Upchurch, D.R.; Wilding, L.P.; Hatfield, J.L. Methods to evaluate spatial variability. In Reclamation of Surface-Mined Land; CRC Press: Boca Raton, FL, USA, 1988; pp. 201–229. [Google Scholar]
- Li, T.; Hao, X.M.; Kang, S.Z. Spatiotemporal variability of soil moisture as affected by soil properties during irrigation cycles. Soil Sci. Soc. Am. J. 2014, 78, 598–608. [Google Scholar] [CrossRef]
- Manns, H.R.; Berg, A.A.; Bullock, P.R.; McNairn, H. Impact of soil surface characteristics on soil water content variability in agricultural fields. Hydrol. Process. 2014, 28, 4340–4351. [Google Scholar] [CrossRef]
- Kravchenko, A.N.; Wang, A.N.W.; Smucker, A.J.M.; Rivers, M.L. Long-term differences in tillage and land use affect intra-aggregate pore heterogeneity. Soil Sci. Soc. Am. J. 2011, 75, 1658–1666. [Google Scholar] [CrossRef] [Green Version]
- McIsaac, G.F.; David, M.B.; Mitchell, C.A. Miscanthus and switchgrass production in central Illinois: Impacts on hydrology and inorganic nitrogen leaching. J. Environ. Qual. 2010, 39, 1790–1799. [Google Scholar] [CrossRef] [Green Version]
- Entekhabi, D.; Rodriguez-Iturbe, I. Analytical framework for the characterization of the space-time variability of soil moisture. Adv. Water Resour. 1994, 17, 35–45. [Google Scholar] [CrossRef]
- Pan, F.; Peters-Lidard, C.D.; Sale, M.J. An analytical method for predicting surface soil moisture from rainfall observations. Water Resour. Res. 2003, 39, 1–12. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).