Digital Mapping of Soil Classes Using Ensemble of Models in Isfahan Region, Iran
Abstract
1. Introduction
- (i)
- compare the performance of different models, including ANN, MnLR, SVM, BN, DT, SMnLR and RF to predict spatial prediction of USDA soil taxonomic classes,
- (ii)
- evaluate the ability of ensemble model with the purpose of yielding an individual and more accurate model for prediction of soil taxonomic classes, and
- (iii)
- evaluate the sensitivity analysis of the true and false prediction of soil class taxa at subgroup level for the individual models and the ensemble model.
2. Materials and Methods
2.1. Study Area
2.2. Soil Data
2.3. Environmental Variables
2.3.1. Digital Elevation Model
2.3.2. Remotely Sensed Optical Satellite Data
2.3.3. Geomorphology Map
2.4. Soil Taxonomic Class Prediction
2.4.1. Traditional Models
Multinomial Logistic Regression (MnLR)
Artificial Neural Networks (ANN)
Support Vector Machines (SVMs)
Decision Tree (DT)
Random Forest (RF)
Bayesian Networks (BN)
Sparse Multinomial Logistic Regression (SMnLR)
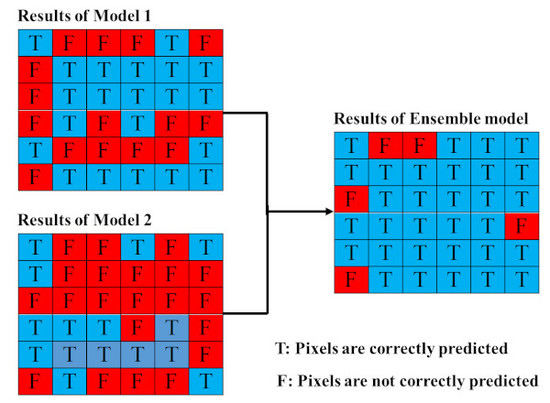
2.4.2. Proposed Ensemble Models
2.5. Validation
3. Results and Discussion
3.1. Soil Taxonomic Class Prediction
3.1.1. Traditional Models
Multinomial Logistic Regression (MnLR)
Artificial Neural Networks (ANN)
Super Vector Machine (SVM)
Decision Tree (DT)
Random Forest (RF)
Bayesian Networks (BN)
Sparse Multinomial Logistic Regression (SMnLR)
3.1.2. Proposed Ensemble Models
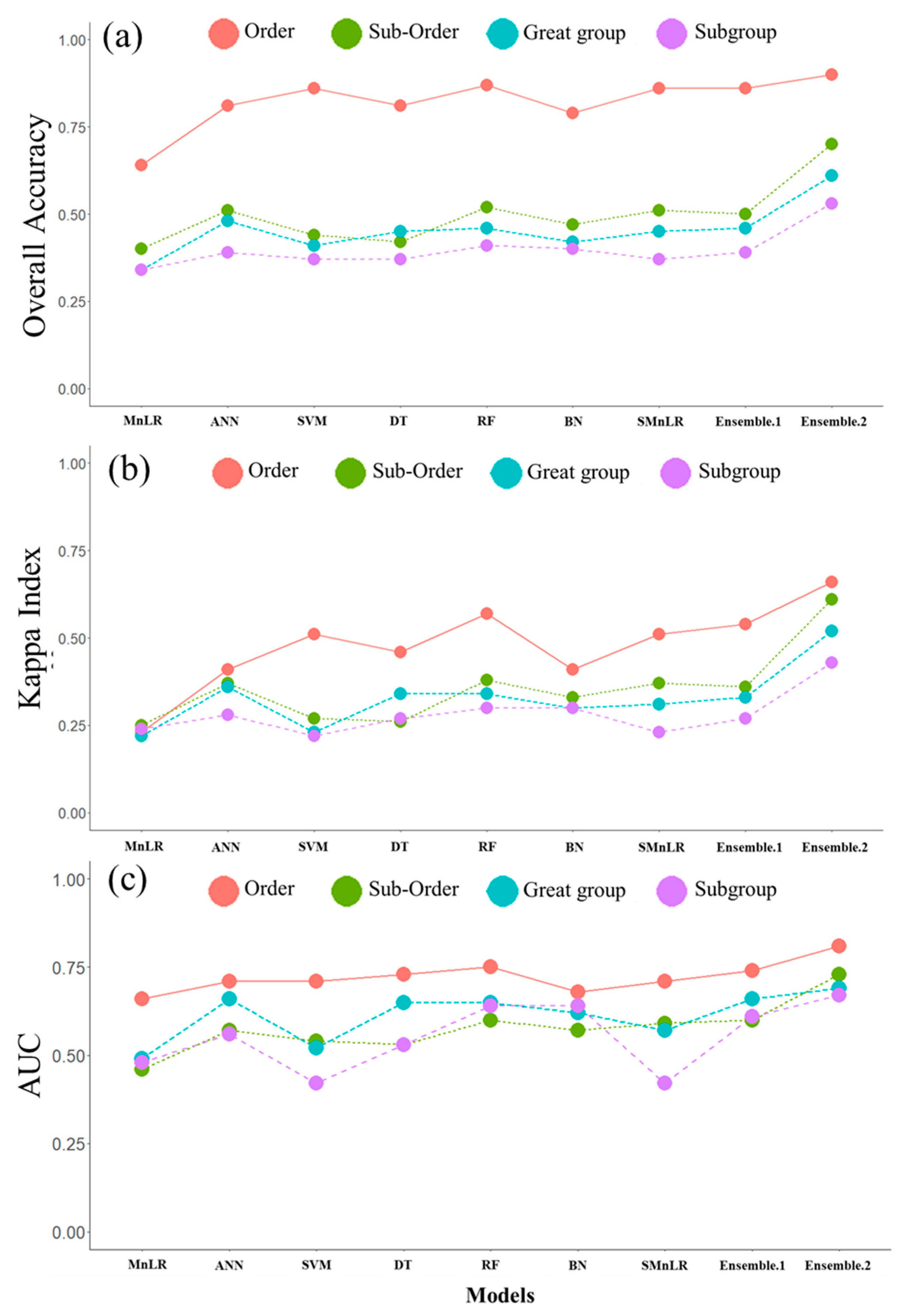
3.1.3. Comparison of Traditional and Ensemble Models
3.2. Environmental Variables
3.3. Spatial Prediction of Soil Classes Using Suggested Ensemble Method
3.4. Land Characteristics, Qualities, Management and Conservation of DSM Soil Taxa Relative to Land Use
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Adhikari, K.; Hartemink, A.E. Linking soils to ecosystem services-A global review. Geoderma 2016, 262, 101–111. [Google Scholar] [CrossRef]
- Dominati, E.; Patterson, M.; Mackay, A. A framework for classifying and quantifying the natural capital and ecosystem services of soils. Ecol. Econ. 2010, 69, 1858–1868. [Google Scholar] [CrossRef]
- Brungard, C.W.; Boettinger, J.L.; Duniway, M.C.; Wills, S.A.; Edwards, T.C. Machine learning for predicting soil classes in three semi-arid landscapes. Geoderma 2015, 239, 68–83. [Google Scholar] [CrossRef]
- Jafari, A.; Finke, P.A.; Van de Wauw, J.; Ayoubi, S.; Khademi, H. Spatial prediction of USDA-great soil groups in the arid Zarand region, Iran: Comparing logistic regression approaches to predict diagnostic horizons and soil types. Eur. J. Soil Sci. 2012, 63, 284–298. [Google Scholar] [CrossRef]
- Pahlavan-Rad, M.R.; Khormali, F.; Toomanian, N.; Brungard, C.W.; Kiani, F.; Komaki, C.B.; Bogaert, P. Legacy soil maps as a covariate in digital soil mapping: A case study from Northern Iran. Geoderma 2016, 279, 141–148. [Google Scholar] [CrossRef]
- Zeraatpisheh, M.; Ayoubi, S.; Jafari, A.; Finke, P. Comparing the efficiency of digital and conventional soil mapping to predict soil types in a semi-arid region in Iran. Geomorphology 2017, 285, 186–204. [Google Scholar] [CrossRef]
- Caubet, M.; Dobarco, M.R.; Arrouays, D.; Minasny, B.; Saby, N.P. Merging country, continental and global predictions of soil texture: Lessons from ensemble modelling in France. Geoderma 2019, 337, 99–110. [Google Scholar] [CrossRef]
- Ma, Y.X.; Minasny, B.; Malone, B.P.; McBratney, A.B. Pedology and digital soil mapping (DSM). Eur. J. Soil Sci. 2019, 70, 216–235. [Google Scholar] [CrossRef]
- McBratney, A.B.; Santos, M.M.; Minasny, B. On digital soil mapping. Geoderma 2003, 117, 3–52. [Google Scholar] [CrossRef]
- Heung, B.; Ho, H.C.; Zhang, J.; Knudby, A.; Bulmer, C.E.; Schmidt, M.G. An overview and comparison of machine-learning techniques for classification purposes in digital soil mapping. Geoderma 2016, 265, 62–77. [Google Scholar] [CrossRef]
- Minasny, B.; McBratney, A.B. Digital soil mapping: A brief history and some lessons. Geoderma 2016, 264, 301–311. [Google Scholar] [CrossRef]
- Adhikari, K.; Minasny, B.; Greve, M.B.; Greve, M.H. Constructing a soil class map of Denmark based on the FAO legend using digital techniques. Geoderma 2014, 214, 101–113. [Google Scholar] [CrossRef]
- Kovačević, M.; Bajat, B.; Gajić, B. Soil type classification and estimation of soil properties using support vector machines. Geoderma 2010, 154, 340–347. [Google Scholar] [CrossRef]
- Behrens, T.; Förster, H.; Scholten, T.; Steinrücken, U.; Spies, E.D.; Goldschmitt, M. Digital soil mapping using artificial neural networks. J. Plant Nutr. Soil Sci. 2005, 168, 21–33. [Google Scholar] [CrossRef]
- Taghizadeh-Mehrjardi, R.; Nabiollahi, K.; Minasny, B.; Triantafilis, J. Comparing data mining classifiers to predict spatial distribution of USDA-family soil groups in Baneh region, Iran. Geoderma 2015, 253, 67–77. [Google Scholar] [CrossRef]
- Górecki, T.; Krzyśko, M. Regression methods for combining multiple classifiers. Commun. Stat.-Simul. C. 2015, 44, 739–755. [Google Scholar] [CrossRef]
- Swiderski, B.; Osowsk, S.; Kruk, M.; Barhoumi, W. Aggregation of classifiers ensemble using local discriminatory power and quantiles. Expert Syst. Appl. 2016, 46, 316–323. [Google Scholar] [CrossRef]
- Román Dobarco, M.; Arrouays, D.; Lagacherie, P.; Ciampalini, R.; Saby, N.P.A. Prediction of topsoil texture for Region Centre (France) applying model ensemble methods. Geoderma 2017, 298, 67–77. [Google Scholar] [CrossRef]
- Diks, C.G.H.; Vrugt, J.A. Comparison of point forecast accuracy of model averaging methods in hydrologic applications. Stoch. Environ. Res. Risk Assess. 2010, 24, 809–820. [Google Scholar] [CrossRef]
- Wasson, T.; Hartemink, A.J. An ensemble model of competitive multi-factor binding of the genome. Genome Res. 2009, 19, 2101–2112. [Google Scholar] [CrossRef]
- Malone, B.P.; Minasny, B.; Odgers, N.P.; McBratney, A.B. Using model averaging to combine soil property rasters from legacy soil maps and from point data. Geoderma 2014, 232, 34–44. [Google Scholar] [CrossRef]
- Padarian, J.; Minasny, B.; McBratney, A.B.; Dalgliesh, N. Predicting and mapping the soil available water capacity of Australian wheatbelt. Geoderma Reg. 2014, 2, 110–118. [Google Scholar] [CrossRef]
- Hartemink, A.E. The use of soil classification in journal papers between 1975 and 2014. Geoderma Reg. 2015, 5, 127–139. [Google Scholar] [CrossRef]
- Taghizadeh-Mehrjardi, R.; Sarmadian, F.; Minasny, B.; Triantafilis, J.; Omid, M. Digital mapping of soil classes using decision tree and auxiliary data in the Ardakan region, Iran. Arid Land Res. Manag. 2014, 28, 147–168. [Google Scholar] [CrossRef]
- Jaafarian, M.A. Past history and evolutionary steps of Zayandeh-rud Valley. Res. J. Isfahan Univ. 1986, 1, 15–31. (In Persian) [Google Scholar]
- Toomanian, N.; Jalalian, A.; Khademi, H.; Eghbal, M.K.; Papritz, A. Pedodiversity and pedogenesis in Zayandeh-rud Valley, central Iran. Geomorphology 2006, 81, 376–393. [Google Scholar] [CrossRef]
- Soil Survey Staff. Keys to Soil Taxonomy, 10th ed.; United States Department of Agriculture: Washington, DC, USA, 2006.
- Conrad, O.; Bechtel, B.; Bock, M.; Dietrich, H.; Fischer, E.; Gerlitz, L. System for Automated Geoscientific Analyses (SAGA) v. 2.1.4. Geosci. Model Dev. 2015, 8, 1991–2007. [Google Scholar] [CrossRef]
- National Cartographic Center; Research Institute of NCC: Tehran, Iran, 2010; Available online: www.ncc.org.ir (accessed on 21 August 2010).
- European Space Agency. GMES Sentinel-2 mission requirements document. In Technical Report Issue 2 Revision 1; European Space Agency: Paris, France, 2010. [Google Scholar]
- Wulder, M.A.; White, J.C.; Loveland, T.R.; Woodcock, C.E.; Belward, A.S.; Cohen, W.B.; Fosnight, E.A.; Shaw, J.; Masek, J.G.; Roy, D.P. The global Landsat archive: Status, consolidation, and direction. Remote Sens. Environ. 2016, 185, 271–283. [Google Scholar] [CrossRef]
- Mulder, V.L.; De Bruin, S.; Schaepman, M.E.; Mayr, T.R. The use of remote sensing in soil and terrain mapping—A review. Geoderma 2011, 162, 1–19. [Google Scholar] [CrossRef]
- Andronikov, V.; Dobrolvshiy, G. Theory and methods for the use of remote sensing in the study of soils. Mapp. Sci. Remote Sens. 1991, 28, 92–101. [Google Scholar]
- Moameni, A.; Zink, J.A. Application of statistical quality control charts and geostatistics to soil quality assessment in a semi-arid environment of south-central Iran. ITC J. 1997, 3, 1–26. [Google Scholar]
- Alpaydin, E. Introduction to Machine Learning; MIT Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Marquardt, D.W. An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Ivanciuc, O. Applications of support vector machines in chemistry. Rev. Comp. Ch. 2007, 23, 291. [Google Scholar]
- Hsu, S.-H.; Hsieh, J.P.A.; Chih, T.C.; Hsu, K.C. A two-stage architecture for stock price forecasting by integrating self-organizing map and support vector regression. Expert Syst. Appl. 2009, 36, 7947–7951. [Google Scholar] [CrossRef]
- Murthy, S.K. Automatic construction of decision trees from data: A multi-disciplinary survey. Data Min. Knowl. Discov. 1998, 2, 345–389. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Amit, Y.; Geman, D. Shape quantization and recognition with randomized trees. Neural Comput. 1997, 9, 1545–1588. [Google Scholar] [CrossRef]
- Rudiyanto, M.B.; Setiawan, B.I.; Saptomo, S.K.; McBratney, A.B. Open digital mapping as a cost-effective method for mapping peat thickness and assessing the carbon stock of tropical peatlands. Geoderma 2018, 313, 25–40. [Google Scholar] [CrossRef]
- Hartemink, A.J. Bayesian networks and informative priors: Transcriptional regulatory network models. In Bayesian Inference for Gene Expression and Proteomics; Do, K., Müller, P., Vannucci, M., Eds.; Cambridge University Press: Cambridge, UK, 2006; pp. 401–424. [Google Scholar]
- Robinson, J.W.; Hartemink, A.J. Learning non-stationary dynamic Bayesian networks. J. Mach. Learn. Res. 2010, 11, 3647–3680. [Google Scholar]
- Taalab, K.; Corstanje, R.; Zawadzka, J.; Mayr, T.; Whelan, M.J.; Hannam, J.A.; Creamer, R. On the application of Bayesian networks in digital soil mapping. Geoderma 2015, 259, 134–148. [Google Scholar] [CrossRef]
- Dlamini, W.M. Application of Bayesian networks for fire risk mapping using GIS and remote sensing data. GeoJournal 2011, 76, 283–296. [Google Scholar] [CrossRef]
- Krishnapuram, B.; Carin, L.; Figueiredo, M.A.T.; Hartemink, A.J. Sparse multinomial logistic regression: Fast algorithms and generalization bounds. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 957–968. [Google Scholar] [CrossRef] [PubMed]
- Narlikar, L.; Hartemink, A. Sequence features of DNA binding sites reveal structural class of associated transcription factor. Bioinformatics 2006, 22, 157–163. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Heuvelink, G.B.M.; Bierkens, M.F.P. Combining soil maps with interpolations from point observations to predict quantitative soil properties. Geoderma 1992, 55, 1–15. [Google Scholar] [CrossRef]
- Granger, C.W.J.; Ramanathan, R. Improved methods of combining forecasts. J. Forecast. 1984, 3, 197–204. [Google Scholar] [CrossRef]
- Giasson, E.; Figueiredo, S.; Tornquist, C.; Clarke, R. Digital soil mapping using logistic regression on terrain parameters for several ecological regions in Southern Brazil. In Digital Soil Mapping with Limited Data; Hartemink, A.E., McBratney, A.B., Mendonça-Santos, M.L., Ahrens, R.L., Eds.; Springer: Cham, Switzerland, 2008; pp. 225–232. [Google Scholar]
- Stum, A.K.; Boettinger, J.L.; White, M.A.; Ramsey, R.D. Random Forests Applied as a Soil Spatial Predictive Model in Arid Utah. In Digital Soil Mapping: Bridging Research, Environmental Application, and Operation; Boettinger, J.L., Howell, D.W., Moore, A.C., Hartemink, A.E., Kienast-Brown, S., Eds.; Springer: Dordrecht, The Netherlands, 2010; pp. 179–190. [Google Scholar]
- Hosmer, D.W.; Lemeshow, S.; Sturdivant, R.X. Applied Logistic Regression; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Buol, S.W.; Southard, R.J.; Graham, R.C.; Mcdaniel, P.A. Soil Genesis and Classification; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2011. [Google Scholar]
- Roozitalab, M.H.; Toomanian, N.; Ghasemi Dehkordi, V.R.; Khormali, F. Major soils, properties, and classification. In The Soils of Iran; Roozitalab, M.H., Siadat, H., Farshad, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2018; pp. 93–147. [Google Scholar]
- Khademi, H.; Mermut, A.R. Micromorphology and classification of Argids and associated gypsiferous Aridisols from central Iran. Catena 2003, 54, 439–455. [Google Scholar] [CrossRef]
- Gharaee, H.A.; Mahjoory, R.A. Characteristics and geomorphic relationships of some representative Aridisols in southern Iran. Soil Sci. Soc. Am. J. 1984, 48, 115–119. [Google Scholar] [CrossRef]





| Order | No. | Sub-Order | No. | Great Group | No. | Subgroup | No. |
|---|---|---|---|---|---|---|---|
| Entisols | 43 | Orthents | 43 | Torriorthents | 43 | Typic Torriorthents | 43 |
| Aridisols | 151 | Salids | 49 | Haplosalids | 49 | Typic Haplosalids | 17 |
| Gypsic Haplosalids | 32 | ||||||
| Argids | 34 | Haploargids | 19 | Typic Haploargids | 19 | ||
| Calciargids | 15 | Typic Calciargids | 15 | ||||
| Haplogypsids | 31 | Typic Haplogypsids | 24 | ||||
| Gypsids | 44 | Calcigypsids | 13 | Lithic Haplogypsids | 7 | ||
| Typic Calcigypsids | 13 | ||||||
| Calcids | 24 | Haplocalcids | 24 | Typic Haplocalcids | 24 |
| Definition | Code |
|---|---|
| Topographic attributes | |
| Slope | SLOPE |
| Aspect | ASPECT |
| LS factor | LS |
| Elevation | Elev |
| Catchments area | CaA |
| Catchment network base level | CNBL |
| Topographic Wetness Index | TWI |
| Altitude above channel network | AaCN |
| Multi-resolution Valley Bottom Flatness Index | MrVBF |
| Multi-resolution of ridge top flatness index | MrRTF |
| Remote sensing attributes | |
| Clay Index: (shortwave IR-1/shortwave IR-2) | Clay.In |
| Blue, green, red, near infrared, shortwave IR-1, shortwave IR-2, | Lan.B1-B7 |
| Normalized Difference Vegetation Index: (Shortwave IR-1—Near infrared)/(Shortwave IR-1+ Near infrared) | NDVI |
| Salinity Index: (Red—Near infrared)/(Red + Near infrared) | Salinity.In |
| Sentinel Bands 1, 2, 3, and 4 | Sen.B1-B4 |
| Geomorphology map | |
| Hierarchical four level classification (geomorphic surfaces) | GEO |
| Methods | Models | Order | Sub-Order | Great Group | Subgroup | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| OA | κ | AUC | OA | κ | AUC | OA | κ | AUC | OA | κ | AUC | ||
| Traditional models | MnLR | 0.64 | 0.23 | 0.66 | 0.40 | 0.25 | 0.46 | 0.34 | 0.22 | 0.49 | 0.34 | 0.24 | 0.48 |
| ANN | 0.81 | 0.41 | 0.71 | 0.51 | 0.37 | 0.57 | 0.48 | 0.36 | 0.66 | 0.39 | 0.28 | 0.56 | |
| SVM | 0.86 | 0.51 | 0.71 | 0.44 | 0.27 | 0.54 | 0.41 | 0.23 | 0.52 | 0.37 | 0.22 | 0.42 | |
| DT | 0.81 | 0.46 | 0.73 | 0.42 | 0.26 | 0.53 | 0.45 | 0.34 | 0.65 | 0.37 | 0.27 | 0.53 | |
| RF | 0.87 | 0.57 | 0.75 | 0.52 | 0.38 | 0.60 | 0.46 | 0.34 | 0.65 | 0.41 | 0.30 | 0.64 | |
| BN | 0.79 | 0.41 | 0.68 | 0.47 | 0.33 | 0.57 | 0.42 | 0.30 | 0.62 | 0.40 | 0.30 | 0.64 | |
| SMnLR | 0.86 | 0.51 | 0.71 | 0.51 | 0.37 | 0.59 | 0.45 | 0.31 | 0.57 | 0.37 | 0.23 | 0.42 | |
| Ensemble models | Ensemble.1 | 0.86 | 0.54 | 0.74 | 0.50 | 0.36 | 0.60 | 0.46 | 0.33 | 0.66 | 0.39 | 0.27 | 0.61 |
| Ensemble.2 | 0.90 | 0.66 | 0.81 | 0.70 | 0.61 | 0.73 | 0.61 | 0.52 | 0.69 | 0.53 | 0.43 | 0.67 | |
| RI (%) * | 3.4 | 15.8 | 7.4 | 34.6 | 60.5 | 17.8 | 27.1 | 44.4 | 4.5 | 29.3 | 43.3 | 4.6 | |
| Methods | Methods | GHS | LHG | TCA | TCG | THA | THC | THG | THS | TTO | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Traditional models | MnLR | Se | 0.66 | 0.29 | 0.40 | 0.00 | 0.68 | 0.17 | 0.33 | 0.29 | 0.16 |
| Sp | 0.88 | 0.95 | 0.88 | 0.97 | 0.89 | 0.94 | 0.92 | 0.97 | 0.85 | ||
| PPV | 0.51 | 0.17 | 0.22 | 0.00 | 0.39 | 0.29 | 0.38 | 0.45 | 0.23 | ||
| ANN | Se | 0.69 | 0.14 | 0.20 | 0.38 | 0.21 | 0.25 | 0.38 | 0.18 | 0.53 | |
| Sp | 0.88 | 0.99 | 0.94 | 0.97 | 0.97 | 0.93 | 0.89 | 0.97 | 0.73 | ||
| PPV | 0.54 | 0.33 | 0.23 | 0.45 | 0.40 | 0.35 | 0.33 | 0.38 | 0.36 | ||
| SVM | Se | 0.72 | 0.14 | 0.00 | 0.08 | 0.21 | 0.17 | 0.12 | 0.06 | 0.81 | |
| Sp | 0.78 | 0.99 | 0.99 | 1.00 | 1.00 | 1.00 | 0.98 | 0.98 | 0.49 | ||
| PPV | 0.40 | 0.50 | 0.00 | 1.00 | 1.00 | 1.00 | 0.43 | 0.20 | 0.31 | ||
| DT | Se | 0.62 | 0.00 | 0.27 | 0.46 | 0.32 | 0.29 | 0.33 | 0.23 | 0.39 | |
| Sp | 0.88 | 0.97 | 0.96 | 0.94 | 0.91 | 0.92 | 0.92 | 0.95 | 0.81 | ||
| PPV | 0.51 | 0.00 | 0.36 | 0.35 | 0.27 | 0.33 | 0.38 | 0.33 | 0.38 | ||
| RF | Se | 0.75 | 0.00 | 0.27 | 0.38 | 0.16 | 0.21 | 0.42 | 0.23 | 0.56 | |
| Sp | 0.89 | 0.99 | 0.95 | 0.97 | 0.96 | 0.93 | 0.90 | 0.97 | 0.97 | ||
| PPV | 0.57 | 0.00 | 0.33 | 0.50 | 0.30 | 0.29 | 0.37 | 0.44 | 0.44 | ||
| BN | Se | 0.75 | 0.00 | 0.27 | 0.00 | 0.00 | 0.08 | 0.42 | 0.06 | 0.06 | |
| Sp | 0.88 | 0.99 | 0.97 | 0.99 | 0.99 | 0.96 | 0.89 | 0.99 | 0.99 | ||
| PPV | 0.54 | 0.00 | 0.44 | 0.00 | 0.00 | 0.22 | 0.36 | 0.33 | 0.33 | ||
| SMnLR | Se | 0.50 | 0.00 | 0.33 | 0.31 | 0.16 | 0.46 | 0.54 | 0.29 | 0.29 | |
| Sp | 0.96 | 0.98 | 0.94 | 0.94 | 0.96 | 0.86 | 0.89 | 0.94 | 0.94 | ||
| PPV | 0.73 | 0.00 | 0.31 | 0.27 | 0.30 | 0.32 | 0.42 | 0.33 | 0.33 | ||
| Ensemble models | Ensemble.1 | Se | 0.72 | 0.00 | 0.27 | 0.31 | 0.16 | 0.17 | 0.37 | 0.18 | 0.18 |
| Sp | 0.87 | 0.99 | 0.97 | 0.96 | 0.97 | 0.95 | 0.90 | 0.98 | 0.98 | ||
| PPV | 0.52 | 0.00 | 0.40 | 0.40 | 0.37 | 0.33 | 0.35 | 0.43 | 0.43 | ||
| Ensemble.2 | Se | 0.69 | 0.29 | 0.13 | 0.23 | 0.47 | 0.50 | 0.50 | 0.23 | 0.23 | |
| Sp | 0.95 | 0.99 | 0.96 | 0.99 | 0.95 | 0.96 | 0.97 | 0.99 | 0.99 | ||
| PPV | 0.73 | 0.50 | 0.22 | 0.75 | 0.53 | 0.63 | 0.75 | 0.67 | 0.67 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taghizadeh-Mehrjardi, R.; Minasny, B.; Toomanian, N.; Zeraatpisheh, M.; Amirian-Chakan, A.; Triantafilis, J. Digital Mapping of Soil Classes Using Ensemble of Models in Isfahan Region, Iran. Soil Syst. 2019, 3, 37. https://doi.org/10.3390/soilsystems3020037
Taghizadeh-Mehrjardi R, Minasny B, Toomanian N, Zeraatpisheh M, Amirian-Chakan A, Triantafilis J. Digital Mapping of Soil Classes Using Ensemble of Models in Isfahan Region, Iran. Soil Systems. 2019; 3(2):37. https://doi.org/10.3390/soilsystems3020037
Chicago/Turabian StyleTaghizadeh-Mehrjardi, Ruhollah, Budiman Minasny, Norair Toomanian, Mojtaba Zeraatpisheh, Alireza Amirian-Chakan, and John Triantafilis. 2019. "Digital Mapping of Soil Classes Using Ensemble of Models in Isfahan Region, Iran" Soil Systems 3, no. 2: 37. https://doi.org/10.3390/soilsystems3020037
APA StyleTaghizadeh-Mehrjardi, R., Minasny, B., Toomanian, N., Zeraatpisheh, M., Amirian-Chakan, A., & Triantafilis, J. (2019). Digital Mapping of Soil Classes Using Ensemble of Models in Isfahan Region, Iran. Soil Systems, 3(2), 37. https://doi.org/10.3390/soilsystems3020037