The Relation between General Relativity’s Metrics and Special Relativity’s Gravitational Scalar Generalized Potentials and Case Studies on the Schwarzschild Metric, Teleparallel Gravity, and Newtonian Potential
Abstract
:1. Introduction
- (i)
- Precession of Mercury’s Perihelion due to Sun gravity;
- (ii)
- Gravitational Deflection of Light;
- (iii)
- Shapiro time delay; and
- (iv)
- Gravitational Red Shift.
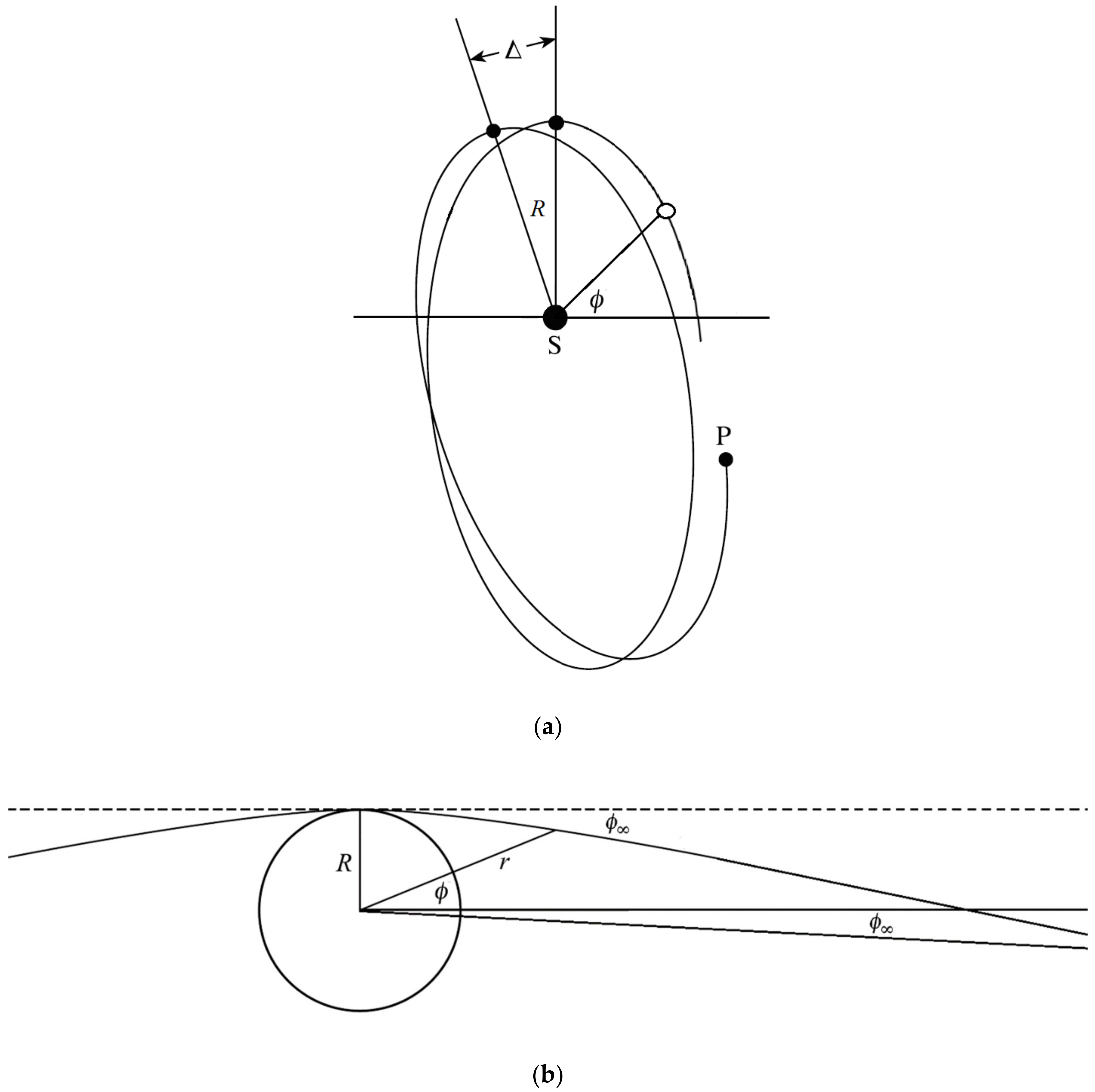
2. SR: Isometric Linear Transformations in Spacetime Endowed with the Lorentz Metric (Minkowski Spacetime)
3. GR: Metrics with Spherical Symmetry and the Schwarzschild Metric
3.1. The Metric of a Static and Centrally Symmetric Gravitational Field
3.2. Schwarzschild Metric: Relativistic Potential, Field Strength, and Isotropic Form
3.3. Schwarzschild Metric: Lagrangian, Geodesics, Equations of Motion, Equation of Trajectory, Precession of Planets’ Perihelion, Deflection of Light, and the Shapiro Time Delay
4. SR: Gravitational Field from the Central Scalar Generalized Potential
4.1. SR Gravitational Central Scalar Generalized Potential, Lagrangian, Equations of Motion, and Correlation to GR Time Dilation
4.2. SR Gravitational Central Scalar Generalized Potential from the GR Time Dilation of the Schwarzschild Metric: Field Strength, Lagrangian, Equations of Motion, Equation of Trajectory, Precession of Planets’ Perihelion, Deflection of Light, and Shapiro Time Delay
4.3. SR Gravitational Central Scalar Generalized Potential from the Time Dilation of Teleparallel Gravity
5. Gravitational Red Shift
6. The Reverse Procedure: GR Metrics from the SR Gravitational Central Scalar Generalized Potential and the Case Study of a Non-Riemannian Metric from the Newtonian Gravitational Potential
7. Discussion
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| EEP | Einstein’s Equivalence Principle |
| GR | General Relativity |
| M4 | Minkowski spacetime |
| NPs | Newtonian Physics |
| RIO | Relativistic Inertial Observer |
| RIO O | RIO with the origin of its frame on the center of gravity O |
| SR | Special Relativity |
| UCM | Uniform Circular Motion |
References
- Phipps, T.E. Mercury’s precession according to special relativity. Am. J. Phys. 1986, 54, 245–247. [Google Scholar] [CrossRef]
- Tsamparlis, M. Special Relativity: An Introduction with 200 Problems and Solutions, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2010; ISBN 978-3-642-03836-5. [Google Scholar]
- Goldstein, H. Classical Mechanics, 2nd ed.; Addison-Wesley: London, UK, 1980; ISBN 0-201-02969-3. [Google Scholar]
- Park, R.S.; Folkner, W.M.; Konopliv, A.S.; Williams, J.G.; Smith, D.E.; Zuber, M.T. Precession of Mercury’s Perihelion from Ranging to the MESSENGER Spacecraft. Astron. J. 2017, 153, 121. [Google Scholar] [CrossRef]
- Einstein, A. Relativity: The Special and General Theory; Robert, W.L., Translator; Henry Holt: New York, NY, USA, 1920. [Google Scholar]
- von Soldner, J.G. Ueber die Ablenkung eines Lichtstrals von seiner geradlinigen Bewegung, durch die Attraktion eines Weltkörpers, an welchem er nahe vorbei geht. Berl. Astron. Jahrb. 1804, 1804, 161–172. [Google Scholar]
- Einstein, A. On the Influence of Gravitation on the Propagation of Light. Ann. Phys. 1911, 35, 898–908. [Google Scholar] [CrossRef] [Green Version]
- Rindler, W. Relativity: Special, General and Cosmological, 2nd ed.; Oxford University Press: New York, NY, USA, 2006; ISBN 978-0-19-856732-5. [Google Scholar]
- Blagojevic, M. Gravitation and Gauge Symmetries; IOP Publishing: Bristol, UK, 2002; ISBN 0750307676. [Google Scholar]
- Utiyama, R. Invariant Theoretical Interpretation of Interaction. Phys. Rev. 1956, 101, 1597–1607. [Google Scholar] [CrossRef]
- Kibble, T.W.B. Lorentz Invariance and the Gravitational Field. J. Math. Phys. 1961, 2, 212–221. [Google Scholar] [CrossRef] [Green Version]
- Lecian, O.M.; Mercuri, S.; Montani, G. Is Torsion a Fundamental Physical Field? In Proceedings of the 11th Marcel Grossmann Meeting on General Relativity, Berlin, Germany, 23–29 July 2006; World Scientific: Singapore, 2008; pp. 2668–2670. [Google Scholar] [CrossRef] [Green Version]
- Lecian, O.M.; Montani, G.; Carlevaro, N. Novel analysis of spinor interactions and non-Riemannian geometry. Eur. Phys. J. Plus 2013, 128, 19. [Google Scholar] [CrossRef] [Green Version]
- Hehl, F.W.; Von Der Heyde, P.; Kerlick, G.D.; Nester, J.M. General relativity with spin and torsion: Foundations and prospects. Rev. Mod. Phys. 1976, 48, 393–416. [Google Scholar] [CrossRef] [Green Version]
- Einstein, A. Riemann-Geometrie mit Aufrechterhaltung des Begriffes des Fernparallelismus; Sitzungsberichte, K., Ed.; Preussische Akademie der Wissenschaften, Phys-math: Berlin, Germany, 1928; pp. 217–221. [Google Scholar]
- Møller, C. Conservation laws and absolute parallelism in general relativity. Mat. Fys. Dan. Vid. Selsk. 1961, 1, 50. [Google Scholar]
- Pellegrini, C.; Plebanski, J. Tetrad fields and gravitational fields. Mat. Fys. SKR. Dan. Vid. Selsk. 1963, 2, 1–39. [Google Scholar]
- Maluf, J.W. The Teleparallel Equivalent of General Relativity and the Gravitational Centre of Mass. Universe 2016, 2, 19. [Google Scholar] [CrossRef] [Green Version]
- Perlick, V. Characterization of standard clocks by means of light rays and freely falling particles. Gen. Relativ. Gravit. 1987, 19, 1059–1073. [Google Scholar] [CrossRef]
- Delhom, A.; Lobo, I.P.; Olmo, G.J.; Romero, C. Conformally invariant proper time with general non-metricity. Eur. Phys. J. C 2020, 80, 415. [Google Scholar] [CrossRef]
- Hayashi, K.; Shirafuji, T. New General Relativity. Phys. Rev. D 1979, 12, 3524–3553. [Google Scholar] [CrossRef]
- Golovko, V. New metrics for the gravitational field of a point mass. Results Phys. 2019, 13, 102288. [Google Scholar] [CrossRef]
- Schwarzschild, K. Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie. Sitz. Königlich Preuss. Akad. Wiss. 1916, 7, 189–196. [Google Scholar]
- Vossos, S.; Vossos, E.; Massouros, C.G. Explanation of Light Deflection, Precession of Mercury’s Perihelion, Gravitational Red Shift and Rotation Curves in Galaxies, by using General Relativity or equivalent Generalized Scalar Gravitational Potential, according to Special Relativity and Newtonian Physics. J. Phys. Conf. Ser. 2021, 1730, 012080. [Google Scholar] [CrossRef]
- Reasenberg, R.D.; Shapiro, I.I.; MacNeil, P.E.; Goldstein, R.B.; Breidenthal, J.C.; Brenkle, J.P.; Cain, D.L.; Kaufman, T.M.; Komarek, T.A.; Zygielbaum, A.I. Viking relativity experiment—Verification of signal retardation by solar gravity. Astrophys. J. 1979, 234, L219–L221. [Google Scholar] [CrossRef]
- Vossos, S.; Vossos, E.; Massouros, C.G. New Central Scalar Gravitational Potential according to Special Relativity and Newtonian Physics, explains the Precession of Mercury’s Perihelion, the Gravitational Red Shift and the Rotation Curves in Galaxies, eliminating Dark Matter. J. Phys. Conf. Ser. 2019, 1391, 012095. [Google Scholar] [CrossRef]
- Williams, D.R. Mercury Fact Sheet. Available online: https://nssdc.gsfc.nasa.gov/planetary/factsheet/mercuryfact.html (accessed on 17 June 2020).
- Lide, D.R. (Ed.) CRC Handbook of Chemistry and Physics, 89th ed.; Internet Version; CRC Press/Taylor and Francis: Boca Raton, FL, USA, 2009. [Google Scholar]
- Williams, D.R. Sun Fact Sheet. Available online: https://nssdc.gsfc.nasa.gov/planetary/factsheet/sunfact.html (accessed on 17 June 2020).
- Williams, D.R. Earth Fact Sheet. Available online: https://nssdc.gsfc.nasa.gov/planetary/factsheet/earthfact.html (accessed on 17 June 2020).
- Lopresto, J.C.; Chapman, R.D.; Sturgis, E.A. Solar gravitational redshift. Sol. Phys. 1980, 66, 245–249. [Google Scholar] [CrossRef]
- Heymans, C. The Dark Universe; IOP Publishing: Bristol, UK, 2017; ISBN 978-0-7503-1373-5. [Google Scholar] [CrossRef]
- Grimshaw, R.; Pelinovsky, D.; Pelinovsky, E. Homogenization of the variable-speed wave equation. Wave Motion 2010, 47, 496–507. [Google Scholar] [CrossRef]
| Mercury | Earth | ||||
|---|---|---|---|---|---|
| SR/cy−1 | GR/cy−1 | SRr (%) | SR/cy−1 | GR/cy−1 | SRr (%) |
| 42.9820(43) (1) | 42.9820(43) (1) | 0 | 3.83893(38) (1) | 3.83893(38) (1) | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vossos, S.; Vossos, E.; Massouros, C.G. The Relation between General Relativity’s Metrics and Special Relativity’s Gravitational Scalar Generalized Potentials and Case Studies on the Schwarzschild Metric, Teleparallel Gravity, and Newtonian Potential. Particles 2021, 4, 536-576. https://doi.org/10.3390/particles4040039
Vossos S, Vossos E, Massouros CG. The Relation between General Relativity’s Metrics and Special Relativity’s Gravitational Scalar Generalized Potentials and Case Studies on the Schwarzschild Metric, Teleparallel Gravity, and Newtonian Potential. Particles. 2021; 4(4):536-576. https://doi.org/10.3390/particles4040039
Chicago/Turabian StyleVossos, Spyridon, Elias Vossos, and Christos G. Massouros. 2021. "The Relation between General Relativity’s Metrics and Special Relativity’s Gravitational Scalar Generalized Potentials and Case Studies on the Schwarzschild Metric, Teleparallel Gravity, and Newtonian Potential" Particles 4, no. 4: 536-576. https://doi.org/10.3390/particles4040039
APA StyleVossos, S., Vossos, E., & Massouros, C. G. (2021). The Relation between General Relativity’s Metrics and Special Relativity’s Gravitational Scalar Generalized Potentials and Case Studies on the Schwarzschild Metric, Teleparallel Gravity, and Newtonian Potential. Particles, 4(4), 536-576. https://doi.org/10.3390/particles4040039








