Abstract
In different areas of mechanics, highly non-equilibrium processes are accompanied by self-organization of various type turbulent structures and localized inhomogeneities at intermediate scale between macro and micro levels. In order to describe the self-organization of the new dynamic structures on the mesoscale, a new problem formulation based on the results of non-equilibrium statistical mechanics, control theory of adaptive systems, and theory of a special type nonlinear operator sets is proposed. Determination of the turbulent structure parameters through constraints imposed on the system in the form of nonlinear functionals is an inverse problem similar to problems on spectra in quantum mechanics. Like in quantum mechanics, the bounded system in response to impact forms a discrete spectrum of the turbulent structure sizes and lifetimes which goes into continuous spectrum close-to-equilibrium. The proposed description of the structure evolution on the intermediate scale level which is valid far from thermodynamic equilibrium bridges the gap between macroscopic theories and quantum mechanics and affirms the unity of the physical laws of nature.
1. Introduction
One of the unsolved problems of modern physics is the behavior of the system at an intermediate scale level between the deterministic behavior of a macroscopic system and the probabilistic one at the micro level of elementary particles. Macroscopic size systems containing a huge number of elementary particles obey the laws of classical physics; the energy and momentum are distributed continuously over the system volume. The microscopic structure and processes occurring at the structural level determine only averaged macroscopic properties of the system. The elementary particles interact according to the laws of quantum mechanics, according to which energy and momentum are transmitted by discrete quanta. The question of what is happening at the intermediate, mesoscopic scale has been raised for a long time, but with the development of nanotechnologies, it has gained practical interest. Studies of the properties of liquids with dispersed nanoparticles or flows in nanochannels have shown that the classical models of continuum mechanics have proved unsuitable for their description [1,2]. It is known that materials with an internal nanoscale structure have new properties that are different from the usual properties of these materials. Developing nanotechnology needs a fundamental theory that could be laid in their basis.
Modern studies of high-speed and short-duration processes in condensed matter [3,4,5,6] have shown that processes on very small space-time scales are also not described by models of continuum mechanics. A correct description of such processes also presents the unsolved fundamental problem of constructing non-equilibrium thermodynamics.
The recent trends in non-equilibrium thermodynamics propose new statistical and phenomenological approaches involving nonlinear, nonlocal, and memory effects to describe high-rate and short-duration processes with large spatial gradients which are used in modern technique and technologies. The main ideas behind the macroscopic approaches to describe the processes out of equilibrium beyond the local equilibrium hypothesis are presented in book [7]. Since non-equilibrium thermodynamics is not considered to be completely constructed, many researchers still use long-established and deeply rooted ideas that implicitly rely on the concept of local thermodynamic equilibrium. Mechanically transferred to the non-equilibrium conditions, these ideas sometimes lead either to contradictions, or simply to incorrect results.
Experimental results, obtained in the study of non-equilibrium processes in different branches of mechanics (hydrodynamics of turbulent flows, multi-phase flows, shock-induced processes in solids, biomechanical processes), show many similar features of the non-classical system response to external perturbations. Far from equilibrium processes are often accompanied by self-organization of new dynamic structures [8,9,10,11,12,13,14,15,16] such as boundary layers, mass velocity pulsations, vortex structures, various localized inhomogeneities, etc. The observable self-organization effects are characterized not only by the medium properties (composition, phase state) but also by the loading and boundary conditions and the system geometry. Because of the finite rate of propagation of disturbances, the medium response always lags behind the impact from outside. Momentum and energy exchange between new degrees of freedom related to the internal structure formed under external influence can give rise to oscillations, instabilities, and formation of feedback between the structure effects and macroscopic properties of the system. The system behavior becomes unstable and poorly predictable. The medium properties become time-dependent, exhibit size effects, and depend on boundary and loading conditions. In order to describe processes far from equilibrium, we need to understand the physical nature of the processes at the intermediate scales, to generalize and revise all the concepts of thermodynamics and to develop a unified mathematical description valid for various media in a wide range of loading conditions with accounting self-organization effects.
An example of such structures is provided in Figure 1. In the research [16], the fracture of polymethylmethacrylate and fluoroplastic cylinders by an electric explosion of wire was studied. The use of the electric-physical approach allowed us to destroy plastic samples with a single mechanical pulse of 1–5 s duration, depending on the features of the experimental design and material properties. It was noticed that the observed abundance of various structures on the fracture surface of the polymethylmethacrylate sample in comparison to a fluoroplastic one corresponds to a more intense damping of the load pulse due to its absorption by the forming structures on the mesoscale.
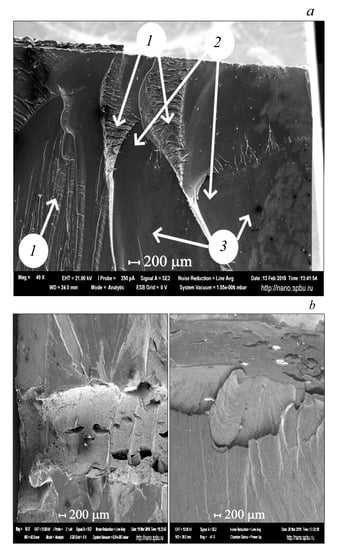
Figure 1.
Structures formed on fracture surfaces of polymethylmethacrylate (a) and fluoroplastic (b) samples being rapidly fractured with electric explosion of wire [16]. Regions of increased roughness (1), mirror areas (2), and areas of geometric shapes (3) were identified for a polymethylmethacrylate sample (a).
In Section 2, the problems arising in the description of shock-induced processes in condensed matter are presented. Experimental studies of shock-wave processes in condensed media characterized by such scales [1,2,3,4,5,6,10,11,15,16,17,18,19,20,21,22,23] show that so-called mesoparticles become carriers of momentum and energy which are much larger than the quantum, but much smaller than the macro-size of the system. At present, even a separate discipline "mesomechanics" has emerged which deals with the study of mesostructures that arise in various materials under the influence of external loading [24,25]. The theoretical description of the mesostructures formation is associated with the description of a non-equilibrium elastic-plastic transition under shock loading and requires entering the region of thermodynamics far from equilibrium, which is currently still being developed [7]. The problem of the emergence and evolution of mesoscopic-scale structures has many interesting practical applications in high-speed technique and technologies for creating materials with desired properties, including nanotechnology, as well as in biomechanics and medicine.
The solution to this problem requires new interdisciplinary approaches based on the rigorous results of non-equilibrium statistical thermodynamics which would allow one to go beyond continuum mechanics into the region of substantial non-equilibrium.
In our work, we relied on non-equilibrium nonlocal thermodynamic relationships with memory between thermodynamic forces and fluxes which were derived in statistical mechanics by Zubarev [26] ab initio using the method of the non-equilibrium statistical operator. The obtained relationships are nonlocal both in space and time and have no restrictions on the scale of processes. However, the generalized integral-differential equations obtained by the method for the volumetric densities of mechanical quantities have not been used in practice for a long time due to the difficulties in describing the space-time correlations included in the integral kernels of these equations.
In papers [13,14,27,28,29,30,31], a new approach to modeling the dynamics of correlations far from thermodynamic equilibrium was proposed based on the Bogolyubov’s principle of decaying correlations [32], the Jaynes’s principle of maximum entropy (MEP) [33], according to which a non-equilibrium system tends to achieve the maximum value of entropy available under the constraints imposed on the system, and the speed gradient principle [34] developed in control theory of adaptive systems which determines the fastest way to achieve this goal. Within the framework of this approach, a connection between the dynamics of correlations and the sizes of forming mesoparticles was revealed. Presented in Section 3, the developed approach is applied to describe mesostructure evolution during shock wave propagation inside the condensed matter.
An explicit approximate solution [6] to the problem of the waveforms evolution during the wave propagation is presented in Section 4. Based on the solution, the interference and formation of wave packets of elastic-plastic waves in media with dispersion is considered in Section 5.
In Section 6, we show that, within the proposed approach, the sizes of mesostucture in multi-scale processes in bounded systems should be discrete.
In Section 7, an evolution of mesostructure during the wave packet propagation is described basing on the results obtained in Section 5 and Section 6. Mathematical apparatus to the problem formulation and solution is given in Section 8.
We found that the mathematical formulation of the problem of determining the sizes of evolving mesoparticles coincides with the formulation of inverse problems of quantum mechanics in the Banach functional space for nonlinear integral operators [35,36]. In addition, the observed behavior of the wave packets propagating along the condensed matter corresponds to the spreading quantum wave packets [37]. This, of course, does not mean that quantum mechanics works in full on the mesoscale. We wanted to show that in such transient processes which are not entirely described by macroscopic laws, the quantum discrete nature of the mesolevel is already partially manifested.
2. Mesoscopic Structure Formation in Shock-Induced Processes
One of such problems is related to shock-induced processes. Experimental study of shock loading of solid materials [3,13,14,17,18,19] shows that the material response can not be explained by continuum mechanics. Specifically, the presented results indicate that mechanical and physical properties of the shocked material are determined by localized deformations occurring on a sub-continuum scale.
For a long time, it was thought that plastic deformation was a macroscopically uniform continuous process. Now we know that the plastic deformation is heterogeneous at all intermediate scales and consists of series of discrete steps reducing the local stress during the relaxation [20,21]. However, numerous attempts to describe mechanical characteristics of crystalline solids by using the failed dislocation theory. Now the situation in the experimental and theoretical study of defective structures in deformable materials has radically changed. Structural studies of solid materials have revealed completely new types of defective structures for different deformation conditions. These formations play the role of independent elementary carriers of momentum and energy. A new area of mechanics called “mesomechanic” [24,25] describes the deformation and destruction of the material as the multi-scale process responsible for the macroscopic properties of materials. According to modern concepts of the physics of strength and plasticity, there is a certain hierarchy of scale levels that defines a change in mechanisms of momentum and energy transport in a deformable solid, depending on the strain rate, boundary and initial conditions, and the material properties [5,14,22,23]. Despite considerable progress in modeling, there is no a first-principle approach capable of describing a whole complex of non-equilibrium processes in a deformable medium responsible for its dynamic macroscopic properties. To develop predictive continuum models, it is necessary to critically examine the fundamental postulates used to interpret shock compression phenomena. A theoretical description of the phenomenon of plasticity under shock loading is associated with serious difficulties connected to specific problems of non-equilibrium transport. The non-equilibrium processes of mass, momentum and energy transport in condensed matter are accompanied by dynamic self-organization processes at intermediate, mesoscopic scales. The observed formation of local inhomogeneities at mesoscopic scale, such as the localized shear bands, microcracks, traces of microflows and rotational structures significantly change the macroscopic properties of the medium. In experiments on shock loading of solid materials [12,22,23], it was found that the formation of dynamic structures inside the propagating waveform is of resonant origin when the wave length coincides with the size of spatial internal structure of the medium. It is impossible to detect if they are reversible or not until behind the wave a part of them remained frozen into the medium. The observed inhomogeneities formed by shock loading are only traces left in the medium by partially reversible mass velocity pulsations and wave structures.
The elastic-plastic transition zone itself is highly turbulent with a collection of eddies, interacting transverse waves, shear layers, and density interfaces [10]. Inside the turbulent transition zone, large pulsations and a strong departure from local equilibrium occur. When the pulsations grow, inertial effects begin to play a significant role. In this case, angular momenta appear associated with internal rotations of the medium—vortex structures. At present, the notion of turbulence differs from that which was commonly adopted earlier. The turbulent state is not random or chaotic, but an orderly structure. A fundamental role in the phenomenon of turbulence is played by internal and external boundaries. It has long been noted that correlations are observed between pulsations at different spatio-temporal points. The turbulence is inherent in non-equilibrium processes in media of various nature. However, up to now, there has been no general theory of turbulent flows of fluids, only various semi-empiric models are used.
Thus, the response of solid materials to shock loading determined by the self-organization effects at mesoscopic scale and multi-scale energy exchange relate to highly non-equilibium processes which can not be described in the framework of the continuum mechanics models since all the special features of turbulence should be included in the description of thermodynamic processes far from equilibrium. Now, we need such a fundamental theory that would explain the formation of turbulent mesoscopic structures in various media under non-equilibrium conditions on a unified theoretical basis.
A new interdisciplinary approach to the problem based on results of non-equilibrium statistical mechanics and control theory of adaptive systems [6,14,27,28,29] was applied to explain the whole complex of non-equilibrium phenomena.
3. New Approach to the Multi-Scale Processes far from Equilibrium
Based on the results of non-equilibrium statistical thermodynamics, a new self-consistent approach was proposed to include self-organization of dynamic structures on the mesoscale into mathematical modeling processes out of equilibrium. Derived in non-equilibrium statistical thermodynamics [26], the nonlocal relationships with memory between thermodynamic forces and fluxes served as the basis for constructing models that describe the dynamics of spatiotemporal correlations depending on the external impact on the system [6,14,27,28,29]. In scope of the approach, it was shown that the self-organization effects at the meso-scale are the result of the correlation dynamics under the constraints imposed. The generalized nonlocal and retarded hydrodynamic equations are used at a macroscopic level and on an intermediate between macro and micro scale the dynamics of the space-time correlations is described by Speed Gradient principle developed in control theory of adaptive systems [34] and Maximum Entropy principle by Jaynes [33]. Interrelations between the correlation scales and dynamic structures of the system allow us to describe the internal structure evolution far from equilibrium. Evolving over time, the constructed model of the correlation function with parameters connected to the correlation scales allow us to take into account all typical features of turbulent structures in any medium. An appropriate mathematical apparatus for nonlocal boundary problems based on the special type nonlinear operator theory [35,36] is developed to describe non-equilibrium phenomena. Inclusion of the constraints imposed on the system and boundary and loading conditions into the modeling makes it possible to describe self-organization of new multi-scale dynamic structures in an open system and to find the scales of the correlations which are not given in advance. In the framework of the developed approach, under highly non-equilibrium conditions, correlations decay at scales that are intermediate between the micro and macro levels where the transfer mechanism combines both wave and diffusion properties. The most common mechanism of momentum transfer is a nonlinear damped wave. The problem of the propagation of a planar elastic-plastic wave is solved in papers [6,27] by using the developed model of dynamics of spatiotemporal correlations. The initial state of a solid is characterized by long-range spatiotemporal correlations; a shock breaks the correlations and induces elastic-plastic wave propagation. The constructed model of momentum transport describes the stress relaxation as a post-shock due to the memory effects included in the correlation function. This conception of the shock-induced elastic-plastic transition based on the non-local theory of non-equilibrium transport processes [27] radically differs from the conventional one. Comparison of the obtained results to the experimental data was shown that all experimentally observed features of the waveforms propagation are described by the model.
4. Integral Model of the Elastic-Plastic Wave Propagation in Condensed Matter
A problem on the shock-induced elastic-plastic wave propagating in condensed matter has been solved by Meshcheryakov and Khantuleva [6]. We give the obtained solution, since it will be used in the future. In case of the planar shock loading when the induced wave propagates along the x-axis in a linear approximation with respect to the parameter , the equations of mass and momentum transfer lead to the equation for mass velocity v
The constitutive equation for the longitudinal component of stress tensor to close the Equation (1) based on the generalized thermodynamic relationships [26] takes a form
Here, is initial unperturbed density, C is longitudinal sound velocity defined by the relationship , where are volume compression and shear elastic modules. is the temporal correlation function for the shear degrees of freedom.
The force is applied only during the time interval , whereas the shear relaxation time is much more for condensed matter. For macroscopic large-size systems when , the nonlocal effects in the transition zone can be omitted. For shock-induced processes of moderate intensity, the plastic deformation in the transition zone is explained by the shear relaxation. In a condensed medium, the shear relaxation time is less than the bulk one . When the elastic limit is exceeded, there is a two-wave structure form, which consists of both an elastic precursor and a plastic front rising behind it. The mass transporting plastic part of the waveform gradually lags from the precursor. Its speed is a group velocity of the wave propagating in a medium with internal structure, evidenced by the experimentally observed in real time the mass velocity dispersion.
In the reference connected to the elastic precursor running at the constant longitudinal sound velocity C, , , an essential simplification of the nonlocal model for the impulse transport (1), is gained on the condition resulted from the experimentally tested evaluation . Here, parameters of relaxation, retardation, and nonlocality are introduced: , , . The separation of typical scales of the process is considered as the necessary condition for self-organization of new structures in the medium [8,9].
On the above conditions, the problem (1)–(2) in the new reference with is reduced to an integral equation for the mass velocity
In papers [14,27,29], the temporal correlation function was introduced to take into account inertial and relaxation post-effects:
Meeting the above conditions, the correlation function describes a range of the wave modes near the elastic limit
The integral Equation (3) with the correlation function (2) has an explicit solution at a constant strain-rate that describes the waveform propagation along the medium.
At the initial stage when , the system response to the loading is elastic
At the final stage when the stress component corresponds to the Newtonian fluid,
After the loading , the solution describes the shear relaxation as a memory effect due to the medium inertia:
In the limit of the non-decaying memory, the stress remains constant
Without the memory effects after the loading, the stress disappears
As experimental data show, the parameters , grow with the distance traveled by the wave and the waveform spreads.
5. Interference of Elastic-Plastic Waves
In a heterogeneous medium, an external action induces a group of waves with different but fairly close frequencies which are recorded in experiments in real time as the mass velocity dispersion. As a result of interference, the waves form a space-time limited wave formation called a wave packet. Due to the dispersion properties of the medium, wave packets propagate at a group velocity which is always less than the phase velocity. In an inertial medium with sufficiently long relaxation and delay times, the wave fronts induced by short-duration pulses can be added up, greatly increasing the velocity and resulting stress [30]. Due to such resonance effects, the resulting wave packet can transfer mass and momentum in an amount significantly exceeding the capabilities of one total pulse at the same strain rate.
In the presence of dispersion in the individual components of the waves, a spread in phase velocities appears which in turn leads to the spreading of the wave packet during its propagation, as in quantum mechanics. Experiments on the shock loading of solid materials show that the plastic front of an elastic-plastic wave actually spreads during propagation [6]. Packets partially reflect from internal and external boundaries and partially penetrate the inter-phase boundaries. For bounded systems, interference of incident and reflected waves can give rise to the resonance effects which form waves with large amplitudes. Propagating at different speeds, the mass flows inside plastic fronts generate high-speed shifts which in turn induce rotational degrees of freedom [38]. The self-organization of vortex-wave structures associated with the phenomenon of turbulence is experimentally observed in solids under shock loading.
All type inhomogeneities including turbulent structures (pulsations, mesoflows, mesoshears, rotations) arise inside the waveform and absorb a part of kinetic energy not due to dissipation (diffusion is too slow for a shock duration) but to dispersion [30,39]. The turbulent structures are only partially irreversible and only a part of the dynamic structures remain frozen into material after passing the wave.
In quantum mechanics, the problem of scattering of a wave packet by potential inhomogeneities is solved [37]. The scattering process on the potential can be considered as the interference of the incident wave and multiply reflected waves from the inhomogeneities of the potential. The interference can give rise to various resonant effects depending on the ratio of wavelengths and distances between potential inhomogeneities.
It was found that, during scattering, the transmitted and reflected wave packets exit with a certain delay. The times and lengths of the delay are determined by the packet pulses and the shape of the potential. The delay of the reflected packet corresponds to the penetration depth of the wave into the potential barrier. In addition, due to the dispersion, wave packets spread out on the inhomogeneities of the potential.
The difference between the oscillations of a discrete chain of atoms and the vibrations of a continuous string is the manifestation of the effects of the internal structure of the system in the form of wave dispersion, which manifests itself in a nonlinear relationship between frequency and wave vector in the dispersion relation. Group velocity occurs only in dispersive media, when the internal structure of the medium affects the process of wave propagation. Group velocity is always less than phase velocity, like wave packet velocity. It can be seen from this that short-wave signals propagate more slowly than long-wave ones. Due to the spreading of the wave packet, they also decay faster than long-wave ones. In the long-wavelength limit, when the dispersion disappears, both speeds coincide and become equal to the speed of sound propagation in the equilibrium system. In the long wavelength limit , when the size of the lattice does not affect the propagation of waves, the medium can be considered as structureless.
In addition, a real material always has various defects of the crystal lattice and other inhomogeneities at the mesoscopic scale level. Obviously, larger structures result in greater dispersion. Since the interaction between the atoms is potential, all the heterogeneities of the material structure are potential heterogeneities. A shock on a solid can be considered as the scattering of a wave packet by the inhomogeneities of its structure after passing through a potential barrier. The parameters of relaxation and delay introduced into the description of an elastic-plastic wave in Section 4 are related to the delays of the wave packet that arose after passing through the potential barrier during the shock.
In experimental study of shock loading of solid materials [11,12], the mass velocity dispersion was recorded inside the waveform on the back side of the metal target. It means that the plastic part of the registered waveform consists of separate mesoscopic mass flows. Due to their velocity dispersion, the plastic waveform presents a wave packet spreading during its propagation. Then, integration over the interval of the mass velocity variation defines the wave packet transmitted into material after the shock
In experiments on the shock loading of solid materials, the wave characteristics are registered at two scales simultaneously. The waveform is recording at a mesoscopic spot compared to the diameter of the laser beam on the target back side. The mass velocity dispersion is registered only on the plastic front [6]. It means that the wave packet consists of movements at the smaller scale than the mesoscale of the registered waveform. Apparently, there is a hierarchy of scales between macro and micro levels on which momentum and energy exchange proceeds into the medium after the shock loading.
6. Discrete Spectra of Meso-Scale Structure in the Shocked Material
The mass velocity waveform and the velocity dispersion are registered in real time on the back side of metal target at , . However, the relaxation and delay parameters , are unknown for the wave packet. In order to define them, it is necessary to find the total momentum loss during the passage along the target. Since the initial waveform is given, it is sufficient to define the total momentum in the final waveform by integration over its duration
We have got a nonlinear Equation (13) with respect to the parameters , . Experimental data [6] show that, during quasi-stationary wave propagation, between the parameters , a linear relationship is established for each material . In this case, the nonlinear Equation (13) defines the parameters at in a non-unique way.
Physical meaning of the parameters is associated with the structure elements lifetimes. The parameter defines the size of each type turbulent structure and the parameter defines inertial properties of the turbulent structure of each size in the obtained spectrum.
The finite-size element, embraced by correlations of the radius , moves like solid particles in multi-phase medium; it can pulsate and in a non-uniform mass velocity field begins to rotate. Such turbulent modes of motions at intermediate scales are observed not only in high-rate flows of fluids but also in solid materials under shock loading [10,11]. Thus, the finite-size elements embraced by the correlations and moving as a quasi-particle can be considered as a real dynamic structure of the system.
Like in quantum mechanics, the bounded system out of equilibrium can have a discrete spectrum of the structure sizes and near equilibrium, where classical hydrodynamic equations are valid, it goes into continuous spectrum. Elements of the discrete dynamic structure of the system become carriers of momentum and energy in the system. Since finite values of the model parameters can represent linear sizes of the system dynamic structure, Equation (16) determines dynamic self-organization of various kinds of turbulent structures in the system. It means that the structuring is a response of the system to the external action that takes the system far from thermodynamic equilibrium. Then, it may be concluded that the self-organization appears to be the necessary component of the transport processes modeling far from equilibrium.
The task of determining the parameters of the structure of the system from its integral characteristics is an inverse problem of quantum mechanics. In quantum mechanics, it is proved that a sufficiently deep potential well should contain discrete energy levels. We can consider that here we have just the same case: a short-duration process in a bounded system should be characterized by the discrete spectrum of temporal parameters associated with mass flows on the mesoscale. Long-duration loading induces continuum spectrum of internal structure. The spreading of the wave packet also leads to continuum spectrum of parameters.
7. Evolution of the Turbulent Structure Lifetimes
In the general case, Equation (13) is not sufficient to define all the parameters at various distances from the shocked surface. When the number of boundary conditions is less than the number of the model parameters, another part evolves in the direction of thermodynamic equilibrium. Generally, the system states far from equilibrium are unstable. It means that spatiotemporal correlations according to the hypothesis by Bogolyubov [32] attenuate due to the degrees of freedom that are not governed by the constraints imposed.
In order to define all the turbulent structure parameters within a wide range of conditions, it is necessary to describe the waveform evolution during its propagation along the medium. The limiting state, the goal of the evolution, is determined by the thermodynamic Maximum Entropy principle by Jaynes [33]. The fastest way to the goal is governed by the Speed Gradient principle by Fradkov developed in the control theory of adaptive systems [34]. By using the Speed-Gradient principle, it became possible to trace the entropy production behavior far from equilibrium. In Ref. [31], it had been shown that, by saving the information about the process history and transforming its internal structure, the system minimizes its irreversible losses. Between the structure evolution on the mesoscale and macroscopic properties of the system, feedback is forming. Stabilization of the states in approaching equilibrium requires the energy dissipation in the form of heat. Stabilization of the non-equilibrium states requires the energy loss to the structure transitions.
The goal is written as a conditional functional
is the Lagrange multiplier. The entropy production inside the waveform for the way along the x-axis , is written as follows:
The finite form of the Speed Gradient algorithm defines the evolutionary set of differential equations with respect to the parameters , :
The gain parameters , are empiric constants connected to the inertial properties of the turbulent structures.
The nonlinear set of differential Equation (16) defines a family of integral curves that describe the evolution paths of the turbulent structures. In order to choose the real paths from them, we need the conditions for each pair of parameters , . The conditions and the gain parameters we can get only from experimental measuring of the new internal structure sizes inside the target material of two close waveforms. Then, we have the completed mathematical formulation of the inverse problem of determining the spectrum of turbulent structures from experimental data. For quasi-stationary wave propagation, the proposed approach results in the evolution paths coinciding with experimental data [40].
8. Mathematical Apparatus to Solve the Problem
A mathematical apparatus similar to the apparatus of quantum mechanics for solving inverse problems was developed in papers [35,36]. We modify it to the case of evolving parameters and apply it to solve the problem in the formulation (16). Integrating the Equation (16) over the way traveled by the wave gives two functional equations for the evolving parameters , :
The goal functional in (17) depends on the evolution coordinate only via the parameters ,
According to Equation (19), the parameters , increase with gradient descent over the surface from the point , and decrease when lifting. In both cases, the wave produces the maximum integral entropy for the propagation way possible under the condition (13) imposed. The case of the quasi-stationary wave propagation with the growing parameters corresponds to the spatiotemporal correlations in solid material. In this case, the limiting state is solid with a new internal structure formed after the shock-induced stress relaxation. Another limiting state after extreme shock is fluid. Presented in Section 4, the solution is not correct in this case.
Within the iteration procedure developed in [35,36], the set (17) in the i-approximation takes a form
Here, , , is nonlinear operators, E is an infinite-dimensional Banach space.
If the initial approximation for the parameters at the distance is given from experiments, the next approximation corresponds to the parameters at the distance down the surface along the path resulted from the Speed Gradient algorithm or at the distance up the surface. The procedure (20) represents a sweep along the wave propagation path. Each iteration defines a step of the system evolution on the mesoscale.
The integral transport Equation (12) allows us to express the mass velocity in i-approximation as a nonlinear functional depending on the model parameters :
Here, is a nonlinear operator, . Equation (21) with the parameters defined by the set (20) describes the waveform evolution as a wave packet. In Refs. [35,36], it was proved that, if the iteration procedure converges, a solution to the problem (21) exists.
Equation (12) and its approximate form (21) describe the wave packet spreading during its propagation. The set (19)–(20) describes the evolution of the discrete internal structure of the packet during its spreading. Between the two scales, there is feedback.
In general, describing the structure formation and evolution on the mesoscale in the formulation (19) is very complicated problem. The mathematical apparatus needs further development. Now, we can not answer some questions regarding the relationship between the step of the iterative procedure and the scale of temporal correlation, between feedback and the delay time, and between the inaccuracy of experimental data and the convergence of the procedure. We consider the proposed sweep of the iteration procedure as one of the possible approaches to future developments.
9. Conclusions
The emergence of various turbulent structures at the intermediate between macro and micro scale levels, as shown by experimental data, accompanies non-equilibrium processes of mass, momentum, and energy transfer in media of various nature. It was experimentally discovered [11,12] that multi-scale and multi-stage energy exchange is a mechanism of the structural evolution of a physical system far from thermodynamic equilibrium. The description of such processes requires solving a whole complex of fundamental problems of modern science: the creation of a theory of turbulence, thermodynamics of highly non-equilibrium processes, and non-equilibrium statistical mechanics of open systems. Obviously, only an interdisciplinary approach is required to solve this global problem.
Developed on the basis of non-equilibrium statistical mechanics [26] and control theory [34], a new approach to describing non-equilibrium processes [27,28,29] allows for constructing mathematical models of the processes that describe the formation and development of turbulent structures, including external influences, dimensions and geometry of the system, as well as take into account the incompleteness of information about the history of the system in the form of the dynamics of spatial-temporal correlations. Similar to the inverse problems of quantum mechanics, the use of the formalism of operators in a Banach space allows us to formulate a problem of the spectrum of spatial-temporal scales of dynamical structures formed in bounded systems due to external action across boundaries. As for a sufficiently deep potential well, the energy spectrum should have discrete levels, and a strong impact on the surface of a condensed medium, experiments show, generates a set of the structure elements of the same type at several intermediate scales. As in quantum mechanics during the propagation of a pulse in an inhomogeneous medium with dispersion, wave packets of elastic-plastic waves are formed, spread, and interfere.
In this paper, on the basis of the integral model of elastic-plastic waves (12) propagating in a dispersive medium, we formulate the problem of the spectrum of relaxation and delay times that evolve when the wave packet spreads. On the basis of the theory of a special type nonlinear operators depending on parameters [35,36], a variant of the iterative procedure sweeping along the system evolution path is proposed, which can make it possible to calculate the dynamics of turbulent structures in media of different nature at different scale levels.
Unfortunately, we were not able to bring the solution of the formulated problem to a number and to demonstrate a specific result. The fact is that our integral operators working at the mesolevel are much more complicated than in inverse problems of quantum mechanics, since they themselves evolve during the wave propagation. We have proposed only a formulation of the problem, which is a new mathematical object. Methods for solving such problems have not yet been developed. In addition, their solution requires the use of consistent experimental data on the evolution of the wave profiles and wave packets. It is also a very time-consuming and complex technical task that will not be solved soon.
In Ref. [41], a much simpler example of discrete values of the structure sizes is presented. By using the same approach in the case of high-speed shear motion of a condensed medium, it was obtained that chains of vortices of the same size arise near the boundaries. This is indeed a whole complex of new problems that require a lot of effort of many researchers. However, we decided that it is worth showing now that new, non-traditional approaches to their solution that will attract the attention of specialists in various disciplines can be promising and give impetus to new technologies in the future.
Author Contributions
Conceptualization, T.A.K.; methodology, T.A.K.; investigation, T.A.K. and V.M.K.; writing—original draft preparation, T.A.K. and V.M.K.; writing—review and editing, V.M.K.; visualization, V.M.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rudyak, V.Y.; Minakov, A.V. Thermophysical properties of nanofluids. Eur. Phys. J. E 2018, 41, 15. [Google Scholar] [CrossRef]
- Rudyak, V.; Belkin, A. Statistical mechanics of transport processes of fluids under confined conditions. Nanosyst. Phys. Chem. Math. 2015, 6, 366–377. [Google Scholar] [CrossRef]
- Asay, J.R.; Chhabildas, L.C. Paradigms and Challenges in Shock Wave Research. In High-Pressure Compression of Solids VI: Old Paradigms and New Challenges; Horie, Y., Davison, L., Thadhani, N.N., Eds.; Springer: New York, NY, USA, 2003; pp. 57–108. [Google Scholar]
- Panin, V.E.; Egorushkin, V.E.; Panin, A.V. Physical mesomechanics of a deformed solid as a multilevel system. 1. Physical fundamentals of the multilevel approach. Phys. Mesomech. 2006, 9, 9–20. [Google Scholar]
- Makarov, P.V. On the hierarchical nature of deformation and fracture of solids. Phys. Mesomech. 2004, 7, 25–34. [Google Scholar]
- Meshcheryakov, Y.I.; Khantuleva, T.A. Nonequilibrium processes in condensed media. Part 1. Experimental studies in light of nonlocal transport theory. Phys. Mesomech. 2015, 18, 228–243. [Google Scholar] [CrossRef]
- Lebon, G.; Jou, D.; Casas-Vazquez, J. Understanding Non-Equilibrium Thermodynamics; Springer: Berlin, Germany, 2008. [Google Scholar]
- Haken, H. Information and Self-Organization. A Macroscopic Approach to Complex Systems; Springer: Berlin, Germany, 2006. [Google Scholar]
- Nicolis, G.; Prigogine, I. Self-Organization in Nonequilibrium Systems. From Dissipative Structure to Order through Fluctuations; Wiley: New York, NY, USA, 1977. [Google Scholar]
- Lee, J. The universal role of turbulence in the propagation of strong shocks and detonation waves. In High-Pressure Compression of Solids VI: Old Paradigms and New Challenges; Horie, Y., Davison, L., Thadhani, N.N., Eds.; Springer: New York, NY, USA, 2003; pp. 121–144. [Google Scholar]
- Meshcheryakov, Y.I.; Divakov, A.K.; Zhigacheva, N.I.; Makarevich, I.P.; Barakhtin, B.K. Dynamic structures in shock-loaded copper. Phys. Rev. B 2008, 78, 064301. [Google Scholar] [CrossRef]
- Meshcheryakov, Y.I.; Divakov, A.K.; Zhigacheva, N.I.; Barakhtin, B.K. Regimes of interscale momentum exchange in shock deformed solids. Int. J. Impact Eng. 2013, 57, 99–107. [Google Scholar] [CrossRef]
- Khantuleva, T.A. The shock wave as a nonequilibrium transport process. In High-Pressure Compression of Solids VI: Old Paradigms and New Challenges; Horie, Y., Davison, L., Thadhani, N.N., Eds.; Springer: New York, NY, USA, 2003; pp. 215–254. [Google Scholar]
- Khantuleva, T.A. Self-organization at the mesolevel at high-rate deformation of condensed media. Khim. Fiz. 2005, 24, 36–48. [Google Scholar]
- Morozov, V.; Kats, V.; Savenkov, G.; Lukin, A. Mechanisms of fracture of ring samples made of FCC metals on loading with magnetic-pulse method. AIP Conf. Proc. 2018, 1959, 100006. [Google Scholar]
- Morozov, V.A.; Bogatko, V.I.; Atroshenko, S.A.; Kats, V.M.; Gazizullina, A.R. Loading, Deformation, and destruction of cylindrical samples of polymethylmethacrylate and fluoroplastic using an electric explosion of conductors. Tech. Phys. 2020, 65, 221–225. [Google Scholar] [CrossRef]
- Chabildas, L.C.; Trott, W.M.; Reinhart, W.D.; Cogar, J.R.; Mann, G.A. Incipient spall studies in tantalum—Microstructural effects. AIP Conf. Proc. 2002, 620, 483–486. [Google Scholar]
- Furnish, M.D.; Trott, W.M.; Mason, J.; Podsednik, J.; Reinhart, W.D.; Hall, C. Assessing mesoscale material response via high resolution line-imaging VISAR. AIP Conf. Proc. 2003, 706, 1159–1163. [Google Scholar]
- Swegle, J.W.; Grady, D.E. Shock velocity and the prediction of shock-wave times. J. Appl. Phys. 1985, 58, 692–699. [Google Scholar] [CrossRef]
- Gilman, J.J. Mechanical states of solids. AIP Conf. Proc. 2002, 620, 36–41. [Google Scholar]
- Gilman, J.J. Response of condensed matter to impact. In High-Pressure Compression of Solids VI: Old Paradigms and New Challenges; Horie, Y., Davison, L., Thadhani, N.N., Eds.; Springer: New York, NY, USA, 2003; pp. 279–296. [Google Scholar]
- Meshcheryakov, Y.I.; Atroshenko, S.A. Multiscale rotations in dynamically deformed solids. Int. J. Solids Struct. 1992, 29, 2761–2778. [Google Scholar] [CrossRef]
- Meshcheryakov, Y.I.; Divakov, A.K. Multiscale kinetics and strain-rate dependence of materials. Dymat J. 1994, 1, 271–287. [Google Scholar]
- Panin, V.E. (Ed.) Physical Mesomechanics and Computer-Aided Design of Materials; Nauka: Novosibirsk, Russia, 1995. [Google Scholar]
- Panin, V.E. Foundations of physical mesomechanics. Phys. Mesomech. 1998, 1, 5–20. [Google Scholar]
- Zubarev, D.N. Non-Equilibrium Statistical Thermodynamics; Springer: New York, NY, USA, 1974. [Google Scholar]
- Khantuleva, T.A. Nonlocal Theory of Nonequilibrium Transport Processes; St Petersburg University Publishing: St Petersburg, Russia, 2013. (In Russian) [Google Scholar]
- Khantuleva, T.A. Thermodynamic evolution far from equilibrium. AIP Conf. Proc. 2018, 1959, 100003. [Google Scholar]
- Khantuleva, T.A. On the description of non-equilibrium transport processes and formation of dynamic structures in liquid media. Fundam. Prikl. Gidrofiz. 2020, 13, 3–14. [Google Scholar]
- Khantuleva, T.A.; Meshcheryakov, Y.I. Mesoscale plastic flow instability in a solid under high-rate deformation. Phys. Mesomech. 2017, 20, 417–424. [Google Scholar] [CrossRef]
- Khantuleva, T.; Shalymov, D. Modelling non-equilibrium thermodynamic systems from the speed-gradient principle. Philos. Trans. Royal Soc. A 2017, 375, 20160220. [Google Scholar] [CrossRef] [PubMed]
- Bogoliubov, N.N. Problems of Dynamic Theory in Statistical Physics; Technical Information Service: Oak Ridge, TN, USA, 1960. [Google Scholar]
- Jaynes, E. The Maximum Entropy Formalism; MIT: Cambridge, MA, USA, 1979. [Google Scholar]
- Fradkov, A.L. Cybernetical Physics: From Control of Chaos to Quantum Control; Springer: Berlin, Germany, 2007. [Google Scholar]
- Vavilov, S.A. Geometric methods of studying the solvability of a class of operator equations. Rus. Acad. Sci. Dokl. Math. 1992, 45, 276–280. [Google Scholar]
- Vavilov, S.A. On the solvability of one class of boundary value problems. Differ. Integral Equ. 1990, 3, 175–179. [Google Scholar]
- Ivanov, M.G. How to Understand Quantum Mechanics; R&C Dynamics: Moscow-Izhevsk, Russia, 2012. (In Russian) [Google Scholar]
- Chaoqun, L.; Yonghua, Y.; Ping, L. Physics of turbulence generation and sustenance in a boundary layer. Comput. Fluids 2014, 102, 353–384. [Google Scholar]
- Ravichandran, G.; Rosakis, A.J.; Hodovany, J.; Rosakis, P. On the convention of plastic work into heat during high-strain-rate deformation. AIP Conf. Proc. 2002, 620, 557–562. [Google Scholar]
- Fradkov, A.L.; Khantuleva, T.A. Cybernetic model of the shock induced wave evolution in solids. Procedia Struct. Integrity 2016, 2, 994–1001. [Google Scholar] [CrossRef]
- Khantuleva, T.; Shalymov, D. Nonlocal hydrodynamic modeling high-rate shear processes in condensed matter. J. Phys. Conf. Ser. 2020, 1560, 012057. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).