Neutron Star Mergers: Probing the EoS of Hot, Dense Matter by Gravitational Waves
Abstract
1. Introduction
2. The New Era of Multi-Messenger Gravitational Wave Astronomy
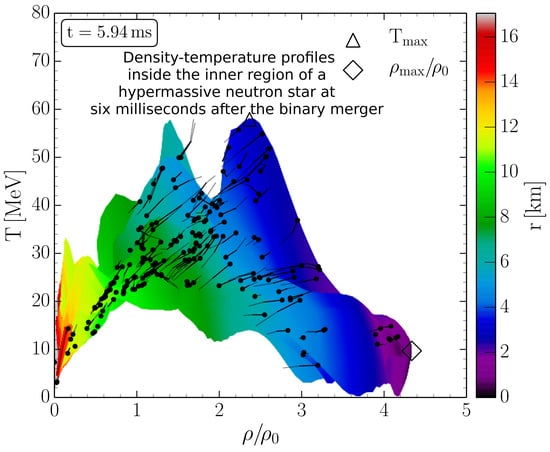
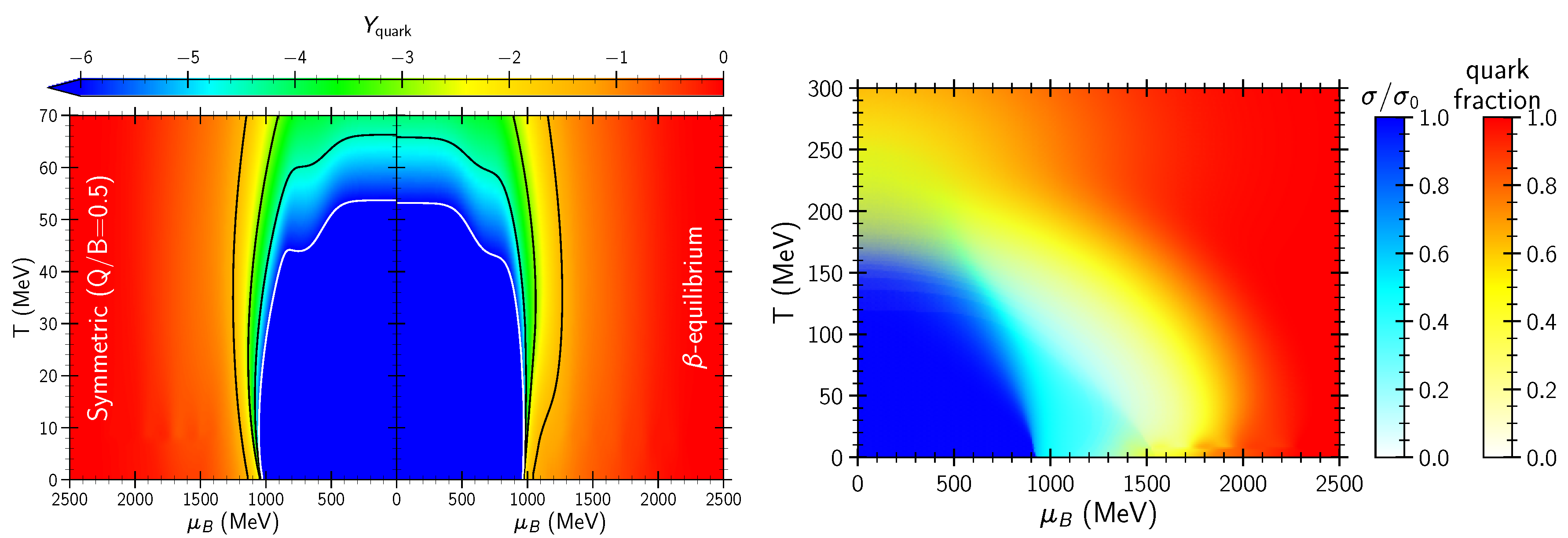
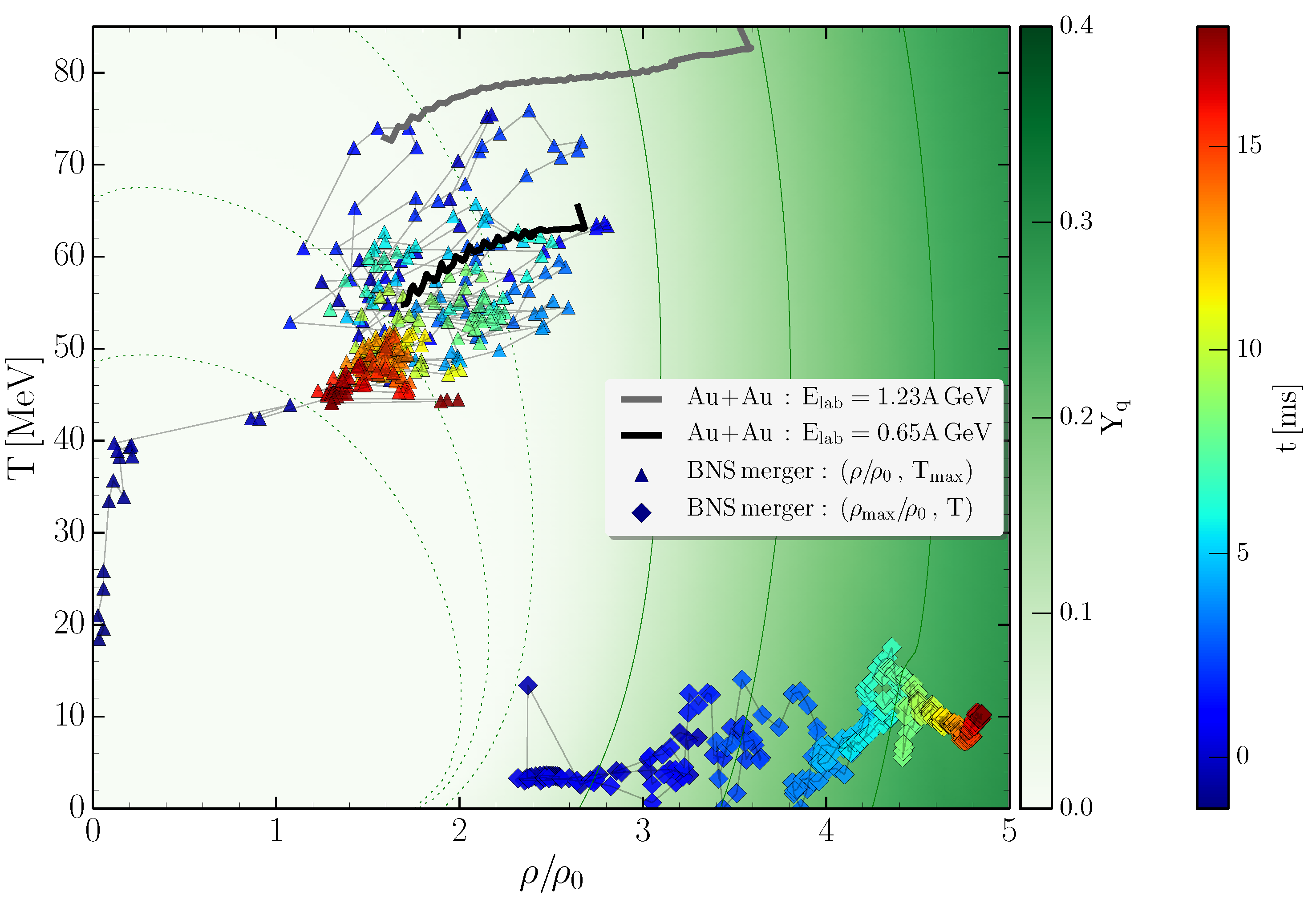
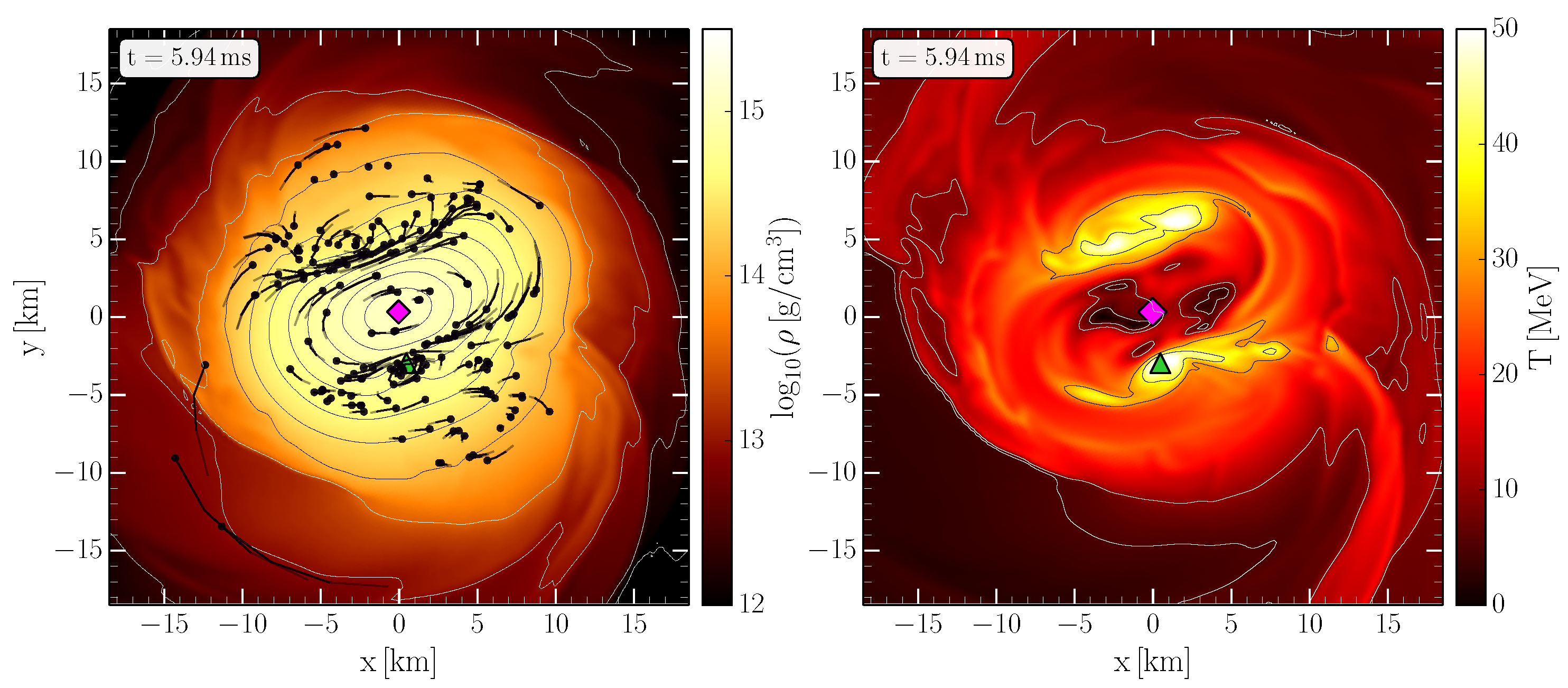
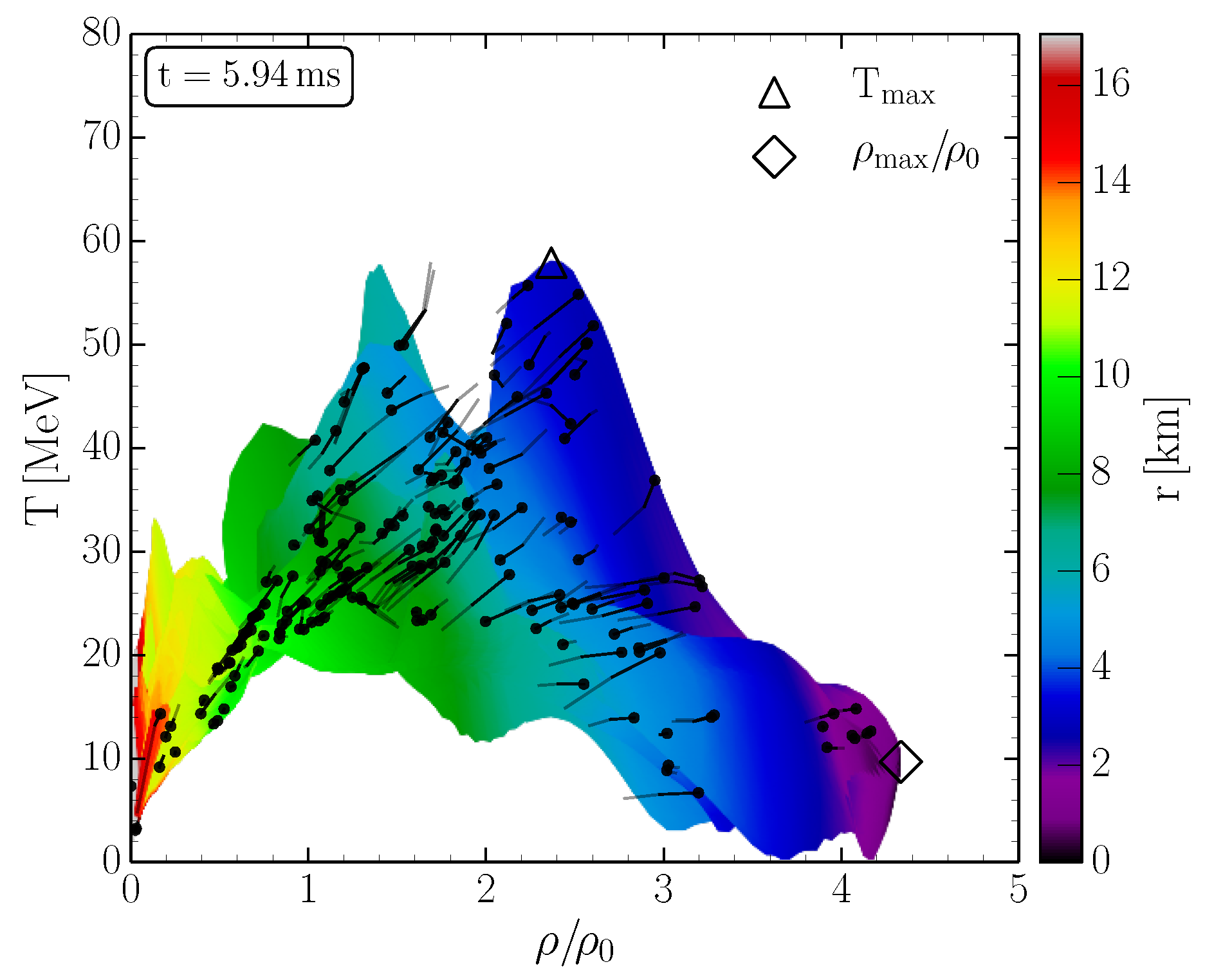
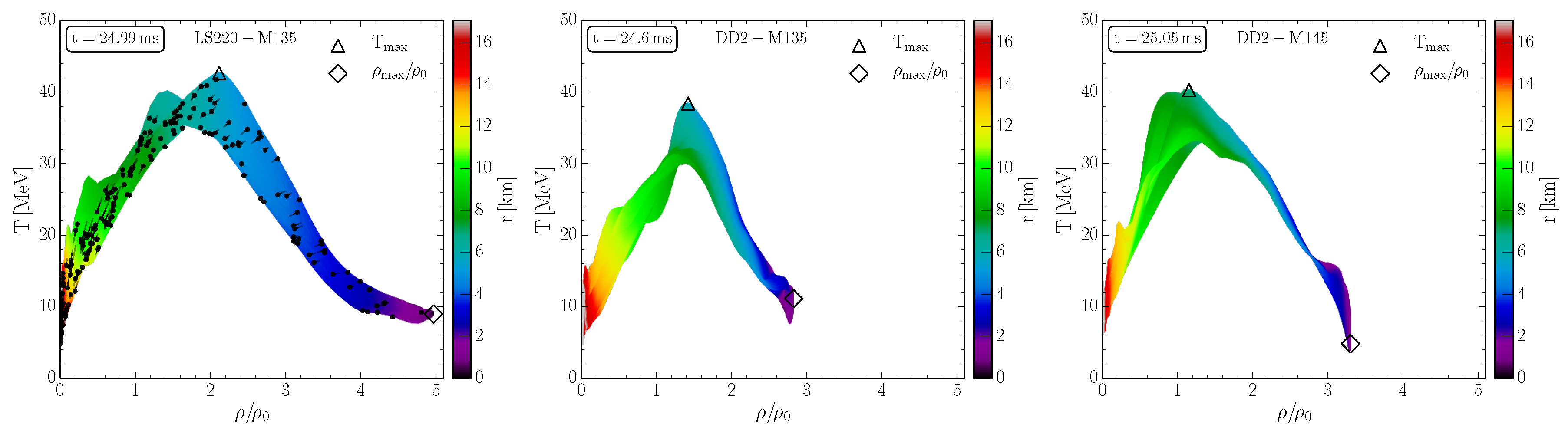
3. Numerical Relativity of Neutron Star Mergers and the Phase Diagram of QCD
4. Summary and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Borsanyi, S.; Endrodi, G.; Fodor, Z.; Jakovac, A.; Katz, S.D.; Krieg, S.; Ratti, C.; Szabo, K.K. The QCD equation of state with dynamical quarks. J. High Energy Phys. 2010, 11, 77. [Google Scholar] [CrossRef]
- Bazavov, A.; Petreczky, P. Deconfinement and chiral transition with the highly improved staggered quark (HISQ) action. J. Phys. Conf. Ser. 2010, 230, 012014. [Google Scholar] [CrossRef]
- Gazdzicki, M.; NA49 Collaboration. Report from NA49. J. Phys. G 2004, 30, S701–S708. [Google Scholar] [CrossRef]
- Gazdzicki, M.; Gorenstein, M.I. On the early stage of nucleus-nucleus collisions. Acta Phys. Pol. 1999, B30, 2705. [Google Scholar]
- Adams, J.; Aggarwal, M.M.; Ahammed, Z.; Amonett, J.; Anderson, B.D.; Arkhipkin, D.; Averichev, G.S.; Badyal, S.K.; Bai, Y.; Balewski, J.; et al. Experimental and theoretical challenges in the search for the quark gluon plasma: The STAR Collaboration’s critical assessment of the evidence from RHIC collisions. Nucl. Phys. 2005, A757, 102–183. [Google Scholar] [CrossRef]
- Arsene, I.; Bearden, I.G.; Beavis, D.; Besliu, C.; Budick, B.; Bøggild, H.; Chasman, C.; Christensen, C.H.; Christiansen, P.; Cibor, J.; et al. Quark gluon plasma and color glass condensate at RHIC? The Perspective from the BRAHMS experiment. Nucl. Phys. A 2005, 757, 1–27. [Google Scholar] [CrossRef]
- Adcox, K.; Adler, S.S.; Afanasiev, S.; Aidala, C.; Ajitanand, N.N.; Akiba, Y.; Al-Jamel, A.; Alexander, J.; Amirikas, R.; Aoki, K.; et al. Formation of dense partonic matter in relativistic nucleus-nucleus collisions at RHIC: Experimental evaluation by the PHENIX collaboration. Nucl. Phys. A 2005, 757, 184–283. [Google Scholar] [CrossRef]
- Aamodt, K.; Quintana, A.A.; Adamová, D.; Adare, A.M.; Aggarwal, M.M.; Rinella, G.A.; Agocs, A.G.; Salazar, S.A.; Ahammed, Z.; Ahmad, N.; et al. Centrality dependence of the charged-particle multiplicity density at mid-rapidity in Pb-Pb collisions at = 2.76 TeV. Phys. Rev. Lett. 2011, 106, 032301. [Google Scholar] [CrossRef] [PubMed]
- Aamodt, K.; Abelev, B.; Quintana, A.A.; Adamova, D.; Adare, A.M.; Aggarwal, M.M.; Rinella, G.A.; Agocs, A.G.; Salazar, S.A.; Ahammed, Z.; et al. Elliptic flow of charged particles in Pb-Pb collisions at 2.76 TeV. Phys. Rev. Lett. 2010, 105, 252302. [Google Scholar] [CrossRef]
- Aamodt, K.; Alice Collaboration. Charged-particle multiplicity density at mid-rapidity in central Pb-Pb collisions at = 2.76 TeV. Phys. Rev. Lett. 2010, 105, 252301. [Google Scholar] [CrossRef]
- Csernai, L.P.; Magas, V.K.; Wang, D.J. Flow vorticity in peripheral high-energy heavy-ion collisions. Phys. Rev. C 2013, 87, 034906. [Google Scholar] [CrossRef]
- Adamczyk, L.; STAR Collaboration. Global Λ hyperon polarization in nuclear collisions. Nature 2017, 548, 62–65. [Google Scholar] [CrossRef] [PubMed]
- Papazoglou, P.; Schramm, S.; Schaffner-Bielich, J.; Stöcker, H.; Greiner, W. Chiral Lagrangian for strange hadronic matter. Phys. Rev. C 1998, 57, 2576. [Google Scholar] [CrossRef]
- Papazoglou, P.; Zschiesche, D.; Schramm, S.; Schaffner-Bielich, J.; Stöcker, H.; Greiner, W. Nuclei in a chiral SU (3) model. Phys. Rev. C 1999, 59, 411. [Google Scholar] [CrossRef]
- Glendenning, N. Compact Stars: Nuclear Physics, Particle Physics, and General Relativity; Astronomy and Astrophysics Library; Springer: New York, NY, USA, 2000. [Google Scholar]
- Weber, F. Pulsars as Astrophysical Laboratories for Nuclear and Particle Physics; IoP: Bristol, UK, 1999. [Google Scholar]
- Hanauske, M. Properties of Compact Stars within QCD-Motivated Models. Ph.D. Thesis, J.W. Goethe-University, Frankfurt, Germany, 2004. [Google Scholar]
- Steinheimer, J.; Schramm, S.; Stöcker, H. An effective chiral hadron-quark equation of state. J. Phys. G Nucl. Phys. 2011, 38, 035001. [Google Scholar] [CrossRef]
- Steinheimer, J.; Schramm, S.; Stöcker, H. Hadronic SU(3) parity doublet model for dense matter and its extension to quarks and the strange equation of state. Phys. Rev. C 2011, 84, 045208. [Google Scholar] [CrossRef]
- Mukherjee, A.; Steinheimer, J.; Schramm, S. Higher-order baryon number susceptibilities: Interplay between the chiral and the nuclear liquid-gas transitions. Phys. Rev. C 2017, 96, 025205. [Google Scholar] [CrossRef]
- Motornenko, A.; Vovchenko, V.; Steinheimer, J.; Schramm, S.; Stoecker, H. QCD at high density: Equation of state for nuclear collisions and neutron stars. In Proceedings of the 27th International Conference on Ultrarelativistic Nucleus-Nucleus Collisions (Quark Matter 2018), Venice, Italy, 14–19 May 2018. [Google Scholar]
- Most, E.R.; Papenfort, L.J.; Dexheimer, V.; Hanauske, M.; Schramm, S.; Stöcker, H.; Rezzolla, L. Signatures of quark-hadron phase transitions in general-relativistic neutron-star mergers. arXiv, 2018; arXiv:1807.03684. [Google Scholar]
- Bauswein, A.; Bastian, N.U.F.; Blaschke, D.B.; Chatziioannou, K.; Clark, J.A.; Fischer, T.; Oertel, M. Identifying a first-order phase transition in neutron star mergers through gravitational waves. arXiv, 2018; arXiv:1809.01116. [Google Scholar]
- Hanauske, M.; Takami, K.; Bovard, L.; Rezzolla, L.; Font, J.A.; Galeazzi, F.; Stöcker, H. Rotational properties of hypermassive neutron stars from binary mergers. Phys. Rev. D 2017, 96, 043004. [Google Scholar] [CrossRef]
- Baiotti, L.; Rezzolla, L. Binary neutron-star mergers: A review of Einstein’s richest laboratory. Rep. Prog. Phys. 2017, 80, 096901. [Google Scholar] [CrossRef] [PubMed]
- Dietrich, T.; Ujevic, M. Modeling dynamical ejecta from binary neutron star mergers and implications for electromagnetic counterparts. Class. Quantum Gravity 2017, 34, 105014. [Google Scholar] [CrossRef]
- Dietrich, T.; Ujevic, M.; Tichy, W.; Bernuzzi, S.; Brügmann, B. Gravitational waves and mass ejecta from binary neutron star mergers: Effect of the mass ratio. Phys. Rev. D 2017, 95, 024029. [Google Scholar] [CrossRef]
- Kastaun, W.; Ciolfi, R.; Giacomazzo, B. Structure of stable binary neutron star merger remnants: A case study. Phys. Rev. D 2016, 94, 044060. [Google Scholar] [CrossRef]
- Siegel, D.M.; Ciolfi, R. Electromagnetic Emission from Long-lived Binary Neutron Star Merger Remnants. I. Formulation of the Problem. Astrophys. J. 2016, 819, 14. [Google Scholar] [CrossRef]
- Siegel, D.M.; Ciolfi, R. Electromagnetic Emission from Long-lived Binary Neutron Star Merger Remnants. II. Lightcurves and Spectra. Astrophys. J. 2016, 819, 15. [Google Scholar] [CrossRef]
- Siegel, D.M.; Metzger, B.D. Three-Dimensional General-Relativistic Magnetohydrodynamic Simulations of Remnant Accretion Disks from Neutron Star Mergers: Outflows and r-Process Nucleosynthesis. Phys. Rev. Lett. 2017, 119, 231102. [Google Scholar] [CrossRef] [PubMed]
- Bauswein, A.; Stergioulas, N. Semi-analytic derivation of the threshold mass for prompt collapse in binary neutron-star mergers. Mon. Not. R. Astron. Soc. 2017, 471, 4956–4965. [Google Scholar] [CrossRef]
- Radice, D.; Bernuzzi, S.; Del Pozzo, W.; Roberts, L.F.; Ott, C.D. Probing Extreme-density Matter with Gravitational-wave Observations of Binary Neutron Star Merger Remnants. Astrophys. J. Lett. 2017, 842, L10. [Google Scholar] [CrossRef]
- Radice, D.; Perego, A.; Hotokezaka, K.; Fromm, S.A.; Bernuzzi, S.; Roberts, L.F. Binary Neutron Star Mergers: Mass Ejection, Electromagnetic Counterparts and Nucleosynthesis. arXiv, 2018; arXiv:1809.11161. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration; The Virgo Collaboration. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed]
- Bauswein, A.; Just, O.; Janka, H.T.; Stergioulas, N. Neutron-star Radius Constraints from GW170817 and Future Detections. Astrophys. J. Lett. 2017, 850, L34. [Google Scholar] [CrossRef]
- Rezzolla, L.; Most, E.R.; Weih, L.R. Using Gravitational-wave Observations and Quasi-universal Relations to Constrain the Maximum Mass of Neutron Stars. Astrophys. J. Lett. 2018, 852, L25. [Google Scholar] [CrossRef]
- Margalit, B.; Metzger, B.D. Constraining the Maximum Mass of Neutron Stars from Multi-messenger Observations of GW170817. Astrophys. J. Lett. 2017, 850, L19. [Google Scholar] [CrossRef]
- Paschalidis, V.; Yagi, K.; Alvarez-Castillo, D.; Blaschke, D.B.; Sedrakian, A. Implications from GW170817 and I-Love-Q relations for relativistic hybrid stars. Phys. Rev. D 2018, 97, 084038. [Google Scholar] [CrossRef]
- Most, E.R.; Weih, L.R.; Rezzolla, L.; Schaffner-Bielich, J. New Constraints on Radii and Tidal Deformabilities of Neutron Stars from GW170817. Phys. Rev. Lett. 2018, 120, 261103. [Google Scholar] [CrossRef] [PubMed]
- De, S.; Finstad, D.; Lattimer, J.M.; Brown, D.A.; Berger, E.; Biwer, C.M. Tidal Deformabilities and Radii of Neutron Stars from the Observation of GW170817. Phys. Rev. Lett. 2018, 121, 091102. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration; The Virgo Collaboration. GW170817: Measurements of Neutron Star Radii and Equation of State. Phys. Rev. Lett. 2018, 121, 161101. [Google Scholar] [CrossRef]
- Abbott, B.; Abbott, R.; Abbott, T.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.; Adya, V.; et al. Properties of the binary neutron star merger GW170817. arXiv, 2018; arXiv:1805.11579. [Google Scholar]
- Christian, J.E.; Zacchi, A.; Schaffner-Bielich, J. Signals in the tidal deformability for phase transitions in compact stars with constraints from GW170817. arXiv, 2018; arXiv:1809.03333. [Google Scholar]
- The LIGO Scientific Collaboration; the Virgo Collaboration; Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; et al. Search for post-merger gravitational waves from the remnant of the binary neutron star merger GW170817. arXiv, 2017; arXiv:1710.09320. [Google Scholar]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Gravitational Waves and Gamma-Rays from a Binary Neutron Star Merger: GW170817 and GRB 170817A. Astrophys. J. Lett. 2017, 848, L13. [Google Scholar] [CrossRef]
- Goldstein, A.; Veres, P.; Burns, E.; Briggs, M.; Hamburg, R.; Kocevski, D.; Wilson-Hodge, C.; Preece, R.; Poolakkil, S.; Roberts, O.; et al. An ordinary short gamma-ray burst with extraordinary implications: Fermi-GBM detection of GRB 170817A. Astrophys. J. Lett. 2017, 848, L14. [Google Scholar] [CrossRef]
- Papenfort, L.J.; Gold, R.; Rezzolla, L. Dynamical ejecta and nucleosynthetic yields from eccentric binary neutron-star mergers. arXiv, 2018; arXiv:1807.03795. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration; the Virgo Collaboration; Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; et al. Multi-messenger Observations of a Binary Neutron Star Merger. Astrophys. J. Lett. 2017, 848, L12. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration; The Virgo Collaboration; Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; et al. Estimating the Contribution of Dynamical Ejecta in the Kilonova Associated with GW170817. arXiv, 2017; arXiv:1710.05836. [Google Scholar]
- Rezzolla, L.; Takami, K. Gravitational-wave signal from binary neutron stars: A systematic analysis of the spectral properties. Phys. Rev. D 2016, 93, 124051. [Google Scholar] [CrossRef]
- Hanauske, M.; Steinheimer, J.; Bovard, L.; Mukherjee, A.; Schramm, S.; Takami, K.; Papenfort, J.; Wechselberger, N.; Rezzolla, L.; Stöcker, H. Concluding Remarks: Connecting Relativistic Heavy Ion Collisions and Neutron Star Mergers by the Equation of State of Dense Hadron-and Quark Matter as signalled by Gravitational Waves. J. Phys. 2017, 878, 012031. [Google Scholar] [CrossRef]
- Janka, H.T.; Zwerger, T.; Mönchmeyer, R. Does artificial viscosity destroy prompt type-II supernova explosions? Astron. Astrophys. 1993, 268, 360–368. [Google Scholar]
- Read, J.S.; Lackey, B.D.; Owen, B.J.; Friedman, J.L. Constraints on a phenomenologically parametrized neutron-star equation of state. Phys. Rev. D 2009, 79, 124032. [Google Scholar] [CrossRef]
- Takami, K.; Rezzolla, L.; Baiotti, L. Spectral properties of the post-merger gravitational-wave signal from binary neutron stars. Phys. Rev. D 2015, 91, 064001. [Google Scholar] [CrossRef]
- Alford, M.; Braby, M.; Paris, M.; Reddy, S. Hybrid Stars that Masquerade as Neutron Stars. Astrophys. J. 2005, 629, 969–978. [Google Scholar] [CrossRef]
- Stergioulas, N.; Bauswein, A.; Zagkouris, K.; Janka, H.T. Gravitational waves and non-axisymmetric oscillation modes in mergers of compact object binaries. Mon. Not. R. Astron. Soc. 2011, 418, 427–436. [Google Scholar] [CrossRef]
- Bernuzzi, S.; Nagar, A.; Balmelli, S.; Dietrich, T.; Ujevic, M. Quasiuniversal Properties of Neutron Star Mergers. Phys. Rev. Lett. 2014, 112, 201101. [Google Scholar] [CrossRef]
- Takami, K.; Rezzolla, L.; Baiotti, L. Constraining the Equation of State of Neutron Stars from Binary Mergers. Phys. Rev. Lett. 2014, 113, 091104. [Google Scholar] [CrossRef] [PubMed]
- Bauswein, A.; Stergioulas, N. Unified picture of the post-merger dynamics and gravitational wave emission in neutron star mergers. Phys. Rev. D 2015, 91, 124056. [Google Scholar] [CrossRef]
- Hanauske, M.; Bovard, L. Neutron star mergers in the context of the hadron-quark phase transition. J. Astrophys. Astron. 2018, 39, 45. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Swesty, F.D. A Generalized Equation of State for Hot, Dense Matter. Nucl. Phys. A 1991, 535, 331–376. [Google Scholar] [CrossRef]
- Bovard, L.; Rezzolla, L. On the use of tracer particles in simulations of binary neutron stars. Class. Quantum Gravity 2017, 34, 215005. [Google Scholar] [CrossRef]
- Alford, M.G.; Bovard, L.; Hanauske, M.; Rezzolla, L.; Schwenzer, K. Viscous Dissipation and Heat Conduction in Binary Neutron-Star Mergers. Phys. Rev. Lett. 2018, 120, 041101. [Google Scholar] [CrossRef]
- Bovard, L.; Martin, D.; Guercilena, F.; Arcones, A.; Rezzolla, L.; Korobkin, O. On r-process nucleosynthesis from matter ejected in binary neutron star mergers. Phys. Rev. D 2017, 96, 124005. [Google Scholar] [CrossRef]
- Rischke, D.H.; Bernard, S.; Maruhn, J.A. Relativistic hydrodynamics for heavy ion collisions. 1. General aspects and expansion into vacuum. Nucl. Phys. 1995, A595, 346–382. [Google Scholar] [CrossRef]
- Hanauske, M.; Yilmaz, Z.S.; Mitropoulos, C.; Rezzolla, L.; Stöcker, H. Gravitational waves from binary compact star mergers in the context of strange matter. In Proceedings of the 17th International Conference on Strangeness in Quark Matter (SQM 2017), Utrecht, The Netherlands, 10–15 July 2017; Volume 171, p. 20004. [Google Scholar] [CrossRef]
- Hanauske, M.; Greiner, W. Neutron Star Properties in a QCD-Motivated Model. Gen. Relat. Gravitat. 2001, 33, 739–755. [Google Scholar] [CrossRef]
- Hanauske, M.; Zschiesche, D.; Eichmann, U.; Satarov, L.M.; Mishustin, I.N.; Schaffner-Bielich, J.; Stoecker, H.; Greiner, W. Theory of Compact Stars. In Proceedings of the XEUS—Studying the Evolution of the Hot Universe, MPE Garching, Germany, 11–13 March 2002; MPE Report 281. Hasinger, G., Boller, T., Parmer, A.N., Eds.; 2003; p. 277. [Google Scholar]
- Hanauske, M. How to detect the Quark-Gluon Plasma with Telescopes. In GSI Annual Report; GSI: Darmstadt, Germany, 2003; p. 96. [Google Scholar]
- Glendenning, N.K.; Pei, S.; Weber, F. Signal of quark deconfinement in the timing structure of pulsar spin-down. Phys. Rev. Lett. 1997, 79, 1603. [Google Scholar] [CrossRef]
- Banik, S.; Hanauske, M.; Bandyopadhyay, D.; Greiner, W. Rotating compact stars with exotic matter. Phys. Rev. D 2004, 70, 123004. [Google Scholar] [CrossRef]
- Banik, S.; Hanauske, M.; Bandyopadhyay, D. Strange matter in rotating compact stars. J. Phys. G Nucl. Phys. 2005, 31, S841–S848. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Ghosh, S.K.; Hanauske, M.; Raha, S. Rotating twin stars and signature of quark-hadron phase transition. Phys. Rev. C 2005, 71, 048801. [Google Scholar] [CrossRef]
- Glendenning, N.K.; Kettner, C. Nonidentical neutron star twins. Astron. Astrophys. 2000, 353, L9. [Google Scholar]
- Mishustin, I.N.; Hanauske, M.; Bhattacharyya, A.; Satarov, L.M.; Stöcker, H.; Greiner, W. Catastrophic rearrangement of a compact star due to the quark core formation. Phys. Lett. B 2003, 552, 1–8. [Google Scholar] [CrossRef]
- Alford, M.; Sedrakian, A. Compact Stars with Sequential QCD Phase Transitions. Phys. Rev. Lett. 2017, 119, 161104. [Google Scholar] [CrossRef]
- Shovkovy, I.; Hanauske, M.; Huang, M. Nonstrange hybrid compact stars with color superconducting matter. Phys. Rev. D 2003, 67, 103004. [Google Scholar] [CrossRef]
- Dexheimer, V.A.; Schramm, S. Novel approach to modeling hybrid stars. Phys. Rev. C 2010, 81, 045201. [Google Scholar] [CrossRef]
- Fischer, T.; Bastian, N.U.F.; Wu, M.R.; Baklanov, P.; Sorokina, E.; Blinnikov, S.; Typel, S.; Klähn, T.; Blaschke, D.B. Quark deconfinement as a supernova explosion engine for massive blue supergiant stars. Nat. Astron. 2018, 2, 980–986. [Google Scholar] [CrossRef]
- Montana, G.; Tolos, L.; Hanauske, M.; Rezzolla, L. Constraining twin stars with GW170817. arXiv, 2018; arXiv:1811.10929. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hanauske, M.; Steinheimer, J.; Motornenko, A.; Vovchenko, V.; Bovard, L.; Most, E.R.; Papenfort, L.J.; Schramm, S.; Stöcker, H. Neutron Star Mergers: Probing the EoS of Hot, Dense Matter by Gravitational Waves. Particles 2019, 2, 44-56. https://doi.org/10.3390/particles2010004
Hanauske M, Steinheimer J, Motornenko A, Vovchenko V, Bovard L, Most ER, Papenfort LJ, Schramm S, Stöcker H. Neutron Star Mergers: Probing the EoS of Hot, Dense Matter by Gravitational Waves. Particles. 2019; 2(1):44-56. https://doi.org/10.3390/particles2010004
Chicago/Turabian StyleHanauske, Matthias, Jan Steinheimer, Anton Motornenko, Volodymyr Vovchenko, Luke Bovard, Elias R. Most, L. Jens Papenfort, Stefan Schramm, and Horst Stöcker. 2019. "Neutron Star Mergers: Probing the EoS of Hot, Dense Matter by Gravitational Waves" Particles 2, no. 1: 44-56. https://doi.org/10.3390/particles2010004
APA StyleHanauske, M., Steinheimer, J., Motornenko, A., Vovchenko, V., Bovard, L., Most, E. R., Papenfort, L. J., Schramm, S., & Stöcker, H. (2019). Neutron Star Mergers: Probing the EoS of Hot, Dense Matter by Gravitational Waves. Particles, 2(1), 44-56. https://doi.org/10.3390/particles2010004