High-Gradient Cherenkov Radiation Based on a New Dielectric-Loaded Waveguide
Abstract
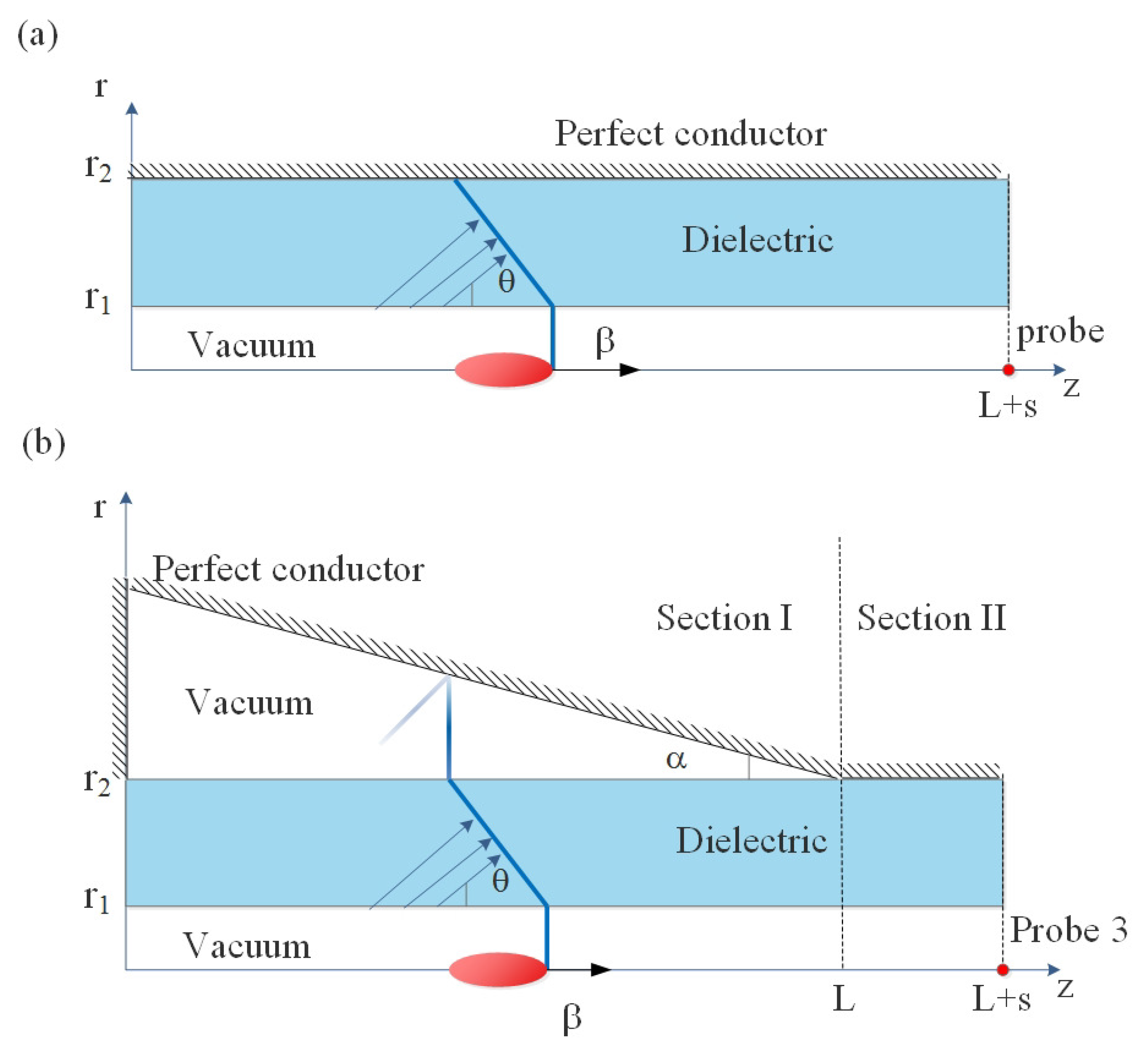
:1. Introduction
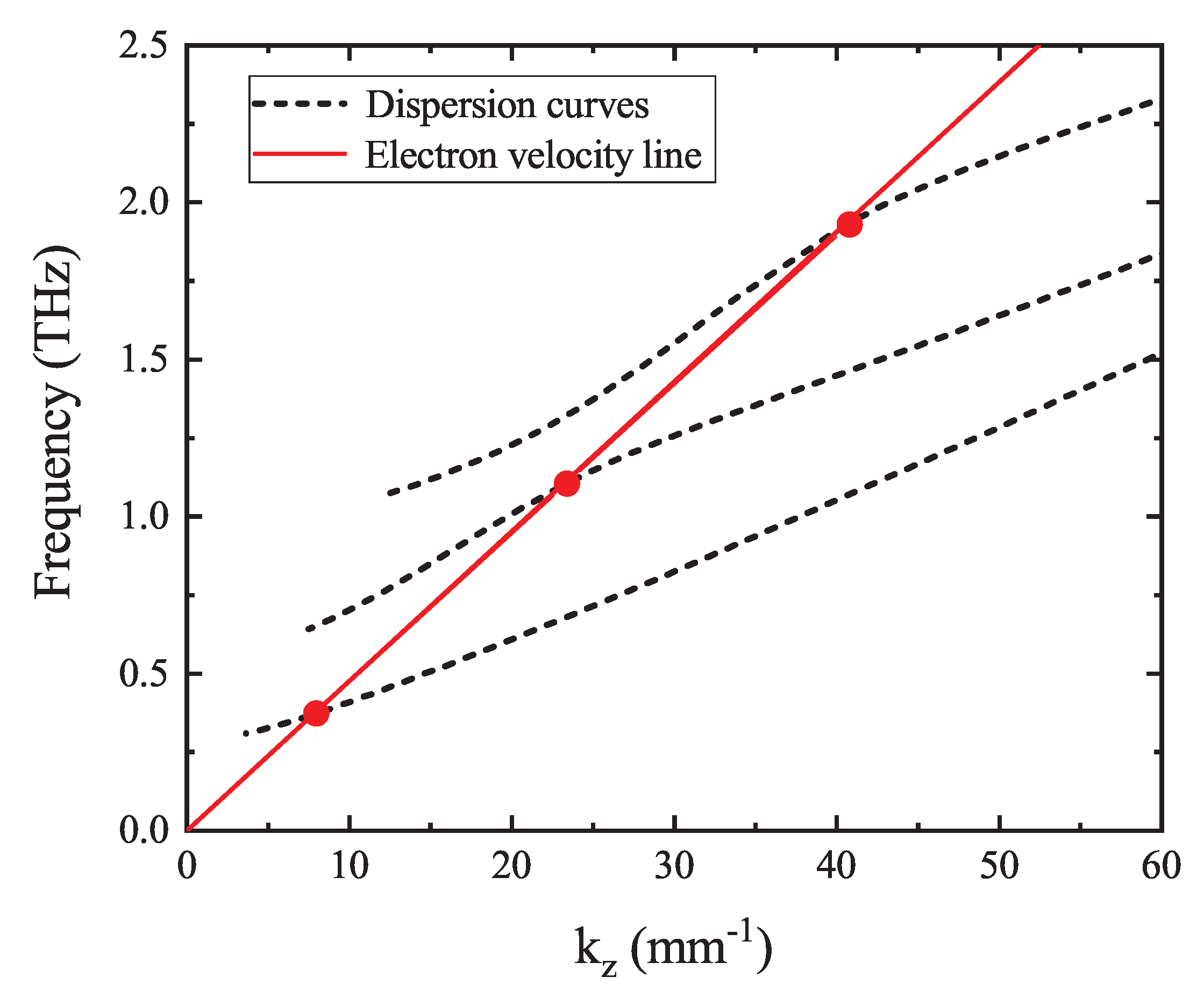
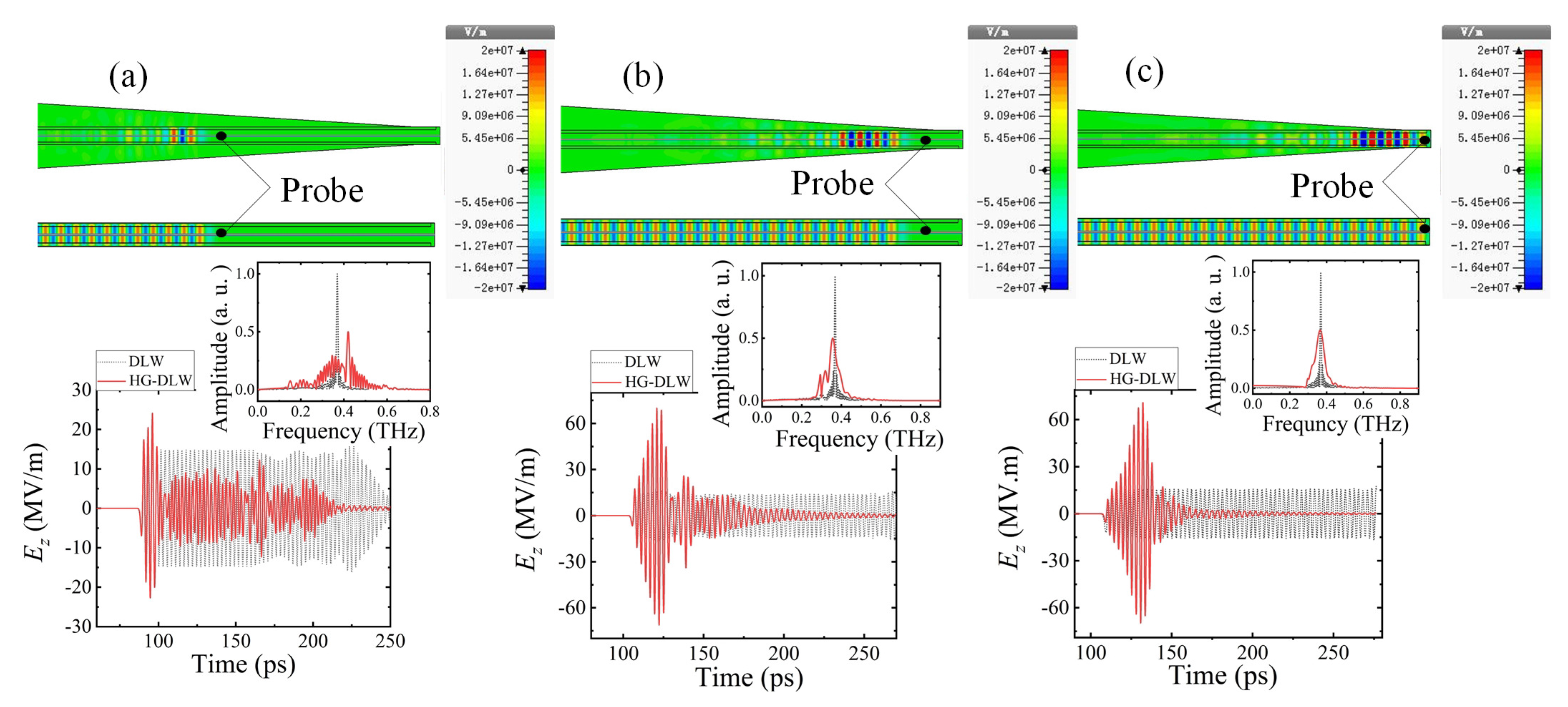
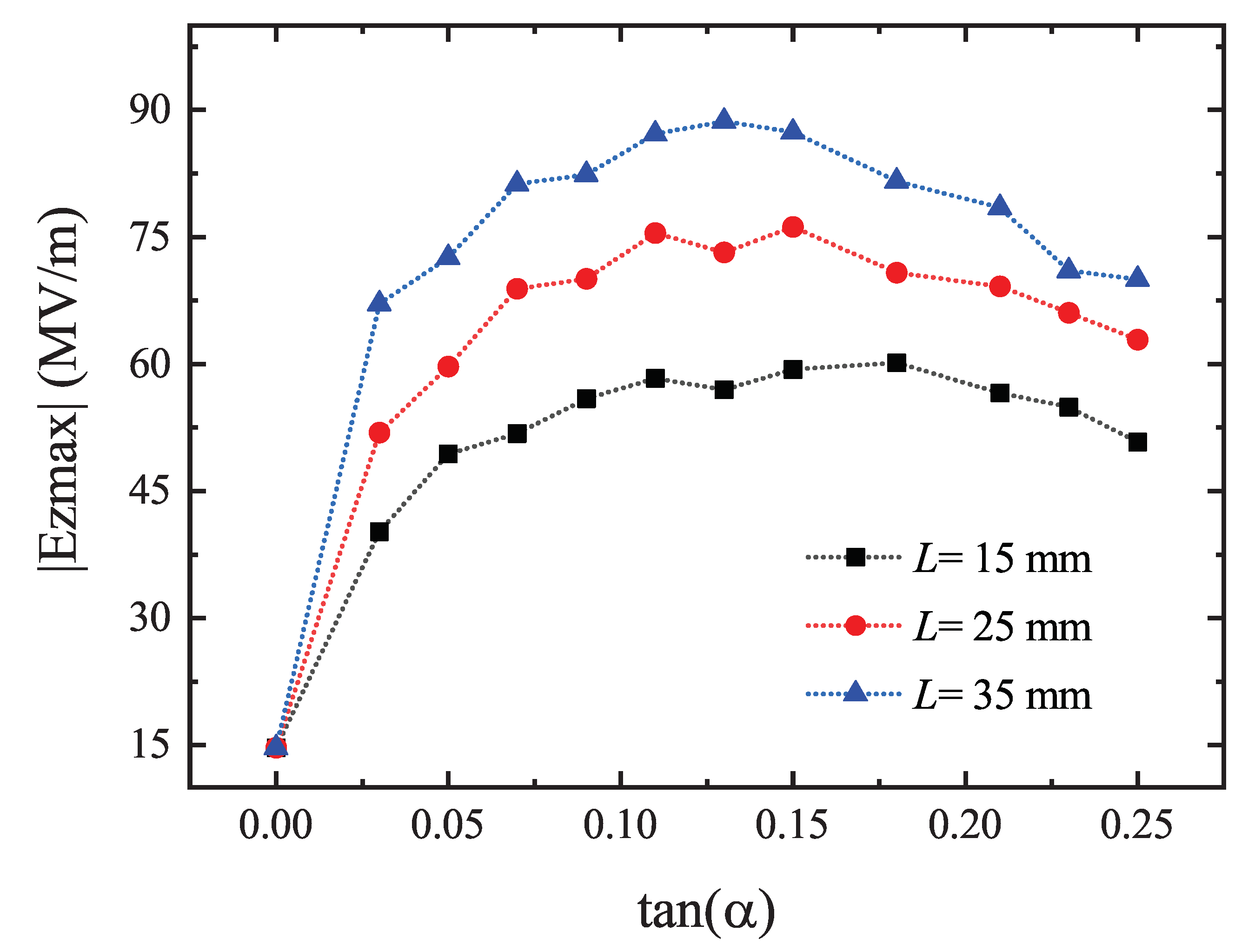
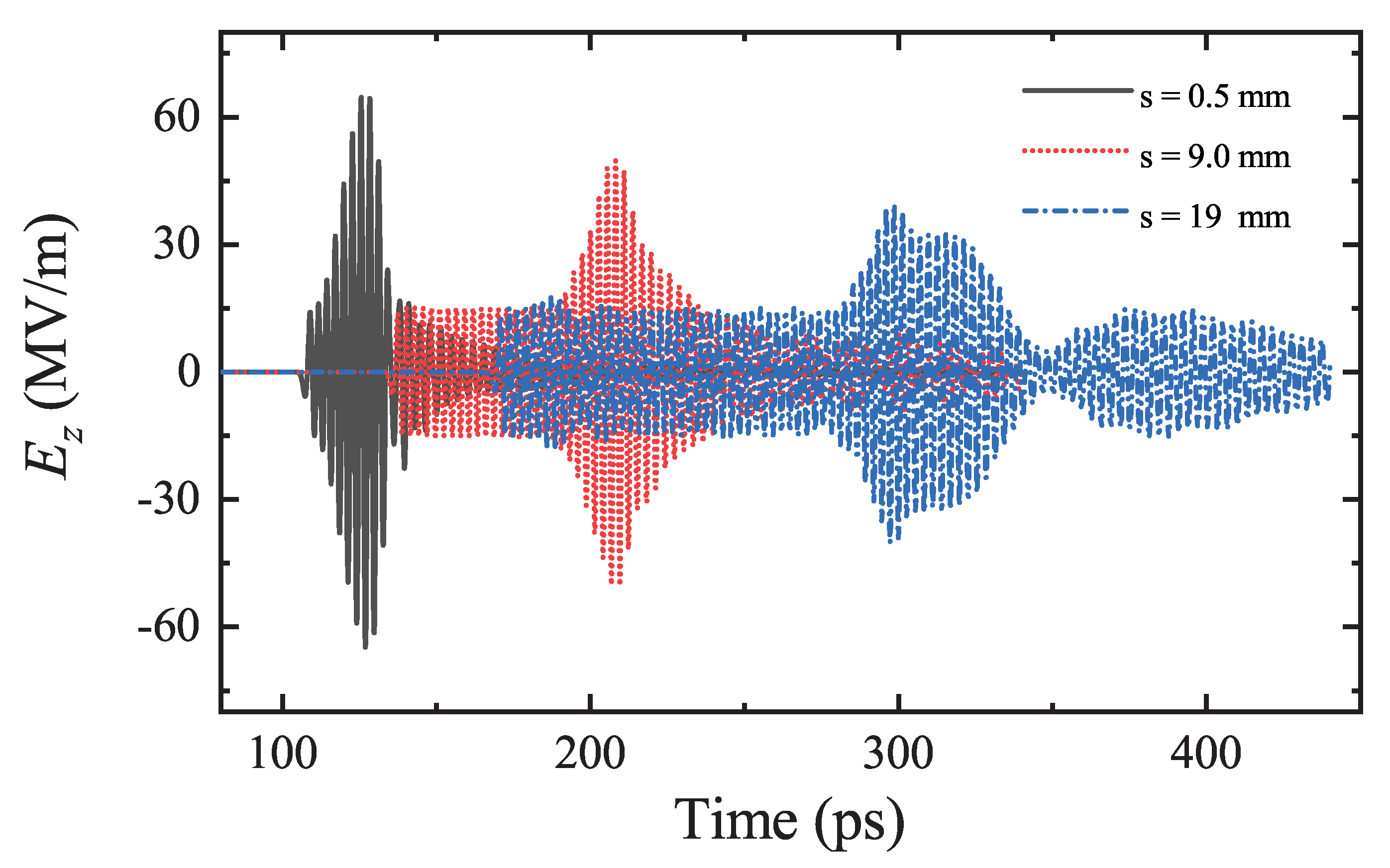
2. Simulation Results
3. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cook, A.; Tikhoplav, R.; Tochitsky, S.Y.; Travish, G.; Williams, O.; Rosenzweig, J. Observation of narrow-band terahertz coherent Cherenkov radiation from a cylindrical dielectric-lined waveguide. Phys. Rev. Lett. 2009, 103, 095003. [Google Scholar] [CrossRef] [PubMed]
- Altmark, A.; Kanareykin, A. The source of THz radiation based on dielectric waveguide excited by sequence of electron bunches. J. Phys. Conf. Ser. 2016, 732, 012037. [Google Scholar] [CrossRef] [Green Version]
- Wiggins, S.; Jaroszynski, D.; McNeil, B.; Robb, G.; Aitken, P.; Phelps, A.; Cross, A.; Ronald, K.; Ginzburg, N.; Shpak, V.; et al. Self-amplification of coherent spontaneous emission in a Cherenkov free-electron maser. Phys. Rev. Lett. 2000, 84, 2393. [Google Scholar] [CrossRef] [PubMed]
- Nie, Y.; Assmann, R.; Dorda, U.; Marchetti, B.; Weikum, M.; Zhu, J.; Hüning, M. Potential applications of the dielectric wakefield accelerators in the SINBAD facility at DESY. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2016, 829, 183–186. [Google Scholar] [CrossRef] [Green Version]
- Jing, C. Dielectric wakefield accelerators. Rev. Accel. Sci. Technol. 2016, 9, 127–149. [Google Scholar] [CrossRef]
- O’Shea, B.; Andonian, G.; Barber, S.; Fitzmorris, K.; Hakimi, S.; Harrison, J.; Hoang, P.; Hogan, M.; Naranjo, B.; Williams, O.; et al. Observation of acceleration and deceleration in gigaelectron-volt-per-metre gradient dielectric wakefield accelerators. Nat. Commun. 2016, 7, 12763. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Antipov, S.; Jing, C.; Kanareykin, A.; Butler, J.E.; Yakimenko, V.; Fedurin, M.; Kusche, K.; Gai, W. Experimental demonstration of wakefield effects in a THz planar diamond accelerating structure. Appl. Phys. Lett. 2012, 100, 132910. [Google Scholar] [CrossRef] [Green Version]
- Antipov, S.; Babzien, M.; Jing, C.; Fedurin, M.; Gai, W.; Kanareykin, A.; Kusche, K.; Yakimenko, V.; Zholents, A. Subpicosecond bunch train production for a tunable mJ level THz source. Phys. Rev. Lett. 2013, 111, 134802. [Google Scholar] [CrossRef] [PubMed]
- Lemery, F.; Piot, P. Ballistic bunching of photoinjected electron bunches with dielectric-lined waveguides. Phys. Rev. Spec. Top.-Accel. Beams 2014, 17, 112804. [Google Scholar] [CrossRef]
- Piot, P. Overview of Alternative Bunching and Current-Shaping Techniques for Low-Energy Electron Beams. Technical Report. 2015. Available online: http://accelconf.web.cern.ch/AccelConf/FEL2015/papers/mod02.pdf (accessed on 24 November 2018).
- Bettoni, S.; Craievich, P.; Lutman, A.; Pedrozzi, M. Temporal profile measurements of relativistic electron bunch based on wakefield generation. Phys. Rev. Accel. Beams 2016, 19, 021304. [Google Scholar] [CrossRef]
- Ferguson, B.; Zhang, X.C. Materials for terahertz science and technology. Nat. Mater. 2002, 1, 26–33. [Google Scholar] [CrossRef] [PubMed]
- Curry, E.; Fabbri, S.; Maxson, J.; Musumeci, P.; Gover, A. Meter-Scale Terahertz-Driven Acceleration of a Relativistic Beam. Phys. Rev. Lett. 2018, 120, 094801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jing, C.; Power, J.; Conde, M.; Liu, W.; Yusof, Z.; Kanareykin, A.; Gai, W. Increasing the transformer ratio at the Argonne wakefield accelerator. Phys. Rev. Spec. Top-Accel. Beams 2011, 14, 021302. [Google Scholar] [CrossRef]
- Wang, D.; Antipov, S.; Jing, C.; Power, J.; Conde, M.; Wisniewski, E.; Liu, W.; Qiu, J.; Ha, G.; Dolgashev, V.; et al. Interaction of an ultrarelativistic electron bunch train with a W-band accelerating structure: High power and high gradient. Phys. Rev. Lett. 2016, 116, 054801. [Google Scholar] [CrossRef] [PubMed]
- Park, S.; Hirshfield, J. Theory of wakefields in a dielectric-lined waveguide. Phys. Rev. E 2000, 62, 1266. [Google Scholar] [CrossRef]
- Baturin, S.; Kanareykin, A. Cherenkov radiation from short relativistic bunches: General approach. Phys. Rev. Lett. 2014, 113, 214801. [Google Scholar] [CrossRef] [PubMed]
- Frank, I.; Tamm, I. Coherent visible radiation of fast electrons passing through matter. In Selected Papers; Springer: New York, NY, USA, 1991; pp. 29–35. [Google Scholar]
- Corp, C. CST PS Tutorials. Available online: http://www.cst-china.cn/ (accessed on 27 October 2018).
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, S.; Li, W.; He, Z.; Jia, Q. High-Gradient Cherenkov Radiation Based on a New Dielectric-Loaded Waveguide. Particles 2018, 1, 279-284. https://doi.org/10.3390/particles1010022
Jiang S, Li W, He Z, Jia Q. High-Gradient Cherenkov Radiation Based on a New Dielectric-Loaded Waveguide. Particles. 2018; 1(1):279-284. https://doi.org/10.3390/particles1010022
Chicago/Turabian StyleJiang, Shimin, Weiwei Li, Zhigang He, and Qika Jia. 2018. "High-Gradient Cherenkov Radiation Based on a New Dielectric-Loaded Waveguide" Particles 1, no. 1: 279-284. https://doi.org/10.3390/particles1010022




