Bulk Viscosity of Hot Quark Plasma from Non-Equilibrium Statistical Operator
Abstract
1. Introduction
2. Bulk Viscosity Formula from the Non-Equilibrium Statistical Operator
2.1. Decomposition into Different Dissipative Processes
2.2. Kubo Formula for the Bulk Viscosity
3. Bulk Viscosity within the Two-Flavor NJL Model
Resummation of the Feynman Diagrams
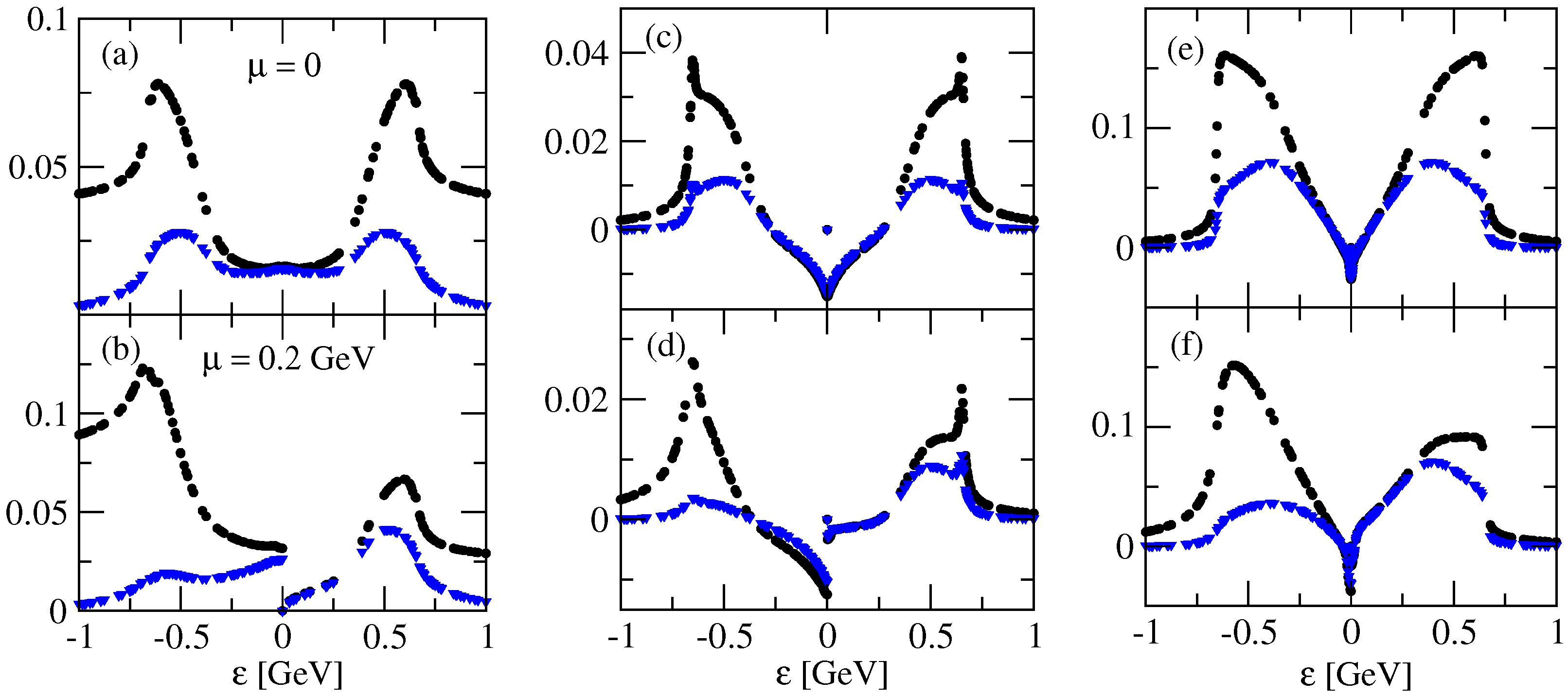
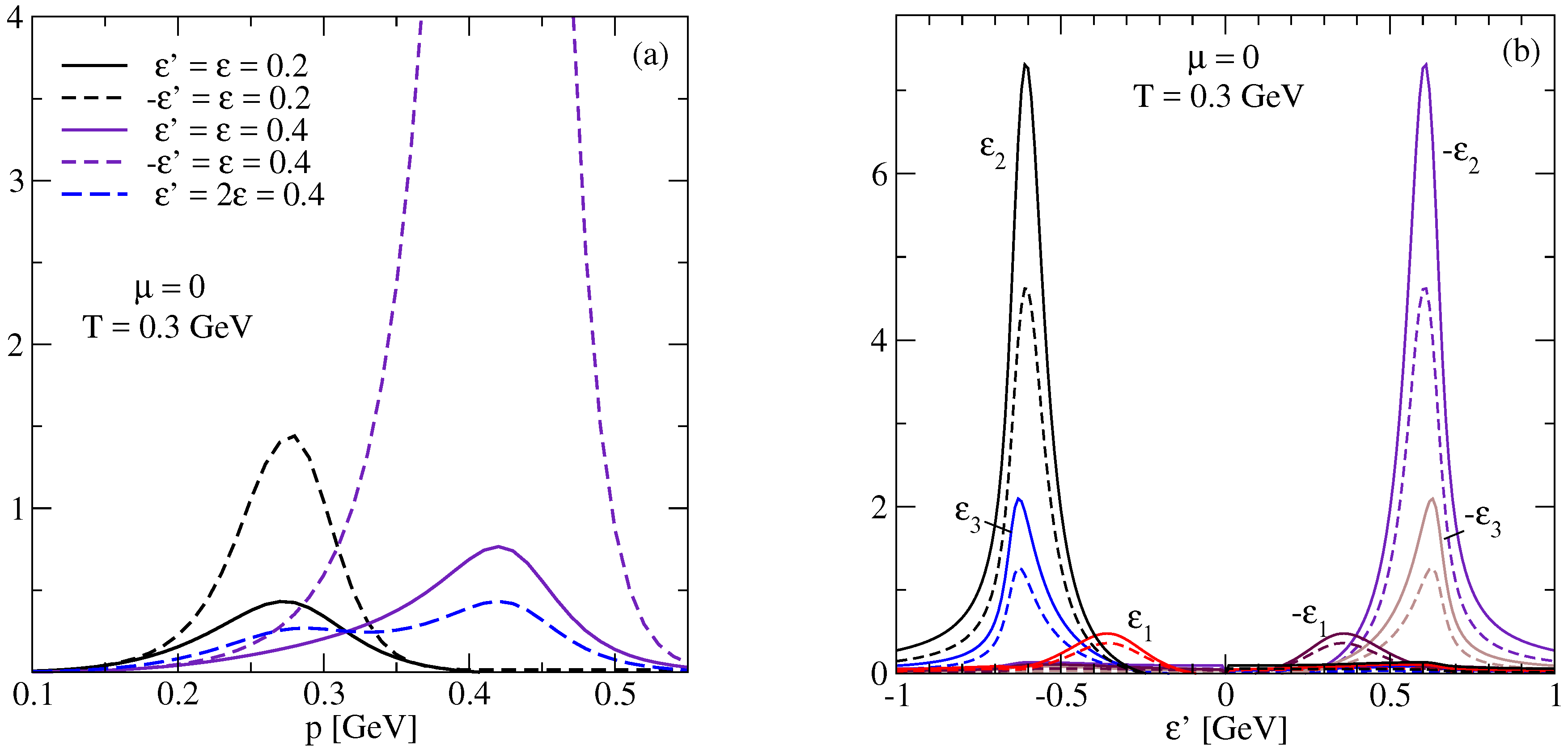
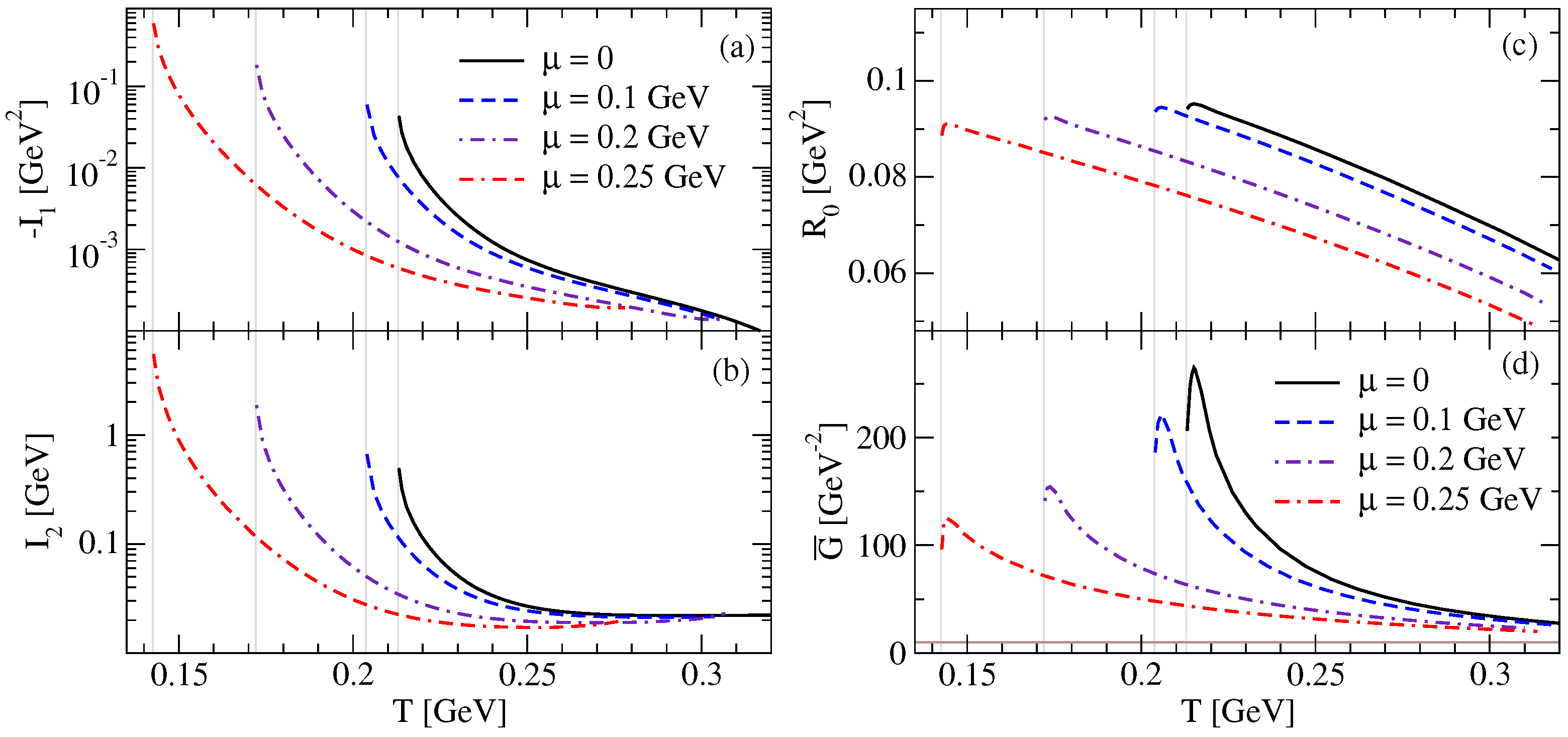
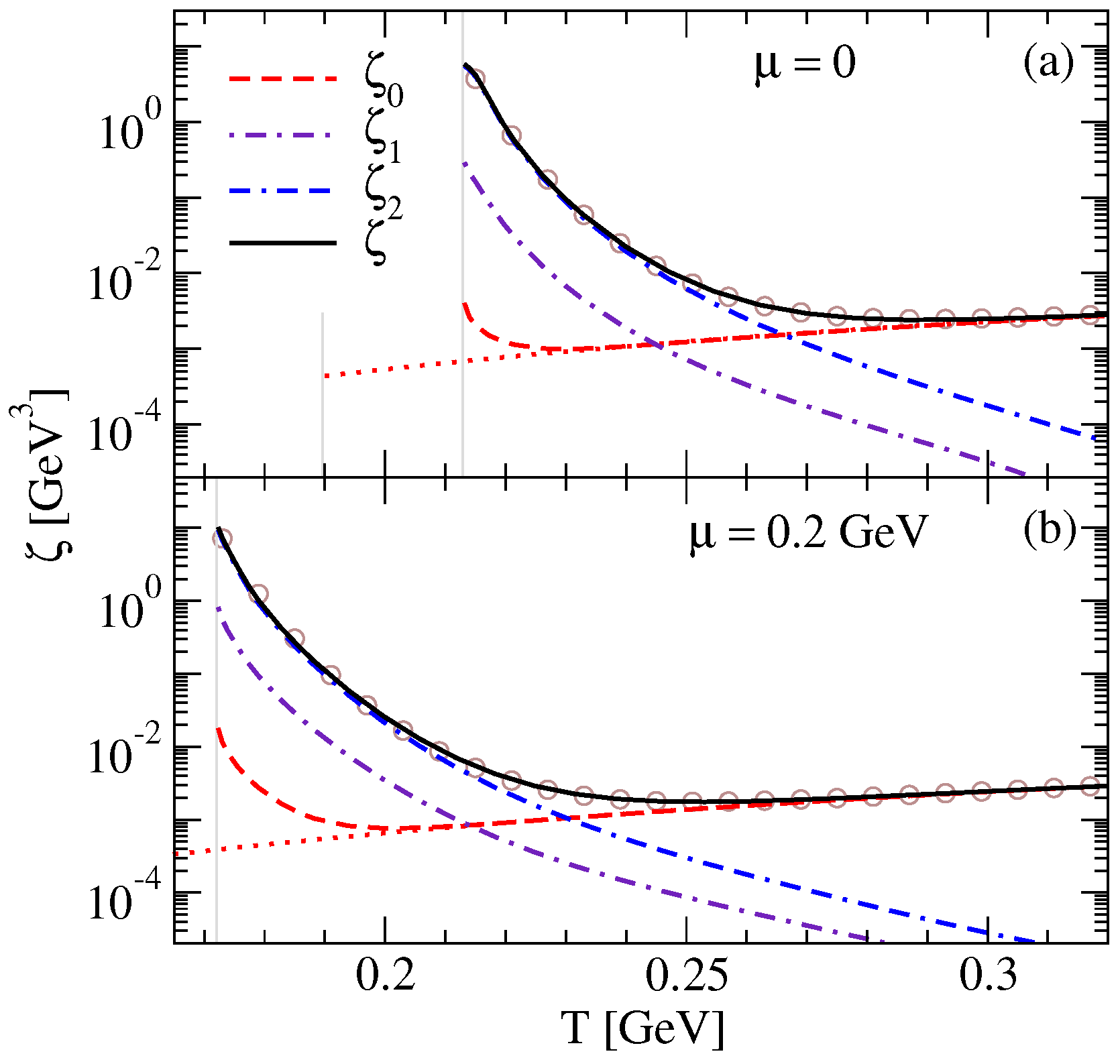
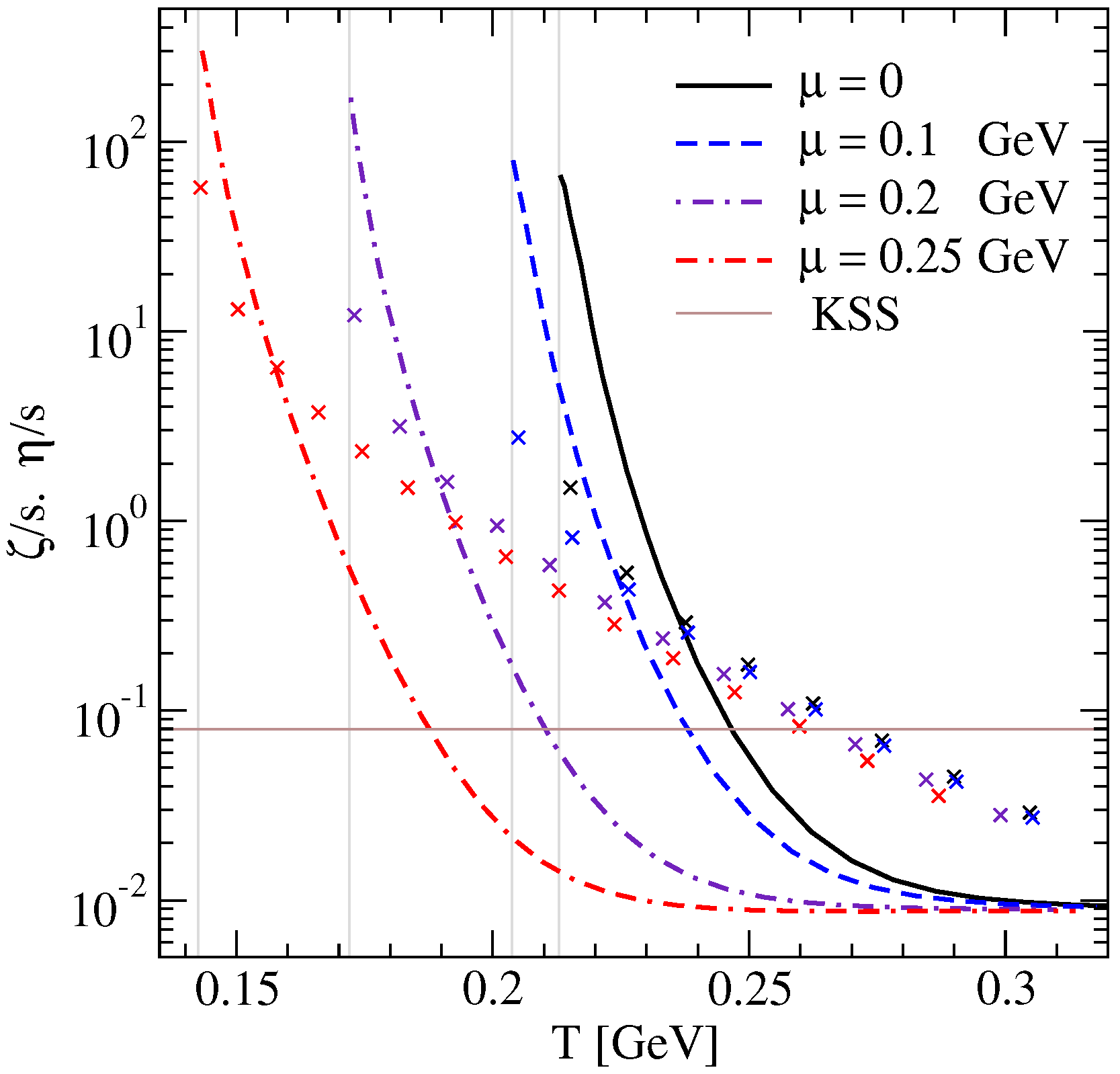
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
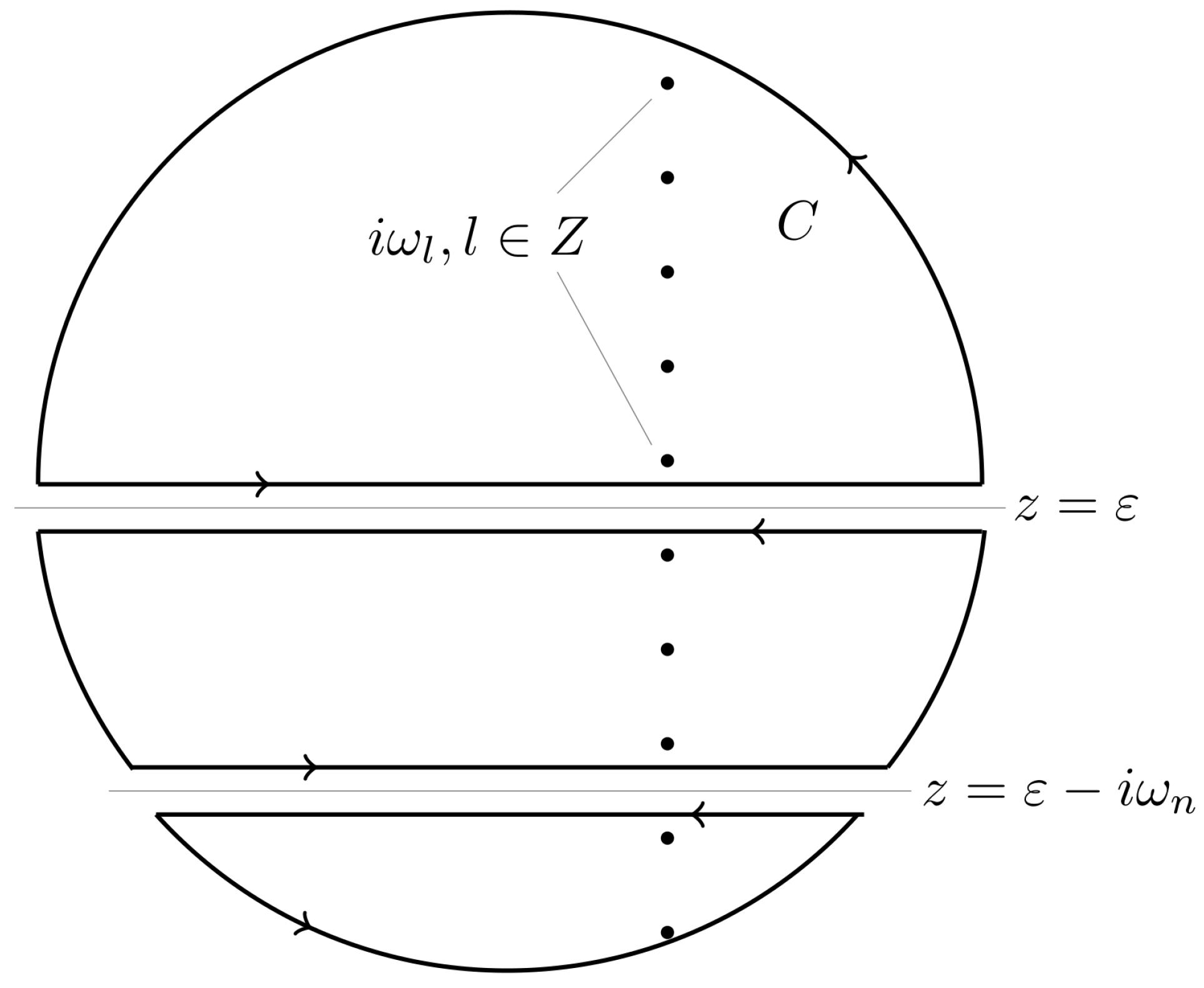
Appendix A. Matsubara Summations
References
- Danielewicz, P.; Gyulassy, M. Dissipative phenomena in quark-gluon plasmas. Phys. Rev. D 1985, 31, 53–62. [Google Scholar] [CrossRef]
- Kovtun, P.; Son, D.; Starinets, A. Viscosity in Strongly Interacting Quantum Field Theories from Black Hole Physics. Phys. Rev. Lett. 2005, 94, 111601. [Google Scholar] [CrossRef] [PubMed]
- Hosoya, A.; Kajantie, K. Transport coefficients of QCD matter. Nucl. Phys. B 1985, 250, 666–688. [Google Scholar] [CrossRef]
- Arnold, P.; Doǧan, Ç.; Moore, G.D. Bulk viscosity of high-temperature QCD. Phys. Rev. D 2006, 74, 085021. [Google Scholar] [CrossRef]
- Moore, G.; Saremi, O. Bulk viscosity and spectral functions in QCD. Phys. Rev. D 2008, 9, 015. [Google Scholar] [CrossRef]
- Chen, J.-W.; Liu, Y.-F.; Song, Y.-K.; Wang, Q. Shear and bulk viscosities of a weakly coupled quark gluon plasma with finite chemical potential and temperature: Leading-log results. Phys. Rev. D 2013, 87, 036002. [Google Scholar] [CrossRef]
- Meyer, H. Calculation of the Bulk Viscosity in SU(3) Gluodynamics. Phys. Rev. D 2008, 100, 162001. [Google Scholar] [CrossRef] [PubMed]
- Paech, K.; Pratt, S. Origins of bulk viscosity in relativistic heavy ion collisions. Phys. Rev. C 2006, 74, 014901. [Google Scholar] [CrossRef]
- Karsch, F.; Kharzeev, D.; Tuchin, K. Universal properties of bulk viscosity near the QCD phase transition. Phys. Lett. B 2008, 663, 217–221. [Google Scholar] [CrossRef]
- Aarts, G. Transport and spectral functions in high-temperature QCD. arXiv, 2007; arXiv:0710.0739. [Google Scholar]
- Sasaki, C.; Redlich, K. Transport coefficients near chiral phase transition. Nucl. Phys. A 2010, 832, 62–75. [Google Scholar] [CrossRef]
- Chakraborty, P.; Kapusta, J. Quasiparticle theory of shear and bulk viscosities of hadronic matter. Phys. Rev. C 2011, 83, 014906. [Google Scholar] [CrossRef]
- Chandra, V. Bulk viscosity of anisotropically expanding hot QCD plasma. Phys. Rev. D 2011, 84, 09402. [Google Scholar] [CrossRef]
- Dobado, A.; Llanes-Estrada, F.; Torres-Rincon, J. Bulk viscosity and energy-momentum correlations in high energy hadron collisions. Eur. Phys. J. C 2012, 72, 1873. [Google Scholar] [CrossRef]
- Marty, R.; Bratkovskaya, E.; Cassing, W.; Aichelin, J.; Berrehrah, H. Transport coefficients from the Nambu-Jona-Lasinio model for SU(3)f. Phys. Rev. C 2013, 88, 045204. [Google Scholar] [CrossRef]
- Harutyunyan, A.; Sedrakian, A. Bulk viscosity of two-flavor quark matter from the Kubo formalism. Phys. Rev. D 2017, 96, 034006. [Google Scholar] [CrossRef]
- Xiao, S.-S.; Guo, P.-P.; Zhang, L.; Hou, D.-F. Bulk viscosity of hot dense Quark matter in the PNJL model. Chin. Phys. C 2014, 38, 054101. [Google Scholar] [CrossRef]
- Ghosh, S.; Peixoto, T.; Roy, V.; Serna, F.; Krein, G. Shear and bulk viscosities of quark matter from quark-meson fluctuations in the Nambu-Jona-Lasinio model. Phys. Rev. C 2016, 93, 045205. [Google Scholar] [CrossRef]
- Harutyunyan, A.; Rischke, D.H.; Sedrakian, A. Transport coefficients of two-flavor quark matter from the Kubo formalism. Phys. Rev. D 2017, 95, 114021. [Google Scholar] [CrossRef]
- Zubarev, D. Nonequilibrium Statistical Thermodynamics; Studies in Soviet Science; Consultants Bureau: New York, NY, USA, 1974. [Google Scholar]
- Zubarev, D.; Morozov, V.; Röpke, G. Statistical Mechanics of Nonequilibrium Processes; Akademie Verlag: Berlin, Germany, 1996. [Google Scholar]
- Quack, E.; Klevansky, S. Effective 1/Nc expansion in the Nambu-Jona-Lasinio model. Phys. Rev. C 1994, 49, 3283–3288. [Google Scholar] [CrossRef]
- Hosoya, A.; Sakagami, M.A.; Takao, M. Nonequilibrium thermodynamics in field theory: Transport coefficients. Ann. Phys. 1984, 154, 229–252. [Google Scholar] [CrossRef]
- Huang, X.G.; Sedrakian, A.; Rischke, D.H. Kubo formulas for relativistic fluids in strong magnetic fields. Ann. Phys. 2011, 326, 3075–3094. [Google Scholar] [CrossRef]
- Landau, L.; Lifshitz, E. Fluid Mechanics; Butterworth-Heinemann: Oxford, UK, 1987. [Google Scholar]
- Eckart, C. The Thermodynamics of Irreversible Processes. III. Relativistic theory of the simple fluid. Phys. Rev. 1940, 58, 919–924. [Google Scholar] [CrossRef]
- Zubarev, D.; Tishchenko, S. Nonlocal hydrodynamics with memory. Physica 1972, 59, 285–304. [Google Scholar] [CrossRef]
- Mori, H. Statistical-Mechanical Theory of Transport in Fluids. Phys. Rev. 1958, 112, 1829–1842. [Google Scholar] [CrossRef]
- Dusling, K.; Schäfer, T. Bulk viscosity, particle spectra, and flow in heavy-ion collisions. Phys. Rev. C 2012, 85, 044909. [Google Scholar] [CrossRef]
- Jeon, S. Hydrodynamic transport coefficients in relativistic scalar field theory. Phys. Rev. D 1995, 52, 3591–3642. [Google Scholar] [CrossRef]
- De Groot, S.; Mazur, P. Non-Equilibrium Thermodynamics; North-Holland Publishing Company: Amsterdam, The Netherlands, 1962. [Google Scholar]
- Lang, R.; Kaiser, N.; Weise, W. Shear viscosities from Kubo formalism in a large-Nc Nambu–Jona-Lasinio model. Eur. Phys. J. A 2015, 51, 127. [Google Scholar] [CrossRef]
- Lang, R.; Weise, W. Shear viscosity from Kubo formalism: NJL model study. Eur. Phys. J. A 2014, 50, 63. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Harutyunyan, A.; Sedrakian, A. Bulk Viscosity of Hot Quark Plasma from Non-Equilibrium Statistical Operator. Particles 2018, 1, 212-229. https://doi.org/10.3390/particles1010016
Harutyunyan A, Sedrakian A. Bulk Viscosity of Hot Quark Plasma from Non-Equilibrium Statistical Operator. Particles. 2018; 1(1):212-229. https://doi.org/10.3390/particles1010016
Chicago/Turabian StyleHarutyunyan, Arus, and Armen Sedrakian. 2018. "Bulk Viscosity of Hot Quark Plasma from Non-Equilibrium Statistical Operator" Particles 1, no. 1: 212-229. https://doi.org/10.3390/particles1010016
APA StyleHarutyunyan, A., & Sedrakian, A. (2018). Bulk Viscosity of Hot Quark Plasma from Non-Equilibrium Statistical Operator. Particles, 1(1), 212-229. https://doi.org/10.3390/particles1010016





