Analysis of Displacement Transmissibility and Bifurcation Behavior in Nonlinear Systems with Friction and Nonlinear Spring
Abstract
1. Introduction
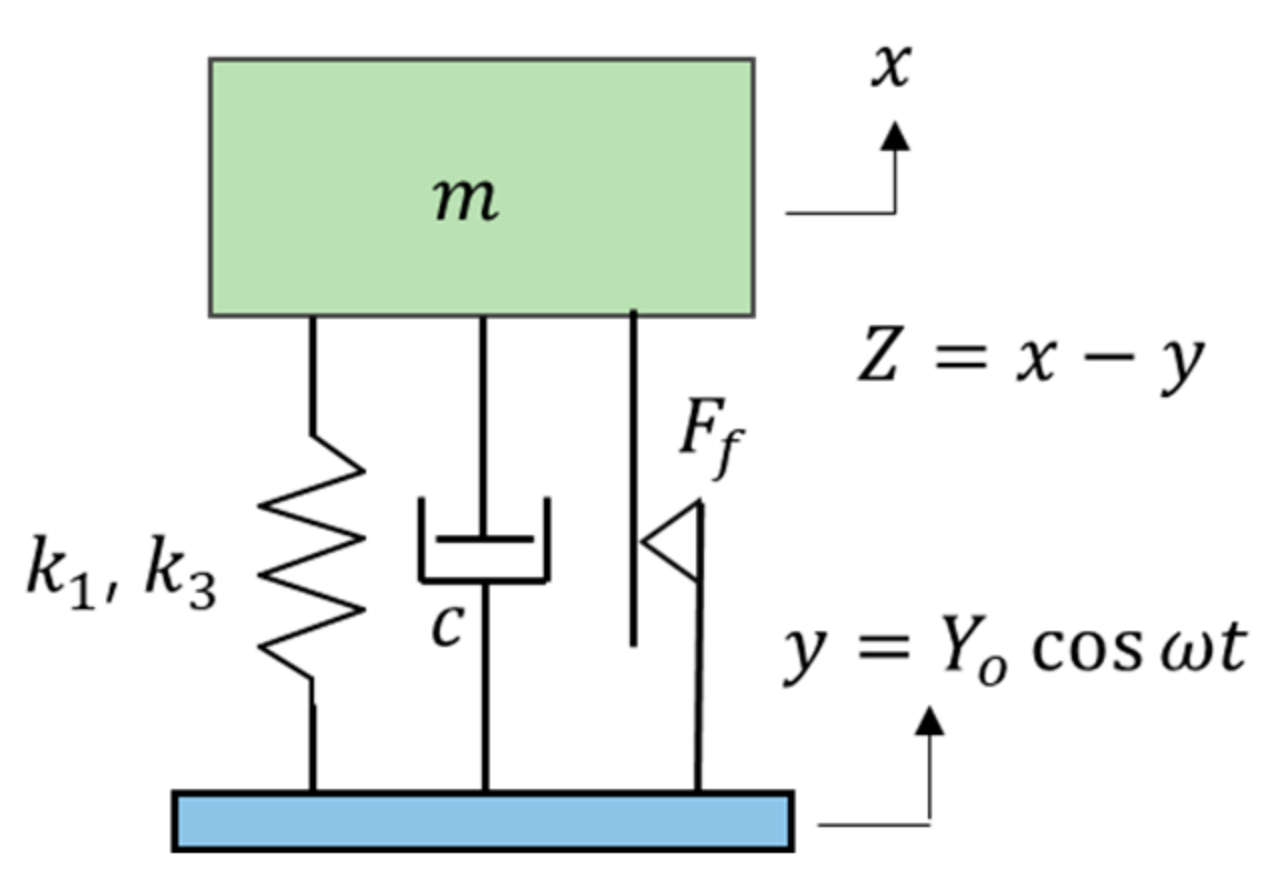
2. Equation of Motion for Base Exited System
3. Response Analysis of Nonlinear Isolation System for Base Excited
4. Results and Discussion
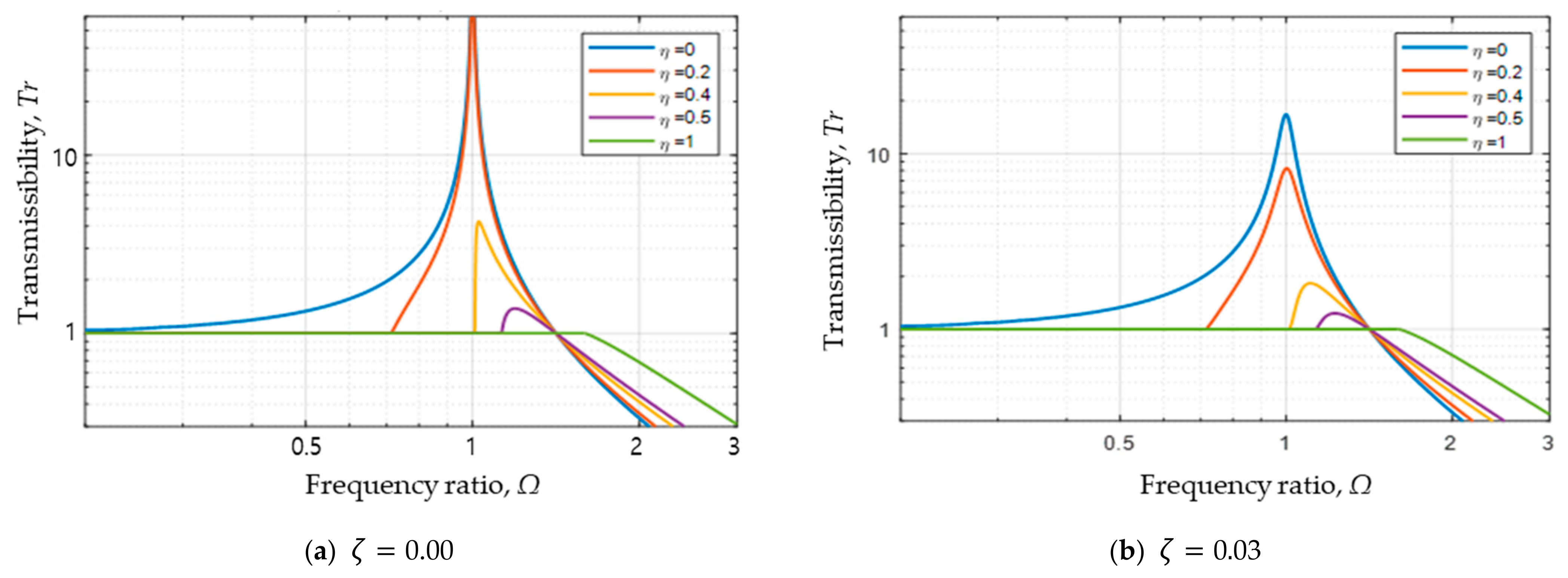
4.1. System with Zero Nonlinear Spring Coefficient (
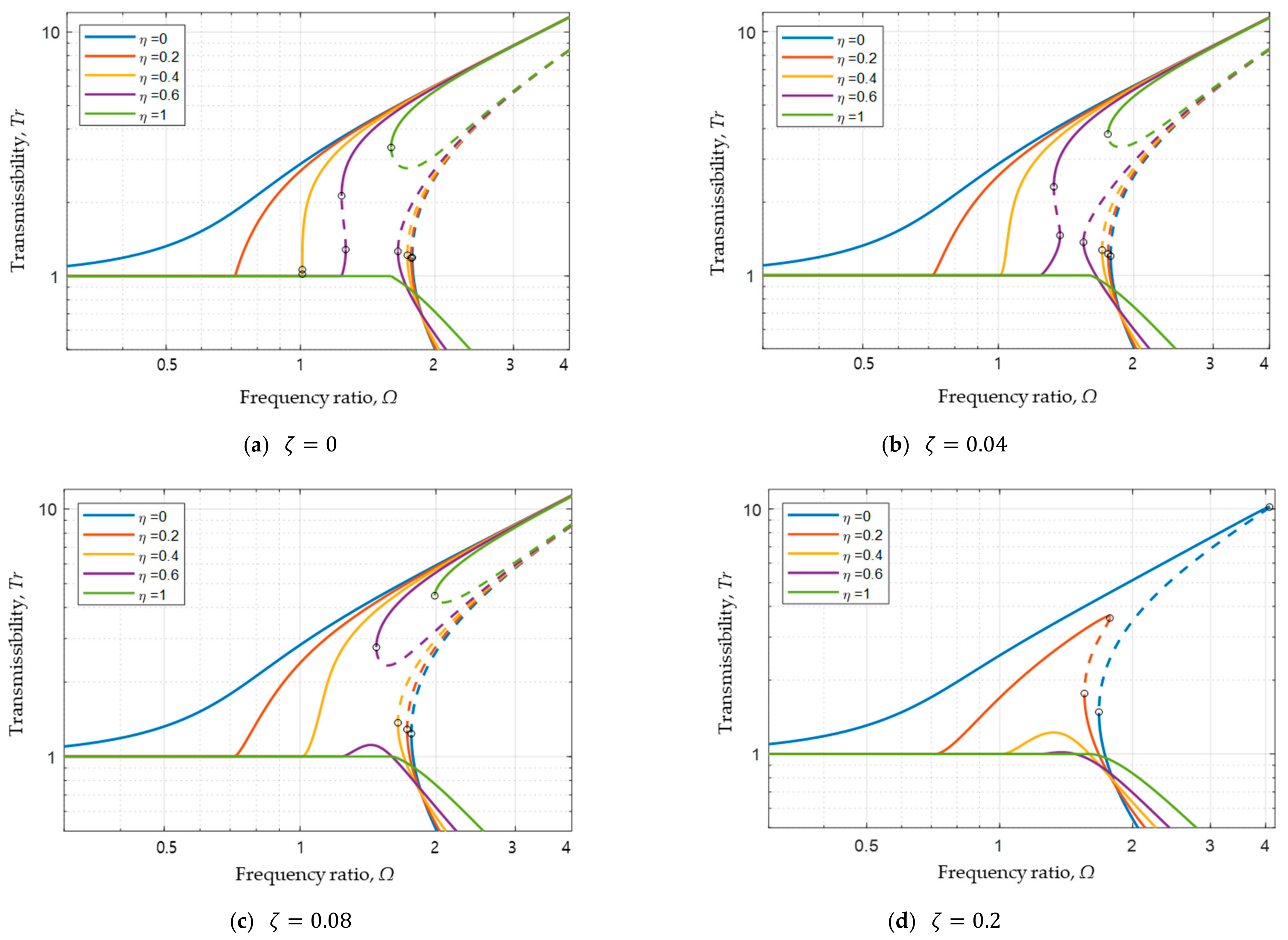
4.2. System with Positive Nonlinear Spring Coefficient (
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| m | mass of system |
| c | viscous damping coefficient |
| stiffness coefficient | |
| coefficient of cubic nonlinear stiffness | |
| friction force | |
| displacement of mass | |
| displacement of base | |
| relative displacement of the mass with respect to the base | |
| excitation frequency | |
| amplitude of base displacement | |
| dimensionless relative displacement | |
| natural frequency | |
| dimensionless time | |
| frequency ratio | |
| damping ratio | |
| friction ratio | |
| coefficient of cubic nonlinearity | |
| amplitude of relative displacement response | |
| phase of relative displacement response | |
| steady-state amplitude of relative displacement response | |
| steady-state phase of relative displacement response | |
| break-loose frequency, starting frequency of motion, or critical frequency | |
| absolute displacement transmissibility (ADTR) | |
| SVAP | slowly varying amplitude and phase |
| DTR | displacement transmissibility |
| LP | Limit Point |
| kink point | |
| critical point | |
| intersection point |
References
- Liu, C.; Jing, X.; Daley, S.; Li, F. Recent advances in micro-vibration isolation. Mech. Syst. Signal Process. 2015, 56–57, 55–80. [Google Scholar] [CrossRef]
- Yan, B.; Yu, N.; Wu, C. A state-of-the-art review on low-frequency nonlinear vibration isolation with electromagnetic mechanisms. Appl. Math. Mech.-Engl. 2022, 43, 1045–1062. [Google Scholar] [CrossRef]
- Santhosh, B.; Narayanan, S.; Padmanabhan, C. Nonlinear Dynamics of Shrouded Turbine Blade System with Impact and Friction. Appl. Mech. Mater. 2014, 76, 81–92. [Google Scholar] [CrossRef]
- Le, T.D.; Ahn, K.K. A vibration isolation system in low frequency excitation region using negative stiffness structure for vehicle seat. J. Sound Vib. 2011, 330, 6311–6335. [Google Scholar] [CrossRef]
- Le, T.D.; Ahn, K.K. Experimental investigation of a vibration isolation system using negative stiffness structure. Int. J. Mech. Sci. 2013, 70, 99–112. [Google Scholar] [CrossRef]
- Lang, Z.Q.; Jing, X.J.; Billings, S.A.; Tomlinson, G.R.; Peng, Z.K. Theoretical study of the effects of nonlinear viscous damping on vibration isolation of sdof systems. J. Sound Vib. 2009, 323, 352–365. [Google Scholar] [CrossRef]
- Yuvaraju, B.A.G.; Srinivas, J.; Nanda, B.K. Nonlinear dynamics of friction-induced regenerative chatter in internal turning with process damping forces. J. Sound Vib. 2023, 544, 117386. [Google Scholar] [CrossRef]
- Ruzicka, J.E.; Derby, T.F. Influence of Damping in Vibration Isolation, SVM-7; Shock and Vibration Information Center: Washington DC, USA, 1971. [Google Scholar]
- Ibrahim, R.A. Recent advances in nonlinear passive vibration isolators. J. Sound Vib. 2008, 314, 371–452. [Google Scholar] [CrossRef]
- Ledezma-Ramírez, D.F.; Tapia-González, P.E.; Ferguson, N.; Brennan, M.; Tang, B. Recent advances in shock vibration isolation: An overview and future possibilities. Appl. Mech. Rev. 2019, 71, 060802. [Google Scholar] [CrossRef]
- Rivin, E.I. Passive Vibration Isolation; ASME Press: New York, NY, USA, 2003. [Google Scholar]
- Hong, S.C.; Hur, D.J. Dynamic behavior of a simple rolling seismic isolator with a position restoring device. Appl. Sci. 2018, 8, 1910. [Google Scholar] [CrossRef]
- Hur, D.J.; Hong, S.C. Analysis of an isolation system with vertical spring-viscous dampers in horizontal and vertical ground motion. Appl. Sci. 2020, 10, 1141. [Google Scholar] [CrossRef]
- Shin, Y.H.; Lee, J.H.; Jung, B.C.; Moon, S.J. Design of passive vibration isolation element by wire mesh material for developing a hybrid mount. Trans. Korean Soc. Noise Vib. Eng. 2020, 30, 75–81. [Google Scholar] [CrossRef]
- Alrajhi, J.; Alhaifi, K.; Alardhi, M.; Alhaifi, N.; Alazmi, J.; Khalfan, A.; Alkhulaifi, K. The numerical analysis of single degree of freedom vibration system with non-linearity. J. Mech. Eng. Autom. 2023, 12, 6–19. [Google Scholar]
- Min, K.W.; Kim, H.S. Performance based design of friction dampers for seismically excited structures. J. Earthq. Eng. Soc. Korea 2003, 7, 17–24. [Google Scholar]
- Krack, M.; Gross, J. Harmonic Balance for Nonlinear Vibration Problems; Springer Nature: Cham, Switzerland, 2019. [Google Scholar]
- Mickens, R.E. Truly Nonlinear Oscillations, Harmonic Balance, Parameter Expansions, Iteration, and Averaging Methods; World Scientific Publishing Company: Danvers, MA, USA, 2010. [Google Scholar]
- Hagedorn, P. Non-Linear Oscillations; Clarendon Press: Oxford, UK, 1981. [Google Scholar]
- Sanders, J.A.; Verhulst, F.; Murdock, J. Averaging Methods in Nonlinear Dynamical Systems, 2nd ed.; Springer: New York, NY, USA, 2007. [Google Scholar]
- Nayfeh, A.H.; Mook, D.T. Nonlinear Oscillations; John Wiley & Sons: Hoboken, NJ, USA, 1995. [Google Scholar]
- Shahraeeni, M.; Sorokin, V.; Mace, B.; Ilanko, S. Effect of damping nonlinearity on the dynamics and performance of a quasi-zero-stiffness vibration isolator. J. Sound Vib. 2022, 526, 116822. [Google Scholar] [CrossRef]
- Ma, Z.; Zhou, R.; Yang, Q. Recent advances in quasi-zero stiffness vibration isolation systems: An overview and future possibilities. Machines 2022, 10, 813. [Google Scholar] [CrossRef]
- Brennan, M.J.; Kovacic, I.; Carrella, A.; Waters, T.P. On the jump-up and jump-down frequencies of the Duffing oscillator. J. Sound Vib. 2008, 318, 1250–1261. [Google Scholar] [CrossRef]
- Carrella, A.; Brennan, M.J.; Waters, T.P.; Lopes, V. Force and displacement transmissibility of a nonlinear isolator with high-static-low-dynamic-stiffness. Int. J. Mech. Sci. 2012, 55, 22–29. [Google Scholar] [CrossRef]
- Barquist, C.S.; Jiang, W.G.; Gunther, K.; Lee, Y. Determining the source of phase noise: Response of a driven Duffing oscillator to low-frequency damping and resonance frequency fluctuations. Phys. D Nonlinear Phenom. 2021, 427, 13299. [Google Scholar] [CrossRef]
- Liu, S.; Peng, G.; Li, Z.; Li, W. Analytical jump-avoidance criteria of Duffing-type vibration isolation systems under base and force excitations based on concave-convex property. J. Vib. Control 2023, 29, 4082–4092. [Google Scholar] [CrossRef]
- Murata, A.; Kume, Y.; Hashimoto, F. Application of catastrophe theory to forced vibration of a diaphragm air spring. J. Sound Vib. 1987, 112, 31–44. [Google Scholar] [CrossRef]
- Kovacic, I.; Brennan, M.J.; Lineton, B. On the resonance response of an asymmetric Duffing oscillator. Int. J. Non-Linear Mech. 2008, 43, 858–867. [Google Scholar] [CrossRef]
- Shi, B.; Yang, J.; Li, T. Enhancing Vibration Isolation Performance by Exploiting Novel Spring-Bar Mechanism. Appl. Sci. 2021, 11, 8852. [Google Scholar] [CrossRef]
- Marino, L.; Cicirello, A.; Hills, D.A. Displacement transmissibility of a Coulomb friction oscillator subject to jointed base-wall motion. Nonlinear Dyn. 2019, 98, 2595–2612. [Google Scholar] [CrossRef]
- Wang, D.; Song, L.; Zhu, R.; Cao, P. Nonlinear dynamics and stability analysis of dry friction damper for supercritical transmission shaft. Nonlinear Dyn. 2022, 110, 3135–3149. [Google Scholar] [CrossRef]
- Uzdin, A.M.; Kuznetsova, I.O.; Frese, M.; Nazarova, S.S.; Nazarov, A.A. Analysis of the behaviour of seismic isolated structure on bearings connected to the structure with a dry friction damper. AIP Conf. Proc. 2023, 2612, 040012. [Google Scholar]
- Benacchio, S.; Giraud-Audine, C.; Thomas, O. Effect of dry friction on a parametric nonlinear oscillator. Nonlinear Dyn. 2022, 108, 1005–1026. [Google Scholar] [CrossRef]
- Zucca, S.; Firrone, C.M. Nonlinear dynamics of mechanical systems with friction contacts: Coupled static and dynamic multi-harmonic balance method and multiple solutions. J. Sound Vib. 2014, 333, 916–926. [Google Scholar] [CrossRef]
- Ferhatoglu, E.; Zucca, S. Determination of periodic response limits among multiple solutions for mechanical systems with wedge dampers. J. Sound Vib. 2021, 494, 115900. [Google Scholar] [CrossRef]
- Ferhatoglu, E.; Groß, J.; Krack, M. Frequency response variability in friction-damped structures due to non-unique residual tractions: Obtaining conservative bounds using a nonlinear-mode-based approach. Mech. Syst. Signal Process. 2013, 201, 110651. [Google Scholar] [CrossRef]
- Starossek, U. Exact analytical solutions for forced cubic restoring force oscillator. Nonlinear Dyn. 2016, 83, 2349–2359. [Google Scholar] [CrossRef]
- Ravindra, B.; Mallik, A.K. Hard Duffing-type Vibration Isolator with Combined Coulomb and Viscous Damping. Int. J. Non-Linear Mech. 1993, 28, 427–440. [Google Scholar] [CrossRef]
- Yu, H.; Zhang, L. Free resonance analysis of bilinear hysteresis dry friction damper. J. Vib. Shock 2016, 3, 92–95. [Google Scholar]
- Huang, X.; Sun, J.; Hua, H.; Zhang, Z. The isolation performance of vibration systems with general velocity-displacement-dependent nonlinear damping under base excitation: Numerical and experimental study. Nonlinear Dyn. 2016, 85, 777–796. [Google Scholar] [CrossRef]
- Yu, H.; Xu, Y.; Sun, X. Analysis of the non-resonance of nonlinear vibration isolation system with dry friction. J. Mech. Sci. Technol. 2018, 32, 1489–1497. [Google Scholar] [CrossRef]
- Dhooge, A.; Govaerts, W.; Kuznetsov, Y.A. MATCONT: A Matlab Package for Numerical Bifurcation Analysis of ODEs. ACM Trans. Math. Softw. 2003, 29, 141–164. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hur, D.J.; Hong, S.C. Analysis of Displacement Transmissibility and Bifurcation Behavior in Nonlinear Systems with Friction and Nonlinear Spring. Vibration 2024, 7, 1210-1225. https://doi.org/10.3390/vibration7040062
Hur DJ, Hong SC. Analysis of Displacement Transmissibility and Bifurcation Behavior in Nonlinear Systems with Friction and Nonlinear Spring. Vibration. 2024; 7(4):1210-1225. https://doi.org/10.3390/vibration7040062
Chicago/Turabian StyleHur, Deog Jae, and Sung Chul Hong. 2024. "Analysis of Displacement Transmissibility and Bifurcation Behavior in Nonlinear Systems with Friction and Nonlinear Spring" Vibration 7, no. 4: 1210-1225. https://doi.org/10.3390/vibration7040062
APA StyleHur, D. J., & Hong, S. C. (2024). Analysis of Displacement Transmissibility and Bifurcation Behavior in Nonlinear Systems with Friction and Nonlinear Spring. Vibration, 7(4), 1210-1225. https://doi.org/10.3390/vibration7040062







