Nonlinear Finite Element Analysis of Tubular Steel Wind Turbine Towers near Man Door and Ventilation Openings to Optimize Design against Buckling
Abstract
1. Introduction
2. Materials and Methods
2.1. Geometry
2.2. Modeling Details
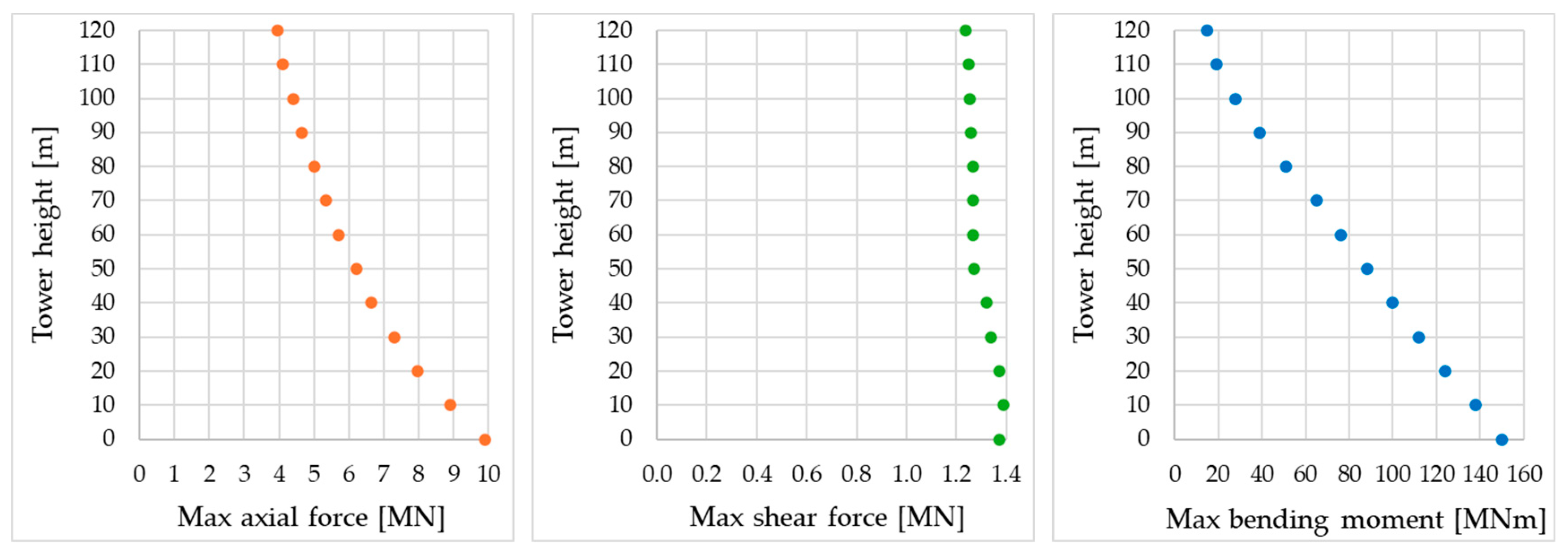
2.3. Loading Details
2.4. Analysis Details
3. Results
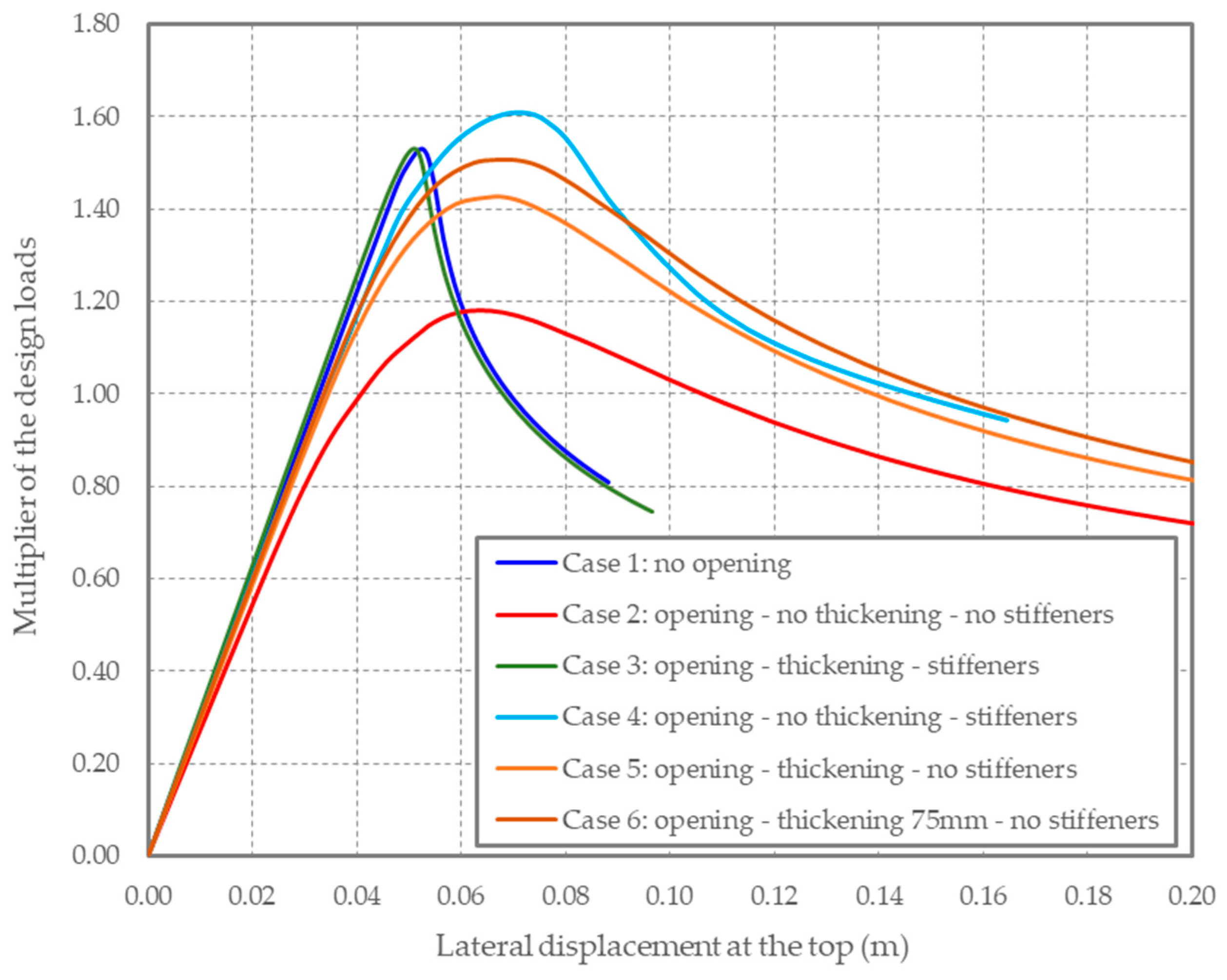
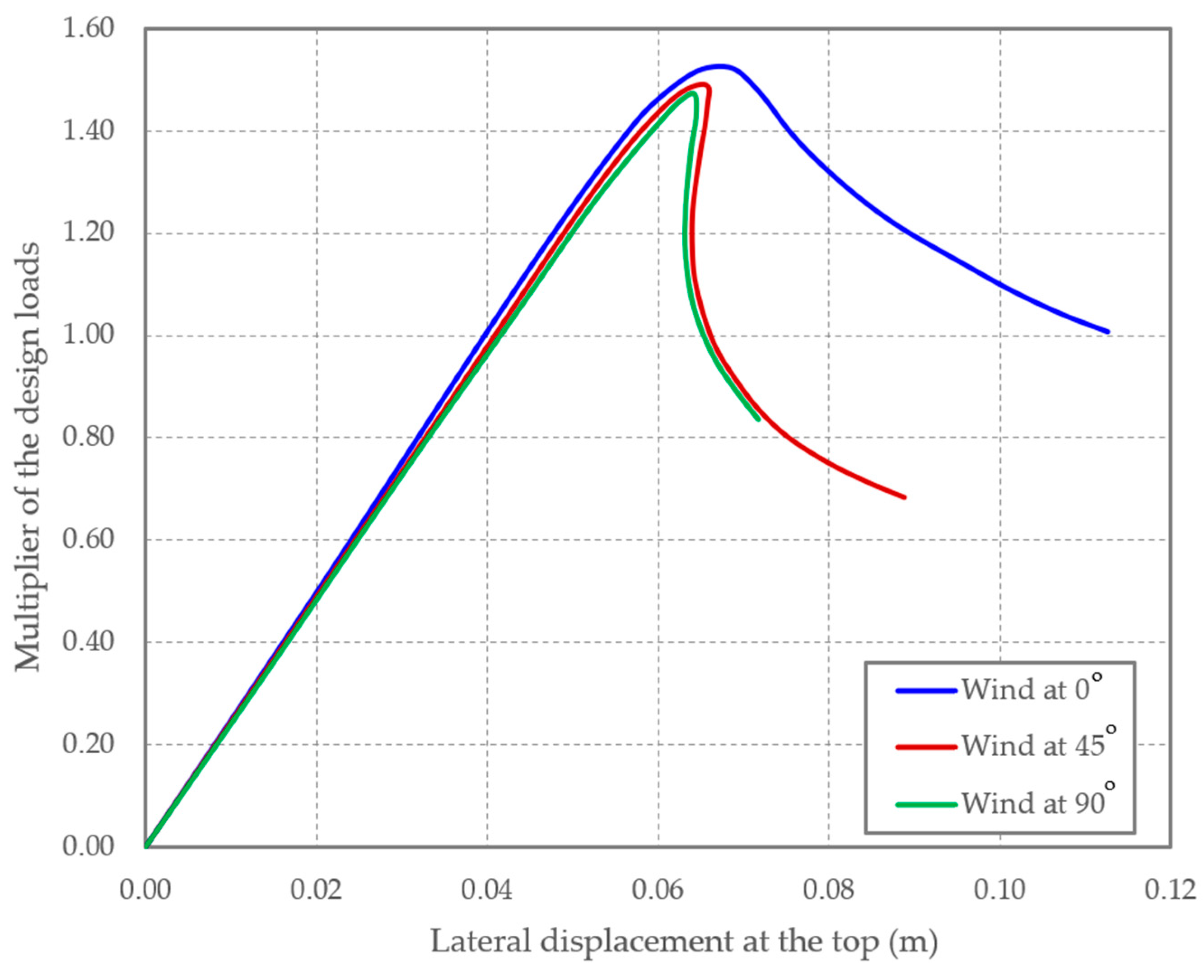
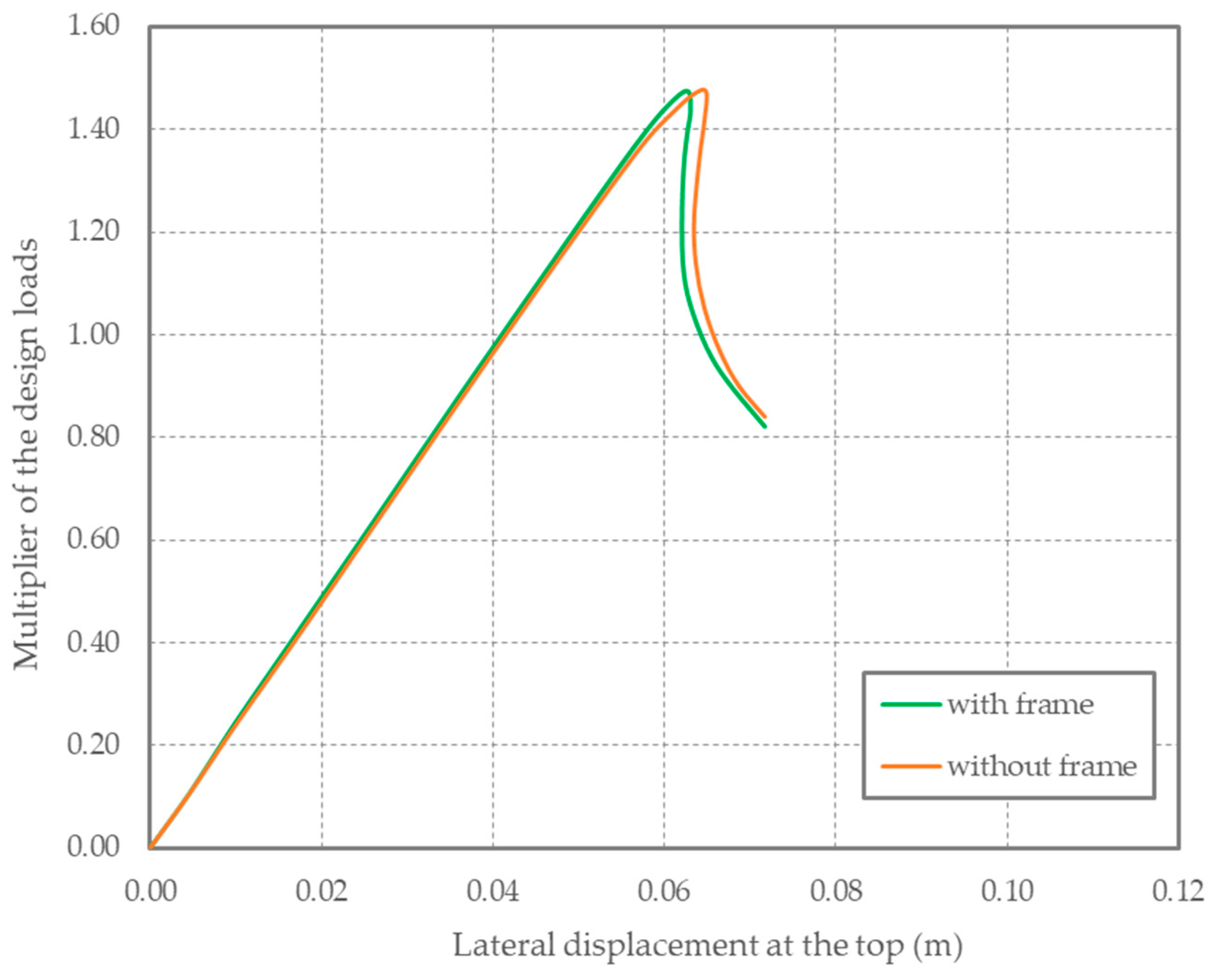
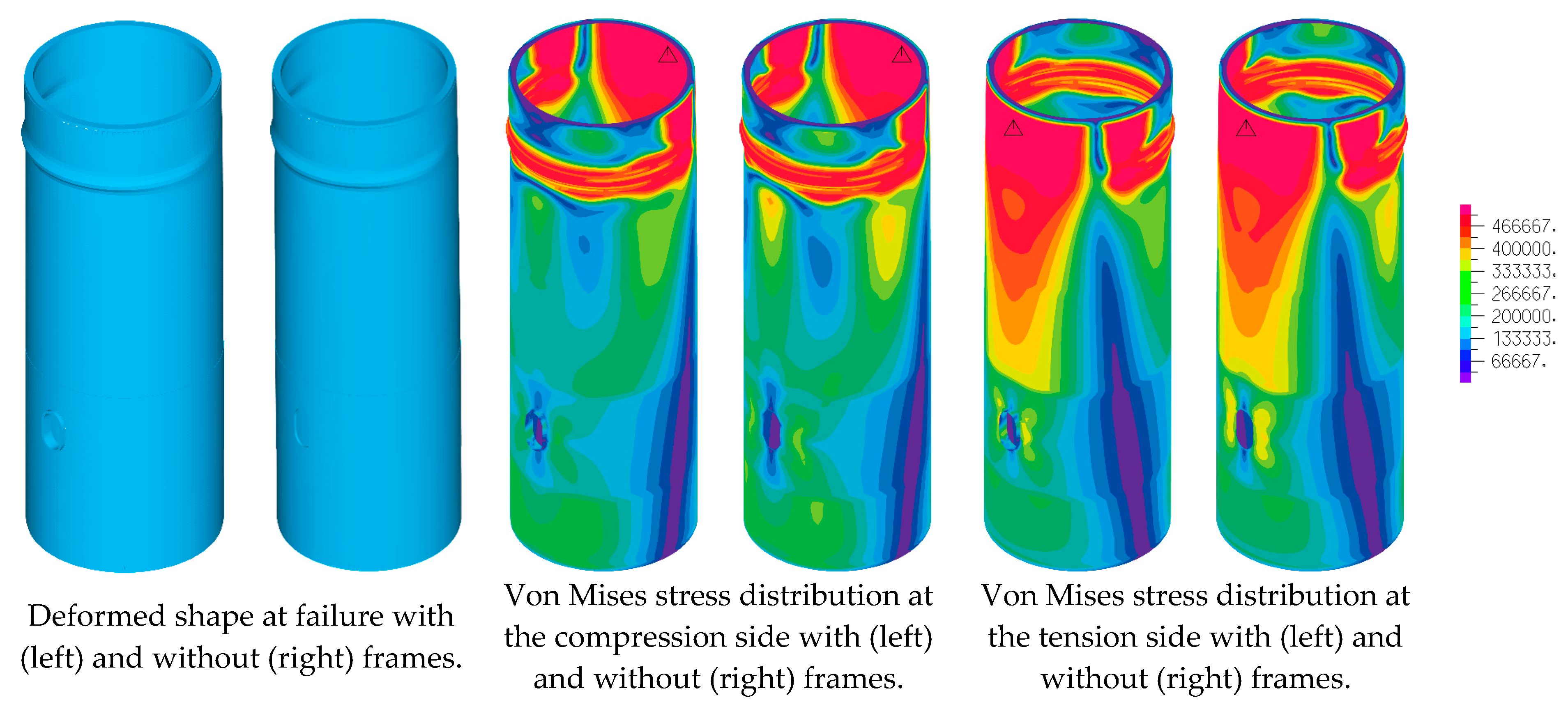
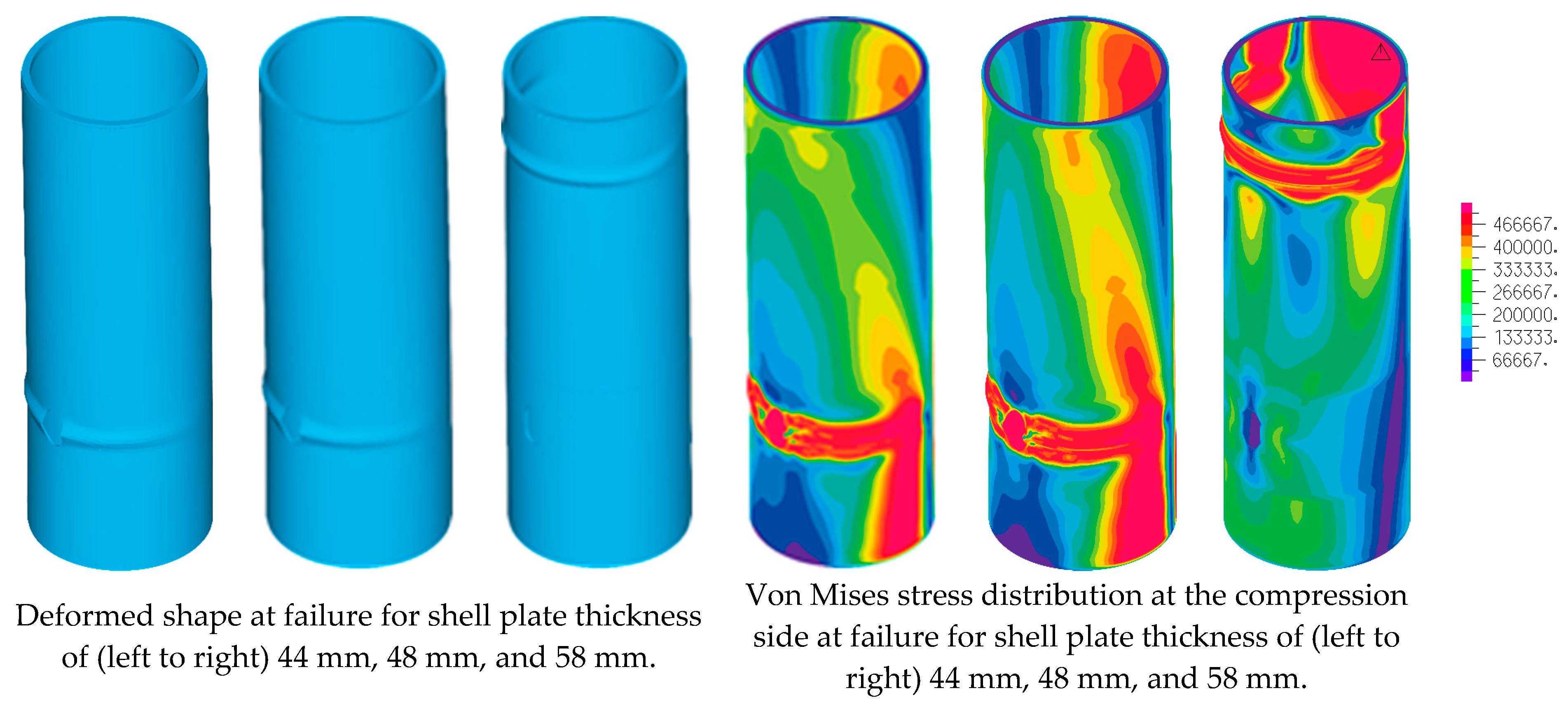
3.1. Section with Man Door Opening
- Case 3: with a 65 mm thick door plate around the man door opening and with a stiffening frame like that illustrated in Figure 3;
- Case 4: without thickening of the door plate around the man door opening but with a stiffening frame, the same as the one illustrated in Figure 3;
- Case 5: with 65 mm thick door plate around the man door opening, but without a stiffening frame;
- Case 6: with 75 mm thick door plate around the man door opening, but without a stiffening frame.
3.2. Section with Two Ventilation Openings
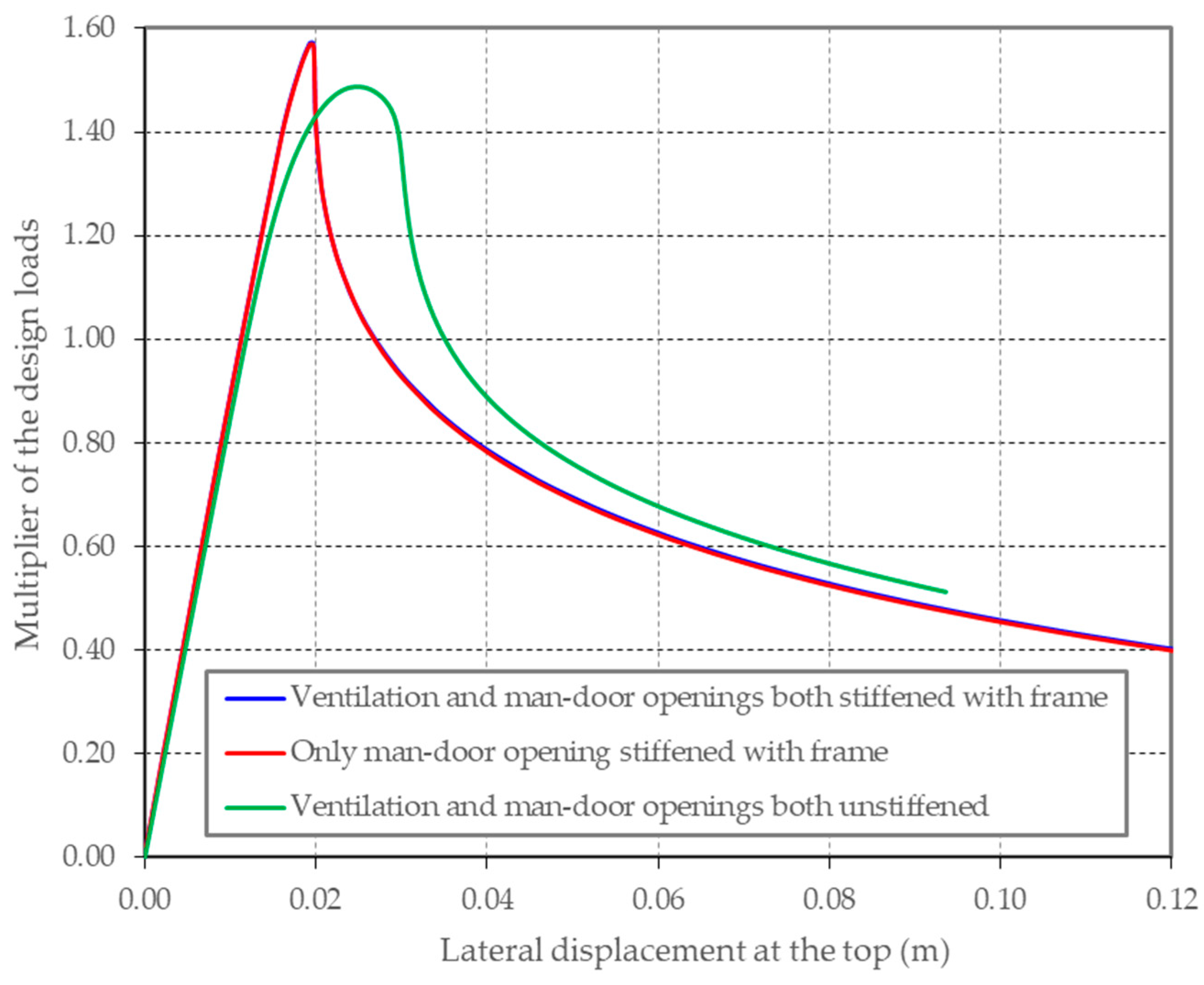
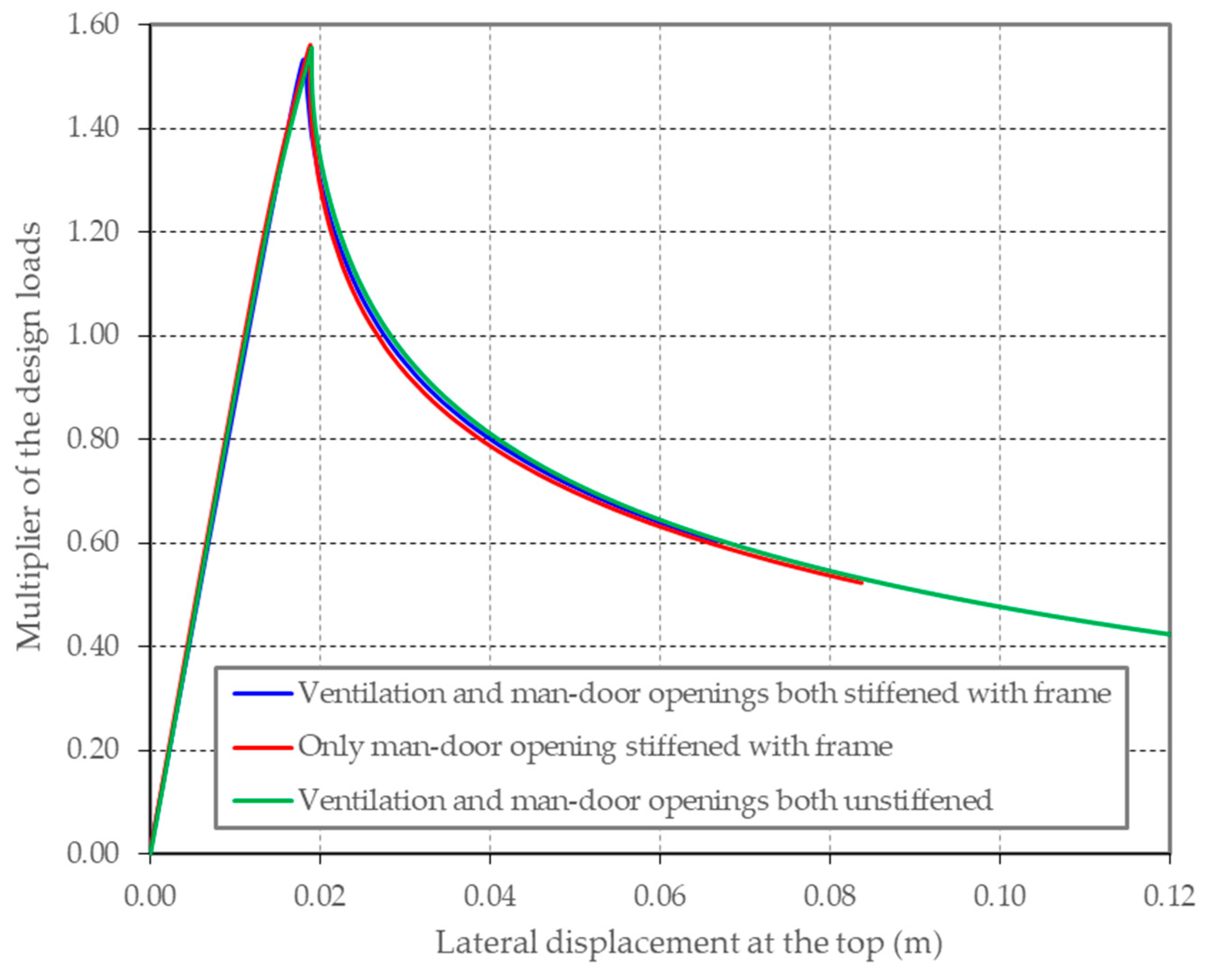
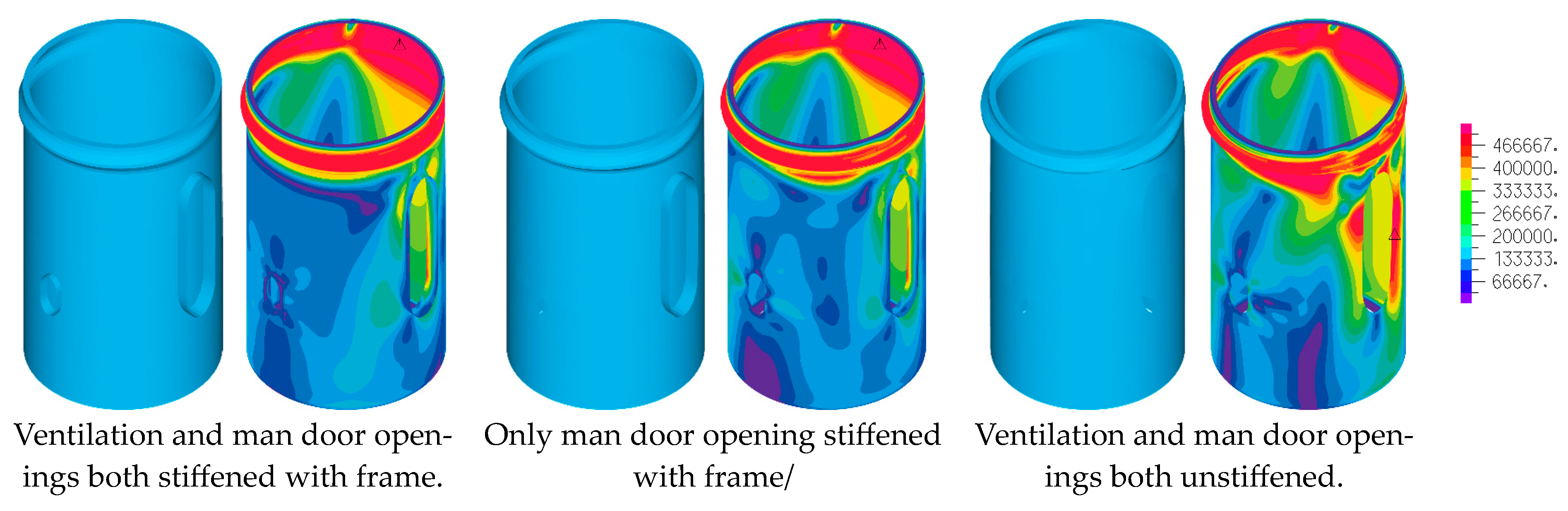
3.3. Section with Man Door and Ventilation Opening
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- 2030 Climate & Energy Framework. Available online: https://ec.europa.eu/clima/policies/strategies/2030_en#tab-0-0 (accessed on 7 December 2023).
- International Energy Agency. Net Zero by 2050—A Roadmap for the Global Energy Sector, 2nd Revision. June 2021. Available online: https://www.iea.org/reports/net-zero-by-2050 (accessed on 7 December 2023).
- Global Wind Energy Council. Global Wind Report 2022. Available online: https://gwec.net/global-wind-report-2022/ (accessed on 7 December 2023).
- Zhao, Z.; Dai, K.; Camara, A.; Bitsuamlak, G.; Sheng, C. Wind turbine tower failure modes under seismic and wind loads. J. Perform. Constr. Facil. 2019, 33, 04019015. [Google Scholar] [CrossRef]
- IEC61400-1:2005; Wind Turbines—Part 1: Design Requirements, International Standard. 3rd ed. International Electrotechnical Commission: Geneva, Switzerland, 2005.
- Germanischer Lloyd. Guideline for the Certification of Wind Turbines; Germanischer Lloyd: Hamburg, Germany, 2010. [Google Scholar]
- Det Norske Veritas (DNV). Wind Energy Department, Risø National Laboratory. Guidelines for Design of Wind Turbines. Available online: https://www.kimerius.com/app/download/5784679452/Guidelines+for+design+of+wind+turbines.pdf (accessed on 9 September 2021).
- DNV GL. DNVGL-ST-0126. Support Structures for Wind Turbines. Available online: https://rules.dnv.com/docs/pdf/DNV/ST/2016-04/DNVGL-ST-0126.pdf (accessed on 9 September 2021).
- EN1993-1-6:2007; Eurocode 3: Design of Steel Structures—Part 1.6: Strength and Stability of Shell Structures. European Committee of Standardization: Brussels, Belgium, 2007.
- EN1993-1-6:2007/A1:2015; Eurocode 3: Design of Steel Structures—Part 1.6: Strength and Stability of Shell Structures—Corrigendum. European Committee of Standardization: Brussels, Belgium, 2015.
- NREL Transforming Energy. Available online: https://www.nrel.gov/wind/nwtc/fast.html (accessed on 26 February 2024).
- Xi, R.; Wang, P.; Du, X.; Xu, C.; Jia, J. Evaluation of an Uncoupled Method for Analyzing the Seismic Response of Wind Turbines Excited by Wind and Earthquake Loads. Energies 2020, 13, 3833. [Google Scholar] [CrossRef]
- ADINA. Available online: https://www.adina.com/index.shtml (accessed on 26 February 2024).
- Dimopoulos, C.A.; Gantes, C.J. Numerical methods for the design of cylindrical steel shells with unreinforced or reinforced cutouts. Thin-Walled Str. 2015, 96, 11–28. [Google Scholar] [CrossRef]
- Dimopoulos, C.A.; Koulatsou, K.; Petrini, F.; Gantes, C.J. Assessment of stiffening type of the cutout in tubular wind turbine towers under artificial dynamic wind actions. J. Comput. Nonlinear Dyn. 2015, 10, 041004. [Google Scholar] [CrossRef]
- Tennyson, R.C. Buckling of circular cylindrical shells in axial compression. AIAA J. 1964, 2, 1351–1353. [Google Scholar] [CrossRef]
- Weingarten, V.I.; Morgan, E.J.; Seide, P. Elastic stability of thin-walled cylindrical and conical shells under axial compression. AIAA J. 1965, 3, 500–505. [Google Scholar] [CrossRef]
- Schneider, M.H., Jr. Investigations of the stability of imperfect cylinders using structural models. Eng. Struct. 1996, 8, 792–800. [Google Scholar] [CrossRef]
- Lee, L.H.N. Inelastic buckling of initially imperfect cylindrical shells subject to axial compression. J. Aerosp. Sci. 1962, 29, 87–95. [Google Scholar] [CrossRef]
- Batterman, S.C. Plastic buckling of axially compressed cylindrical Shells. AIAA J. 1965, 3, 316–325. [Google Scholar] [CrossRef]
- Bardi, F.C.; Yun, H.D.; Kyriakides, S. On the axisymmetric progressive crushing of circular tubes under axial compression. Int. J. Solids Struct. 2003, 40, 3137–3155. [Google Scholar] [CrossRef]
- Sherman, D.R. Tests of circular steel tubes in bending. ASCE J. Struct. Div. 1976, 102, 2181–2195. [Google Scholar] [CrossRef]
- Reddy, B.D. An experimental study of the plastic buckling of circular cylinders in pure bending. Int. J. Solids Struct. 1979, 15, 669–685. [Google Scholar] [CrossRef]
- Kyriakides, S.; Shaw, P.K. Inelastic buckling of tubes under cyclic bending. ASME J. Press. Vessel. Technol. 1987, 109, 169–178. [Google Scholar] [CrossRef]
- Kyriakides, S.; Ju, G.T. Bifurcation and localization instabilities in cylindrical shells under bending. Int. J. Solids Struct. 1992, 29, 1117–1142. [Google Scholar] [CrossRef]
- Koulatsou, K.G.; Chondrogiannis, K.-A.; Gantes, C.J. Structural optimization of tubular steel wind turbine towers with respect to buckling. In Proceedings of the IASS Annual Symposium 2019—Structural Membranes 2019, Form and Force, Barcelona, Spain, 7–10 October 2019. [Google Scholar]
- Gantes, C.J.; Koulatsou, K.G.; Chondrogiannis, K.-A. Alternative ring flange models for buckling verification of tubular steel wind turbine towers via advanced numerical analysis and comparison to code provisions. Structures 2023, 47, 1366–1382. [Google Scholar] [CrossRef]
- Sadowski, A.J.; Seidel, M.; Al-Lawati, H.; Azizi, E.; Balscheit, H.; Böhm, M.; Chen, L.; van Dijk, I.; Doerich-Stavridis, C.; Fajuyitan, O.K.; et al. 8-MW wind turbine tower computational shell buckling benchmark. Part 1: An international ‘round-robin’ exercise. Eng. Fail. Anal. 2023, 148, 107124. [Google Scholar] [CrossRef]
- Sadowski, A.J.; Seidel, M. 8-MW wind turbine tower computational shell buckling benchmark. Part 2: Detailed reference solution. Eng. Fail. Anal. 2023, 148, 107133. [Google Scholar] [CrossRef]
- Brogan, F.; Almorth, B.O. Buckling of cylinders with cutout. AIAA J. 1970, 8, 236–240. [Google Scholar] [CrossRef]
- Almorth, B.O.; Holmes, A.M.C. Buckling of shells with cutouts, experiment and analysis. Int. J. Solids Struct. 1972, 8, 1057–1071. [Google Scholar] [CrossRef]
- Starnes, J.H., Jr. Effect of a slot on the buckling load of a cylindrical shell with a circular cutout. AIAA J. 1972, 10, 227–229. [Google Scholar] [CrossRef]
- Bennett, J.G.; Dove, R.C.; Butler, T.A. An investigation of buckling of steel cylinders with circular reinforced cutouts. Nucl. Eng. Des. 1982, 69, 229–239. [Google Scholar] [CrossRef]
- Toda, S. Buckling of cylinders with cutouts under axial compression. Exp. Mech. 1983, 23, 414–417. [Google Scholar] [CrossRef]
- Shariati, M.; Rokhi, M.M. Numerical and experimental investigations on buckling of steel cylindrical shells with elliptical cutout subject to axial compression. Thin Walled Struct. 2008, 46, 1251–1261. [Google Scholar] [CrossRef]
- Knödel, P.; Schulz, U. Zur Stabilität von Schornsteinen mit Fuchsöffnungen. Stahlbau 1988, 57, 13–21. [Google Scholar]
- Yeh, M.K.; Lin, M.C.; Wu, W.T. Bending buckling of an elastoplastic cylindrical shell with a cutout. Eng. Struct. 1999, 21, 996–1005. [Google Scholar] [CrossRef]
- Dimopoulos, C.A.; Gantes, C.J. Experimental investigation of buckling of wind turbine tower cylindrical shells with opening and stiffening under bending. Thin Walled Struct. 2012, 54, 140–155. [Google Scholar] [CrossRef]
- Dimopoulos, C.A.; Gantes, C.J. Comparison of stiffening types of the cutout in tubular wind turbine towers. J. Constr. Steel Res. 2013, 83, 62–74. [Google Scholar] [CrossRef]
- Tran, A.; Veljkovic, M.; Rebelo, C.; Simões da Silva, L. Resistance of door openings in towers for wind turbines. In Proceedings of the SEECCM III—3rd South-East European Conference on Computational Mechanics—An ECCOMAS and IACM Special Interest Conference, Kos Island, Greece, 12–14 June 2013; Papadrakakis, M., Kojic, M., Tuncer, I., Papadopoulos, V., Eds.; SEECCM 2013: Kos Island, Greece, 2013. [Google Scholar] [CrossRef]
- Alsalah, A.; Holloway, D.; Ghanbari Ghazijahani, T. Recovery of capacity lost due to openings in cylindrical shells under compression. J. Constr. Steel Res. 2017, 137, 169–179. [Google Scholar] [CrossRef]
- Koulatsou, K.G.; Chondrogiannis, K.-A.; Gantes, C.J. Buckling verification of manhole area of tubular steel wind turbine towers via non-linear finite element analysis. Ce/Papers 2021, 4, 261–268. [Google Scholar] [CrossRef]
- Gantes, C.J.; Vernardos, S.; Koulatsou, K.G.; Doğanli, A.E.; Güneş, O. Optimization of mandoor and ventilation openings of tubular steel wind turbine towers with respect to buckling. In Proceedings of the 6th Izmir Wind Symposium and Exhibition, Izmir, Turkey, 23–24 September 2021. [Google Scholar]
- Gantes, C.J.; Fragkopoulos, K.A. Strategy for numerical verification of steel structures at the ultimate limit state. Struct. Infrastruct. Eng. 2010, 6, 225–255. [Google Scholar] [CrossRef]
- Quan, C.; Walport, F.; Gardner, L. Equivalent geometric imperfections for the design of steel and stainless steel beam-columns by GMNIA. J. Constr. Steel Res. 2024, 215, 108502. [Google Scholar] [CrossRef]
- Dimopoulos, C.A.; Gantes, C.J. Comparison of alternative algorithms for buckling analysis of slender steel structures. Struct. Eng. Mech. 2012, 44, 219–238. [Google Scholar] [CrossRef]
- Bathe, K.J.; Cimento, A.P. Some practical procedures for the solution of nonlinear finite element equations. Comput. Methods Appl. Mech. Eng. 1980, 22, 59–85. [Google Scholar] [CrossRef]


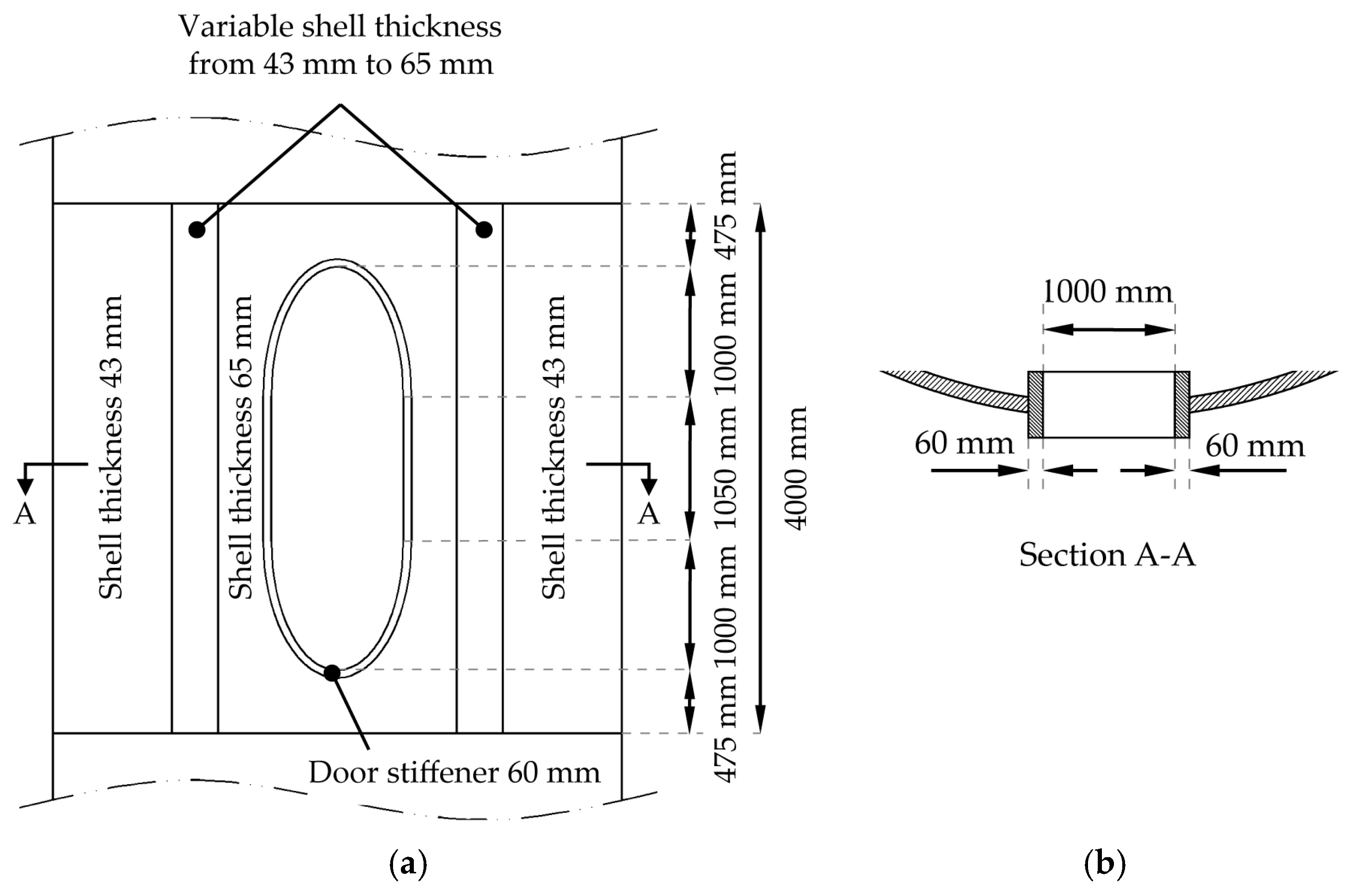
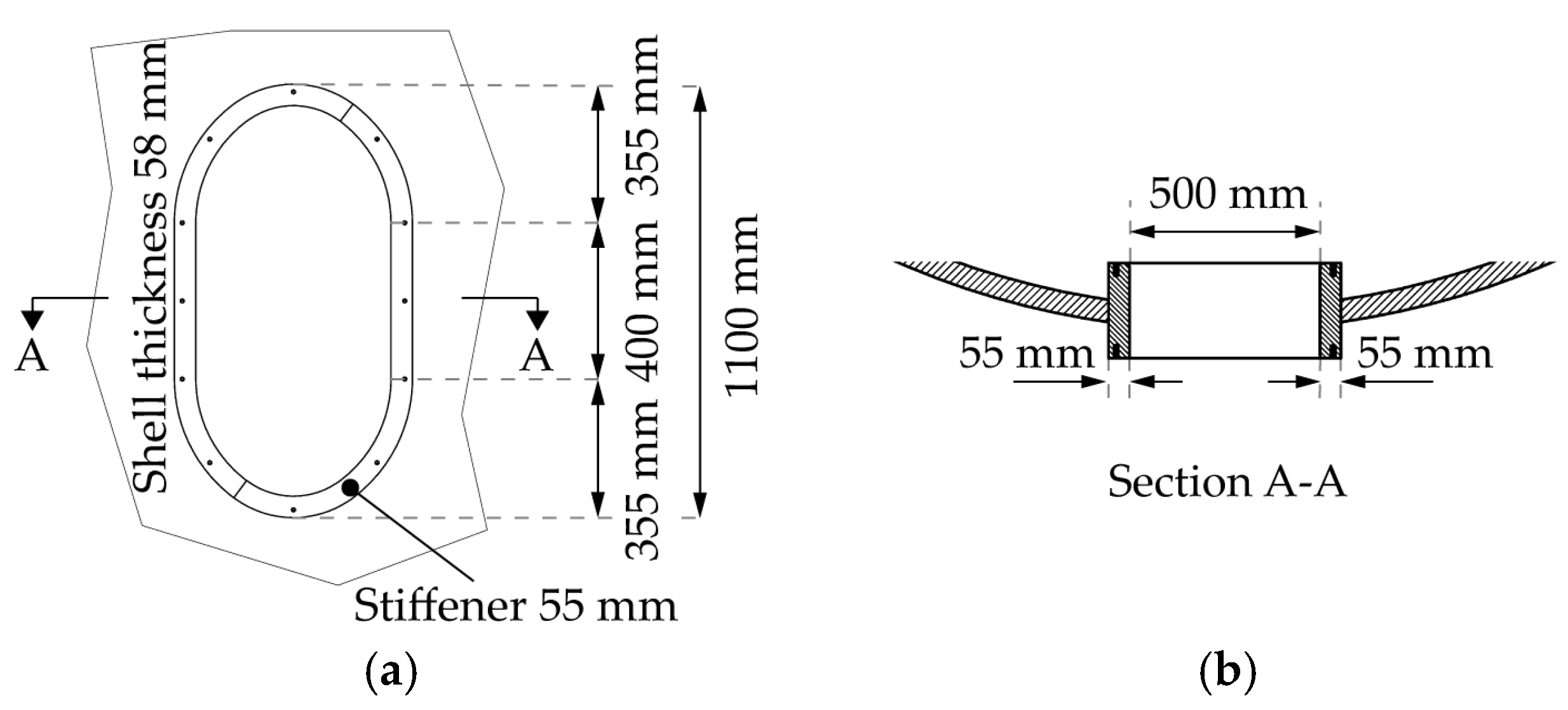






| Man Door | Ventilation | |
|---|---|---|
| Width [mm] | 1000 | 500 |
| Height [mm] | 3050 | 1110 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gantes, C.J.; Vernardos, S.M.; Koulatsou, K.G.; Gül, S. Nonlinear Finite Element Analysis of Tubular Steel Wind Turbine Towers near Man Door and Ventilation Openings to Optimize Design against Buckling. Vibration 2024, 7, 212-228. https://doi.org/10.3390/vibration7010012
Gantes CJ, Vernardos SM, Koulatsou KG, Gül S. Nonlinear Finite Element Analysis of Tubular Steel Wind Turbine Towers near Man Door and Ventilation Openings to Optimize Design against Buckling. Vibration. 2024; 7(1):212-228. https://doi.org/10.3390/vibration7010012
Chicago/Turabian StyleGantes, Charis J., Stelios M. Vernardos, Konstantina G. Koulatsou, and Semih Gül. 2024. "Nonlinear Finite Element Analysis of Tubular Steel Wind Turbine Towers near Man Door and Ventilation Openings to Optimize Design against Buckling" Vibration 7, no. 1: 212-228. https://doi.org/10.3390/vibration7010012
APA StyleGantes, C. J., Vernardos, S. M., Koulatsou, K. G., & Gül, S. (2024). Nonlinear Finite Element Analysis of Tubular Steel Wind Turbine Towers near Man Door and Ventilation Openings to Optimize Design against Buckling. Vibration, 7(1), 212-228. https://doi.org/10.3390/vibration7010012







