Parametric Instability of Functionally Graded Porous Cylindrical Panels under the Effect of Static and Time-Dependent Axial Loads
Abstract
:1. Introduction
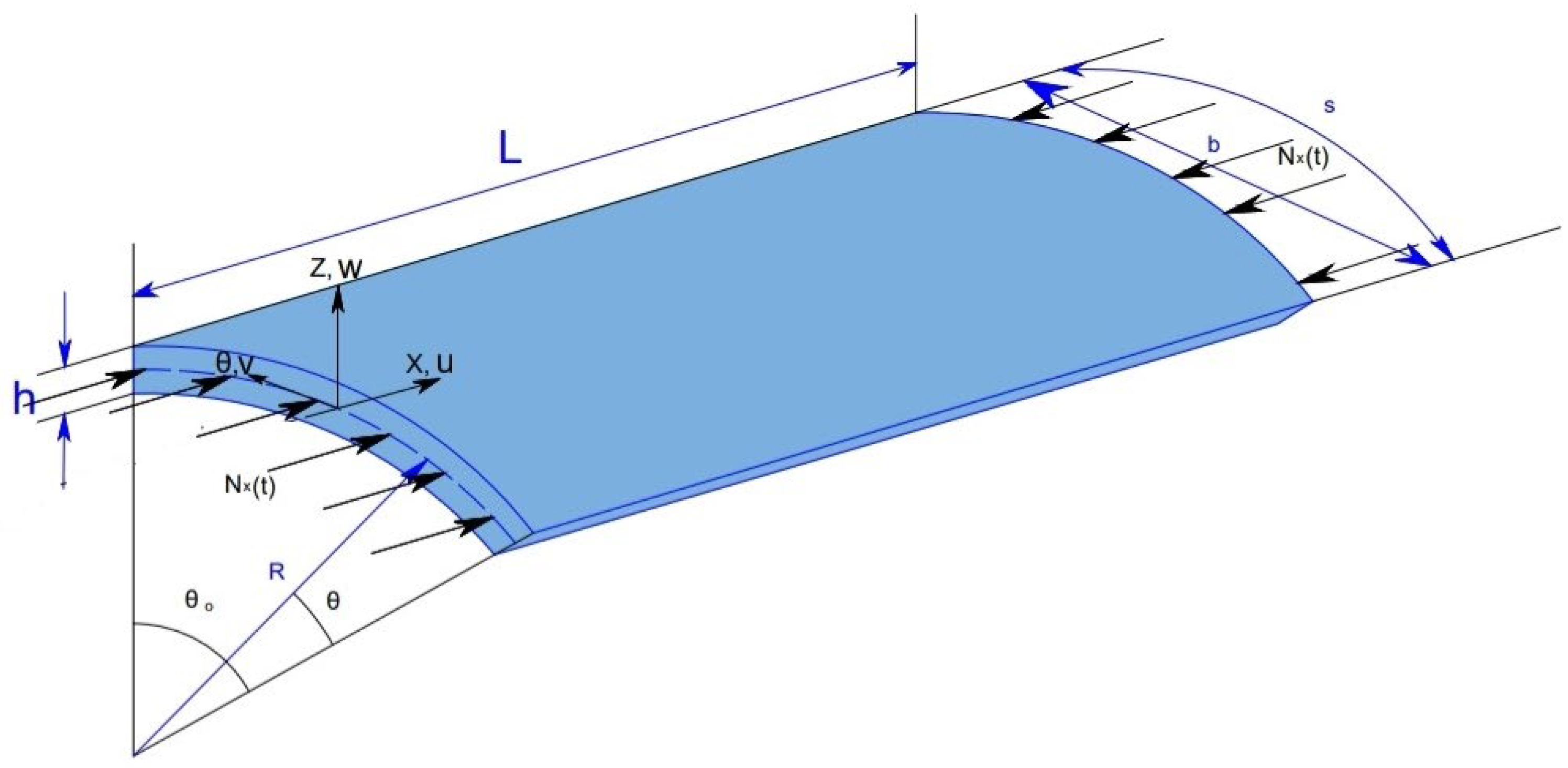
2. Theoretical Approach
2.1. The Governing Equations of the Distribution of Porosity
2.2. Formulation of Dynamic Stability
3. Numerical Results and Discussions
3.1. Validation
3.2. Results of the Present Study
3.2.1. The Effect of Porosity Distribution
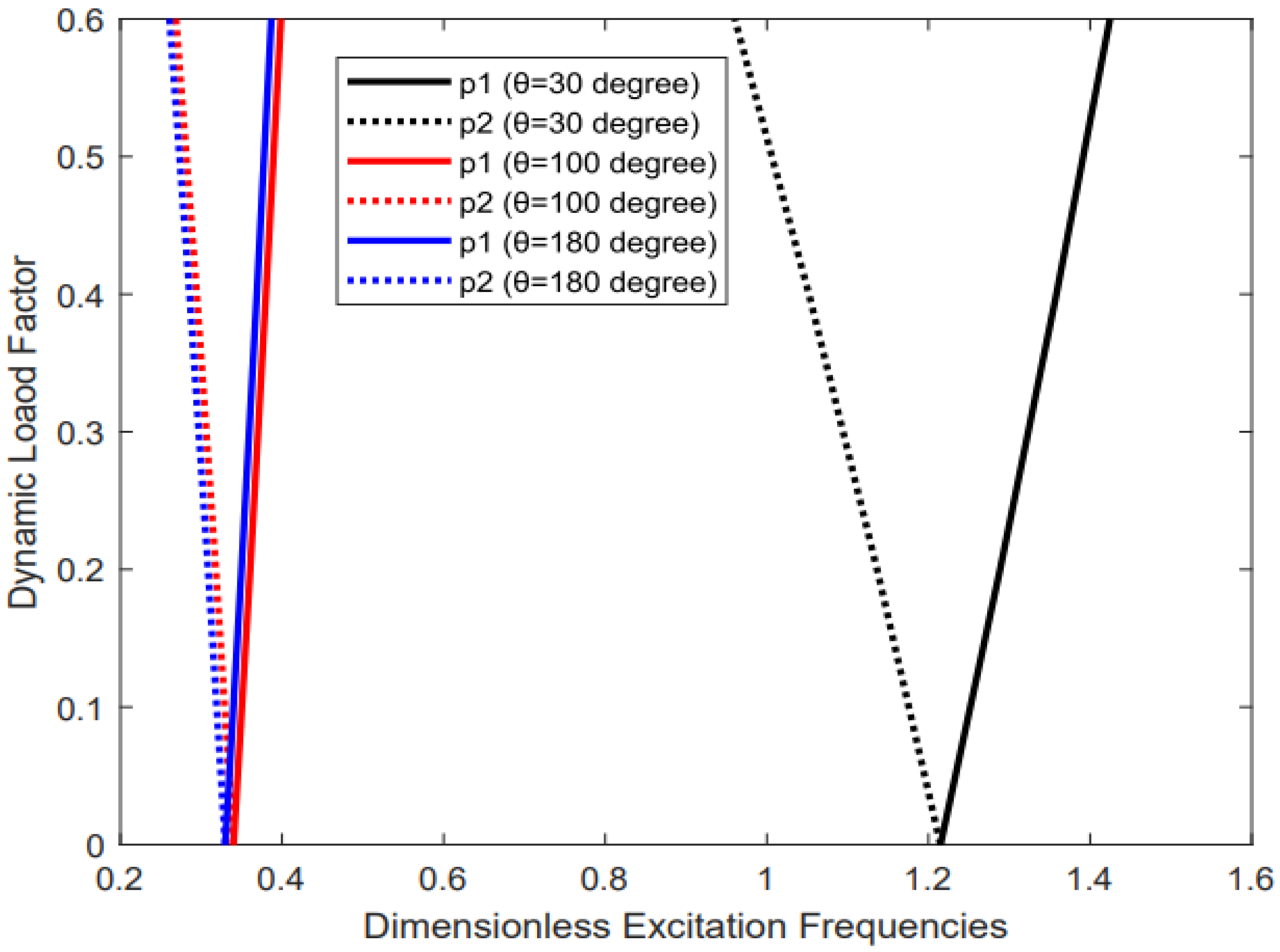
3.2.2. The Effect of the Panel’s Angle
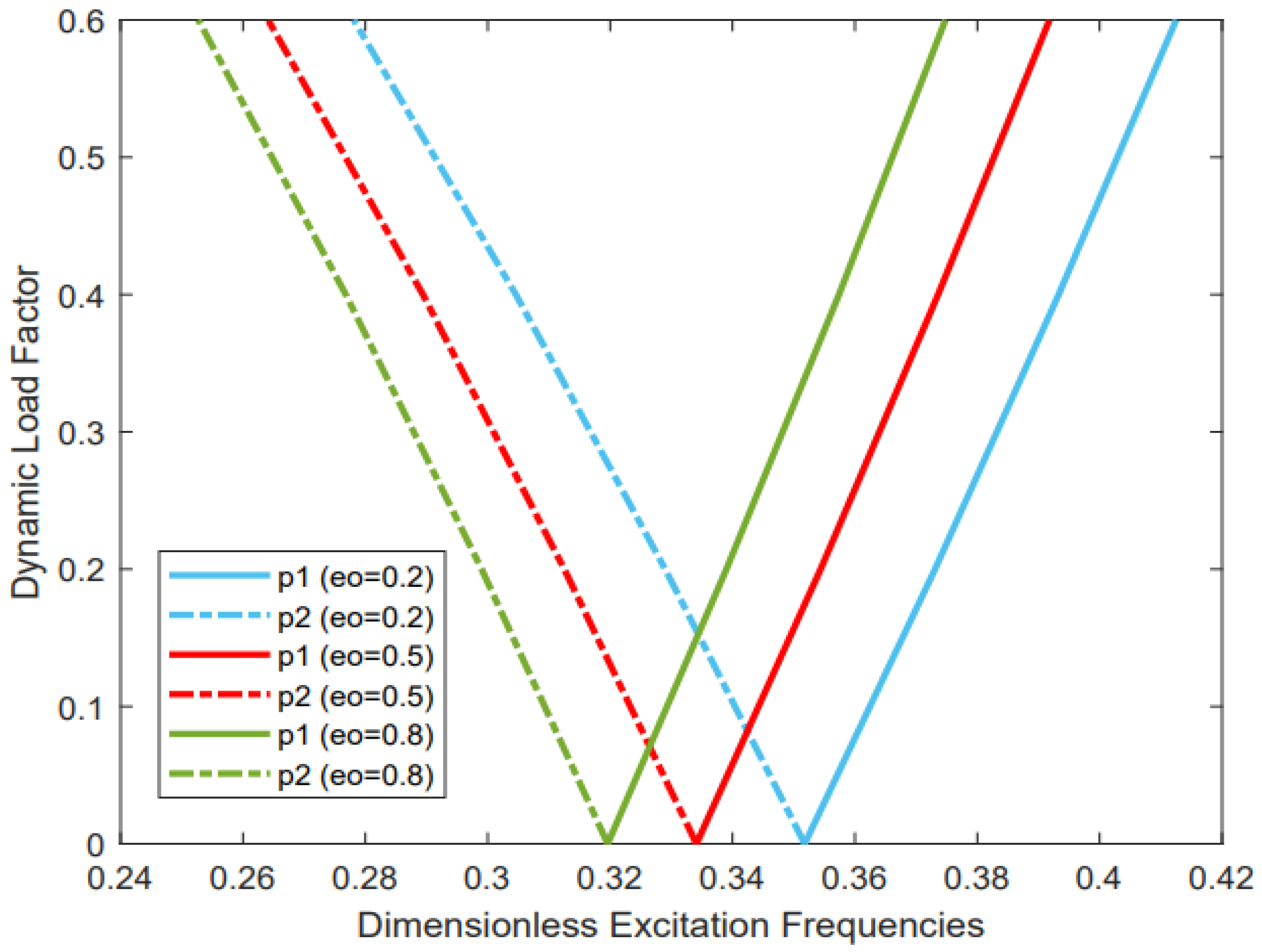
3.2.3. The Effect of the Porosity Coefficient
3.2.4. The Effect of Static and Dynamic Load Factors
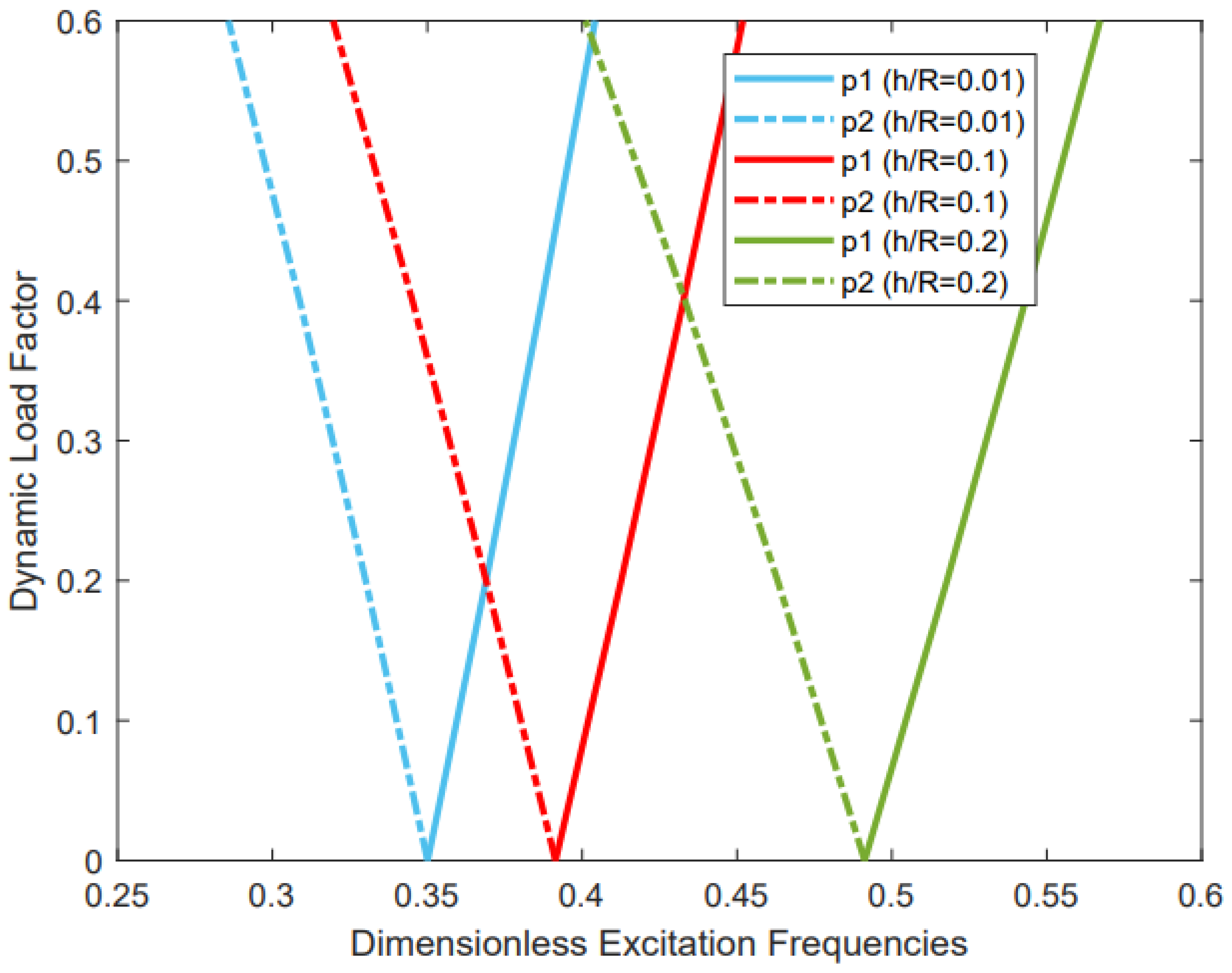
3.2.5. The Effect of the h/R Ratio
3.2.6. The Effect of the L/S Ratio
3.2.7. The Effect of the Circumferential Wave Number
4. Conclusions
- According to the results shown, it may be concluded that the symmetric porosity distribution around the midplane (i.e., Type 2) has more stiffness and results in the excitation frequency shifting forward to a high value, so it is preferred over the rest of the types.
- A small angle (i.e., ) of the panel results in a large excitation frequency, but it is more influenced by the dynamic load. This behavior is fully reversed when the angle of the panel is large.
- By increasing the circumferential wave number, the excitation frequencies decrease and then increase when the angle of the panel is large (i.e., ), but when the angle of the panel is small (i.e., ) the excitation frequencies increase by increasing the circumferential wave number.
- The excitation frequencies increase when the static load factor decreases. Additionally, the width of instability increases as the static load factor and dynamic load factor increase.
- The structure is less stable when it has porosity, and the weakness of the structure increases with an increase in the porosity.
- For design purposes, care should be taken to decide the values of the static load factor and the porosity coefficient because a wrong selection leads to instability and then an early failure in the structure.
- The dimensionless excitation frequencies and width of the instability region have a large value when the thickness is large and when the length is small.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Babaei, M.; Hajmohammad, M.H.; Asemi, K. Natural frequency and dynamic analyses of functionally graded saturated porous annular sector plate and cylindrical panel based on 3D elasticity. Aeros. Sci. Technol. 2020, 96, 105524. [Google Scholar] [CrossRef]
- Mirzaei, M.; Kiani, Y. Free vibration of functionally graded carbon nanotube reinforced composite cylindrical panels. Compos. Struct. 2016, 142, 45–56. [Google Scholar] [CrossRef]
- Li, H.; Pang, F.; Chen, H.; Du, Y. Vibration analysis of functionally graded porous cylindrical shell with arbitrary boundary restraints by using a semi analytical method. Compos. Part B Eng. 2019, 164, 249–264. [Google Scholar] [CrossRef]
- Chu, H.-N. Influence of Large Amplitudes on Flexural Vibrations of a Thin Circular Cylindrical Shell. J. Aerosp. Sci. 1961, 28, 602–609. [Google Scholar] [CrossRef]
- Bich, D.H.; Xuan Nguyen, N. Nonlinear vibration of functionally graded circular cylindrical shells based on improved Donnell equations. J. Sound Vib. 2012, 331, 5488–5501. [Google Scholar] [CrossRef]
- Quoc, T.H.; Tham, V.; Van Tu, T.M. Free Vibration of Stiffened Functionally Graded Porous Cylindrical Shell Under Various Boundary Conditions. In Modern Mechanics and Applications; Springer: Singapore, 2022; pp. 347–361. [Google Scholar]
- Wang, Y.; Wu, D. Free vibration of the functionally graded porous cylindrical shell using a sinusoidal shear deformation theory. Aerosp. Sci. Technol. 2017, 66, 83–91. [Google Scholar] [CrossRef]
- Dang, X.H.; Nguyen, V.L.; Tran, M.T.; Nguyen Thi, B. Free Vibration Characteristics of Rotating Functionally Graded Porous Circular Cylindrical Shells with Different Boundary Conditions. Iran J. Sci. Technol. Trans. Mech. Eng. 2020, 46, 167–183. [Google Scholar] [CrossRef]
- Liew, K.M.; Ng, T.Y.; Zhao, X.; Reddy, J.N. Harmonic reproducing kernel particle method for free vibration analysis of rotating cylindrical shells. Comput. Methods Appl. Mech. Eng. 2002, 191, 4141–4157. [Google Scholar] [CrossRef]
- Sun, S.; Chu, S.; Cao, D. Vibration characteristics of thin rotating cylindrical shells with various boundary conditions. J. Sound Vib. 2012, 331, 4170–4186. [Google Scholar] [CrossRef]
- Xiang, S.; Li, G.C.; Zhang, W.; Yang, M.S. Natural frequencies of rotating functionally graded cylindrical shells. Appl. Math. Mech. 2012, 33, 345–356. [Google Scholar] [CrossRef]
- Zohar, A.; Aboudi, J. The free vibrations of a thin circular finite rotating cylinder. Int. J. Mech. Sci. 1973, 15, 269–278. [Google Scholar] [CrossRef]
- Lam, K.Y.; Loy, C.T. Free Vibrations of a Rotating Multi-Layered Cylindrical Shell. Int. J. Solids Struct. 1995, 32, 647–663. [Google Scholar] [CrossRef]
- Sheng, G.G.; Wang, X. The non-linear vibrations of rotating functionally graded cylindrical shells. Nonlinear Dyn. 2017, 87, 1095–1109. [Google Scholar] [CrossRef]
- Hosseini-Hashemi, S.; Ilkhani, M.R.; Fadaee, M. Accurate natural frequencies and critical speeds of a rotating functionally graded moderately thick cylindrical shell. Int. J. Mech. Sci. 2013, 76, 9–20. [Google Scholar] [CrossRef]
- Soldatos, K.P. Hadjigeorgiou vthree-dimensional solution of the free vibration problem of homogeneous isotropic cylindrical shells and panels. J. Sound Vib. 1990, 137, 369–384. [Google Scholar] [CrossRef]
- Keleshteri, M.M.; Jelovica, J. Nonlinear vibration behavior of functionally graded porous cylindrical panels. Compos. Struct. 2020, 239, 112028. [Google Scholar] [CrossRef]
- Loy, C.T.; Lam, K.Y. Vibrations of Rotating Thin Cylindrical Panels. Appl. Acoust. 1995, 46, 327–343. [Google Scholar] [CrossRef]
- Xie, F.; Tang, J.; Wang, A.; Shuai, C.; Wang, Q. Free vibration of functionally graded carbon nanotube reinforced composite cylindrical panels with general elastic supports. Curved Layer. Struct. 2018, 5, 95–115. [Google Scholar] [CrossRef]
- Zhang, H.; Shi, D.; Wang, Q.; Qin, B. Free vibration of functionally graded parabolic and circular panels with general boundary conditions. Curved Layer. Struct. 2017, 4, 52–84. [Google Scholar] [CrossRef]
- Dong, Y.H.; Zhu, B.; Wang, Y.; Li, Y.H.; Yang, J. Nonlinear free vibration of graded graphene reinforced cylindrical shells: Effects of spinning motion and axial load. J. Sound Vib. 2018, 437, 79–96. [Google Scholar] [CrossRef]
- Li, X.; Li, Y.H.; Xie, T.F. Vibration characteristics of a rotating composite laminated cylindrical shell in subsonic air flow and hygrothermal environment. Int. J. Mech. Sci. 2019, 150, 356–368. [Google Scholar] [CrossRef]
- Liew, K.M.; Yang, J.; Wu, Y.F. Nonlinear vibration of a coating-FGM-substrate cylindrical panel subjected to a temperature gradient. Comput. Methods Appl. Mech. Eng. 2006, 195, 1007–1026. [Google Scholar] [CrossRef]
- Safar Pour, H.; Ghanbari, B.; Ghadiri, M. Buckling and free vibration analysis of high speed rotating carbon nanotube reinforced cylindrical piezoelectric shell. Appl. Math. Model 2019, 65, 428–442. [Google Scholar] [CrossRef]
- Chen, Y.; Jin, G.; Ye, T.; Lee, H. Three-dimensional vibration analysis of rotating pre-twisted cylindrical isotropic and functionally graded shell panels. J. Sound Vib. 2022, 517, 116581. [Google Scholar] [CrossRef]
- Chan, D.Q.; Van Hoan, P.; Trung, N.T.; Hoa, L.K.; Huan, D.T. Nonlinear buckling and post-buckling of imperfect FG porous sandwich cylindrical panels subjected to axial loading under various boundary conditions. Acta Mech. 2021, 232, 1163–1179. [Google Scholar] [CrossRef]
- NGT, Y.; Lam, K.Y.; Reddy, J.N. parametric resonance of a rotating cylindrical shell subjected to periodic axial loads. J. Sound Vib. 1998, 214, 513–529. [Google Scholar]
- Liew, K.M.; Hu, Y.G.; Ng, T.Y.; Zhao, X. Dynamic stability of rotating cylindrical shells subjected to periodic axial loads. Int. J. Solids Struct. 2006, 43, 7553–7570. [Google Scholar] [CrossRef]
- Dai, Q.; Cao, Q. Parametric instability of rotating cylindrical shells subjected to periodic axial loads. Int. J. Mech. Sci. 2018, 146–147, 1–8. [Google Scholar] [CrossRef]
- Heydarpour, Y. Malekzadeh Dynamic Stability of Rotating FG-CNTRC Cylindrical Shells under Combined Static and Periodic Axial Loads. Int. J. Struct. Stab. Dyn. 2018, 18, 1850151. [Google Scholar] [CrossRef]
- Han, Q.; Chu, F. Parametric resonance of truncated conical shells rotating at periodically varying angular speed. J. Sound Vib. 2014, 333, 2866–2884. [Google Scholar] [CrossRef]
- Li, X.; Du, C.C.; Li, Y.H. Parametric resonance of a FG cylindrical thin shell with periodic rotating angular speeds in thermal environment. Appl. Math. Model 2018, 59, 393–409. [Google Scholar] [CrossRef]
- Li, X.; Jiang, W.T.; Chen, X.C. Parametric Instability of Rotating Functionally Graded Graphene Reinforced Truncated Conical Shells Subjected to Both Mechanical and Thermal Loading Conditions. Int. J. Struct. Stab. Dyn. 2022, 22, 2250067. [Google Scholar] [CrossRef]
- Phu, K.; Van Bich, D.H.; Doan, L.X. Nonlinear Dynamic Stability of Variable Thickness FGM Cylindrical Shells Subjected to Mechanical Load. In Modern Mechanics and Applications; Springer: Singapore, 2022; pp. 506–521. [Google Scholar]
- Zhao, S.; Yang, Z.; Kitipornchai, S.; Yang, J. Dynamic instability of functionally graded porous arches reinforced by graphene platelets. Thin-Walled Struct. 2020, 147, 106491. [Google Scholar] [CrossRef]
- Han, Q.; Qin, Z.; Zhao, J.; Chu, F. Parametric instability of cylindrical thin shell with periodic rotating speeds. Int. J. Non-Linear Mech. 2013, 57, 201–207. [Google Scholar] [CrossRef]
- Pellicano, F.; Amabili, M. Stability and vibration of empty and fluid-filled circular cylindrical shells under static and periodic axial loads. Int. J. Solids Struct. 2003, 40, 3229–3251. [Google Scholar] [CrossRef]
- Ng, T.Y.; Lam, K.Y.; Liew, K.M.; Reddy, J.N. Dynamic stability analysis of functionally graded cylindrical shells under periodic axial loading. Int. J. Solids Struct. 2001, 38, 1295–1309. [Google Scholar] [CrossRef]
- Sofiyev, A.H.; Kuruoglu, N. Parametric instability of shear deformable sandwich cylindrical shells containing an FGM core under static and time dependent periodic axial loads. Int. J. Mech. Sci. 2015, 101–102, 114–123. [Google Scholar] [CrossRef]
- Sofiyev, A.H. Influences of shear stresses on the dynamic instability of exponentially graded sandwich cylindrical shells. Compos. Part B Eng. 2015, 77, 349–362. [Google Scholar] [CrossRef]
- Dong, Y.H.; Li, Y.H.; Chen, D.; Yang, J. Vibration characteristics of functionally graded graphene reinforced porous nanocomposite cylindrical shells with spinning motion. Compos. Part B Eng. 2018, 145, 1–13. [Google Scholar] [CrossRef]




| h/b | (degree) | Soldatos and Hadjigeorgiou [16] | Present Study |
|---|---|---|---|
| 0.1 | 30 | 0.7001 | 0.6393 |
| 60 | 0.8096 | 0.7589 | |
| 90 | 0.9574 | 0.9296 | |
| 0.2 | 30 | 1.2032 | 1.1158 |
| 60 | 1.1979 | 1.1462 | |
| 90 | 1.2199 | 1.2143 | |
| 0.3 | 30 | 1.5947 | 1.4945 |
| 60 | 1.528 | 1.4804 | |
| 90 | 1.4699 | 1.4864 |
| d = 0.5 | |||||
|---|---|---|---|---|---|
| (m,n) | Nt1 | SofIiyev [39] | Kuruoglu | Present Study | |
| P1 | P2 | P1 | P2 | ||
| (1,1) | 0 | 66.5 | 66.55 | 67.421 | 67.421 |
| 0.1 | 66.964 | 66.132 | 67.8412 | 66.9984 | |
| 0.3 | 67.786 | 65.29 | 68.6736 | 66.1449 | |
| 0.5 | 68.598 | 64.436 | 69.4961 | 65.2802 | |
| d = 2 | |||||
| (1,3) | 0 | 60.196 | 60.571 | 60.588 | 60.966 |
| 0.1 | 60.196 | 59.819 | 60.588 | 60.209 | |
| 0.3 | 61.314 | 59.056 | 61.714 | 62.453 | |
| 0.5 | 62.049 | 58.284 | 59.442 | 58.664 | |
| n | Porosity Coefficient | Yuewu and Dafang [7] | Present Study |
|---|---|---|---|
| 1 | 0 | 1.2429 | 1.2465 |
| 0.2 | 1.2155 | 1.2191 | |
| 0.4 | 1.1893 | 1.1931 | |
| 0.6 | 1.1677 | 1.1718 | |
| 0.8 | 1.1633 | 1.1682 | |
| 4 | 0 | 1.2256 | 1.246 |
| 0.2 | 1.2006 | 1.2208 | |
| 0.4 | 1.1772 | 1.1974 | |
| 0.6 | 1.159 | 1.1795 | |
| 0.8 | 1.1591 | 1.1805 |
| θ (Degree) | Porosity Coefficient | (m,n) = (1,1) | (m,n) = (1,2) | (m,n) = (1,3) |
|---|---|---|---|---|
| p (Type 2) | p (Type 2) | p (Type 2) | ||
| 30 | 0.1 | 1.181 | 3.6808 | 7.594 |
| 0.3 | 1.1767 | 3.6665 | 7.542 | |
| 0.5 | 1.1783 | 3.6726 | 7.526 | |
| 0.7 | 1.1956 | 3.725 | 7.591 | |
| 0.9 | 1.2659 | 3.9365 | 7.954 | |
| 100 | 0.1 | 0.3461 | 0.3367 | 0.723 |
| 0.3 | 0.3349 | 0.3355 | 0.722 | |
| 0.5 | 0.3235 | 0.3416 | 0.726 | |
| 0.7 | 0.313 | 0.3625 | 0.739 | |
| 0.9 | 0.3103 | 0.787 | ||
| 180 | 0.1 | 0.3368 | 0.1271 | 0.212 |
| 0.3 | 0.3253 | 0.1246 | 0.211 | |
| 0.5 | 0.3134 | 0.1224 | 0.212 | |
| 0.7 | 0.3021 | 0.1212 | 0.216 | |
| 0.9 | 0.2978 | 0.1243 | 0.23 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaidan, S.M.; Hasan, H.M. Parametric Instability of Functionally Graded Porous Cylindrical Panels under the Effect of Static and Time-Dependent Axial Loads. Vibration 2022, 5, 570-584. https://doi.org/10.3390/vibration5030033
Zaidan SM, Hasan HM. Parametric Instability of Functionally Graded Porous Cylindrical Panels under the Effect of Static and Time-Dependent Axial Loads. Vibration. 2022; 5(3):570-584. https://doi.org/10.3390/vibration5030033
Chicago/Turabian StyleZaidan, Salah M., and Hamad M. Hasan. 2022. "Parametric Instability of Functionally Graded Porous Cylindrical Panels under the Effect of Static and Time-Dependent Axial Loads" Vibration 5, no. 3: 570-584. https://doi.org/10.3390/vibration5030033
APA StyleZaidan, S. M., & Hasan, H. M. (2022). Parametric Instability of Functionally Graded Porous Cylindrical Panels under the Effect of Static and Time-Dependent Axial Loads. Vibration, 5(3), 570-584. https://doi.org/10.3390/vibration5030033











