1. Introduction
Piezo-actuators are used extensively in high precision positioning devices due to their various desirable proprieties, such as high positioning accuracy, nanometre repeatable displacement resolution and a high level of stiffness [
1,
2]. They produce large forces, relatively high bandwidth and frictionless motion [
3]. Precision positioning stages currently have widespread use due to their popularity and use in a variety of applications [
4,
5]. Their uses include Atomic Force Microscope (AFM), such as biological manipulation [
6]. Another popular application is scanning probe microscopy, where the nanopositioner moves the surface in a raster pattern, which is used to generate a topographic image of the surface with a nanometre scale. This image is beneficial as it provides qualitative information about the sample surface, which could be useful in investigating the magnetic or electrical properties of the surface [
7].
A piezo-driven nanopositioner is an electromechanical mechatronics device that exploits the properties of piezo-actuators to provide precise motion. The two-axis nanopositioner is used to generate the raster scan in the
x-axis (fast axis) and
y-axis (slow axis) with the aid of piezoelectric stack actuators. The raster pattern is the most common scanning trajectory employed by nanopositioning systems when precise tracking of periodic references is necessary. Scanning ramp-like signals (high-frequency component) will therefore be required in order to drive the nanopositioner to scan as fast as possible without generating significant positioning errors. The triangular wave is popularly employed to drive the
x-axis of the nanopositioner and generate the raster pattern. A piezo-driven nanopositioner is a lightly-damped system. Lightly-damped resonant systems are prone to excitation of the resonant modes [
8]. The performance of many mechatronics systems is substantially degraded due to unwanted excitation of system resonance, thereby producing vibrations [
9]. The performance of the entire positioning stage is limited by the vibration effect of the lightly-damped resonant dynamics behaviour. The occurrence of a sharp resonant peak accompanied by a rapid-phase transition in the dynamics leads to a low stability margin in the structure. This peak compounds the effect of high-frequency dynamics and exhibits vibration problems, particularly if the structure is driven by a high-frequency component signal. This is an obstacle, especially when driving the positioning stage with a triangular signal.
There are numerous issues with controlling a piezo-driven stage nanopositioner to deliver the desired accurate positioning. For example, structural vibration (resonance) [
10], sensor noise [
11], thermal drift [
12], cross-coupling [
13], time delay (phase-shift) [
14], and nonlinearities such as hysteresis [
15] and creep [
16]. Controlling the piezo-driven positioning stage is not an easy task due to various issues associated with the piezo-actuators, as noted above. The control object in nanopositioning applications is there to keep the tracking error to a minimum and to maintain robust closed-loop stability. Conventional sensor-based linear feedback controls, such as PI and I, on their own are not suitable to meet high-speed nanopositioning accuracy and robustness. This is because they are limited in bandwidth due to the mechanical resonance of the positioning stage. In order to overcome this limitation, the control design procedures combine both damping and tracking control. The traditional approach is to use a damping controller to treat the resonance and tracking controller to address induced nonlinearity (hysteresis).
The aim of damping control is to obtain a flat frequency response in the closed-loop at a low frequency in order to preserve most of the harmonic that forms the triangle wave. The closed-loop frequency response must also roll off at higher frequencies in order to reduce the effect of higher order dynamics and noise [
17]. Flattening the frequency response is achieved by damping the system’s first resonant mode, as a result, increasing the gain margin of the system [
18]. Damping control techniques are useful for artificially increasing the damping ratio of a system, and this will provide the capacity to increase the feedback gain and closed-loop bandwidth [
19]. The damping controllers are still unable to raise the bandwidth beyond the resonance frequency. These controllers have the advantage of being insensitive to variation in the resonance frequency. There are many types of damping controllers in the literature, such as the Integral Force Feedback (IFF) [
20], Integral Resonant Controller (IRC) [
21], Positive Velocity and Position Feedback (PVPF) [
22], Shunt Control [
23], Robust Control [
24], Positive Position Feedback (PPF), Direct Velocity Feedback (DVF) [
25] and Resonant Control (RC) [
26]. In this article, the IRC is used to dampen the mechanical resonance of the nanopositioner due to its simplicity and robustness.
After damping control, conventional Proportional Integral (PI) or Integral (I) control algorithms are able to achieve accurate tracking control in nanopositioning applications. There are numerous attempts in the literature to employ a double integral, as reported in [
27,
28]. However, these control methods increase the order of the system and introduce a phase shift in the tracking control. Although a low-order control scheme is reported in [
29], the use of this feedback control law is limited in nanopositioning applications due to bandwidth. Therefore, it does not meet the requirement for an ultra-precise application.
This paper uses the IRC in the damping loop, combined with a PI controller in the tracking loop. The PI tracking-based strategic placement of the zero is proposed. This will improve the positioning bandwidth and result in reduced tracking error. An overview of the system model is presented in
Section 2; the traditional and proposed control schemes are described in detail in
Section 3; the experimental results in the frequency- and time-domains are reported in
Section 4; and the paper ends with concluding remarks in
Section 5.
2. System Modelling
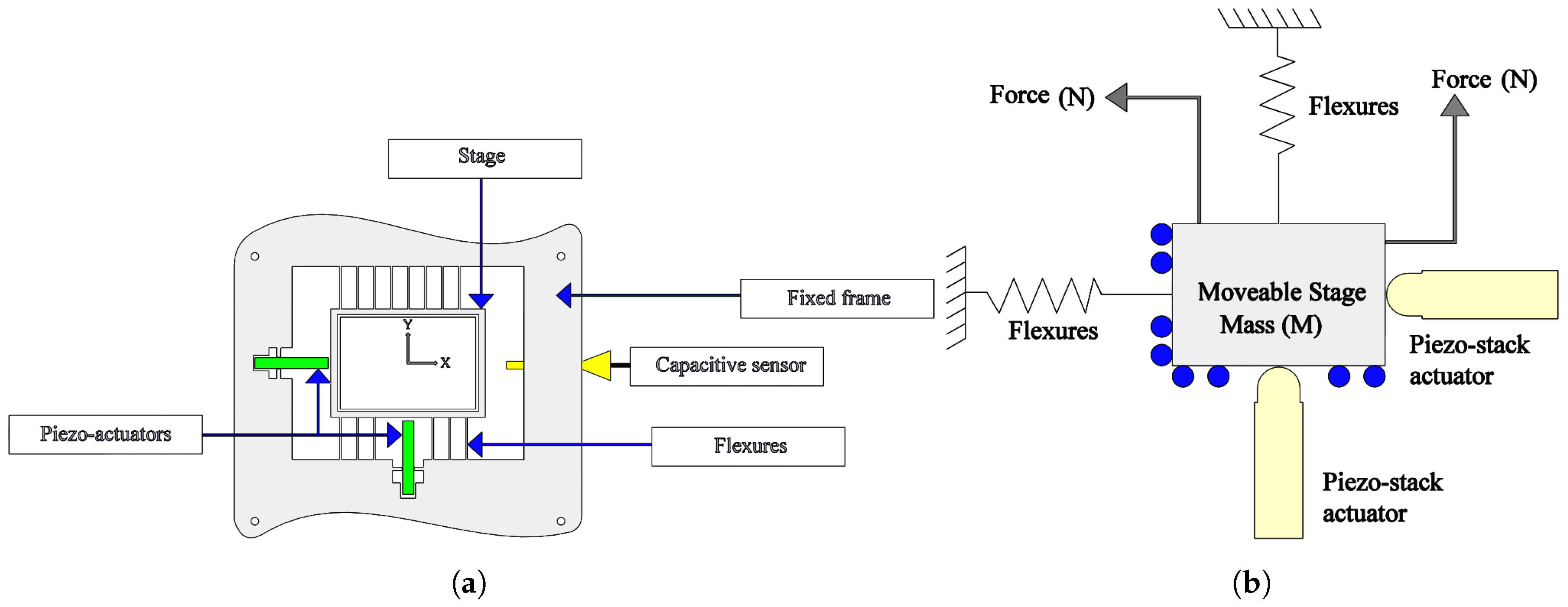
The employed nanopositioner is presented in
Figure 1a and can be modelled from the mechanical perspective as a mass spring damper by virtue of its constituent piezoelectric effect and restoring force flexures. A schematic representation of the nanopositioner in the form of a simplified mechanical model is illustrated in
Figure 1b.
As shown in
Figure 1a, the axis of the piezo-driven stage is equipped with a capacitive sensor for position measurement. The two axes (
x and
y) are driven by piezo stack flexure-based actuators. Each actuator is capable of generating 40
m of motion along each axis with the aid of flexures.
The dynamic system can be described by the linear differential equation. The equation of motion is formulated using Newton’s law as follows:
The simplified system is characterised by the stiffness and the damping of the flexures, referred to as
and
, whilst the inertia (mass) of the stage is denoted as
. The system dynamics is regulated by the piezo-actuator force that moves the nanopositioning stage and is called
, and the stiffness is
. The displacement of the stage is referred to as
d. As the flexures and the actuators are mechanically parallel, their stiffness can be combined, as in the equation below:
where
k denotes the combined stiffness. Therefore, the following transfer function describes the relationship between the applied force of actuator
and the displacement of the stage by taking the Laplace transform of Equation (
2).
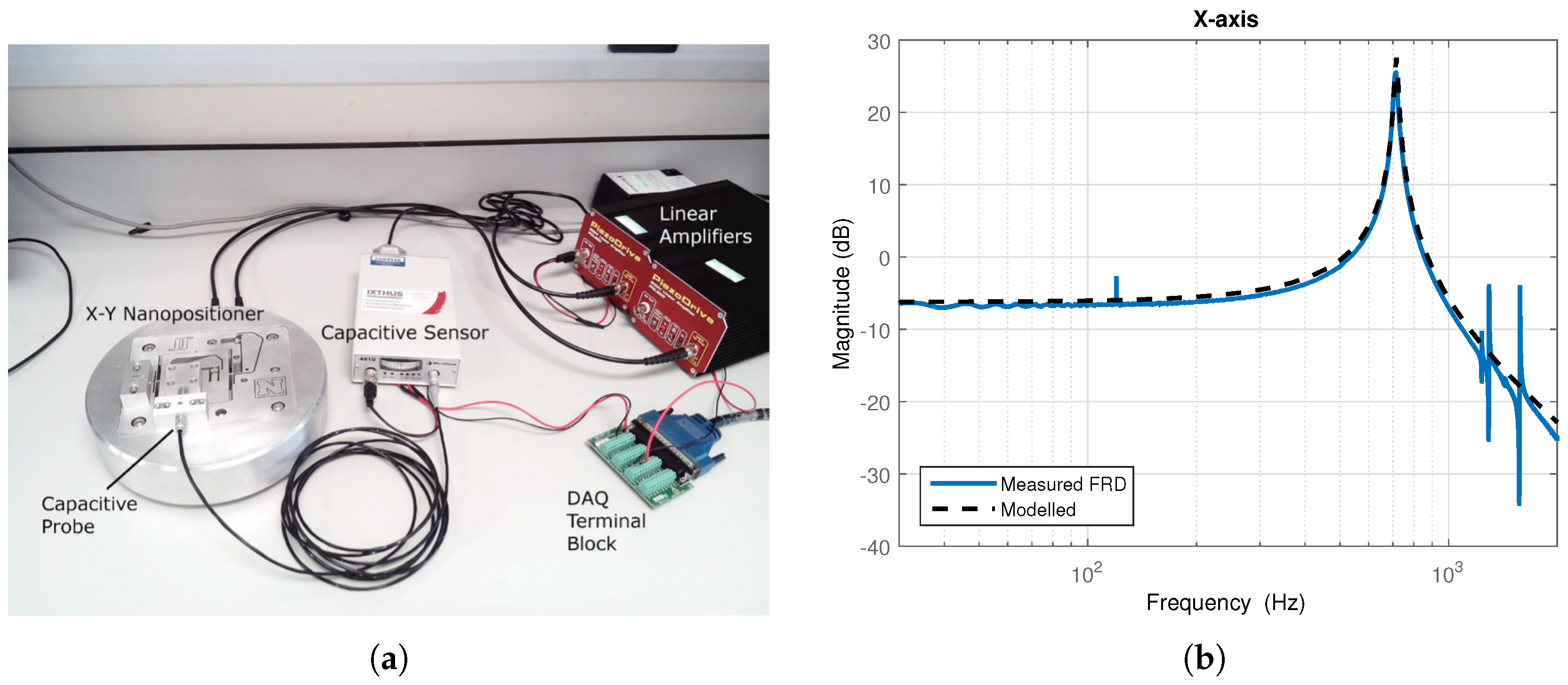
Figure 2a presents a snapshot of the experimental setup, and it consists of a two-axis (
x and
y) serial kinematic piezoelectric stack-driven flexure-based nanopositioner. Each axis is driven by a 10-mm 200-V piezoelectric stack actuator capable of generating 40
m of motion along each axis. The nanopositioner also provides integrated mounts for capacitive sensor probes. The MicroSense 6810 capacitive displacement sensor and 6504-01 probe with a sensitivity of 5
m/V provide a voltage signal proportional to the displacement sensed along each axis. The piezoelectric stack actuators are driven by two PiezoDrive PDL200 voltage amplifiers with a gain of 20. All the open-loop and closed-loop experiments and consequent time-domain data are captured using a real-time module at a sampling frequency of 20 kHz. The frequency response data are recorded using an HP 35670A FFT Dynamic Signal Analyser (DSA). The open-loop frequency response of one axis of the nanopositioner is obtained by sending a band-limited random noise input generated by the DSA of amplitude 0.25
within the frequency range 20 Hz–2 kHz. This signal was fed to the voltage amplifier as the input, and the output of the amplifier was used to excite the piezoelectric stack. This input corresponds to a displacement within 0 and 2
m, or 5% of the total range of the stage. The open-loop transfer function-based model for the
x-axis of the piezo-driven nanopositioner is presented in
Figure 2b. The system is characterised by the resulting first dominant resonance of the
x-axis, which appears at 716 Hz, as is clear from
Figure 2b.
The resulting mechanical frequency response can be described as in the following dynamic system transfer function using the frequency response analysis:
where
is the damping ratio,
is the natural frequency, and
is chosen to adjust the gain of the stage at 0-Hz frequency. The transfer function of the stage is identified solely based on the first dominant mode, as in the following transfer function:
This is because a simple second-order transfer function with a suitably low damping coefficient and the correct resonant frequency is sufficient to capture the dominant in-bandwidth dynamics of a nanopositioner axis. This model will be used in the design of the controllers in this article. There are a couple of low-magnitude modes seen within the bandwidth of interest, but these are beyond the dominant mode. These can be safely ignored due to their small dynamic range compared to that of the dominant mode at 716 Hz. Consequently, the measured magnitude response looks similar to that exhibited by a typical second-order system with low damping. As the identification was done from 20 Hz onwards, the effect of creep was eliminated due to the absence of any low-frequency components. The piezoelectric stack actuator for the other axis was shorted to eliminate its cross-coupling effect. The sensor and the operational amplifier can be modelled by a first-order low-pass filter with a cut-off frequency of 10,000 Hz and 5000 Hz, respectively. The system identification process for a linear dynamic model of the considered system is thus completed.
In order to allow for an accurate description of the system, this work utilises a nonlinear hysteresis model for the nanopositioner. Bouc–Wen is a popular hysteresis modelling technique to approximate the physical hysteretic behaviour of the system. It uses a first-order nonlinear differential equation with displacement as its input variable and restoring force as its output variable, as shown in Equation (
6) [
30]:
The applied voltage can be denoted as
u and
x as the displacement of the piezoelectric actuator;
m,
b,
k and
d represent the effective mass, damping coefficient, mechanical stiffness and effective piezoelectric coefficients (
m per volt), respectively.
h represents the nonlinear relationship between the lag force (the applied voltage) and the displacement. The parameters
,
and
are identified simultaneously in order to represent the hysteresis loop’s magnitude and shape, where
,
and
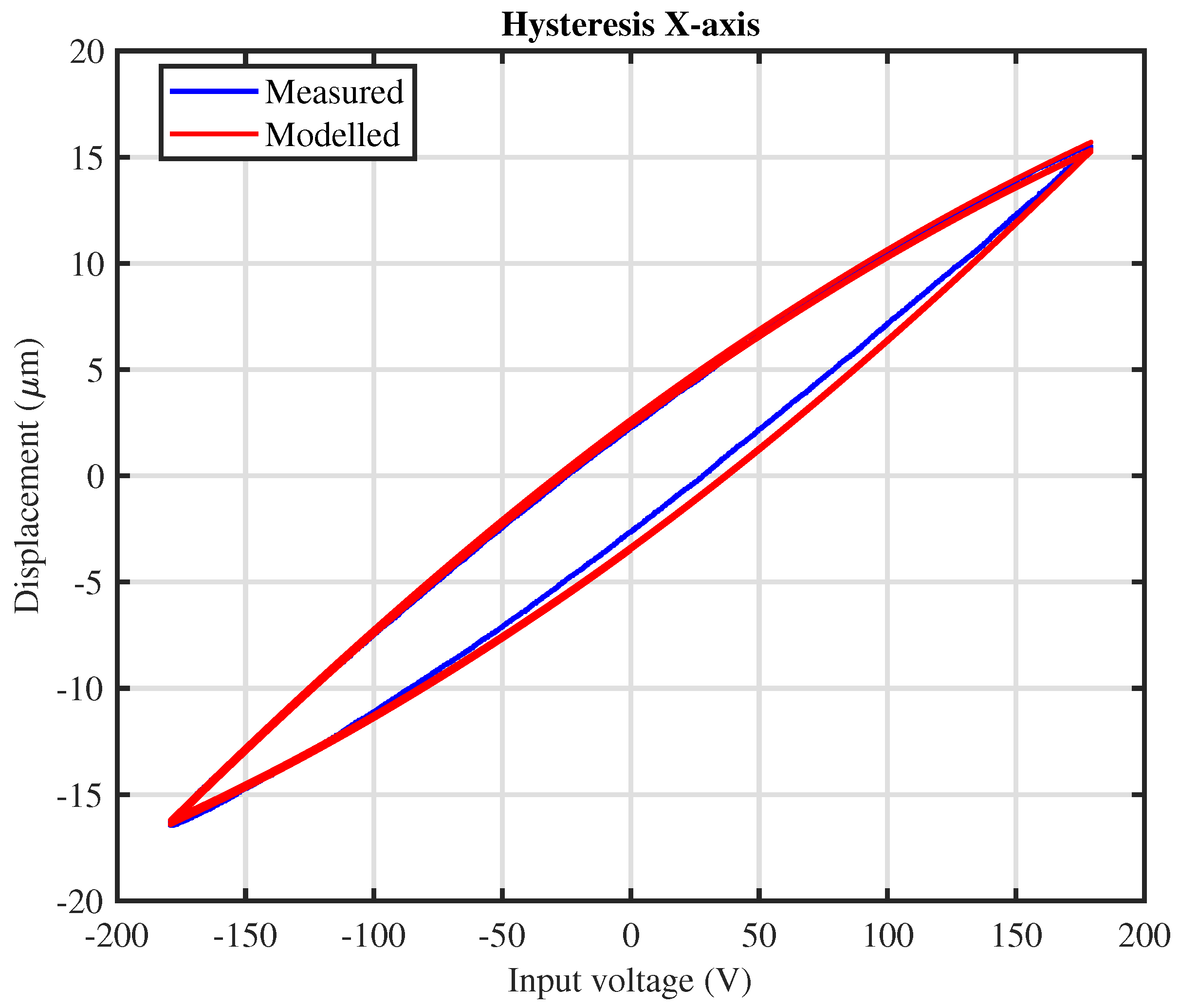
, which capture the major hysteresis cycles. The identified Bouc–Wen hysteresis model represents the nonlinear behaviour, and the above equations are realised in MATLAB Simulink, as in the following figure. The proposed hysteresis model is investigated by applying a 180-V peak amplitude sinusoidal signal of 10 Hz to the nanopositioner. A comparison of recorded and simulated displacement profiles is performed in open-loop, as is evident in
Figure 3.
A nonlinear rate-independent relationship is found to exist between the control voltages applied to the piezo-actuators and their displacements (10 m). From the figure, it can be observed that the output of the nanopositioner is independent of the input. As the sinusoidal input alternates between an increasing and decreasing condition, the output of the nanopositioner diverges from its desired path, resulting in a hysteresis loop. The hysteresis loop is a measure of the deformation of the piezo-driven nanopositioner displacement in response to the sinusoidal input voltage. As mentioned above with regard to precise positioning, this behaviour should be modelled and eliminated. The following section presents the traditional control of the piezo-driven nanopositioner.
4. Experimental Results
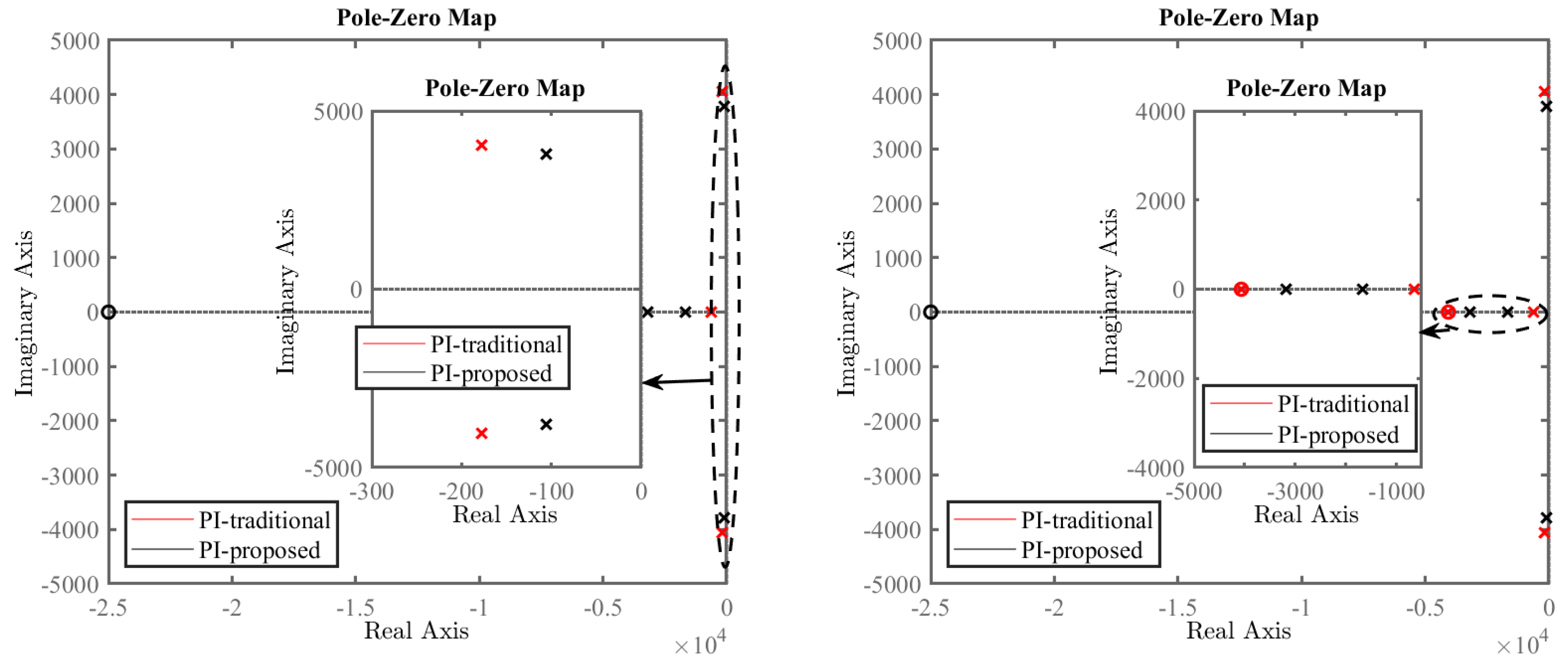
In this section, experimental-based tuning values for the tracking gain and placement of the PI zero are proposed. The pole-zero maps of the traditional and proposed control methods are plotted in
Figure 5. The closed-loop was asymptotically stable using both the conventional and proposed methods. The pole of the IRC was precisely cancelled by the tracking controller using the traditional method, as is clear from
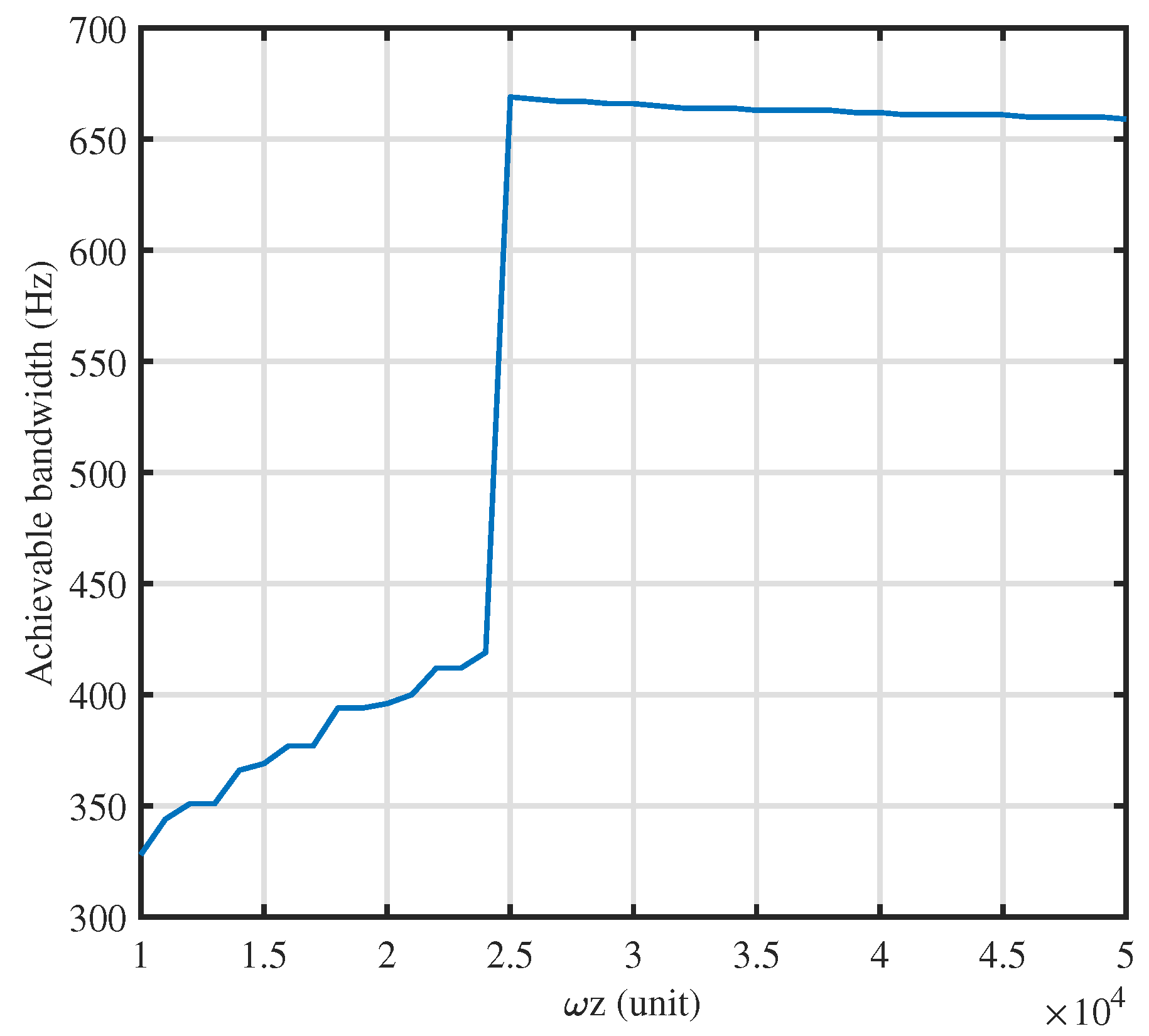
Figure 5. Using the proposed method, the pole of the tracking controller was placed at a significant distance from the IRC pole in accordance with the best achievable bandwidth, as in
Figure 6. From the figure, it can be observed that placing the PI zero at a significant distance from the IRC pole was important for increasing the bandwidth. It should be noted that, in order to guarantee stability, it is recommended that
10,000
for the selected value of
, as in
Table 1. With regard to the value of the integral gain,
is selected to provide a sufficient phase margin for the system to account for time delay and provide a reasonable gain margin for uncertainties.
Table 1 lists the controller parameters obtained experimentally for both the traditional and the proposed method. The table shows that the arrangement of the PI zero in such a way as to cancel exactly the IRC pole (
) is not beneficial.
Using the traditional method for the selected value of
=
, in order to guarantee stability and provide a reasonable stability margin, the value of the tracking gain
was chosen to be around 1300. Thus, the maximum allowable value of the tracking gain
was 1300. As shown in
Table 1, the achievable bandwidth using the traditional method was limited to around 110 Hz. As mentioned above, the selected value of the PI zero to cancel exactly the pole of the IRC restricted the gain margin. On the other hand, placing the PI zero at a significant distance from the IRC pole increased the gain margin, and as a result, a higher value of the tracking gain can be chosen. Therefore, improvement in positioning bandwidth was obtained around 668 Hz, as is clear in
Table 1. The table presents the achievable bandwidth such that the closed-loop response must not deviate from ±3 dB. Error was reduced using the proposed method as a result of the higher bandwidth obtained.
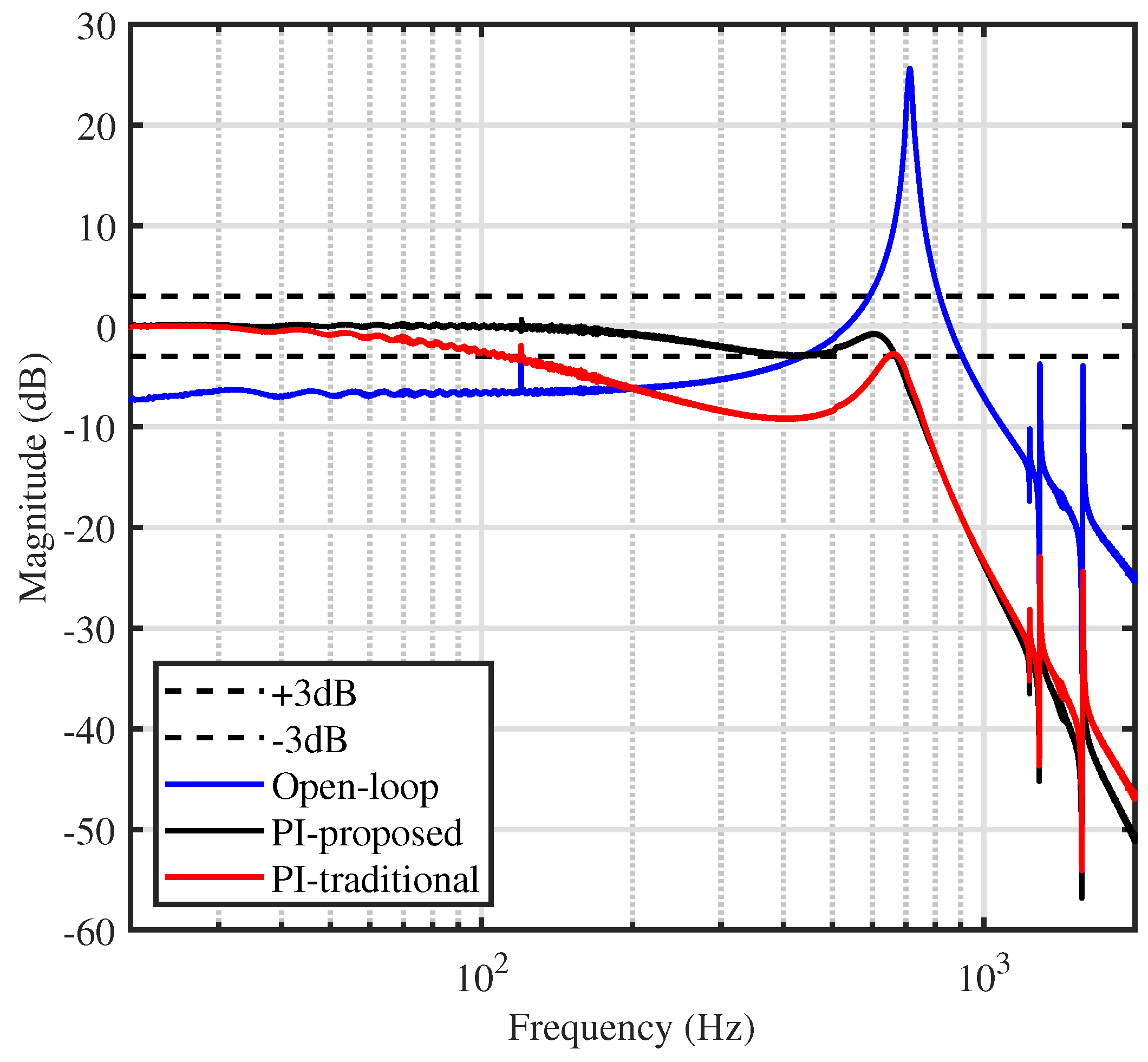
Figure 7 shows the open- and closed-loop frequency response obtained experimentally for the traditional and proposed methods. It can be observed that significant improvement in the closed-loop bandwidth was achieved. This improvement was so effective at capturing the frequencies that it formed the triangular wave.
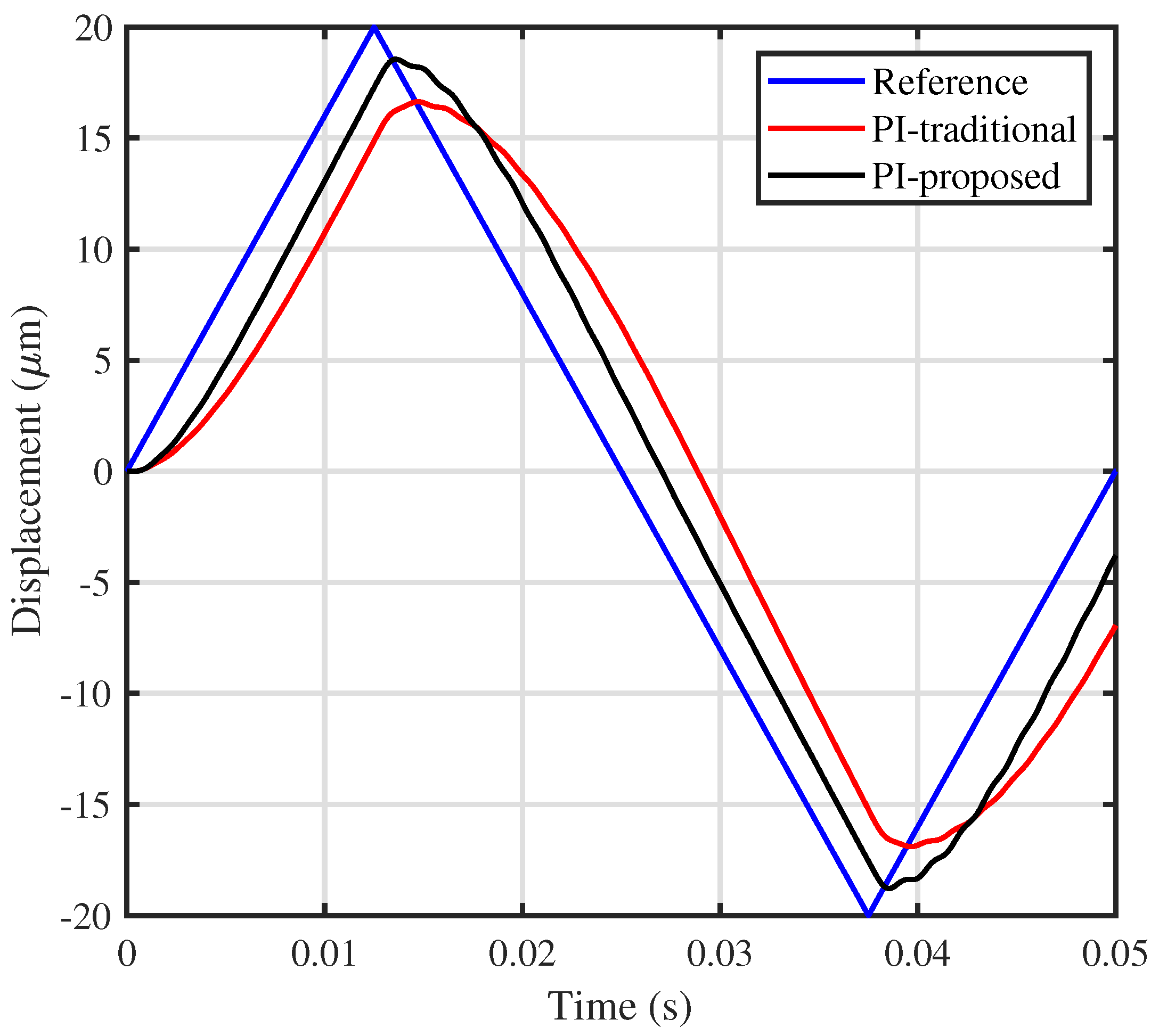
In order to inspect the obtained bandwidth in the time-domain and in the presence of disturbances such as hysteresis, the time-domain tracking is plotted in
Figure 8 for a 20-Hz triangular reference. It can be seen that a significant improvement in tracking performance was achieved using the proposed method.
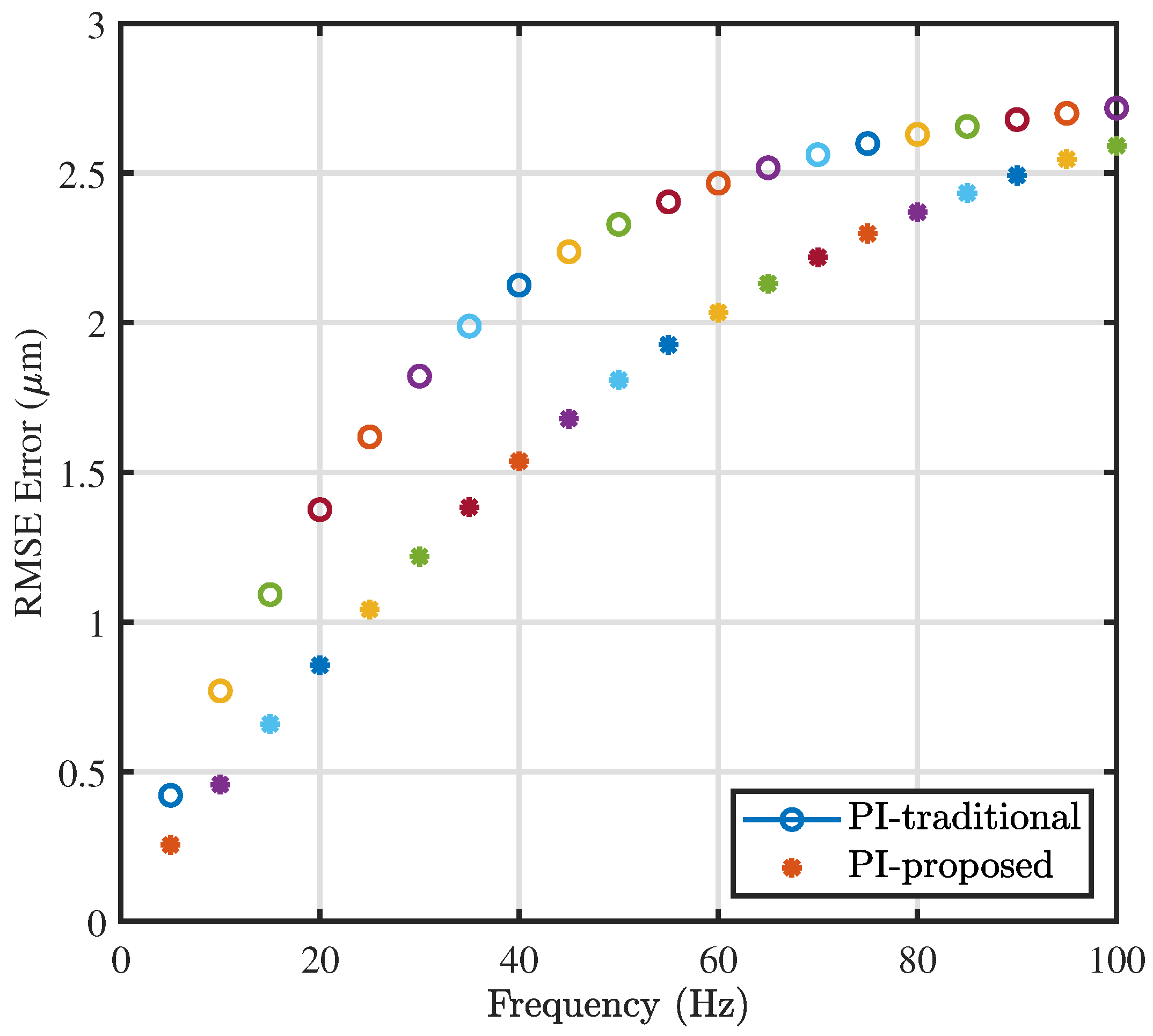
In order to further show the significant improvement,
Figure 9 provides the root mean squared error (RMSE) for tracking triangular trajectories. The error was reduced remarkably using the proposed method.
In order to account for uncertainties, such as unmodelled dynamics and latency due to amplifier and sensor circuitry, the tuned controller parameters offered a reasonably stable system. The experimental results provided a sufficient phase margin to account for time delay in the system and GM to account for uncertainties. The greater the stability margins, the more stable the system in the closed-loop. The nanopositioning stage was susceptible to parameter changes due to loading, and therefore, sufficient GM can cope with the loading condition.
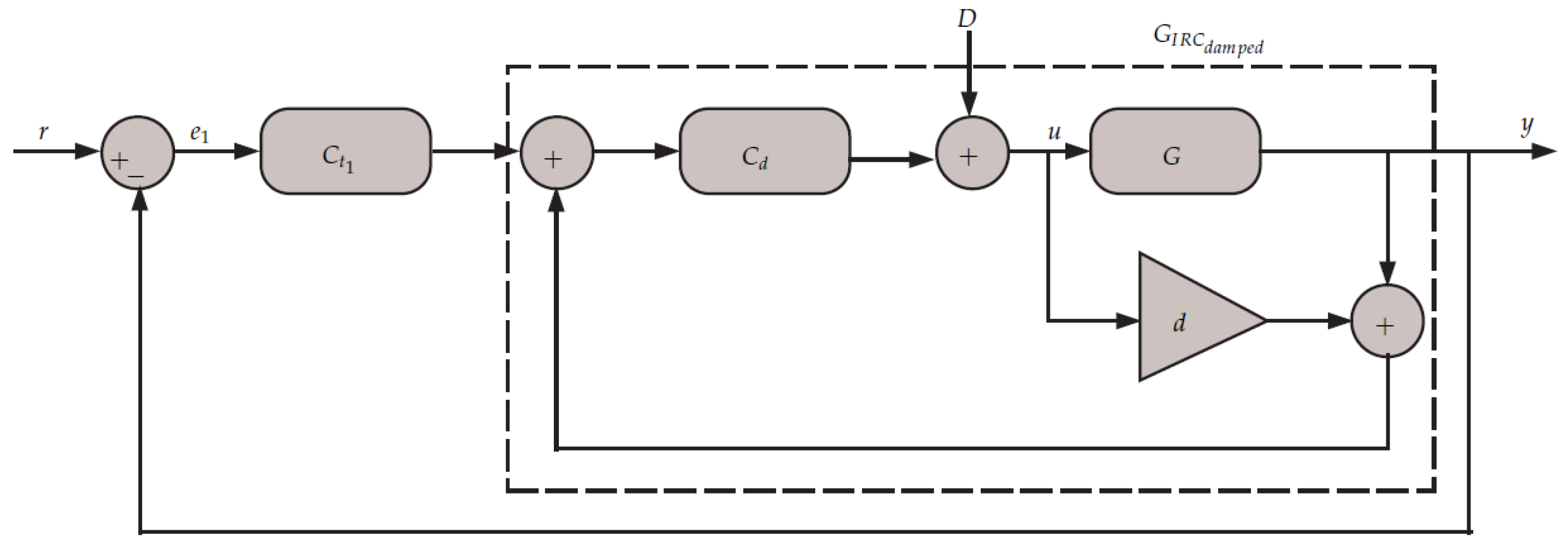
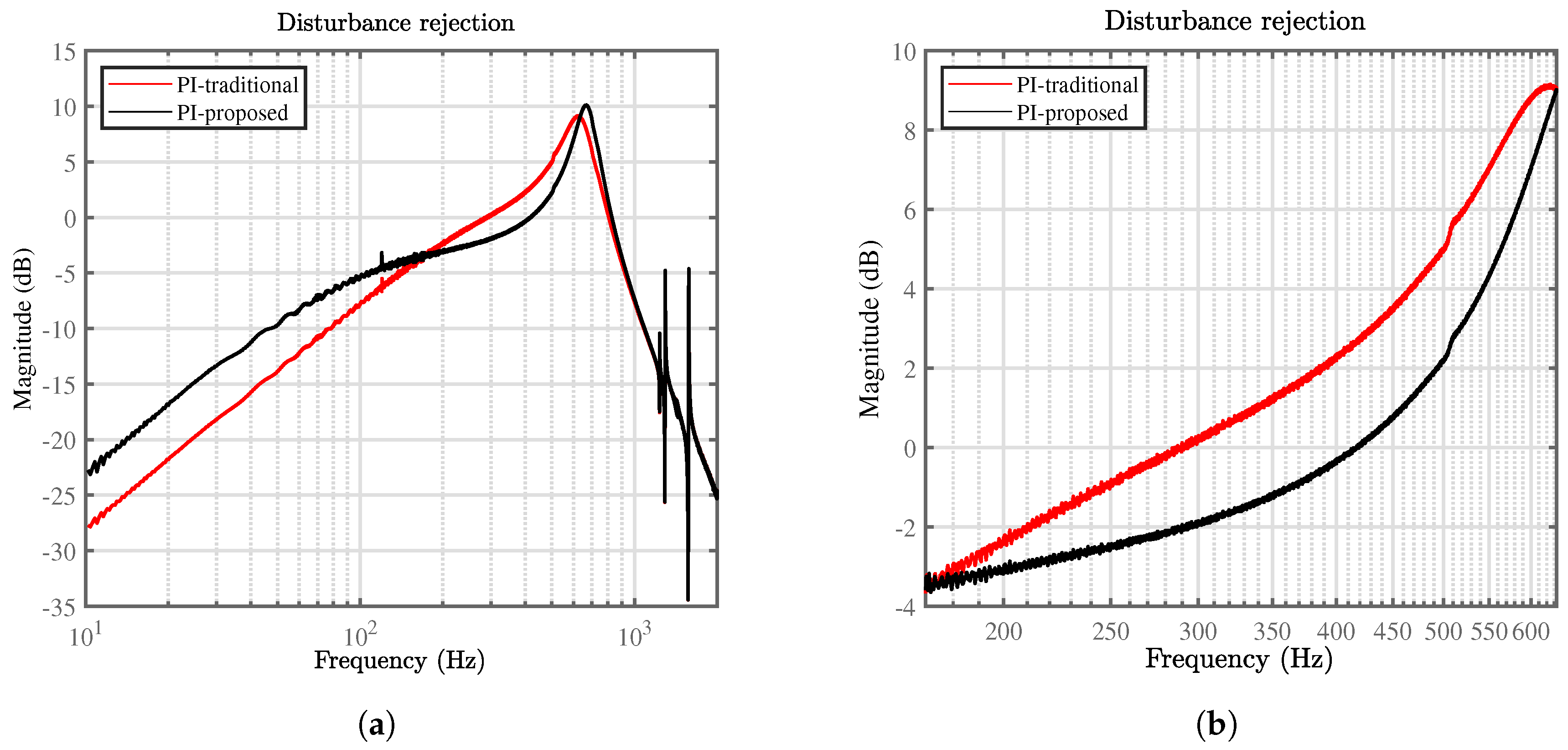
The disturbance rejection profile of the proposed method can be obtained by substituting
r = 0 in
Figure 4 and calculating
D, as in Equation (
15):
The above transfer function was tested experimentally and is plotted in
Figure 10a,b.
Significant disturbance rejection was provided over the bandwidth of interest. The capability of the traditional control method was minimal within the bandwidth of interest, while the proposed method offered higher disturbance. It should be noted that the disturbance profile of the proposed method was minimal around the resonant.