Thermophy: A Chebyshev Polynomial-Based Tool for Transport Property Estimation in Multicomponent Gas Systems

Abstract

The accurate computation of the thermophysical properties of gases and gas mixtures is critical for combustion analysis but remains challenging due to the precision and numerical stability required across wide temperature ranges. In this study, we present Thermophy, a computational framework based on Chebyshev polynomial fitting, developed to calculate thermal conductivity, viscosity, and binary diffusion coefficients for pure gases and multicomponent mixtures. Unlike conventional tools that rely on low-order polynomial approximations, Thermophy applies Chebyshev fitting over defined temperature intervals, enabling higher accuracy, improved numerical stability, and computational efficiency. Thermophy is validated through four case studies involving pure gases, binary mixtures, and ternary mixtures relevant to combustion applications. For pure gases and air, deviations in thermal conductivity and viscosity were found to be 1.22–4.25% and 0.11–4.71%, respectively. For ternary mixtures, viscosity deviations ranged from 0.11 to 0.24%, while binary mixtures showed deviations of 2.60% and 0.20% for viscosity and thermal conductivity, respectively. Binary diffusion coefficients exhibited an overall deviation of approximately 3.35%. The combination of flexible input handling, extensibility, and high-fidelity calculations positions Thermophy as a robust and efficient alternative for integration into combustion modeling and other gas-phase simulation frameworks, including gasification, pyrolysis, global carbon cycle analysis, environmental systems, and fire modeling.

1. Introduction

Improving combustion efficiency while minimizing environmental pollutants remains a critical goal in energy and process industries. This pursuit underlines the growing demand for highly efficient, low-emission combustion technologies [1,2]. Combustion, playing a crucial role in low-carbon economy in today’s society, research on combustion characteristics, as well as fire and explosion safety prevention have become popular [3,4,5]. Combustion is a complex phenomenon involving fluid flow, heat transfer, and chemical reactions [6]. The most commonly used form of combustion is turbulent, and the main forms of heat transfer are not only conduction and convection but also radiation. Moreover, the elementary reaction processes of many ion and radical species in a short time period dominate the combustion reaction [2]. Although experimental techniques provide valuable insights, they are often limited in their ability to resolve individual steps of the combustion process. Consequently, a complete understanding of combustion phenomena remains elusive [7,8]. However, the accuracy and scope of application of various models that mathematically describe the physical phenomena of combustion, as well as the fundamental physical properties that govern the combustion state are improved with the development of numerical analysis methods, computer performance and programs [9].

To simulate combustion phenomena accurately, reliable thermophysical property data are essential. These properties vary with temperature, pressure, and gas composition, and must be calculated with high precision. Over a wide range of temperatures for various substances related to the combustion phenomenon, combustion reactions are described in terms of dozens or even hundreds of elementary reaction processes [9]. During combustion analysis, these transport properties of the gases or gas mixtures should be calculated according to the temperature, pressure, and mixture component ratios. Traditionally, thermophysical data are taken from the literature on combustion reactions or from the JANAF Thermochemical Properties Tables [10] and the CHEMKIN Thermodynamic Database [11]. These are the tables containing collision integrals and potential parameters for components obtained from the Kinetic Theory of Gases. The potential parameters of the components show the molecular structure, potential well depth, collision diameter, dipole moment, polarizability and rotational relaxation number. However, the growing number of species involved in combustion systems, many of which have never been experimentally studied, necessitates the development of predictive methods for estimating transport properties. While experimental methods are the most accurate, they are often costly and time-consuming. Thus, a significant number of correlations were developed in order to determine viscosity, thermal conductivity, and diffusion coefficients of gases since experimental methods are typically not cost-effective and time-consuming although they are the most accurate approaches [12,13,14,15,16,17].

Recent advances in computing power, such as increased memory capacity, faster processors, and parallel computing techniques, now allow for high-accuracy calculations that were previously infeasible. This study hypothesizes that a new computational tool, grounded in kinetic theory and capable of utilizing species-specific parameters, can accurately compute the thermophysical properties of pure gases and gas mixtures without the time and cost burdens associated with experimental methods. Thus, in this study, we developed Thermophy, a tool implemented in FORTRAN, widely used in high-performance computing, to compute viscosity, thermal conductivity, and binary diffusion coefficients for both reacting and non-reacting gas mixtures. The Thermophy algorithm is implemented by potential parameters of species, collision integral tables, and NASA Glenn coefficients to calculate the thermophysical properties. Users or developers can easily use Thermophy with little effort by entering the mixture temperature, number of species in the mixture, and mole fractions of the species data of gas mixtures.

To date, several tools currently exist for combustion modeling, most notably CHEMKIN [18] and Cantera [19]. CHEMKIN, a commercial package, and Cantera, an open-source alternative, both use polynomial approximations to evaluate transport properties, typically third-order and fourth-order polynomials, respectively [20,21]. It is important that algorithms are developed that are numerically stable when implemented in the software [22]. However, the increasing number of interpolation nodes make the computation efficiency low with large interpolation precision. Chebyshev polynomial fitting is used to construct high precision in order to improve the accuracy and effectiveness [23,24]. In this regard, concerning the achievement of speed-up processes with accuracy during curve fitting for each transport property, Chebyshev polynomial fitting is suggested as a superior alternative to commercial tools, for accurate curve fitting for the calculation of the thermophysical properties of gases and gas mixtures.

Thus, we present Thermophy which follows the approach of a separate curve fitting using Chebyshev polynomials with a defined number of intervals between inlet and equilibrium temperatures for each transport property value. Unlike conventional tools such as CHEMKIN and Cantera, which use low-order polynomial fits, Thermophy employs piecewise Chebyshev polynomial fitting to achieve superior numerical stability and precision across wide temperature ranges. The use of Chebyshev polynomials represents a significant methodological advancement, especially in the context of scalable combustion simulations. By achieving experimental-level accuracy with reduced computational cost, Thermophy addresses a critical need in combustion modeling and other gas-phase processes where reliable transport property estimation is essential. This shows the novelty of Thermophy where it has the ability to address the requirements of the efficient computations of each chemical species and transport properties for gas mixtures in order to avoid costly exponential evaluations later. Implemented in FORTRAN for high-performance computing, Thermophy is lightweight, modular, and user-extensible, making it suitable for integration as a subroutine in broader combustion simulation frameworks.

In the present study, four case studies were performed via Thermophy involving the computation of viscosity, thermal conductivity, and binary diffusion coefficients of gases and gas mixtures. Viscosities and thermal conductivity values of C₂H₆, CH₄, CO₂, He gases and air, viscosity values of N₂-Ar-CO₂ and N₂-CO₂-CH₄ ternary gas mixtures with different molar compositions, viscosities and thermal conductivity values of the Xe-He binary gas mixture, and the binary diffusion coefficients of gases including He, Xe, CH₄, C₂H₄, N₂, H₂, CO₂, H₂O, Ar, CO and NO₂ are calculated by Thermophy at different temperatures. The computed results are compared with experimental and/or established computational data from the literature to assess the accuracy and robustness of the tool.

2. Theory and Calculations

The thermophysical properties (viscosity, thermal conductivity, and binary diffusion coefficients) of gases and gas mixtures can be calculated using collision integrals [25] and potential parameters [26,27] for components from the Kinetic Theory of Gases which show the molecular structure, potential well depth, collision diameter, dipole moment, polarizability, and rotational relaxation number.

2.1. Viscosity

The viscosity coefficient for a single component gas is given by [25],

$${\mu }_i=2.6693\times {10}^{-6}{\displaystyle \frac{{\left(W_{i}T\right)}^{1/2}}{{\sigma }_i^2{\Omega }_{i,i}^{\left(\mathrm{2,2}\right)*}(T^{*};{\delta }^{*})}}$$

(1)

where μ_i is viscosity, W_i is molecular weight, T is temperature, σ_i is the Lennard-Jones collision diameter, Ω_i,i is the collision integral, T^* is the reduced temperature, and δ^* is the reduced dipole moment of the ith species and,

$$T^{*}=k^{o}T/{ϵ}_i,{\delta }^{*}={\displaystyle \frac{1}{2}}{\displaystyle \frac{d_i^2}{{ϵ}_i{\sigma }_i^3}}$$

(2)

where $k^o$ is the Boltzmann constant, d_i is the dipole moment, and ε_i is the Lennard-Jones potential well depth of the ith species. δ^* = 0 for nonpolar gases since d_i = 0 for them.

Viscosity of a N-component gas mixture can be calculated from the equation below [28]:

$${ \mu }_{mix}={\sum }_{i=1}^N{\mu }_i{\left(1+{\sum }_{\begin{array}{c}j=1\\ j\ne i\end{array}}^N{A}_{ij}{\displaystyle \frac{X_j}{X_i}}\right)}^{-1}$$

(3)

where $X_i$ and $X_j$ are the mole fractions of the related species of the component and $A_{ij}$ is defined as

$$A_{ij}={\displaystyle \frac{L}{K}}{\left({\displaystyle \frac{{\mu }_i{W}_j}{{\mu }_j{W}_i}}\right)}^{0.5}\left\{1+{\displaystyle \frac{\frac{W_i}{W_j}-{\left(\frac{{\mu }_j{W}_i}{{\mu }_i{W}_j}\right)}^{0.5}}{2\left(1+\frac{W_i}{W_j}\right)+\frac{1+{\left(\frac{{\mu }_j{W}_i}{{\mu }_i{W}_j}\right)}^{0.5}}{K+L}L}}\right\}$$

(4)

where $W_i$ and $W_j$ are molecular weights, and ${\mu }_i$ and ${\mu }_j$ are the viscosities of the related species of the component. The other variables in Equation (4) are given below:

$$L={\left\{{\displaystyle \frac{4W_i{W}_j}{{\left(W_i+W_j\right)}^2}}\right\}}^{0.25}$$

(5)

To calculate K, when W_i > W_He:

$$K_1=1+0.0138\left({\displaystyle \frac{W_j}{W_i}}-1.4\right),K=K_1\mathrm{e}\mathrm{x}\mathrm{p}(-0.0066\alpha /L)$$

(6)

when W_i ≤ W_He:

$$K_1=2-\mathrm{e}\mathrm{x}\mathrm{p}\left\{-0.00011 {\left({\displaystyle \frac{W_j}{W_i}}\right)}^{1.5}\right\}, K=K_1\mathrm{e}\mathrm{x}\mathrm{p}\left\{-0.00975{\displaystyle \frac{\sqrt{\alpha }}{L}}(1-\beta )\right\}$$

(7)

And complementary equations for Equations (6) and (7) are

$$\alpha ={\displaystyle \frac{W_j}{W_i}}\left({\displaystyle \frac{T}{T_0}}-1\right), \beta =\exp \left(5-{\displaystyle \frac{W_j}{W_i}}\right), T_0=298 K$$

(8)

2.2. Thermal Conductivity

Thermal conductivity of a single component gas is given by [29,30]:

$$k_i={\displaystyle \frac{{\mu }_i}{W_i}}{(f_{trans}{C}_{\upsilon ,trans}+f_{rot}{C}_{\upsilon ,rot}+f_{vib}{C}_{\upsilon ,vib})}_i$$

(9)

where k_i is the thermal conductivity, W_i is the molecular weight and ${\mu }_i$ is the viscosity of the ith species. C_v is specific heat at a constant volume and trans, rot, and vib subscripts mean translational, rotational, and vibrational contributions. C_v contributions depends on the linearity of the species (i.e., linear molecule, non-linear molecule, or single atom). If the given the species is a single atom, then $C_{\upsilon ,trans}$= ${\displaystyle \frac{3}{2}}R$, $C_{\upsilon ,rot}=0$, and $C_{\upsilon ,vibe}=0$. If the given species is a linear molecule, then $C_{\upsilon ,trans}$= ${\displaystyle \frac{3}{2}}R$, $C_{\upsilon ,rot}=R,$ and $C_{\upsilon ,vibe}=C_{\upsilon }-{\displaystyle \frac{5}{2}}R$. If the given species is a non-linear molecule, then $C_{\upsilon ,trans}$= ${\displaystyle \frac{3}{2}}R$, $C_{\upsilon ,rot}={\displaystyle \frac{3}{2}}R$, and $C_{\upsilon ,vibe}=C_{\upsilon }-3R$.

$$f_{trans}={\displaystyle \frac{5}{2}}(1-{\displaystyle \frac{2}{\pi }}{\displaystyle \frac{C_{\upsilon ,rot}}{C_{\upsilon ,trans}}}{\displaystyle \frac{A}{B}})$$

(10)

$$f_{rot}={\displaystyle \frac{\rho D_{ii}}{{\mu }_i}}(1+{\displaystyle \frac{2}{\pi }}{\displaystyle \frac{A}{B}})$$

(11)

$$f_{vib}={\displaystyle \frac{\rho D_{ii}}{{\mu }_i}}$$

(12)

where $\rho$ is the density obtained from the equation of state with perfect gas assumption and $D_{ii}$, the self-diffusion coefficient, is expressed as [31]

$$D_{ii}={\displaystyle \frac{{0.00266T}^{1.5}}{P_{bar}\sqrt{W_i}{\sigma }_i^2\left[{\mathsf{\Omega }}_i^{\left(\mathrm{1,1}\right)*}\left(T^{*};{\delta }^{*}\right)\right]}}$$

(13)

A and B constants are expressed as

$$A={\displaystyle \frac{5}{2}}-{\displaystyle \frac{\rho D_{ii}}{{\mu }_i}}, B=Z_{rot}+{\displaystyle \frac{2}{\pi }}\left({\displaystyle \frac{5}{3}}{\displaystyle \frac{C_{\upsilon ,rot}}{R}}+{\displaystyle \frac{\rho D_{ii}}{{\mu }_i}}\right)$$

(14)

and $Z_{rot}$ can be calculated from the equations below:

$$Z_{rot}\left(T\right)=Z_{rot}\left(298\right){\displaystyle \frac{F\left(298\right)}{F\left(T\right)}}, F(T)=1+{\displaystyle \frac{{\pi }^{3/2}}{2}}{({\displaystyle \frac{ϵ/k^o}{T}})}^{1/2}+({\displaystyle \frac{{\pi }^2}{4}}+2)({\displaystyle \frac{ϵ/k^o}{T}})+{\pi }^{3/2}{({\displaystyle \frac{ϵ/k^o}{T}})}^{3/2}$$

(15)

where $Z_{rot}(T$) is the relaxation collision number at 298 K for species i.

For a gas mixture of N components with the molar ratio X, thermal conductivity of the mixture is calculated from the equation given below [32]:

$$k_{mix}={\sum }_{i=1}^N{\displaystyle \frac{X_i{k}_i}{\sum _{j=1}^N{X}_j{\Phi }_{ij}}}$$

(16)

and

$${\Phi }_{ij}={\displaystyle \frac{1}{\sqrt{8}}}{\left(1+{\displaystyle \frac{W_i}{W_j}}\right)}^{-0.5}{\left[1+{\left({\displaystyle \frac{{\mu }_i}{{\mu }_j}}\right)}^{0.5}{\left({\displaystyle \frac{W_j}{W_i}}\right)}^{0.25}\right]}^2$$

(17)

2.3. Diffusion Coefficient

Binary diffusion coefficient is given by [31]:

$$D_{ij}={\displaystyle \frac{{0.00266T}^{1.5}}{P_{bar}\sqrt{W_{ij}}{\sigma }_{i,j}^2[{\mathsf{\Omega }}^{\left(\mathrm{1,1}\right)*}\left(T^{*};{\delta }_{i,j}^{*}\right)]}}$$

(18)

and

$$W_{ij}=2{[({\displaystyle \frac{1}{W_i}}+{\displaystyle \frac{1}{W_j}})]}^{-1}$$

(19)

where P is the pressure in [bar] unit and $W_{ij}$ and $W_{ij}$ are molecular weights of the i and j species.

For a gas mixture of N components with i species, average diffusion coefficient is calculated from the equation given below [29]:

$${ D}_{i,mix}={\displaystyle \frac{1-\frac{X_i{W}_i}{\overline{W}}}{\sum _{\begin{array}{c}j=1\\ j\ne i\end{array}}^N\frac{X_j}{D_{ii}}}}$$

(20)

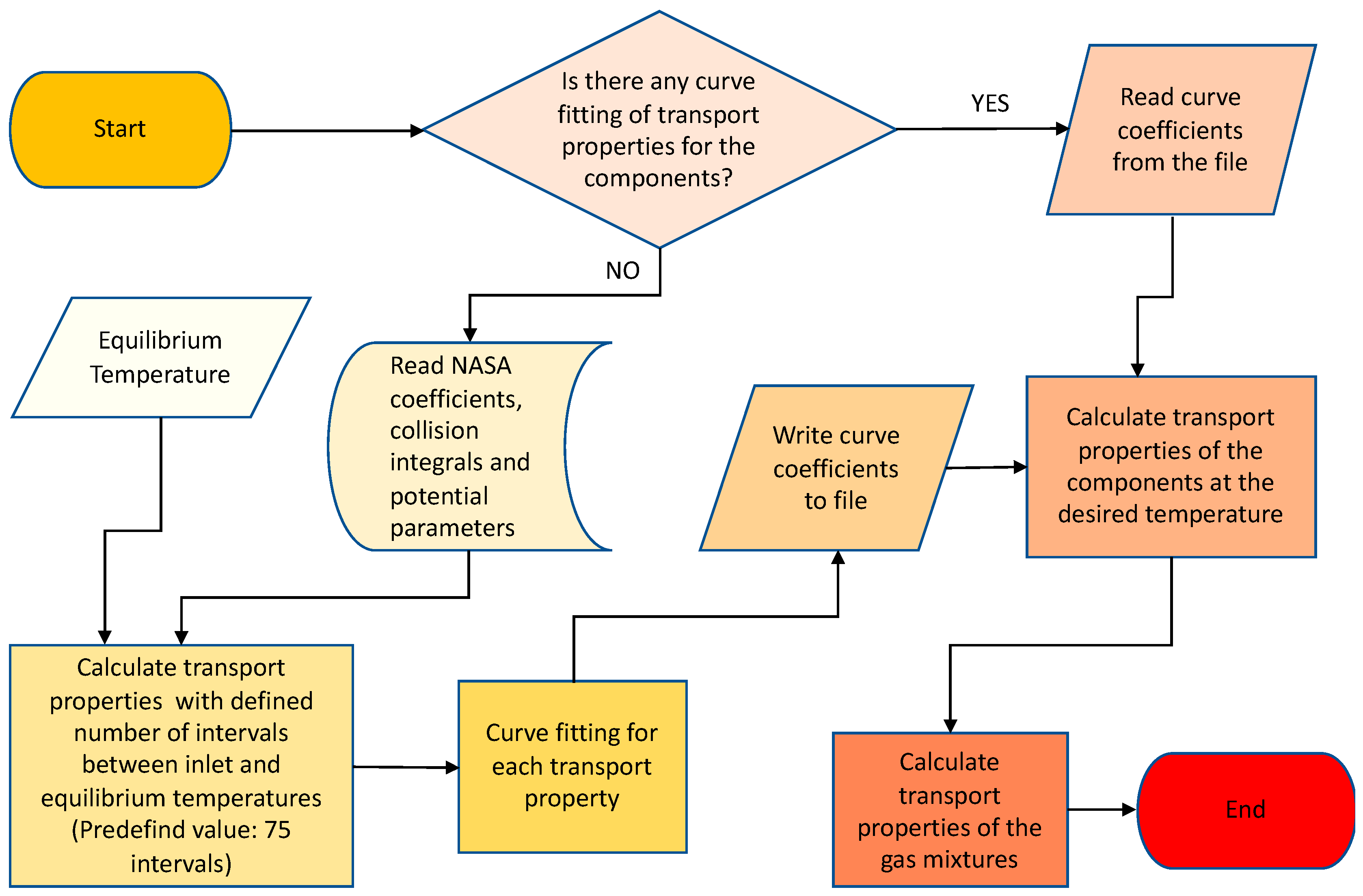
2.4. Program Algorithm

Thermophy is constructed in order to determine viscosity, thermal conductivity, and diffusion coefficients of pure gases and gas mixtures for combustion simulations. For the architecture of the molecular structure, three kinds of pairs are considered: atom pair 0, linear molecule 1, and non-linear molecule 2. Our preliminary results showed sufficient accuracy with the literature data (deviation is below 5%). However, the program appears to be a processing load within the first version when it is used as a subroutine program for combustion analysis. In this case, the transport properties of pure gases were recalculated at each temperature change, while iterative solutions were made. Thus, the equations (given in Section 2) used for the calculation of the transport properties of pure gases were repeated for each iteration, which leads to the repetition of both linear interpolation and bilinear interpolation of the table values of the transport properties. So, we changed our mental model in order to solve the problem above to construct a program friendly to users. It is known that the temperature obtained after the equilibrium solution is the theoretically highest temperature of an adiabatic system and the inlet temperature is the lowest temperature. In this regard, transport properties were calculated at the temperatures specified by the user between these two temperatures. Moreover, for each transport property value, a separate curve was fitted using Chebyshev polynomials that can also be changed by the user. For curve fitting and the recalculation of fitted curves with coefficients, subprograms were implemented from the literature in FORTRAN language [33,34]. Calculated transport values of pure gases were written in a separate file, thus, the required computational time limitation will prevent a user from computing during further iterations or different computing studies with the same components. Thus, a computation of the transport property data is performed with the recalculation of fitted curves with coefficients. The main structure of the program is shown in Figure 1. Since the algorithm of the program is presented, researchers can easily reproduce with their codes using whatever language is chosen (i.e., Python).

The structure and performance of Thermophy is assessed by computing the transport properties using Chebyshev polynomials via four case studies. Thermophy is presented so as to demonstrate the success of computing thermophysical properties of pure gases and gas mixtures with regard to thermal conductivity, viscosity, and diffusion coefficients. Then calculated data is compared with theoretical and experimental data obtained from the literature.

3. Results and Discussion

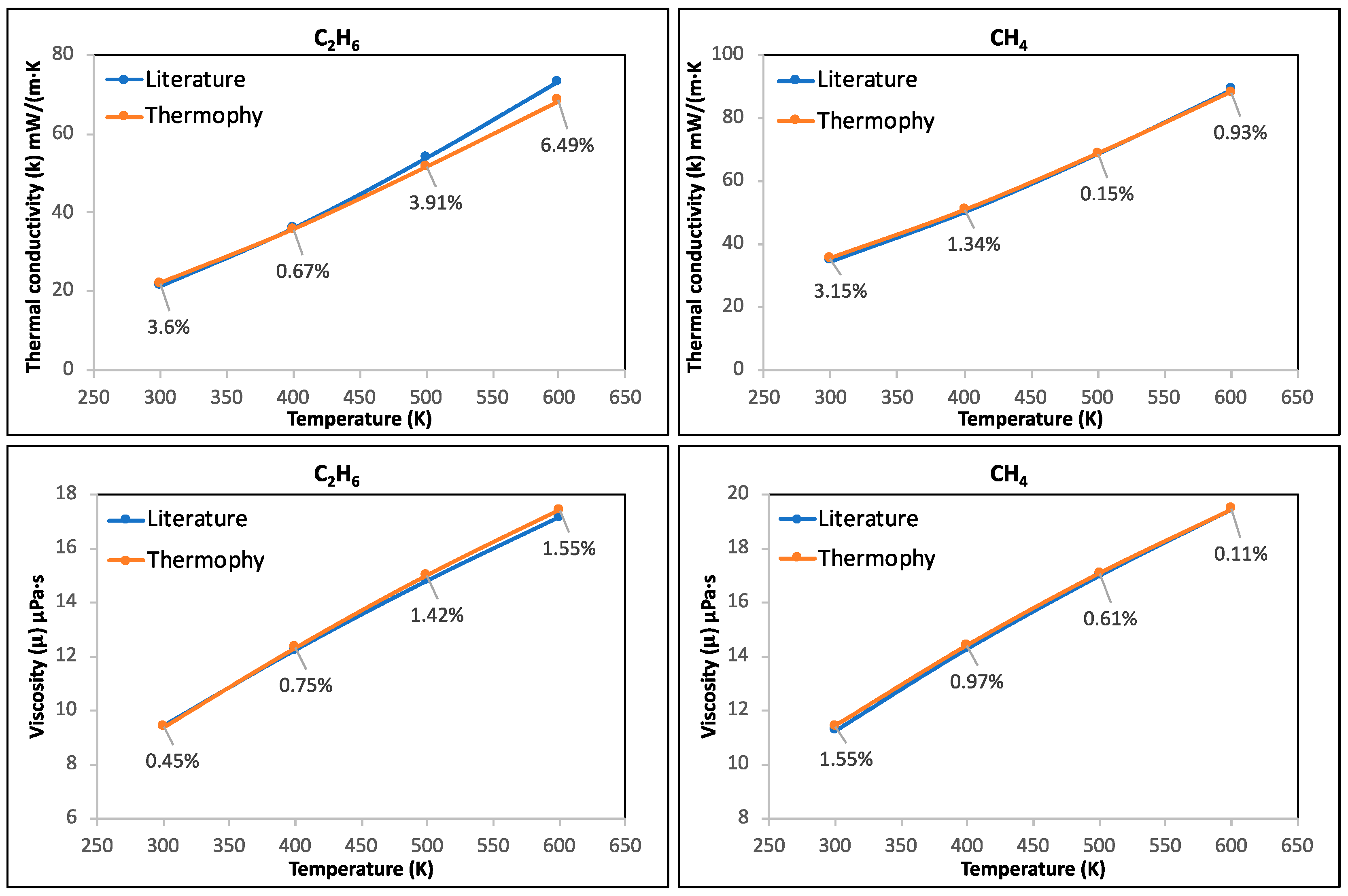
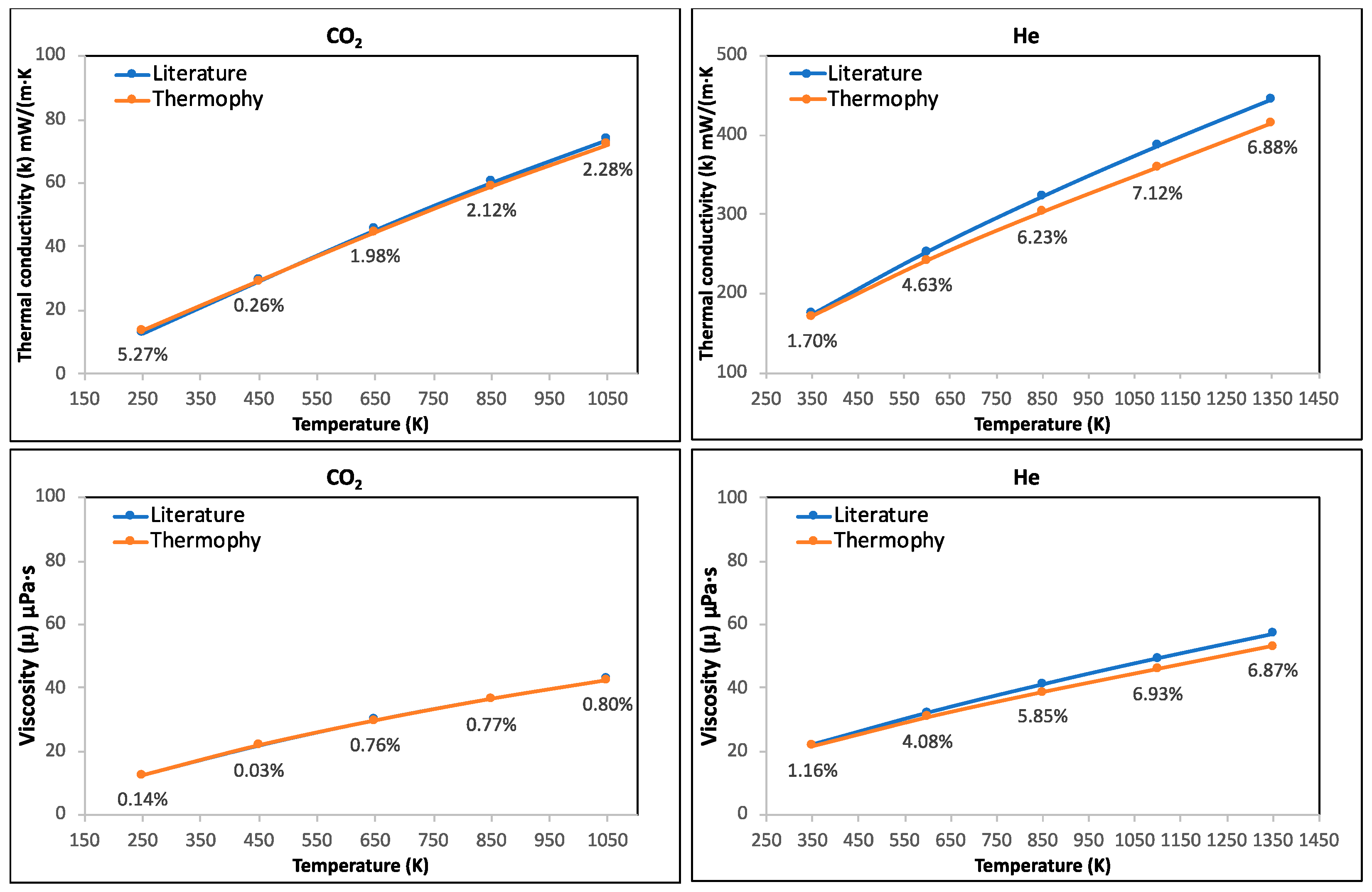
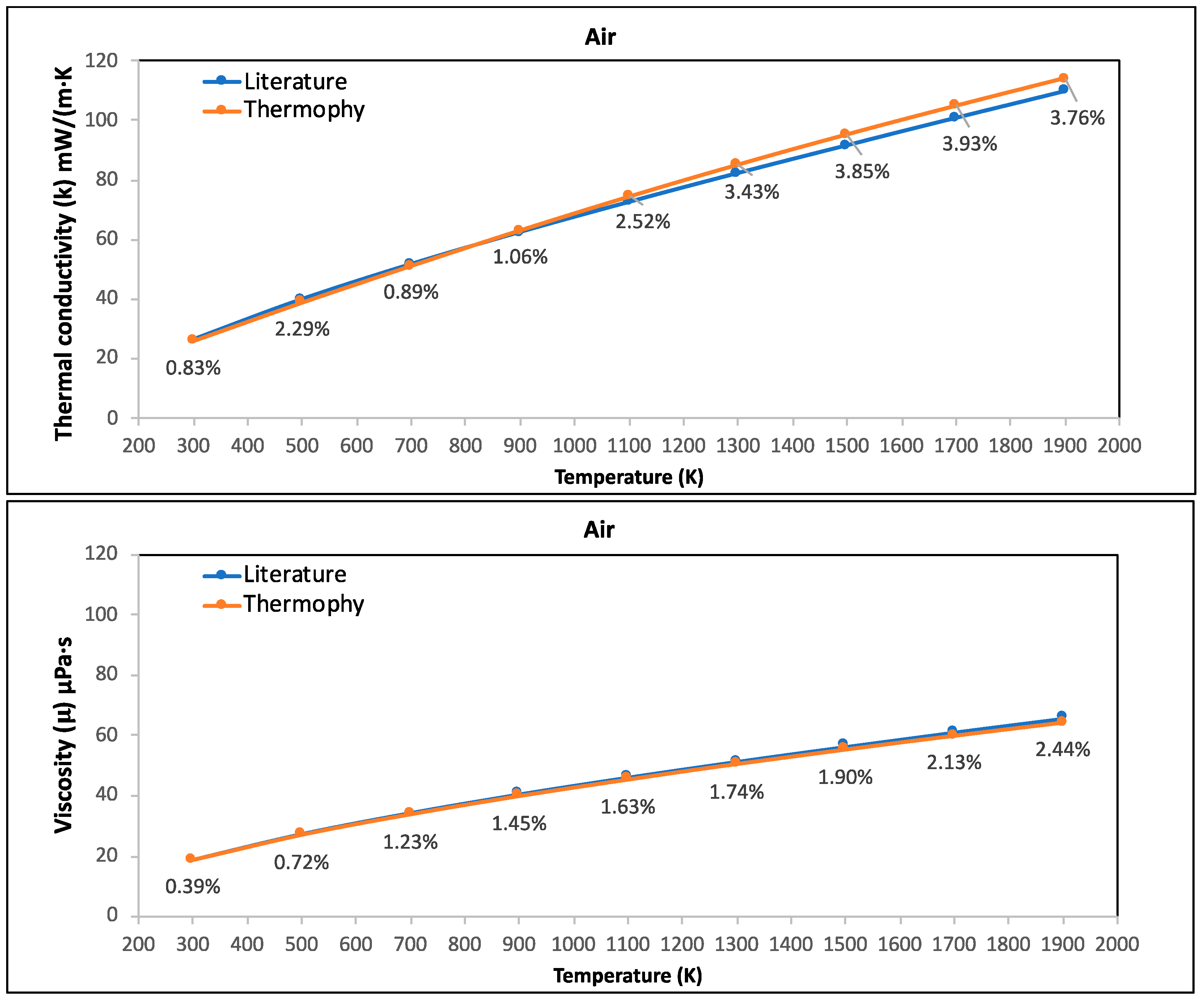
3.1. Case Study 1: Thermal Conductivity and Viscosity of C₂H6, CH₄, CO_2, and He Pure Gases and Air

With Thermophy, we compute the values of viscosity and thermal conductivity of some pure gases and air using transport properties [26,27,35], which is compared with the tabulated data from the literature [36]. Figure 2 shows thermal conductivity–temperature and viscosity–temperature curves of C₂H₆ and CH₄ gases obtained from tabulated data [36] and Thermophy.

Results showed that theoretical computation confirms thermal conductivity and viscosity data at temperatures between (300 and 600) K for C₂H₆ and CH₄ (Figure 2). Considering the deviation between the literature data and computational data of thermal conductivity of C₂H₆ and CH₄ at given temperatures, maximum deviation was calculated as 6.49% and 3.15%, respectively. For computational viscosity data of C₂H₆ and CH₄ gases at given temperatures, maximum deviation of 1.55% was calculated compared to tabulated data. Thermal conductivity–temperature and viscosity–temperature data of CO₂ and He gases obtained from Thermophy data confirmed the tabulated data [36] which is presented in Figure 3.

The calculated Thermophy data agrees with the tabulated data [36] at temperatures between (250 and 1050) K for CO₂ with maximum deviations of 5.27% and 0.80% regarding thermal conductivity and viscosity, respectively (Figure 3). For He at temperatures between (350 and 1350) K, thermal conductivity and viscosity data maximum deviations were calculated as 7.12% and 6.93%, respectively (Figure 3). These errors are not random but systematically increase with temperature, pointing to limitations in the high-temperature regime which explain the increased deviation observed in both viscosity and thermal conductivity. Due to He’s extremely low molecular mass and small collision diameter, helium’s transport properties are highly sensitive to the accuracy of molecular interaction parameters and collision integrals [31], which may limit Thermophy calculations.

Figure 4 represents thermal conductivity–temperature and viscosity–temperature curves of air obtained from tabulated data [36] and Thermophy data. It is assumed that the air consists of N₂, O_2, and Ar with molar ratios of 0.7812, 0.2096, and 0.0092, respectively. The calculated Thermophy data are in a good parallel with the tabulated data [36] at temperatures between (300 and 1900) K with maximum deviations of 3.93% and 2.44% regarding thermal conductivity and viscosity, respectively (Figure 4). Overall deviations obtained from thermal conductivity values considering each point of temperature were 4.25%, 1.22%, 2.62%, 4.02%, and 1.38% for C₂H₆, CH₄, CO₂, He, and air, respectively. For viscosity values, overall deviations considering each point of temperature were 0.21%, 0.27%, 0.11%, 4.71%, and 0.34% for C₂H₆, CH₄, CO₂, He, and air, respectively. All deviation values are sufficient for engineering calculations, which indicates the success of Thermophy.

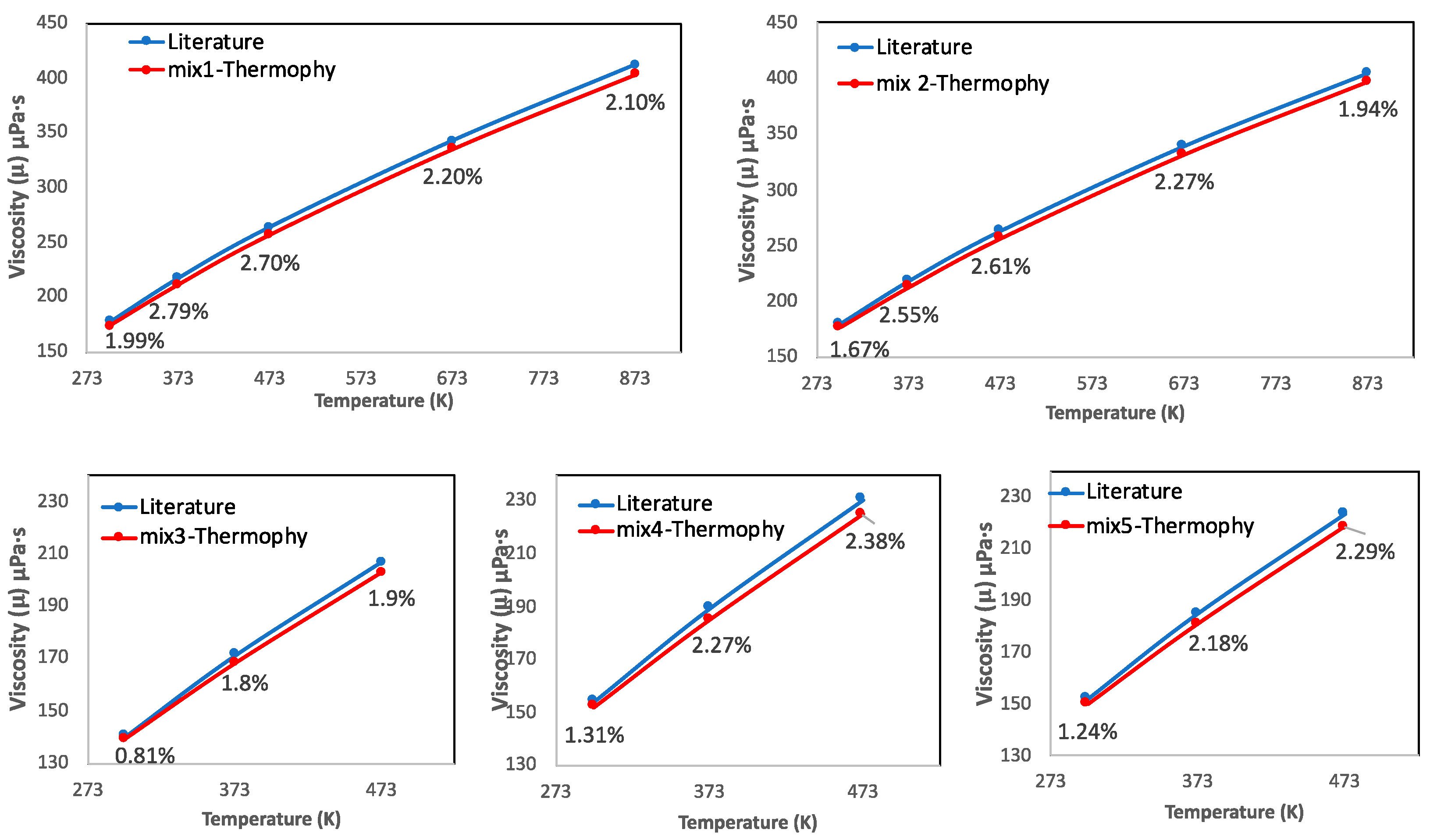
3.2. Case Study 2: Viscosity of N₂-Ar-CO₂ and N₂-CO₂-CH₄ Ternary Gas Mixtures

We compute the viscosity values of N₂-Ar-CO₂ and N₂-CO₂-CH₄ ternary gas mixtures with different molar compositions via Thermophy, which is compared with experimental data from the literature [37]. N₂-Ar-CO₂ ternary gas mixture with different molar ratios of $X_{N_2}=0.1869, X_{Ar}=0.2842, X_{{CO}_2}=0.5289$ and $X_{N_2}=0.4535, X_{Ar}=0.2049, { X}_{{CO}_2}=0.3416$ were denoted as Mixture 1 (mix1) and Mixture 2 (mix2). N₂-CO₂-CH₄ ternary gas mixture with different molar ratios of $X_{N_2}=0.2002, { X}_{{CO}_2}=0.2713, { X}_{{CH}_4}=0.5285$, $X_{N_2}=0.2654, X_{{CO}_2}=0.5588, { X}_{{CH}_4}=0.1758$ and $X_{N_2}=0.3429, X_{{CO}_2}=0.3456, { X}_{{CH}_4}=0.3115$ were denoted as Mixture 3 (mix3), Mixture 4 (mix4), and Mixture 5 (mix5). Experimental viscosity values [37] and Thermophy calculated viscosity values of mix1-5 were presented in Figure 5. Viscosity values of mix1 and mix2 at temperatures between (298 and 873) K and viscosity values of mix3, mix4, and mix5 at temperatures between (298 and 473) K, determined from Thermophy computation, showed very low deviation from the experimental data (maximum deviation of mix1, mix2, mix3, mix4, and mix5 are calculated as 2.79%, 2.61%, 1.9%, 2.38%, and 2.29%, respectively) (Figure 5). Overall deviations obtained from viscosity values considering each point of temperature were 0.11%, 0.13%, 0.24%, 0.23%, and 0.22% for mix1, mix2, mix3, mix4, and mix5, respectively. These results indicate the success of Thermophy in this study and the solutions are achieved without any processing load during computation.

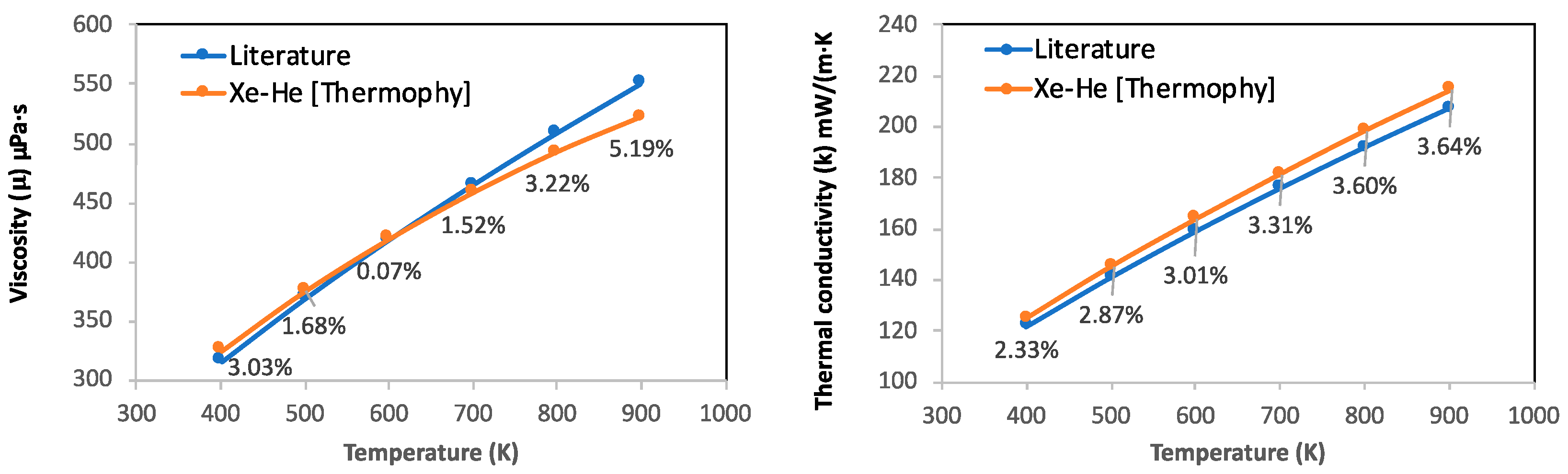
3.3. Case Study 3: Viscosity and Thermal Conductivity of Xe-He Binary Gas Mixture

The values of viscosity and thermal conductivity of Xe-He binary gas mixtures with a molar composition of $X_{Xe}=1271 \mathrm{a}\mathrm{n}\mathrm{d} X_{He}=0.8729$ via Thermophy, which is compared with the data obtained from the literature [38]. Thermophy calculated viscosity data at temperatures between (400 and 900) K confirm the viscosity data from the literature with a maximum deviation of 5.19% (Figure 6). Similarly, thermal conductivity of the computed Thermophy data at temperatures between (400 and 900) K agrees with the literature data considering the maximum deviation of 3.64% (Figure 6). Overall deviations obtained from viscosity and thermal conductivity values considering each point of temperature were 2.60% and 0.20% for Xe-He, respectively. It is noteworthy to mention that in this study, Thermophy confirms the maximum deviation value of 5% given in our preliminary study with the first version of Thermophy where some problems were encountered from processing. However, in this study, Thermophy achieves successful computing of the thermophysical values of the gas mixtures that is consequently suggested to be useful and sufficient data for combustion analysis.

3.4. Case Study 4: Diffusion Coefficients of Binary Gases

Table 1. Binary diffusion coefficient of gas mixtures.

Binary Gas System	Literature	Temperature (K)	Experimental DAB (cm2/s)	Thermophy DAB (cm2/s)	Deviation (%)
Ar-CH4	[39]	298	0.205	0.214	4.39
Ar-H2	[39]	295	0.840	0.790	5.95
Ar-He	[39]	276	0.655	0.654	0.15
Ar-Xe	[39]	378	0.180	0.173	3.89
CO2-He	[39]	298	0.620	0.610	1.61
CO2-He	[39]	498	1.433	1.446	0.91
CO-N2	[39]	373	0.322	0.302	6.21
H2-N2	[39]	294	0.773	0.751	2.85
H2-N2	[39]	573	2.449	2.317	5.39
He-H2O	[39]	352	1.136	1.176	3.52
He-N2	[39]	298	0.696	0.709	1.87
CH4-He	[40]	273.15	0.618	0.596	3.56
C2H4-He	[40]	273.15	0.497	0.498	0.20
NO2-N2	[40]	273.15	0.145	0.146	0.69
C3H8-CH4	[41]	293.29	0.118	0.119	1.42
C3H8-CH4	[41]	313.59	0.138	0.136	1.92
CO2-CH4	[43]	298.45	0.173	0.167	3.47

represents the binary diffusion coefficients for different gases at different temperatures obtained from the experimental data in the literature [39,40,41] and calculated data from Thermophy. According to the results, Thermophy greatly calculates diffusion coefficient values obtained from all gas mixtures presented in this study with a minimum deviation of 0.15% for Ar-He and maximum deviation of 6.21% for CO-NO₂ (Table 1). The relatively large deviation of 6.21% observed in the CO–N₂ binary diffusion coefficient may be because of measurement uncertainty but appears to stem primarily from the specific intermolecular interactions between CO and N₂. The polar nature of CO and the quadrupolar nature of N₂ introduce anisotropic interactions [42] that may not be captured by Thermophy in this study, which is a limitation. Thermophy computation of the combustion gases of alkane–alkane systems resulted in a deviation <2% [41]. Moreover, calculated Thermophy values of CO₂-CH₄ were in a good agreement (Table 1) with the experimental values of the mutual diffusion coefficient of CH₄ in CO₂ obtained from the spectroscopic method [43]. Overall deviation for binary diffusion coefficients of all the computed gas mixtures is 3.35%. Consequently, in this study, Thermophy computation achieves successful determination of diffusion coefficients of binary gases and is suggested as a useful tool for multicomponent gas systems.

3.5. Error Analysis: Accuracy and Efficiency

In this study, “Thermophy” is proposed as an efficient tool for calculating the properties of combustion/gas mixtures through curve fitting based on the Chebyshev polynomial. Results showed a certain level of improvement in accuracy compared to the existing literature data. However, we compared Thermophy results for the viscosity of N₂-Ar-CO₂ and N₂-CO₂-CH₄ ternary gas mixtures (Case 2) with a commercial/open source tool (Cantera) [19] to indicate the accuracy and computational efficiency of Thermophy. Thus, an error analysis is performed, and overall deviations are calculated and presented in

Table 2. Error analysis for viscosities of N₂-Ar-CO₂ and N₂-CO₂-CH₄ ternary gas mixtures compared to data from the literature [37].

Ternary Gas Mixtures	Molar Compositions	Overall Deviation (%) Compared to Thermophy	Overall Deviation (%) Compared to Cantera
Mixture 1	$X_{N_2}=0.1869, X_{Ar}=0.2842, X_{{CO}_2}=0.5289$	0.11	3.54
Mixture 2	$X_{N_2}=0.4535, X_{Ar}=0.2049, X_{{CO}_2}=0.3416$	0.13	1.29
Mixture 3	$X_{N_2}=0.2002, X_{{CO}_2}=0.2713, X_{{CH}_4}=0.5285$	0.24	0.23
Mixture 4	$X_{N_2}=0.2654, X_{{CO}_2}=0.5588, X_{{CH}_4}=0.1758$	0.23	0.88
Mixture 5	$X_{N_2}=0.3429, X_{{CO}_2}=0.3456, X_{{CH}_4}=0.3115$	0.22	0.28

.

According to Table 2, Thermophy improves in accuracy and remains clearly reliable in this case. It is noteworthy to mention that although Cantera deviations are also reasonable, the largest contributor of the error cause analysis may likely stem from the temperature-dependence of collision integrals at higher temperatures, especially for polar gases like CO₂. The strong temperature dependence for quadrupolar molecules like CO₂ compared to monoatomic or non-polar gases was previously explained [44]. Thus, the greater temperature sensitivity of CO₂’s collision integrals may show its stronger impact on mixture viscosities at elevated temperatures, whether interacting with CH₄, N₂, or Ar. However, this limitation seems to be overcome via Thermophy computing that applies Chebyshev fitting over defined temperature intervals, enabling higher accuracy, improved numerical stability, and computational efficiency since Chebyshev expansions provide a numerically stable and accurate interpolation of complex thermodynamic surfaces [45].

It is noteworthy to mention that error cause analysis and user scalability are key factors that should be considered. In summary, Thermophy performs with overall deviations <0.25% from experimental data (Table 2). The dominant error sources relate to non-ideal molecular interactions and fit the resolution since overall deviations are in the range of 0.11–0.24% between mixtures showing numerical stability. Moreover, a parameter sensitivity analysis for Chebyshev fitting specially looks at a number of polynomial segments and polynomial order per segment. Thus, best practice with a minimum error is performed using three segments with an order of 5 and 7. In addition, a consistency of errors across compositions of N₂-Ar-CO₂ and N₂-CO₂-CH₄ ternary gas mixtures shows composition-independent scalability. This may lead to general-purpose transport property evaluations across complex ternary systems. To design combustion systems that are both efficient and environmentally responsible, it is essential to develop computational methods that can accurately reproduce the complex interactions of flow, chemical reactions, and heat transfer within a flame. Improving the fidelity of combustion simulations requires high-accuracy thermophysical property data over a wide temperature range [2]. Thus, the primary objective of this study is to develop a robust and extensible computational program capable of generating a high-accuracy database of essential thermophysical properties. Such a tool supports the advancement of combustion modeling and contributes to the broader goals of environmental conservation and sustainable resource use for the future.

4. Conclusions and Future Direction

In this study we presented Thermophy, an extensible FORTRAN library that computes the transport properties (thermal conductivity, viscosity, diffusion coefficient) of various pure gases, air, and gas mixtures. The key molecular insights are as follows:

• Thermophy leverages Chebyshev polynomial fitting to provide numerically stable and accurate estimations of transport properties. Users only need to supply the temperature, number of species, and their mole fractions to perform calculations efficiently.
• Thermophy correctly calculated the thermal conductivity and viscosity of C₂H₆, CH₄, CO_2, and He pure gases and air while considering all temperatures, highlighting its potential in calculating the thermophysical properties of other various gases.
• Thermophy computation showed very low deviation from the experimental viscosity data of ternary gas mixtures (overall deviation of mix1, mix2, mix3, mix4, and mix5 are calculated as 0.11%, 0.13%, 0.24%, 0.23%, and 0.22%, respectively, considering each point of temperature) without any processing load during computation.
• Thermal conductivity and viscosity values of the Xe-He binary gas mixture were successfully determined from Thermophy which highlights the potential of using Thermophy in combustion simulations.
• Diffusion coefficients of various binary gas systems were successfully calculated using Thermophy, as confirmed from the literature.

The present version of Thermophy can successfully compute the thermophysical properties of gases and gas mixtures and help to improve the performance of combustion modeling. Thus, Thermophy offers practical value for researchers and engineers in combustion modeling, gasification, pyrolysis, and related fire and explosion safety prevention processes. It is noteworthy to mention that the current version primarily considers atmospheric or constant-pressure conditions. Future versions will include pressure correction algorithms to support high-pressure combustion environments, such as those encountered in engines or gas turbines. Accordingly, future work will focus on coupling Thermophy with full-scale combustion solvers to enhance the accuracy of reactive flow simulations and promote the development of clean and efficient combustion technologies.