Asymmetric Flow Induced by the Longitudinal Position of the Fire Source Under Different Ambient Pressures
Abstract
1. Introduction
2. Materials and Methods
2.1. FDS Model
2.2. Boundary Condition
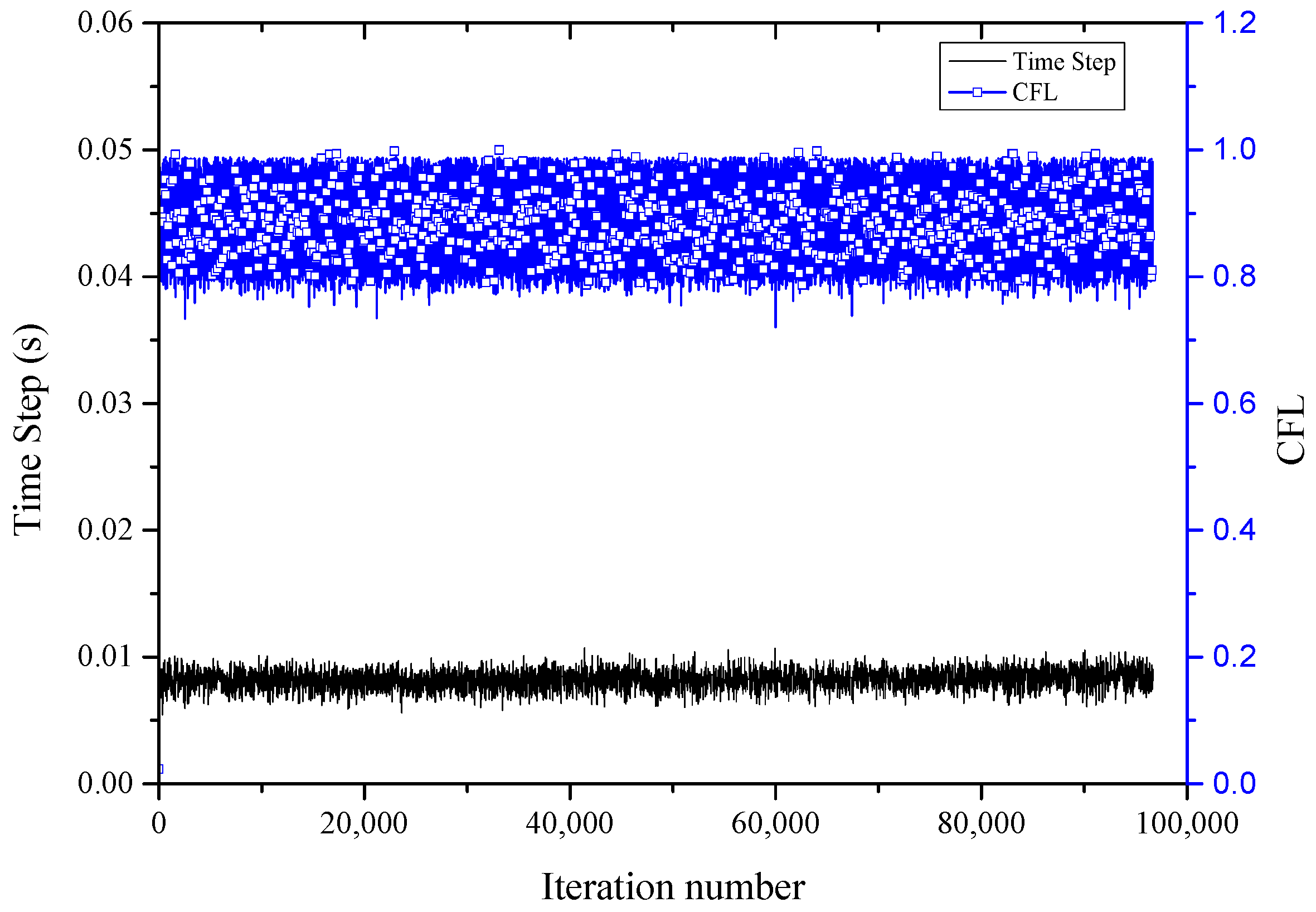
2.3. Mesh Systeml
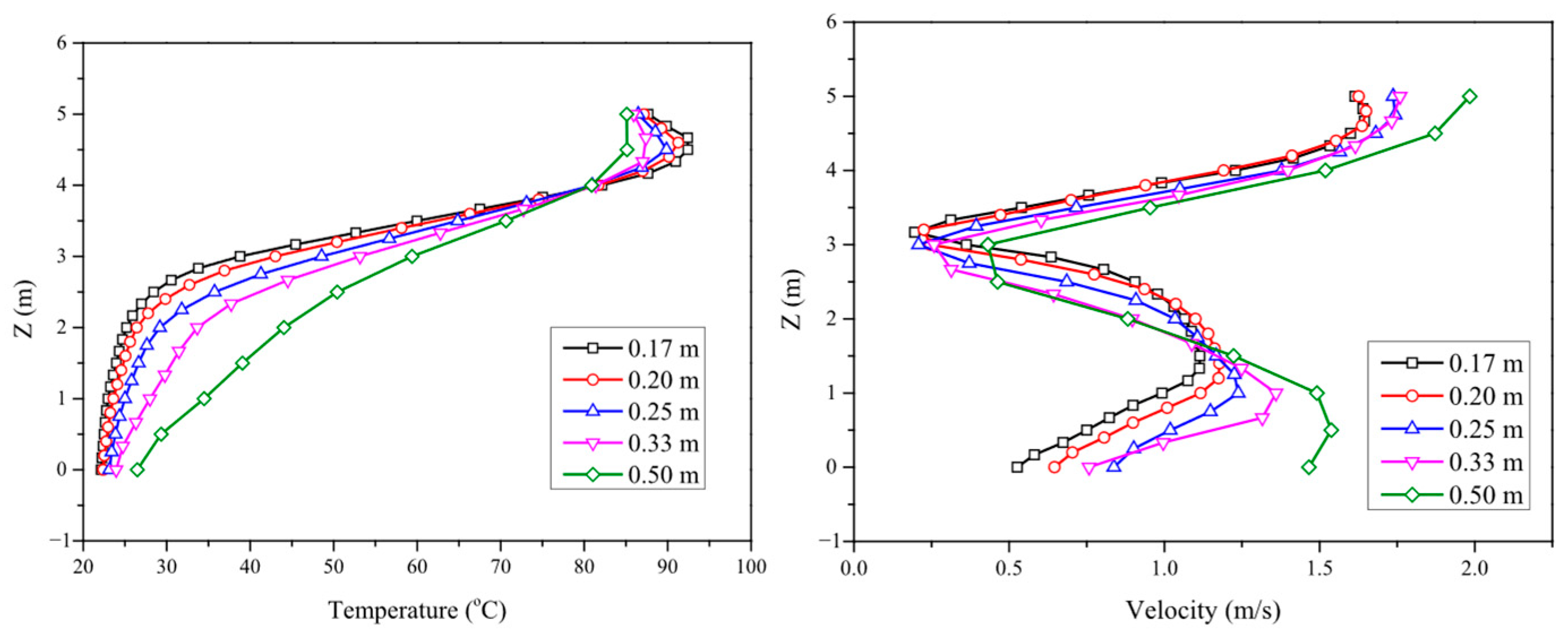
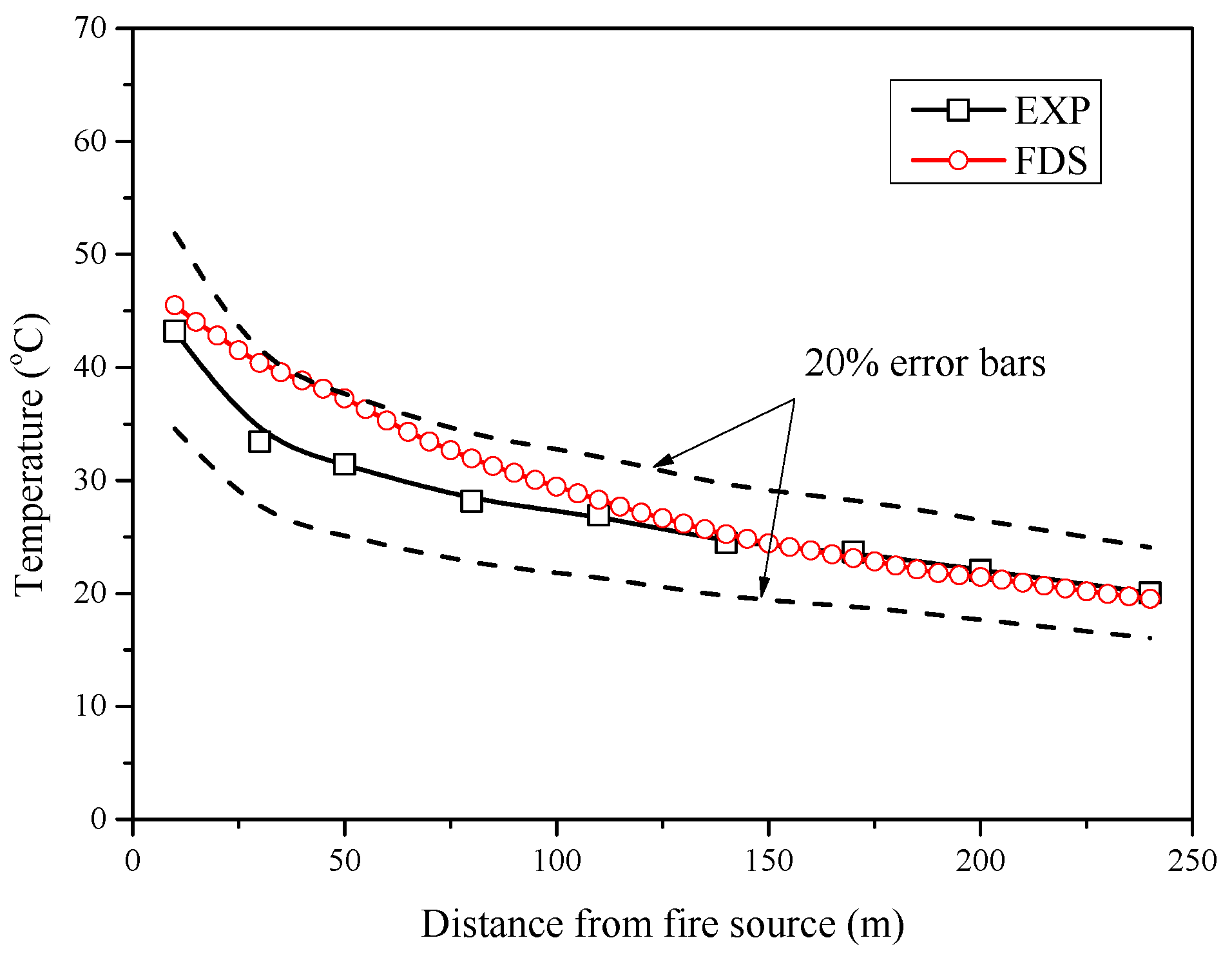
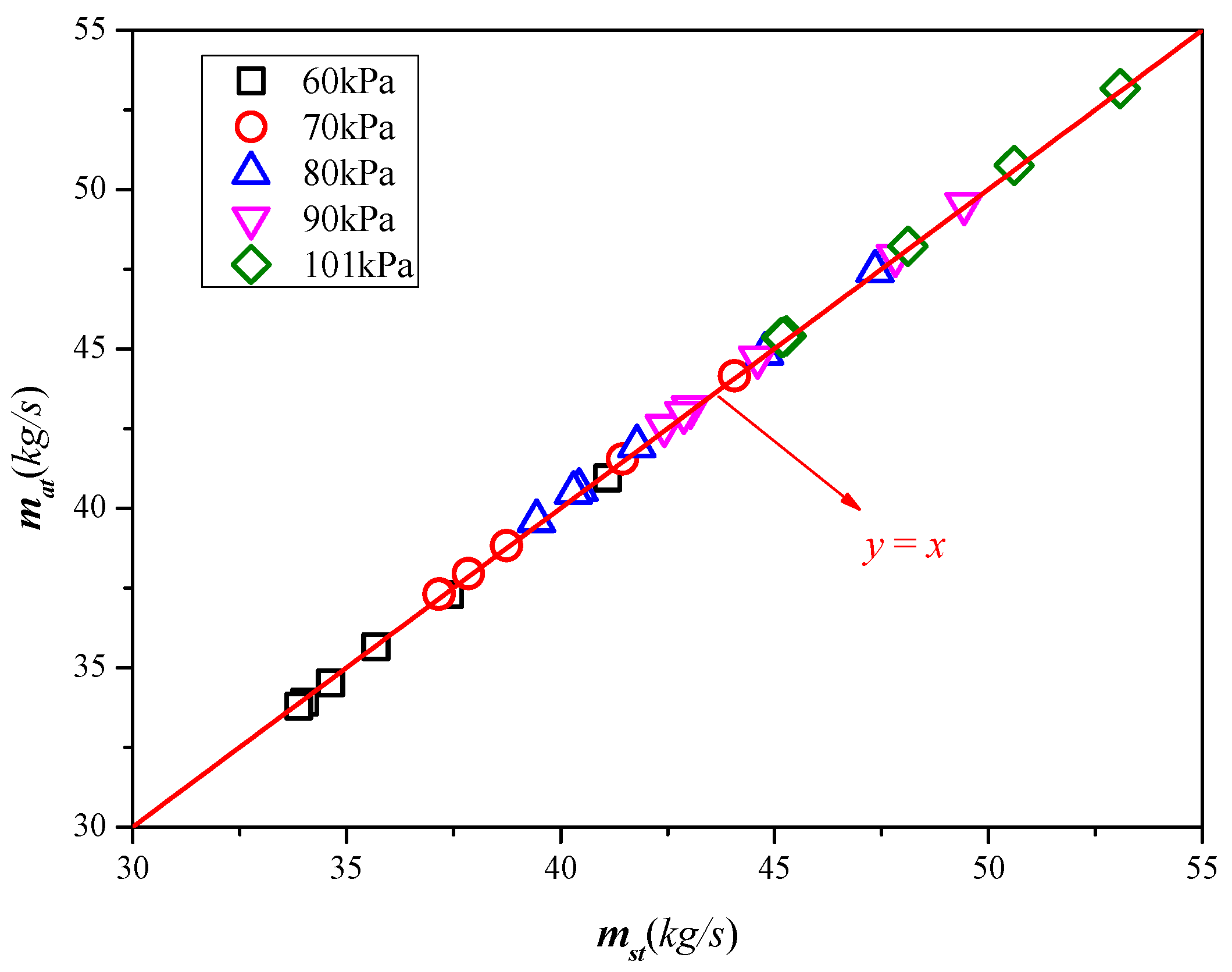
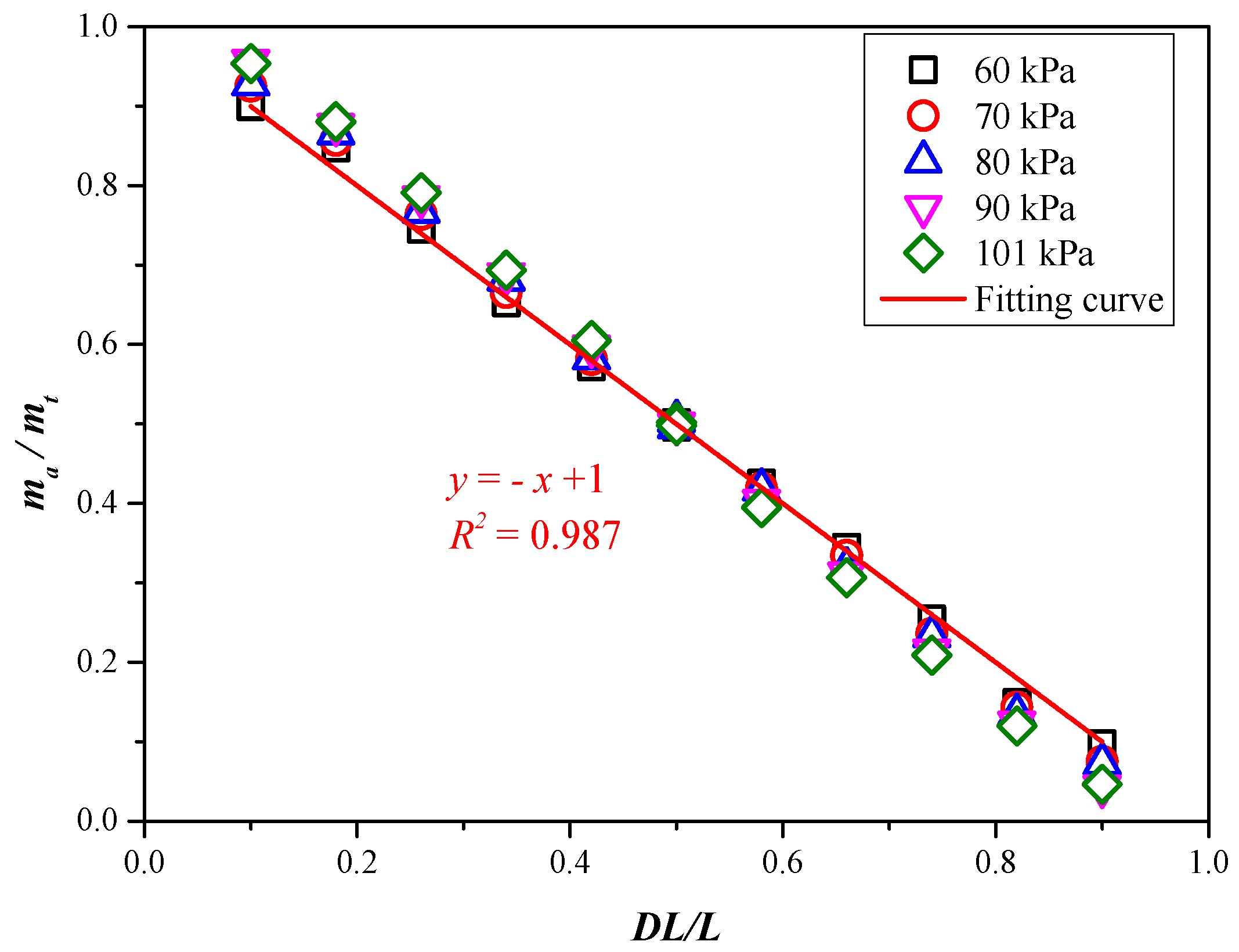
2.4. Validation
3. Results and Discussions
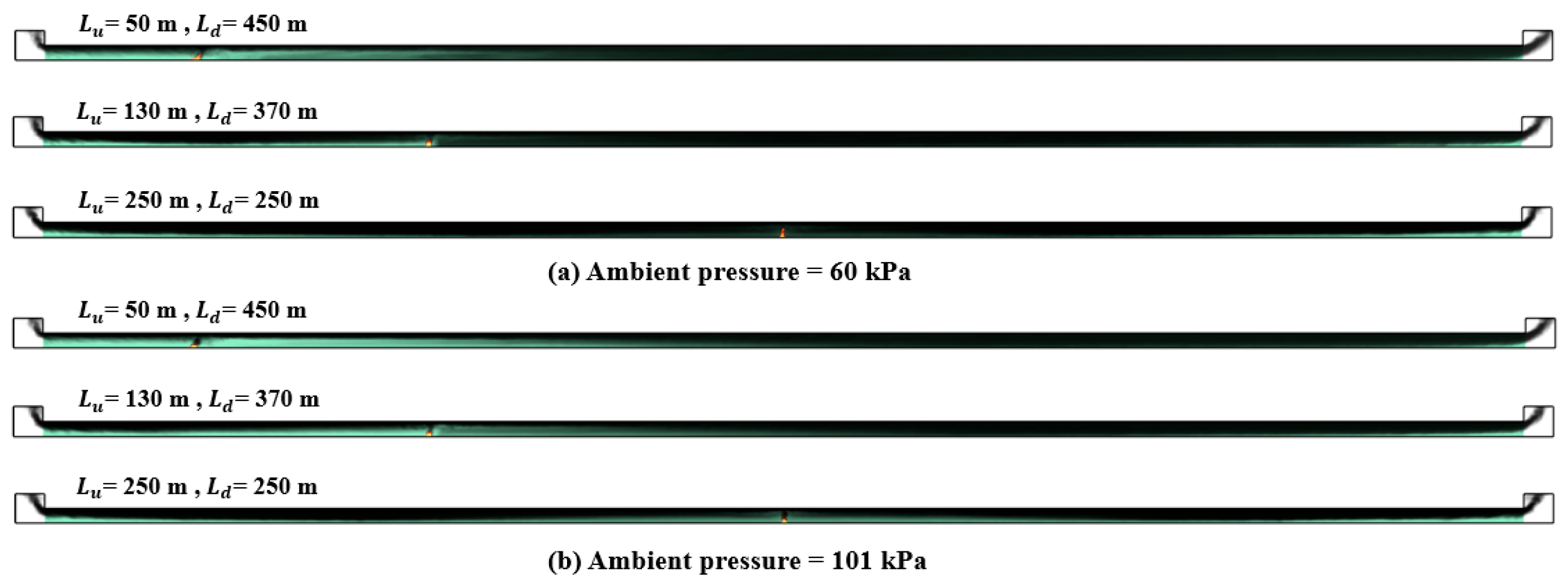
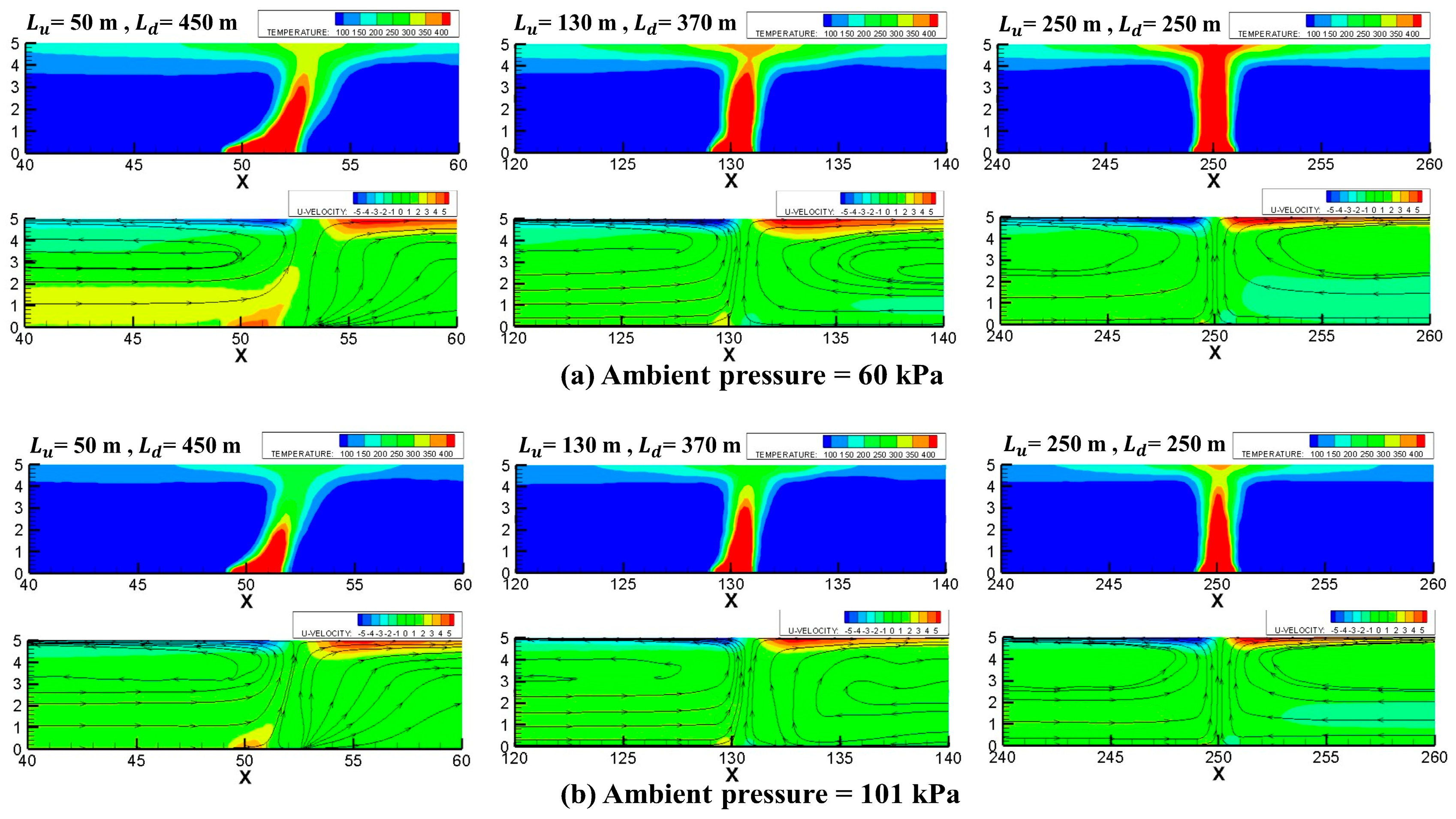
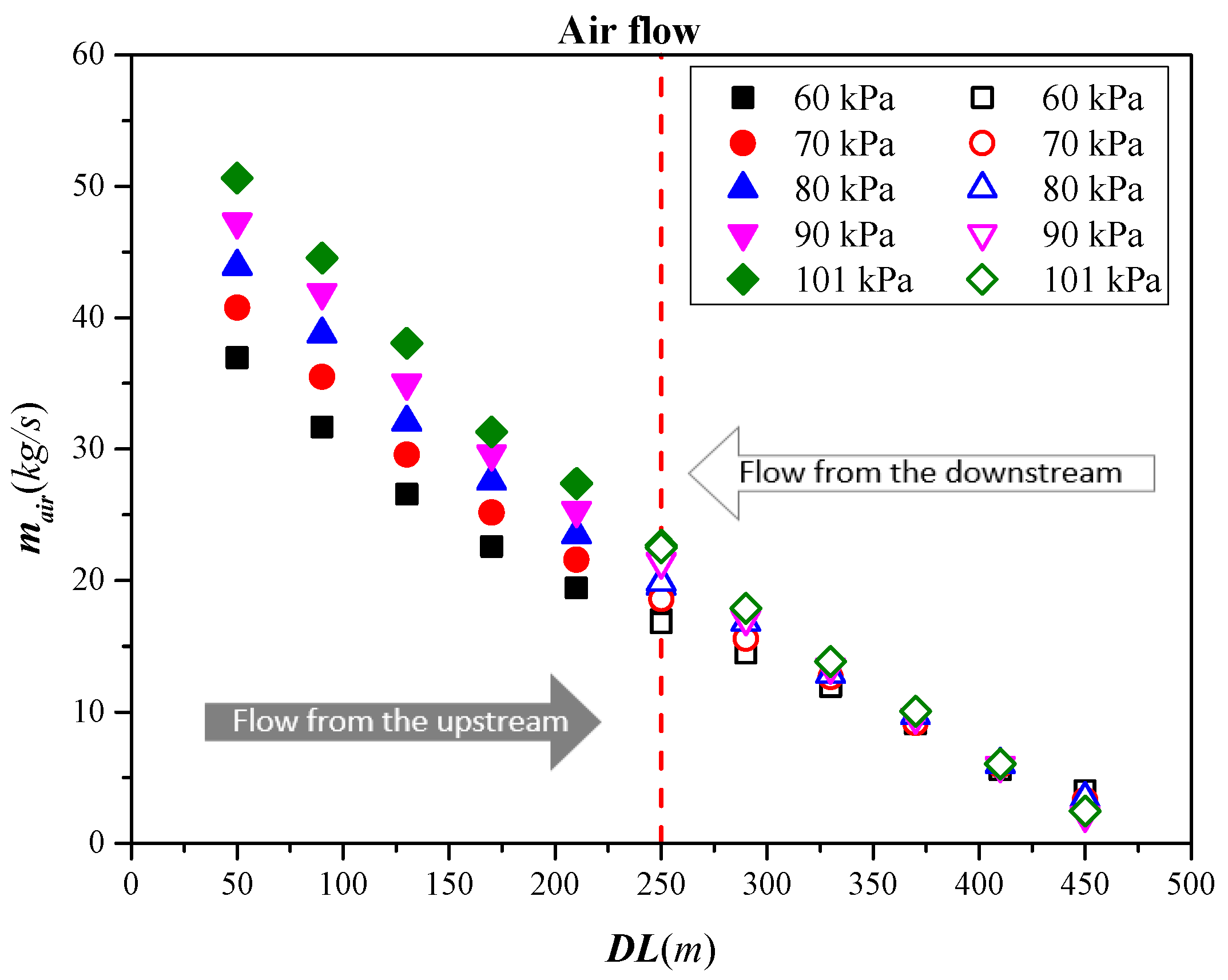
3.1. Asymmetric Flow Under Different Ambient Pressures
3.2. The Impact of Ambient Pressure on
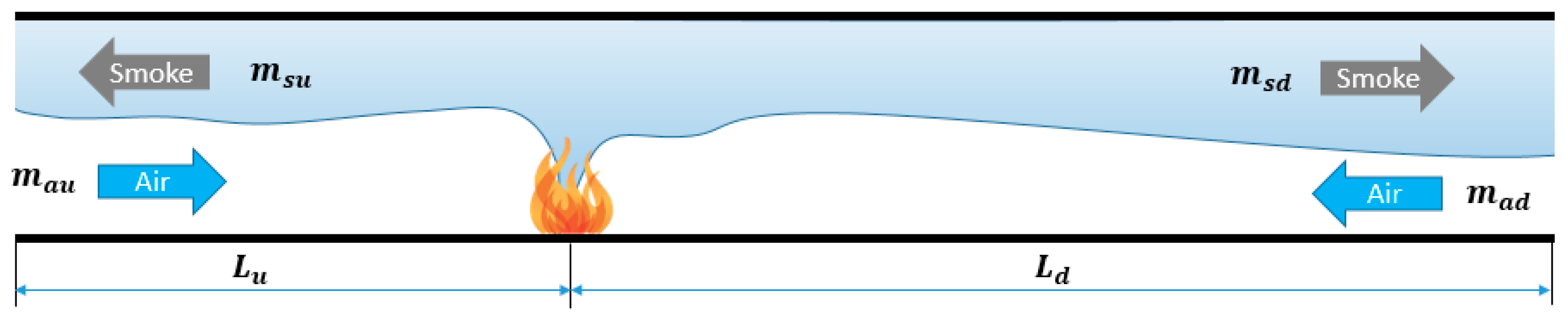
3.3. Distribution of Mass Flow Rate Smoke and Air
4. Conclusions
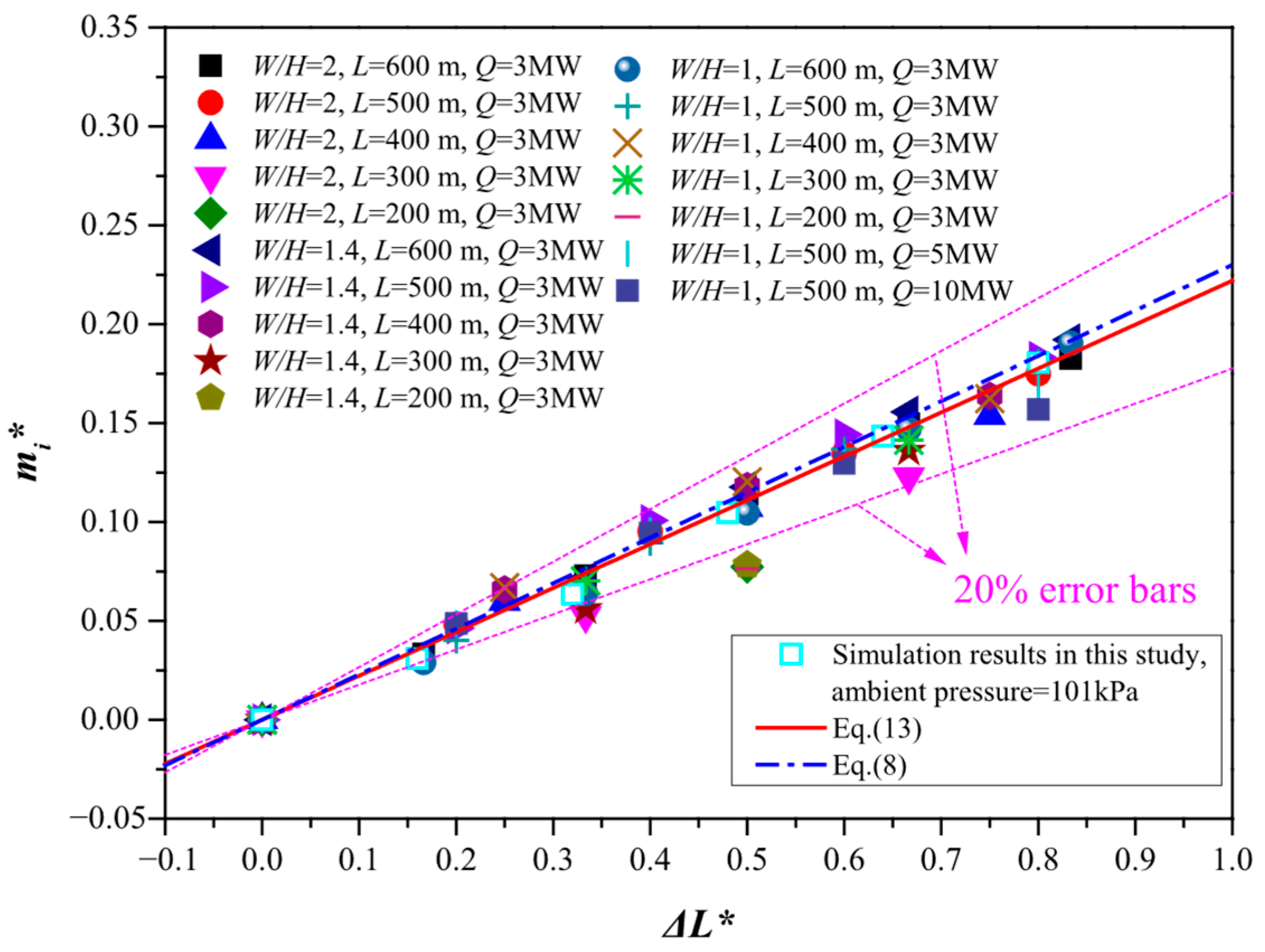
- (1)
- Asymmetric flow resulting from varying longitudinal positions of the fire source is observable under different ambient pressures. Ambient pressure affects the dynamics of smoke and air diffusion inside tunnels. An increase in ambient pressure results in a rise in both emitted smoke and incoming air.
- (2)
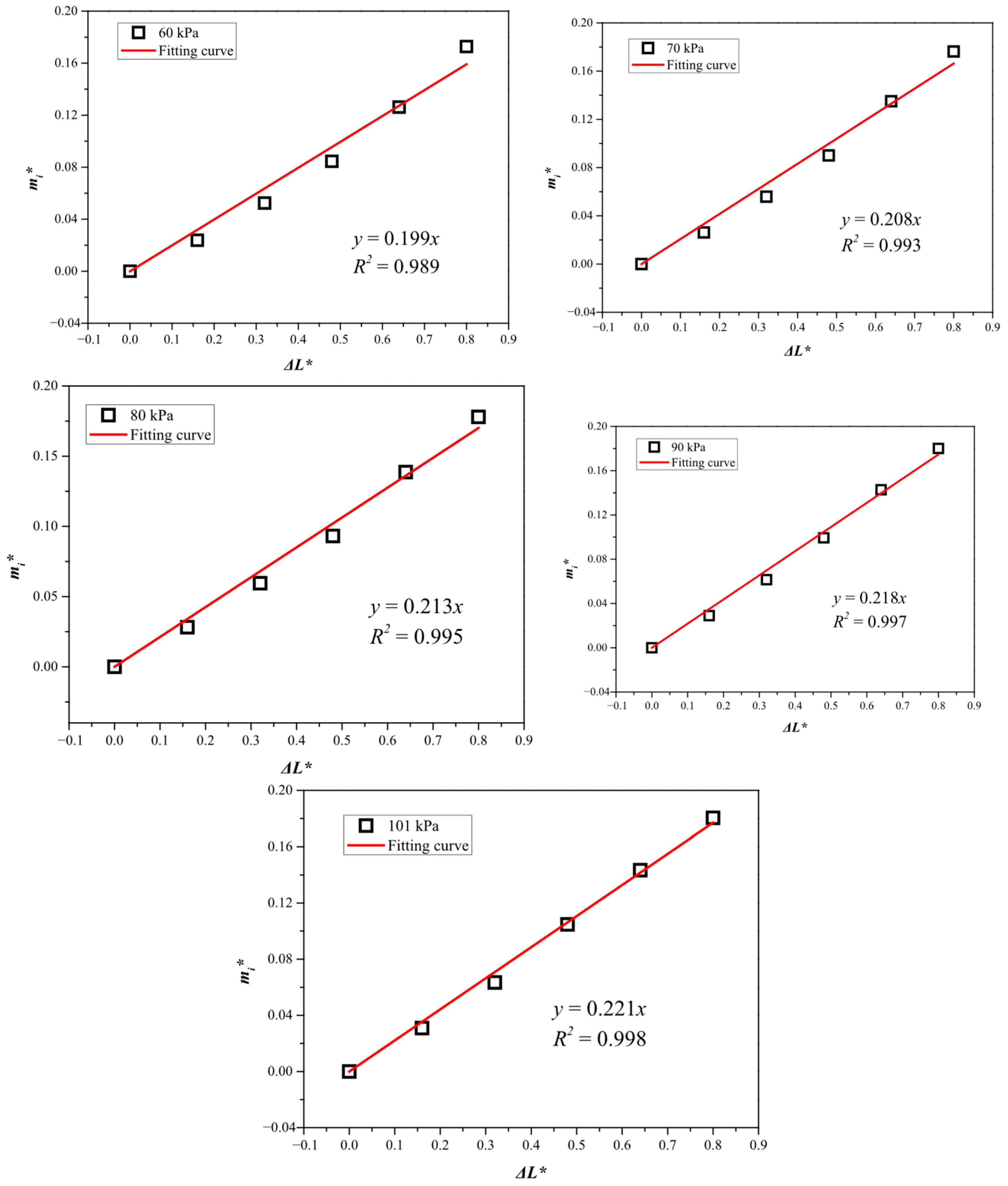
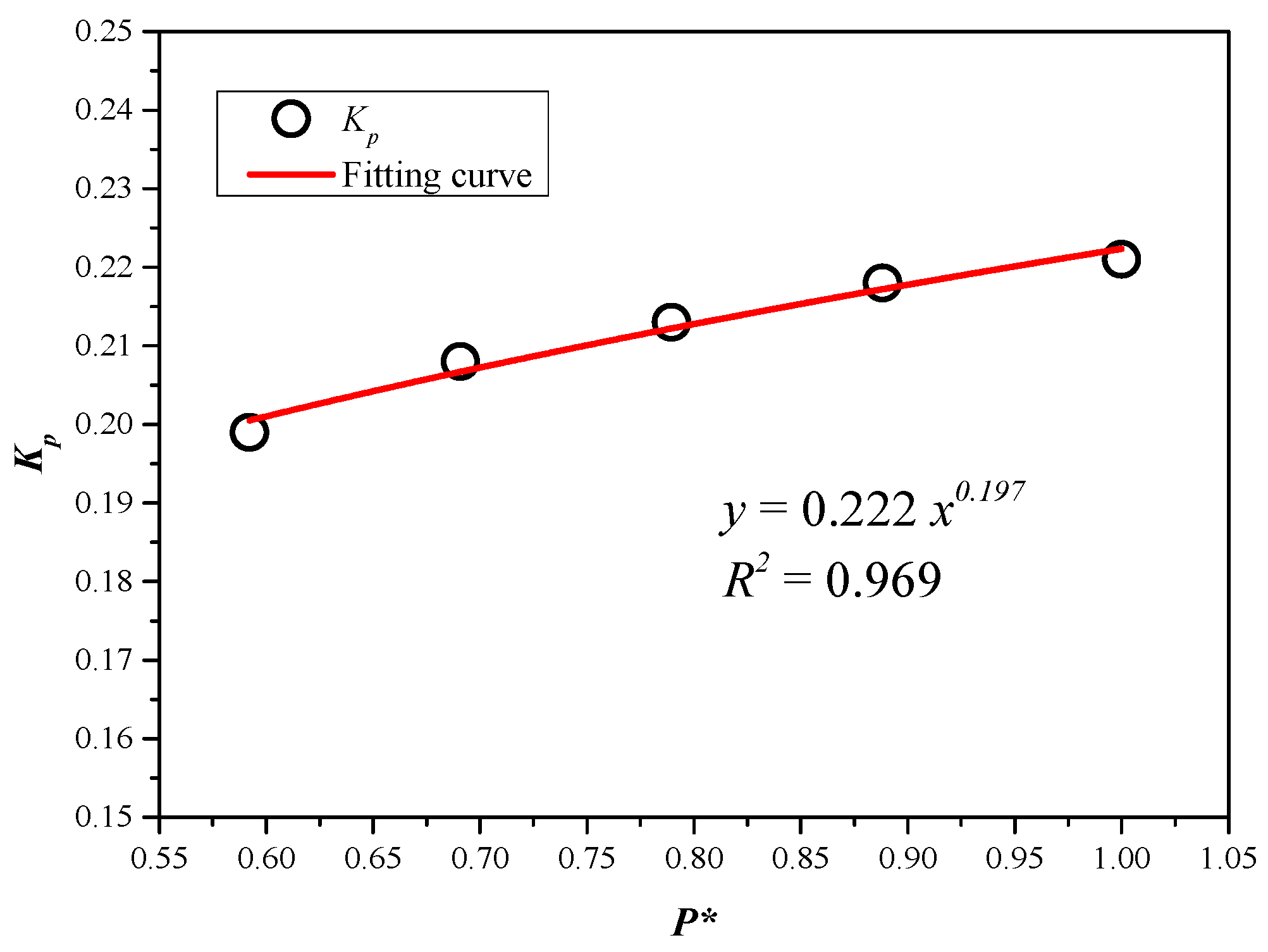
- The parameter of induced longitudinal flow mass rate characterizes the intensity of asymmetric flow effects at varying ambient pressures. A prediction model for calculating the mass flow rate of induced longitudinal flow was developed by using dimensionless ambient pressure to quantify its impact.
- (3)
- The ambient pressure has an impact on the mass flow values of smoke and airflow in tunnel fires but has little effect on their basic distribution laws. A predictive model has been proposed for the distribution laws of smoke overflow and air inflow under different ambient pressures.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Meng, N.; Liu, X.; Li, X.; Liu, B. Effect of blockage ratio on backlayering length of thermal smoke flow in a longitudinally ventilated tunnel. Appl. Therm. Eng. 2018, 132, 1–7. [Google Scholar] [CrossRef]
- Ji, J.; Gao, Z.H.; Fan, C.G.; Sun, J.H. Large Eddy Simulation of stack effect on natural smoke exhausting effect in urban road tunnel fires. Int. J. Heat Mass Transf. 2013, 66, 531–542. [Google Scholar] [CrossRef]
- Ji, J.; Wang, Z.; Ding, L.; Yu, L.; Gao, Z.; Wan, H. Effects of ambient pressure on smoke movement and temperature distribution in inclined tunnel fires. Int. J. Therm. Sci. 2019, 145, 106006. [Google Scholar] [CrossRef]
- Yu, L.; Wan, H.; Ji, J. Asymmetric flow effect in a horizontal natural ventilated tunnel with different aspect ratios under the influence of longitudinal fire locations. Build. Simul. 2020, 14, 1311–1323. [Google Scholar] [CrossRef]
- Wu, Y.; Atkinson, G.T.; Stoddard, J.P.; James, P. Effect of Slope on Control of Smoke Flow in Tunnel Fires. In Proceedings of the FIRE SAFETY SCIENCE—5, Tsukuba, Japan, 3–7 March 1997; pp. 1225–1236. [Google Scholar]
- He, L.; Liao, K.; Zhou, Y.; Tao, H.; Ming, Y.; Wang, X.; Zhang, H.; Zhu, G. Study on the influence of the longitudinal position of the fire source on the movement behavior of the asymmetric flow field. Therm. Sci. Eng. Prog. 2023, 39, 101753. [Google Scholar] [CrossRef]
- Gao, Z.; Li, L.; Sun, C.; Zhong, W.; Yan, C. Effect of longitudinal slope on the smoke propagation and ceiling temperature characterization in sloping tunnel fires under natural ventilation. Tunn. Undergr. Space Technol. 2022, 123, 104396. [Google Scholar] [CrossRef]
- Yu, L.; Lei, X.; Huang, P.; Liu, C.; Zhang, H.; Yang, F. Study on the combination effect of tunnel slope and longitudinal fire location on the asymmetric flow fields in a naturally ventilated tunnel. Tunn. Undergr. Space Technol. 2024, 146, 105623. [Google Scholar] [CrossRef]
- Ji, J.; Guo, F.Y.; Gao, Z.H.; Zhu, J.P.; Sun, J.H. Numerical investigation on the effect of ambient pressure on smoke movement and temperature distribution in tunnel fires. Appl. Therm. Eng. 2017, 118, 663–669. [Google Scholar] [CrossRef]
- Zhang, Y.; Yao, Y.; Ren, F.; Zhu, H.; Zhang, S.; Jiang, L. Effects of ambient pressure on smoke propagation in inclined tunnel fires under natural ventilation. Environ. Sci. Pollut. Res. 2023, 30, 65074–65085. [Google Scholar] [CrossRef] [PubMed]
- Yan, Z.G.; Guo, Q.H.; Zhu, H.H. Full-scale experiments on fire characteristics of road tunnel at high altitude. Tunn. Undergr. Space Technol. 2017, 66, 134–146. [Google Scholar] [CrossRef]
- Ji, J.; Guo, F.; Gao, Z.; Zhu, J. Effects of ambient pressure on transport characteristics of thermal-driven smoke flow in a tunnel. Int. J. Therm. Sci. 2018, 125, 210–217. [Google Scholar] [CrossRef]
- Yao, Y.; Zhang, Y.; Zhu, H.; Han, Z.; Zhang, S.; Zhang, X. Effects of ambient pressure on characteristics of smoke movement in tunnel fires. Tunn. Undergr. Space Technol. 2023, 134, 104981. [Google Scholar] [CrossRef]
- Tang, F.; Hu, L.H.; Yang, L.Z.; Qiu, Z.W.; Zhang, X.C. Longitudinal distributions of CO concentration and temperature in buoyant tunnel fire smoke flow in a reduced pressure atmosphere with lower air entrainment at high altitude. Int. J. Heat Mass Transf. 2014, 75, 130–134. [Google Scholar] [CrossRef]
- Liu, B.; Mao, J.; Xi, Y.; Hu, J. Effects of altitude on smoke movement velocity and longitudinal temperature distribution in tunnel fires. Tunn. Undergr. Space Technol. 2021, 112, 103850. [Google Scholar] [CrossRef]
- Gao, Z.; Cai, J.; Wang, P.; Liu, M.; Li, L. Smoke exhaust characteristics under stack effect of natural ventilation by shaft in high-altitude tunnel. Therm. Sci. Eng. Prog. 2024, 48, 102397. [Google Scholar] [CrossRef]
- Gannouni, S.; Ben Maad, R. CFD analysis of smoke backlayering dispersion in tunnel fires with longitudinal ventilation. Fire Mater. 2017, 41, 598–613. [Google Scholar] [CrossRef]
- Fan, C.; Zhang, L.; Jiao, S.; Yang, Z.; Li, M.; Liu, X. Smoke spread characteristics inside a tunnel with natural ventilation under a strong environmental wind. Tunn. Undergr. Space Technol. 2018, 82, 99–110. [Google Scholar] [CrossRef]
- Fan, C.; Chen, J.; Zhou, Y.; Liu, X. Effects of fire location on the capacity of smoke exhaust from natural ventilation shafts in urban tunnels. Fire Mater. 2018, 42, 974–984. [Google Scholar] [CrossRef]
- Ji, J.; Tan, T.; Gao, Z.; Wan, H.; Zhu, J.; Ding, L. Numerical Investigation on the Influence of Length–Width Ratio of Fire Source on the Smoke Movement and Temperature Distribution in Tunnel Fires. Fire Technol. 2019, 55, 963–979. [Google Scholar] [CrossRef]
- Yao, Y.; Li, Y.Z.; Ingason, H.; Cheng, X. Numerical study on overall smoke control using naturally ventilated shafts during fires in a road tunnel. Int. J. Therm. Sci. 2019, 140, 491–504. [Google Scholar] [CrossRef]
- Hu, L.H.; Huo, R.; Wang, H.B.; Yang, R.X. Experimental and Numerical Studies on Longitudinal Smoke Temperature Distribution Upstream and Downstream from the Fire in a Road Tunnel. J. Fire Sci. 2007, 25, 23–43. [Google Scholar] [CrossRef]
- McGrattan, K.; Hostikka, S.; McDermott, R.; Floyd, J.; Weinschenk, C.; Overholt, K. FDS Technical Reference Guide; National Institute of Standards and Technology: Washington, DC, USA, 2016. [Google Scholar]
- Hong, L.J.; Liu, C.J. Review of Research on Tunnel Fire Safety. Chin. J. Undergr. Space Eng. 2005, 1, 149–155. [Google Scholar]
- Wang, F.; Weng, M.; Han, J.; Obadi, I.; Liu, F. Effect of metro train on the critical driving force for preventing smoke back-layering in tunnel fires. Fire Mater. 2021, 46, 927–942. [Google Scholar] [CrossRef]
- Wang, F.; Liu, F.; Obadi, I.; Weng, M. Study on the smoke propagation characteristics of metro tunnel fire under the effects of piston wind. Indoor Built Environ. 2021, 32, 149–169. [Google Scholar] [CrossRef]
- McGrattan, K.; Hostikka, S.; McDermott, R.; Floyd, J.; Weinschenk, C.; Overholt, K. Fire Dynamics Simulator User’s Guide; National Institute of Standards and Technology: Washington, DC, USA, 2016. [Google Scholar] [CrossRef]
- Zhao, S.; Yang, H.; Xu, T.; Wang, F.; Li, C.; Xu, L. Effects of ambient pressure on fire-induced buoyancy driven plume dispersion and re-entrainment behavior in a street canyon. Atmos. Pollut. Res. 2023, 14, 101733. [Google Scholar] [CrossRef]
- Huang, P.; Ye, S.; Xie, J.; Chen, M.; Liu, C.; Yu, L. Study on the maximum and longitudinal distribution of ceiling gas temperature in a naturally ventilated tunnel: The effect of longitudinal fire location. Int. J. Therm. Sci. 2023, 185, 108037. [Google Scholar] [CrossRef]
- Zhao, S.; Xu, L.; Obadi, I.; Wang, F.; Liu, F.; Weng, M. Plug-holing height and complete plug-holing phenomenon in naturally ventilated tunnel fires with vertical shaft. Tunn. Undergr. Space Technol. 2021, 107, 103631. [Google Scholar] [CrossRef]
- Merci, B.; Beji, T. Fluid Mechanics Aspects of Fire and Smoke Dynamics in Enclosures; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
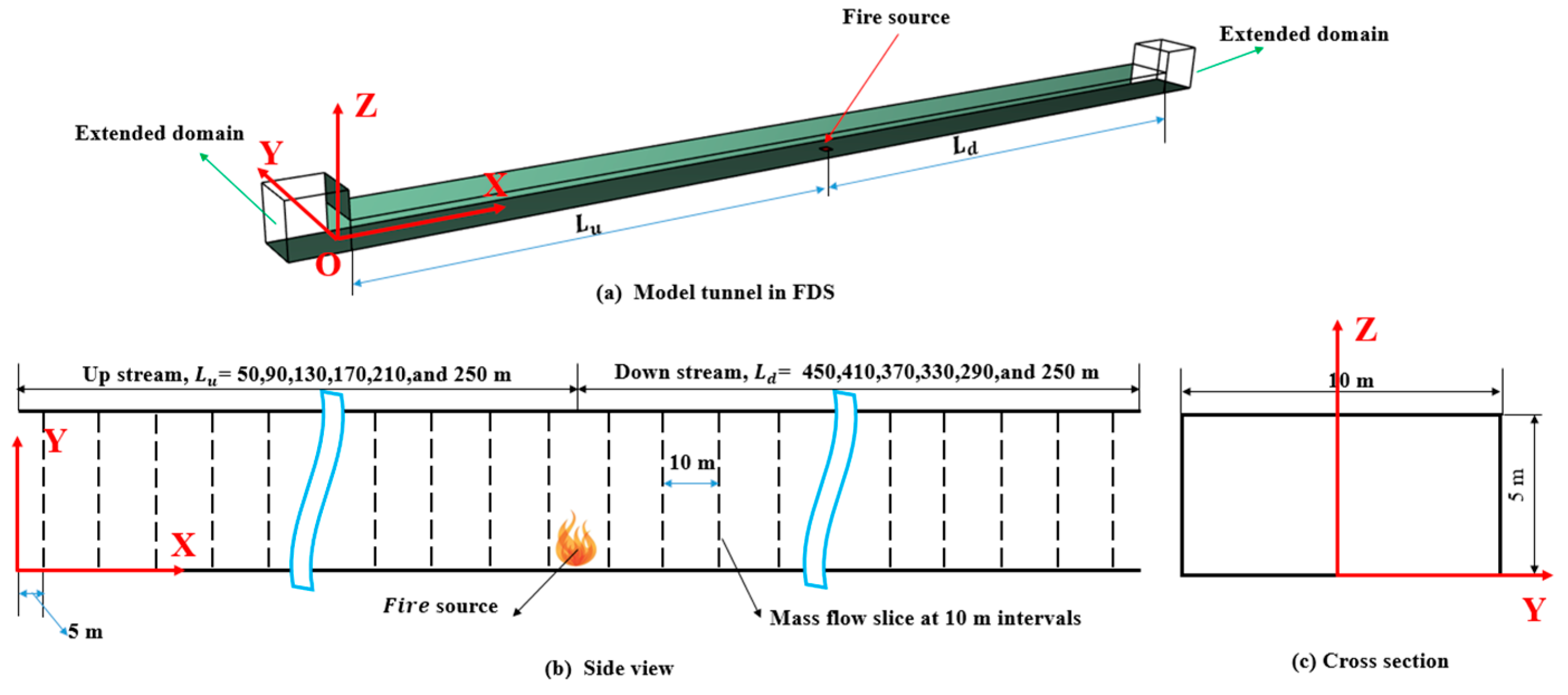





| Case No | (m) | (m) | Ambient Pressure (kPa) | HRR (MW) |
|---|---|---|---|---|
| 1–6 | 50 | 450 | 50, 60, 70, 80, 90, 101 | 5 |
| 7–12 | 90 | 410 | ||
| 13–18 | 130 | 370 | ||
| 19–24 | 170 | 330 | ||
| 25–30 | 210 | 290 | ||
| 31–36 | 250 | 250 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Liu, T.; Xu, L.; Cheng, C.; Chen, H.; He, X.; Zhao, S. Asymmetric Flow Induced by the Longitudinal Position of the Fire Source Under Different Ambient Pressures. Fire 2025, 8, 364. https://doi.org/10.3390/fire8090364
Wang F, Liu T, Xu L, Cheng C, Chen H, He X, Zhao S. Asymmetric Flow Induced by the Longitudinal Position of the Fire Source Under Different Ambient Pressures. Fire. 2025; 8(9):364. https://doi.org/10.3390/fire8090364
Chicago/Turabian StyleWang, Fei, Tianji Liu, Lin Xu, Chunjie Cheng, Haisheng Chen, Xingsen He, and Shengzhong Zhao. 2025. "Asymmetric Flow Induced by the Longitudinal Position of the Fire Source Under Different Ambient Pressures" Fire 8, no. 9: 364. https://doi.org/10.3390/fire8090364
APA StyleWang, F., Liu, T., Xu, L., Cheng, C., Chen, H., He, X., & Zhao, S. (2025). Asymmetric Flow Induced by the Longitudinal Position of the Fire Source Under Different Ambient Pressures. Fire, 8(9), 364. https://doi.org/10.3390/fire8090364







