Research on Fire Evacuation in University Libraries Based on the Fuzzy Ant Colony Optimization Algorithm
Abstract
1. Introduction
2. The Impact of Psychological Factors on Evacuation Speed
2.1. Factors Affecting Evacuation Psychology
2.2. Correction for Evacuation Speed
3. The Impact of Fire Environment Factors on Evacuation Speed
3.1. The Effect of Fire Products on Evacuation
3.2. Quantification of the Diminution in Evacuation Speed Due to Fire Products
4. Path Optimization Based on ACO
4.1. Fundamentals of ACO
4.2. Improvement of ACO
4.2.1. Improvement of the Heuristic Function
4.2.2. Enhancement of the Pheromone Update Method
4.3. Simulation Experiments and Analysis
- (1)
- Combination of and
- (2)
- Combination of
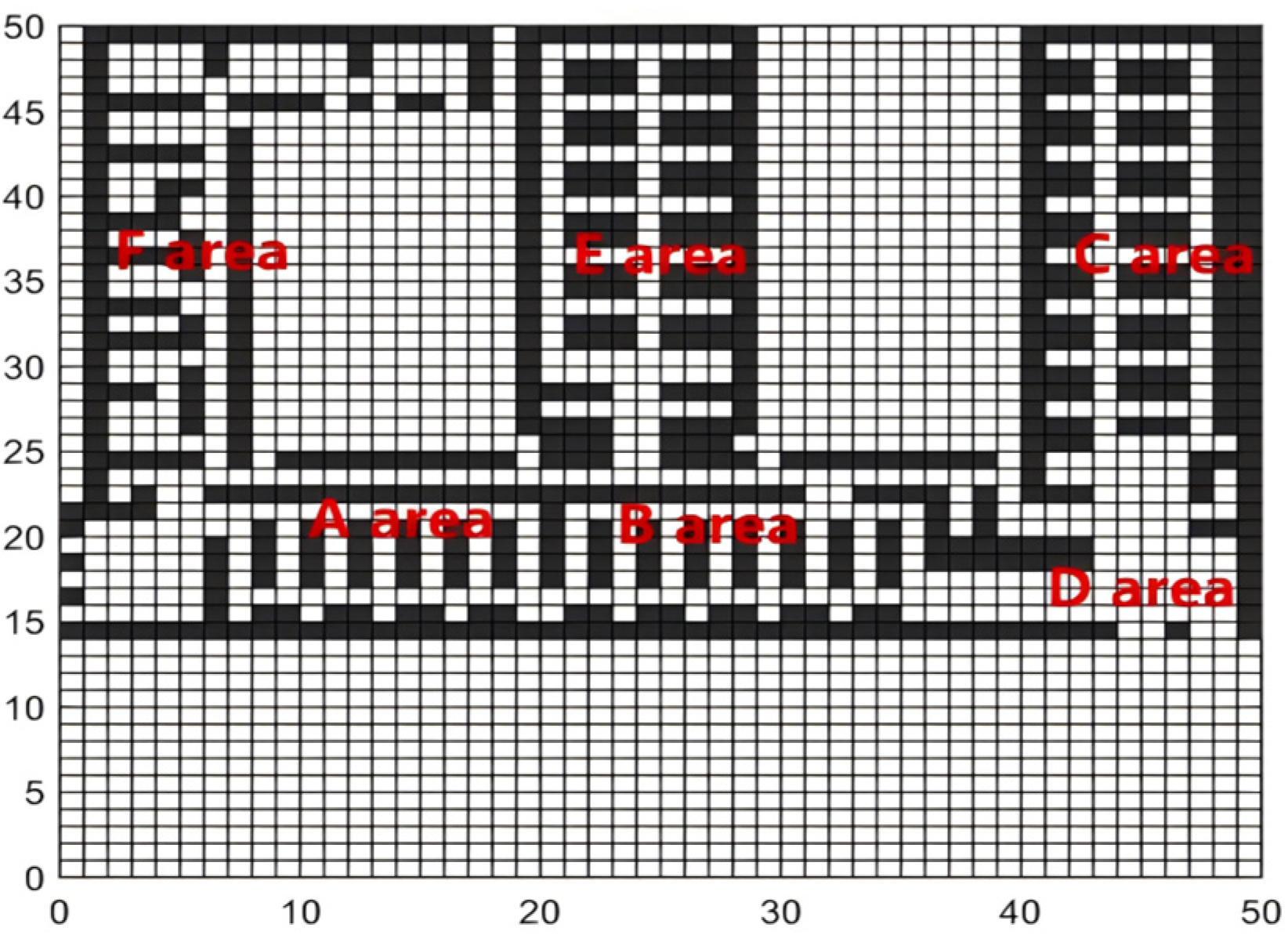
5. Practical Cases
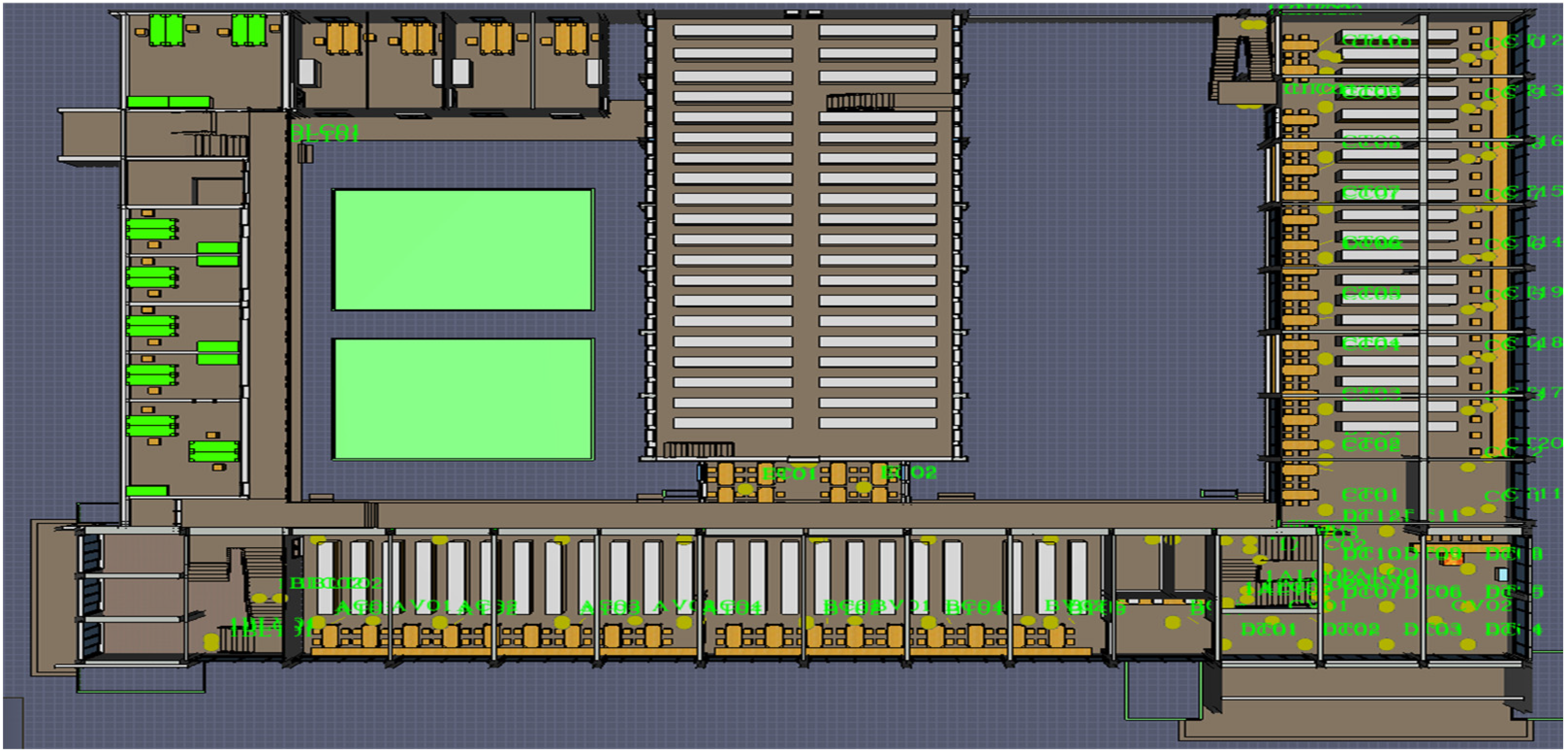
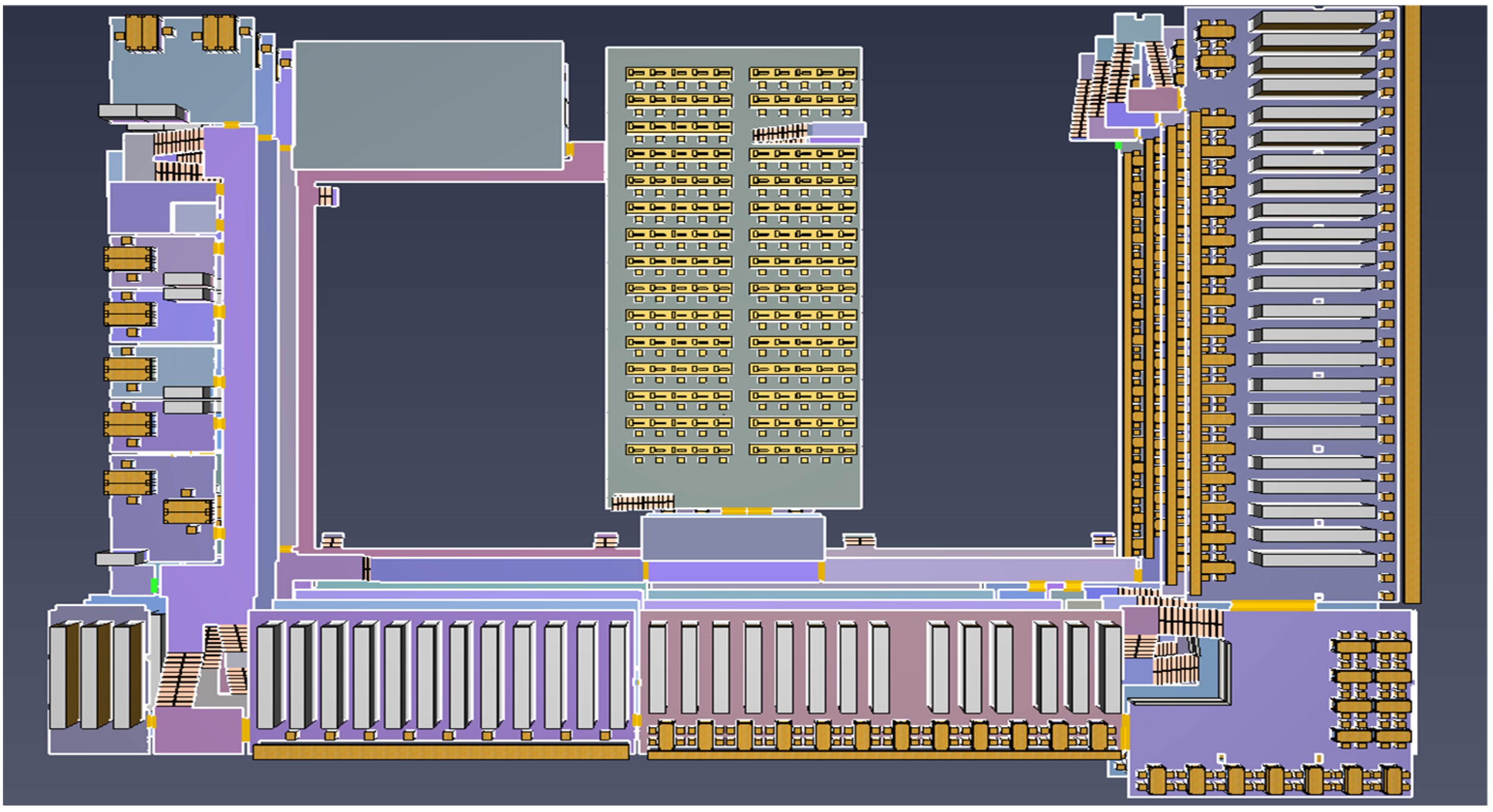
5.1. Building Information
5.2. Personnel Initial Evacuation Speed Correction
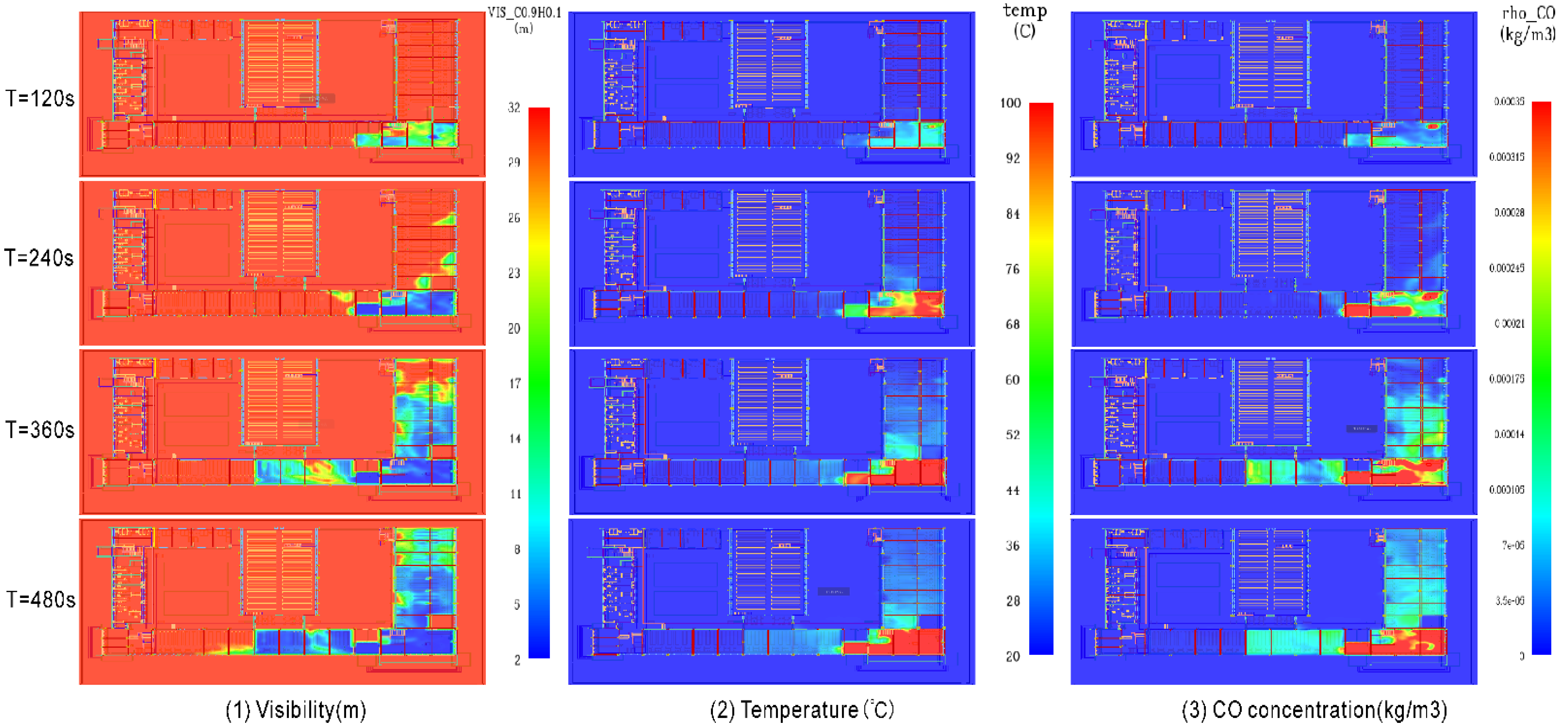
5.3. Derogation of the Speed of Evacuation
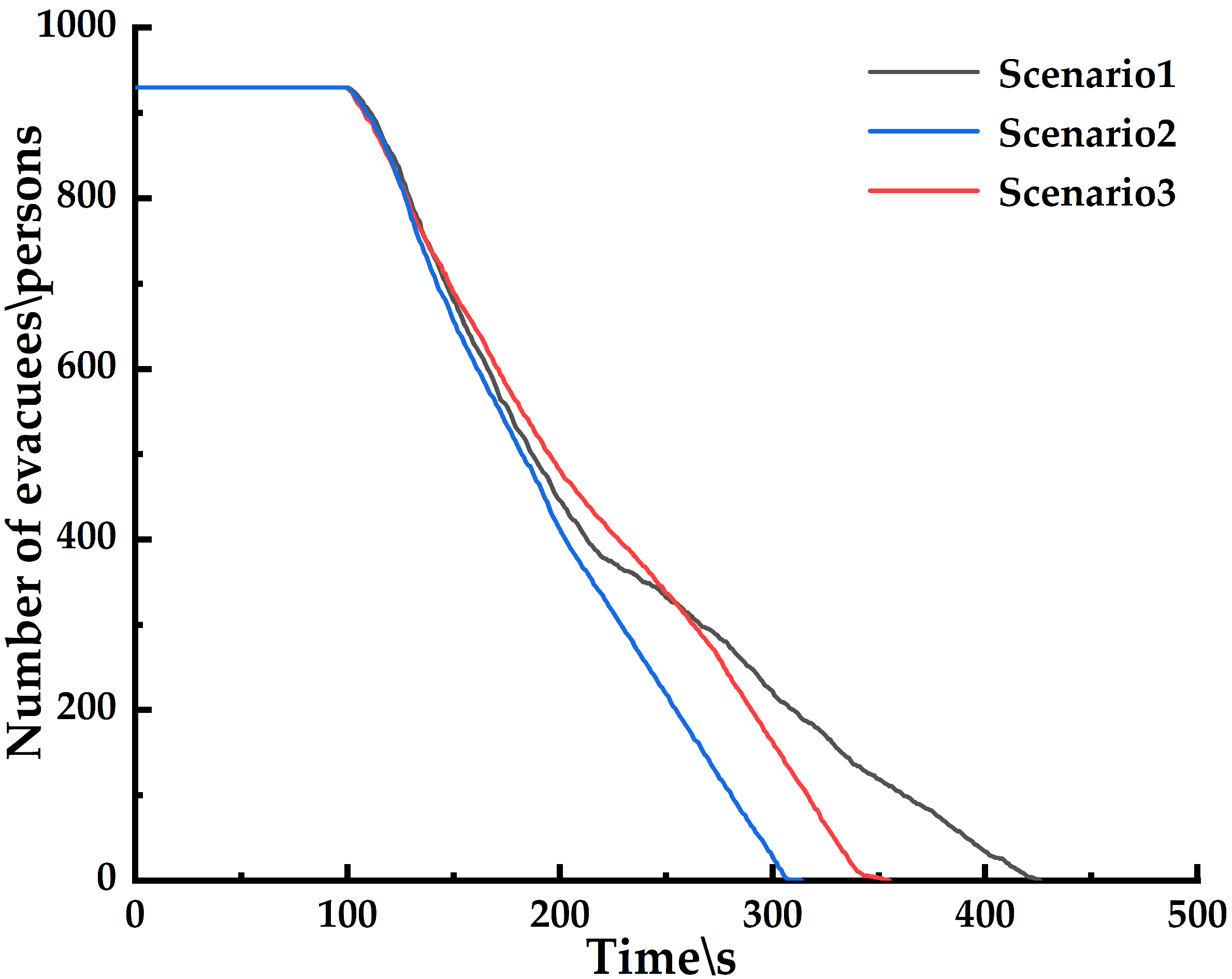
5.4. Comparison of Results from Personnel Evacuation Simulation Analysis
6. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, J.N.; Li, Y.H.; Du, H.B. Study of psychological and behavior characteristics of people during fire accident. J. Saf. Sci. Technol. 2007, 3, 35–38. [Google Scholar]
- Chen, J.; Long, Z.; Wang, L.; Xu, B.; Bai, Q.; Zhang, Y.; Liu, C.; Zhong, M. Fire evacuation strategy analysis in long metro tunnels. Saf. Sci. 2022, 147, 105603. [Google Scholar] [CrossRef]
- Yan, Z.; Wang, Y.; Chao, L.; Guo, J. Study on Evacuation Strategy of Commercial High-Rise Building under Fire Based on FDS and Pathfinder. CMES-Comput. Model. Eng. Sci. 2024, 140, 1077. [Google Scholar] [CrossRef]
- Juřík, V.; Uhlík, O.; Snopková, D.; Kvarda, O.; Apeltauer, T.; Apeltauer, J. Analysis of the use of behavioral data from virtual reality for calibration of agent-based evacuation models. Heliyon 2023, 9, e14275. [Google Scholar] [CrossRef]
- Cotfas, L.A.; Delcea, C.; Iancu, L.D.; Ioanăş, C.; Ponsiglione, C. Large event halls evacuation using an agent-based modeling approach. IEEE Access 2022, 10, 49359–49384. [Google Scholar] [CrossRef]
- Feng, Z.; You, Q.; Chen, K.; Song, H.; Peng, H. Research on Passenger Evacuation Behavior in Civil Aircraft Demonstration Experiments Based on Neural Networks and Modeling. Aerospace 2024, 11, 221. [Google Scholar] [CrossRef]
- Alidmat, O.; Abu Owida, H.; Yusof, U.K.; Almaghthawi, A.; Altalidi, A.; Alkhawaldeh, R.S.; Abuowaida, S.; Alshdaifat, N.; AlShaqsi, J. Simulation of crowd evacuation in asymmetrical exit layout based on improved dynamic parameters model. IEEE Access 2024, 13, 7512–7525. [Google Scholar] [CrossRef]
- Luo, Q.; Wang, H.; Zheng, Y.; He, J. Research on path planning of mobile robot based on improved ant colony algorithm. Neural Comput. Appl. 2020, 32, 1555–1566. [Google Scholar] [CrossRef]
- Asare, F.K.; Moniri-Morad, A.; Augustine, P.C.; Sattarvand, J. Vehicle-augmented evacuation integer programming model for improving safety and efficiency in underground mines. J. Saf. Sci. Resil. 2025, 6, 21–28. [Google Scholar] [CrossRef]
- Lei, M.; Zhang, W.; Zhang, J.; Wang, D.; Yang, M.; Li, X. Modeling of Safe Evacuation Conditions at the Construction Site for Building Type “I”. Buildings 2023, 13, 2121. [Google Scholar] [CrossRef]
- Lei, M.; Yang, M.; Gao, F.; Wang, D.; Zhang, J.; Qin, Z.; Zhang, W. Analysis and optimization of fire evacuation safety of university laboratory building based on Pyrosim and Pathfinder. Saf. Environ. Eng. 2023, 30, 36–44. [Google Scholar] [CrossRef]
- Gao, S.; Chang, C.; Liu, Q.; Zhang, M.; Yu, F. Study on the optimization for emergency evacuation scheme under fire in university building complex. Heliyon 2023, 9, e14277. [Google Scholar] [CrossRef]
- Yan, W.D.; Zhang, X.L. Research on the influence of personnel’s cognitive level on evacuation psychology and behavior during building fire. China Saf. Prod. Sci. Technol. 2010, 6, 108–113. [Google Scholar]
- Kobes, M.; Helsloot, I.; de Vries, B.; Post, J.G. Building safety and human behaviour in fire: A literature review. Fire Saf. J. 2010, 45, 1–11. [Google Scholar] [CrossRef]
- Siyam, N.; Alqaryouti, O.; Abdallah, S. Research issues in agent-based simulation for pedestrians evacuation. IEEE Access 2019, 8, 134435–134455. [Google Scholar] [CrossRef]
- Kinateder, M.; Comunale, B.; Warren, W.H. Exit choice in an emergency evacuation scenario is influenced by exit familiarity and neighbor behavior. Saf. Sci. 2018, 106, 170–175. [Google Scholar] [CrossRef]
- Zhang, Y.; Kinateder, M.; Huang, X.; Warren, W.H. Modeling competing guidance on evacuation choices under time pressure using virtual reality and machine learning. Expert Syst. Appl. 2025, 262, 125582. [Google Scholar] [CrossRef]
- Yuan, Y.; Wang, D. Multi-objective path selection model and algorithm for emergency evacuation. In Proceedings of the 2007 IEEE International Conference on Automation and Logistics, Jinan, China, 18–21 August 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 340–344. [Google Scholar]
- Zhang, Y.; Yan, Z.; Zhu, H.; Shen, Y.; Guo, Q.; Guo, Q. Experimental investigation of pedestrian evacuation using an extra-long steep-slope evacuation path in a high altitude tunnel fire. Sustain. Cities Soc. 2019, 46, 101423. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Shi, K.; Wu, Z.; Jiang, B.; Karimi, H.R. Dynamic path planning of mobile robot based on improved simulated annealing algorithm. J. Frankl. Inst. 2023, 360, 4378–4398. [Google Scholar] [CrossRef]
- Smarandache, F.; Vladareanu, L.; Broumi, S.; Bakali, A.; Akram, M. Applying Dijkstra Algorithm for Solving Neutrosophic Shortest Path Problem. In Proceedings of the 2016 International Conference on Advanced Mechatronic Systems, Melbourne, Australia, 30 November–3 December 2016; pp. 1–26. [Google Scholar]
- Singal, P.; Chhillar, R.S. Dijkstra shortest path algorithm using global position system. Int. J. Comput. Appl. 2014, 101, 12–18. [Google Scholar] [CrossRef]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A formal basis for the heuristic determination of minimum cost paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Chakraborty, S.; Sharma, S.; Saha, A.K.; Saha, A. A novel improved whale optimization algorithm to solve numerical optimization and real-world applications. Artif. Intell. Rev. 2022, 55, 4605–4716. [Google Scholar] [CrossRef]
- Dorigo, M.; Maniezzo, V.; Colorni, A. Ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man Cybern. Part B Cybern. 1996, 26, 29–41. [Google Scholar] [CrossRef]
- Wu, S.; Dong, A.; Li, Q.; Wei, W.; Zhang, Y.; Ye, Z. Application of ant colony optimization algorithm based on farthest point optimization and multi-objective strategy in robot path planning. Appl. Soft Comput. 2024, 167, 112433. [Google Scholar] [CrossRef]
- Wu, L.; Huang, X.; Cui, J.; Liu, C.; Xiao, W. Modified adaptive ant colony optimization algorithm and its application for solving path planning of mobile robot. Expert Syst. Appl. 2023, 215, 119410. [Google Scholar] [CrossRef]
- Li, X.; Feng, S.; Qian, J.; Lu, F. Research on parameter tuning method of robust PID controller based on artificial fish swarm algorithm. Inf. Control 2004, 33, 112–115. [Google Scholar]
- Chouridis, I.; Mansour, G.; Papageorgiou, V.; Mansour, M.T.; Tsagaris, A. Enhanced Hybrid Artificial Fish Swarm Algorithm for Three-Dimensional Path Planning Applied to Robotic Systems. Robotics 2025, 14, 32. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, W.; Wang, T.; Liu, J.; Wang, X.; Sean, M.; Yang, Z.; Wang, J. Dynamic optimisation of evacuation route in the fire scenarios of offshore drilling platforms. Ocean. Eng. 2022, 247, 110564. [Google Scholar] [CrossRef]
- Zheng, Y.; Yu, L.; Li, N.; Lu, Y. An ant colony algorithm applied to path planning in fire environment. J. Shanxi Univ. Nat. Sci. Ed. 2017, 40, 690–701. [Google Scholar]
- Banerjee, A.V. A simple model of herd behavior. Q. J. Econ. 1992, 107, 797–817. [Google Scholar] [CrossRef]
- Chen, C.; Qin, W.; Tong, Y.; Chen, Y. Investigation and analysis of personnel evacuation psychology and behavior under sudden fire. China Saf. Prod. Sci. Technol. 2018, 14, 35–40. [Google Scholar]
- Yu, X.; Xie, K.; Liang, B. A study on the relationship between emergency shelter perception and evacuation behavior. J. Manag. 2020, 17, 931–936. [Google Scholar]
- Zhao, H.; Zhang, Y.; Gou, Y. Simulation study of personnel evacuation considering environment familiarity and panic propagation. China Saf. Prod. Sci. Technol. 2024, 20, 124–130. [Google Scholar]
- Xie, B.; Zhou, L.; Zhao, J. A simulation method for fire evacuation in subway stations with the interaction of panic and evacuation behavior. China Saf. Prod. Sci. Technol. 2024, 20, 20–25. [Google Scholar]
- Wang, L.-X.; Yang, Z.-Z. A study of library fire evacuation behavior considering psychological latent variables. Fire Sci. Technol. 2023, 42, 658–664. [Google Scholar]
- Kirchner, A.; Klüpfel, H.; Nishinari, K.; Schadschneider, A.; Schreckenberg, M. Discretization effects and the influence of walking speed in cellular automata models forpedestrian dynamics. J. Stat. Mech. Theory Exp. 2004, 2004, P10011. [Google Scholar] [CrossRef]
- Yuan, C.; Wang, K.; Chen, H.; Liu, X.; Lang, Y. Study on correctin method of fire evacuation speed based on personel psychological and environmental factors. J. Saf. Sci. Technol. 2020, 15, 112–118. [Google Scholar]
- Saatchi, R. Fuzzy Logic Concepts, Developments and Implementation. Information 2024, 15, 656. [Google Scholar] [CrossRef]
- Takagi, T.; Sugeno, M. Fuzzy identification of systemsand its applications to modeling and control. IEEE Trans-Actions Syst. Man Cybern. 1985, 15, 116–132. [Google Scholar] [CrossRef]
- Cheng, H.D.; Chen, J.R. Automatically determine the membership function based on the maximum entropy principle. Inf. Sci. 1997, 96, 163–182. [Google Scholar] [CrossRef]
- Fridolf, K.; Nilsson, D.; Frantzich, H.; Ronchi, E.; Arias, S. Walking speed in smoke: Representation in life safety verifications. In Proceedings of the 12th International Performance-Based Codes and Fire Safety Design Methods Conference, Oahu, HI, USA, 23–26 April 2018; pp. 23–27. [Google Scholar]
- Qiu, R.; Fan, W. Biotoxicity of common hazardous combustion products in fires (I)—CO, hydrogen cyanide. Fire Sci. 2001, 10, 154–158. [Google Scholar]
- Dorigo, M.; Blum, C. Ant colony optimization theory: A survey. Theor. Comput. Sci. 2005, 344, 243–278. [Google Scholar] [CrossRef]
- Du, Y.; Zhang, Y.; Zhao, H. Research on Robot Path Planning Based on Parameter Optimized ant Colony algorithm. Mod. Manuf. Eng. 2020, 7–14. [Google Scholar] [CrossRef]
- Yang, R.; Wang, Y. Research on the basic principle and parameter setting of ant colony algorithm. South. Agric. Mach. 2018, 49, 38–39. [Google Scholar]
- Sun, H.; Zhu, K.; Zhang, W.; Ke, Z.; Hu, H.; Wu, K.; Zhang, T. Emergency path planning based on improved ant colony algorithm. J. Build. Eng. 2025, 100, 111725. [Google Scholar] [CrossRef]
- Li, M.-X.; Zhu, S.-B.; Wang, J.-H.; Zhou, Z. Research on Fire Safety Evacuation in a University Library in Nanjing. Procedia Eng. 2018, 211, 372–378. [Google Scholar] [CrossRef]
- Chen, N.; Wang, S.; Zhao, J.; Zhong, W.; Zhang, L. Simulation and optimization of emergency evacuation of student apartments in higher education. Ind. Saf. Environ. Prot. 2017, 43, 62–64+87. [Google Scholar]
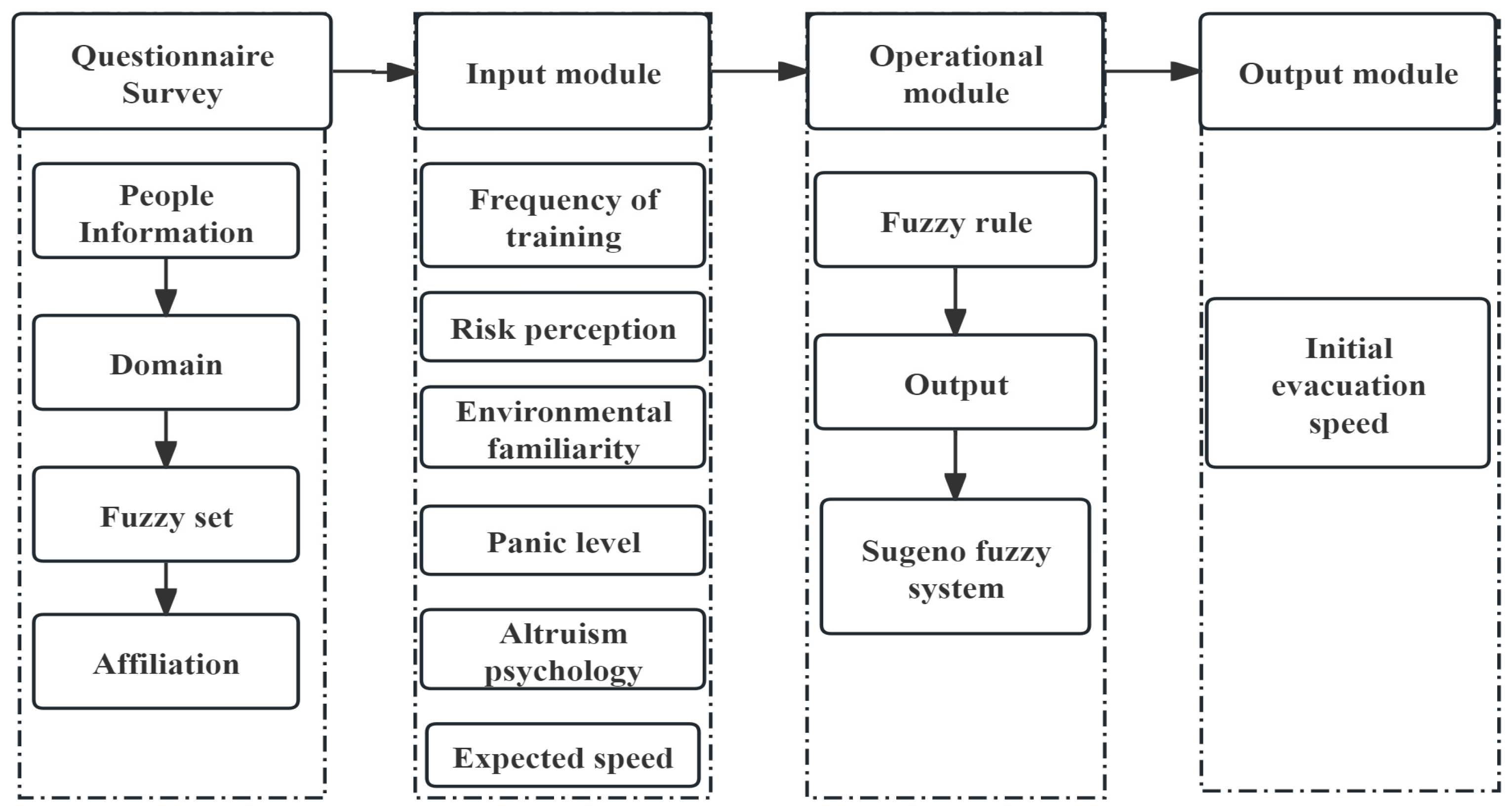




| Factors | Concept |
|---|---|
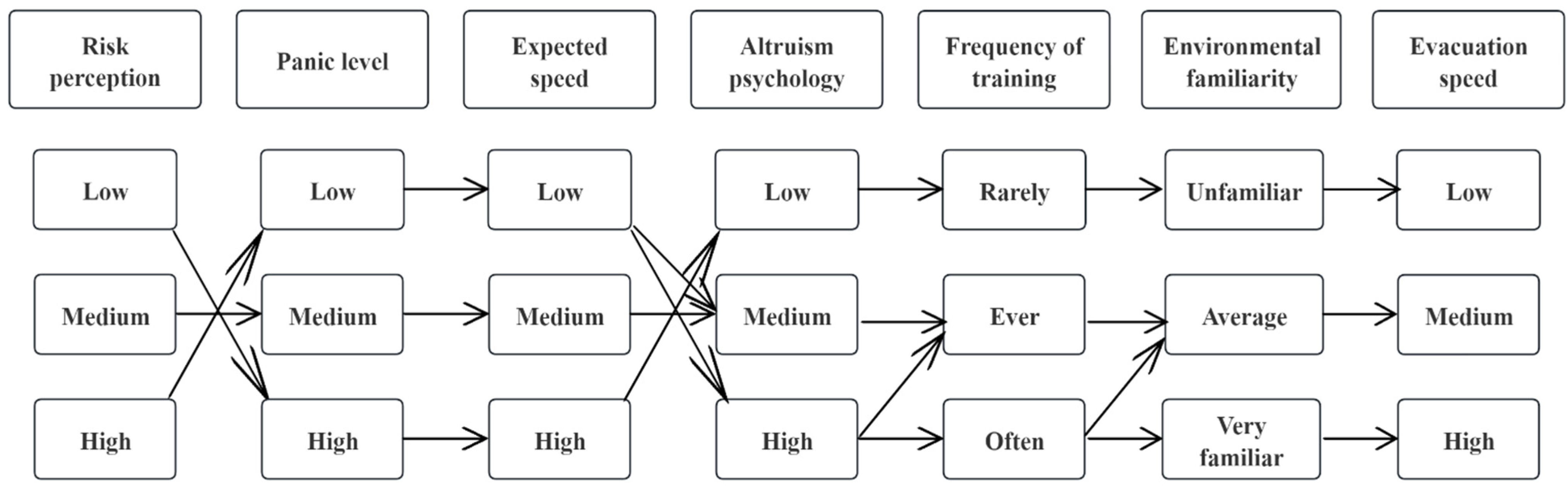
| Frequency of training | Increasing the frequency of evacuation education and training for individuals enhances their confidence in evacuation knowledge and broadcast orders, reduces panic levels, and improves their ability to evacuate [35]. |
| Risk perception | Risk perception has a substantial beneficial influence on evacuation behavior. As personnel’s risk perception increases, the evacuation characteristics become more evident [36]. |
| Environmental familiarity | Enhanced environmental familiarity will reduce the spread of fear and promote crowd evacuation [37]. |
| Panic level | Following a fire in a building, a lack of awareness of the fire circumstances and insufficient evacuation experience may easily arouse fear, which impairs judgment and results in the phenomena of crowd gathering and unthinkingly following others through the evacuation process [38]. |
| Altruism psychology | It is a psychological tendency of evacuees to give assistance to those who need it during evacuation regardless of other factors, and helping behavior can improve the efficiency of evacuation to a certain extent [39]. |
| Expected speed | The required evacuation speed of individuals may significantly change owing to differences in their physical health and psychological behavior [40]. |
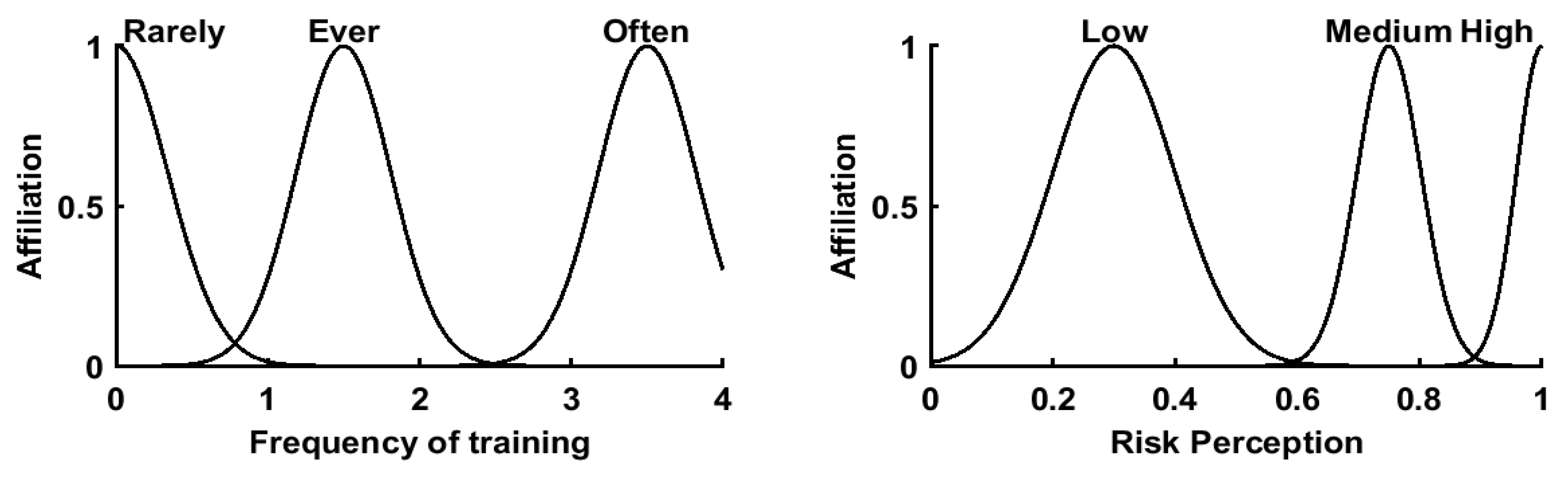
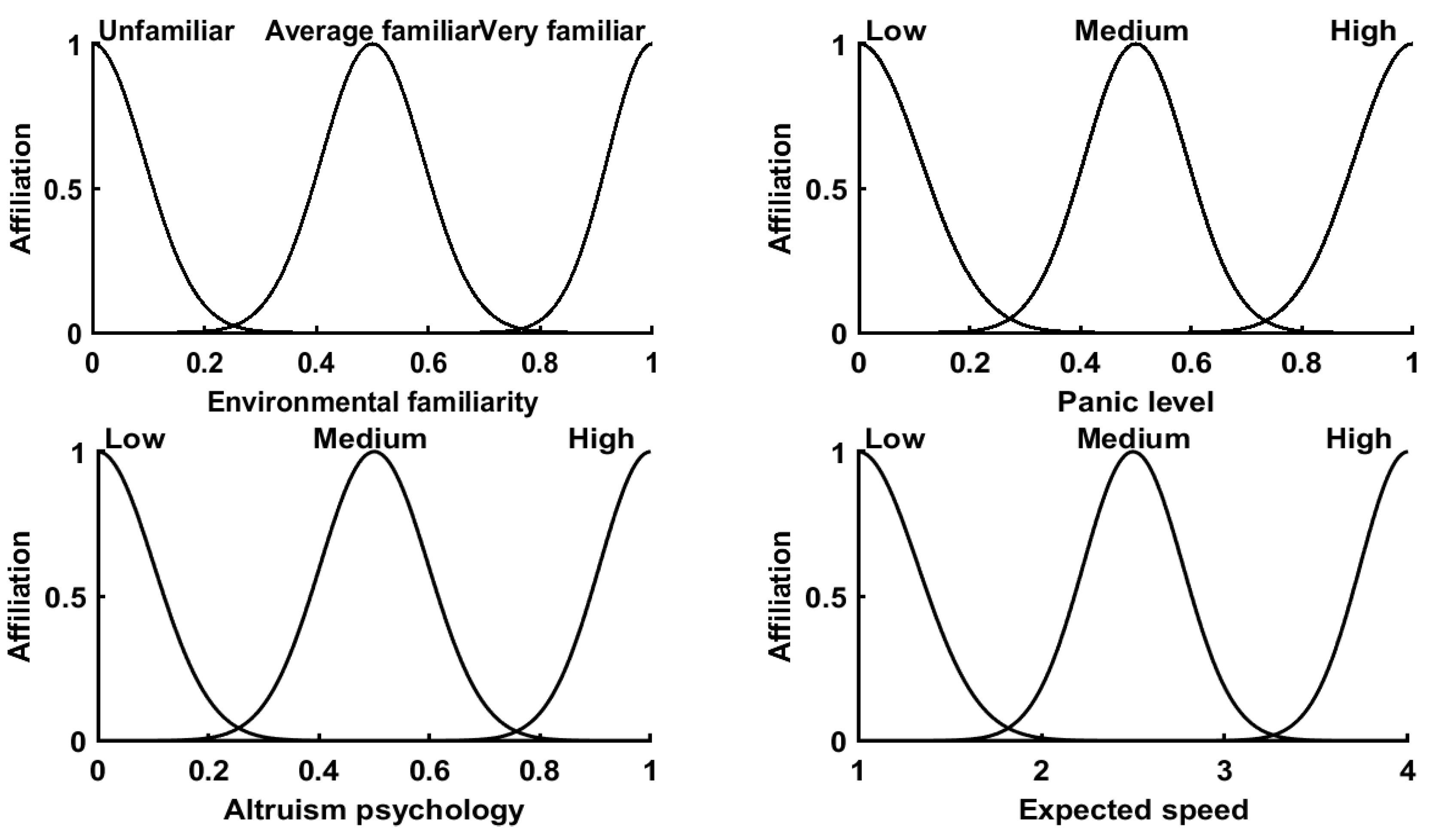
| Factors | Domain (Math.) | Fuzzy Sets (Plurality) |
|---|---|---|
| Frequency of training | (0, 4) | Rarely (0), Ever (1.5), Often (3.5) |
| Risk perception | (0, 1) | Low (0.3), Medium (0.75), High (0.96) |
| Environmental familiarity | (0, 1) | Unfamiliar (0), Average (0.5), Very Familiar (0.95) |
| Panic level | (0, 1) | Low (0.05), Medium (0.5), High (1) |
| Altruism psychology | (0, 1) | Low (0.05), Medium (0.5), High (1) |
| Expected speed | (1, 4) | Low (1), Medium (2.5), High (4) |
| Parameter Value | Average Length | ||||
|---|---|---|---|---|---|
| 28.50 | 25.82 | 24.67 | 24.42 | 24.13 | |
| 27.10 | 24.93 | 23.96 | 24.09 | 23.91 | |
| 24.49 | 24.20 | 23.64 | 24.09 | 23.92 | |
| 25.90 | 24.31 | 24.57 | 24.45 | 24.28 | |
| 25.25 | 24.40 | 24.76 | 24.37 | 24.64 | |
| 27.10 | 24.97 | 24.50 | 24.66 | 24.66 | |
| Parameter Value | Average Length | |||
|---|---|---|---|---|
| Q | M = 50 | M = 100 | M = 150 | |
| 0.4 | 1 | 24.06 | 23.59 | 23.65 |
| 50 | 24.36 | 24.01 | 23.45 | |
| 100 | 24.61 | 23.97 | 23.95 | |
| 150 | 24.87 | 24.26 | 23.72 | |
| 0.5 | 1 | 24.14 | 23.98 | 23.55 |
| 50 | 24.72 | 24.23 | 24.12 | |
| 100 | 24.26 | 24.25 | 24.02 | |
| 150 | 24.21 | 23.78 | 24.03 | |
| 0.6 | 1 | 24.17 | 23.89 | 23.51 |
| 50 | 24.91 | 24.01 | 24.03 | |
| 100 | 24.84 | 23.87 | 23.66 | |
| 150 | 24.56 | 24.64 | 23.96 | |
| Starting Point | Exit | Distance for ACO | Number of Iterations for ACO | Distance for IACO | Number of Iterations for IACO |
|---|---|---|---|---|---|
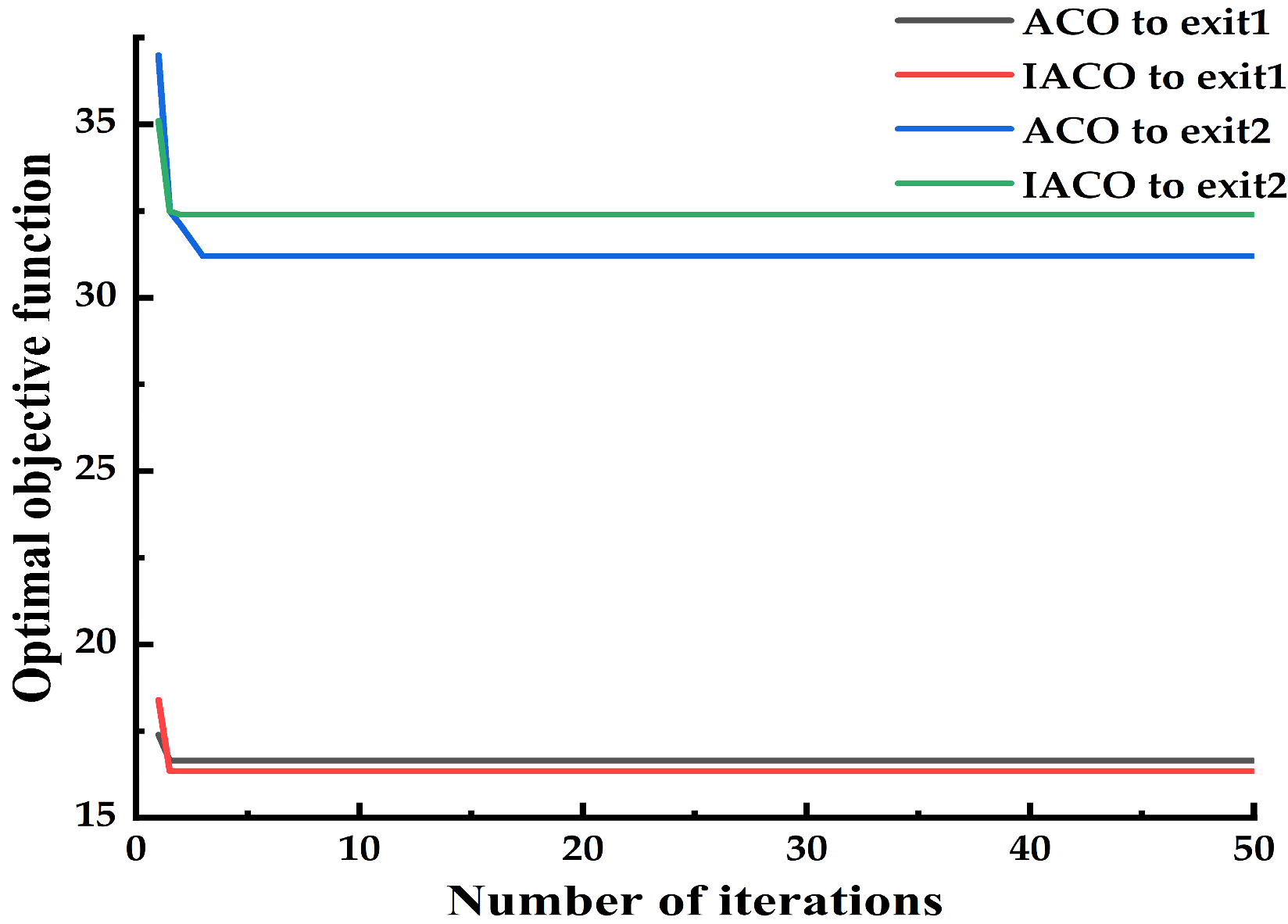
| A | 1 | 17.99 | 21.49 | 17.99 | 21.49 |
| 2 | 31.11 | 35.14 | 30.71 | 35.38 | |
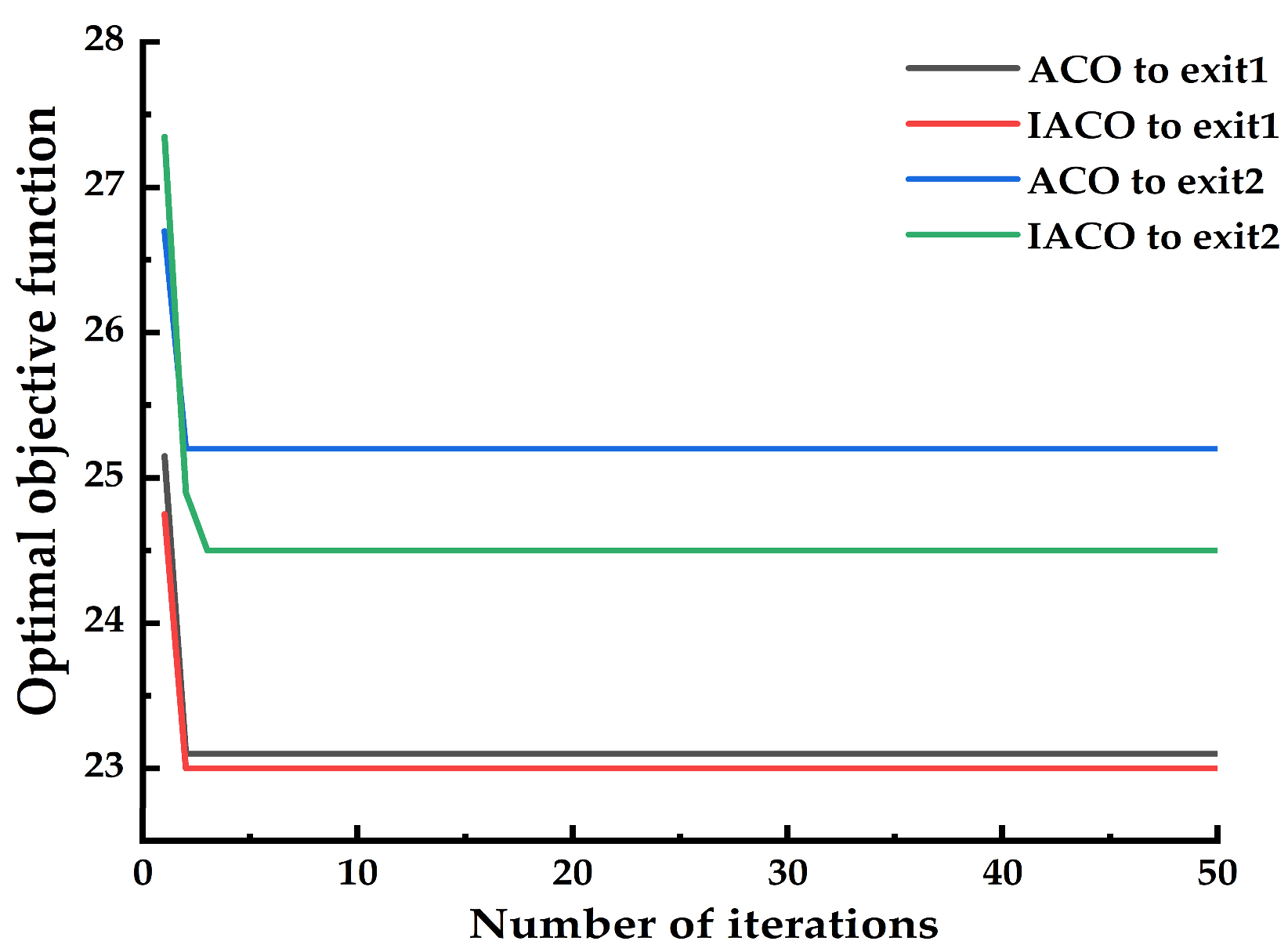
| B | 1 | 23.05 | 27.31 | 22.99 | 26.49 |
| 2 | 25.18 | 28.73 | 24.51 | 28.14 | |
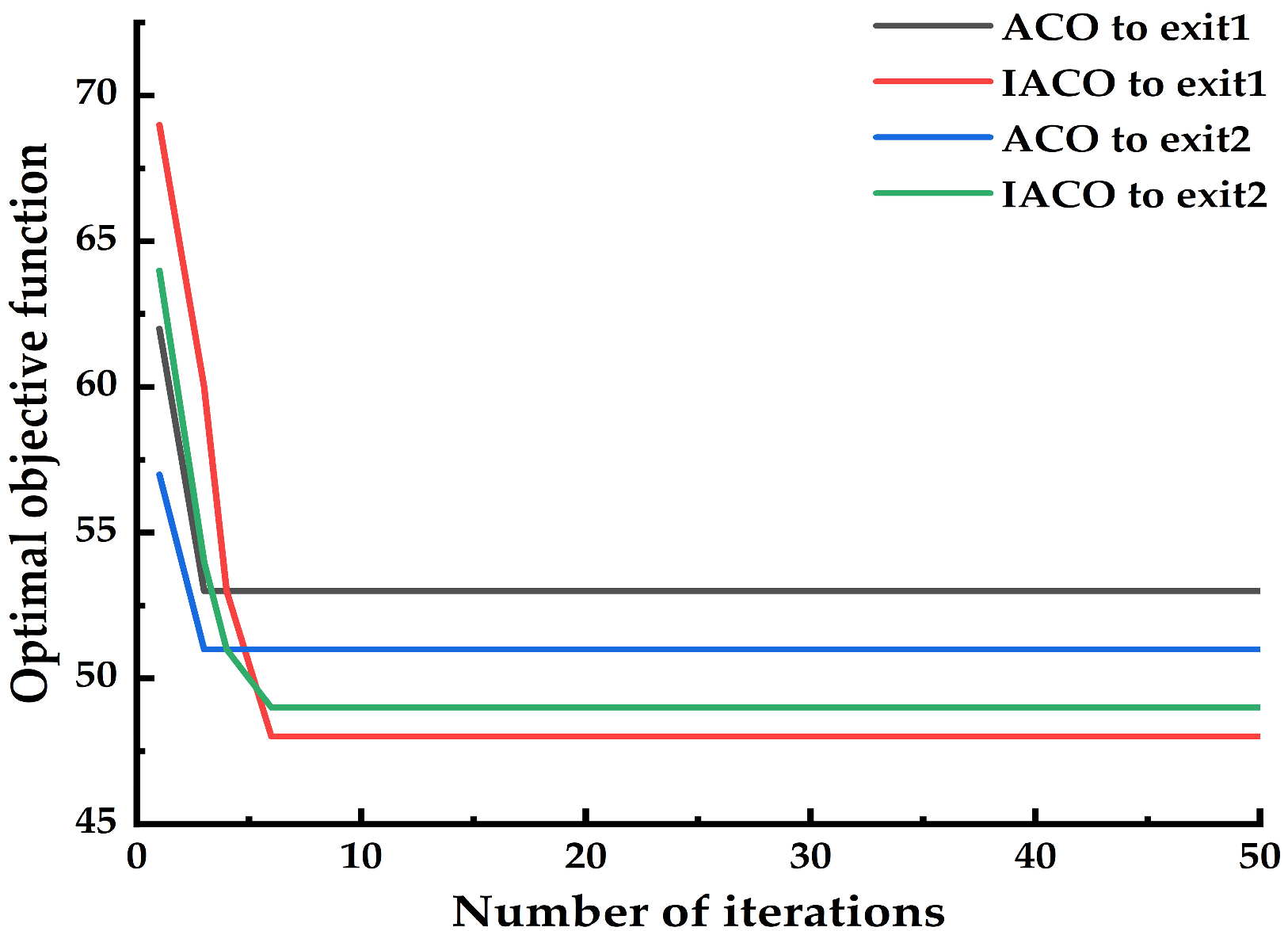
| C | 1 | 95.52 | 50.03 | 92.29 | 47.5 |
| 2 | 43.45 | 39.7 | 40.14 | 36.42 | |
| E | 1 | 62.79 | 52.78 | 57.72 | 47.63 |
| 2 | 64.69 | 51.56 | 64.45 | 48.53 |
| Frequency of Training | Risk Perception | Environmental Familiarity | Panic Level | Altruism Psychology | Expected Speed (m/s) | Initial Evacuation Speed | |
|---|---|---|---|---|---|---|---|
| Man | 2 | 0.87 | 0.37 | 0.44 | 0.67 | 2.9 | 1.2 |
| Woman | 2 | 0.85 | 0.36 | 0.58 | 0.68 | 3.0 | 1.12 |
| Area\Time(s) | 60 | 120 | 180 | 240 | 300 | 360 | 420 | 480 |
|---|---|---|---|---|---|---|---|---|
| A | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0.83 |
| B | 1 | 1 | 1 | 1 | 1.02 | 1.14 | 1.24 | 0.93 |
| C | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| D | 1 | 0.79 | 0.3 | 0.4 | 0.66 | 0.62 | 0.57 | 0.54 |
| E | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| F | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1st floor stairs | 1 | 1 | 1.32 | 2.97 | 1.48 | 0.67 | 0.34 | 0.02 |
| 2nd floor stairs | 1 | 1.02 | 1.09 | 1.05 | 0.98 | 0.31 | 0.16 | 0.02 |
| 3rd floor stairs | 1 | 1 | 1 | 0.58 | 0.55 | 0.66 | 0.62 | 0.64 |
| 4th floor stairs | 1 | 1 | 0.88 | 0.44 | 0.55 | 0.65 | 0.61 | 0.62 |
| Type of Personnel | Height/m | Shoulder Width/m | 1st Floor/Person | 2nd Floor/Person | 3rd Floor/Person | 4th Floor/Person |
|---|---|---|---|---|---|---|
| Middle-aged men | 1.667 | 0.433 | 4 | 3 | 4 | 2 |
| Middle-aged women | 1.560 | 0.405 | 6 | 5 | 3 | 4 |
| Young men | 1.686 | 0.427 | 105 | 133 | 114 | 73 |
| Young women | 1.580 | 0.391 | 115 | 127 | 126 | 87 |
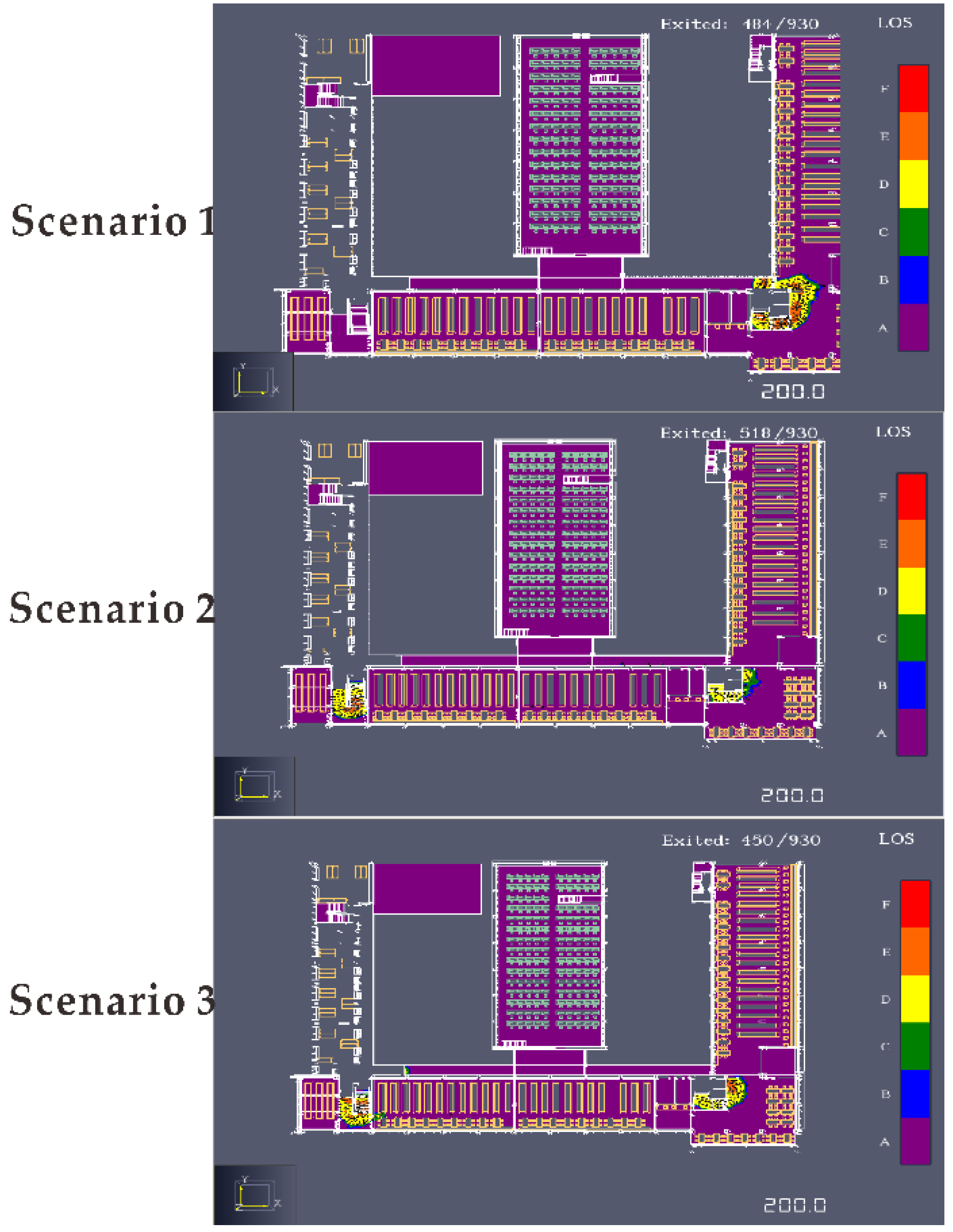
| Scenario | Total Evacuation Time\s | Anyone Trapped | Evacuation Efficiency (Curve Slope) | 100–220 s (Curve Slope) | 100–300 s (Curve Slope) |
|---|---|---|---|---|---|
| 1 | 426 | no | High in the first half of slope | −4.947 ± 0.032 | −1.948 ± 0.022 |
| 2 | 313.3 | no | Always high | −5.222 ± 0.032 | −3.688 ± 0.030 |
| 3 | 356.8 | no | High in the second half of slope | −4.430 ± 0.027 | −3.200 ± 0.289 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, M.; Huang, M.; Wang, D.; Zhang, W.; Cheng, S.; Dong, W. Research on Fire Evacuation in University Libraries Based on the Fuzzy Ant Colony Optimization Algorithm. Fire 2025, 8, 329. https://doi.org/10.3390/fire8080329
Lei M, Huang M, Wang D, Zhang W, Cheng S, Dong W. Research on Fire Evacuation in University Libraries Based on the Fuzzy Ant Colony Optimization Algorithm. Fire. 2025; 8(8):329. https://doi.org/10.3390/fire8080329
Chicago/Turabian StyleLei, Ming, Mengke Huang, Dandan Wang, Wei Zhang, Sixiang Cheng, and Wenhui Dong. 2025. "Research on Fire Evacuation in University Libraries Based on the Fuzzy Ant Colony Optimization Algorithm" Fire 8, no. 8: 329. https://doi.org/10.3390/fire8080329
APA StyleLei, M., Huang, M., Wang, D., Zhang, W., Cheng, S., & Dong, W. (2025). Research on Fire Evacuation in University Libraries Based on the Fuzzy Ant Colony Optimization Algorithm. Fire, 8(8), 329. https://doi.org/10.3390/fire8080329





