Finite Element Analysis of Flat Plate Structures in Fire
Abstract
1. Introduction
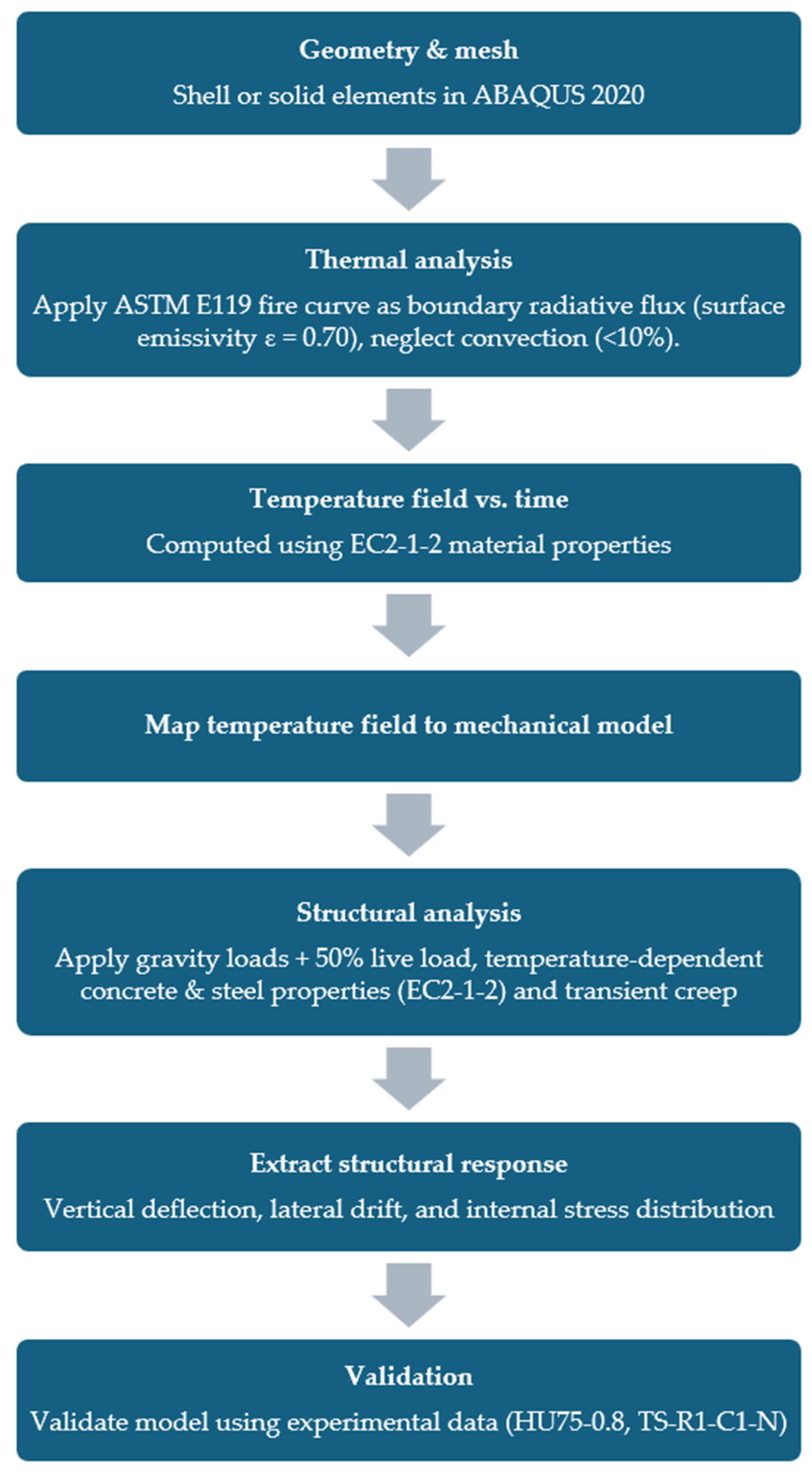
2. General Thermo-Structural Analysis Procedures
- Concrete degradation due to reasons other than fire temperature was ignored. This assumption was made to allow the analysis to continue for the duration of the fire. According to the structural strength failure criteria in BS 476-20:1987 [22,23], horizontal elements are considered to have failed when deflection limits (Δ) in Equations (2) and (3) are reached. Therefore, in this study, failure was judged based on these criteria. The clear span (L) and the depth of section (d) were used in these calculations. Adopting these failure criteria ensures alignment with widely accepted practices in structural fire engineering and consistency with experimental methodologies. This approach bridges the gap between numerical modelling and experimental validation by providing a clear, standardized, practical framework for assessing structural failure under fire conditions.
- Concrete spalling was excluded due to its limited occurrence in normal-strength concrete.
- The elevated temperatures do not affect the bond of the steel rebars to the concrete.
- The slab is uniformly exposed to fire.
- Columns are assumed to be thermally protected and unaffected by the fire. Their properties were assigned based on an ambient temperature of 20 °C.
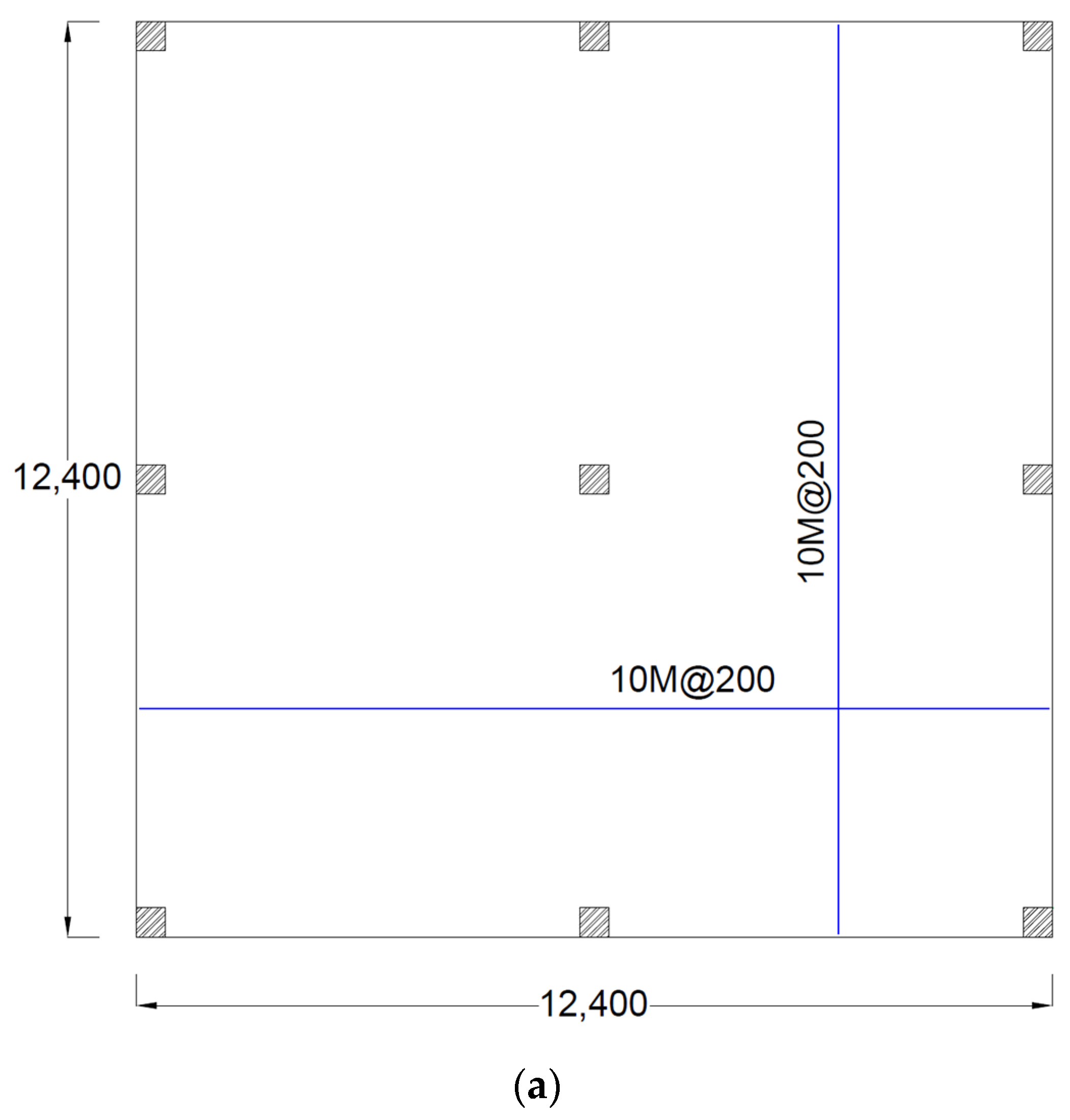
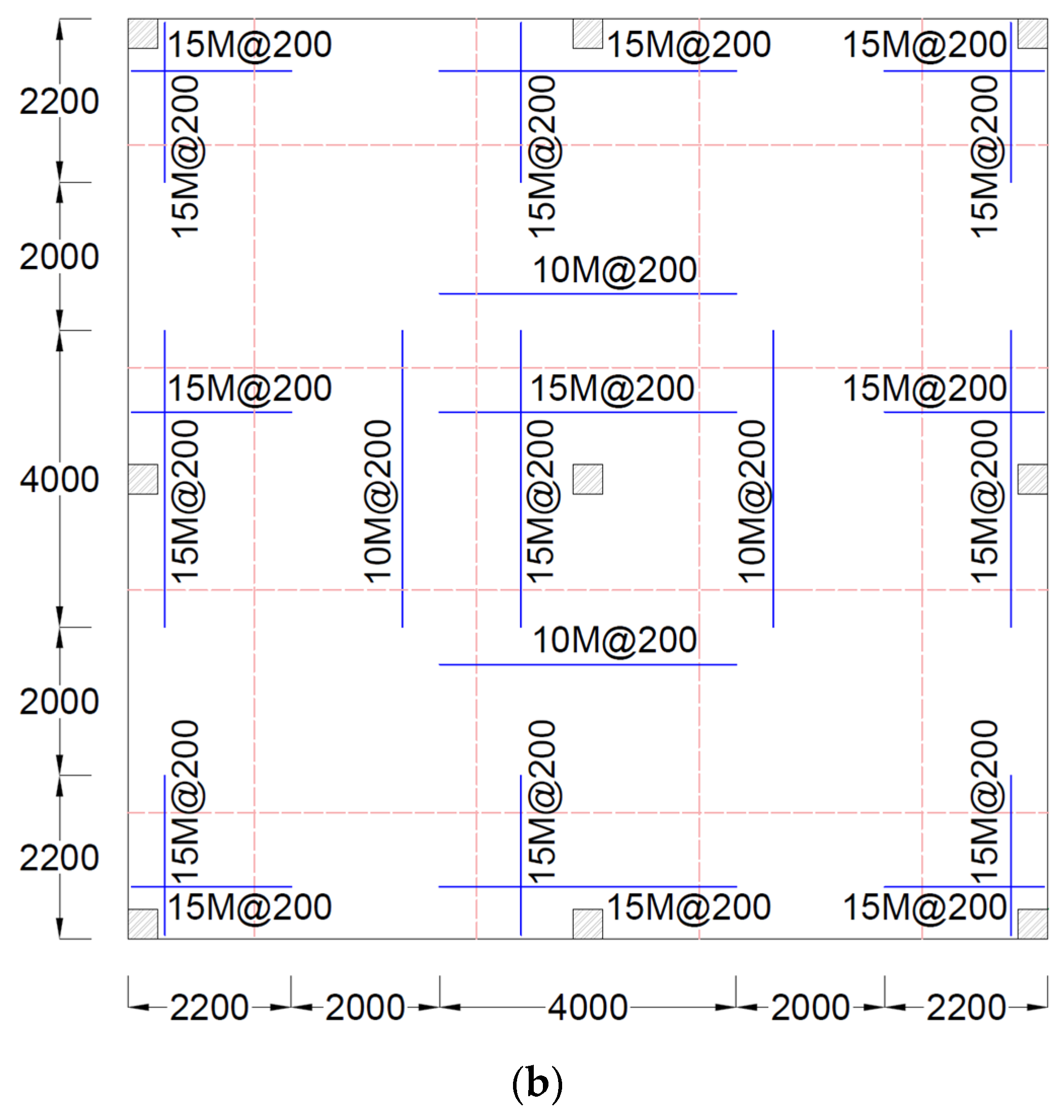
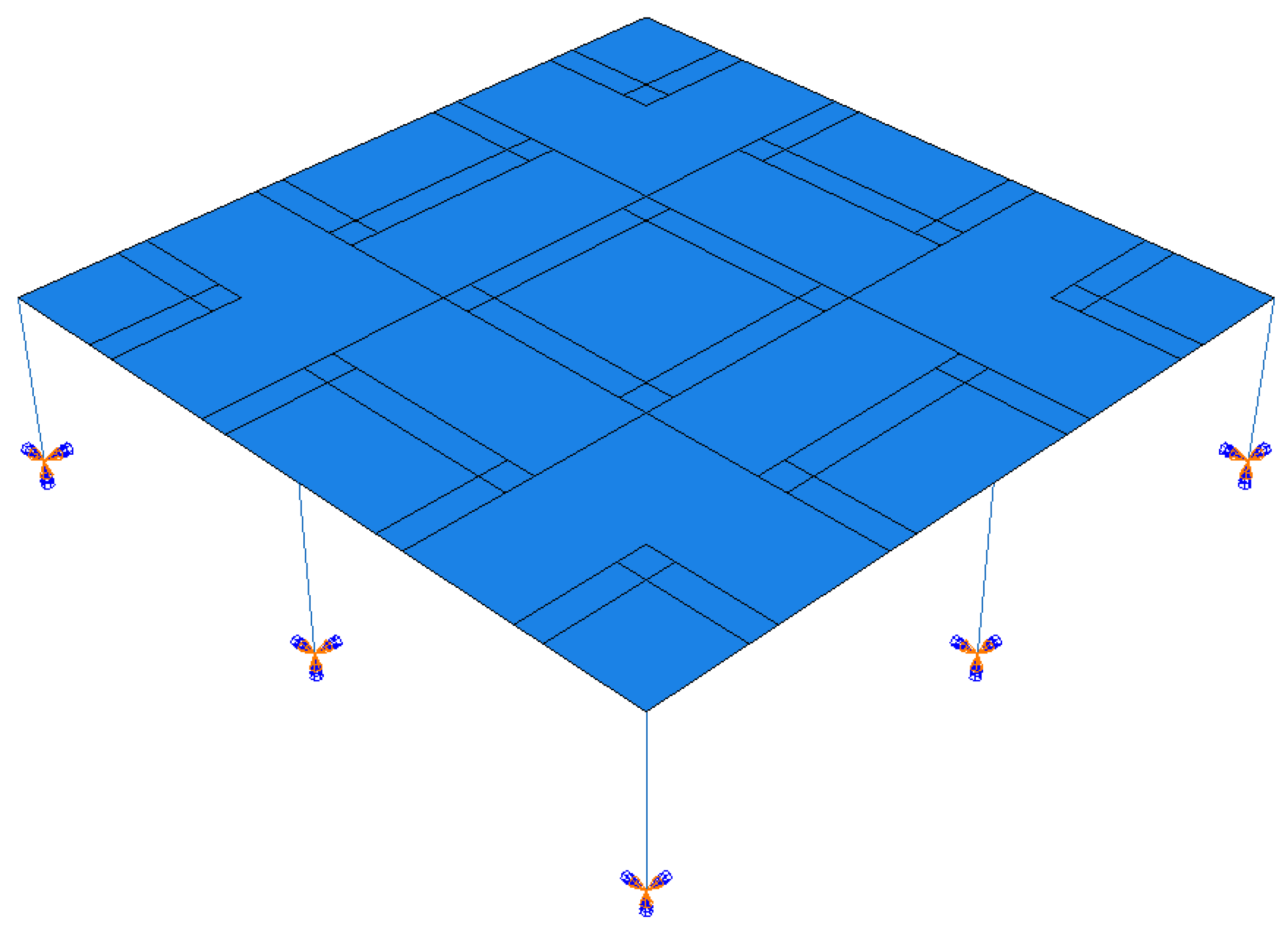
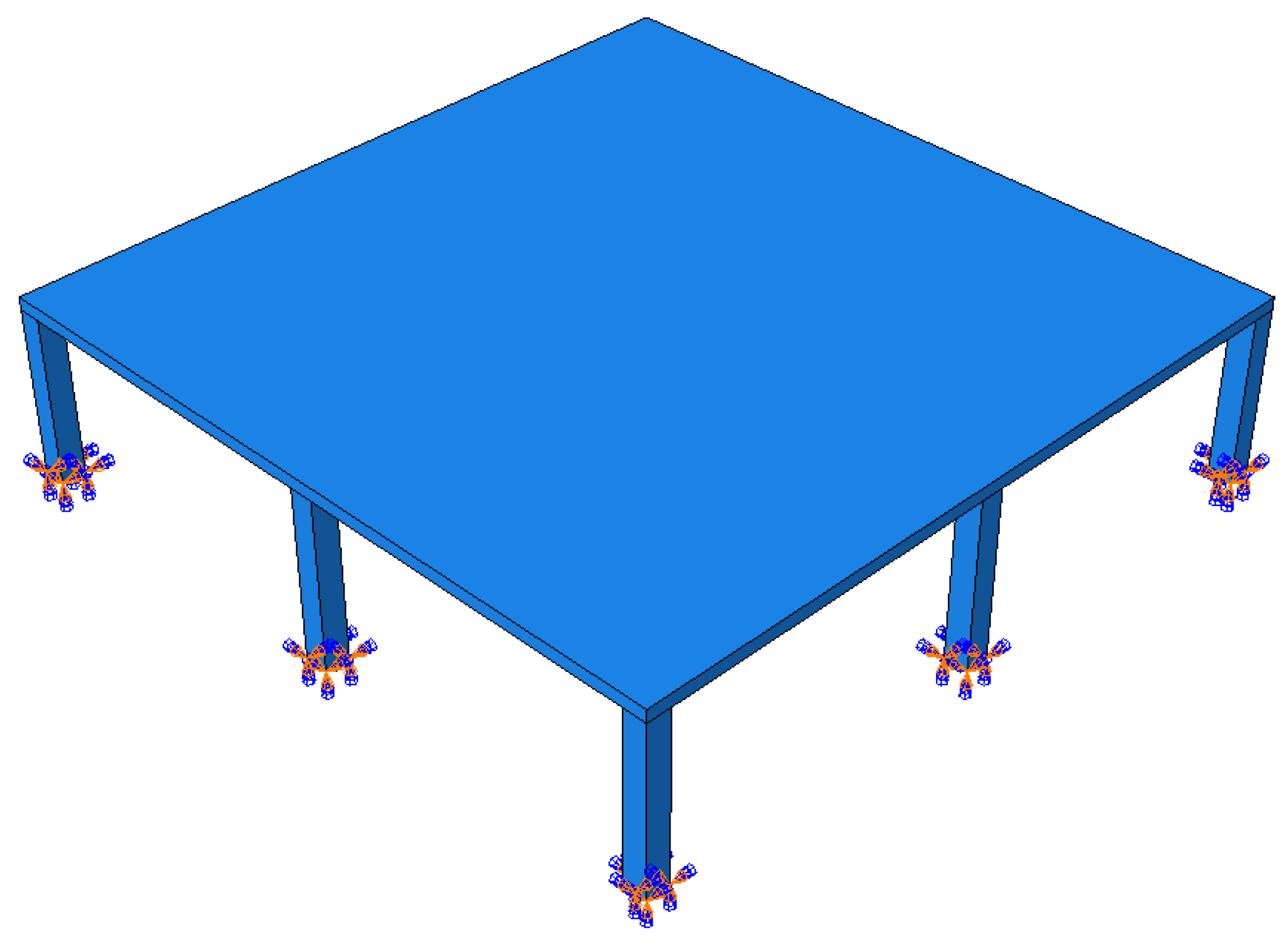
3. Flat Building Structure (Prototype)
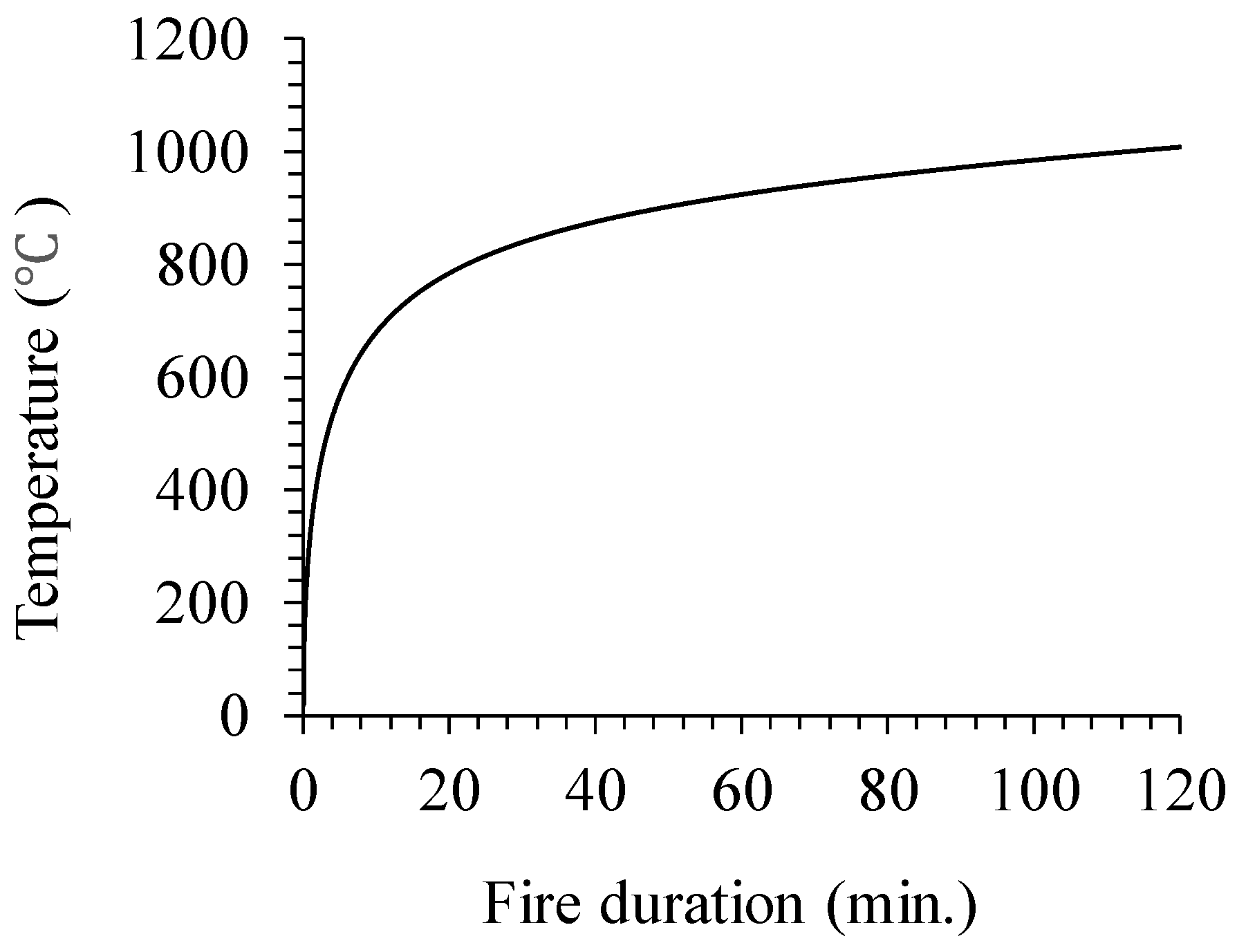
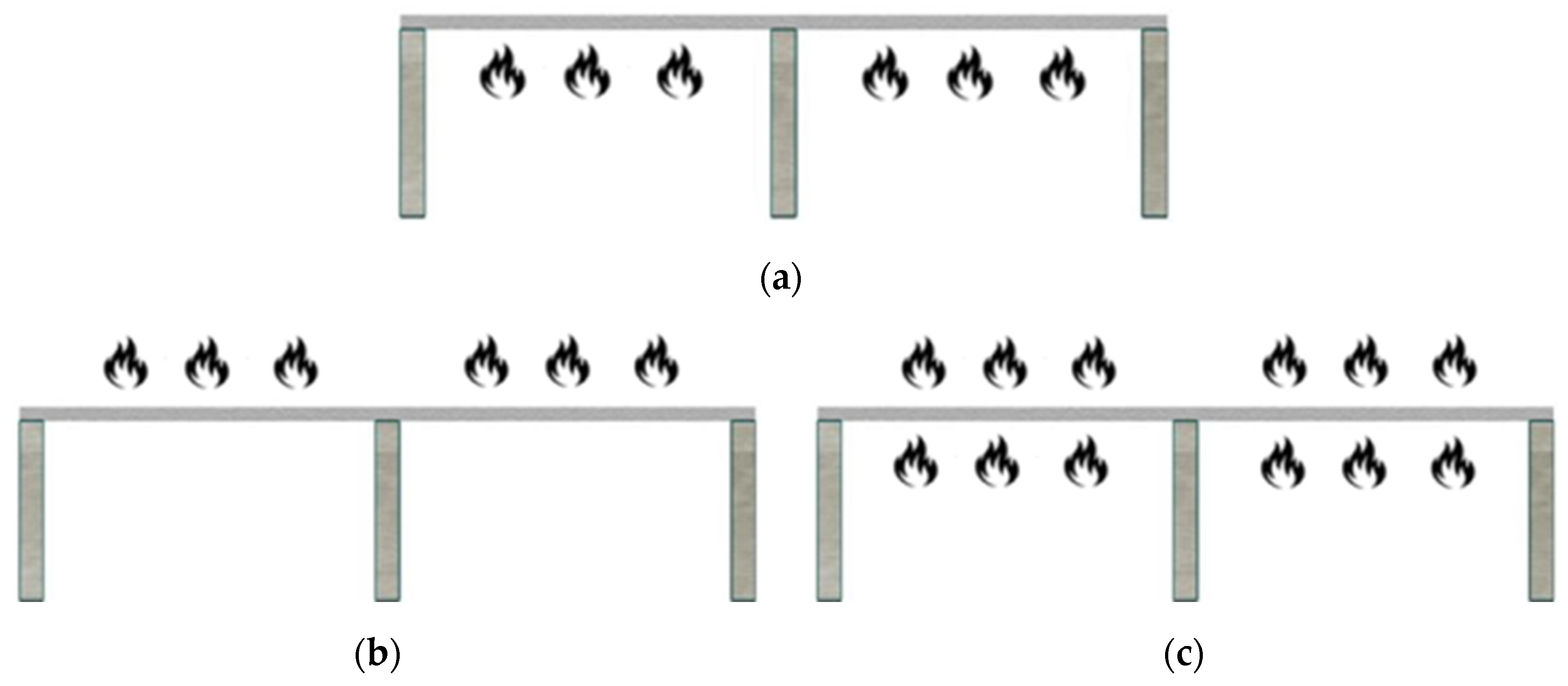
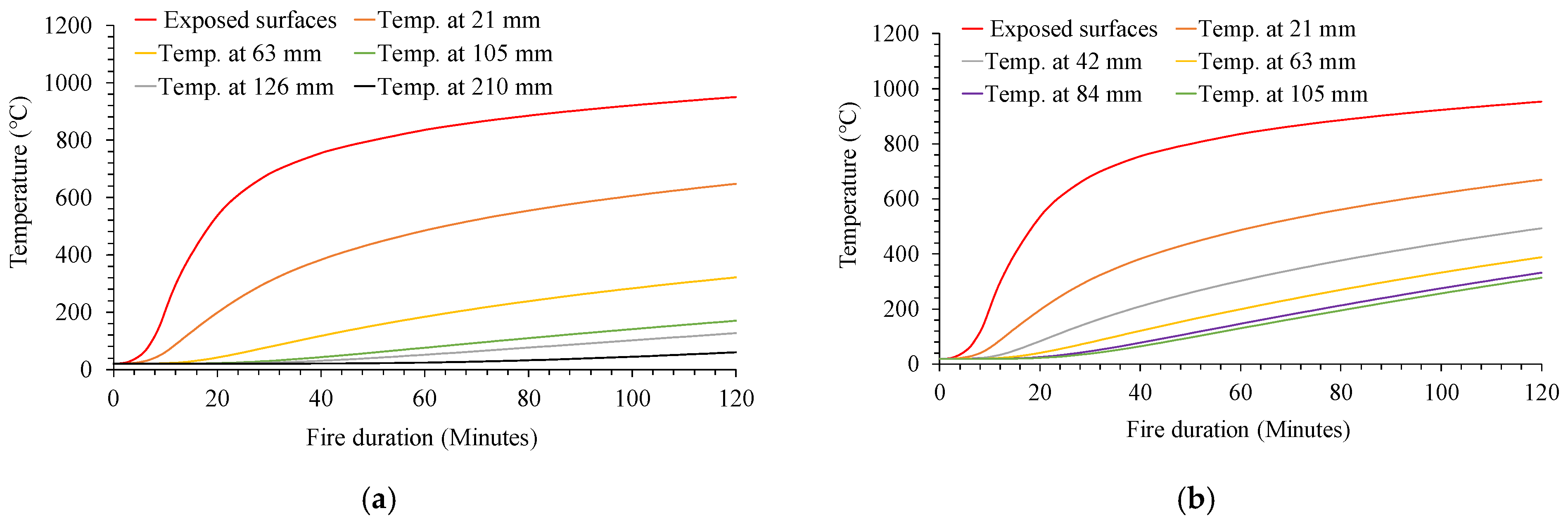
4. Fire Scenarios
5. Modelling Procedure for Flat Plate Structures Subjected to Fire
6. Shell Modelling of Prototype
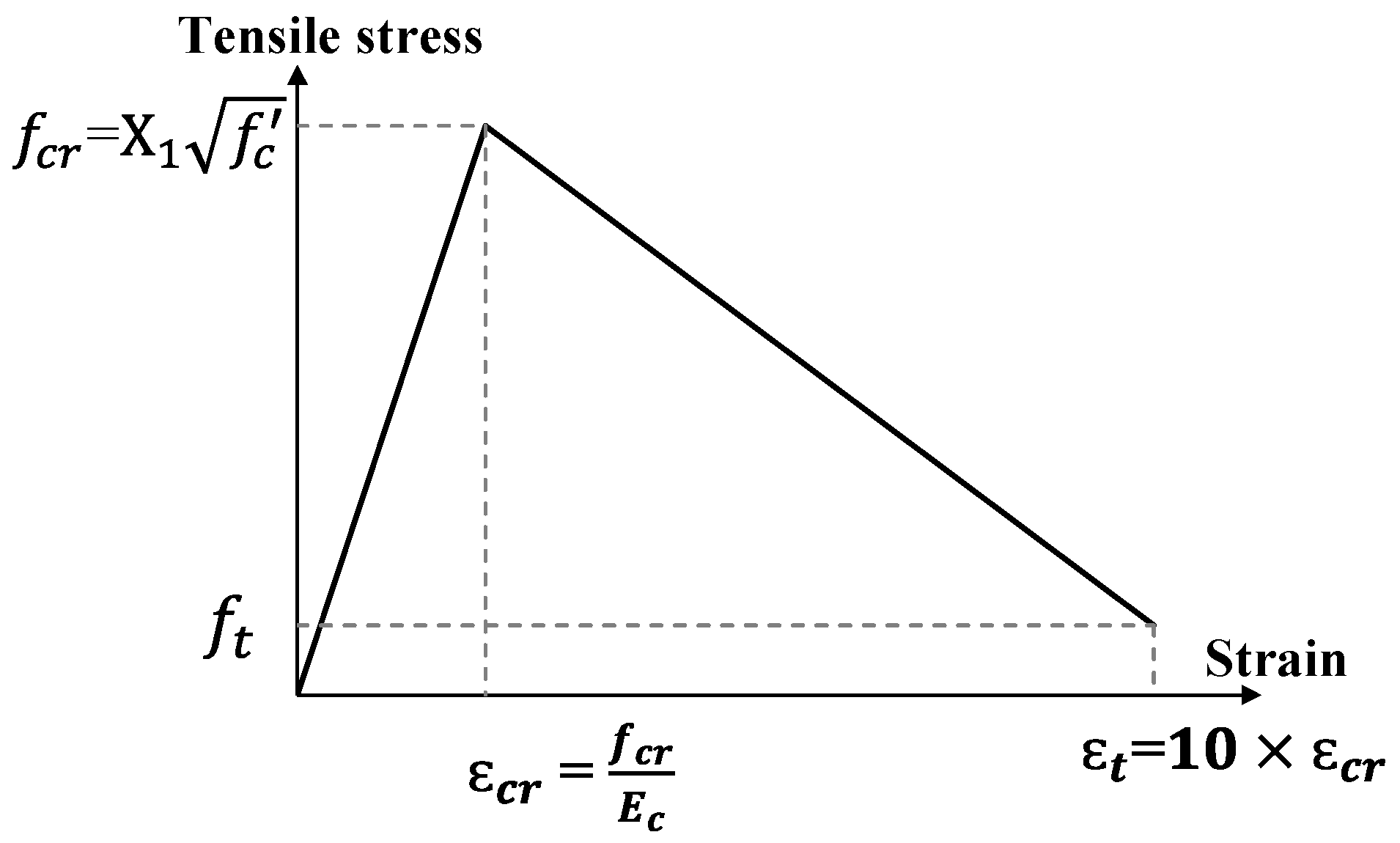
6.1. Impact of Concrete Tensile Stress on the FE Predictions
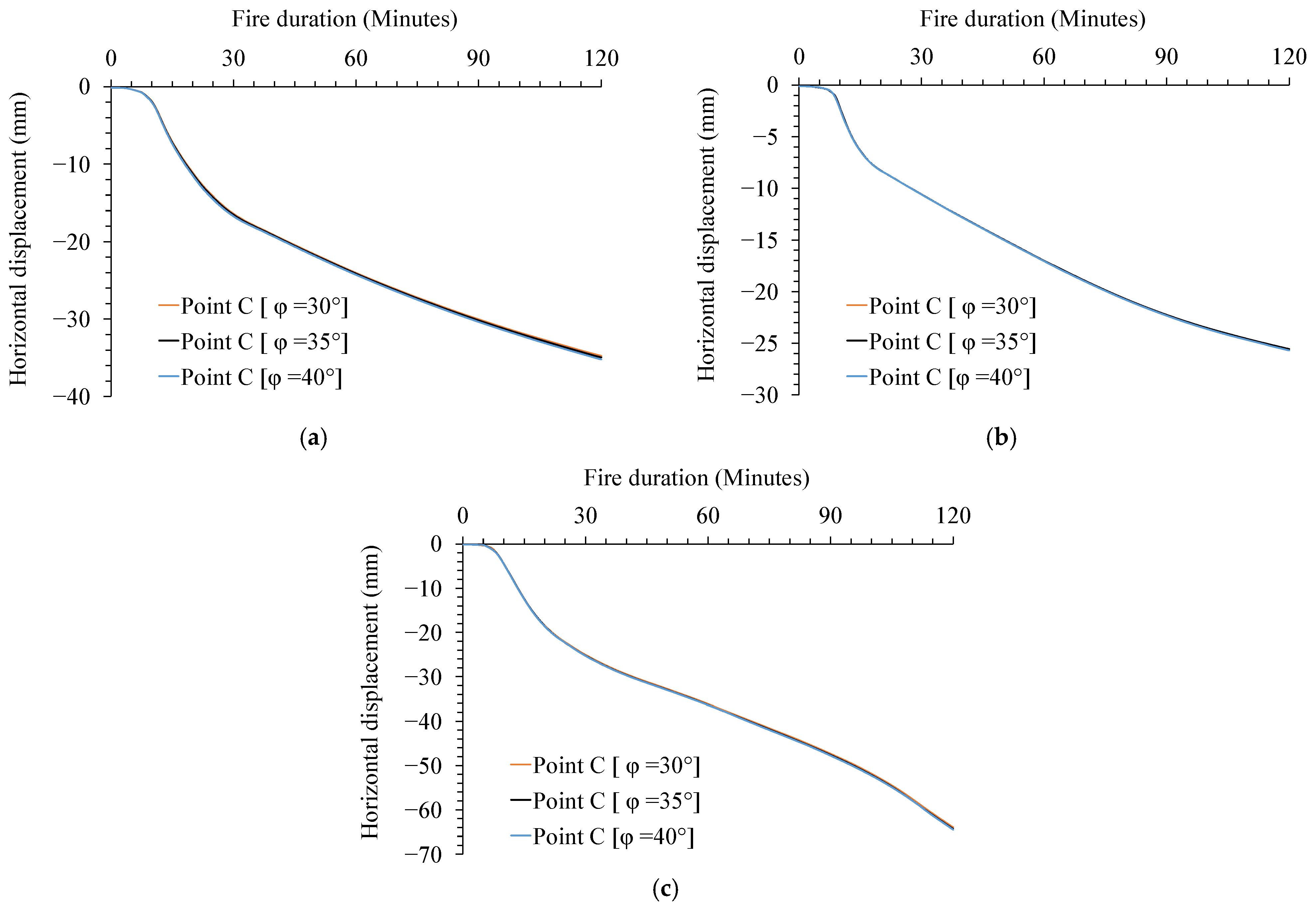
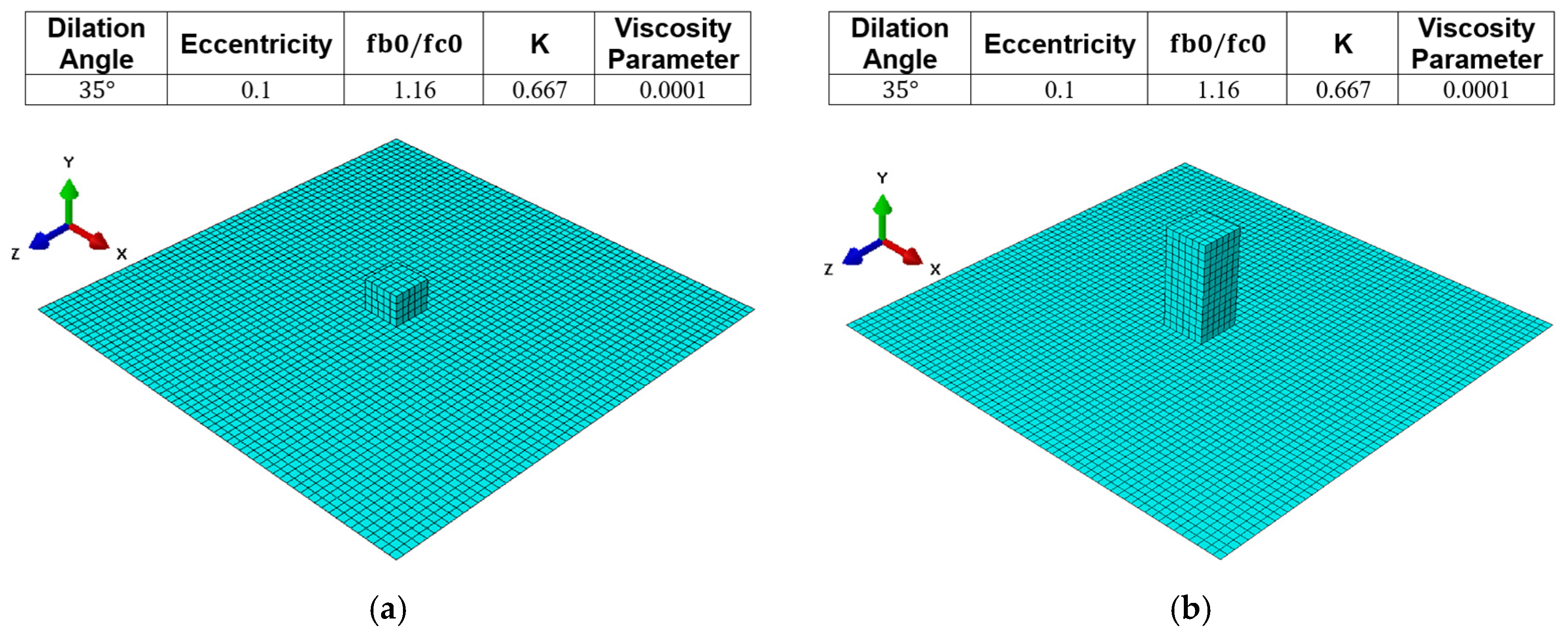
6.2. Impact of the Dilation Angle on the FE Predictions
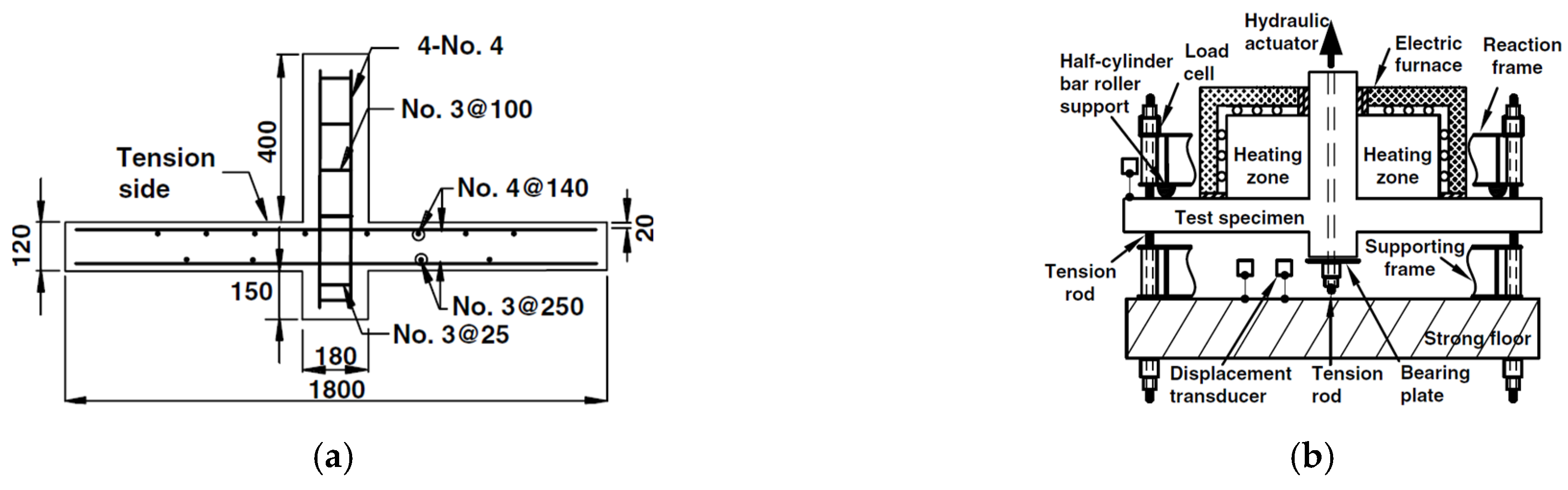
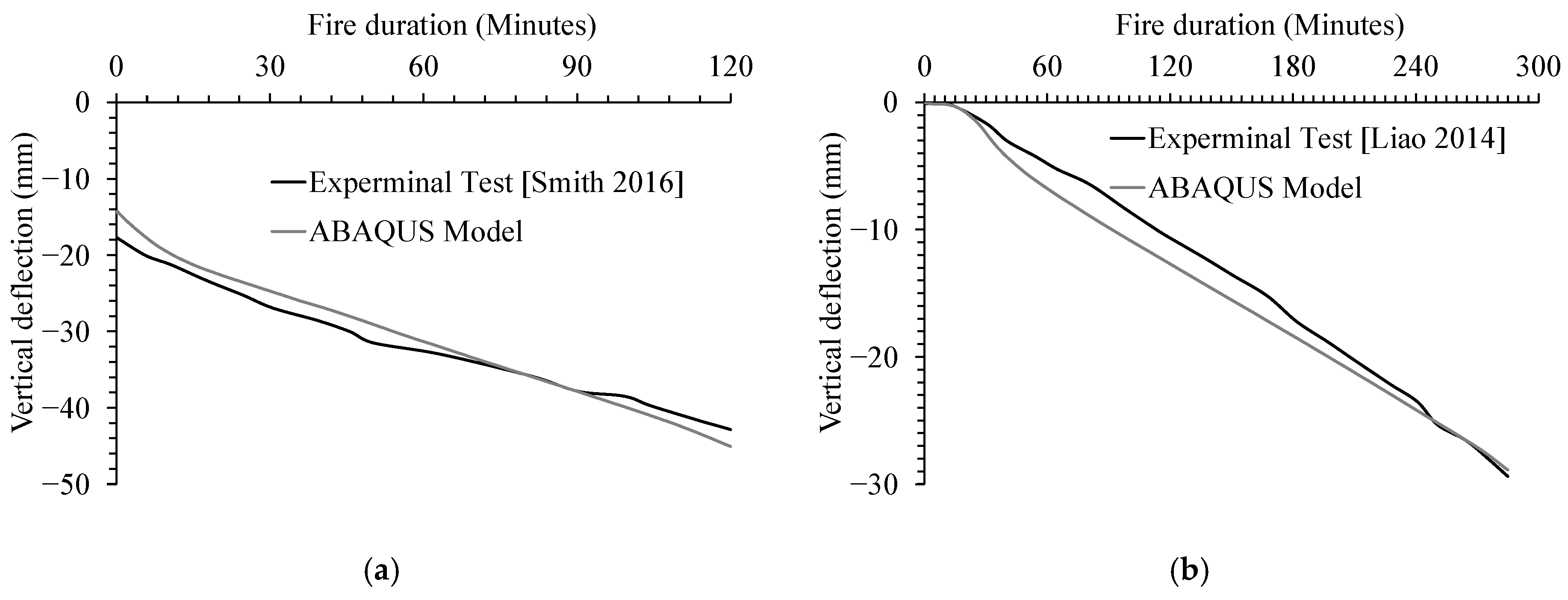
6.3. Validation
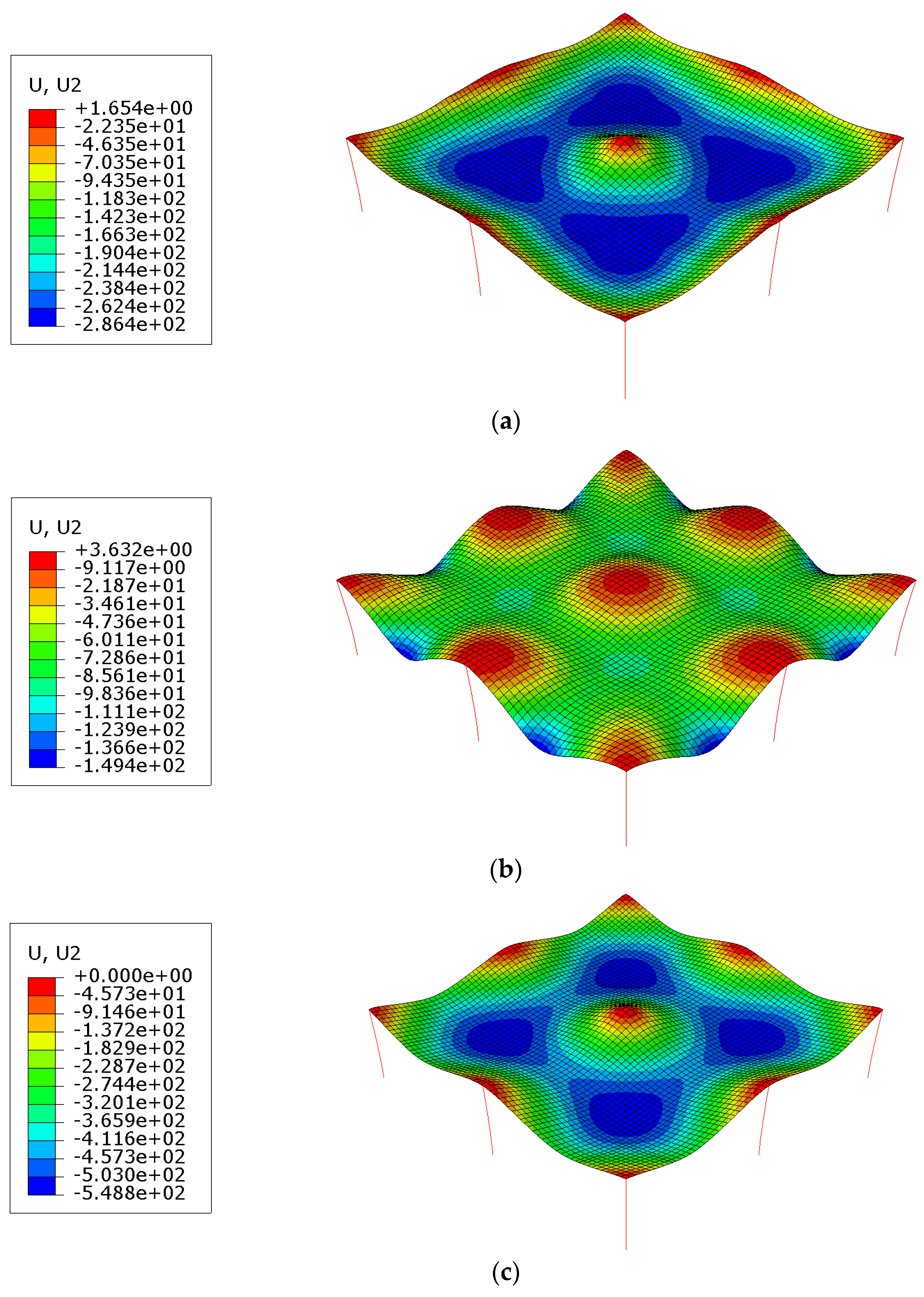
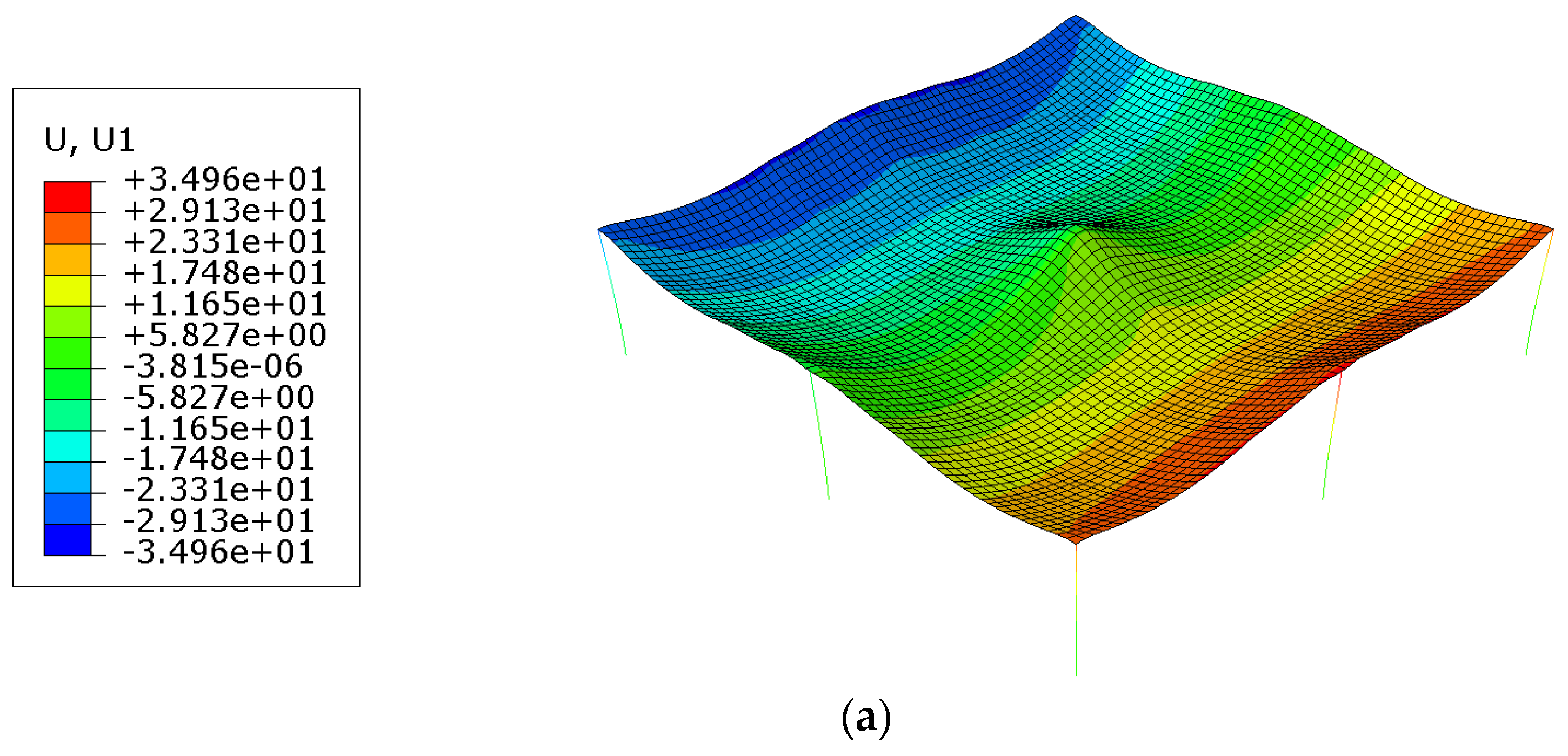
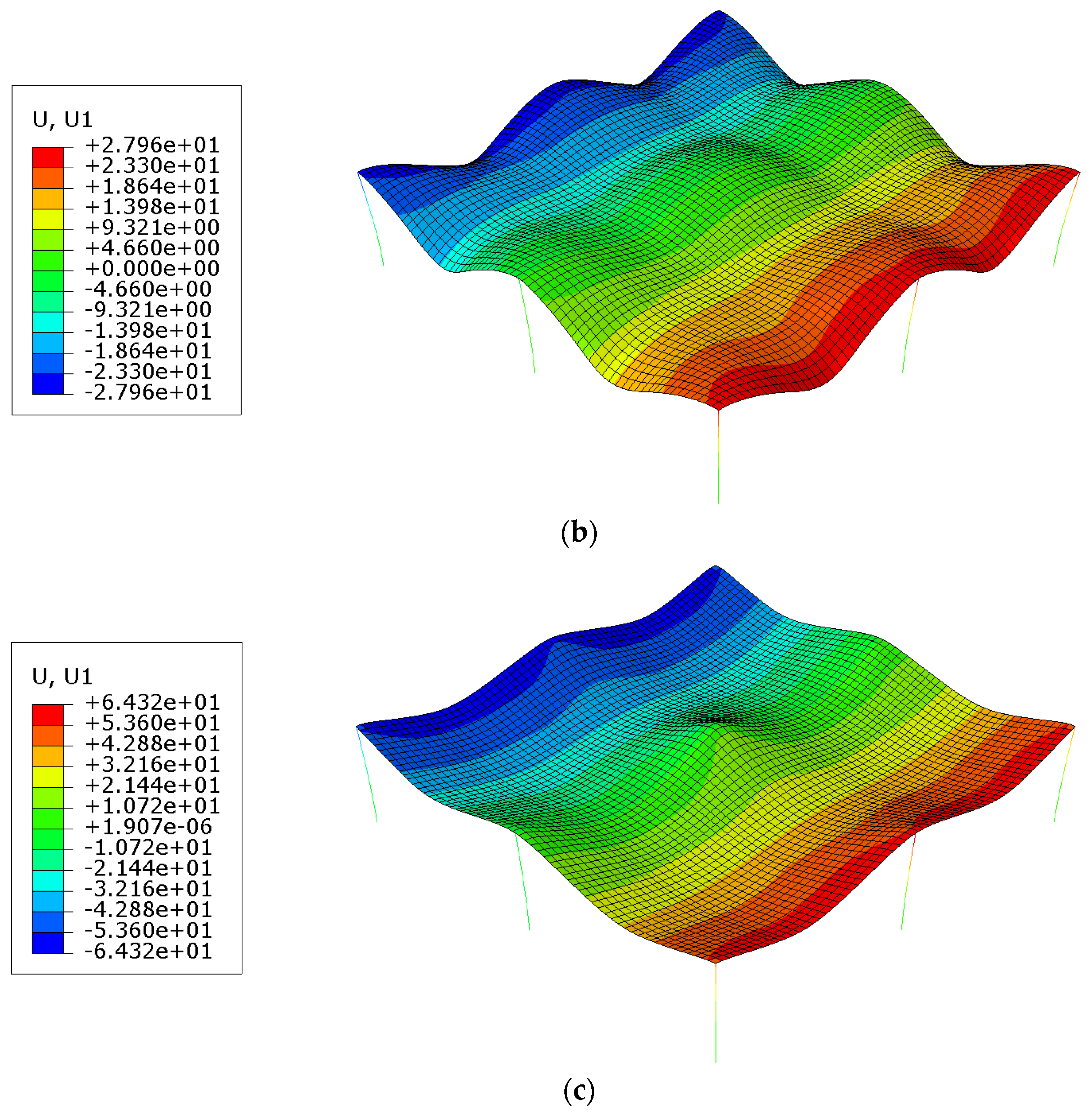
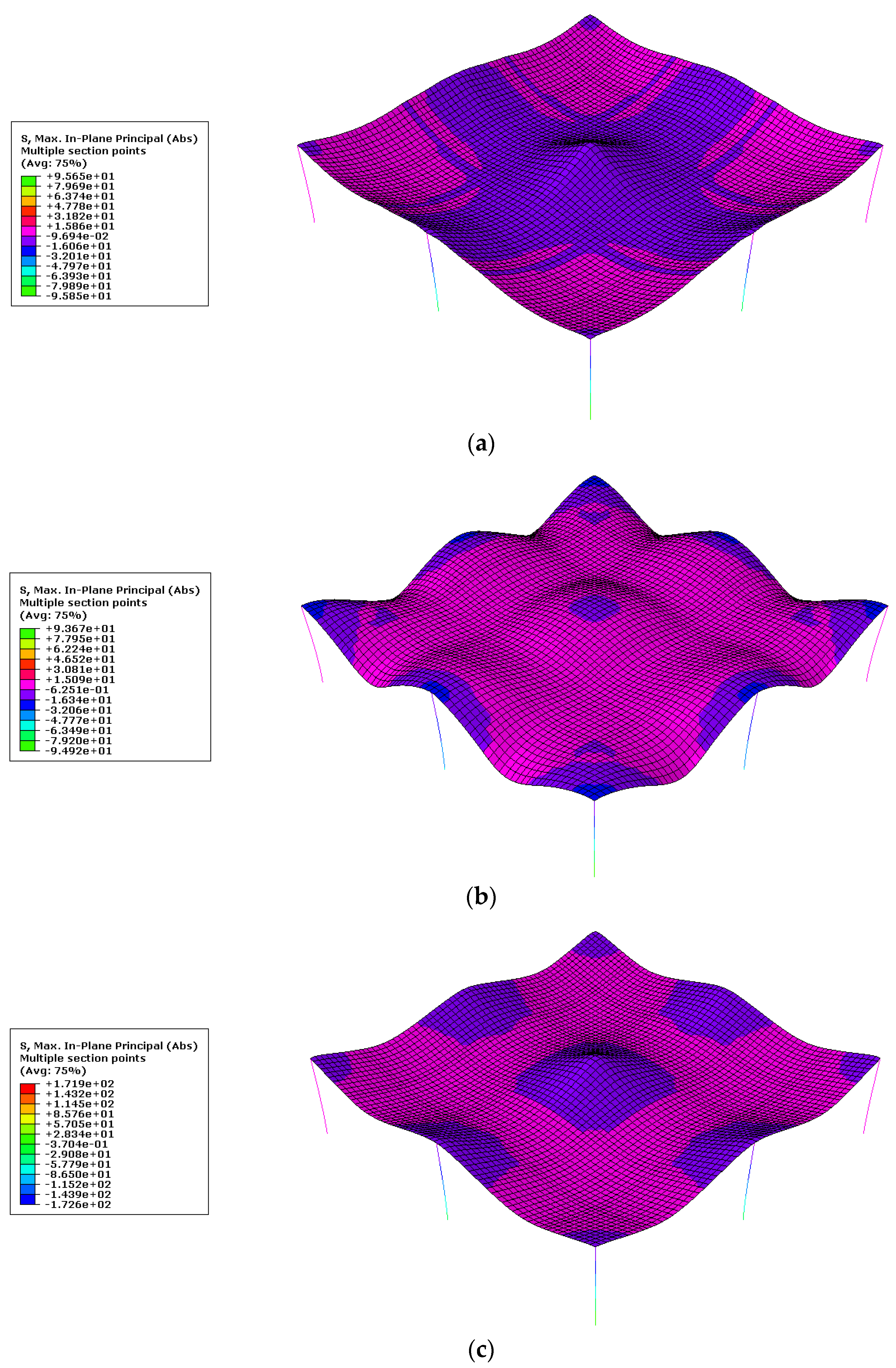
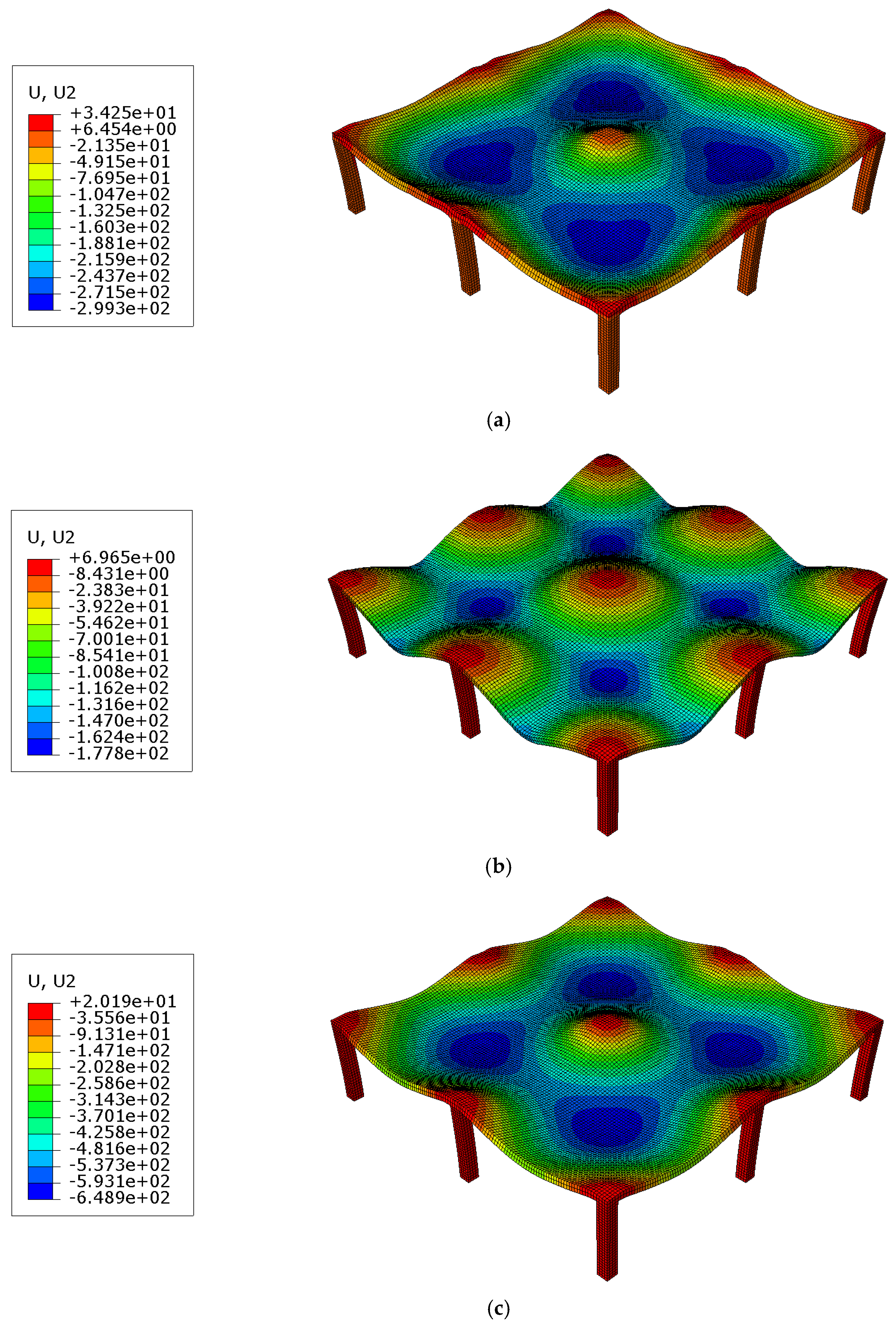
6.4. Detailed Results for the Prototype Slab
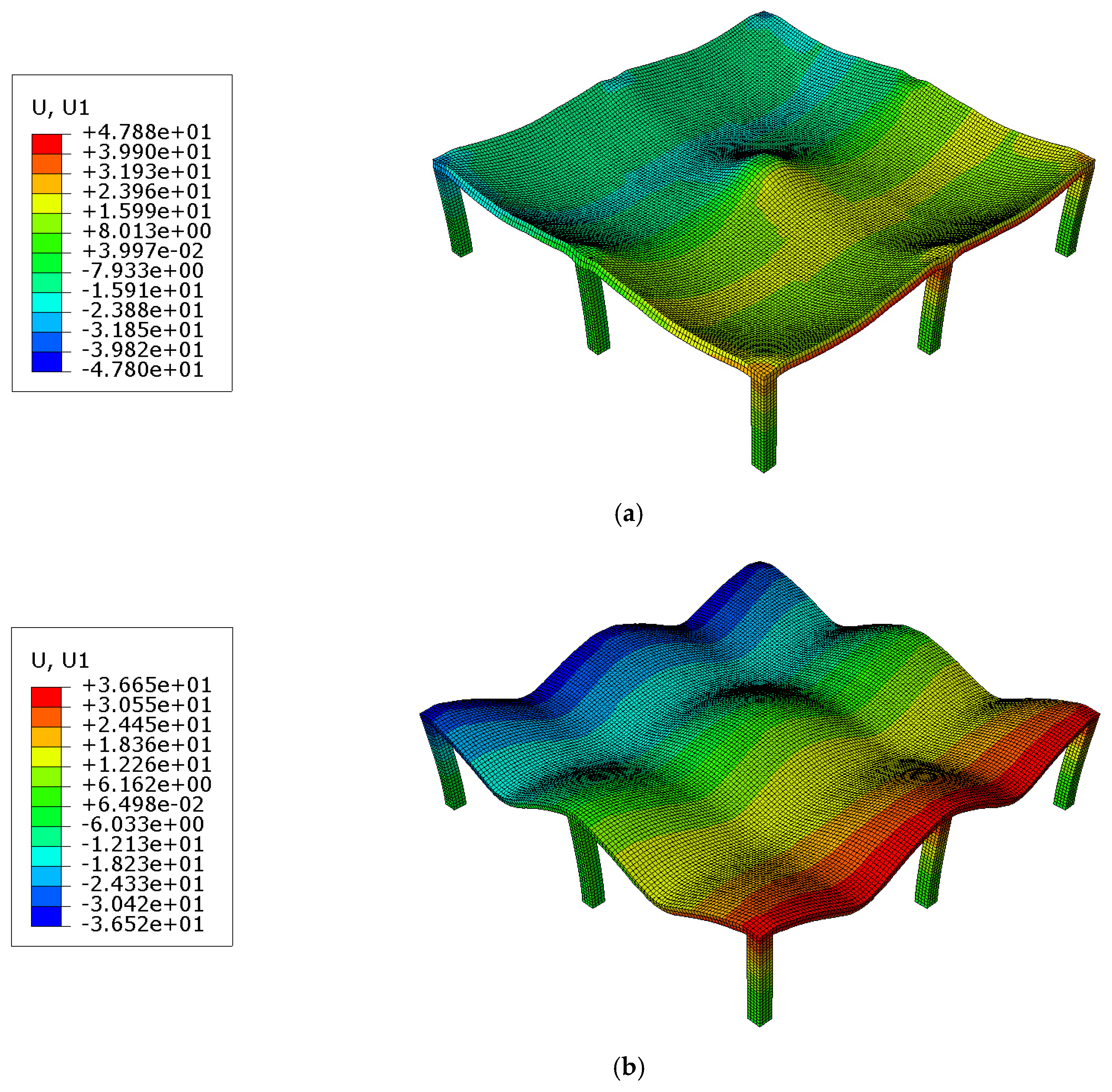
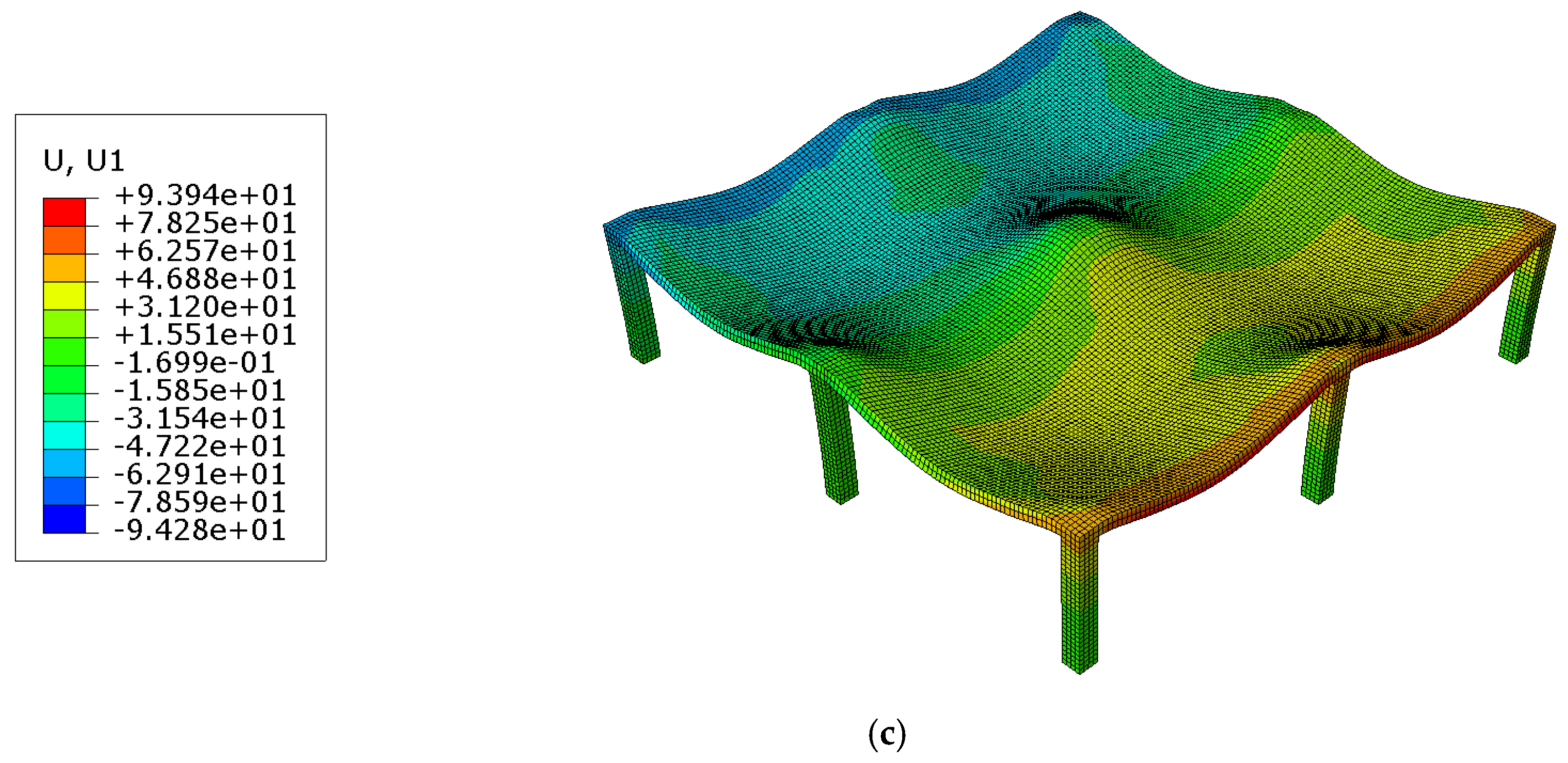
7. FE Solid Modelling of Prototype
FE Solid Performance
8. Modelling Decision Framework: Shell vs. Solid Elements
8.1. Shell Elements
8.2. Solid Elements
8.3. Comparative Analysis
8.4. Decision Criteria
- Global Structural Behaviour: Utilize shell elements for efficient modelling of overall deformation and load distribution.
- Localized Stress Analysis: Employ solid elements to capture detailed stress variations and potential failure zones.
- Computational Resources: Consider the available computational capacity, as solid models require significantly more resources.
9. Summary and Conclusions
- Material Modelling: The tensile strength of concrete has a significant influence on its structural response. A peak stress value of provided a balanced representation between stiffness and flexibility, aligning well with experimental observations.
- Dilation Angle Sensitivity: Variations in the dilation angle between 30° and 40° had a negligible impact on deflection outcomes, suggesting that this parameter may be less critical in certain fire scenarios.
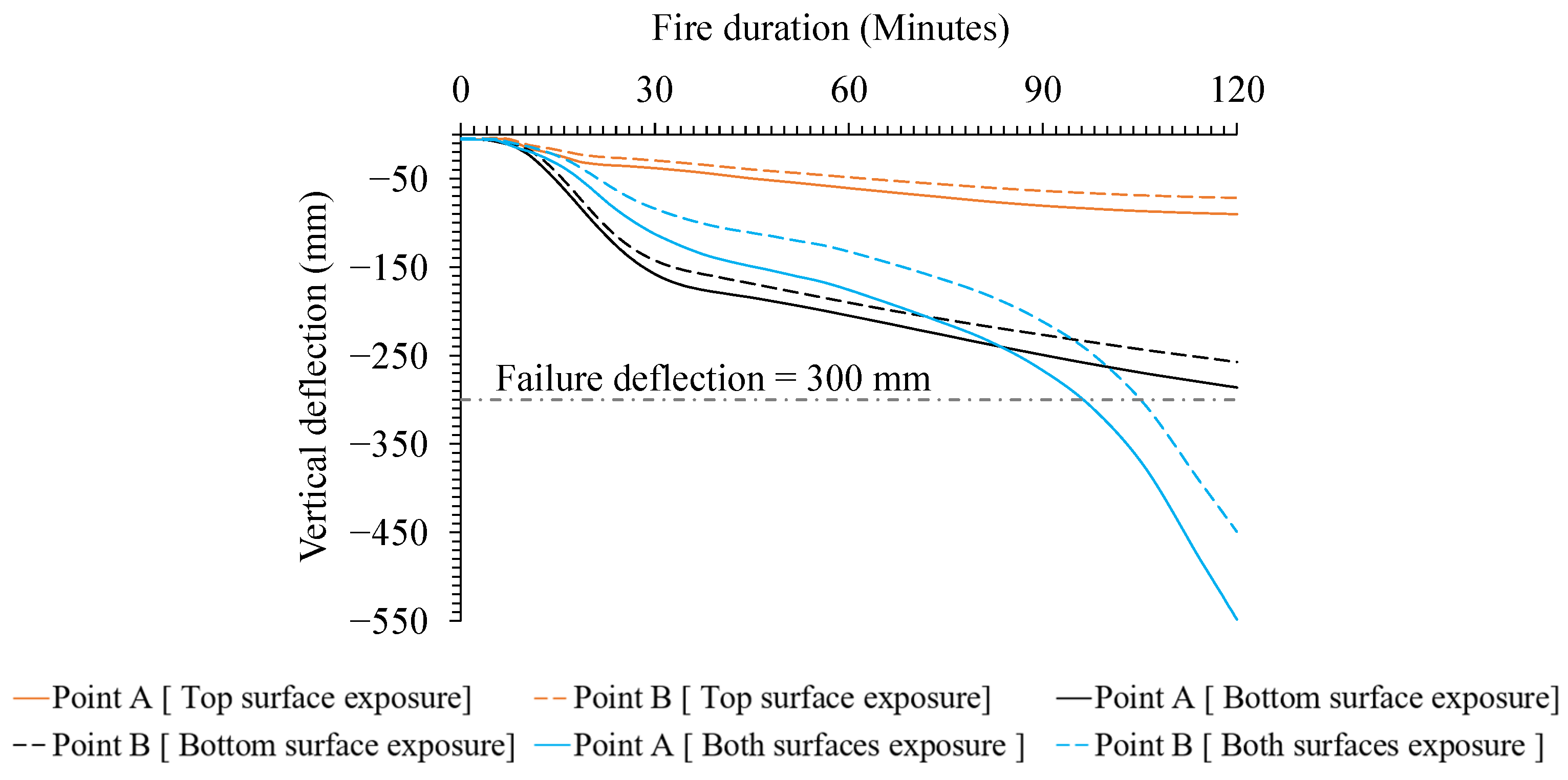
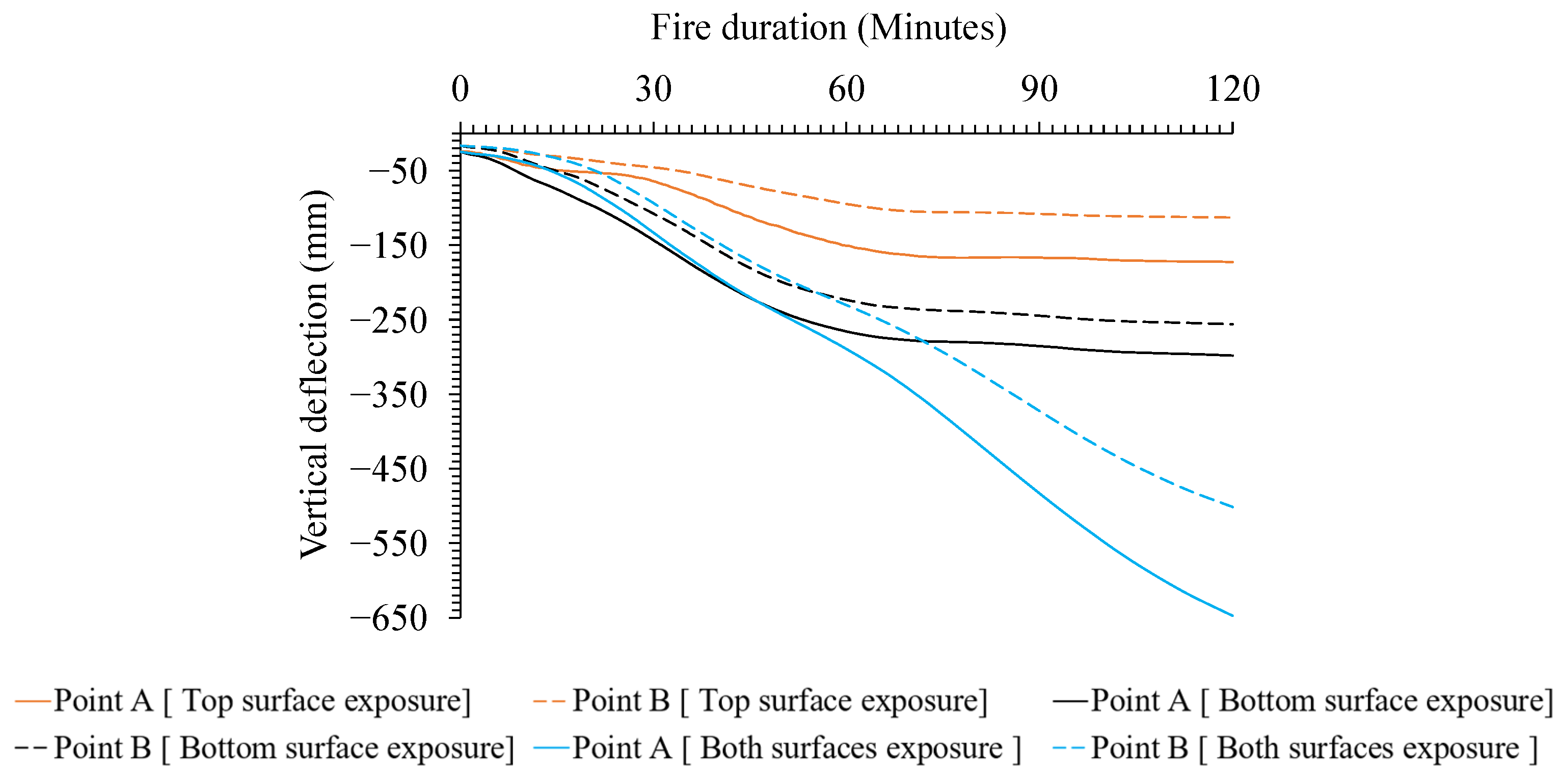
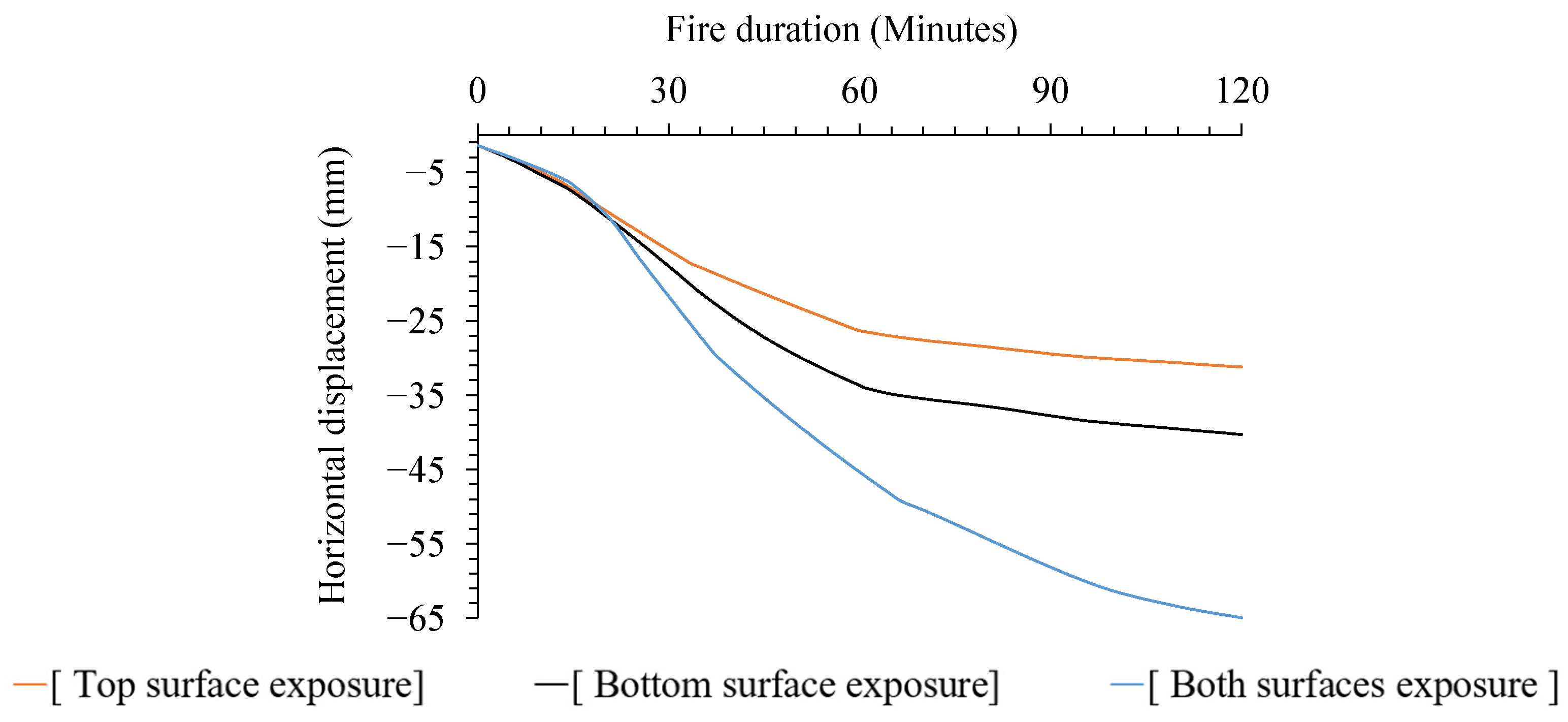
- Fire Exposure Scenarios: Two-sided fire exposure resulted in significantly higher deflections and thermal elongations compared to single-sided exposures. This increase is attributed to the elimination of temperature gradient-induced curvature restraint, a more uniform reduction in concrete stiffness across the slab thickness, and greater overall thermal expansion. These factors collectively led to approximately 1.9 times the deflection observed in bottom-only fire scenarios. This finding underscores the importance of considering dual-sided fire exposure in design assessments to ensure structural resilience.
- Column Displacements: Thermal elongation led to substantial horizontal displacements in columns, with two-sided exposure cases exhibiting up to 2.5 times greater displacement than top-sided exposure scenarios.
- Mesh Sensitivity: Solid models demonstrated sensitivity to mesh refinement, particularly in capturing through-thickness stress gradients. Incorporating temperature-dependent fracture energy models could enhance the accuracy of these simulations.
10. Future Work
- Incorporation of Temperature-Dependent Fracture Energy and Spalling Effects: Developing models that account for the degradation of concrete fracture energy at elevated temperatures is essential for accurately predicting crack propagation and failure mechanisms [38]. Additionally, integrating spalling phenomena into simulations can provide a more comprehensive understanding of structural integrity during fire events.
- Exploration of Non-Uniform and Travelling Fire Scenarios: Future studies should consider the impact of non-uniform fire exposures, such as travelling fires [39,40], on flat-plate structures. This research involves modelling varying fire intensities and durations across different slab areas to assess their impact on structural behaviour and failure modes.
- Analysis of Cooling Phase Effects: Investigating the structural response during the cooling phase after fire exposure is crucial, as residual stresses and potential re-cracking can significantly impact the long-term performance and safety of the structure.
- Validation Against Diverse Experimental Data: Expanding the validation of numerical models through comparison with a broader range of experimental results, including full-scale fire tests, will enhance the reliability and generalizability of simulation outcomes.
- Assessment of Alternative Structural Systems: Examining the fire performance of flat plate systems integrated with different lateral load-resisting mechanisms, such as shear walls or braced frames, and exploring the behaviour of post-tensioned slabs under fire conditions can provide insights into designing more resilient structures.
- Development of Simplified Design Tools: Creating user-friendly, simplified analytical methods or design charts based on validated finite element models can aid practicing engineers in assessing the fire performance of flat plate structures without resorting to complex simulations.
- Integration of Advanced Computational Techniques: Leveraging machine learning and artificial intelligence to predict structural responses under fire exposure can offer rapid assessment tools. Training models on extensive simulation and experimental data sets can facilitate the development of predictive algorithms for structural performance.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Earij, A.; Alfano, G.; Cashell, K.; Zhou, X. Nonlinear three-dimensional finite-element modelling of reinforced-concrete beams: Computational challenges and experimental validation. Eng. Fail. Anal. 2017, 82, 92–115. [Google Scholar] [CrossRef]
- Ab-Kadir, M.A.; Awal, A.A. Finite element modelling of reinforced concrete slab at elevated temperature using ABAQUS. Appl. Mech. Mater. 2015, 752, 623–627. [Google Scholar] [CrossRef]
- Al Hamd, R.K.S. Punching Shear in Heated Interior Reinforced Concrete Slab-Column Connections. Ph.D. Thesis, The University of Manchester, Manchester, UK, 2018. [Google Scholar]
- Buchanan, A.H.; Abu, A.K. Structural Design for Fire Safety; John Wiley & Sons: Chichester, UK, 2017. [Google Scholar]
- Webster, B. Which Abaqus Element Type Should My Finite Element Analysis (FEA) Simulation Use? Fidelis, 2021. Available online: https://www.fidelisfea.com/post/which-abaqus-element-type-should-my-finite-element-analysis-fea-simulation-use (accessed on 5 April 2024).
- George, S.J. Structural Performance of Reinforced Concrete Flat-Plate Buildings Subjected to Fire. Master’s Thesis, University of Nevada, Las Vegas, NV, USA, 2012. [Google Scholar]
- Grassl, P.; Jirásek, M. Plastic model with non-local damage applied to concrete. Int. J. Numer. Anal. Methods Geomech. 2006, 30, 71–90. [Google Scholar] [CrossRef]
- Puddicome, T. Finite Element Analysis of Reinforced Concrete and Steel Fiber Reinforced Concrete Slabs in Punching Shear. Ph.D. Thesis, Memorial University of Newfoundland, St. John’s, NL, Canada, 2018. [Google Scholar]
- Genikomsou, A.S.; Polak, M.A. Finite-element analysis of reinforced concrete slabs with punching shear reinforcement. J. Struct. Eng. 2016, 142, 04016129. [Google Scholar] [CrossRef]
- Annerel, E.; Taerwe, L.; Merci, B.; Jansen, D.; Bamonte, P.; Felicetti, R. Thermo-mechanical analysis of an underground car park structure exposed to fire. Fire Saf. J. 2013, 57, 96–106. [Google Scholar] [CrossRef]
- Arna’ot, F.H.; Abid, S.R.; Özakça, M.; Tayşi, N. Review of concrete flat plate-column assemblies under fire conditions. Fire Saf. J. 2017, 93, 39–52. [Google Scholar] [CrossRef]
- El-Tayeb, E.H.M.; El-Metwally, S.E.; Askar, H.H.; Yousef, A.M. Analysis of RC flat slab system for thermal loads. Int. J. Eng. Innov. Technol. 2015, 4, 62–73. [Google Scholar]
- George, S.J.; Tian, Y. Structural performance of reinforced concrete flat plate buildings subjected to fire. Int. J. Concr. Struct. Mater. 2012, 6, 111–121. [Google Scholar] [CrossRef]
- Moss, P.J.; Dhakal, R.P.; Wang, G.; Buchanan, A.H. The fire behaviour of multi-bay, two-way reinforced concrete slabs. Eng. Struct. 2008, 30, 3566–3573. [Google Scholar] [CrossRef]
- ISO 834; Fire-Resistance Tests—Elements of Buildingonstruction. ISO: Geneva, Switzerland, 1975.
- Wahid, N.; Stratford, T.; Bisby, L. Calibration of concrete damage plasticity model parameters for high temperature modelling of reinforced concrete flat slabs in fire. Appl. Struct. Fire Eng. 2019, 1, 1–8. [Google Scholar]
- Lim, L.; Buchanan, A.; Moss, P.; Franssen, J.-M. Numerical modelling of two-way reinforced concrete slabs in fire. Eng. Struct. 2004, 26, 1081–1091. [Google Scholar] [CrossRef]
- ENV 1992-1-2; Eurocode 2. Design of Concrete Structures, Part 1–2: General Rules—Structural Fire Design. European Committee for Standardization: Brussels, Belgium, 2004.
- Genikomsou, A.S.; Polak, M.A. Finite element analysis of punching shear of concrete slabs using damaged plasticity model in ABAQUS. Eng. Struct. 2015, 98, 38–48. [Google Scholar] [CrossRef]
- Lie, T.T. (Ed.) Structural Fire Protection; ASCE Manuals and Reports on Engineering Practice No. 78; American Society of Civil Engineers: Reston, VA, USA, 1992. [Google Scholar]
- ASTM E119; Standard Test Methods for Fire Tests of Building Construction and Materials. ASTM International: West Conshohocken, PA, USA, 2007; Volume 4, p. 436.
- BS 476-20:1987; Fire Tests on Building Materials and Structures—Part 20: Method for Determination of the Fire Resistance of Elements of Construction (General Principles). BSI: London, UK, 1987.
- Elshorbagi, M.; AlHamaydeh, M. Simulation of RC beams during fire events using a nonlinear numerical fully coupled thermal-stress analysis. Fire 2023, 6, 57. [Google Scholar] [CrossRef]
- Canadian Standards Association. Design of Concrete Structures (CSA A23.3-19); CSA Group: Mississauga, ON, Canada, 2019. [Google Scholar]
- Collins, M.P.; Mitchell, D. Prestressed Concrete Basics; Canadian Prestressed Concrete Institute: Ottawa, ON, Canada, 1987. [Google Scholar]
- Burgess, I.; Sahin, M. Tensile Membrane Action of Lightly-Reinforced Rectangular Composite Slabs in Fire. Structures 2018, 16, 176–197. [Google Scholar] [CrossRef]
- Smith, H.K.M. Punching Shear of Flat Reinforced-Concrete Slabs under Fire Conditions. Ph.D. Thesis, The University of Edinburgh, Edinburgh, UK, 2016. [Google Scholar]
- Liao, J.S.; Cheng, F.P.; Chen, C.C. Fire resistance of concrete slabs in punching shear. J. Struct. Eng. 2014, 140, 04013025. [Google Scholar] [CrossRef]
- Dassault Systèmes Simulia Corp. ABAQUS/Standard User’s Manual, Version 6.14; Dassault Systèmes Simulia Corp.: Providence, RI, USA, 2014. [Google Scholar]
- Malm, R. Shear Cracks in Concrete Structures Subjected to In-Plane Stresses. Ph.D. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2006. [Google Scholar]
- Cornelissen, H.; Hordijk, D.; Reinhardt, H. Experimental determination of crack softening characteristics of normalweight and lightweight concrete. Heron 1986, 31, 45–56. [Google Scholar]
- Rafi, M.M.; Nadjai, A.; Ali, F. Analytical modeling of concrete beams reinforced with carbon FRP bars. J. Compos. Mater. 2007, 41, 2675–2690. [Google Scholar] [CrossRef]
- CEB-FIP. Design of Concrete Structures: CEB-FIP Model Code 1990; British Standards Institution: London, UK, 1993. [Google Scholar]
- Wittmann, F.H. Crack formation and fracture energy of normal and high strength concrete. Sadhana 2002, 27, 413–423. [Google Scholar] [CrossRef]
- Brameshuber, W.; Hilsdorf, H.K. Development of strength and deformability of very young concrete. In Fracture of Concrete and Rock; Shah, S.P., Swartz, S.E., Eds.; Springer: New York, NY, USA, 1989; pp. 23–35. [Google Scholar]
- Rafi, M.M.; Nadjai, A.; Ali, F. Analytical behaviors of steel and CFRP reinforced concrete beams in fire. J. ASTM Int. 2010, 7, JAI102641. [Google Scholar] [CrossRef]
- De Borst, R.; Peeters, P.P. Analysis of concrete structures under thermal loading. Comput. Methods Appl. Mech. Eng. 1989, 77, 293–310. [Google Scholar] [CrossRef]
- Gernay, T.; Franssen, J.-M. A formulation of the Eurocode 2 concrete model at elevated temperature that includes an explicit term for transient creep. Fire Saf. J. 2012, 51, 1–9. [Google Scholar] [CrossRef]
- Bolina, F.L.; Fachinelli, E.G.; Rodrigues, J.P.C. Analysis of Building Structures Subjected to Electric Vehicle Fires. J. Build. Eng. 2025, 107, 112769. [Google Scholar] [CrossRef]
- Yuzbasi, J.; Arslan, H.M. Applied Element Method and Finite Element Method for Progressive Collapse Assessment: A Comparative Study on the Influence of Slab Types, Thicknesses, and Damping via Three Incremental Column Removals. Structures 2025, 73, 108358. [Google Scholar] [CrossRef]
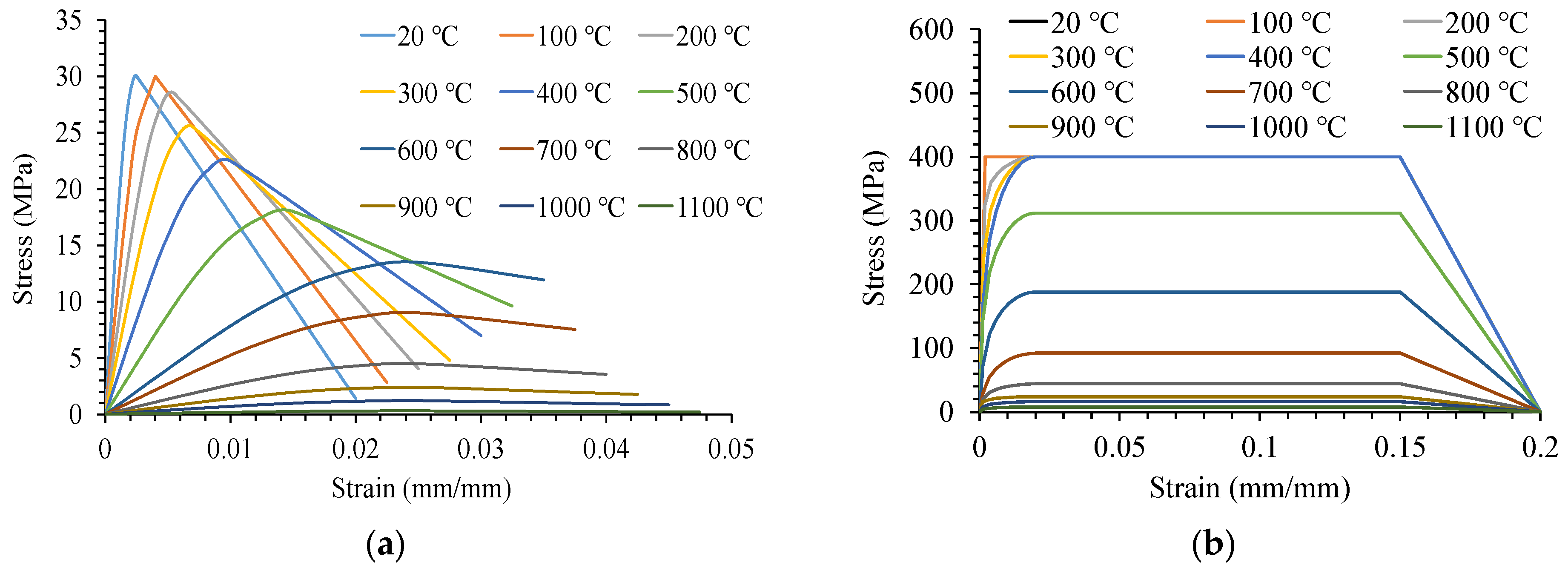







| Thermal Properties | Value | Temperature Range | Ref. |
|---|---|---|---|
| (kg/m3) | [18] | ||
| Heat Capacity, Cc (J/kg K) | [18] | ||
| (W/m K) | [18] | ||
| [20] | |||
| ] | = 1 | [18] | |
| = 0 | |||
| ] | = 1 | [18] | |
| Thermal Properties | Value | Temperature Range | Ref. |
|---|---|---|---|
| (kg/m3) | 7850 | Constant | [18] |
| Heat Capacity, Cs (J/kg K) | [18] | ||
| (W/m K) | [18] | ||
| [18] | |||
| Table 3.2a within Section 3 of EN 1992-1-2 | [18] | ||
| Property | Slab HU75-0.8 [27] | Slab TS-R1-C1-N [28] |
|---|---|---|
| Dimensions | 1400 mm × 1400 mm | 1800 mm × 1800 mm |
| Thickness | 75 mm | 120 mm |
| Column’s Dimensions | 120 mm × 120 mm | 180 × 180 mm |
| Tension RFT | 0.29% | 0.92% |
| Compression RFT | __ | 0.18% |
| Concrete cover | 11 mm | 20 mm |
| Steel elastic modulus | 185 GPa | 200 GPa |
| Steel yield strength | 549 MPa | 420 MPa |
| Concrete Compressive Strength | 32.1 MPa | 32.0 MPa |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hesien, M.; Youssef, M.A.; El-Fitiany, S. Finite Element Analysis of Flat Plate Structures in Fire. Fire 2025, 8, 252. https://doi.org/10.3390/fire8070252
Hesien M, Youssef MA, El-Fitiany S. Finite Element Analysis of Flat Plate Structures in Fire. Fire. 2025; 8(7):252. https://doi.org/10.3390/fire8070252
Chicago/Turabian StyleHesien, Mohamed, Maged A. Youssef, and Salah El-Fitiany. 2025. "Finite Element Analysis of Flat Plate Structures in Fire" Fire 8, no. 7: 252. https://doi.org/10.3390/fire8070252
APA StyleHesien, M., Youssef, M. A., & El-Fitiany, S. (2025). Finite Element Analysis of Flat Plate Structures in Fire. Fire, 8(7), 252. https://doi.org/10.3390/fire8070252







