Numerical Studies on the Combined Effect of Curvature and Area Expansion Rate on Gaseous Detonation Propagation in Curved Channels
Abstract
1. Introduction
2. Numerical Methodology
2.1. Governing Equations
2.2. Numerical Methods
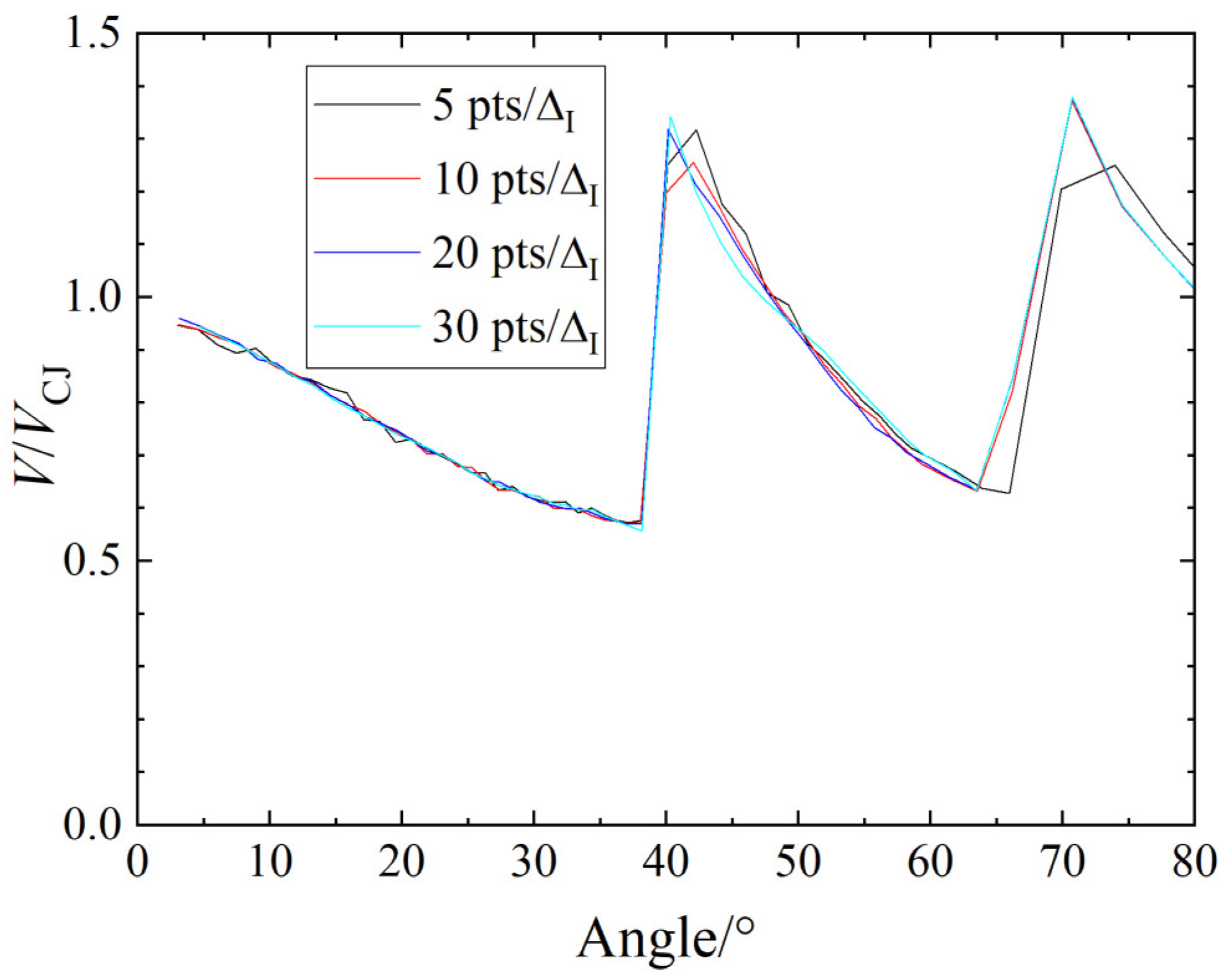
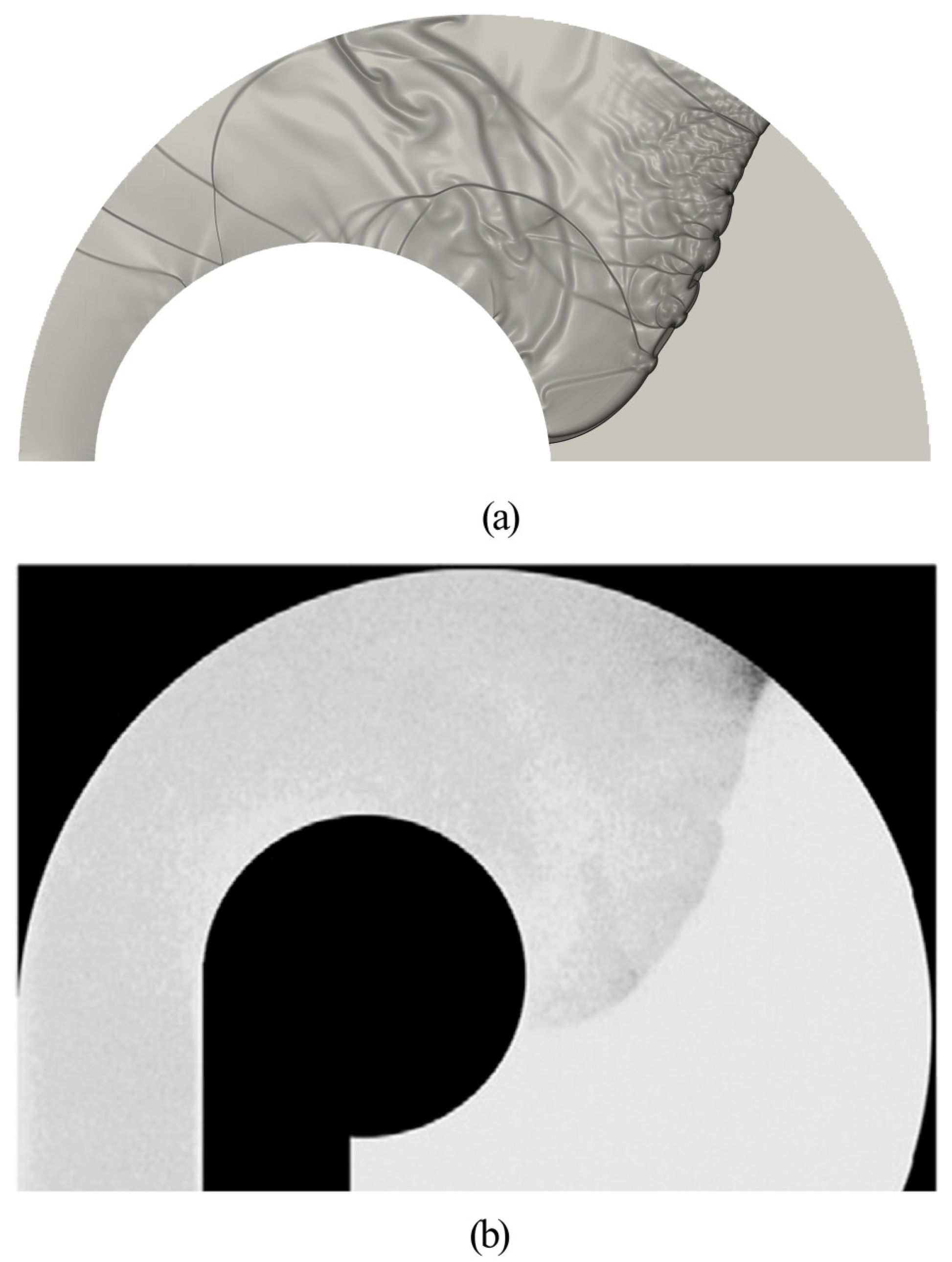
2.3. Resolution Test
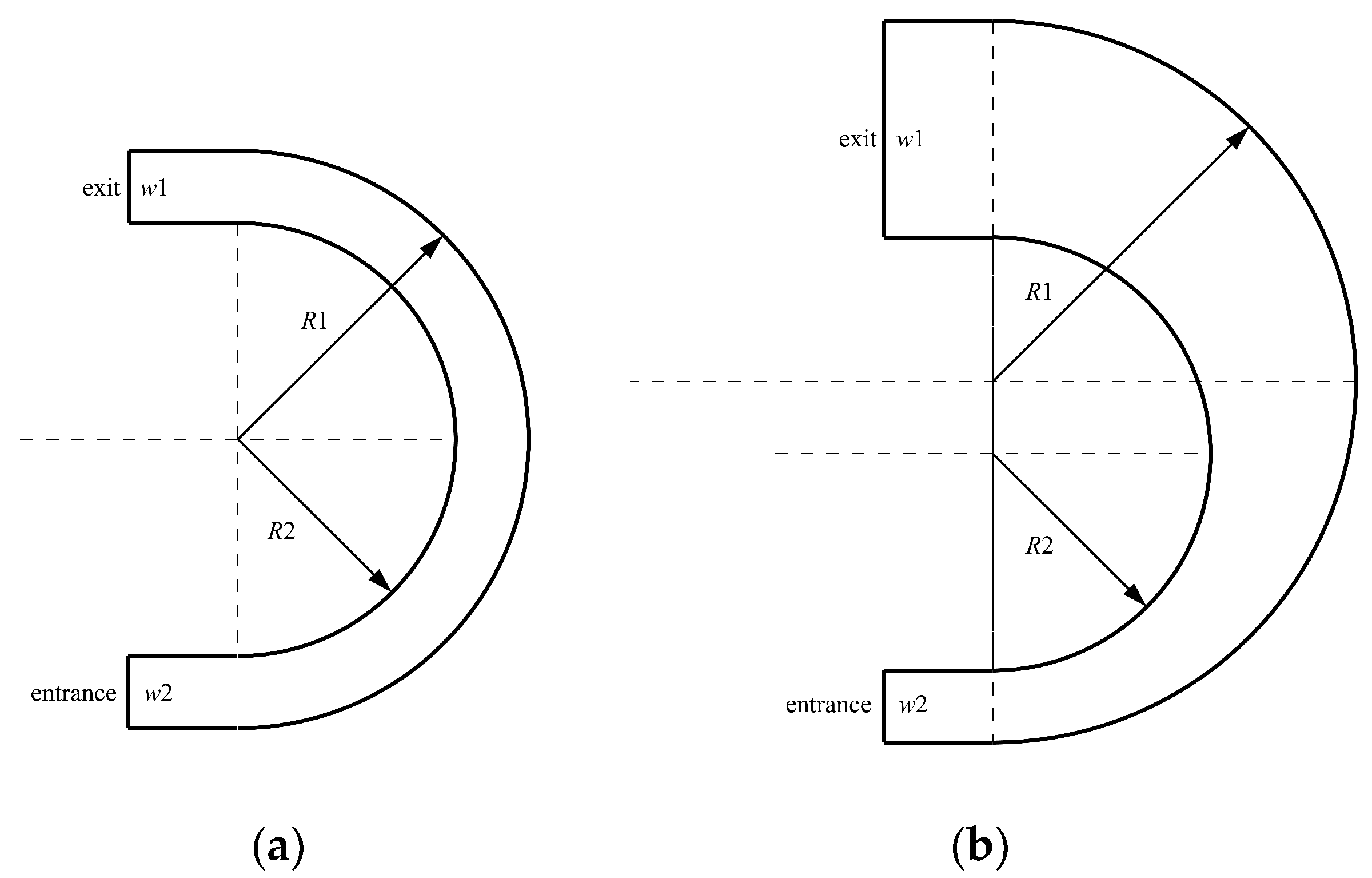
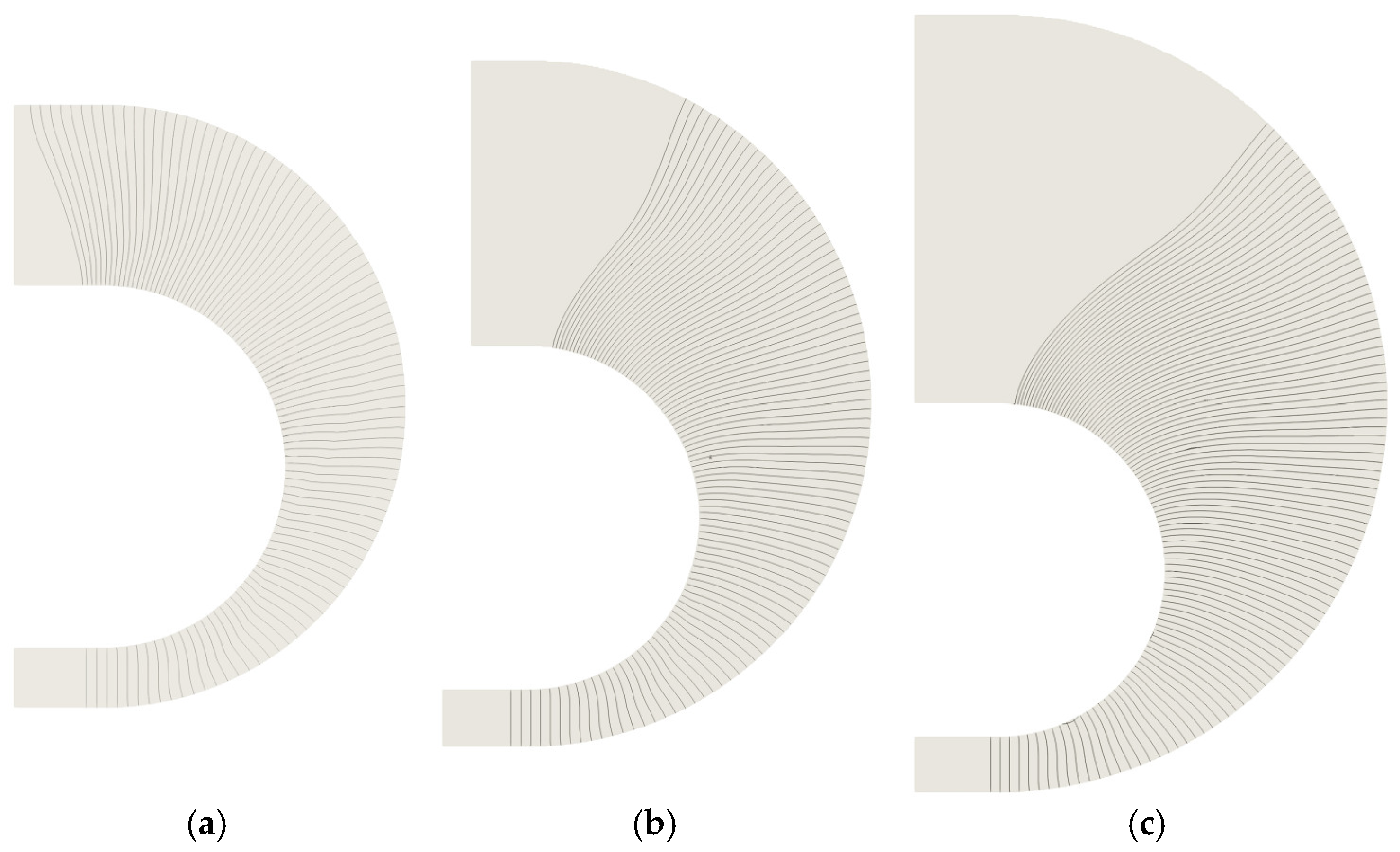
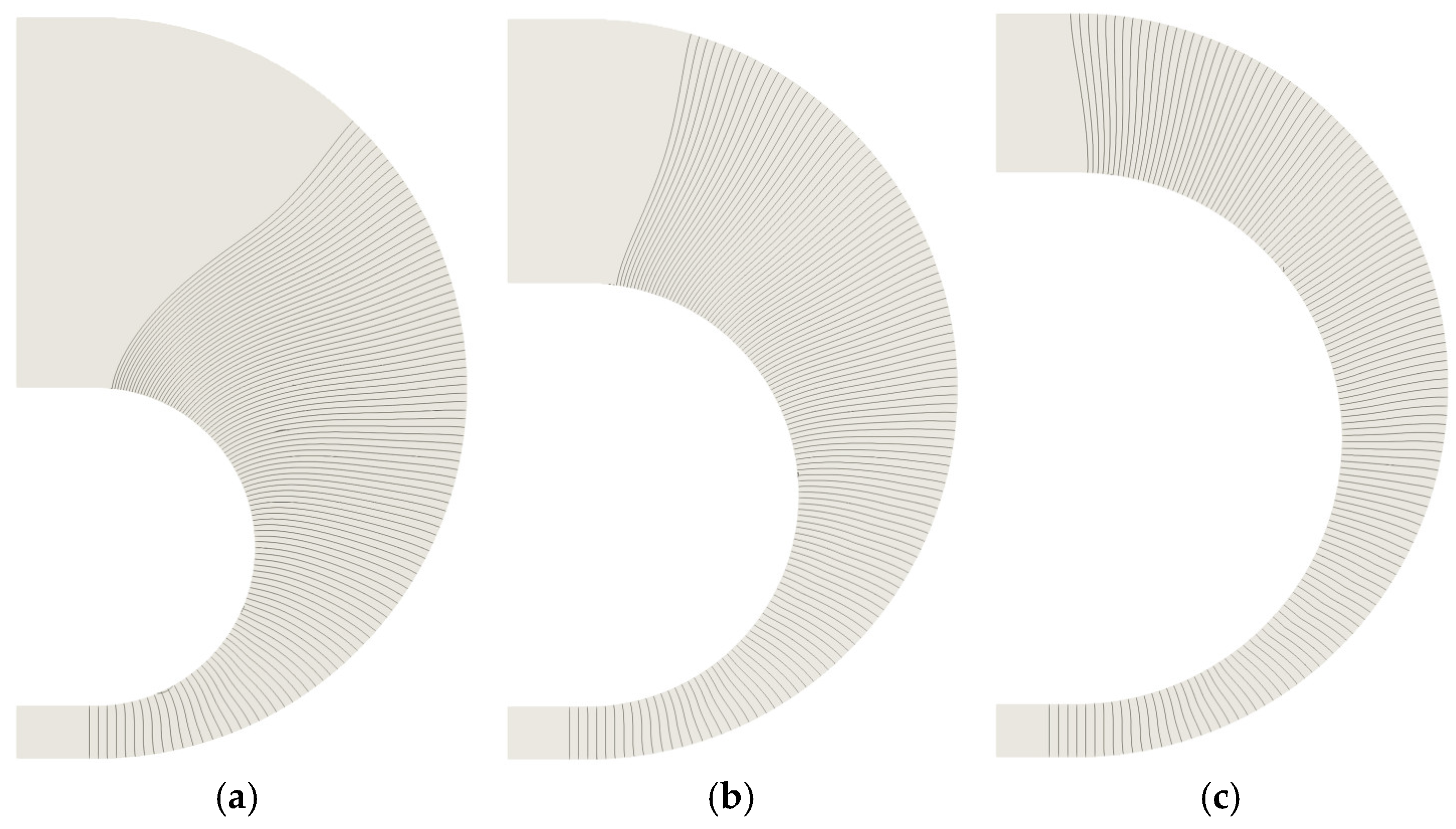
2.4. Numerical Setups
3. Results and Discussions
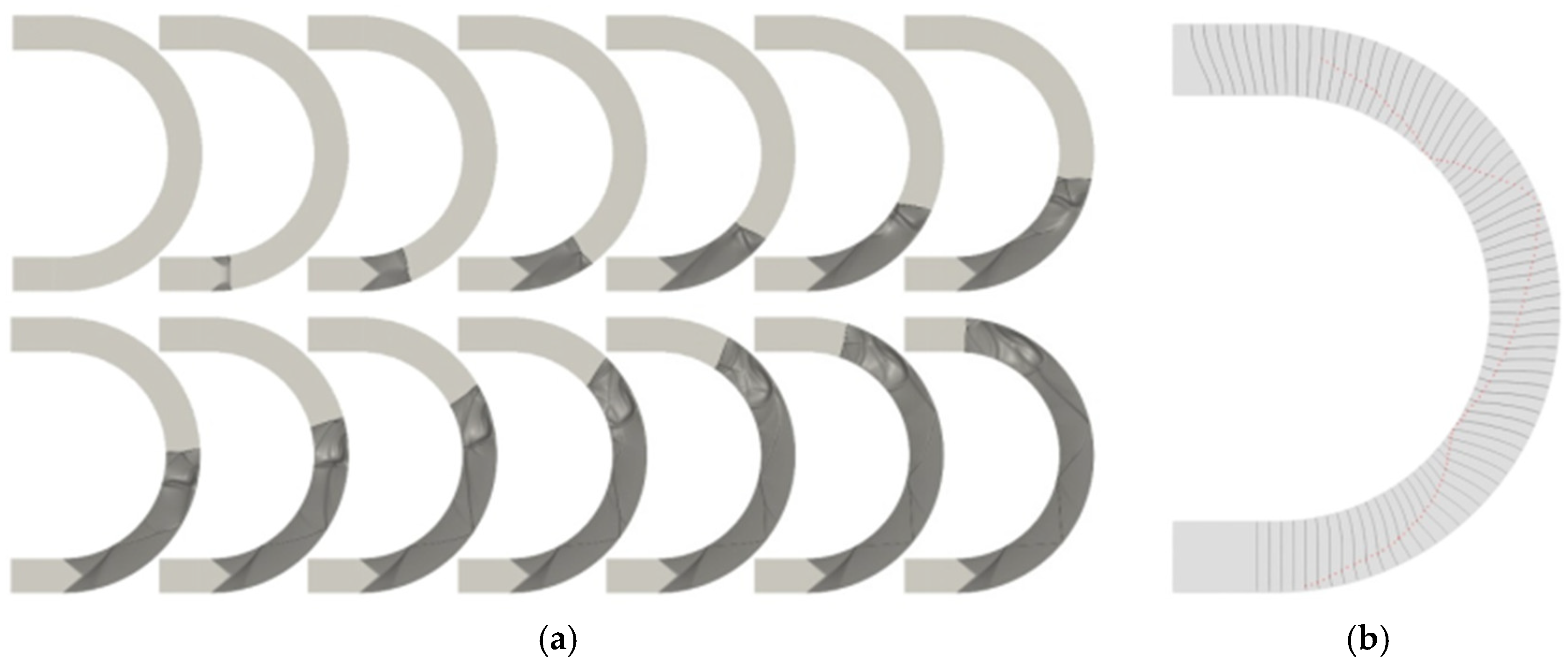
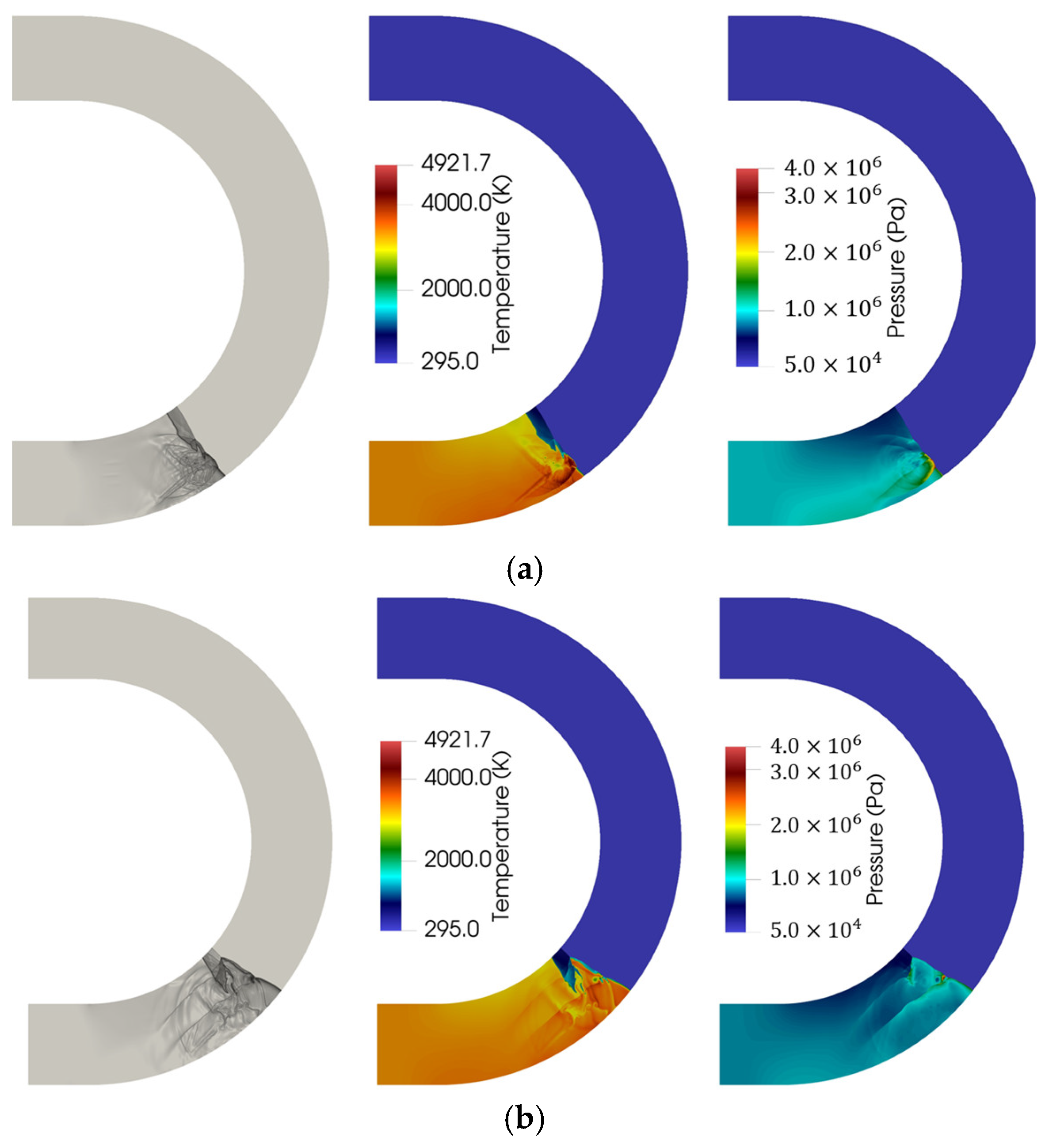
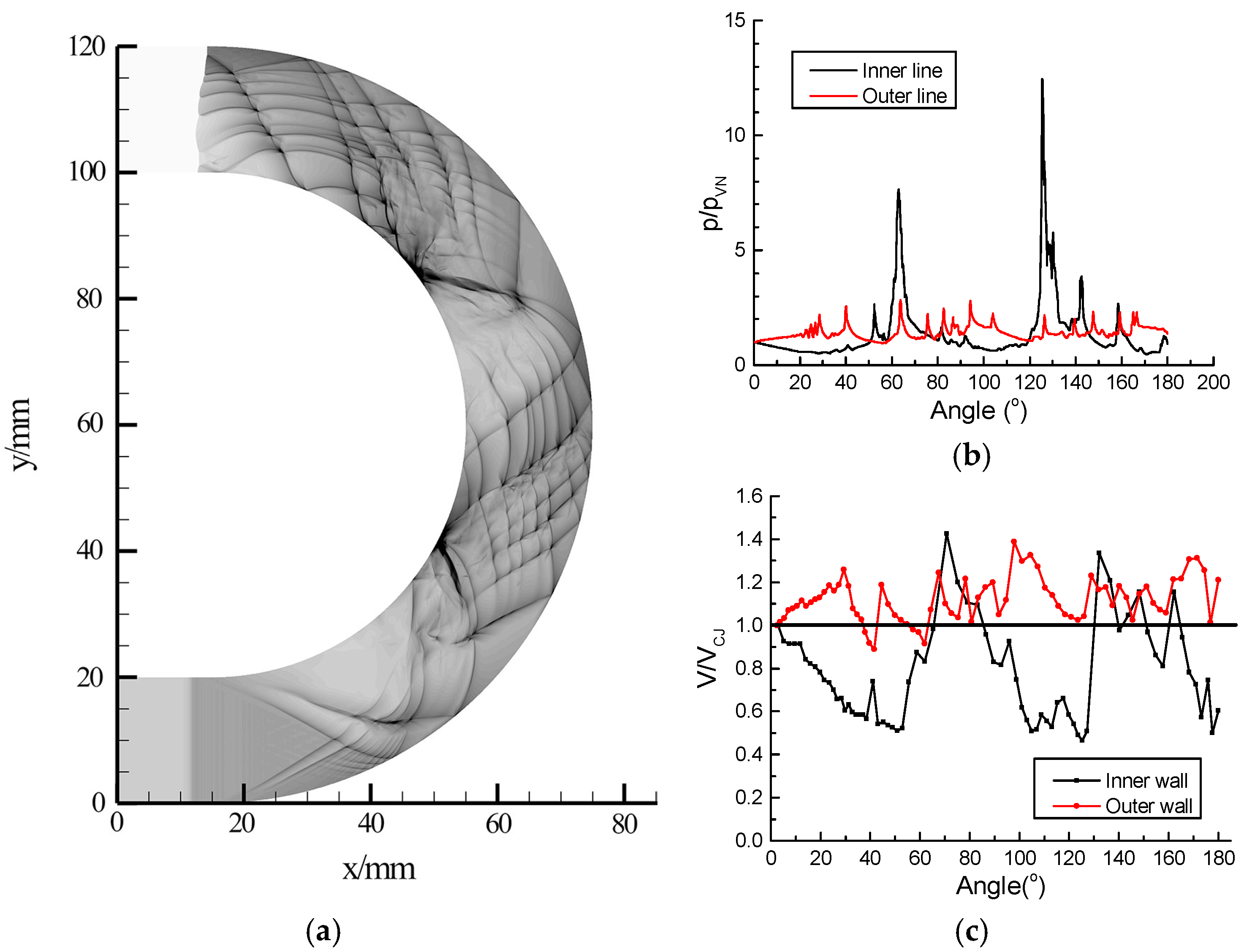
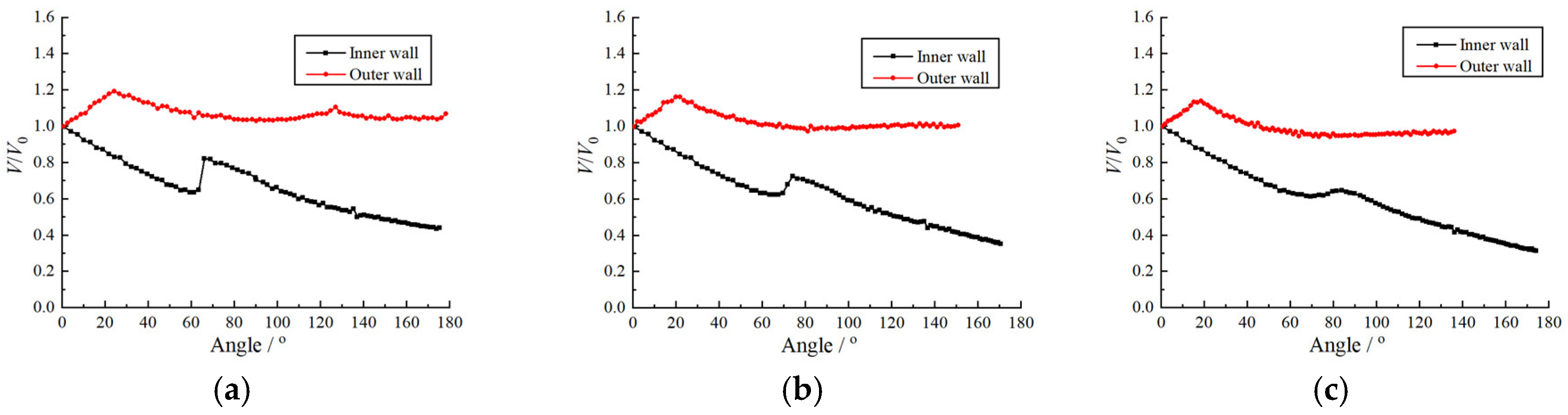
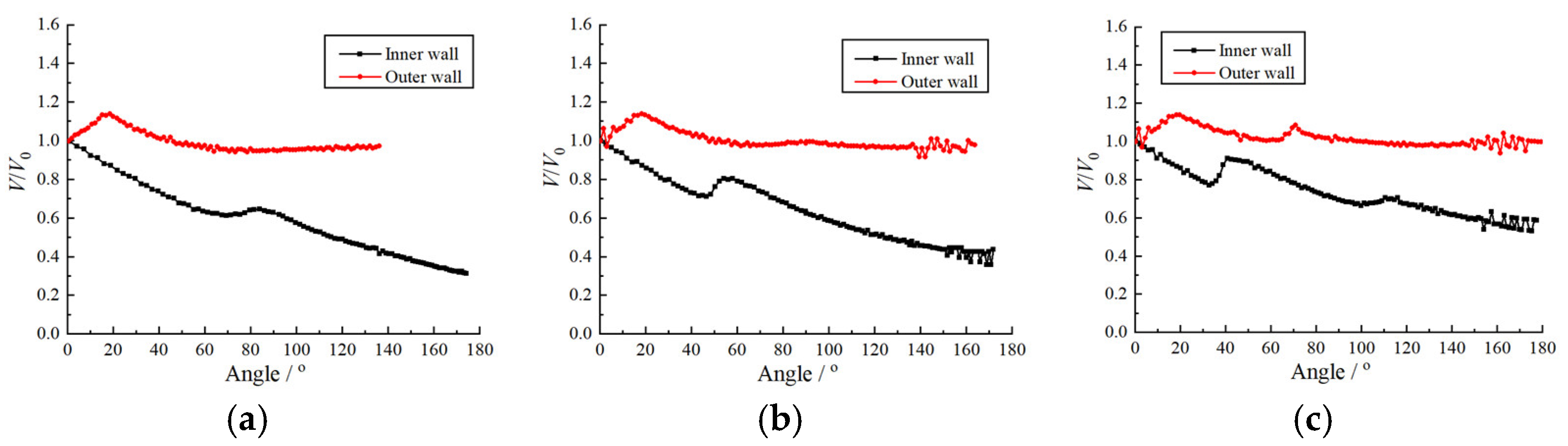
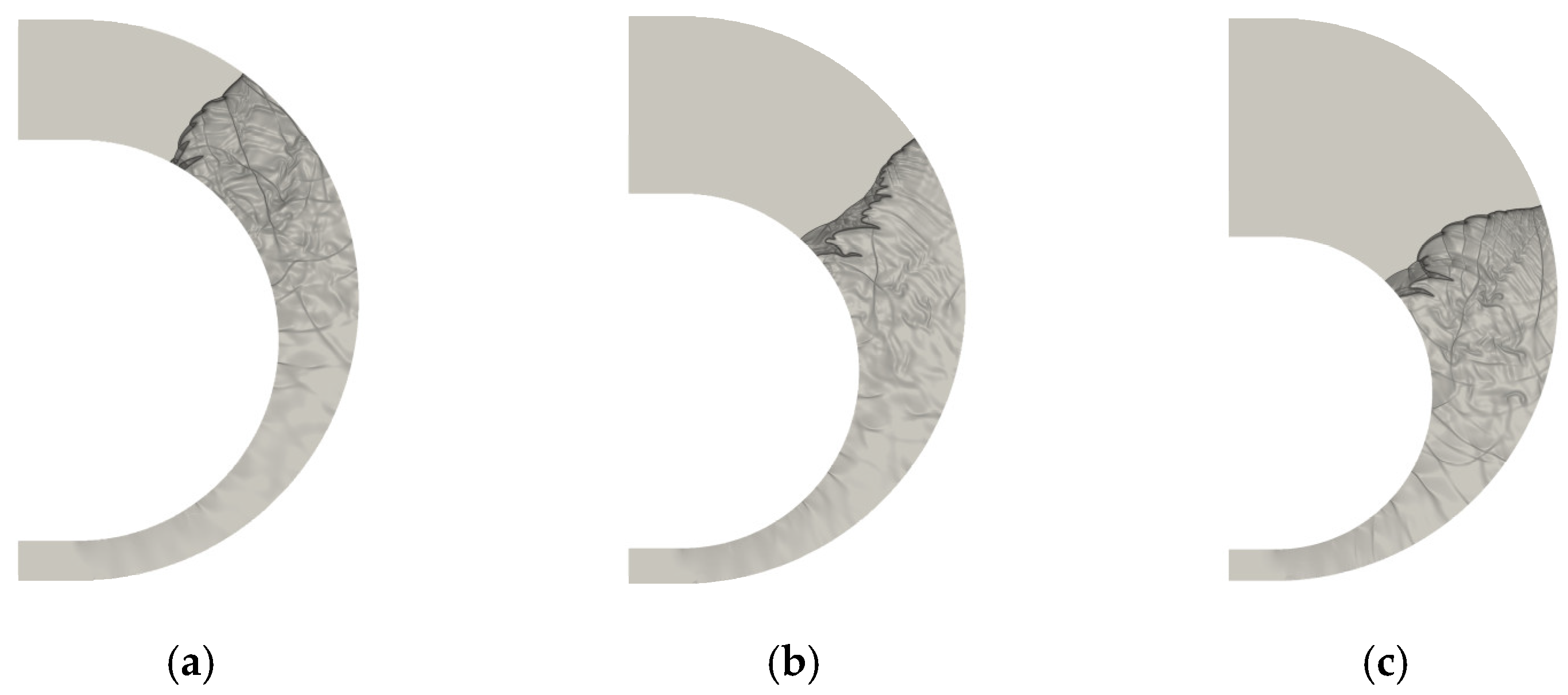
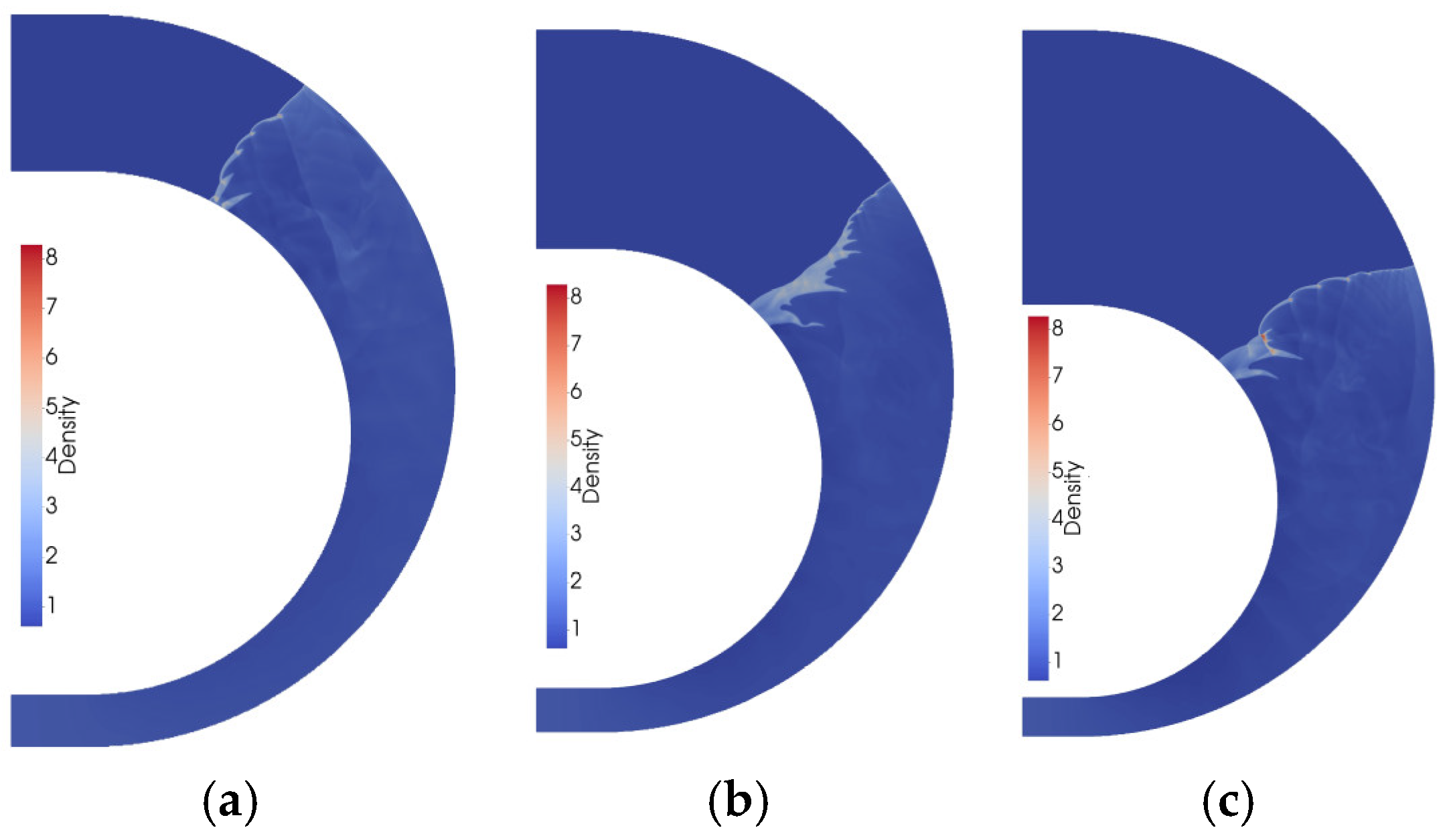
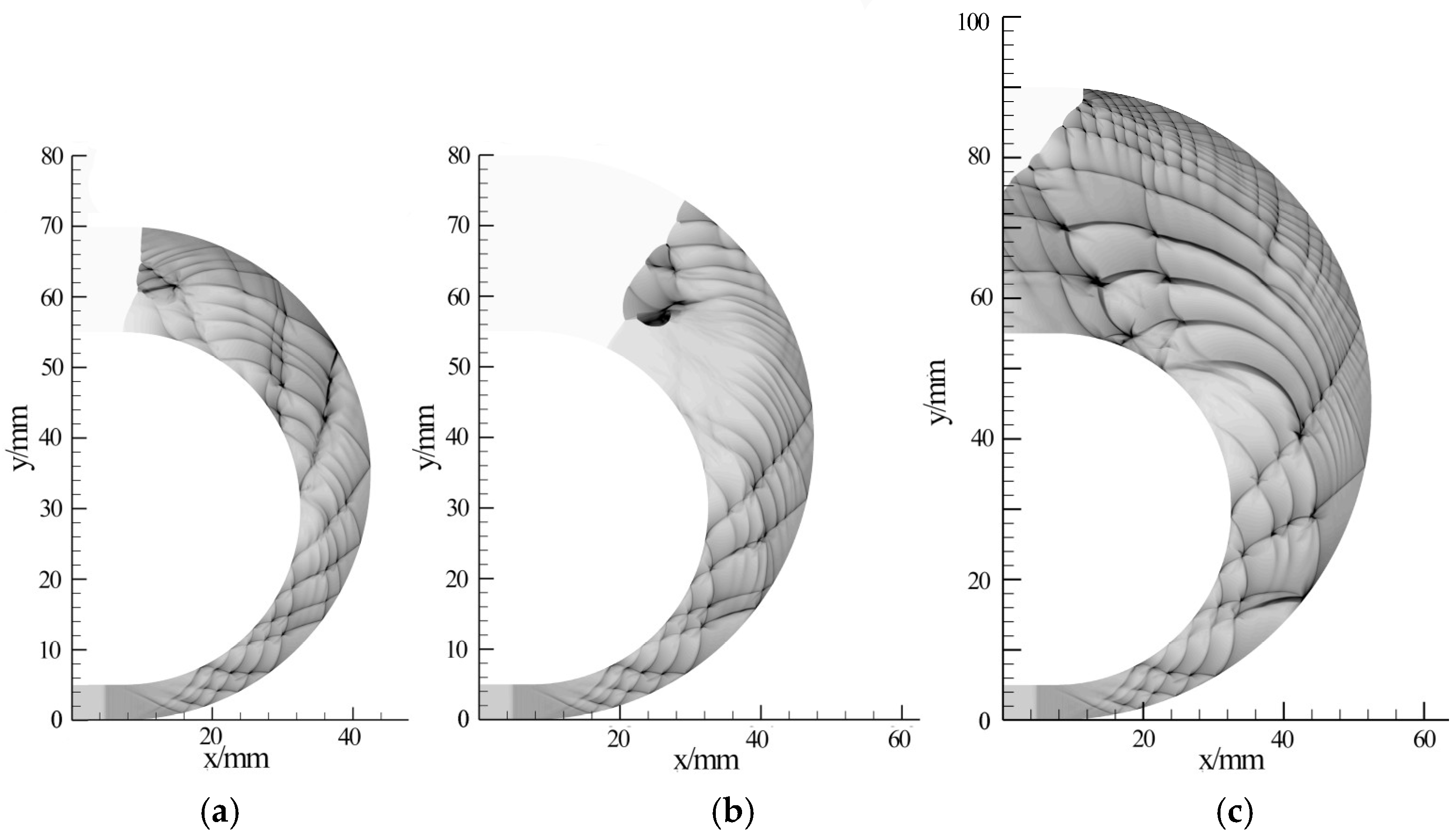
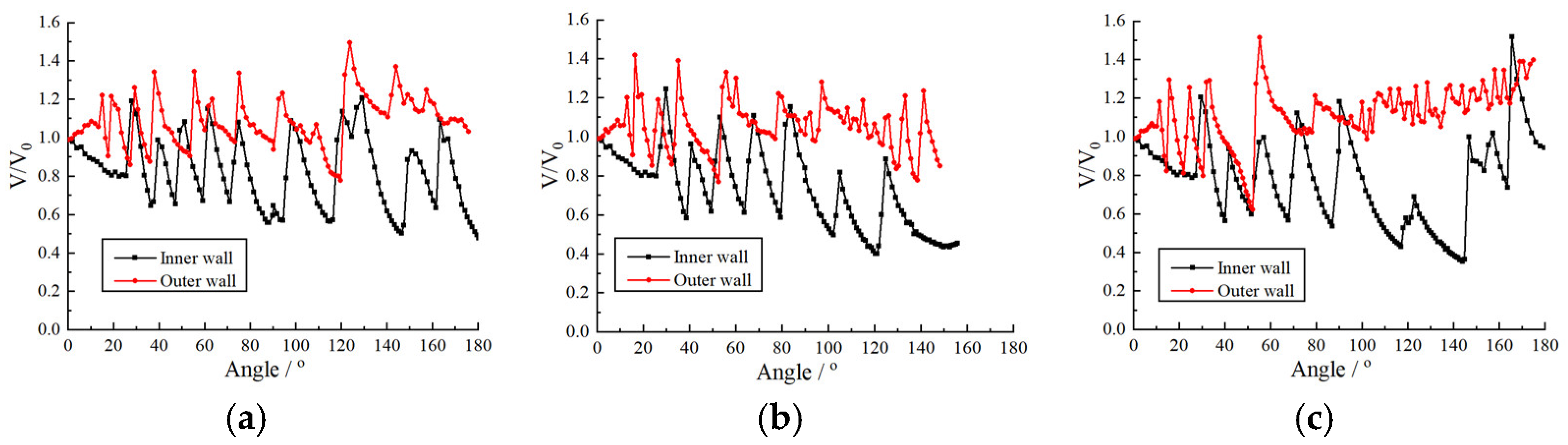
3.1. Shock Propagation in Coverture Bend with Constant Cross-Section Area
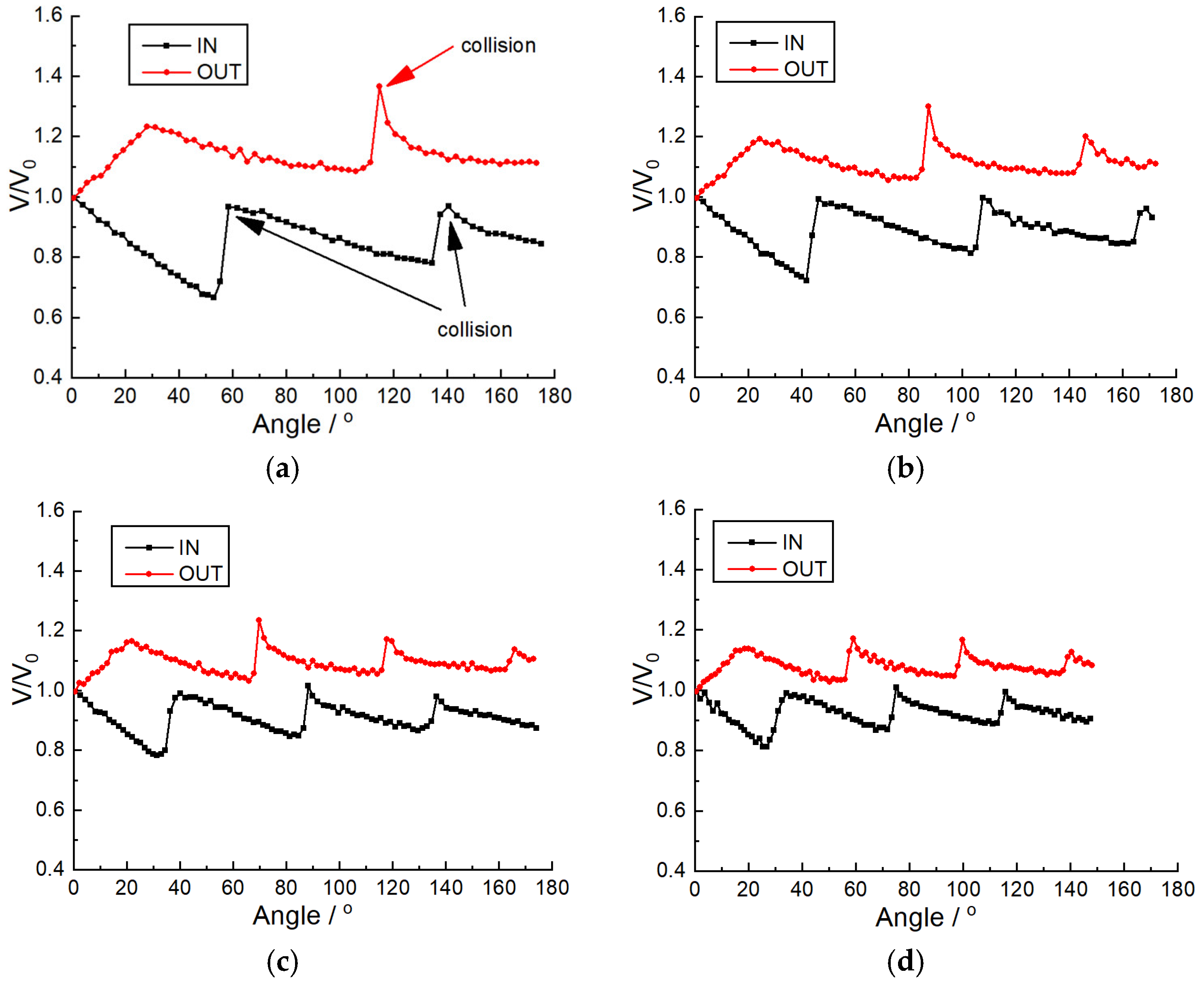
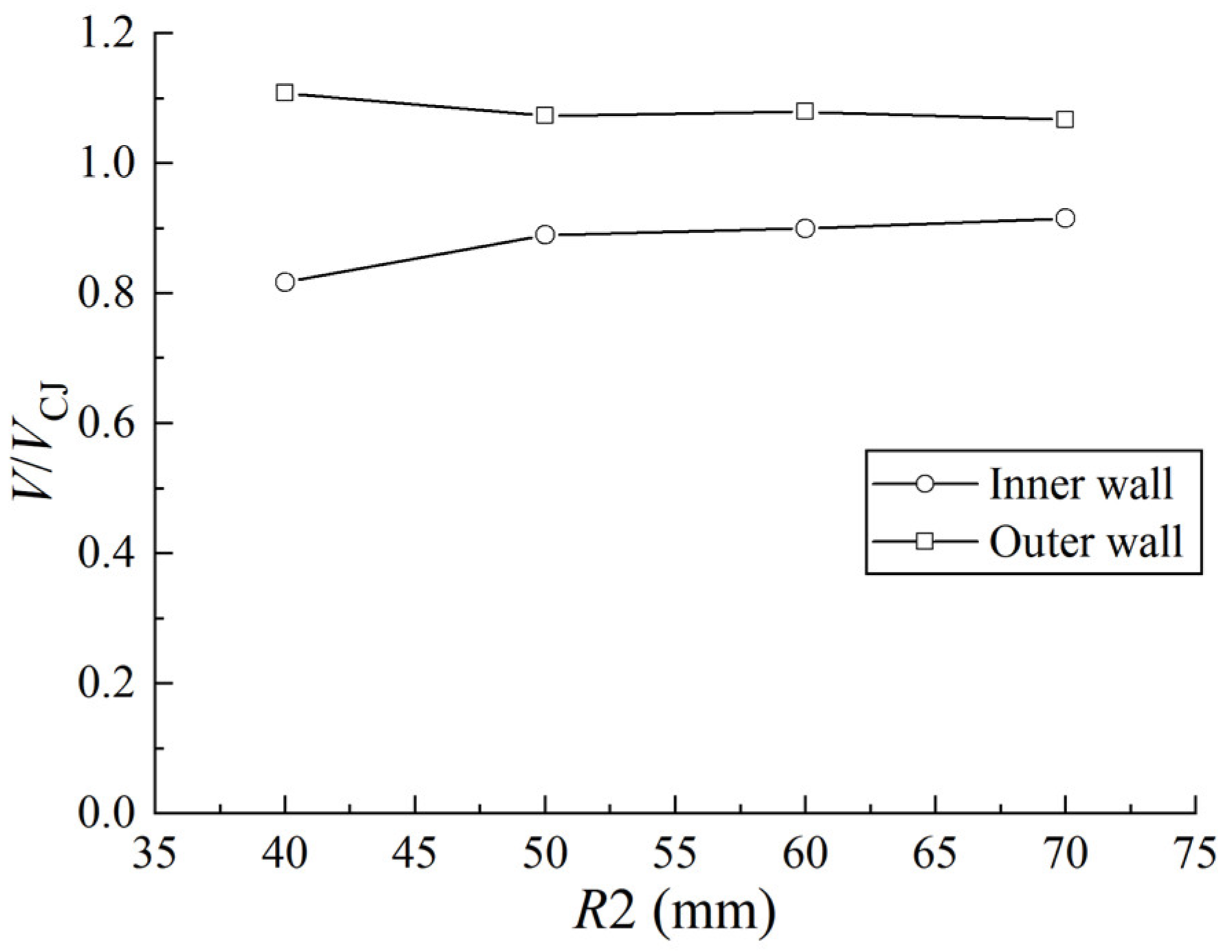
3.2. Detonation Propagation in Curvature Bends with a Constant Cross-Sectional Area
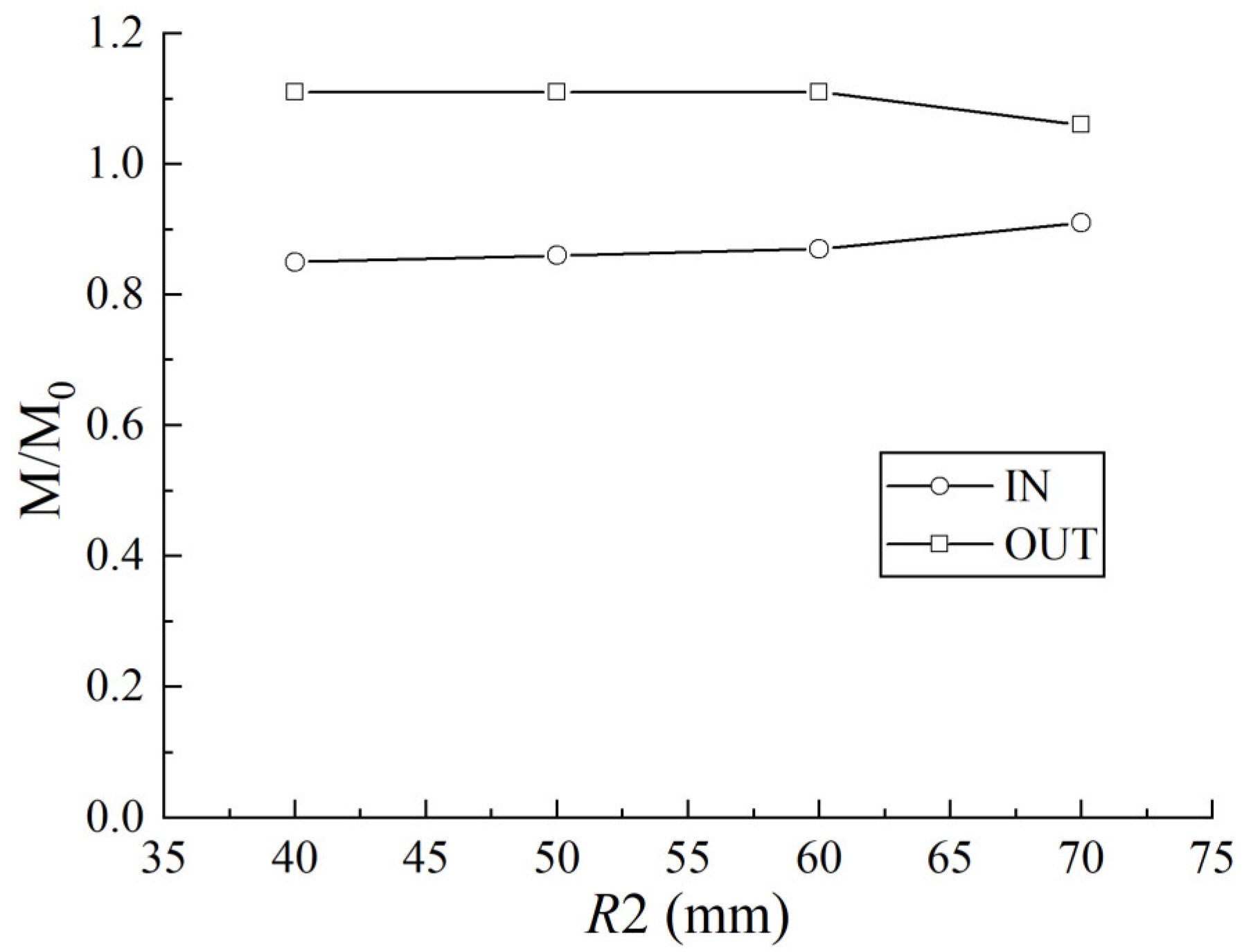
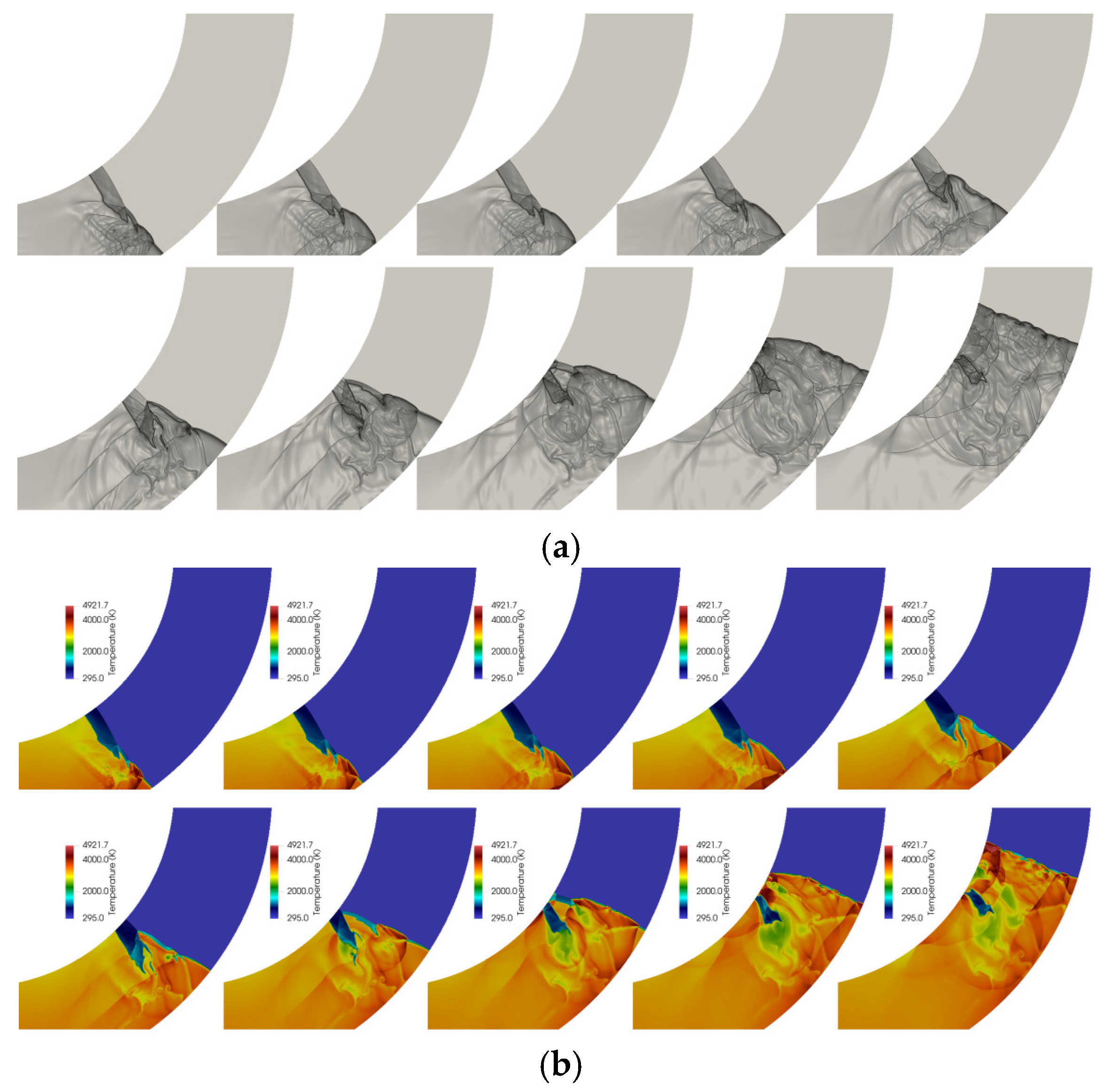
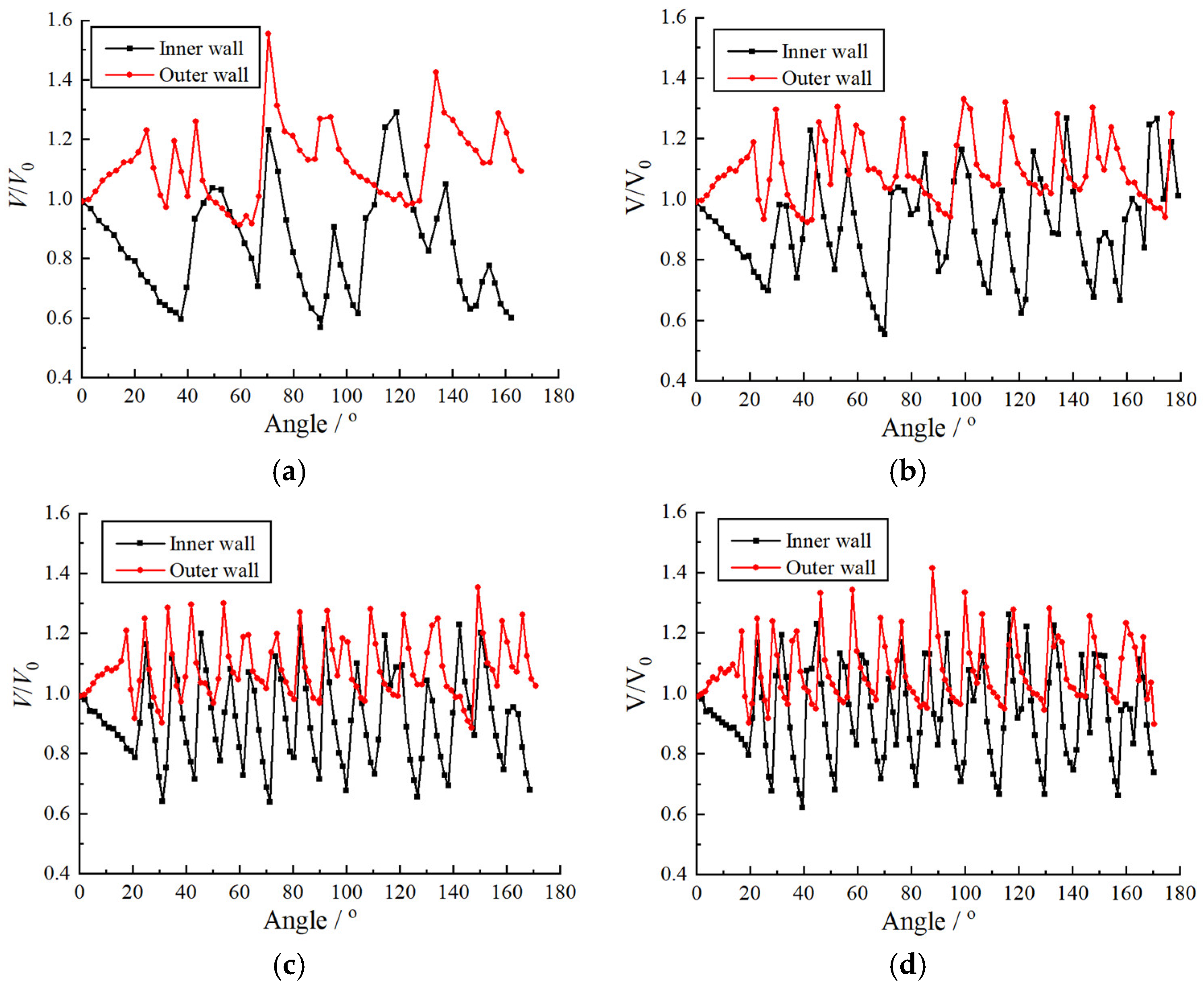
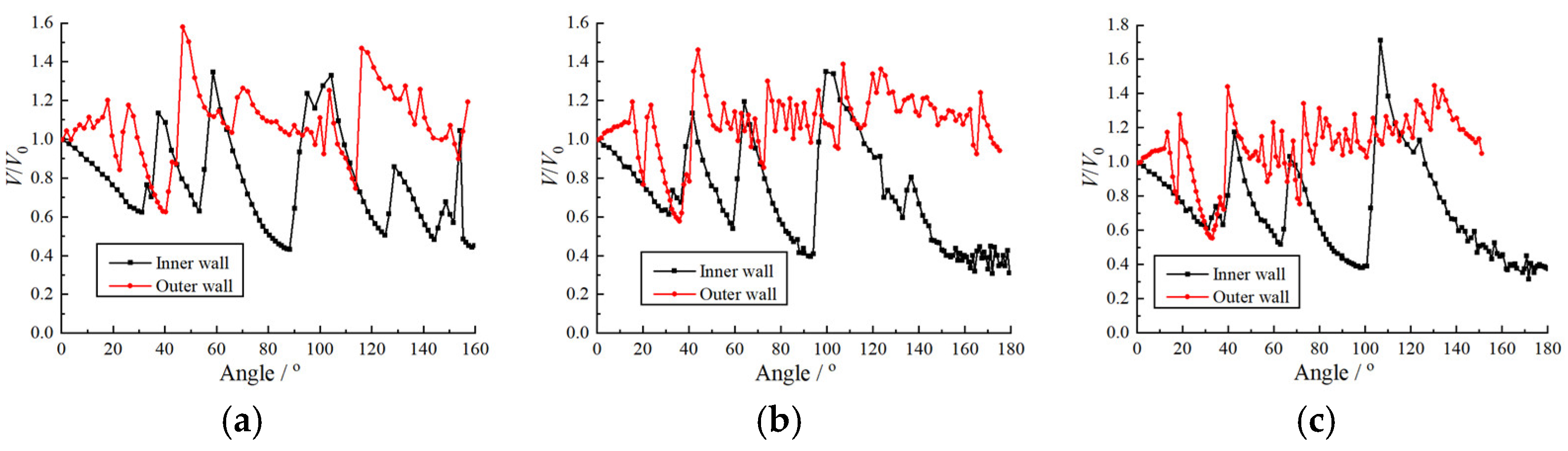
3.3. Shock Propagation in Curvature Bends with a Varying Cross-Sectional Area
3.4. Detonation Propagation in Curvature Bends with Varying Cross-Sectional Area
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yuan, X.; Zhou, J.; Lin, Z.; Cai, X. Adaptive simulations of detonation propagation in 90-degree bent tubes. Int. J. Hydrogen Energy 2016, 41, 18259–18272. [Google Scholar] [CrossRef]
- Li, J.; Ren, H.; Ning, J. Numerical application of additive Runge-Kutta methods on detonation interaction with pipe bends. Int. J. Hydrogen Energy 2013, 38, 9016–9027. [Google Scholar] [CrossRef]
- Li, J.; Ning, J.-G.; Zhao, H.; Hao, L.; Wang, C. Numerical Investigation on the Propagation Mechanism of Steady Cellular Detonations in Curved Channels. Chin. Phys. Lett. 2015, 32, 144–147. [Google Scholar] [CrossRef]
- Edwards, D.H.; Thomas, G.O. The diffraction of detonation waves in channels with 90° bends. Combustions 1983, 3, 65–76. [Google Scholar]
- Mitrofanov, V.V.; Soloukhin, R.I. The Diffraction of Multifront Detonation Waves. Sov. Phys. Dokl. 1965, 9, 1055–1058. [Google Scholar]
- Zhang, B.; Mehrjoo, N.; Ng, H.D.; Lee, J.H.S.; Bai, C. On the dynamic detonation parameters in acetylene–oxygen mixtures with varying amount of argon dilution. Combust. Flame 2014, 161, 1390–1397. [Google Scholar] [CrossRef]
- Meredith, J.; Ng, H.D.; Lee, J.H.S. Detonation diffraction from an annular channel. Shock Waves 2010, 20, 449–455. [Google Scholar] [CrossRef]
- Li, J.; Ning, J.; Lee, J.H.S. Mach reflection of a ZND detonation wave. Shock Waves 2015, 25, 293–304. [Google Scholar] [CrossRef]
- Li, J.; Lee, J.H.S. Numerical simulation of Mach reflection of cellular detonations. Shock Waves 2016, 26, 673–682. [Google Scholar] [CrossRef]
- Li, J.; Ren, H.; Wang, X.; Ning, J. Length scale effect on Mach reflection of cellular detonations. Combust. Flame 2018, 189, 378–392. [Google Scholar] [CrossRef]
- Takayama, K.; Honda, M.; Onoders, O. Shock propagation along 90 degree bends. Rep. Inst. High Speed Mech. 1977, 35, 83–111. [Google Scholar]
- Achasov, O.V.; Penyaz’kov, O.G. Investigation of the dynamic properties of the cellular structure of a gas-detonation wave. J. Eng. Phys. Thermophys. 2000, 73, 915–920. [Google Scholar] [CrossRef]
- Frolov, S.M.; Aksenov, V.S.; Shamshin, I.O. Shock wave and detonation propagation through U-bend tubes. Proc. Combust. Inst. 2007, 31, 2421–2428. [Google Scholar] [CrossRef]
- Thomas, G.O.; Williams, R.L. Detonation interaction with wedges and bends. Shock Waves 2002, 11, 481–492. [Google Scholar] [CrossRef]
- Sato, K.; Sakai, Y.; Chiga, M. Flame Propagation Along 90° Bend in an Open Duct. In Twenty-Sixth Symposium (International) on Combustion; Combustions Institute: Naples, Italy, 1996; pp. 931–937. [Google Scholar]
- Kudo, Y.; Nagura, Y.; Kasahara, J.; Sasamoto, Y.; Matsuo, A. Oblique detonation waves stabilized in rectangular-cross-section bent tubes. Proc. Combust. Inst. 2011, 33, 2319–2326. [Google Scholar] [CrossRef]
- Nakayama, H.; Moriya, T.; Kasahara, J.; Matsuo, A.; Sasamoto, Y.; Funaki, I. Stable detonation wave propagation in rectangular cross-section curved channels. Combust. Flame 2012, 159, 859–869. [Google Scholar] [CrossRef]
- Nakayama, H.; Kasahara, J.; Matsuo, A.; Funaki, I. Front shock behavior of stable curved detonation waves in rectangular-cross-section curved channels. Proc. Combust. Inst. 2013, 34, 1939–1947. [Google Scholar] [CrossRef]
- Sugiyama, Y.; Nakayama, Y.; Matsuo, A.; Nakayama, H.; Kasahara, J. Numerical investigations on detonation propagation in a Two-Dimensional Curved Channel. Combust. Sci. Technol. 2014, 186, 1662–1679. [Google Scholar] [CrossRef]
- Thomas, G.; Edwards, D.; Lee, J.; Knystautas, R.; Moen, I.; Wei, Y. Detonation diffraction by divergent channels. Dyn. Explos. Prog. Astronaut. Aeronaut. 1986, 106, 144–154. [Google Scholar]
- Sorin, R.; Zitoun, R.; Khasainov, B.; Desbordes, D. Detonation diffraction through different geometries. Shock Waves 2009, 19, 11–23. [Google Scholar] [CrossRef]
- Monnier, V.; Rodriguez, V.; Vidal, P.; Zitoun, R. Three-dimensional dynamics of detonation cells in linearly diverging channels: Experimental analysis of the cross-sectional shape and a detonation-shock dynamics interpretation. Exp. Fluids 2024, 65, 154. [Google Scholar] [CrossRef]
- Ng, H.D.; Radulescu, M.I.; Higgins, A.J.; Nikiforakis, N.; Lee, J.H.S. Numerical investigation of the instability for one-dimensional Chapman-Jouguet detonations with chain-branching kinetics. Combust. Theory Model. 2003, 9, 385–401. [Google Scholar] [CrossRef]
- Deiterding, R. Parallel Adaptive Simulation of Multi-Dimensional Detonation Structures. Doctoral Thesis, Brandenburgische Technische Universität Cottbus, Cottbus, Germany, 2003. [Google Scholar]
- Berger, M.J.; Colella, P. Local adaptive mesh refinement for shock hydrodynamics. J. Comput. Phys. 1989, 8, 64–84. [Google Scholar] [CrossRef]
- Melguizo-Gavilanes, J.; Rodriguez, V.; Vidal, P.; Zitoun, R. Dynamics of detonation transmission and propagation in a curved chamber: A numerical and experimental analysis. Combust. Flame 2021, 223, 460–473. [Google Scholar] [CrossRef]




| Model Parameters | Value | Unit |
|---|---|---|
| R | 218.79 | J/kg·K |
| 50.0 | kPa | |
| 295 | K | |
| 0.775 | kg/m3 | |
| 19.7 | ||
| 1.44 | ||
| 5.6 | ||
| 4.8 | ||
| 1.0 | ||
| 1.3875 | ||
| 2.0 |
| R1 (mm) | R2 (mm) | w1 (mm) | |
|---|---|---|---|
| Case 1.1 | 30 | 40 | 10 |
| Case 1.2 | 40 | 50 | 10 |
| Case 1.3 | 50 | 60 | 10 |
| Case 1.4 | 60 | 70 | 10 |
| R1 (mm) | R2 (mm) | w1 (mm) | |
|---|---|---|---|
| Case 2.1 | 20 | 40 | 20 |
| Case 2.2 | 30 | 50 | 20 |
| Case 2.3 | 40 | 60 | 20 |
| Case 2.4 | 30 | 40 | 10 |
| Case 2.5 | 40 | 50 | 10 |
| Case 2.6 | 50 | 60 | 10 |
| Case 2.7 | 60 | 70 | 10 |
| R1 (mm) | R2 (mm) | w1 (mm) | w2 (mm) | (mm/rad) | (1/rad) | |
|---|---|---|---|---|---|---|
| Case 3.1 | 30 | 50 | 10 | 20 | 10 | 0.20 |
| Case 3.2 | 30 | 60 | 10 | 30 | 20 | 0.33 |
| Case 3.3 | 30 | 70 | 10 | 40 | 30 | 0.43 |
| Case 3.4 | 40 | 70 | 10 | 30 | 20 | 0.29 |
| Case 3.5 | 50 | 70 | 10 | 20 | 10 | 0.14 |
| R1 (mm) | R2 (mm) | w1 (mm) | w2 (mm) | (mm/rad) | (1/rad) | |
|---|---|---|---|---|---|---|
| Case 4.1 | 30 | 50 | 10 | 20 | 10 | 0.20 |
| Case 4.2 | 30 | 60 | 10 | 30 | 20 | 0.33 |
| Case 4.3 | 30 | 70 | 10 | 40 | 30 | 0.43 |
| Case 4.4 | 40 | 60 | 10 | 20 | 10 | 0.17 |
| Case 4.5 | 40 | 70 | 10 | 30 | 20 | 0.29 |
| Case 4.6 | 40 | 80 | 10 | 40 | 30 | 0.38 |
| Case 4.7 | 50 | 70 | 10 | 20 | 10 | 0.14 |
| Case 4.8 | 50 | 80 | 10 | 30 | 20 | 0.25 |
| Case 4.9 | 50 | 90 | 10 | 40 | 30 | 0.33 |
| κ = 0.14 | κ = 0.17 | κ = 0.20 | κ = 0.25 | κ = 0.29 | κ = 0.33 | κ = 0.33 | κ = 0.38 | κ = 0.43 | |
|---|---|---|---|---|---|---|---|---|---|
| o | o | o | |||||||
| x | x | o | |||||||
| x | x | x |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, P.; Bao, L.; Dang, W.; Ge, C.; Yu, A. Numerical Studies on the Combined Effect of Curvature and Area Expansion Rate on Gaseous Detonation Propagation in Curved Channels. Fire 2025, 8, 218. https://doi.org/10.3390/fire8060218
Wang P, Bao L, Dang W, Ge C, Yu A. Numerical Studies on the Combined Effect of Curvature and Area Expansion Rate on Gaseous Detonation Propagation in Curved Channels. Fire. 2025; 8(6):218. https://doi.org/10.3390/fire8060218
Chicago/Turabian StyleWang, Peng, Lei Bao, Wenyi Dang, Chuntao Ge, and Anfeng Yu. 2025. "Numerical Studies on the Combined Effect of Curvature and Area Expansion Rate on Gaseous Detonation Propagation in Curved Channels" Fire 8, no. 6: 218. https://doi.org/10.3390/fire8060218
APA StyleWang, P., Bao, L., Dang, W., Ge, C., & Yu, A. (2025). Numerical Studies on the Combined Effect of Curvature and Area Expansion Rate on Gaseous Detonation Propagation in Curved Channels. Fire, 8(6), 218. https://doi.org/10.3390/fire8060218






