Study on the Influence of Expansion Ratio on the Effectiveness of Foam in Suppressing Forest Surface Fires
Abstract
:1. Introduction
2. Materials and Methods
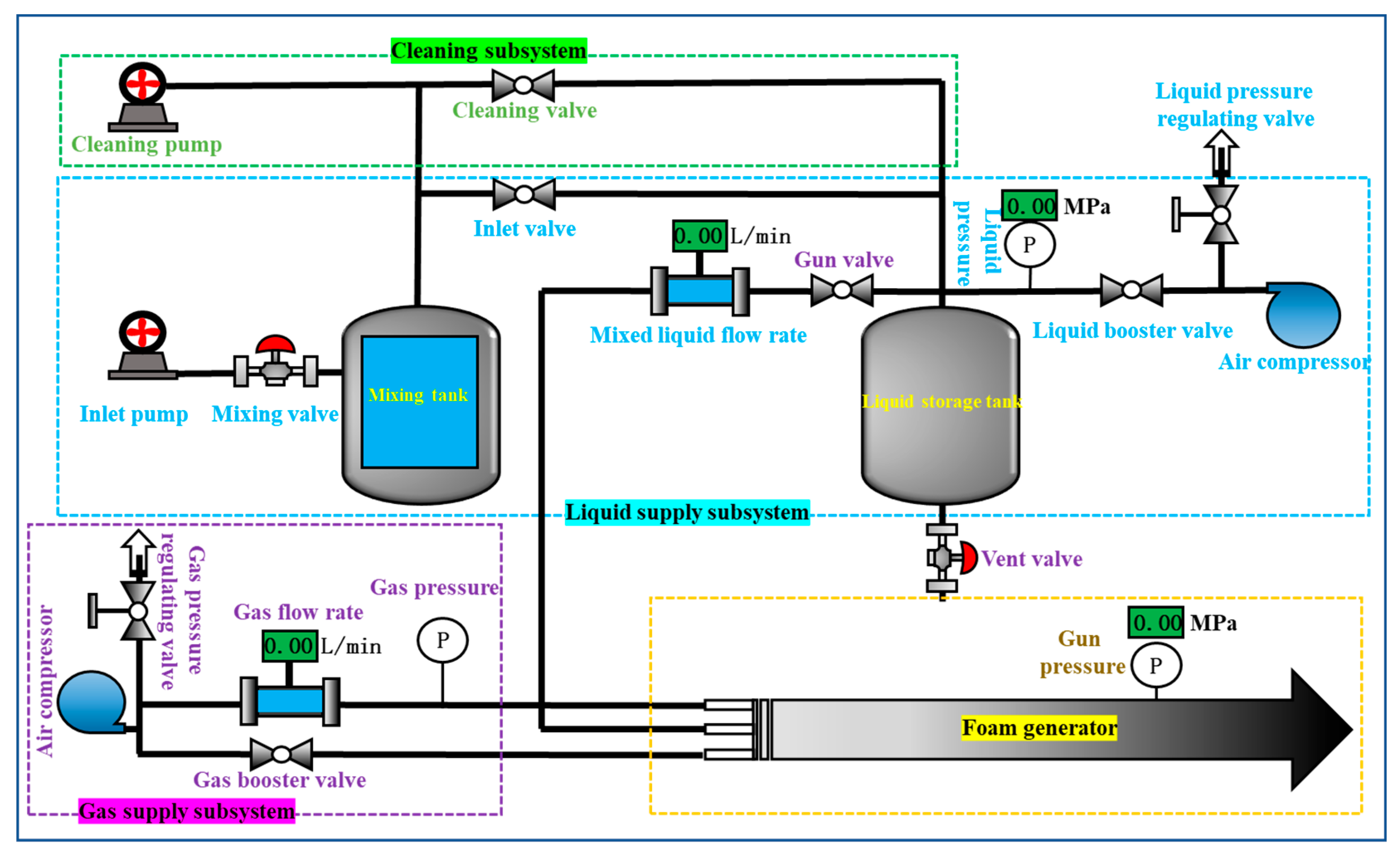
2.1. Foam Generation System
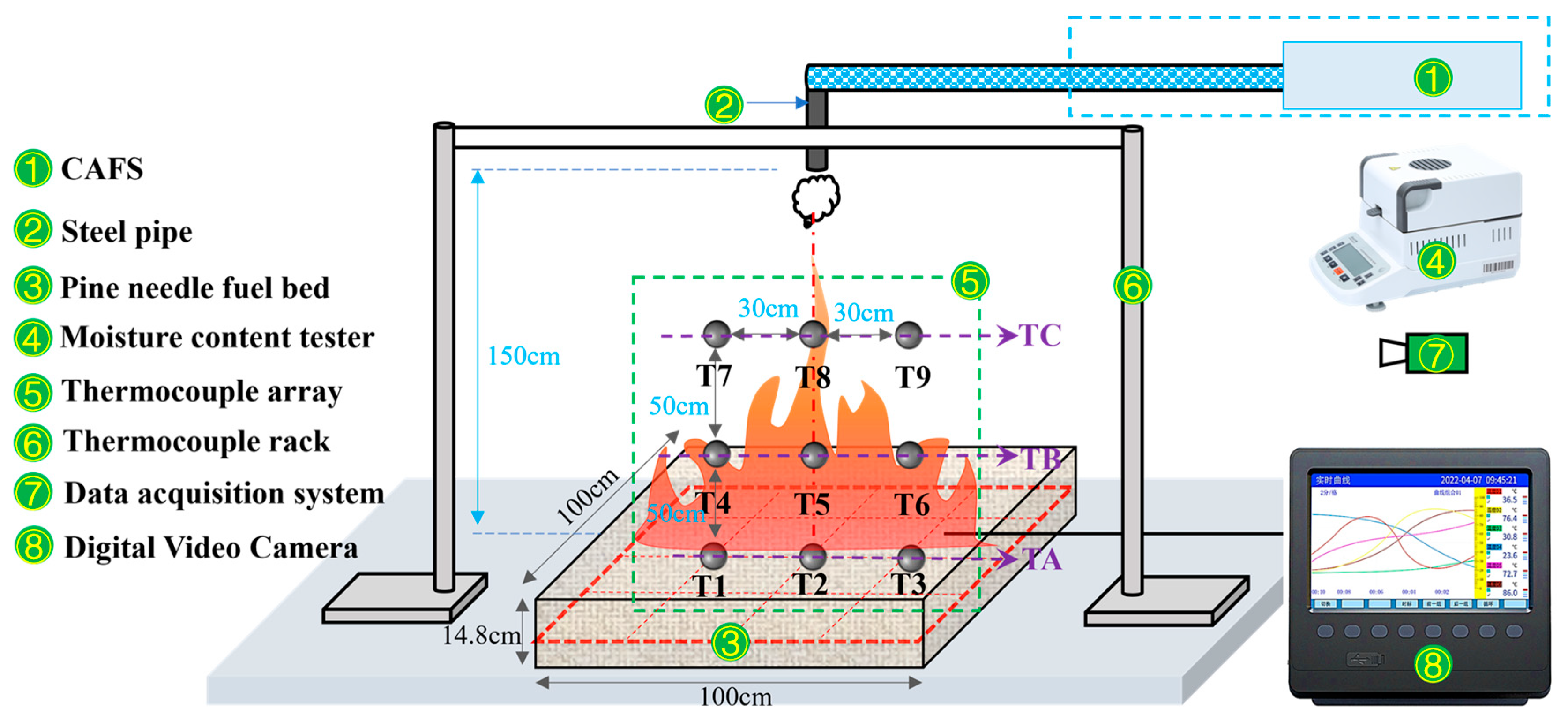
2.2. Experimental Methods
2.2.1. Foam Expansion Ratio
2.2.2. Fire Extinguishing Experiment
3. Experimental Results and Analysis
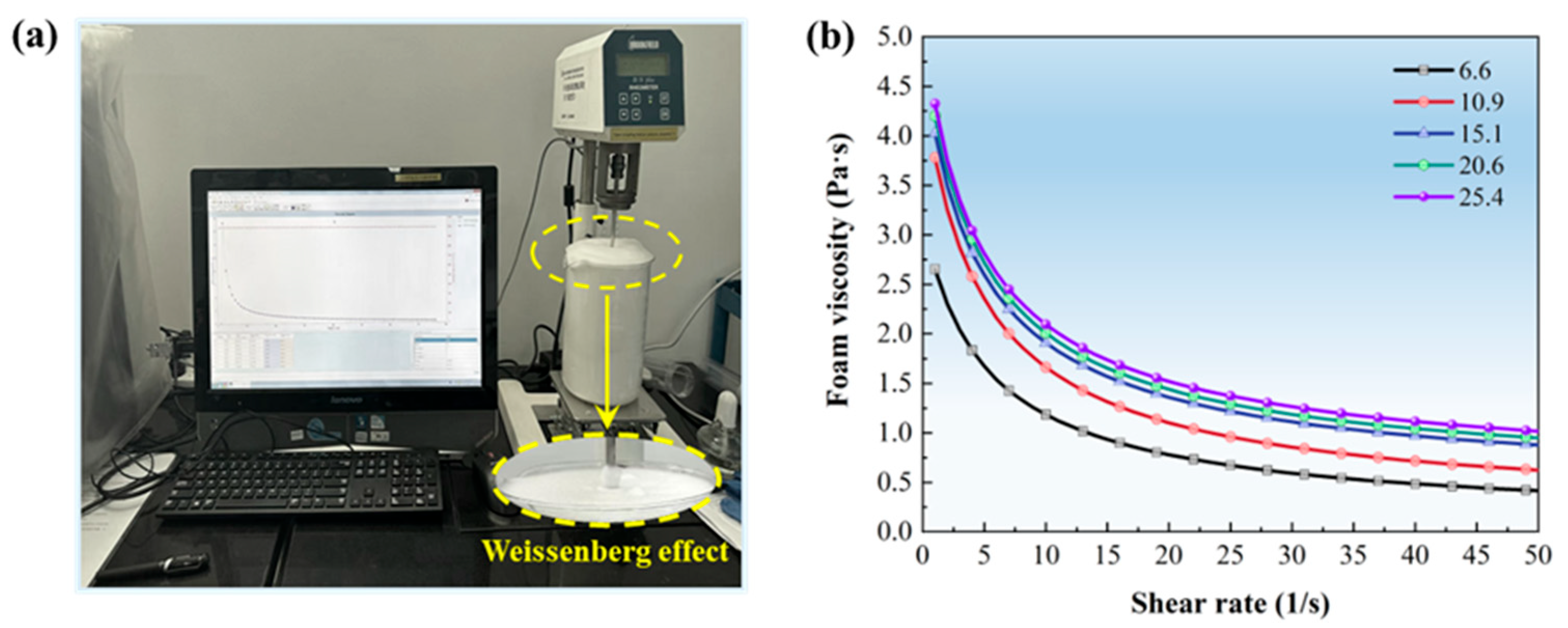
3.1. Basic Properties of Foam
3.2. Combustion Characteristics of the Fuel Bed
3.3. Effect of Foam Expansion Ratio
3.3.1. Coverage Fire Suppression Capability
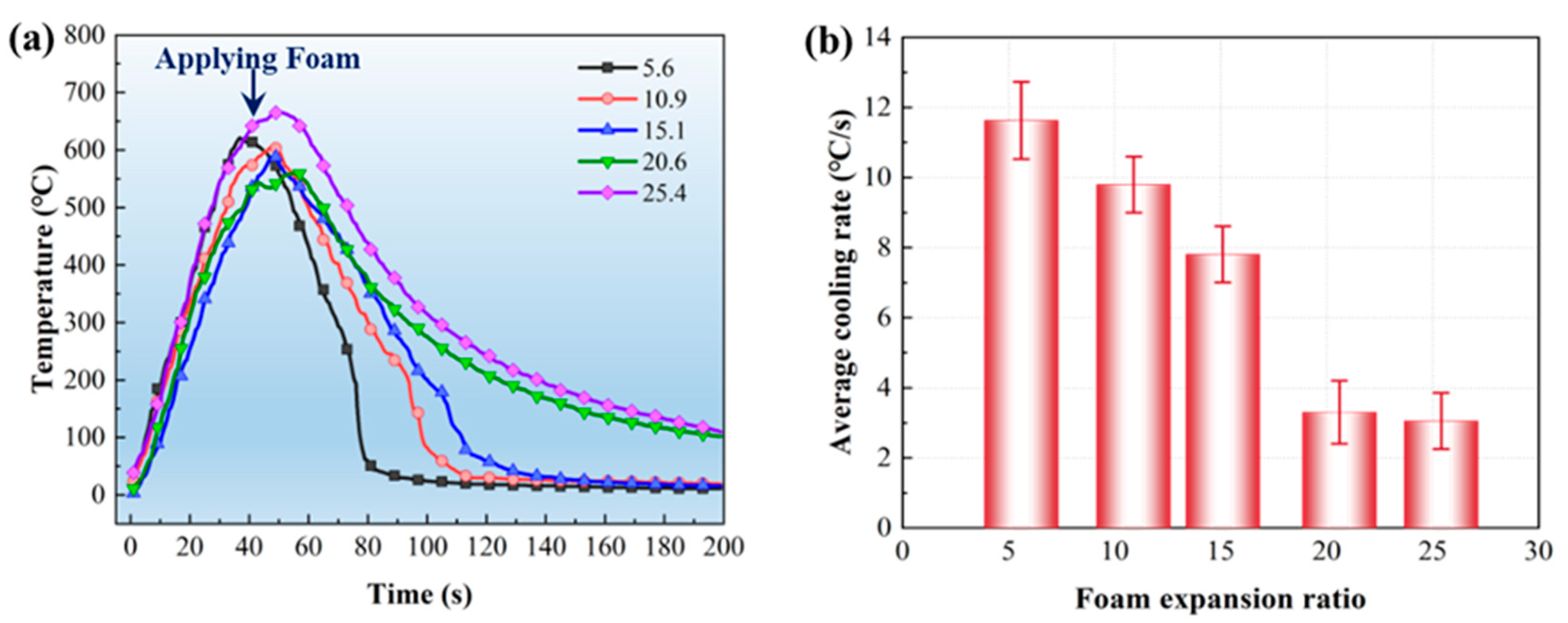
3.3.2. Cooling Capability
3.3.3. Re-Ignition Resistance Capability
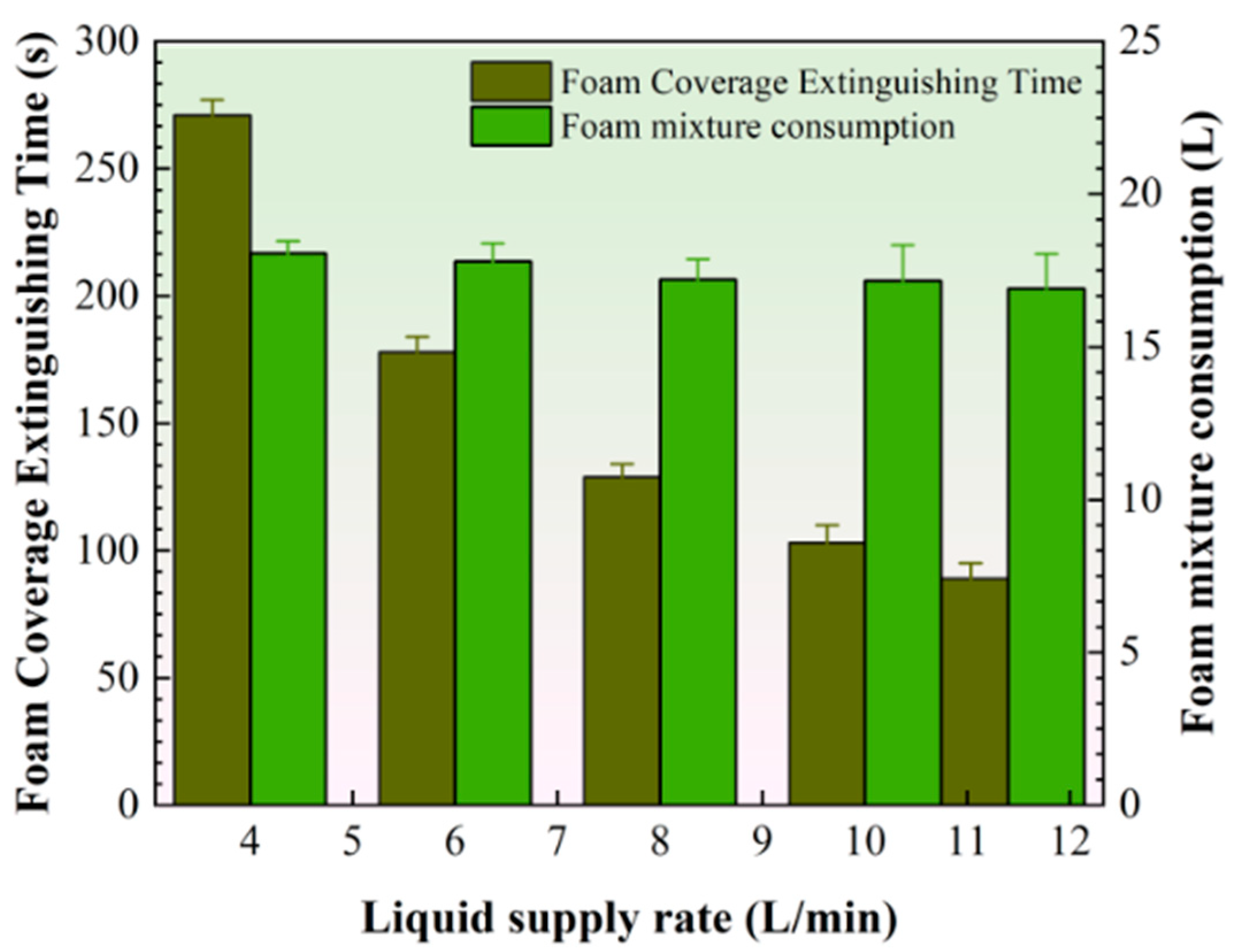
3.4. Influence of Liquid Flow Rate
4. Discussion
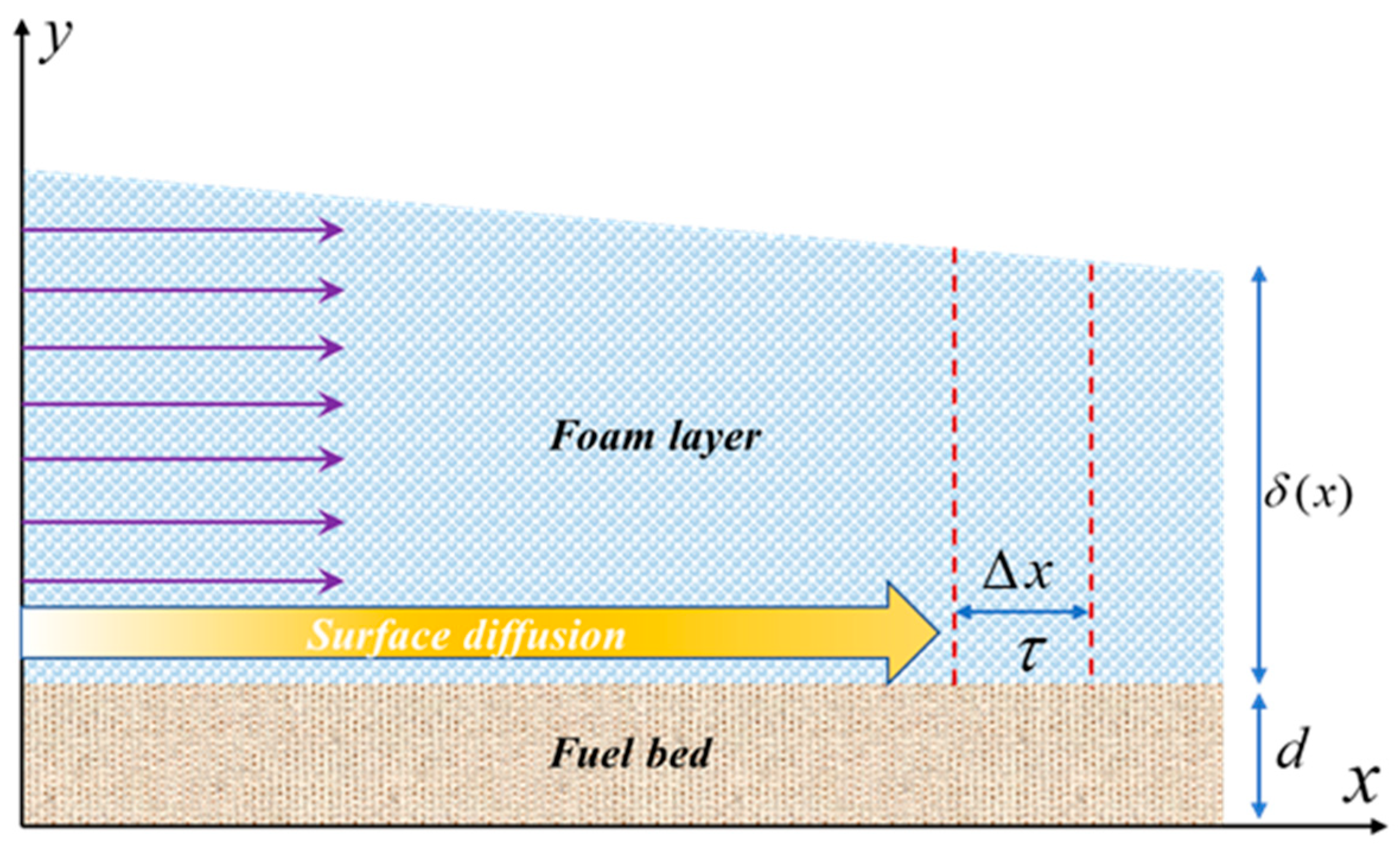
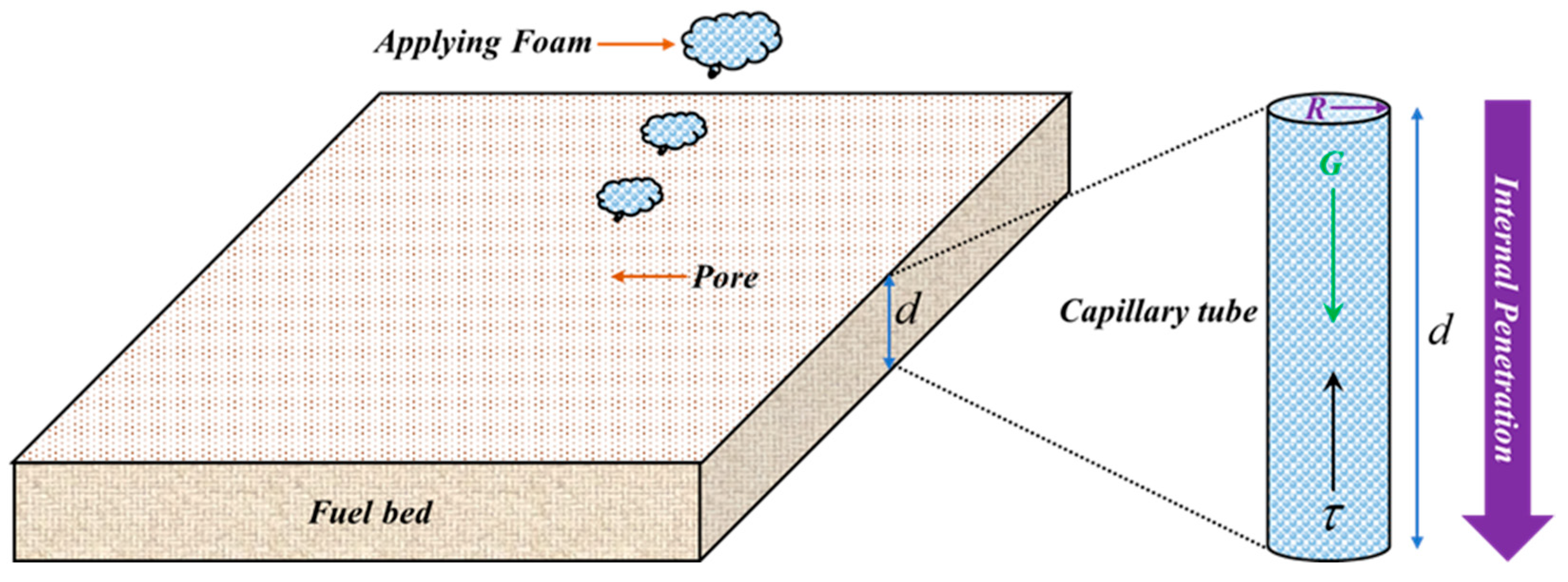
4.1. Diffusion and Penetration of Foam
4.2. Control and Extinction Fire Characteristic Indicators
4.3. Multi-Criteria Comprehensive Evaluation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Prăvălie, R. Major perturbations in the Earth’s forest ecosystems. Possible implications for global warming. Earth Sci. Rev. 2018, 185, 544–571. [Google Scholar] [CrossRef]
- Anthwal, A.; Gupta, N.; Sharma, A.; Anthwal, S.; Kim, K.-H. Conserving biodiversity through traditional beliefs in sacred groves in Uttarakhand Himalaya, India. Resour. Conserv. Recycl. 2010, 54, 962–971. [Google Scholar] [CrossRef]
- Ekins, P.; Simon, S.; Deutsch, L.; Folke, C.; De Groot, R. A framework for the practical application of the concepts of critical natural capital and strong sustainability. Ecol. Econ. 2003, 44, 165–185. [Google Scholar] [CrossRef]
- Rihan, M.; Bindajam, A.A.; Talukdar, S.; Shahfahad; Naikoo, M.W.; Mallick, J.; Rahman, A. Forest fire susceptibility mapping with sensitivity and uncertainty analysis using machine learning and deep learning algorithms. Adv. Space Res. 2023, 72, 426–443. [Google Scholar] [CrossRef]
- Gajendiran, K.; Kandasamy, S.; Narayanan, M. Influences of wildfire on the forest ecosystem and climate change: A comprehensive study. Environ. Res. 2024, 240, 117537. [Google Scholar] [CrossRef]
- Tan, C.; Feng, Z. Mapping forest fire risk zones using machine learning algorithms in Hunan province, China. Sustainability 2023, 15, 6292. [Google Scholar] [CrossRef]
- Benfer, M.; Williams, E. Assessing the impact of fire extinguisher agents on cultural resource materials. Fire Technol. 2018, 54, 289–311. [Google Scholar] [CrossRef]
- Stern, J.; Routley, J.G. Class A foam for structural firefighting. In Federal Emergency Management Agency; US Fire Administration: Emmitsburg, MD, USA, 1997. [Google Scholar]
- Dahlbom, S.; Mallin, T.; Bobert, M. Fire test performance of eleven PFAS-free class B firefighting foams varying fuels, admixture, water types and foam generation techniques. Fire Technol. 2022, 58, 1639–1665. [Google Scholar] [CrossRef]
- Jahura, F.T.; Setiawan, H.; Yildiz, D.; Yu, J.; Turek, E.; Liyanaarachchi, S.; Yu, B.; Peiris, T.; Wijayawardena, H.; Sarker, F. Exploring the Prospects and Challenges of Fluorine-Free Firefighting Foams (F3) as Alternatives to Aqueous Film-Forming Foams (AFFF): A Review. ACS Omega 2024, 9, 37430–37444. [Google Scholar] [CrossRef]
- Kim, A.K.; Crampton, G.P. Evaluation of the fire suppression effectiveness of manually applied compressed-air-foam (CAF) system. Fire Technol. 2012, 48, 549–564. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, F.; Cheng, X.; Chen, T.; Gou, H.; Tao, J.; Lu, Z.; He, K. Multi-scale experimental study on properties of compressed air foam and pressure drop in the long-distance vertical pipe. J. Build. Eng. 2024, 96, 110397. [Google Scholar] [CrossRef]
- Dong, S.; Lu, X.; Wang, D.; Wang, H.; Zheng, K.; Shi, Q.; Chen, M. Experimental investigation of the fire-fighting characteristics of aqueous foam in underground goaf. Process Saf. Environ. Prot. 2017, 106, 239–245. [Google Scholar] [CrossRef]
- Wang, K.; Fang, J.; Shah, H.R.; Mu, S.; Lang, X.; Wang, J.; Zhang, Y. A theoretical and experimental study of extinguishing compressed air foam on an n-heptane storage tank fire with variable fuel thickness. Process Saf. Environ. Prot. 2020, 138, 117–129. [Google Scholar] [CrossRef]
- Wu, C.; Zhou, T.; Chen, B.; Liu, Y.; Liang, P. Experimental study on burning characteristics of the large-scale transformer oil pool fire with different extinguishing methods. Fire Technol. 2021, 57, 461–481. [Google Scholar] [CrossRef]
- Zhang, J.; Shang, F.; Zhang, S.; Wang, L.; Ke, Y.; Huang, J.; Su, W.; Liu, R.; Sheng, Y. Research on Key Parameters and Fire Extinguishing Effectiveness of Compressed Air Foam System Used for UHV Substation. Fire Technol. 2024. [Google Scholar] [CrossRef]
- Rappsilber, T.; Below, P.; Krüger, S. Wood crib fire tests to evaluate the influence of extinguishing media and jet type on extinguishing performance at close range. Fire Saf. J. 2019, 106, 136–145. [Google Scholar] [CrossRef]
- Huang, C.; Dai, Z.; Jiang, Z.; Chen, Y.; Zhong, M. Wood stack fire tests to evaluate the influence of extinguishing medium and driving pressure on fire extinguishing efficacy of forest trees. Therm. Sci. Eng. Prog. 2024, 49, 102464. [Google Scholar] [CrossRef]
- Dai, Z.; Huang, C.; Chen, Y.; Zhong, M.; He, W. Experimental study on fire extinguishing efficiency of polymer hydrogel fire extinguishing agent in pine-fire mixed coniferous forest fires. Case Stud. Therm. Eng. 2024, 64, 105413. [Google Scholar] [CrossRef]
- Qiao, Y.; Zhang, H.; Yang, J.; Chen, H.; Liu, N.; Xu, M.; Zhang, L. Transition from smouldering to flaming combustion of pine needle fuel beds under natural convection. Proc. Combust. Inst. 2024, 40, 105343. [Google Scholar] [CrossRef]
- Guo, H.; Xiang, D.; Kong, L.; Gao, Y.; Zhang, Y. Upslope fire spread and heat transfer mechanism over a pine needle fuel bed with different slopes and winds. Appl. Therm. Eng. 2023, 229, 120605. [Google Scholar] [CrossRef]
- Sullivan, A.L.; Surawski, N.; Crawford, D.; Hurley, R.; Volkova, L.; Weston, C.; Meyer, C. Effect of woody debris on the rate of spread of surface fires in forest fuels in a combustion wind tunnel. For. Ecol. Manag. 2018, 424, 236–245. [Google Scholar] [CrossRef]
- Mueller, E.V.; Gallagher, M.R.; Skowronski, N.; Hadden, R.M. Convective heat transfer in pine forest litter beds. Int. J. Heat Mass Transf. 2022, 195, 123057. [Google Scholar] [CrossRef]
- Morvan, D.; Dupuy, J.-L. Modeling of fire spread through a forest fuel bed using a multiphase formulation. Combust. Flame 2001, 127, 1981–1994. [Google Scholar] [CrossRef]
- Tian, F.; Fang, J.; Tao, S.; Wang, K.; Shah, H.R.; Lang, X.; Tian, Z.; Tang, F. Flame spreading and burning of high-and low-flash point fuels under compressed air foam suppression. Case Stud. Therm. Eng. 2024, 64, 105527. [Google Scholar] [CrossRef]
- Tian, F.; Fang, J.; Fang, L.; Shah, H.R.; Lang, X.; Tian, Z.; Tang, F. Experimental study on mass loss mechanism and cooling effect of compressed air foam on fuel surface at different temperatures. Case Stud. Therm. Eng. 2023, 52, 103747. [Google Scholar] [CrossRef]
- Zhang, J.; Shang, F.; Wang, L.; Su, W.; Kong, D.; Wang, D.; Guo, Y. Effect of the foam flow rate on extinguishing process for low-expansion foam AFFF, FP, and S based on CAF system. Therm. Sci. Eng. Prog. 2024, 53, 102737. [Google Scholar] [CrossRef]
- Zhou, B.; Yang, W.; Yoshioka, H.; Chen, T.; Wang, K.; Hao, D.; Jiang, C.; Cui, K. Research on suppression effectiveness of compressed air foam for oil-immersed transformer hot oil fire. Case Stud. Therm. Eng. 2023, 49, 103272. [Google Scholar] [CrossRef]
- Chen, T.; Fu, X.-C.; Bao, Z.-M.; Xia, J.-J.; Wang, R.-J. Experimental study on the extinguishing efficiency of compressed air foam sprinkler system on oil pool fire. Procedia Eng. 2018, 211, 94–103. [Google Scholar] [CrossRef]
- Xu, Z.; Guo, X.; Yan, L.; Kang, W. Fire-extinguishing performance and mechanism of aqueous film-forming foam in diesel pool fire. Case Stud. Therm. Eng. 2019, 17, 100578. [Google Scholar] [CrossRef]
- Ding, F.; Kang, W.; Yan, L.; Xu, Z.; Guo, X. Influence of gas–liquid ratio on the fire-extinguishing efficiency of compressed gas protein foam in diesel pool fire. J. Therm. Anal. Calorim. 2021, 146, 1465–1472. [Google Scholar] [CrossRef]
- Carrier, V.; Destouesse, S.; Colin, A. Foam drainage: A film contribution? Phys. Rev. E 2002, 65, 061404. [Google Scholar] [CrossRef] [PubMed]
- Kruglyakov, P.M.; Karakashev, S.I.; Nguyen, A.V.; Vilkova, N.G. Foam drainage. Curr. Opin. Colloid Interface Sci. 2008, 13, 163–170. [Google Scholar] [CrossRef]
- Wang, J.; Nguyen, A.V.; Farrokhpay, S. A critical review of the growth, drainage and collapse of foams. Adv. Colloid Interface Sci. 2016, 228, 55–70. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Zhang, Q. A significant review of froth stability in mineral flotation. Chem. Eng. Sci. 2024, 302 Pt A, 120738. [Google Scholar] [CrossRef]
- Gu, M.; Mohanty, K.K. Rheology of polymer-free foam fracturing fluids. J. Pet. Sci. Eng. 2015, 134, 87–96. [Google Scholar] [CrossRef]
- Bashir, A.; Haddad, A.S.; Rafati, R. An experimental investigation of dynamic viscosity of foam at different temperatures. Chem. Eng. Sci. 2022, 248, 117262. [Google Scholar] [CrossRef]
- Faroughi, S.A.; Pruvot, A.J.-C.J.; McAndrew, J. The rheological behavior of energized fluids and foams with application to hydraulic fracturing. J. Pet. Sci. Eng. 2018, 163, 243–263. [Google Scholar] [CrossRef]
- Conroy, M.W.; Ananth, R. Fuel surface cooling by aqueous foam: A pool fire suppression mechanism. Fire Technol. 2015, 51, 667–689. [Google Scholar] [CrossRef]
- Tian, F.; Fang, J.; Shah, H.R.; Lang, X.; Tian, Z.; Tang, F. Experimental Study on Foam Spreading on Fuel Layers with Different Thicknesses. Fire Technol. 2024. [Google Scholar] [CrossRef]
- Fay, J.A. Physical processes in the spread of oil on a water surface. In Proceedings of the International Oil Spill Conference, Online, 10–14 May 2021; Volume 1971, pp. 463–467. [Google Scholar]





| Fuel Load (kg/m2) | Fuel Depth (cm) | Bulk Density (g/cm3) |
|---|---|---|
| 3.0 | 14.8 | 0.203 |
| Storage Temperature (°C) | Fire-Extinguishing Mixture Ratio (%) | Thermal Insulation Mixture Ratio (%) |
|---|---|---|
| −5~50 | 0.5 | 1 |
| Foam Expansion Ratio | Fitting Parameters | ||
|---|---|---|---|
| K | n | R2 | |
| 5.1 | 3.06 | 0.54 | 0.95 |
| 10.9 | 4.31 | 0.55 | 0.96 |
| 15.1 | 4.49 | 0.60 | 0.98 |
| 20.6 | 4.68 | 0.61 | 0.98 |
| 25.4 | 4.78 | 0.62 | 0.98 |
| Foam expansion ratio | 5.6 | 10.9 | 15.1 | 20.6 | 25.4 |
| Foam coverage extinguishing time [s] (SD) | 128(10) | 114(7) | 68(12) | 56(15) | 45(9) |
| Foam Expansion Ratio | 5.6 | 10.9 | 15.1 | 20.6 | 25.4 |
|---|---|---|---|---|---|
| Reignition resistance time [s] (SD) | - | - | - | 154(9) | 126(7) |
| Foam Expansion Ratio | Foam Coverage and Extinguishing Capability (Normalization) | Cooling Capability (Normalization) | Re-Ignition Resistance Capability (Normalization) |
|---|---|---|---|
| 5.6 | 0 | 1 | 1 |
| 10.9 | 0.1613 | 0.8398 | 1 |
| 15.1 | 0.7097 | 0.5542 | 1 |
| 20.6 | 0.7742 | 0.0286 | 0 |
| 25.4 | 1 | 0 | 0 |
| Foam expansion ratio | 5.6 | 10.9 | 15.1 | 20.6 | 25.4 |
| S | 0.6 | 0.6604 | 0.7471 | 0.2649 | 0.33 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Zhang, J.; Zhong, H.; Chen, L. Study on the Influence of Expansion Ratio on the Effectiveness of Foam in Suppressing Forest Surface Fires. Fire 2025, 8, 171. https://doi.org/10.3390/fire8050171
Wang H, Zhang J, Zhong H, Chen L. Study on the Influence of Expansion Ratio on the Effectiveness of Foam in Suppressing Forest Surface Fires. Fire. 2025; 8(5):171. https://doi.org/10.3390/fire8050171
Chicago/Turabian StyleWang, Haiyan, Junzhao Zhang, Hongbin Zhong, and Lei Chen. 2025. "Study on the Influence of Expansion Ratio on the Effectiveness of Foam in Suppressing Forest Surface Fires" Fire 8, no. 5: 171. https://doi.org/10.3390/fire8050171
APA StyleWang, H., Zhang, J., Zhong, H., & Chen, L. (2025). Study on the Influence of Expansion Ratio on the Effectiveness of Foam in Suppressing Forest Surface Fires. Fire, 8(5), 171. https://doi.org/10.3390/fire8050171






