Estimating Maximum Dwell Time for Firefighting Teams Based on Ambient Temperature and Radiant Heat Exposure
Abstract
1. Introduction
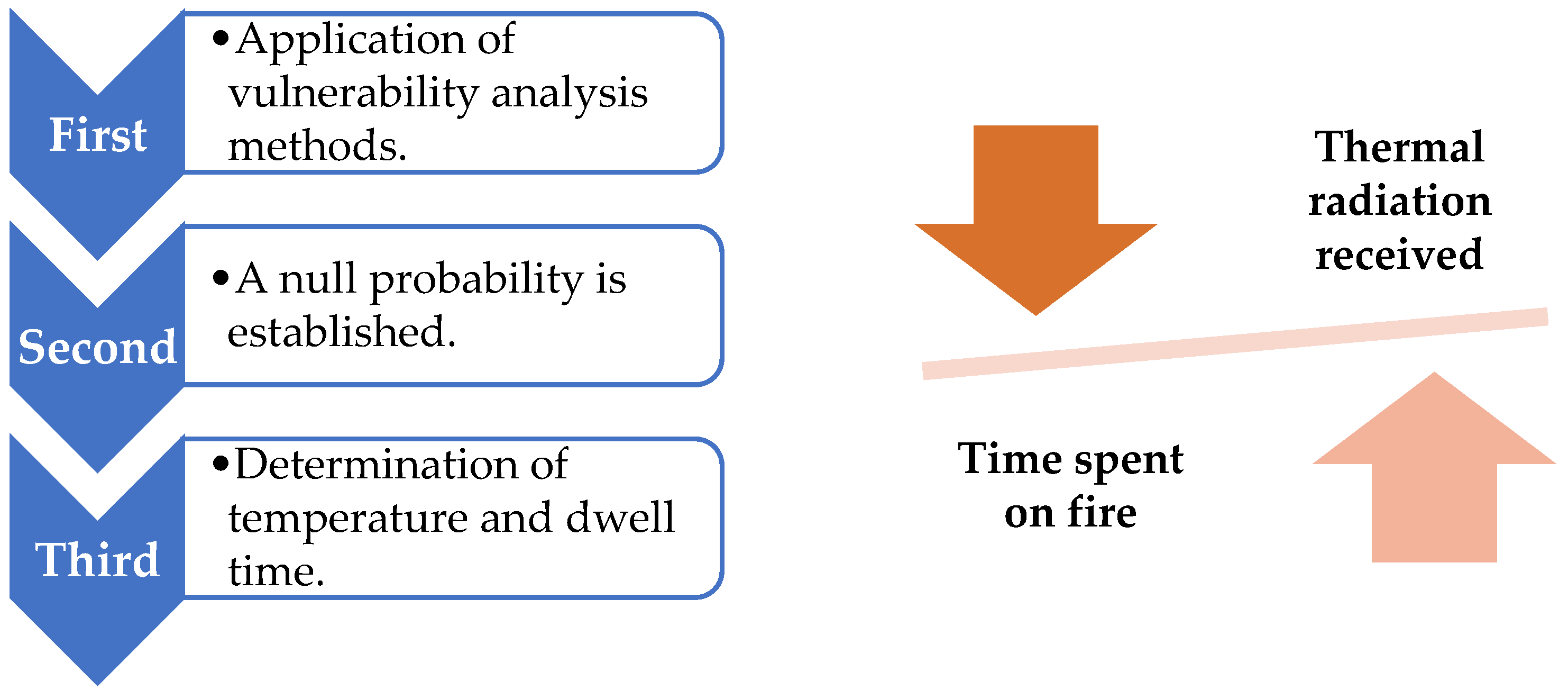
2. Method
Theory and Calculation
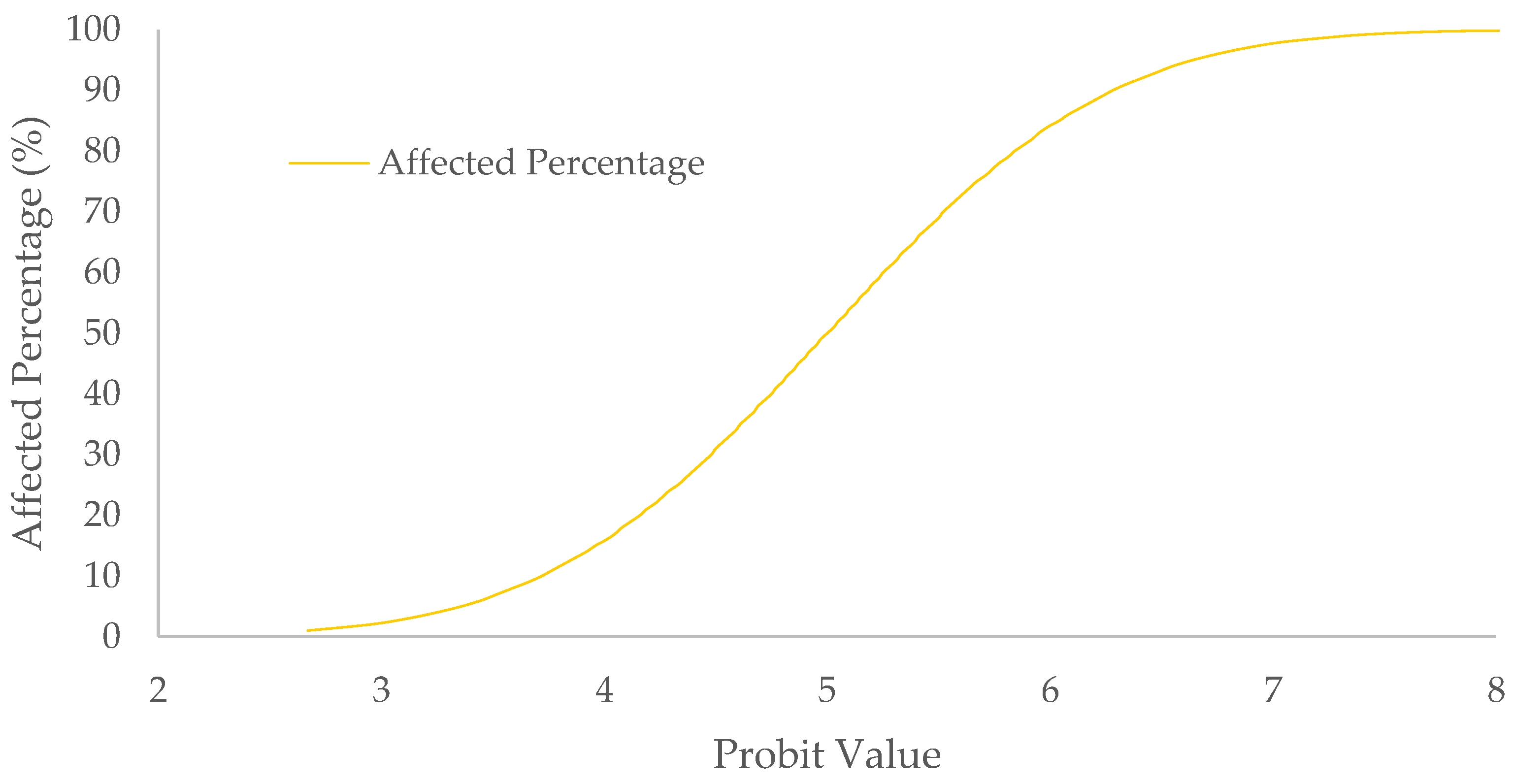
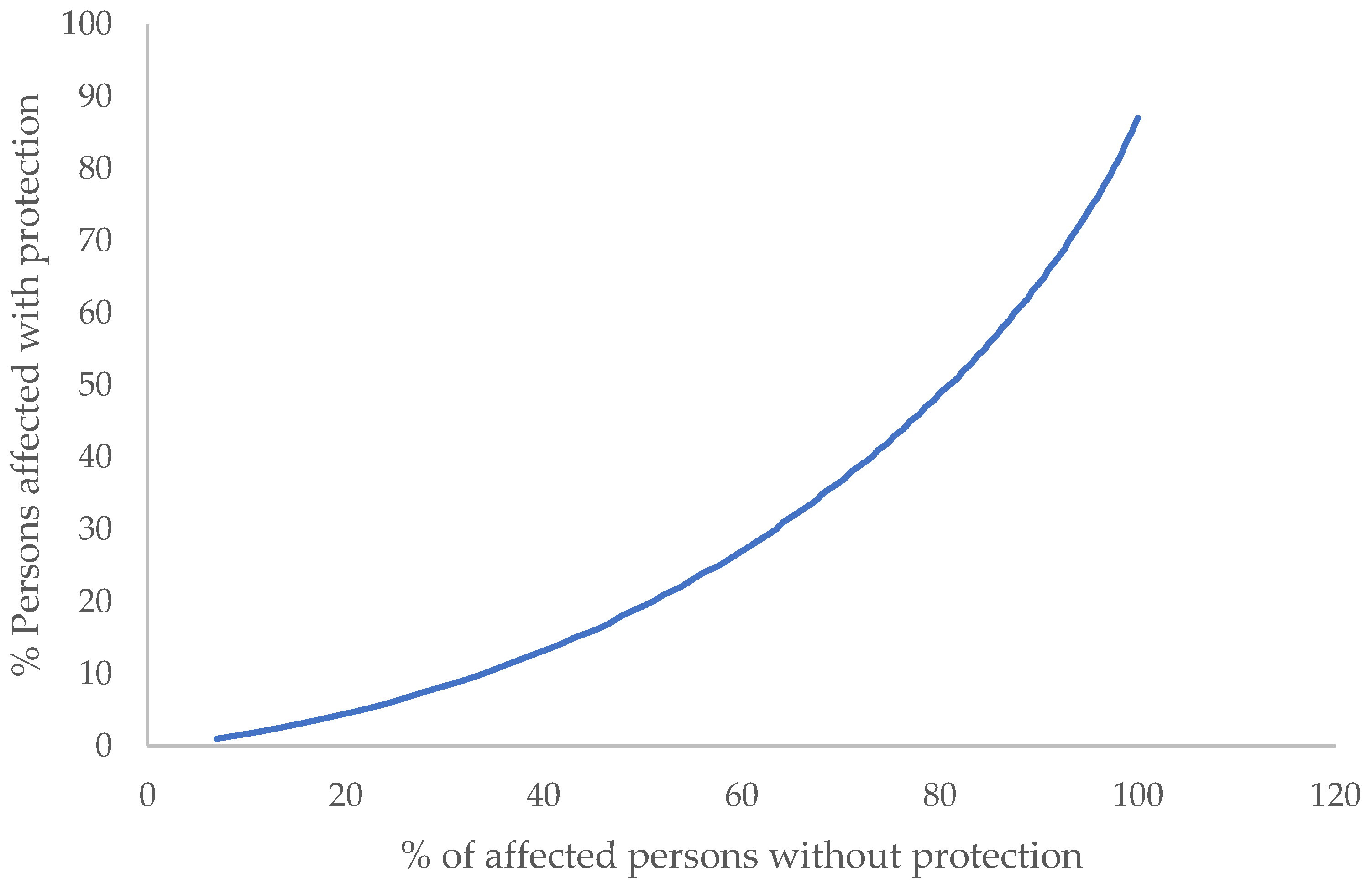
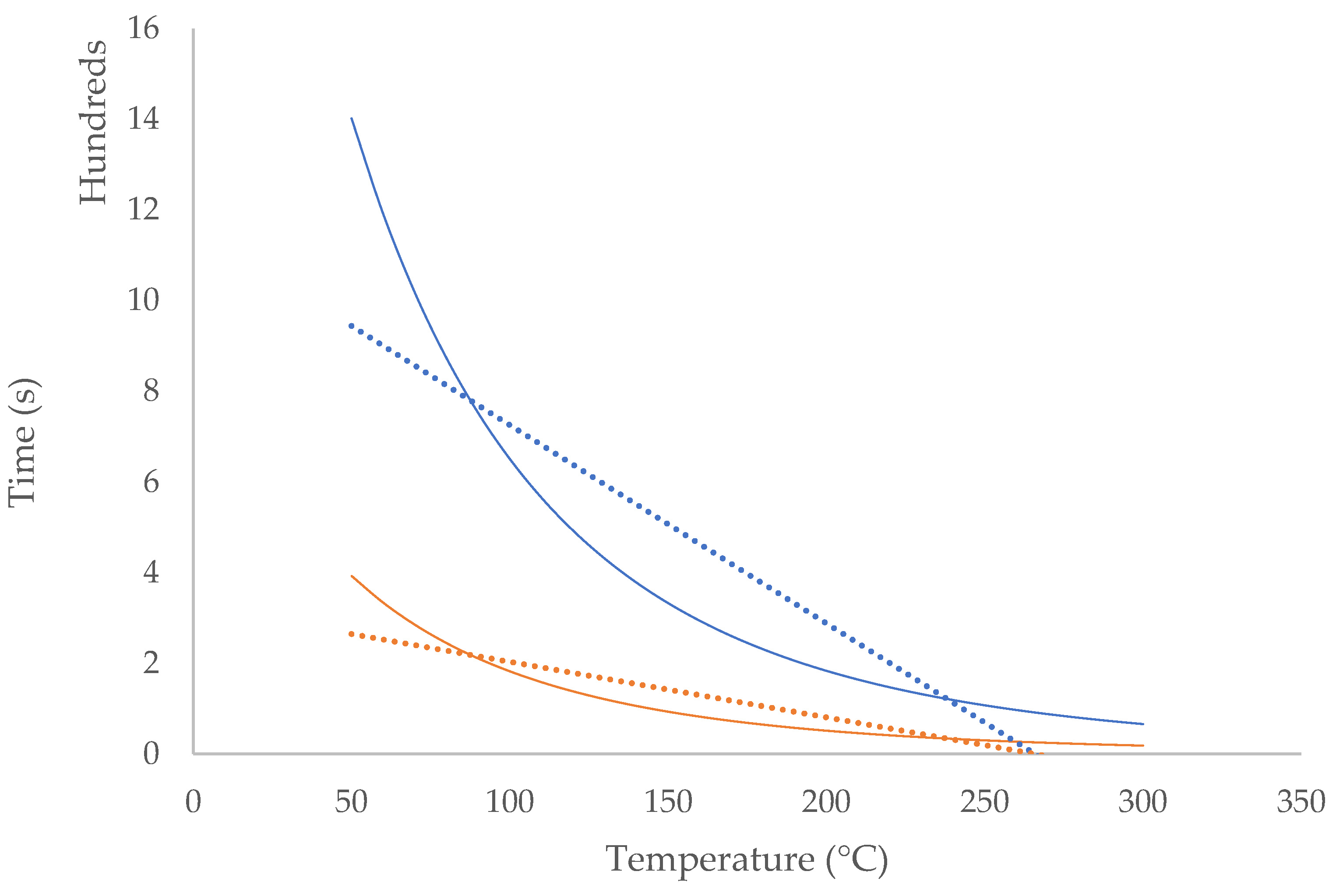
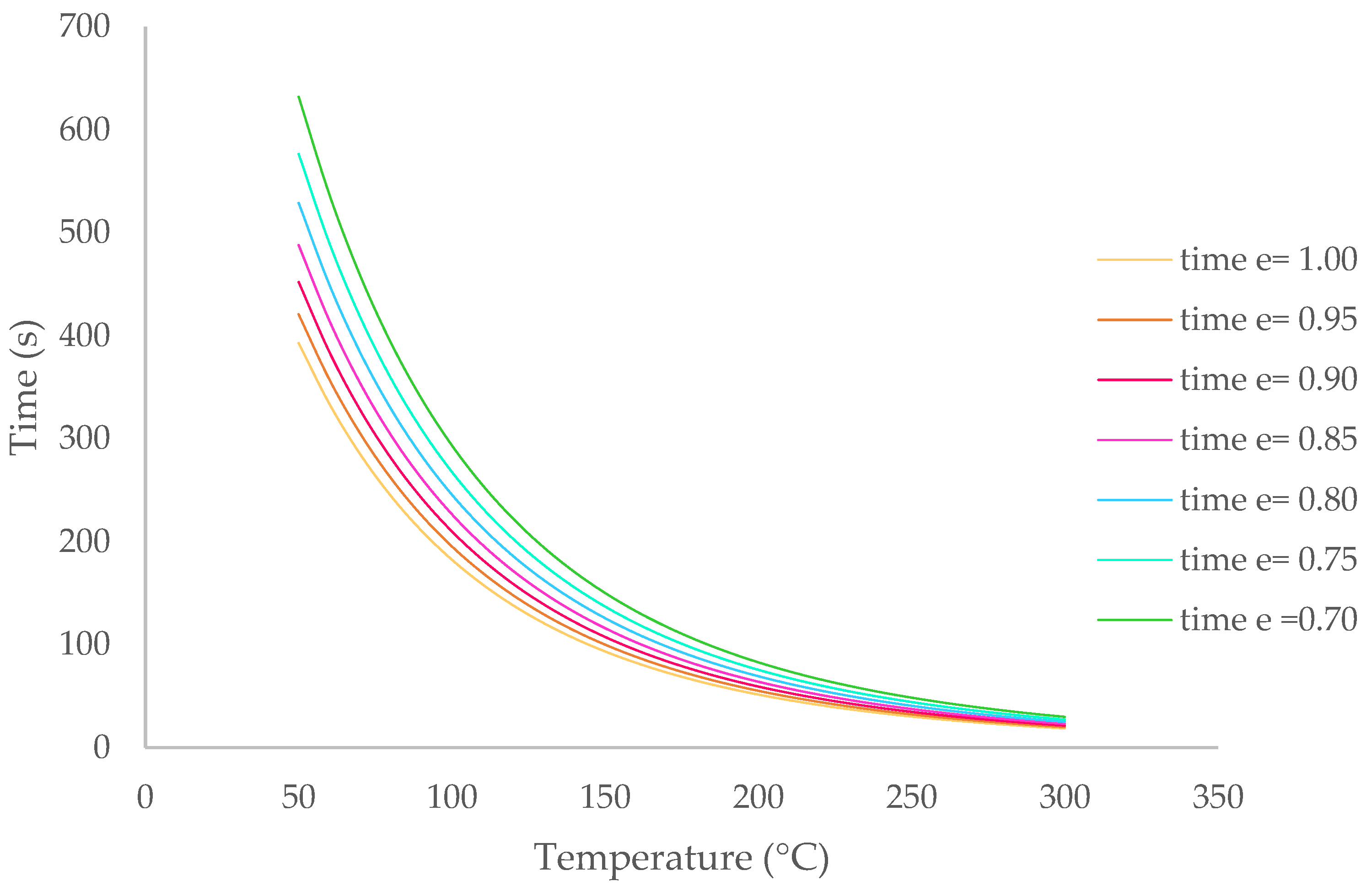
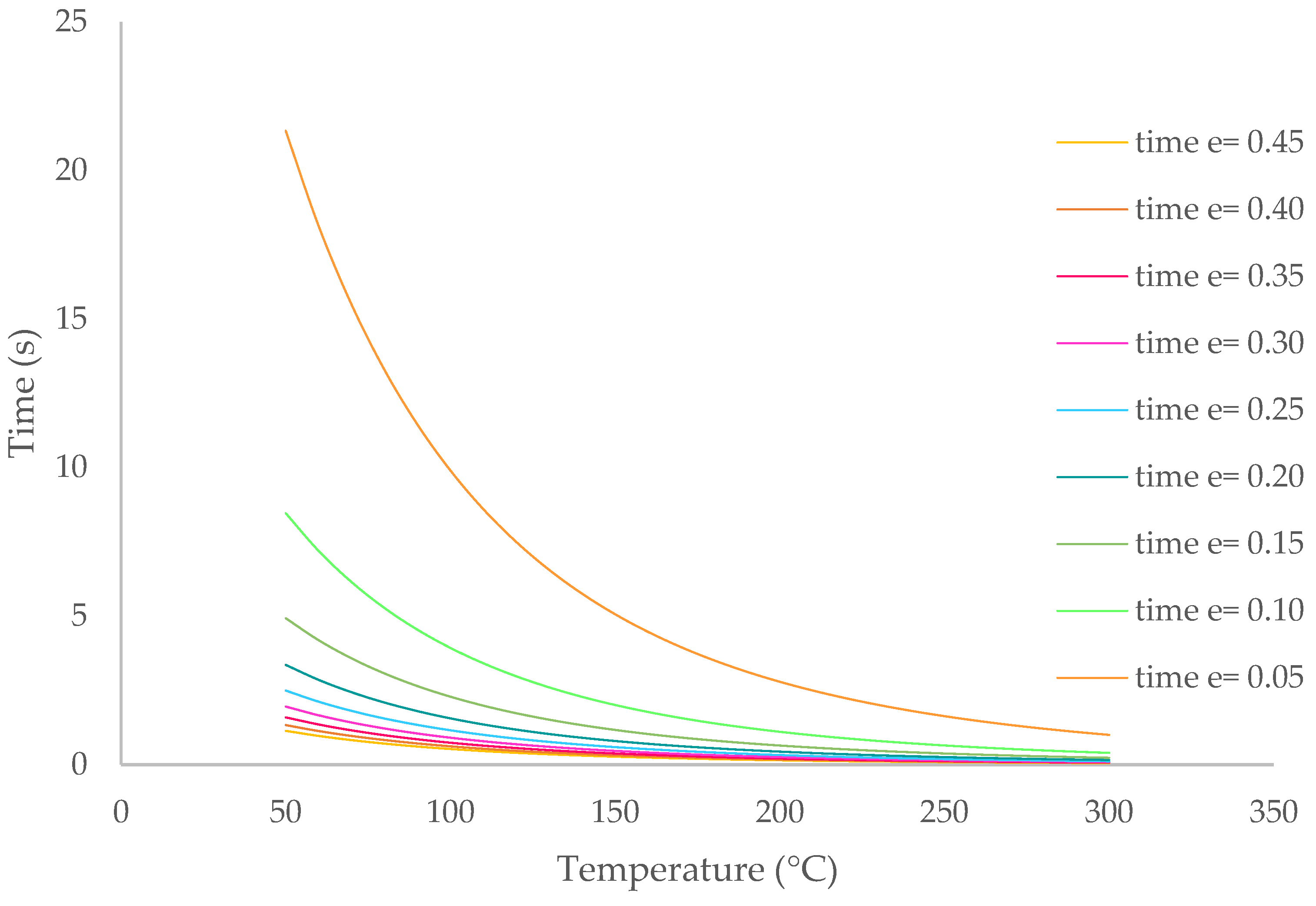
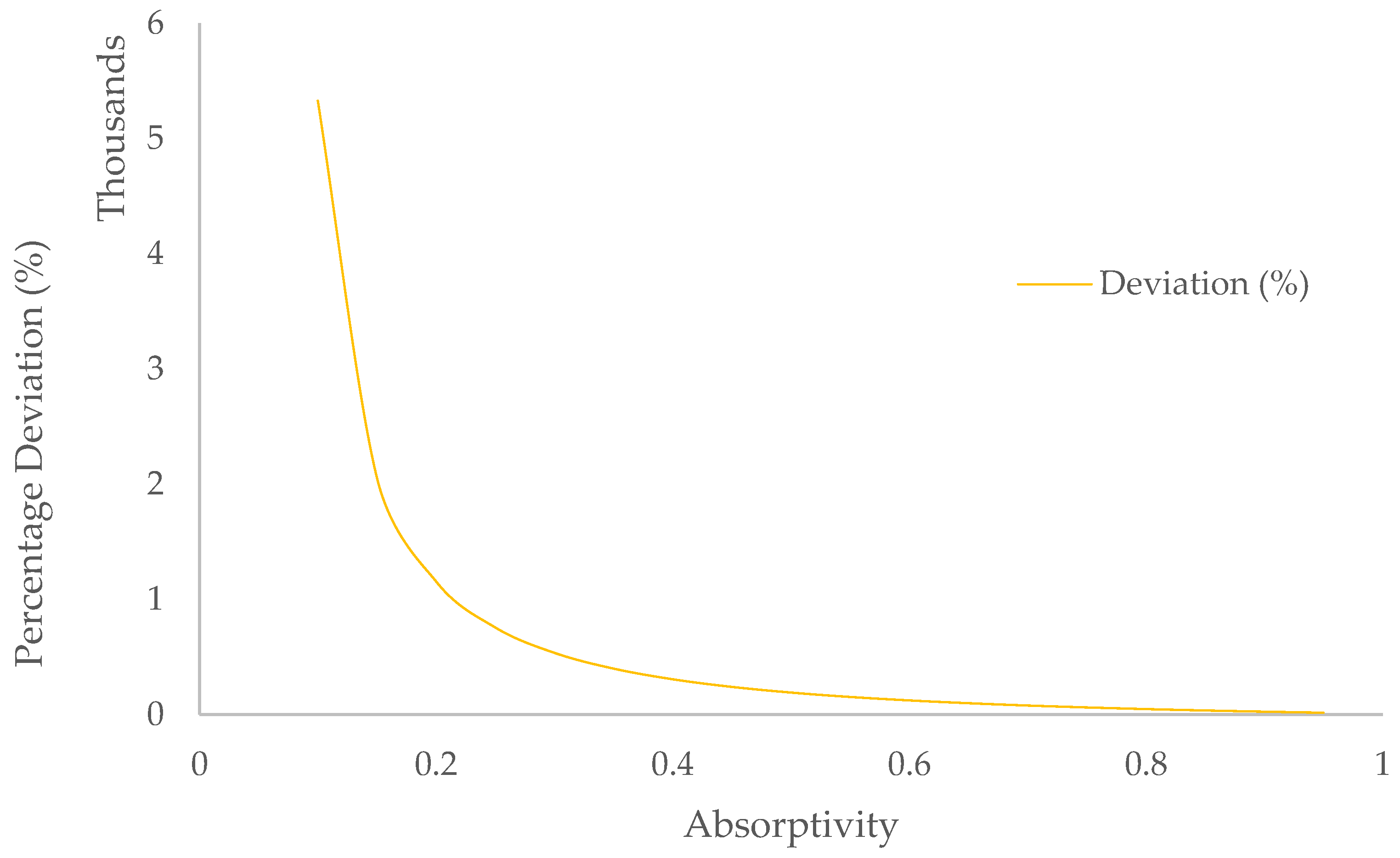
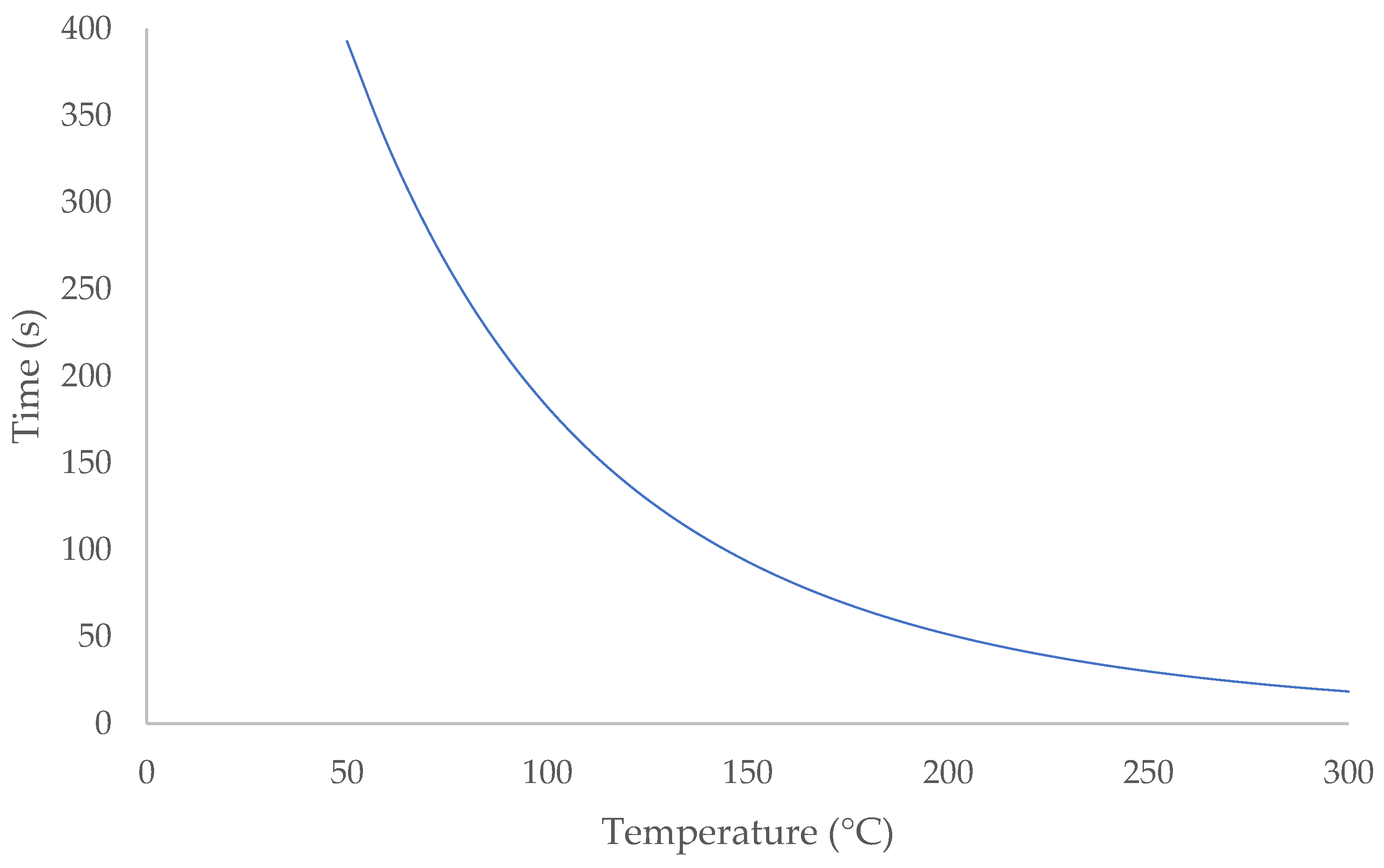
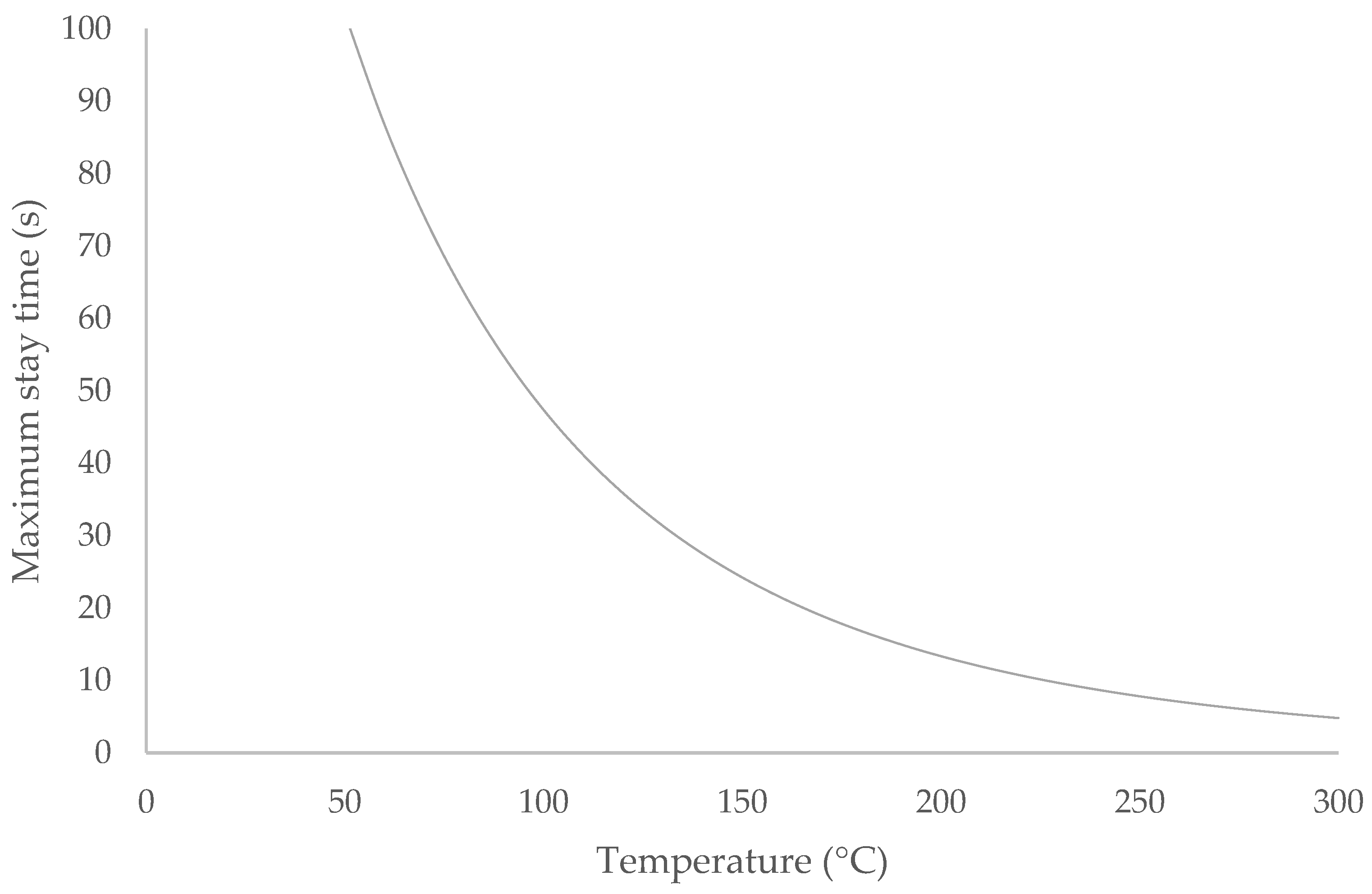
3. Results
- -
- For second-degree burns:
- -
- For first-degree burns:
- -
- For second-degree burns:
- -
- For first-degree burns:
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Park, H.; Meacham, B.J.; Dembsey, N.A.; Goulthorpe, M. Integration of Fire Safety and Building Design. Build. Res. Inf. 2014, 42, 696–709. [Google Scholar] [CrossRef]
- Bjelland, H.; Njå, O.; Heskestad, A.W.; Braut, G.S. The Concepts of Safety Level and Safety Margin: Framework for Fire Safety Design of Novel Buildings. Fire Technol. 2015, 51, 409–441. [Google Scholar] [CrossRef]
- Maluk, C.; Woodrow, M.; Torero, J.L. The Potential of Integrating Fire Safety in Modern Building Design. Fire Saf. J. 2017, 88, 104–112. [Google Scholar] [CrossRef]
- Song, L.Z.; Zhu, J.; Liu, S.T.; Qu, Z.J. Recent Fire Safety Design of High-Rise Buildings. J. Urban Dev. Manag. 2022, 1, 50–57. [Google Scholar] [CrossRef]
- Schüller, J.C.H.; Brinkman, J.L.; Van Gestel, P.J.; Van Otterloo, R.W. Methods for Determining and Processing Probabilities. In Red Book; CPR 12E; Committee for the Prevention of Disasters by Hazardous Materials, Ministry of Transport, Public Works and Water Management: Holland, The Netherlands, 1997; ISBN 9012085438. [Google Scholar]
- Cowlard, A.; Bittern, A.; Abecassis-Empis, C.; Torero, J. Fire Safety Design for Tall Buildings. Procedia Eng. 2013, 62, 169–181. [Google Scholar] [CrossRef]
- Fu, F. Fire Safety Design for Tall Buildings, 1st ed.; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar] [CrossRef]
- Cvetković, V.M.; Dragašević, A.; Protić, D.; Janković, B.; Nikolić, N.; Milošević, P. Fire Safety Behavior Model for Residential Buildings: Implications for Disaster Risk Reduction. Int. J. Disaster Risk Reduct. 2022, 76, 102981. [Google Scholar] [CrossRef]
- Cuenca, M.F.; Ramírez, C.O. Occupational Hazards in Firefighting: Systematic Literature Review. Saf. Health Work 2023, 14, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Burke, P. Preventing Firefighter Exposure Hazards. Doctoral Thesis, Naval Postgraduate School, Monterey, CA, USA, 2017. Available online: https://hdl.handle.net/10945/56108 (accessed on 6 March 2024).
- Kobes, M.; Helsloot, I.; De Vries, B.; Post, J.G. Building Safety and Human Behaviour in Fire: A Literature Review. Fire Saf. J. 2010, 45, 1–11. [Google Scholar] [CrossRef]
- Tan, L.; Hu, M.; Lin, H. Agent-Based Simulation of Building Evacuation: Combining Human Behavior with Predictable Spatial Accessibility in a Fire Emergency. Inf. Sci. 2015, 295, 53–66. [Google Scholar] [CrossRef]
- Jevtic, R.B. Fire and Evacuation in High Residential Buildings. Facta Univ. Ser. Work. Living Environ. Prot. 2019, 15, 123–134. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, Y.; Ding, S.; Huang, X. Optimizing Phased-Evacuation Strategy for High-Rise Buildings in Fire. J. Build. Eng. 2024, 95, 110084. [Google Scholar] [CrossRef]
- Dabous, S.A.; Shikhli, A.; Shareef, S.; Mushtaha, E.; Obaideen, K.; Alsyouf, I. Fire Prevention and Mitigation Technologies in High-Rise Buildings: A Bibliometric Analysis from 2010 to 2023. Ain Shams Eng. J. 2024, 15, 103010. [Google Scholar] [CrossRef]
- Kong, D.; Zhao, X.; Chen, J.; Yang, H.; Du, J. Study on Hazard Characteristics and Safety Distance of Small-Scale Boilover Fire. Int. J. Therm. Sci. 2021, 164, 106888. [Google Scholar] [CrossRef]
- Rossi, J.L.; Simeoni, A.; Moretti, B.; Leroy-Cancellieri, V. An Analytical Model Based on Radiative Heating for the Determination of Safety Distances for Wildland Fires. Fire Saf. J. 2011, 46, 520–527. [Google Scholar] [CrossRef]
- Shi, L.; Chew, M.Y.L.; Liu, X.; Cheng, X.; Wang, B.; Zhang, G. An Experimental and Numerical Study on Fire Behaviors of Charring Materials Frequently Used in Buildings. Energy Build. 2017, 138, 140–153. [Google Scholar] [CrossRef]
- Thevega, T.; Jayasinghe, J.A.S.C.; Robert, D.; Bandara, C.S.; Kandare, E.; Setunge, S. Fire Compliance of Construction Materials for Building Claddings: A Critical Review. Constr. Build. Mater. 2022, 361, 129582. [Google Scholar] [CrossRef]
- European Union. Council Directive 96/82/EC of 9 December 1996 on the Control of Major-Accident Hazards Involving Dangerous Substances. Available online: http://data.europa.eu/eli/dir/1996/82/oj (accessed on 12 March 2024).
- Real Decreto 1196/2003, de 19 de Septiembre, por el que se Aprueba la Directriz Básica de Protección Civil para el Control y Planificación ante el Riesgo de Accidentes Graves en los que Intervienen Sustancias Peligrosas. Ministerio del Interior, Gobierno de España. 2003. Available online: https://www.boe.es/eli/es/rd/2003/09/19/1196/con (accessed on 2 April 2024).
- Águeda, A.; Pastor, E.; Pérez, Y.; Planas, E. Experimental Study of the Emissivity of Flames Resulting from the Combustion of Forest Fuels. Int. J. Therm. Sci. 2010, 49, 543–554. [Google Scholar] [CrossRef]
- Sikanen, T.; Hostikka, S. Modeling and Simulation of Liquid Pool Fires with In-Depth Radiation Absorption and Heat Transfer. Fire Saf. J. 2016, 80, 95–109. [Google Scholar] [CrossRef]
- Mercx, W.P.M.; Van den Berg, A.C. Vapour Cloud Explosion in Methods for the Calculation of Physical Effects of the Escape of Dangerous Material (Liquids and Gases). In Yellow Book; CPE 14E; Ministry of Social Affairs and Employment: Holland, The Netherlands, 2005; Available online: https://rapidn.jrc.ec.europa.eu/reference/72 (accessed on 14 March 2024).
- Liu, J.; Li, J.; Fan, C. A Bibliometric Study of Pool Fire Related Publications. J. Loss Prev. Process. Indust. 2020, 63, 104030. [Google Scholar] [CrossRef]
- Finney, M.A.; Grumstrup, T.P.; Grenfell, I. Flame Characteristics Adjacent to a Stationary Line Fire. Combust. Sci. Technol. 2022, 194, 2212–2232. [Google Scholar] [CrossRef]
- Chen, Y.; Fang, J.; Zhang, X.; Miao, Y.; Lin, Y.; Tu, R.; Hu, L. Pool Fire Dynamics: Principles, Models and Recent Advances. Prog. Energy Combust. Sci. 2023, 95, 101070. [Google Scholar] [CrossRef]
- Rhatigan, J.L.; Bedir, H.; James, S. Gas-Phase Radiative Effects on the Burning and Extinction of a Solid Fuel. Combust. Flame 1998, 112, 231–241. [Google Scholar] [CrossRef]
- Gonome, H.; Takagi, Y.; Nagao, T.; Ono, M. Effect of Soot on Thermal Radiation Shielding Performance of Water Mist. Fire Saf. J. 2021, 123, 103363. [Google Scholar] [CrossRef]
- Hightower, M.; Gritzo, L.; Luketa-Hanlin, A.; Covan, J.; Tieszen, S.; Wellman, G.; Irwin, M.; Kanesshige, M.; Melof, B.; Morrow, C.; et al. Guidance on Risk Analysis and Safety Implications of a Large Liquefied Natural Gas (LNG) Spill over Water; Sandia National Laboratories: Albuquerque, NM, USA, 2004; p. 167. Available online: https://www.osti.gov/servlets/purl/882343 (accessed on 29 April 2024).
- Page, W.G.; Butler, B.W. An Empirically Based Approach to Defining Wildland Firefighter Safety and Survival Zone Separation Distances. Int. J. Wildland Fire 2017, 26, 655–667. [Google Scholar] [CrossRef]
- Raj, P.K. A Review of the Criteria for People Exposure to Radiant Heat Flux from Fires. J. Hazard. Mater. 2008, 159, 61–71. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.H.; Wang, W.C.; Wang, K.C.; Shih, S.Y. Applying Building Information Modeling to Support Fire Safety Management. Autom. Constr. 2015, 59, 158–167. [Google Scholar] [CrossRef]
- Anikin, S.N.; Danilov, M.M.; Denisov, A.N. The Management of Alternatives of Choosing in Reference Decision Making in Fire Extinguishing Tactics. Comput. Nanotechnol. 2020, 7, 39–47. [Google Scholar] [CrossRef]
- Sullivan, E.A.; McDonald, A.G. Mathematical Model and Sensor Development for Measuring Energy Transfer from Wildland Fires. Int. J. Wildland Fire 2014, 23, 995–1004. [Google Scholar] [CrossRef]
- Asensio, M.I.; Cascón, J.M.; Prieto, D.; Ferragut, L. An Historical Review of the Simplified Physical Fire Spread Model PhyFire: Model and Numerical Methods. Appl. Sci. 2023, 13, 2035. [Google Scholar] [CrossRef]
- Hoddinott, J.; Quisumbing, A. Methods for Microeconometric Risk and Vulnerability Assessment. In Risk, Shocks, and Human Development: On the Brink; Palgrave Macmillan: London, UK, 2010; pp. 62–100. [Google Scholar]
- Ballantyne, E.R.; Hill, R.K.; Spencer, J.W. Probit Analysis of Thermal Sensation Assessments. Int. J. Biometeorol. 1977, 21, 29–43. [Google Scholar] [CrossRef] [PubMed]
- Andersson, K.; Johansson, R.; Hjärtstam, S.; Johnsson, F.; Leckner, B. Radiation Intensity of Lignite-Fired Oxy-Fuel Flames. Exp. Therm. Fluid Sci. 2008, 33, 67–76. [Google Scholar] [CrossRef]
- Landucci, G.; Cozzani, V.; Birk, M. Heat Radiation Effects. In Domino Effects in the Process Industries; Elsevier: Amsterdam, The Netherlands, 2013; pp. 70–115. [Google Scholar] [CrossRef]
- Sheikhani, H.; Ajam, H.; Ghazikhani, M. A Review of Flame Radiation Research from the Perspective of Factors Affecting the Flame Radiation, Measurement and Modeling. Eur. Phys. J. Plus 2020, 135, 343. [Google Scholar] [CrossRef]
- Zhou, K.; Wang, X. Thermal Radiation Modelling of Pool Fire with Consideration on the Nonuniform Temperature in Flame Volume. Int. J. Therm. Sci. 2019, 138, 12–23. [Google Scholar] [CrossRef]
- Casal, J.; Montiel, H.; Planas, E.; Vílchez, J.A. Análisis del Riesgo en Instalaciones Industriales; Ediciones Universidad Politécnica de Cataluña: Barcelona, Spain, 2021; ISBN 84-8301-227-8. [Google Scholar]
- Eisenberg, N.A.; Lynch, C.J.; Breeding, R.J. Vulnerability Model. A Simulation System for Assessing Damage Resulting from Marine Spills; Final Report No. AD-A-015245; Enviro Control, Inc.: Rockville, MD, USA, 1975. [Google Scholar]
- Resolución de 30 de Enero de 1991, por la que se Aprueba la Directriz Básica para la Elaboración y Homologación de los Planes Especiales del Sector Químico. Ministerio del Interior, Gobierno de España. 1991. Available online: https://www.boe.es/buscar/doc.php?id=BOE-A-1991-3208 (accessed on 11 March 2024).
- van Geel, P.L.B.A. Guideline for Quantitative Risk Assessment. In Methods for Determining Possible Damage: Methods for Determining Possible Damage to People and Goods Due to the Release of Hazardous Substances; TNO—The Netherlands Organization of Applied Scientific Research, Ministry of the Interior and Kingdom Relations, Hazardous Substances, Commission for Disaster Prevention: South Holland, The Netherlands, 2005. [Google Scholar]
- NFPA 59ª; Standard for the Production, Storage and Handling of Liquefied Natural Gas (LNG). National Fire Protection Association: Boston, MA, USA, 2019. Available online: https://img.antpedia.com/standard/files/pdfs_ora/20230614/NFPA/59A-2019.pdf (accessed on 15 April 2024).
- Grossel, S.S. Guidelines for Chemical Process Quantitative Risk Analysis. J. Loss Prev. Process. Indust. 2001, 14, 438–439. [Google Scholar] [CrossRef]
- Code of Federal Regulations, Title 49. NFPA 59A Standard and the Federal Regulation, 49 CFR Part 193, Liquefied Natural Gas Facilities, 45 FR 9203, 11 February, 1980. Available online: http://ecf.gov/current/title-49/subtitle-B/chapter-I/subchapter-D/part-193 (accessed on 15 April 2024).
- Code of Federal Regulations, 24 CFR, Section 51.204. Part 51: Environmental Criteria and Standards, 44 FR 40861, July 12 1979. Available online: http://ecf.gov/current/title-24/subtitle-A/part-51 (accessed on 15 April 2024).
- Uijt de Haag, P.A.M.; Ale, B.J.M. Guideline for Quantitative Risk Assessment. In Purple Book; CPR 18E; TNO—The Netherlands Organization of Applied Scientific Research, Ministry of the Interior and Kingdom Relations, Hazardous Substances, Commission for Disaster Prevention: South Holland, The Netherlands, 2005. [Google Scholar]
- Rossetto, T.; Ioannou, I.; Grant, D.N.; Maqsood, T. Guidelines for the Empirical Vulnerability Assessment; GEM Foundation: Pavia, Italy, 2014; Available online: https://discovery.ucl.ac.uk/id/eprint/1449624/ (accessed on 7 March 2024).
- Van den Bosch, C.J.H. Methods for the Calculations of the Physical Effects Due to Releases of Hazardous Materials (Liquids and Gases). In Yellow Book; CPR 14E; TNO—The Netherlands Organization of Applied Scientific Research, Ministry of Transport, Public Works and Water Management, Commission for Disaster Prevention: South Holland, The Netherlands, 1979. [Google Scholar]
- Center for Chemical Process Safety (CCPS). Guidelines for Chemical Process Quantitative Risk Analysis; American Institute of Chemical Engineers: New York, NY, USA, 2000. [Google Scholar]
- EN 469:2020; Protective Clothing for Firefighters—Performance Requirements for Protective Clothing for Firefighting Activities. European Committee for Standardization (CEN): Brussels, Belgium, 2020.
- EN 367:1994; Protective Clothing—Protection against Heat and Fire—Method of Determining Heat Transmission on Exposure to Flame. European Committee for Standardization (CEN): Brussels, Belgium, 1994.
- EN ISO 7933:2023; Ergonomics of the Thermal Environment—Analytical Determination and Interpretation of Heat Stress Using Calculation of the Predicted Heat Strain. European Committee for Standardization (CEN): Brussels, Belgium, 2023.
- EN ISO 7243:2017; Ergonomics of the Thermal Environment—Assessment of Heat Stress Using the WBGT (Wet Bulb Globe Temperature). European Committee for Standardization (CEN): Brussels, Belgium, 2017.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Romero-Barriuso, Á.; Ballesteros-Álvarez, J.M.; Villena-Escribano, B.M.; Fuentes-Bargues, J.L.; González-Gaya, C. Estimating Maximum Dwell Time for Firefighting Teams Based on Ambient Temperature and Radiant Heat Exposure. Fire 2025, 8, 89. https://doi.org/10.3390/fire8030089
Romero-Barriuso Á, Ballesteros-Álvarez JM, Villena-Escribano BM, Fuentes-Bargues JL, González-Gaya C. Estimating Maximum Dwell Time for Firefighting Teams Based on Ambient Temperature and Radiant Heat Exposure. Fire. 2025; 8(3):89. https://doi.org/10.3390/fire8030089
Chicago/Turabian StyleRomero-Barriuso, Álvaro, Jesús Manuel Ballesteros-Álvarez, Blasa María Villena-Escribano, José Luis Fuentes-Bargues, and Cristina González-Gaya. 2025. "Estimating Maximum Dwell Time for Firefighting Teams Based on Ambient Temperature and Radiant Heat Exposure" Fire 8, no. 3: 89. https://doi.org/10.3390/fire8030089
APA StyleRomero-Barriuso, Á., Ballesteros-Álvarez, J. M., Villena-Escribano, B. M., Fuentes-Bargues, J. L., & González-Gaya, C. (2025). Estimating Maximum Dwell Time for Firefighting Teams Based on Ambient Temperature and Radiant Heat Exposure. Fire, 8(3), 89. https://doi.org/10.3390/fire8030089








