Modeling Firebrand Spotting in WRF-Fire for Coupled Fire–Weather Prediction

Abstract

This study develops, implements, and evaluates the Firebrand Spotting parameterization within the WRF-Fire coupled fire–atmosphere modeling system. Fire spotting is an important mechanism characterizing fire spread in wind-driven events. It can accelerate the rate of spread and enable the fire to spread over streams and barriers such as highways. Without the capability to simulate fire spotting, wind-driven fire simulations cannot accurately represent fire behavior. In the Firebrand Spotting parameterization, firebrands are generated with a set of fixed properties, from locations vertically aligned with the leading fire line. Firebrands are transported using a Lagrangian framework accounting for particle burnout (combustion) through an MPI-compatible implementation within WRF-Fire. Fire spots may occur when firebrands land on unburned grid points. The parameterization is verified through idealized simulations and its application is demonstrated for the 2021 Marshall Fire, Colorado. The simulations are assessed using the observed fire perimeter and time of arrival at multiple locations identified from social media footage and official documents. All simulations using a range of ignition thresholds outperform the control without spotting. Simulations accounting for fire spots show more accurate fire arrival times (i.e., reflecting a better fire rate of spread), despite producing a generally larger fire area. The Heidke Skill Score (Cohen’s Kappa) for the burn area ranges between 0.62 and 0.78 for simulations with fire spots compared to 0.47 for the control. These results show that the parameterization consistently improves the fire forecast verification metrics, while also underscoring future work priorities, including advancing the generation and ignition components.

1. Introduction

Firebrands or embers are burning pieces of materials (e.g., branches, bark, building materials) generated at a fire source and carried with the wind and convection. Fire spotting occurs when firebrands are lofted into the air, land on unburned areas, and ignite new fires [1]. Spot fires are considered short-range within a few hundred meters from the source fire, or long-range, with reports of spotting distances as high as 35 km [2]. Short-range spotting accelerates the fire rate of spread by expanding the fire perimeters beyond the fire front, whereas long distance spotting can ignite new fires several kilometers downwind. Fires driven by high wind speed combined with low relative humidity and flammable vegetation often result in high fire intensities, rapid growth rates, and showers of embers that can start new fires. Intense spotting increases danger to fire crews, affects fire behavior predictability, and exacerbates the emergency response management.

When firebrands are not represented in fire behavior simulations, the predicted fire area can be considerably smaller than the observed. This is because the absence of spotting can underestimate the simulated fire rate of spread, while fuel barriers such as streams and infrastructure can prevent the simulated fire from spreading. DeCastro et al. [3] showed that some fire areas can be significantly different depending on the location of the ignition relative to nearby barriers. In the case of the 416 Fire (Colorado, U.S.), when ignition points were placed west of US 550, the fire area was significantly reduced because the fire spread towards the east was contained by the road.

Fire spotting can be modeled using different approaches depending on the fire behavior model with which it is integrated. The existing fire behavior models range from explicitly resolved models on one end of the spectrum to empirical models used in operational applications on the other end of spectrum. Explicitly resolved models include combustion processes and coupled atmospheric domain, but are limited to simulating small spatial domains due to their high computational demand (e.g., FIRETEC [4], and WFDS [5]). Fire spotting in these models include, for example, the implementation by Koo et al. [6] in FIRETEC and the coupled stochastic parametric model of firebrand transport by Tohidi & Kaye [7], which provide high fidelity results comparable to wind-tunnel experiments.

Empirical models, on the other hand, rely on simplified parameterizations mainly based on the fire rate of spread formulation by Rothermel [8] or the cellular automata modeling framework (e.g., FARSITE now incorporated into FlamMap [9,10], Prometheus [11], BehavePlus [12], and QUIC-Fire [4]). These fire behavior models typically use atmospheric fields (winds, temperature, humidity) from numerical weather prediction models or wind simulators [13] without fire–atmosphere coupling [14], which can lead to discrepancies between simulated and observed fire characteristics [15]. To be feasible for operational applications, firebrand spotting effects in these models are largely based on empirical methods, for example using spotting distance and probability of ignition [16,17,18,19,20,21,22], or empirical models incorporated into cellular automata fire-spread framework [23,24].

At the middle of the fire modeling spectrum, fire behavior coupled with Numerical Weather Prediction (NWP) models such as WRF-Fire [25,26,27], WRF-SFIRE [28], FOREFIRE [29], and ARPS/DEVS-Fire [30] have the ability to resolve winds in complex terrain and account for fire-induced perturbations in the atmosphere [31]. Among these models, WRF-Fire refers to the fire behavior modeling component in the official distribution of the WRF-ARW modeling system. WRF-Fire serves a distinct role amongst fire behavior models given WRF-ARW’s broadscale use in weather research, industry, and forecasting applications (e.g., the NOAA HRRR operational forecast [32]. The WRF-ARW model couples multiple earth system’s components, such as cloud microphysics, radiation, and land surface, from subsurface layers to the lower stratosphere. Within the Earth system, fires affect local circulation and vertical convection, interfering with cloud processes and precipitation [33,34,35] and impacting weather and air quality downstream. The capability to simulate fire processes within a mesoscale NWP model is critical to advance our understanding of fire–atmosphere interactions and improve local and regional forecasts surrounding and downstream of active fires. Nevertheless, WRF-Fire currently lacks a spotting parameterization, and implementing a framework for firebrand spotting in WRF-Fire is a key contribution of this work.

The Firebrand Spotting parameterization allows us to demonstrate that spotting can be a critical fire spread mechanism. In this study, we show that it can improve the representation of the fire physics, as it allows fire spots to accelerate the fire spread and initiate fires across fuel barriers. It is developed to operate within the WRF-ARW model to help address important fire behavior modeling limitations identified by the WRF and WRF-Fire user community, such as accurately simulating wind-driven fires, where ember showers are a primary fire spread mechanism. The parameterization includes three main components: (1) generation, (2) transport and combustion, and (3) landing and ignition. A key contribution of this work is the parallelization of the Lagrangian particle transport framework within the Eulerian infrastructure of WRF-ARW. The framework allows for future contributions, such as those described by Manzello et al. [36] and Wadhwani et al. [37], including for example the implementation of a more sophisticated generation process, advection and burnout (combustion) of non-spherical particles, and empirical ignition criteria, which would improve the model capability. This article is intended to validate the framework and serve as reference for continuing developments in future version releases.

In this article, we use idealized simulations to describe the parameterization implementation, and demonstrate its application with a simulation experiment of the Marshall Fire. The article is divided into five sections: (1) Introduction; (2) Implementation of the Firebrand Spotting parameterization, where we describe the parameterization components and associated methods; (3) Idealized Simulations, where we demonstrate the parameterization components through various idealized numerical experiments; (4) Marshall Fire Simulations, where we apply the parameterization to forecast the fire spread and quantify its accuracy; and (5) Conclusions.

2. Materials and Methods

2.1. Implementation of the Firebrand Spotting Parameterization

The objective of the work is to implement the Firebrand Spotting parametrization within WRF-Fire. The parameterization processes include three components as shown in Figure 1. For this parametrization, a Lagrangian framework is adopted, in which firebrands are generated individually, are advected with the atmospheric flow while burning out, and may ignite fire spots at landing when pre-defined ignition conditions are met. The main aspects of the parameterization are described in detail in the subsections of this section.

The Firebrand Spotting parameterization is consistent with the modeling scale and resolution of WRF-Fire. WRF-Fire is typically run in a nested domain configuration, downscaling from 3 km HRRR inputs to about 100 m atmospheric grid resolution for the large-eddy simulation (LES) in the inner domain [38]. The fire processes in the fire behavior component are 2-D (i.e., only at the surface level) and run at a more refined grid than the atmosphere (e.g., 30 m), which we refer to as the fire grid. While the fire behavior processes, including the fire rate of spread [8], fuel burn rate [39,40], and fire front propagation [26,27] are calculated at the fire grid, the atmospheric variables, such as wind components (U, V, W), are computed on the coarser atmospheric grid. Although there are no intrinsic restrictions to increasing the grid resolution, the computational cost to run the model’s atmospheric grid solution at LES scales is a limiting factor. As a result, subgrid scale processes are not explicitly resolved and complex formulations are often simplified (e.g., WRF-Fire does not resolve flame or combustion processes), aligning with the premise of all other physical parameterization (also known as schemes) in WRF.

It should also be noted that the parameterization accesses limited information from the fire behavior, which are needed to characterize the fire-related environment, such as fire rate of spread (ROS) and fuels, while the fire behavior is unaware of firebrand processes. The only interaction between them is through the fire spot ignitions initiated by the Firebrand Spotting parameterization. Even though these components are implemented independently of each other, because firebrands respond to the fire propagated by the fire behavior, the parameterization is subject to the same spatial scales, input data, and fire propagation methods currently available within WRF-Fire. Therefore, this work focuses on developing a framework with processes that are consistent with the horizontal, vertical, and temporal scales of fire–weather applications that WRF-Fire supports.

Finally, the source code is written in Fortran 2003 consistent with the WRF model coding standards. It consists of two modules, one containing the main Firebrand Spotting code and associated routines, and another, for specific Message Passing Interface (MPI) routines that are not part of the WRF model. Both modules are included within the WRF physics, distinct from WRF-Fire’s fire behavior source code. The Firebrand Spotting parameterization described here is integrated into the WRF-ARW source code version V4.5.1, available at https://github.com/NCAR/WRF-FirebrandSpotting, last updated on 21 March of 2025.

2.1.1. Generation

The implemented firebrand generation component depends on a number of distinct user-defined and internal parameters. These include generation locations, which are independently defined in the horizontal and vertical spaces, initial firebrand properties and momentum, and firebrand generation limit, which controls the maximum number of firebrands in the simulation, intended to limit computational demand and memory use. It should be noted that the firebrand generation module is largely based on user-defined parameters, except for the generation source locations, which are associated with the location of the fire front. Further research is needed to develop a firebrand generation model that best represents the physical fire and fuel characteristics.

• Horizontal Generation

Firebrands are generated from grid points along the fire front, which is identified through grid points where the fire rate-of-spread (ROS) is above a specified threshold (fs_ROSthresh), representing the advancing fireline. In its current version, the generation does not account for fire intensity and background wind. All grid points representing the advancing fireline generate a firebrand from each vertical level. The frequency of generation cycles is defined by the generation period parameter (fs_firebrand_gen_dt) and generation sources comprise the 2-D grid points along the firefront (i.e., points where ROS is greater than the threshold) during a given timestep. Although indicated by McArthur and Wadhwani et al. [16,37] that firebrand generation is related to the fire ROS and can likely be a function of fire intensity, fuel type, and background wind, we do not intend to characterize these relationships in this work. The ROS threshold is implemented with the intent to reduce the computational cost of transporting thousands of firebrands that could be generated at every timestep from every active fire grid point of a large fire. Although the computational cost is largely dependent on the simulated fire size and computer hardware, the default value of 0.1 m s⁻¹ is sufficiently low to prevent generation in grid points where embers are unlikely to travel beyond the generating point.

• Vertical Generation

The number of vertical levels per source is set by the levels parameters (fs_gen_levels) and an associated maximum generation height (fs_firebrand_gen_maxhgt). Firebrands are evenly distributed between the maximum generation height and 1 m above the landing height (fs_firebrand_land_hgt) by default, or can be randomly distributed between these levels if specified (fs_firebrand_gen_levrand, fs_firebrand_gen_levrand_seed).

• Initial Firebrand Properties

Initial property parameters are set at time of generation and change during transport as the particles burn out. These parameters comprise diameter, effective diameter, temperature, and terminal velocity (fs_firebrand_gen_prop_diam, fs_firebrand_gen_prop_effd, fs_firebrand_gen_prop_temp, fs_firebrand_gen_prop_tvel), and are used during transport to parameterize burnout and terminal velocity. Currently, firebrand generation is limited to spherical particles with properties set by the user. Although it is known that firebrands have different shapes, spherical particles are common assumptions in physical processes parameterizations (such as hydrometeors in microphysics parameterizations, e.g., [41,42], and particle dispersion models for dust and volcanic ash, e.g., [43,44]. This approach is adopted to reduce computational cost and will be revisited in future work.

• Initial Firebrand Momentum

A computationally inexpensive solution is implemented to account for firebrand initial momentum by accelerating particles downwind, which is the equivalent of allowing firebrands to travel without burning out or settling (fs_firebrand_gen_mom3d_dt) for a set number of timesteps. This option is implemented in lieu of effectively calculating an initial momentum to individual particles, which will be the subject of future research.

• Generation Limit

The number of generation locations (i.e., sources in the horizontal grid) is defined by a source limit parameter (fs_firebrand_gen_lim), which is applied to the model’s patch/tile when compiled for distributed memory parallel (dmpar) execution, or over the domain when compiled for serial execution. This limit is meant to prevent overuse of memory and is patch/tile independent to decrease non-essential MPI communication.

2.1.2. Transport and Physics

After generation, the particles are transported in the three-dimensional space with the atmospheric flow, and burnout as advected. During transport, firebrands may burn out entirely or land, when trajectories descend below a given height threshold.

• Advection

During transport, firebrands follow the resolved atmospheric flow as they burn out and fall. Particle density and char density (fs_firebrand_dens, fs_firebrand_dens_char) are the only user-defined parameters associated with firebrand physics. Firebrands may burn out entirely during transport, reach a maximum allowed lifetime (fs_firebrand_max_life_dt), or land.

During advection, the meteorological variables (wind, temperature, pressure, and air density) from the WRF model are interpolated from an Arakawa-C atmospheric [45]) grid to each individual particle position using a bilinear method implemented following the particle trajectory model described in [46].

The source code for particle advection follows the approach implemented by the Hybrid Single Particle Lagrangian Integrated Trajectory (HYSPLIT) model [47,48], which uses an improved Euler method, also known as Heun’s method [49], to advect particles by the atmospheric wind. The method calculates the position after a full timestep by taking the average between the derivative (i.e., wind speed) at the starting position and the derivative at a full step forward:

$$x_0^{t+1}=x^t+U_x^t\Delta \mathrm{t}$$

(1)

$$x^{t+1}=x^t+{\displaystyle \frac{\Delta \mathrm{t}}{2}}(U_x^t+U_{x_0^{t+1}}^t)$$

(2)

where $x_0^{t+1}$ corresponds to the position calculated at the first pass for the timestep forward $t+1$, $x_{t+1}$ is the final advection position calculated at the second pass, $x^t$ is the starting position at the starting timestep $t$, $U_x^t$ and $U_{x_0^{t+1}}^t$ are the wind speed at the starting position and first-pass position, respectively, and $\Delta \mathrm{t}$ is the timestep.

Particles are advected in the 3-D space using zonal, meridional, and vertical components of the wind (U, V, W), followed by an update of particle properties due to burnout and fall speed.

• Burnout

As the firebrand is transported by the ambient flow, its mass and volume (and consequently its diameter) decrease due to pyrolysis (i.e., decomposition of material at high temperature). In this case, woody material is pyrolyzed through both heterogeneous (glowing) combustion on the outer surface and homogeneous gas-phase oxidation of volatiles diffusing from within the firebrand [19]. The pyrolysis front, which marches inward toward the particle center as woody material is converted into char, closely marks the region where heterogeneous combustion occurs. This demarcation is used to track what is referred to as the effective mass diameter, $d_{\mathrm{eff}}$, as described in Tse & Fernandez-Pello and Bhutia et al. [50,51]. It can be derived as:

$$d_{eff}=\sqrt{(d_{eff}^{t-1}{)}^2-\beta \Delta \mathrm{t}}$$

(3)

where the notation $t-1$ indicates the variable value in the previous timestep, $\beta$ is a modified burning rate constant calculated as $\beta ={\beta }^0\left(1+0.276R{e}^{1/2}S{c}^{1/3}\right)$, ${\beta }^0$ is an empirically derived burning rate constant (${\beta }^0$ = 4.8 × 10⁻⁷s⁻¹) from the data of Tarifa et al. [18], and $\mathrm{Sc}$ is the Schmidt number (assumed to be 0.7 for air; Bhutia et al. [51]), and Re is the Reynolds number, which is calculated as in Tse & Fernandez-Pello [50]:

$$Re=|W_r|{\displaystyle \frac{d_p}{0.5\left(\frac{{\nu }_{\mathrm{air}}}{{\rho }_a}+\frac{{\nu }_p}{{\rho }_{\mathrm{ap}}}\right)}}$$

(4)

where $\left|W_r\right|$ is the relative velocity between the firebrand terminal velocity and the ambient vertical velocity, $d_p$ is the particle diameter, ${\rho }_{\mathit{ap}}$ is the air density surrounding the particle, ${\rho }_a$ is the air density, ${\nu }_{\mathit{air}}$ and ${\nu }_p$ are the ambient kinematic viscosity and the kinematic viscosity immediately surrounding the firebrand, respectively. The air density surrounding the particle is obtained using the ideal gas equation, ${\rho }_{\mathit{ap}}=P_a{\left(R_d{T}_p\right)}^{-1}$, where $T_p$ is the particle temperature, $R_d$ is gas constant for dry air, and $P_a$ is the atmospheric pressure at the particle position. The kinematic viscosities are calculated as:

$$\nu =B{\displaystyle \frac{T^{3/2}}{T+S}}$$

(5)

in which T represents the air or particle temperature, accordingly, and B = 1.458 × 10⁻³ g (msK^0.5)⁻¹ and S = 110.4 K are the Sutherland’s coefficients.

The firebrand particle mass is then calculated as:

$$m_p={\displaystyle \frac{{\rho }_{\mathrm{wp}}\pi d_{\mathrm{eff}}^3}{6}}$$

(6)

where ${\rho }_{\mathit{wp}}$ is the particle’s wood density (a user-defined parameter with default value set to fs_firebrand_dens = 513 kg m⁻³). The particle volume V_p is then calculated as $V_p=m_p/{\rho }_{\mathit{wp}}$ and the updated diameter is derived by

$$d_p^4=(d_p^{t-1}{)}^4-{\beta }^2{\Delta \mathrm{t}}^2$$

(7)

In general, once a hot firebrand particle is generated and begins its traverse through the atmosphere, it cools due to convective and radiative heat losses. The temperature rate of change for a spherical wooden particle is calculated based on the influence of two heat transfer processes on the particle temperature using the energy equation:

$${\rho }_{\mathit{ap}}{V}_p{c}_p{\displaystyle \frac{d{T}_p}{\mathit{dt}}}=-S_p(q_{\mathit{conv}}+q_{\mathit{rad}})$$

(8)

where $V_p,c_p$, $T_p$ and $S_p$ are the volume, specific heat capacity, temperature, and the surface area of the firebrand particle, and $q_{\mathit{conv}}$ and $q_{\mathit{rad}}$ are the convective and radiative heat fluxes, respectively, directed from the particle to the ambient air.

The net flux of heat transferred from a firebrand particle to the ambient flow due to convective processes is represented by:

$$q_{\mathit{conv}}=\underset{\_}{h}\left(T_p-T_a\right)$$

(9)

where $T_a$ the ambient temperature near the particle and $\underset{\_}{h}$ is the average convection heat transfer coefficient, determined using the Nuselt number, $\underset{\_}{h}=Nu{k}_{\mathit{air}}/d_p$, such that $k_{\mathrm{air}}$ is the air thermal conductivity (k_air = 27). For a solid sphere, $\mathit{N}\mathit{u}$ can be calculated as:

$$\mathit{Nu}=2+0.6R{e}^{1/2}P{r}^{1/3}$$

(10)

where $\mathit{Pr}$ is the Prandtl number (Pr = 0.7).

The net flux of heat transferred from a firebrand particle to the ambient flow due to radiative processes is represented by:

$$q_{\mathit{rad}}=\sigma ϵ\left(T_p^4-T_a^4\right)$$

(11)

where $\sigma$ is the Stefan-Boltzmann constant and $ϵ$ is the emissivity of the firebrand.

We estimate c_p as the weighted average between wood and charcoal

$$c_p={\displaystyle \frac{d_{\mathit{eff}}}{d}}{c}_{p_w}+\left(1-{\displaystyle \frac{d_{\mathit{eff}}}{d}}{c}_{p_c}\right)$$

(12)

where $c_{p_w}$ is the specific heat capacity for wood ($c_{p_w}$ = 1466 J kgK⁻¹) and $c_{p_c}$ for charcoal ($c_{p_c}$ = 712 J kgK⁻¹).

Lastly, the rate of change in firebrand temperature at each timestep is calculated as:

$$\Delta T_p=-{\displaystyle \frac{6}{{\rho }_{\mathit{ap}}{V}_p{c}_p{d}_p}}\left(\underset{\_}{h}(T_p-T_a)+\sigma ϵ(T_p^4-T_a^4)\right)\Delta \mathrm{t}$$

(13)

• Fall Velocity

It is assumed that the particle fall speed is equal to its terminal settling velocity, which for a spherical particle may be written as:

$$V_t=\sqrt{{\displaystyle \frac{{\rho }_p{d}_{p}g}{0.5({\rho }_a+{\rho }_{ap})3C_D}}}$$

(14)

where g is gravitational acceleration, and C_D is the drag coefficient. As in previous studies (e.g., [50,51], we assume C_D = 0.45. Our assumption that firebrand fall speed is immediately equal to V_t is reasonable considering that the firebrands typically reach their terminal velocity within seconds [18].

2.1.3. Landing and Ignition

Firebrands land when their vertical position reaches a defined height threshold (fs_firebrand_land_hgt) over an unignited grid point. This height would physically be related to fuel bed characteristics (e.g., canopy height); however, these potential dependencies are not considered in this study and the height threshold is left as a user-defined parameter. A spotfire is ignited when firebrands land on a given grid point with nonzero fuel load and meet two empirically defined ignition criteria based on the spatial concentration and accumulation of firebrands. For this purpose, two parameters are calculated. Parameter N, defined in Equation (15), represents the number of grid points where a spatial concentration of firebrands occurs. Parameter T, defined in Equation (16), represents the total number of firebrands landing on a central grid point and its adjacent neighbors. The ignition criteria is met when N > fs_ignneighb and T > fs_ignthresh, where fs_ignneighb and fs_ignthresh are user-defined thresholds.

$$N=1,\mathrm{i}\mathrm{f}(f_{\mathrm{ij}}>0)AND(fuelloa{d}_{\mathrm{ij}}>0)$$

(15)

$$T=f_{\mathrm{ij}},\mathrm{i}\mathrm{f}(fuelloa{d}_{\mathrm{ij}}>0)$$

(16)

where i and j are the grid point indices in the fire refined grid, N represents the number of neighbors, T is the total number of landing firebrands, f_ij represents the number of landed firebrands on the corresponding grid point during the current timestep (i.e., no accumulation of firebrands over time is currently considered), and fuelload is the fuel load on the corresponding grid point during the current timestep.

The set value for fs_ignneighb can be as low as 1, referring to the central grid point ij itself, and as high as 9, referring to the central grid point and the 8 adjacent neighbors. When either fs_ignneighb or fs_ignthresh are set to zero, ignitions do not occur.

It is worth noting that spot fire ignition is a complex thermo-dynamical process, which can be modeled as a function of mass and temperature of landing firebrands combined with fuel bed characteristics and local environment conditions [52]. Due to the complexity of this physical process and its dependence on firebrand generation, we implement a simple user-defined trigger until refined models are developed by the research community, and this parameterization component can be improved.

2.1.4. Lagrangian Transport Parallelization

A new set of Message Passing Interface (MPI) routines allow the Lagrangian transport framework to be compatible with WRF’s parallel process distribution. In WRF, the parallelization divides the domain into multiple patches, based on the number of compute processing units (CPU) available to the model. In general, patch computations are independent within each CPU, such that communications among patches are handled by WRF’s framework at designated times. Typically, communication calls happen among adjacent patches to exchange array elements at grid points around patch edges, known as halo. Halo communications are set for specific model variables needed for finite difference computations or by specific physics parameterizations, and happen in between calls to the physics parameterizations within the model’s timestep computations. A comprehensive description of the parallelization implemented in WRF-Fire, also describing the general WRF-ARW parallelization, can be found in Mandel et al. [26].

The new MPI subroutines implemented for the Lagrangian transport of firebrands (phys/module_firebrand_spotting_mpi.F) enable “on-demand” communication, allowing array elements to be exchanged between individual grid points (instead of all points in the halo zone) when needed, and called directly from the Firebrand Spotting module (phys/module_firebrand_spotting.F). In this case, communication only happens when particles move between patches during transport. Specifically, when particles move into the halo zone (i.e., beyond the grid points of the patch), a signal is sent to the adjacent CPU informing the number of particles to be transferred, followed by the 3-D particle positions and associated property arrays (i.e., properties characterizing diameter, density, and temperature). In addition to communications during transport, the new MPI routines enable CPU communication required for firebrand generation, informing the number of active fire points across the domain, and fire spot ignition, counting landing firebrands in adjacent cells. Here, we follow the official WRF model convention to parallelize using distributed tasks but no shared memory. Hence, the parameterization source code does not support shared memory, and consequently, we do not distinguish between tiles and patches.

3. Results

3.1. Idealized Simulations

Idealized simulations allow us to verify the code implementation and the physical processes by using controlled conditions that help isolate cause-effect relationships and are easier to interpret. In this section we analyze a set of idealized simulations to show that the parameterization’s source code works within the WRF framework and the individual components (generation, transport, ignition) behave as expected. These simulations are produced with WRF-ARW v4.5.1, configured following those in the analysis by [27]. Here, we use two idealized scenarios to simulate particularly distinct environments:

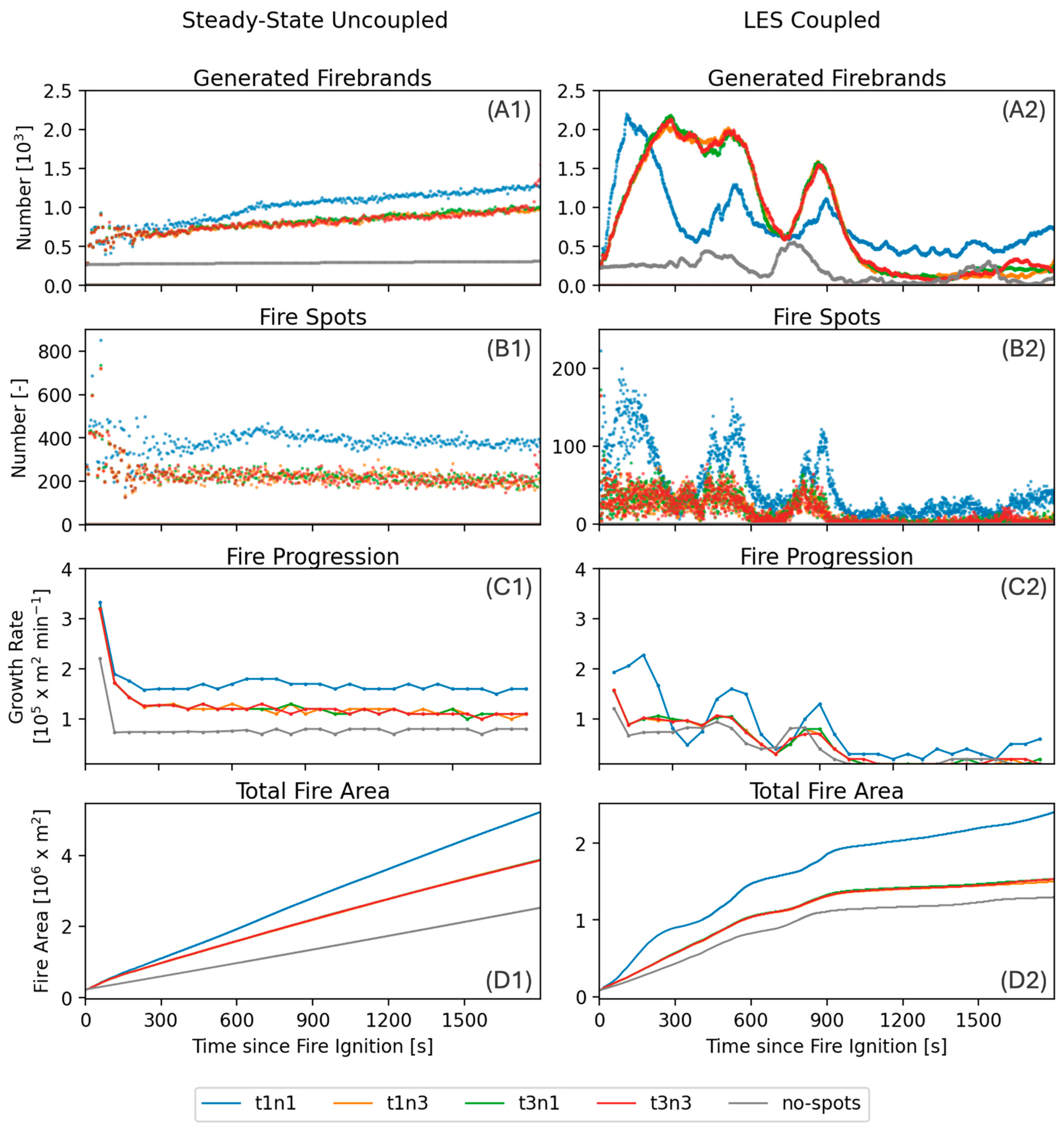
• Steady-state atmosphere with uncoupled fire processes (Steady-State Uncoupled). In the Steady-State Uncoupled scenario, the feedback from the fire to the atmosphere (i.e., the release of fire heat fluxes to the atmosphere) is turned off, and the surface boundary condition is set to be free-slip. The frictionless condition between atmosphere and surface produces uniform wind speed and direction, and no turbulence is generated. This scenario eliminates nonlinear factors that can affect firebrand generation and transport (i.e., wind variability and turbulence), allowing the validation of firebrand processes in a uniform environment in which cause-effect relationships are more evident.
• LES atmosphere with coupled fire processes (LES Coupled). In the LES Coupled scenario, the feedback from the fire to the atmosphere is turned on, in that the fire fluxes are transferred to the atmosphere allowing for turbulent eddies and a fire-induced atmospheric circulation. The intention for this scenario is to show the firebrands’ response in a turbulent environment, where generation occurs on a non-homogeneous fire front, and fluctuating winds (horizontal and vertical) affect transport, burnout, and landing.

The idealized configuration for the scenarios is summarized in

Table 1. Scenario configurations for the idealized simulations.

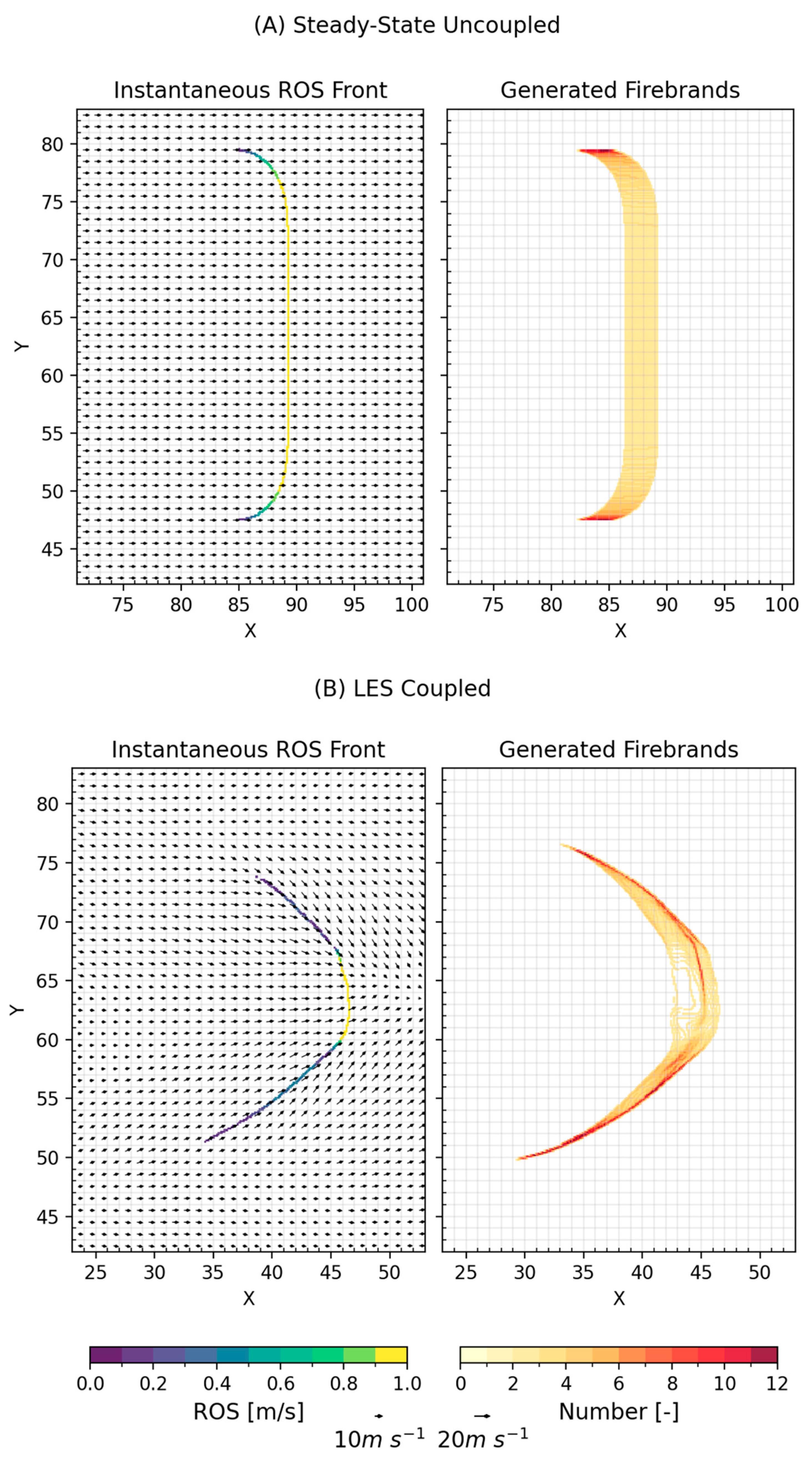
Parameter	Steady-State Uncoupled Fire	LES Coupled Fire
Horizontal grid spacing	40 m	10 m
fire grid refinement	5 m	5 m
Vertical layers	51 uniformly spaced	51 stretched
Model top	2 km	2 km
Timestep	0.5 s	0.125 s
Lateral boundary conditions	Open	Periodic
Temperature profile	305 K at surface, 300 K from surface to 1 km, 310 K at model top increasing linearly after 1 km	305 K at surface, 300 K from surface to 1 km, 310 K at model top increasing linearly after 1 km
Fire ignition	Ignition after 10 s 1 km × 100 m file line	Ignition after 30 min 1 km × 40 m fire line
Fire fuel	Anderson’s 13-fuel model, category 10 (timber litter with understory)	Anderson’s 13-fuel model, category 10 (timber litter with understory)
Surface friction	Free-slip surface (frictionless)	0.005 drag coefficient applied to the surface
Zonal wind speed	Uniform speed of 10 m s−1	Initial speed of 10 m s−1
Perturbations	-	Deardorff’s turbulent kinetic energy subgrid-scale model, coefficient 0.1
	-	Surface Heat Flux of 100 W m−2 + coupled fire heat flux
	-	Temperature perturbation bubble of 0.5 K with 40 m depth
	-	Physics options for LES [27]

, and the Firebrand Spotting parameterization settings are given in

Table 2. Firebrand Spotting parameterization settings for the idealized scenarios and default values.

Firebrand Process	Parameter Category	Namelist Parameter	Default Value	Value in Ideal Scenarios
-	Maximum Array Size	fs_array_maxsize	100,000	100,000
Generation	Generation Limit	fs_firebrand_gen_lim	0 (off, no firebrands)	100,000
Generation	2-D Horizontal Generation Threshold	fs_ROSthresh	0.1 m s−1	0.1 m s−1
Generation	2-D Horizontal Generation Period	fs_firebrand_gen_dt	5 timesteps	10 timesteps
Generation	Vertical Generation	fs_firebrand_gen_levels	5	1
Generation	Vertical Generation	fs_firebrand_gen_maxhgt	15 m	10 m
Generation	Vertical Generation Random Levels	fs_firebrand_gen_levrand	false	false
Generation	Vertical Generation Random Levels	fs_firebrand_gen_levrand_seed	1	1
Generation	Generation Momentum	fs_firebrand_gen_mom3d_dt	0	0
Generation	Initial Firebrand Properties	fs_firebrand_gen_prop_diam	10 mm	3.6 mm
Generation	Initial Firebrand Properties	fs_firebrand_gen_prop_effd	10 mm	3.6 mm
Generation	Initial Firebrand Properties	fs_firebrand_gen_prop_temp	900 K	900 K
Generation	Initial Firebrand Properties	fs_firebrand_gen_prop_tvel	0 m/s	0 m/s
Transport and Physics	Constant Firebrand Properties	fs_firebrand_dens	513,000 g/m3	513,000 g/m3
Transport and Physics	Constant Firebrand Properties	fs_firebrand_dens_char	299,000 g/m3	299,000 g/m3
Transport and Physics	Advection	fs_firebrand_max_life_dt	200 timesteps	200 timesteps
Landing and Ignition	Landing	fs_firebrand_land_hgt	0.15 m	0.15 m
Landing and Ignition	Ignition	fs_ignneighb	0 (no ignition)	0
Landing and Ignition	Ignition	fs_ignthresh	0 (no ignition)	0

. In both scenarios, fire spot ignitions remain off to reduce degrees of freedom and allow a proper assessment of the parameterization components. In the LES Coupled scenario, we include some parameters (surface heat flux, drag coefficient, temperature perturbation bubble) to accelerate the development of domain-wide turbulence. Even though turbulence can be generated simply by coupling the fire with the environment, it would take significant time, and the fire would reach the domain boundaries before we could see its effects. Moreover, the fire line is ignited 30 min after the model initialization, so the fire starts in a developed turbulent environment, and a finer spatial resolution is used to better resolve eddies.

The firebrand generation sources correspond to grid points representing the fire front, which are identified by thresholding the fire ROS. The fire ROS and corresponding number of generated firebrands 40 min after ignition are shown in Figure 2. The figures show a sequence of generation cycles for the Steady-State Uncoupled and LES Coupled cases. On the left side, the figure shows the fire ROS at a single timestep (i.e., instantaneous at the corresponding file output time), and on the right side, the number of generated firebrands, accumulated within a 2 min window defined by the model’s output history interval. The figure shows the fire ROS advancing with wind direction. In the Steady-State Uncoupled simulation, the fire ROS is mostly uniform with a decreasing rate near the y-axis edges, which is a result of the fire front propagation through the level set method. This curvature effect near the edges depends on the level-set viscosity coefficient, the method of level set propagation, and level set reinitialization, as discussed in Munoz-Esparza et al. [27]. The accumulation of firebrands generated over the 2 min output window shows the accumulation is denser over areas where the fire ROS is slower. This happens because firebrands are generated more frequently from the same grid points during the accumulation interval. Conversely, in areas where the fire ROS is faster, firebrands are generated less frequently from the same grid points, resulting in a generation band that extends over a wider area. While in the Steady-State Uncoupled simulation the fire ROS is symmetrical and winds are uniform, in the LES Coupled simulation, the wind speed and direction are influenced by the fire heat fluxes, which in turn drives an asymmetrical ROS. The fire ROS is higher near the middle of the fire line, where the wind vectors show converging higher wind speeds, leading to firebrands being generated over a wider area where ROS is faster, and more frequent generation where ROS is slower.

We illustrate transport through firebrand travel distances and trajectories from a set of simulations configured with various background wind speed and particle properties (diameter, temperature, and density). The parameters values in the sensitivity tests are chosen to be representative of real-world scenarios. Specifically, firebrand density and diameter are chosen to result in typical firebrand mass of 0.01 g to 1 g based on the available data in the literature [53,54]. For firebrand temperature, we selected a range based on reasonable values for smoldering and flaming combustion, as firebrand generation temperature data are not available in the literature. Lastly, the background wind speed upper range is limited by the small simulation domain, in that in higher wind speeds, the fire reaches the domain boundaries, forcing the termination of the simulation.

The sensitivity of firebrand travel distance to temperature, diameter, density, and background wind speed are shown in Figure 3. The results are presented in violin plots to show the data density, median, interquartile range, and statistical outliers of each sensitivity test. The travel distances correspond to the Euclidean distances between firebrands’ generation and landing positions, aggregated over a 30 min window after the simulations’ spin-up time. The figure shows results for a baseline configuration (Base, T = 900 K, d = 3.6 mm, ρ = 513 kg m⁻³, and U = 10 m s⁻¹), and 8 sensitivity tests each modifying a single parameter from the Base configuration. All firebrands are generated at the same height of 10 m. In the Steady-State Uncoupled scenario, travel distances among firebrands generated at the same heights do not vary within simulations because firebrand properties are fixed, the atmosphere profile is homogeneous, and the wind field is constant and homogeneous. In the LES Coupled scenarios, travel distances vary due to turbulence, which intensifies as the fire heat perturbs the wind field. Firebrands will travel farther if generated where the local flow is enhanced vertically and/or horizontally.

In the Steady-State Uncoupled simulations, the travel distances are illustrated by the solid horizontal lines across each violin. These simulations show that for the same wind speed (10 m s⁻¹) and for the range of parameters simulated, cooler or smaller firebrands travel farther than hotter or larger particles. As discussed in Bhutia et al. [51], smaller particles face lower initial drag; whereas hotter particles attain a higher terminal velocity due to the lower air density surrounding the particle. The travel distance increases by 5 m when firebrands start with the coolest temperature, and by up to 15 m when particles are smaller. As expected, lower density particles (all spherical particles in this case) also travel farther distances (up to 15 m), with wind speed being the primary factor affecting firebrands’ reach. The travel distance varies by 30 m between 5 and 15 m s⁻¹.

The sensitivities for the LES Coupled simulations show that in most cases, firebrands travel shorter distances than the corresponding Steady-State Uncoupled runs (shown by the median and 75th percentile below the solid horizontal lines). Even though turbulence tends to decrease the range of most firebrands, it facilitates a small number of firebrands to reach farther distances. Considering the statistical outlier range (i.e., beyond 1.5 points above the upper quartile), firebrands can reach distances of up to 103 m, which corresponds to 37% farther than the median distance.

The number of firebrands in these simulations is summarized in

Table 3. Bulk firebrand summary and travel distance statistics for a 30 min simulation window for each of the sensitivity tests in the LES Coupled scenario.

	Total Generated	Total Landed	Total Burned Out	Median Distance [m]	Outlier Max Distance [m, % Increase]	Total Outlier [%]	Steady State Uncoupled Distance [m]
Base	281,746	279,796	1950 (1%)	24	70, 34%	2.6%	30
T = 300 K	281,746	250,034	31,712 (11%)	30	78, 38%	2.3%	35
T = 600 K	281,746	279,430	2316 (1%)	26	75, 35%	2.8%	30
d= 10 mm	281,746	280,316	1430 (1%)	14	31, 45%	1.6%	15
d = 2.6 mm	281,746	48,725	233,021 (83%)	30	54, 55%	0.6%	33
ρ = 200 kg m−3	281,746	233,692	48,054 (17%)	38	103, 37%	2.5%	45
ρ = 350 kg m−3	281,746	278,698	3048 (1%)	30	90, 33%	3.3%	35
U = 15 m s−1	415,278	410,937	4341 (1%)	29	94, 31%	2.5%	45
U = 5 m s−1	266,934	265,227	1707 (1%)	20	56, 36%	1.1%	15

, along with a summary of travel distances. These totals show that while cooler, smaller, and less dense firebrands travel farther, they also burn out more frequently. In these simulations, diameter is the most susceptible parameter to burning out before landing (~83%), followed by density (~17%) and temperature (11%). With respect to wind speed, the data show firebrand generation increases exponentially with an increasing background wind speed. This happens because firebrands are generated where the fire is actively spreading (i.e., where the fire ROS is above a minimal threshold), whereas the fire rate of spread is a function of wind speed. Hence the number of firebrands generated increases as we increase the background wind speed.

Figure 4 shows the vertical cross-section of particle trajectories from a random atmospheric grid point for each of the sensitivity experiments. The trajectories for the Steady-State Uncoupled are shown in A and for the LES Coupled in B. In the uncoupled cases, the trajectories of particles with the same initial properties are identical regardless of the generating grid point because the environment is homogeneous and, thus, particles travel the same distances. Whether they land or burn out depends only on their initial properties and height from where they are released, not on the environment.

The particles’ position at each model timestep is indicated by the circle markers, informing the duration of the particle’s trajectory, from generation until one timestep prior to landing. Because the timesteps are different between the two scenarios, the number of timesteps in the trajectories of each particle is also different. For example, the figure shows the lower density particle (brown) remains airborne for at least 8 full timesteps (4 s) in the Steady-State Uncoupled and at least 36 timesteps (4.5 s) in the LES Coupled; the particle under higher wind speed (gray) remains airborne for at least 5 timesteps (2.5 s) in the Steady-State Uncoupled and at least 17 timesteps (2.125 s) in the LES Coupled; while the larger particle (red) remains airborne for at least 2 full timesteps (1 s) in the Steady-State Uncoupled and at least 11 timesteps (1.375 s) in the LES Coupled. All particles land during the subsequent timestep.

In the LES Coupled cases, the trajectories depend on the particle’s interaction with the local wind. The trajectories in the figure are all generated from the same grid point (corresponding to the atmospheric grid point at x = 176, y = 225) to illustrate particles traveling under the same environment conditions, as is the case for all simulations using 10 m s⁻¹ background wind speed. When we change the background wind speed of the coupled simulations to 15 and 5 m s⁻¹, the time of generation of the particles also changes (from 9 min to 7 and 20 min after ignition, respectively), because the fire front advances through the selected x, y grid point at different times. The different background wind speeds create different turbulence fields, which affect environmental properties such as vertical velocity and wind direction.

The effect of different ignition criteria on the resulting fire behavior is shown in Figure 5. The ignition criteria are configured with total thresholds and number of neighbors of 1 or 3, such that t indicates the total threshold and n the number of neighbors (i.e., t1n1, t3n1, t1n3, t3n3). The Steady-State Uncoupled and LES Coupled scenarios are shown on the left (1) and right (2) columns, respectively. The number of generated firebrands is shown on the first row (A), the number of fire spots on the second row (B), the fire progression is represented by the fire growth rate on the third row (C), and the fire area on the fourth row (D). The total numbers (A, B) are aggregated in 1 s intervals, the fire progression (C) is aggregated in 1 min intervals, and the fire area is instantaneous. The gray lines show the simulations without fire spots, i.e., firebrands are generated and transported but do not ignite fire spots.

Overall, these sensitivity tests show the simulation configured with the most favorable spotting criteria (t1n1, blue) exhibits more rapid fire progression (C1, C2) and achieves the larger fire area (D1, D2). Conversely, the simulations without fire spots (gray) show the slowest fire progression and smaller fire areas. For the 30 min fire duration in these simulations, there is no visible distinction among t1n3 (orange), t3n1 (green), and t3n3 (red).

The figure shows the fire progression is largely modulated by the number of generated firebrands, which in turn determine the number of fire spots, as indicated by the various aligned peaks in A2, B2, and C2, more prominently shown by t1n1 (blue) but also depicted by t1n3, t3n1, and t3n3 (orange, green, red) with a reduced amplitude caused by the stricter filtering criteria.

The no-spots simulation (gray) also shows an oscillating behavior in the fire progression (C2) and firebrand generation (A2). Due to the encoded correspondence between firebrand generation and grid points comprising the fire front, we can relate the variations in firebrand generation with a longer or wider fire front, which in this case is solely due to turbulence, rather than nonlinear effects of fire spotting in the fire propagation. Slight oscillations are also seen in C1, which are due to the fire viscosity coefficient used to propagate the level set function in WRF-Fire [27], rather than caused by the environment.

In summary, the idealized case studies illustrated the main processes within the parameterization components for generation, transport and burnout, and ignition. The steady-state and turbulent case studies facilitated the assessment of the effects of different modeling assumptions. The presented results were supported by physics-based explanations, which served to verify the implementation.

To quantify the computational cost of these simulations, we present a summary in

Table 4. Computational cost for 30 min simulations of idealized experiments.

Experiment	Domain Size [x, y]	Derecho HPC Allocation	Configuration	Number of Requested Processes (Used CPU)	Execution Time	Simulation Cost [Core-Hours]
LES fire off	1001, 501	10 nodes, 128 CPU each	-	1275	23 min	477
LES-Coupled			Spotting off	1275	27 min	566
			Spotting on	1275	30 min	622
Steady-State Uncoupled	251, 126	1 node, 128 CPU	Spotting off	80	18 min	39
			Spotting on	80	21 min	44

. In the table, we include a simulation intended to assess the cost of the fire behavior component on its own (i.e., WRF-Fire versus WRF-LES) to show that most of the cost associated with WRF-Fire simulations are in fact due to the LES configuration rather than the fire itself. Based on the simulations’ cost expressed in core-hours, the fire behavior component (without spotting) contributes 18% of the computational cost, whereas the Firebrand Spotting parameterization (with the firebrand configuration used in these simulations) adds 10% to the computational cost of the fire behavior simulation. Yet, it is important to note the Firebrand Spotting parameterization cost is highly dependent on the fire size (i.e., the length of the fire line from where firebrands are generated) and the user settings for the parameterization, such as the number of vertical levels set for firebrand generation and generation interval.

In general, the computational cost of these simulations is also dependent on the parallel job submission configuration. In these tests, we configure each job considering the number of parallel tasks is limited by the WRF model’s domain size (patches cannot be smaller than 10 points in each x, y direction). While we could have configured domain patches with approximate the minimal size, it is known that processing speed is lost due to the increased communications cost. So for the LES, we set the number of CPU to compute 51 segments in x and 25 in y, corresponding to patches of approximately 20 by 20 grid points each, also considering the number of CPU per node in order to reduce the computational cost on Derecho HPC (128 CPU per node, non-shared nodes). For the Steady State Uncoupled domain, we use the corresponding number of grid points per CPU (approximately 393 points per CPU) to have similar patch dimensions as the LES Coupled simulation. Lastly, for these tests we omit all output files because the frequency and number of variables in the outputs written to disk increase the execution time.

3.2. Marshall Fire Simulations

In this section, we evaluate and quantify the firebrand parameterization impact on the fire spread forecast for the Marshall Fire. The Marshall Fire started in the outskirts of Boulder, Colorado on 30 December 2021, approximately at 18Z (11 AM MT) and reached the residential area in about one hour. To this date, the Marshall Fire is the most destructive fire in Colorado’s State history, with 1084 homes destroyed and 149 damaged. According to the Boulder County Operational After-Action Report [55], the fire initiated from two distinct sources, a downed utility line and a shed on fire in the same area.

That particular year had an unusually wet and warm spring season, which allowed grasses to grow tall and thick; but from June to December, the area experienced the warmest and driest year on record, leading to favorable fuel conditions [56]. The fast spread of fire was driven by a downslope windstorm, with wind gusts records of 100 mph, relative humidity around 20%, and cured grass fuel. The event was described by Fovell et al. [57] as “a perfect storm of fast winds and drought conditions as the combination of historically warm temperatures and low precipitation along the Front Range of the Rocky Mountains left the grasses in a state of extreme dryness”.

We know from social media records and the analysis in the OAAR that the fire’s devastating behavior was exacerbated by ember showers produced by extreme wind speeds. We chose the Marshall fire to demonstrate the parameterization due to the relatively small scale of the fire (under 10 h, extending over an area under 6000 acres) and the minimal fire suppression, which is not accounted for in WRF-Fire and typically leads to overestimated fire spreads. This model implementation and Marshall Fire analysis concludes the preliminary work by Frediani et al. [57], where we “manually” encoded four spotting ignitions in WRF-Fire, representing strategic fire spot locations that allowed the fire to spread across roads and Hwy36. Following that preliminary work, Juliano et al. [58] simulated and analyzed the physical drivers of the fire spread, and evaluate the simulated atmospheric flow characteristics using Doppler on Wheels (DOW) observations.

3.2.1. Simulation Configuration

The Marshall Fire is simulated on Derecho HPC [59] using WPS v4.5, WRF v4.5.1, and a developmental version of the Firebrand Spotting parameterization. The simulations are configured with two nested domains (parent and child, Figure 6), with one-way feedback between domains, at horizontal grid intervals of 1000 and 111 m, using a mesoscale to microscale configuration [60], in which the inner nest runs in LES mode. We use a fixed 3 s timestep, 45 vertical levels, model top at 200 hPa, fire grid refinement of 4, and boundary conditions from the High-Resolution Rapid Refresh (HRRR) model [32,61] at 3-hourly intervals. The physics suite included the following parameterizations: WRF Single-Moment 6-class scheme as the microphysics [62], RRTMG [63] and Dudhia scheme [64] for long and shortwave radiation, Yonsei University scheme [65] for Planetary Boundary Layer (in parent domain only), revised MM5 for surface layer [66], and Noah Land Surface Model [67].

To simulate the fire behavior, we used fuels from the Anderson 13-fuel models obtained from the LANDFIRE database (13 Anderson Fire Behavior Fuel Models, LF 1.4.0 [68]), and a 100 m ignition line at (start: 105.230189 W, 39.956029 N) and (end: 105.230784 W, 39.956225 N), representing the approximate location considered during police investigations, ignited 5 min after model initialization. The fuel moisture content fraction was left as the model’s default value of 8%.

The Firebrand Spotting parameterization was configured with firebrands generated at every other timestep (fs_firebrand_gen_dt = 2), 10 evenly distributed vertical levels (fs_firebrand_gen_levels = 10), firebrand momentum of 6 timesteps (fs_firebrand_gen_mom3d_dt = 6), and 3 m land height corresponding to the approximate height in meters of the infrastructure in the area (fs_firebrand_land_hgt = 3).

The ignition sensitivity experiments are configured with various combinations of fs_ignthresh and fs_ignneighb, such that t indicates the value used for fs_ignthresh (t for total) and n indicates the value for fs_ignneighb (n for neighbor) (

Table 5. Fire-Spots experiments.

Name	Total Firebrands	Number of Neighbors
t5n1	5	1
t5n2	5	2
t5n3	5	3
t3n3	3	3
t10n1	10	1
t10n2	10	2
t10n3	10	3
t15n3	15	3
t3n5	3	5
t5n5	5	5
t10n5	10	5
t6n6	6	6

). Hereafter we refer to these experiments as “txny Fire-Spots” experiments.

3.2.2. Verification Methods

In atmospheric sciences, forecast verification refers to the process of assessing the quality of forecasts through methods involving comparisons between forecasts and observations [69,70,71,72]. In this subsection, we describe the observations and methods used to quantify the accuracy of the forecasted fire behavior.

Ember showers were mentioned in multiple news sources, including on the OAAR, and also appeared in multiple social media videos; however, firebrands were not directly measured or estimated. Considering that embers were a primary fire spread mechanism in this fire, we verify the simulated fire spread instead. The fire spread is verified against the observed fire perimeter and point observations compiled from recorded footage.

The official containment fire perimeter was timestamped four days later, once the fire was 100% contained. However, according to the OAAR, most of the fire spread occurred during the daytime on the ignition day: “at approximately 6:30 PM, the wind decreased to 25–30 mph and the fire behavior decreased in intensity and rate of spread.” The report indicates that at 8 PM MT “weather conditions had notably changed from the prior 9 h”, and although crews continued to fight fires through the night, we have not found records that indicated significant fire spread overnight. With that in mind, we consider the official fire perimeter was not substantially different from a perimeter that would have been produced on the night of December 30th.

In addition to the fire perimeter, the simulated fire spread is assessed using timestamps from recorded footage, compiled by a special project by 9News in Denver (KUSA-TV, Burned The Story Behind the Marshall Fire [73]), combined with records from the operational response in the OAAR. We used footage that enabled us to define approximate timestamps at fixed and explicitly identifiable locations within the footage. The timestamps and locations are summarized in

Table 6. Summary of timestamps used in the simulations’ verification. Locations are referred to by the name in bold font.

Approx. Coordinates of Report	Reported Local Time [MST]	Reported Location	Source	Reassigned Coordinates	Corresponding Model Output Time [MST]
(105.1745 W, 39.9557 N)	12:18 PM	Parking lot of Costco, Superior	OAAR	(105.1781 W, 39.9553 N)	12:45 PM
	12:56 PM	Bill Fudale, 6th and W. Charles St., Superior	9News Timeline
(105.1687 W, 39.9603 N)	12:45 PM	Home Depot in Louisville (northeast side of Hwy 36)	OAAR	(105.1716 W, 39.9609 N)	12:45 PM
(105.1940 W, 39.9865 N)	12:46 PM	S. Boulder and 68th	OAAR	(105.1933 W, 39.9850 N)	12:45 PM
(105.1664 W, 39.9728 N)	1:33 PM	Hillside neighborhood, Louisville	9News Timeline	(105.1716 W, 39.9736 N)	1:30 PM
(105.1495 W, 39.9546 N)	4:07 PM	Troon Ct., Louisville	9News Timeline	(105.1528 W, 39.9541 N)	4:00 PM
(105.1644 W, 39.9309 N)	4:32 PM	McCaslin Blvd. and Coalton Rd.	9News Timeline	(105.1675 W, 39.9311 N)	4:30 PM
(105.1644 W, 39.9779 N)	4:36 PM	South of Harper Lake	9News Timeline	(105.1669 W, 39.9781 N)	4:30 PM
(105.1580 W, 39.9714 N)	7:12 PM	Vista Ln. Louisville	9News Timeline	(105.1579 W, 39.9721 N)	7:15 PM
fire perimeter	20:00 PM	Weather conditions notably changed	OAAR	fire perimeter	20:00 PM

.

To align the observations with the model output, we reassigned the reported time to the closest model output time and moved the location coordinates to the nearest point where fuel load was greater than zero, still inside the fire perimeter. The locations had to be slightly moved because the Anderson fuels used by the model had a considerable number of points categorized as urban fuels (corresponding to a category with no fuel load), which would result in the model being unable to spread the fire to the exact observed location.

The observation locations are used to quantify model timing and spatial agreement. Model timing is quantified through arrival times, i.e., the absolute difference between the time of observation at each of the locations and the time the simulated fire arrives at the corresponding point:

$$ArrivalTime=t(FireAre{a}_{ij}>0)$$

(17)

where t is time, FireArea_ij is the fire area at the ij grid point corresponding to an observation coordinate.

To quantify the spatial accuracy of the simulated fire area against the fire perimeter, we use a contingency table as described in Wilks [69]. The table summarizes the counts of combinations of possible forecast and event pairs (Figure 7). Results are analyzed in terms of the hit frequency, miss frequency, false alarm frequency, and Heidke Skill Score (HSS), also known as Cohen’s Kappa.

HSS is a skill score that reflects the proportion correct that would be achieved by random forecasts that are statistically independent of the observation. HSS is 1 for perfect forecasts, forecasts equal to chance receive zero, and forecasts worse than chance receive negative scores. It is calculated as:

$$HSS={\displaystyle \frac{2(ad-bc)}{(a+c)(c+d)+(a+b)(b+d)}}$$

(18)

where the parameters a, b, c, and d correspond to the event pairs in the contingency table.

The hit frequency corresponds to the joint probability of a positive forecast and a positive outcome, the miss frequency corresponds to the joint probability of a negative forecast and a positive outcome, and the false alarm frequency corresponds to the joint probability of a positive forecast and a negative outcome, as illustrated in Figure 7.

3.2.3. Forecast Evaluation

The fire forecasts are assessed by comparing a control simulation (CTRL) using a standard configuration of WRF-Fire without fire spots with simulations using the Firebrand Spotting parameterization configured with the ignition criteria specified in Table 5.

A comparison between CTRL and one of the experiments using ignition criteria t5n2 is shown in Figure 8. In the CTRL experiment, the fire front is partially contained or delayed by the local road mesh, because it is represented by a no-fuel category in the Anderson Fuels. In the Fire-Spots experiment, the fire front spreads over the north and south sides of Marshall Road immediately after ignition and reaches Hwy 36 within the first hour in the simulation. For a period of 9 h from ignition time, the Fire-Spots simulation most accurately reaches the observation locations timestamps when compared to CTRL.

Firebrand spotting can be an important mechanism to increase the fire ROS, particularly in wind-driven fires, as noted by Wadhwani et al. [37] and references therein. Figure 9 shows that spotting played a fundamental role in the rapid spread of the fire: the fire front in the Fire-Spots experiment arrives at Hwy 36 within the first simulated hour (at 12 PM MST), whereas in the CTRL experiment, the fire front arrives 9 h later (at 9 PM MST).

The road containment depicted in the CTRL simulation is simply the model’s response to the fuels’ characteristics in the specified fuel layer. It is known that fuel layers such as the Anderson 13-fuels (current default in WRF-Fire) and Scott and Burgan 40-fuels, are inaccurate, incomplete, and static over multiple years [3]. The fuels in these layers are simplified representations of various vegetation types, used to solve the Rothermel’s surface fire spread equation [8], and allowing for rapid application in the field, e.g., for emergency response. In the region encompassed by our fire behavior domain, the Anderson 13-fuels classifies urban fuels in a “no-fuels” category (i.e., with fuel load equal to 0 kg m⁻²), with the area containing the suburbs burned down by the Marshall Fire surrounded by short grass, hardwood litter, timber, and closed timber litter (i.e., fuel loads of 0.166, 0.78, 0.896, and 1.12 kg m⁻², respectively). Even though the Marshall fire burned through urban areas, the simulations in this study do not simulate urban fire. WRF-Fire is not capable of propagating fire through urban fuels due to the zero-fuel load, so the fire rate of spread (ROS) calculated by WRF-Fire is also zero. Therefore, the fire ignites and advances only over fuel categories representing grass, litter, and timber.

Despite the limitations associated with the fuels, the dataset realistically represents the main local roads. The results obtained with the Fire-Spots simulations indicate that for this particular case, the lack of urban fuel representation is not the primary limitation to a more accurate simulation of fire spread. The limitation arises from the fire not being able to spot, preventing the fire front from advancing across barriers and underestimating the fire ROS.

The forecast verification for arrival times is shown in Figure 10. Figure 10A shows the arrival times at each location in Table 6 for each of the simulations, and Figure 10B displays the median times for each of the simulations, with the number of locations reached by the simulated fire indicated below the corresponding bars. The fire in CTRL reaches Superior with a 6 h delay and it is the only location it reaches by 9 PM MT. None of the simulations is able to reach TroonCt and VistaLn, and only the simulations which favor more fire spots reach McCxCoalton (t5n1, t5n2, t3n3, t5n3, t10n1).

As expected, an increase in the thresholds for spotting leads to slower fire propagation. For example, t15n3 only reaches 4 locations. In most cases, configurations with the same total threshold but with fewer neighbors propagate faster to the observation locations (e.g., t5n1 arrives faster than t5n2 at all locations). Similarly, configurations with the same number of neighbors and lower total thresholds also propagate faster than CTRL (e.g., t5n2 propagates faster than t10n2). In the simulations t3n5 and t5n5 the front arrives at the same time in all locations, suggesting that five neighbors is a high threshold for these simulations, such that the total threshold does not affect the results.

The simulations t10n2 and t10n3 show an opposite pattern—for the same total threshold, the higher number of neighbors actually decreases the arrival time. This is because small differences in the first hours of the simulation lead to different spotting patterns, which in turn affect the fire ROS at different locations. As shown in Figure 11, t10n2 shows a higher concentration of spot ignitions in the fire area south of Marshall Rd, whereas t10n3 shows a dense ignition area by Hwy 36 breaching the highway barrier. This is a consequence of firebrand generation being a function of fire ROS and illustrates that the outcome of these simulations is ultimately nonlinear.

The overall spatial metrics calculated for the final fire perimeter are shown in Figure 12. Figure 12A shows the frequency of hits, misses, and false alarms relative to the number of grid points in the domain, comparing the fire perimeter and simulations at 9 PM MT. As corroborated by the point-based analysis (Figure 10), the simulations favoring more spot fires (i.e., those with fewer neighbors, and lower total threshold, e.g., t5n1, t5n2, t5n3) display a higher frequency of hits, indicating there is more overlap between the observed and simulated fire areas, whereas the fewer the number of spot fires (e.g., t15n3, t3n5, t5n5, t10n5, t6n6), the lower the hit frequency, with CTRL having the least hits. Similarly, the miss frequency indicates that more of the observed perimeter is represented by the Fire-Spot simulations, with miss frequency increasing with decreasing number of spot fires. Conversely, the higher the number of spot fires, the higher the frequency of false alarms. This is because a higher number of simulated spot fires translates into a generally larger fire spread, so the tendency to overpredict is higher.

Figure 12B shows the corresponding HSS with respect to the final fire perimeter at 15 min intervals. The HSS shows that between t = 0 and t = 27 (4:45 PM MST), t5n1, t5n2, t3n3 are overall the most accurate predictions. This reflects the fact that the fast fire spread in these simulations produces a larger simulated fire, which is closer to the observed perimeter than the other simulations. Between t = 30 (6:30 PM MST) and t = 38 (8:30 PM MST), t5n3 becomes slightly more accurate, indicating that misses and false alarms in t5n1, t5n2, t3n3 are becoming more frequent as the simulated fire approaches the observed perimeter. At t = 40 (9 PM MST), t10n1 yields a marginally more accurate fire spread than t5n3, whereas the prediction skill of t5n1, t5n2, t3n3 slightly decrease (by 0.13, 0.06, and 0.09, respectively) as the simulated fire becomes larger than the observed perimeter due to a high number of fire spots. This result suggests that a mechanism to modulate the ignition criteria could improve the overall accuracy of the parameterization and also simplify the user-defined parameter configuration.

4. Discussion

This study described the Firebrand Spotting parameterization in the WRF-Fire modeling system, evaluated the parameterization through idealized simulations, and applied it to a real-case study to quantify the forecast skill gained by the new model component.

In the implemented parameterization, firebrands are generated along the fire front, are advected with the atmospheric flow while burning out, and ignite fire spots at landing when pre-defined ignition conditions are met. The three parameterization components are (1) generation, (2) transport and burnout, and (3) landing and ignition. Firebrands are generated according to user-defined initial properties (i.e., diameter, density, temperature) from grid points associated with the advancing fire front, which is propagated in WRF-Fire. Firebrands are transported using a Lagrangian framework designed to be compatible with the process parallelization of the WRF model. The individual firebrand particles follow the atmospheric flow, which is informed by WRF’s atmospheric component, and burn out along their trajectory. As firebrands land, a pair of user-defined thresholds and fuel conditions determine whether a spot fire is ignited.

Two idealized scenarios were used to illustrate the firebrand processes in a steady-state atmosphere with uncoupled fire processes, and in a turbulent environment with coupled fire processes. The idealized experiments demonstrated the effect of firebrand generation properties combined with fire–atmosphere interactions in ember transport, combustion, and landing, which in turn determined whether spot ignitions could occur. We showed that although turbulence decreased the travel range of most firebrands, it facilitated a small number of firebrands to reach farther distances, up to 37% farther than the median. The number of fire spots, and consequent fire rate of spread was largely modulated by the number of generated firebrands, regardless of the ignition criteria configuration. This result emphasized the importance of understanding and modeling ember generation as a precursor to improving forecasts of ember driven fires.

The implemented parameterization was then applied to assess its effect on a real-case simulation of the most destructive fire in the state of Colorado, the Marshall Fire, in which spot fires played a significant role in spreading the fire. The fire spread forecasts were quantified using objective metrics typically applied in forecast verification of numerical weather prediction models. The forecasts were verified against observations comprising a set of locations and timestamps compiled by 9News (Denver, KUSA-TV) from witnesses’ recorded footage, an After-Action Review compiled by Boulder County officials, and the official fire perimeter.

The Marshall Fire simulation experiments indicated spotting played a fundamental role in the rapid spread of the Marshall Fire, consistent with the fire records and scientific literature stating that firebrands are an important mechanism to increase fire rate of spread in wind-driven fires. We compared a control forecast against twelve Fire-Spots simulations, and assessed them in terms of arrival time and spatial metrics. The Fire-Spot simulations were configured with varying spot ignition criteria, ranging between more to less favorable to spotting. All twelve Fire-Spots simulations outperformed the control in all metrics. While the simulated fire in the control simulation was substantially delayed by the local roads, reaching only one observation location with a 6 h delay, the Fire-Spot simulations reached multiple observation locations within more accurate times. The simulations with more fire spots showed a higher frequency of hits combined with lower frequency of misses, indicating there was more agreement between the observed and simulated fire areas. Conversely, these simulations also showed a higher false alarm rate, indicating that more fire spots resulted in a generally larger fire spread. Finally, the assessment of the Heidke Skill Score (Cohen’s Kappa) showed that the simulations’ skill varied with time, with simulations having more fire spots performing better in the early stages of the fire, whereas simulations with fewer spots performed better in the later stages. This result suggests the parameterization would likely improve with an internally modulated approach to control generation and ignition criteria based on environment and fire properties, rather than user-defined thresholds.

The numerical experiments in this study also showed that spotting is a highly nonlinear process, which suggests it can be best represented by an ensemble of simulations. We showed that small differences in the first hours of the simulations led to different spotting patterns, which in turn affected the fire rate of spread at different locations, introducing variability in the fire spread patterns and timing. Although this study did not explore ensemble forecasts, it indicated that spotting can be a significant source of uncertainty in simulating fire spread of wind-driven fires, and could potentially improve forecast probabilities and representation of uncertainties.

Our results showed that the model’s ability to spot can be critical for modeling fire spread over barriers. Although it is known that simulated fire spread is intrinsically dependent on the model’s fuels (i.e., category, temporal and spatial accuracy, and resolution), when barriers such as highways and streams are depicted in the fuels, the simulated fire cannot spread without a spotting capability. This leads to an underprediction of the fire spread, an issue often attributed to the use of an empirical fire rate of spread and associated fuels, which, as we showed, can also be caused by the model’s incomplete representation of fire spread processes. While the Firebrand Spotting parameterization allowed the simulated fire to jump over roads, structures with combustible materials were not represented in the fuel inputs. The simulation near these structures did not account for ember accumulation and did not generate embers from these structures.

At this stage, the Firebrand Spotting parameterization relies on a number of user-defined parameters to control its components. Firebrands are represented as spherical particles with fixed initial properties; ignitions are determined from user-defined thresholds; and height variations due to vegetation structure are not accounted for. While real-world firebrands vary in size, shape, and density, and spotting ignitions depends on multiple physical and ecological factors, this choice is a first-implementation compromise that ensures computational tractability. This decision was also driven by the various unknowns associated with firebrand processes, primarily due to lack of observations in a non-laboratory environment to support empirical modeling and validation of results at NWP spatial and temporal scales. This model capability is in the early stages of development and our results were based on a single case study, in which urban fuels were not represented. Recent observation advancements from radars and image processing of high-resolution recordings will facilitate further development of the modeling components, such as a more sophisticated generation process, transport and burnout of non-spherical particles, and modulated ignition criteria based on internal model parameters and environment. This will lead to a more robust parameterization overall and facilitate the parameterization configuration by users. The present study represents a foundational step toward physically based firebrand spotting in WRF-Fire, with ample opportunities for refinement as data become available and the modular design of our framework allows for incorporation of more complex physics in future work.