Prediction of Ceiling Temperature Rise in High-Voltage Cable Trenches with Identification of Ignition Points
Abstract
1. Introduction
2. Materials and Methods
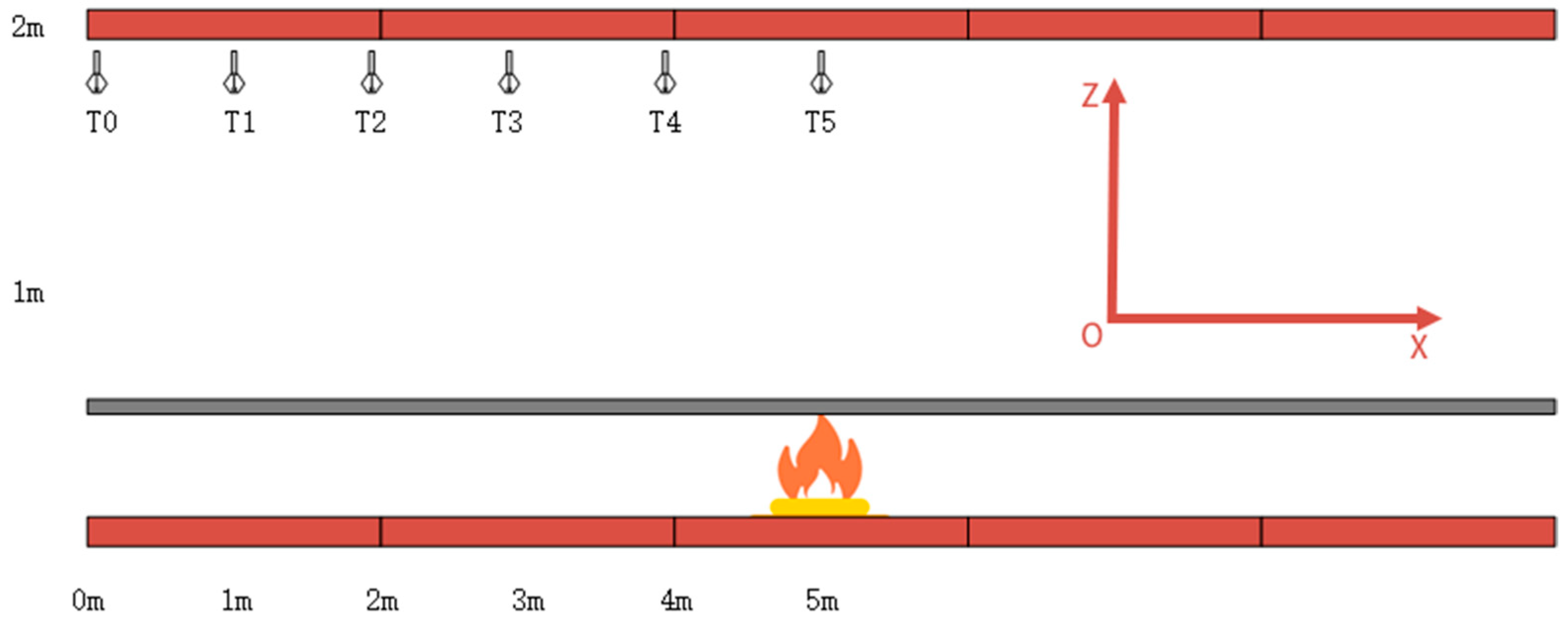
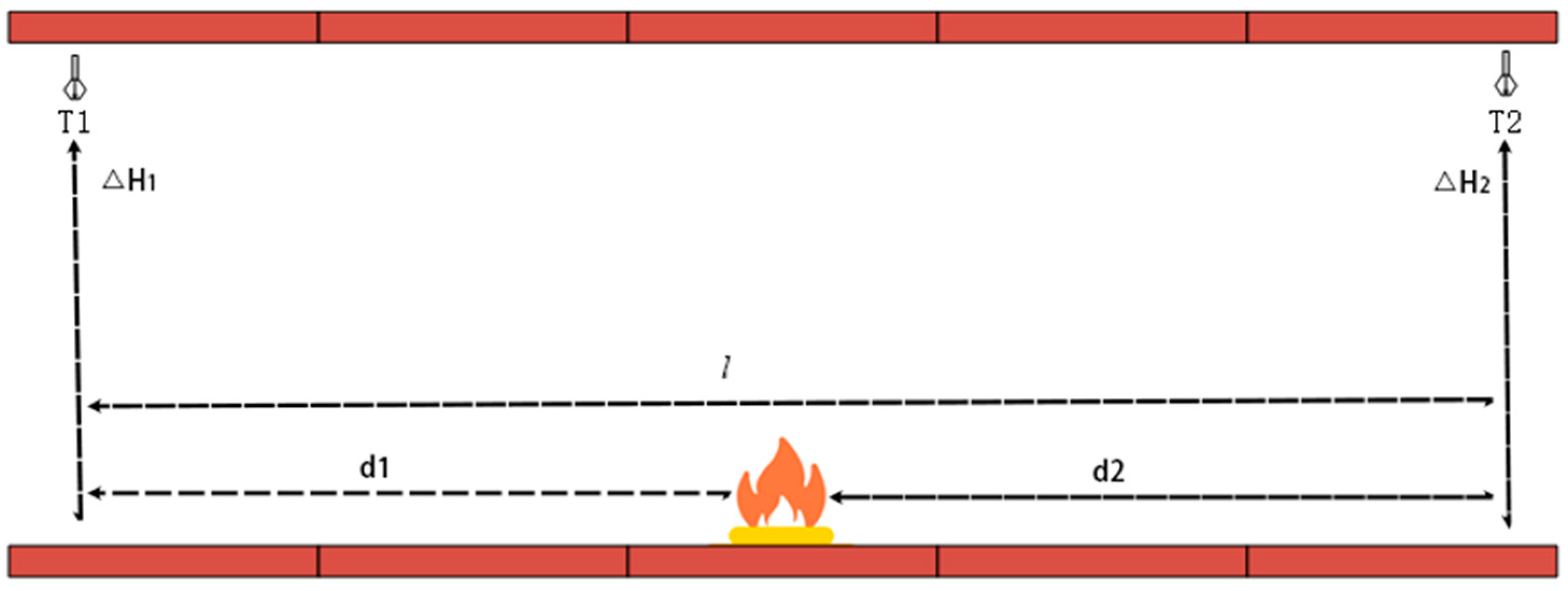
2.1. Cable Trench Fire Experimental Platform
2.2. Longitudinal Temperature Distribution Law of Cable Trench Ceiling
- Material factors: there are differences between the materials used in experimental fires and simulations, such as differences in fuel conductivity and combustion characteristics.
- Environmental factors: there are differences between a series of environmental conditions such as airflow, humidity, and pressure in experimental fires and simulations.
- Theoretical factors: the combustion process of experimental fires is complex, with factors such as diffusion of combustion products and gas convection making it difficult to accurately simulate them all.
3. Results and Discussion
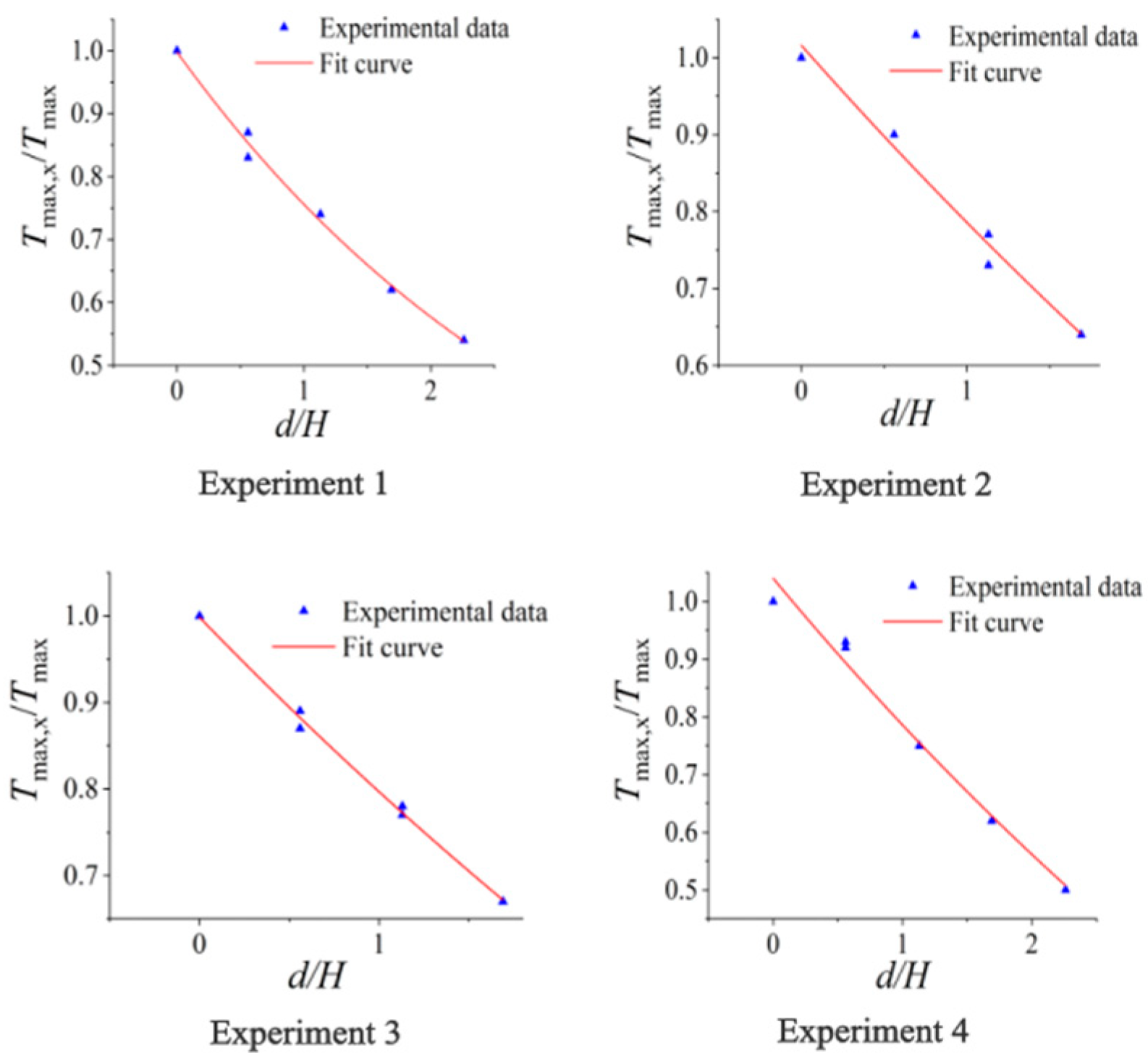
3.1. Fitting Function for Longitudinal Temperature of Ceiling
3.2. Verification of Ignition Point Location and Maximum Temperature Prediction Method
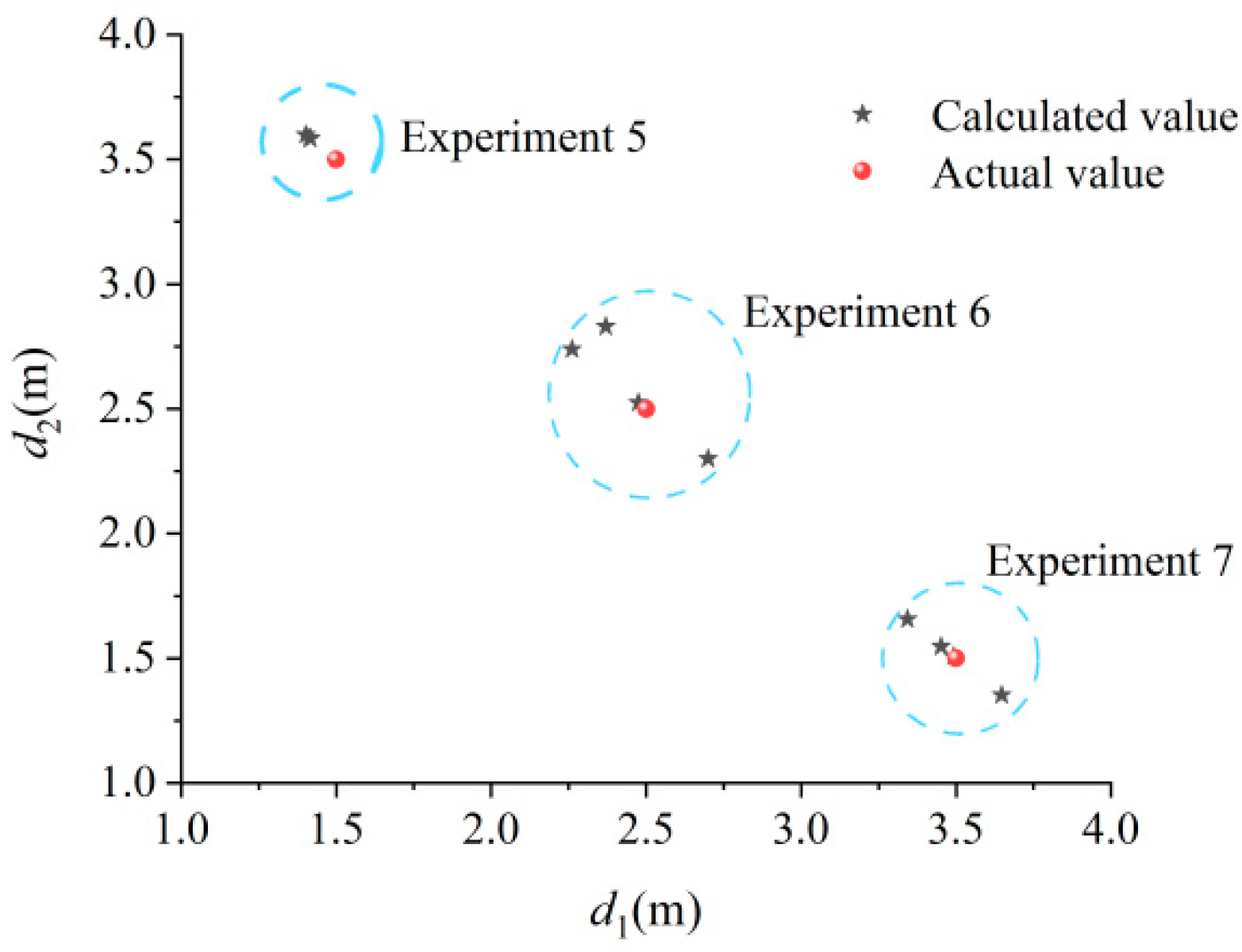
3.2.1. Method for Locating Ignition Points
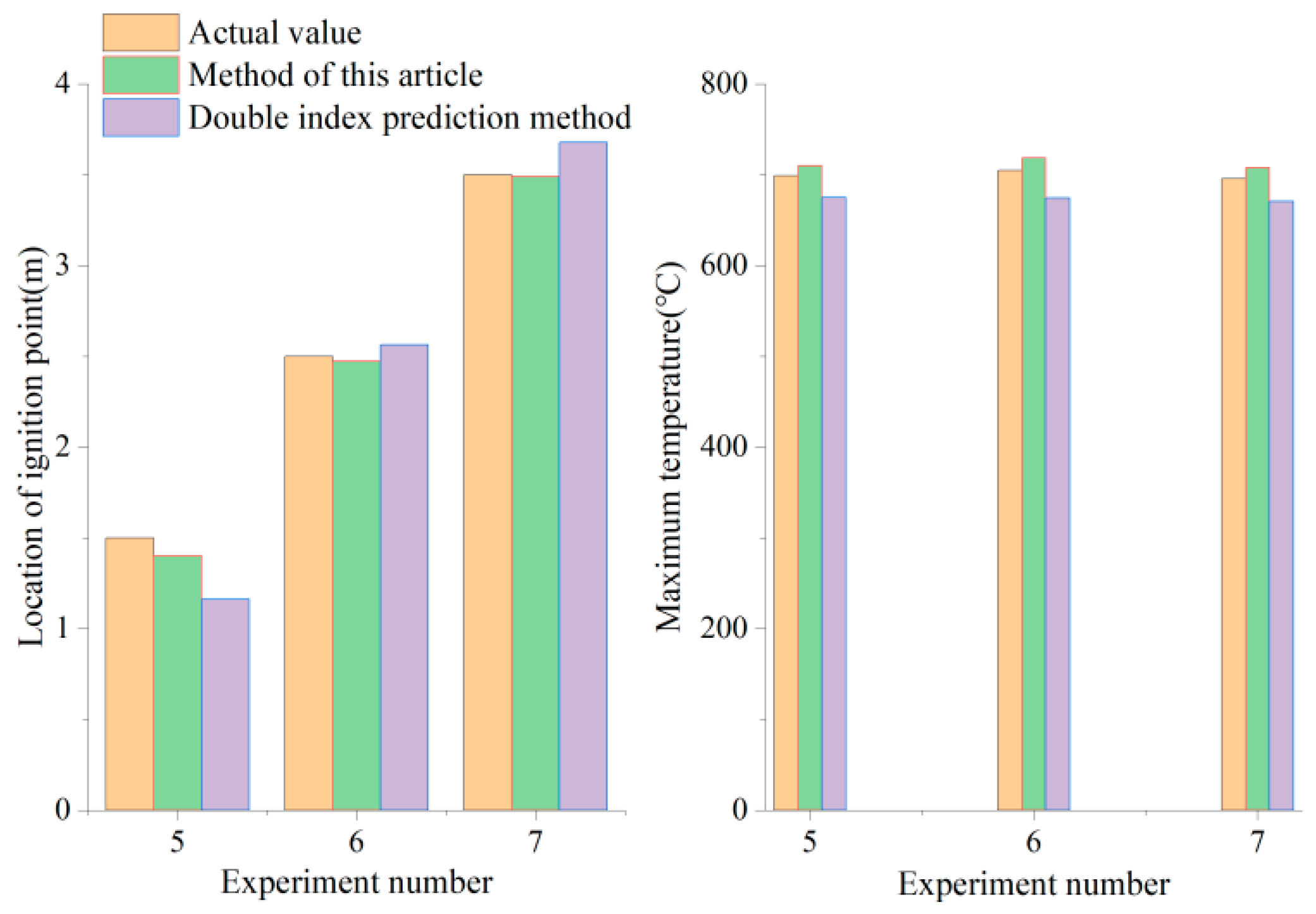
3.2.2. Maximum Temperature Prediction Method
4. Conclusions
- Through experiments and simulations with different fire source powers, it was observed that the maximum temperature of the ceiling directly above the ignition point corresponds to the highest temperature within the cable trench. Within the same location range, the temperature changes more rapidly as it becomes closer to the ignition point.
- Utilizing four sets of experimental data on cable trench fires at various ignition points, we proposed a parameterized exponential function fitting method. This method uses the ratio of the longitudinal distance between the ignition point and the temperature sensor to the vertical height difference of the trench as the independent variable. The dependent variable is the ratio of the maximum temperature rise at the sensor to the maximum temperature rise in the cable trench. The resulting sets of functions demonstrate a high degree of fitting accuracy.
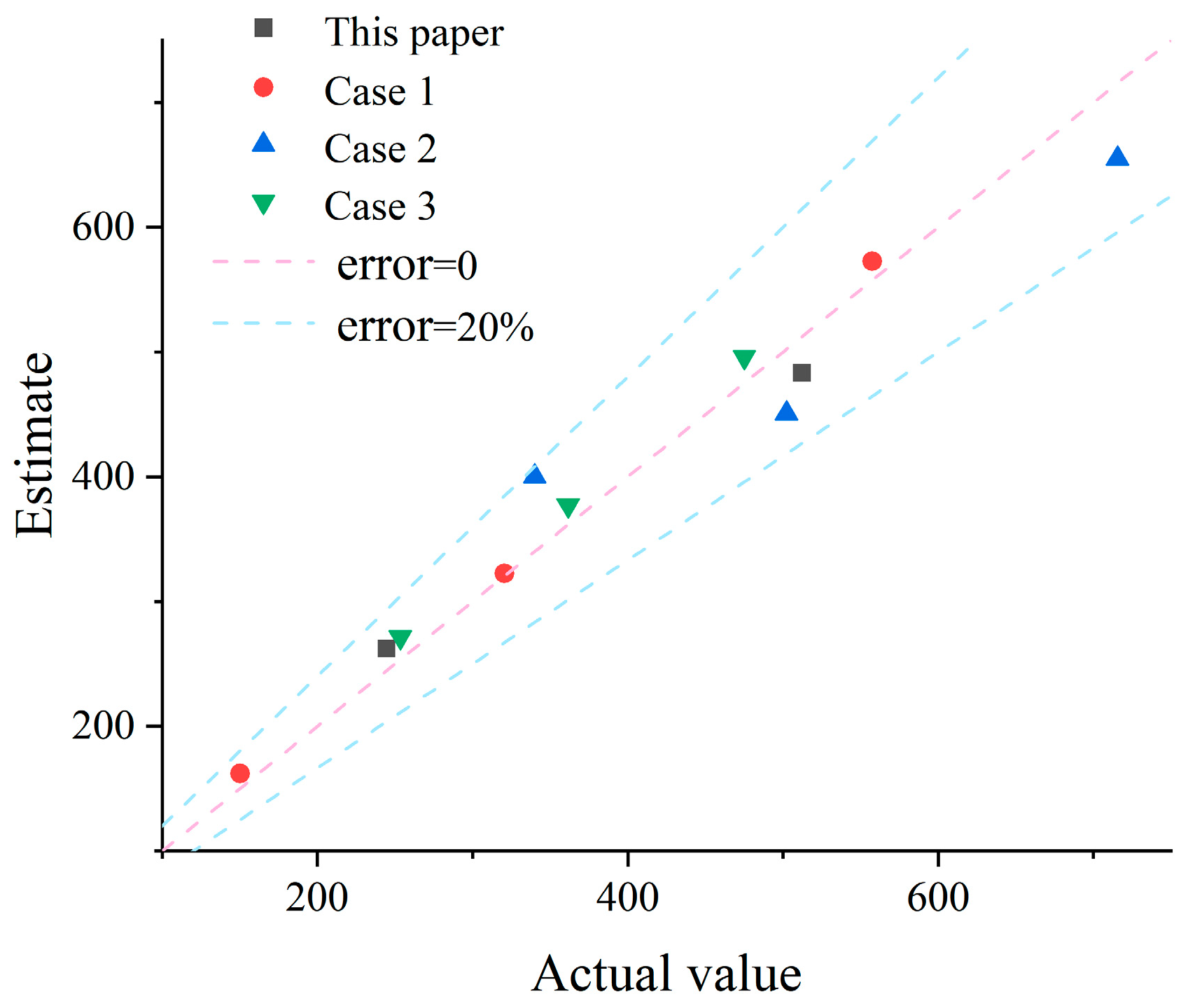
- The deviation between the calculation results of the ignition point identification method and the experimental results is small, with a positional deviation of within 0.098 m, and an average accuracy of 98.77%. The maximum temperature prediction method for the ceiling has a maximum temperature deviation of within 14 °C, with an average accuracy of 98.3%. Compared with traditional methods for predicting the position and maximum temperature rise of cable trenches, this method takes into account the influence of the fire temperature propagation coefficient and cable tunnel structural parameters, enabling more accurate positioning and prediction and providing a scientific basis and theoretical guidance for cable trench fire prevention.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, L.; Ye, K. A review of fire safety standards and fire research in urban comprehensive pipe galleries. Chin. J. Saf. Sci. 2021, 31, 132–140. [Google Scholar]
- Miao, X. The Fire Spread Law and Fire Sealing Improvement Methods of High Voltage Cable Trenches in Substations. Master’s Thesis, Shandong University, Jinan, China, 2021. [Google Scholar]
- Song, Z. Fire Spread Characteristics and Ignition Point Identification Method for High-Voltage Cable Trenches in Substations. Master’s Thesis, Shandong University, Jinan, China, 2022. [Google Scholar]
- Song, Z.; Wang, X.; Tan, Z.; Miao, X.; Zou, L. Analysis of Distribution Law of Fire Gas Concentration in Underground Cable Tunnel of Substation. In Proceedings of the 2020 IEEE International Conference on High Voltage Engineering and Application (ICHVE), Beijing, China, 6–10 September 2020; pp. 1–4. [Google Scholar]
- Wang, M.; Sun, Q.; Zhang, H.; Lu, Y.; Xu, D.; Zhang, Z. The study of fire spread trend in cable tunnels with different firewall spacing settings. In Proceedings of the 2022 IEEE 3rd China International Youth Conference on Electrical Engineering (CIYCEE), Wuhan, China, 3–5 November 2022; pp. 1–6. [Google Scholar]
- Wang, S.; Zhu, K.; Yao, Z.; Zhao, S.; Chen, Y.; Song, Z. Study on Combination Scheme of Cable Laying and Fire Prevention Measures in High Voltage Cable Trench. In Proceedings of the 2021 International Conference on Advanced Electrical Equipment and Reliable Operation (AEERO), Beijing, China, 15–17 October 2021; pp. 1–5. [Google Scholar]
- Ding, B.; Nie, X.; Lv, X.; Zhou, Y.; Su, Y.; Yang, H. Simulation of Fire Spread in Cable Tunnel with Different Fire Barriers. In Proceedings of the 2021 International Conference on Advanced Electrical Equipment and Reliable Operation (AEERO), Beijing, China, 15–17 October 2021; pp. 1–4. [Google Scholar]
- Ding, B.; Nie, X.; Lv, X.; Zhou, Y.; Su, Y.; Yang, H. Preparation and Properties Study on Geopolymer Fire Compartmentation Materials for Cable Trench. In Proceedings of the 2021 4th International Symposium on Traffic Transportation and Civil Architecture (ISTTCA), Suzhou, China, 12–14 November 2021; pp. 591–594. [Google Scholar]
- Cheng, Y.; Mou, C.; Chen, K.; Bai, H.; Liu, Y.; Zhang, Y. Experimental Study on Fire Extinguishing Effect of Water-based Fixed Fire Extinguishing System in full-Scale Bus Cabin. In Proceedings of the 2019 9th International Conference on Fire Science and Fire Protection Engineering (ICFSFPE), Chengdu, China, 18–20 October 2019; pp. 1–6. [Google Scholar]
- Zhu, H.; Chi, Q.; Sun, H.; Zhao, X. Study on Temperature Field of Cable Tunnel Fire. In Proceedings of the 2019 9th International Conference on Fire Science and Fire Protection Engineering (ICFSFPE), Chengdu, China, 18–20 October 2019; pp. 1–5. [Google Scholar]
- Liang, K. Research on Fire Spread Behavior and Smoke Flow Characteristics of Urban Underground Comprehensive Pipe Gallery Cables. Master’s Thesis, China University of Mining and Technology, Beijing, China, 2020. [Google Scholar]
- Li, Z.; Leng, X.; Yin, Q. Research on temperature distribution characteristics of tunnel fires based on distributed fiber optic monitoring. Mod. Tunn. Technol. 2022, 59, 132–139. [Google Scholar]
- Zhao, Y.; Zhu, G.; Gao, Y. Research on the smoke temperature field of urban underground comprehensive pipe gallery fires. Fire Sci. Technol. 2017, 36, 37–40. [Google Scholar]
- Wang, Z. Research on the Influencing Factors of Smoke Spread in Underground Comprehensive Pipe Gallery Fires. Master’s Thesis, Anhui University of Science and Technology, Huainan, China, 2019. [Google Scholar]
- Peng, Y. Numerical simulation of smoke movement under typical cable fire conditions. Shipbuild. Mar. Eng. 2016, 45, 65–68+73. [Google Scholar]
- Hao, G. Simulation Study on Fire and Smoke in Cable Cabin of Comprehensive Pipe Gallery. Master’s Thesis, Xi’an University of Architecture and Technology, Xi’an, China, 2017. [Google Scholar]
- Cram, D.; Hatch, C.E.; Tyler, S.; Ochoa, C. Use of Distributed Temperature Sensing Technology to Characterize Fire Behavior. Sensors 2016, 16, 1712. [Google Scholar] [CrossRef] [PubMed]
- Jain, J.P.; Singh, S.; Tyagi, N.S.; Singh, H.; Singh, I. Performance of ceramic-block fire stops for power cable installations. Fire Technol. 1996, 32, 272–280. [Google Scholar] [CrossRef]
- O’Halloran, B.M.; Papakonstantinou, N.; Van Bossuyt, D.L. Cable routing modeling in early system design to prevent cable failure propagation events. In Proceedings of the 2016 Annual Reliability and Maintainability Symposium (RAMS), Tucson, AZ, USA, 25–28 January 2016; pp. 1–6. [Google Scholar]
- Yun, X.; Ju, Z.; Zhang, Y.; Kong, F.; Ma, C.; Duan, X. Insulation Performance of Polyimide Materials Under Cable Arc. In Proceedings of the 18th Annual Conference of China Electrotechnical Society; ACCES 2023, Beijing, China, 15–17 September 2023; Yang, Q., Li, Z., Luo, A., Eds.; Lecture Notes in Electrical Engineering. Springer: Singapore, 2024; Volume 1167. [Google Scholar]
- Gong, H.; Guo, S.; Cheng, Y.; Tang, Z. Research on the Impact of Fire Source Location on High Voltage Cable Trench Fire Based on FDS. Ind. Saf. Environ. Prot. 2023, 49, 21–25. [Google Scholar]
- Tokarski, M.; Buczyński, R. Heat Transfer Analysis for Combustion under Low-Gradient Conditions in a Small-Scale Industrial Energy Systems. Energies 2024, 17, 186. [Google Scholar] [CrossRef]
- Yang, H. Fire Prevention, Flame Retardancy, and Fire Source Localization Methods for Power Cable Tunnels. Master’s Thesis, Shandong University, Jinan, China, 2023. [Google Scholar]
- GB/T 31431-2015; Standard Burning Items for Class A Fire Test of Extinguishing Systems. Standardization Press of China: Beijing, China, 2015.
- Li, Y.; Lei, B.; Ingason, H. The maximum temperature of buoyancy-driven smoke flow beneath the ceiling in tunnel fires. Fire Saf. J. 2011, 46, 204–210. [Google Scholar] [CrossRef]

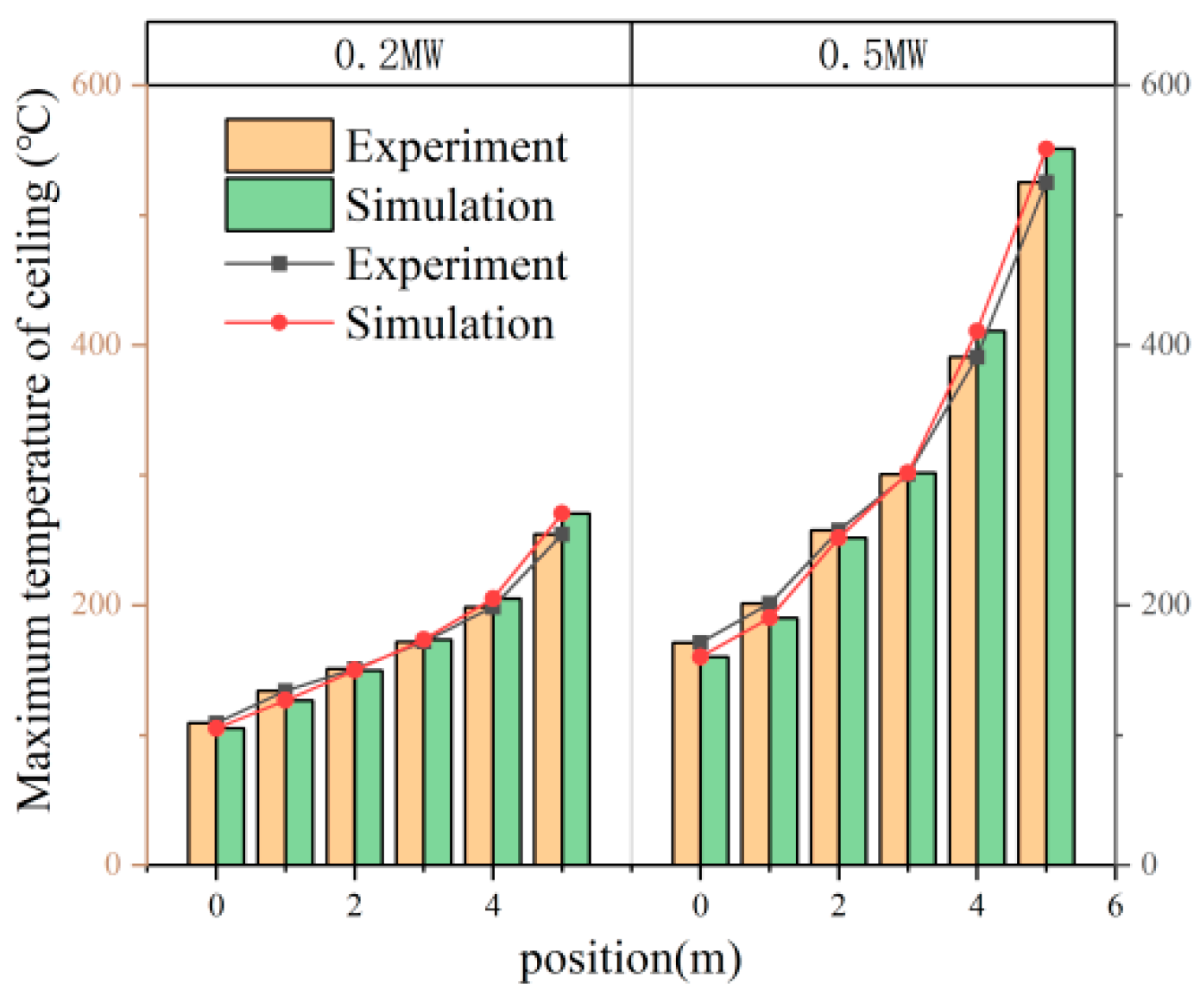


| Temperature Sensor Location | 0.2 MW | 0.5 MW |
|---|---|---|
| T0 (°C) | 109.3 | 171.2 |
| T1 (°C) | 134.1 | 201.3 |
| T2 (°C) | 151.2 | 257.5 |
| T3 (°C) | 171.8 | 300.8 |
| T4 (°C) | 198.5 | 390.8 |
| T5 (°C) | 254.5 | 525.2 |
| Variable | 0.2 MW | 0.5 MW |
|---|---|---|
| Tmax (°C) | 254.5 | 525.2 |
| ΔTmax (°C) | 244.5 | 515.2 |
| Q2/3 | 34.19 | 62.99 |
| H5/3 | 2.28 | 2.28 |
| α | 16.30 | 18.65 |
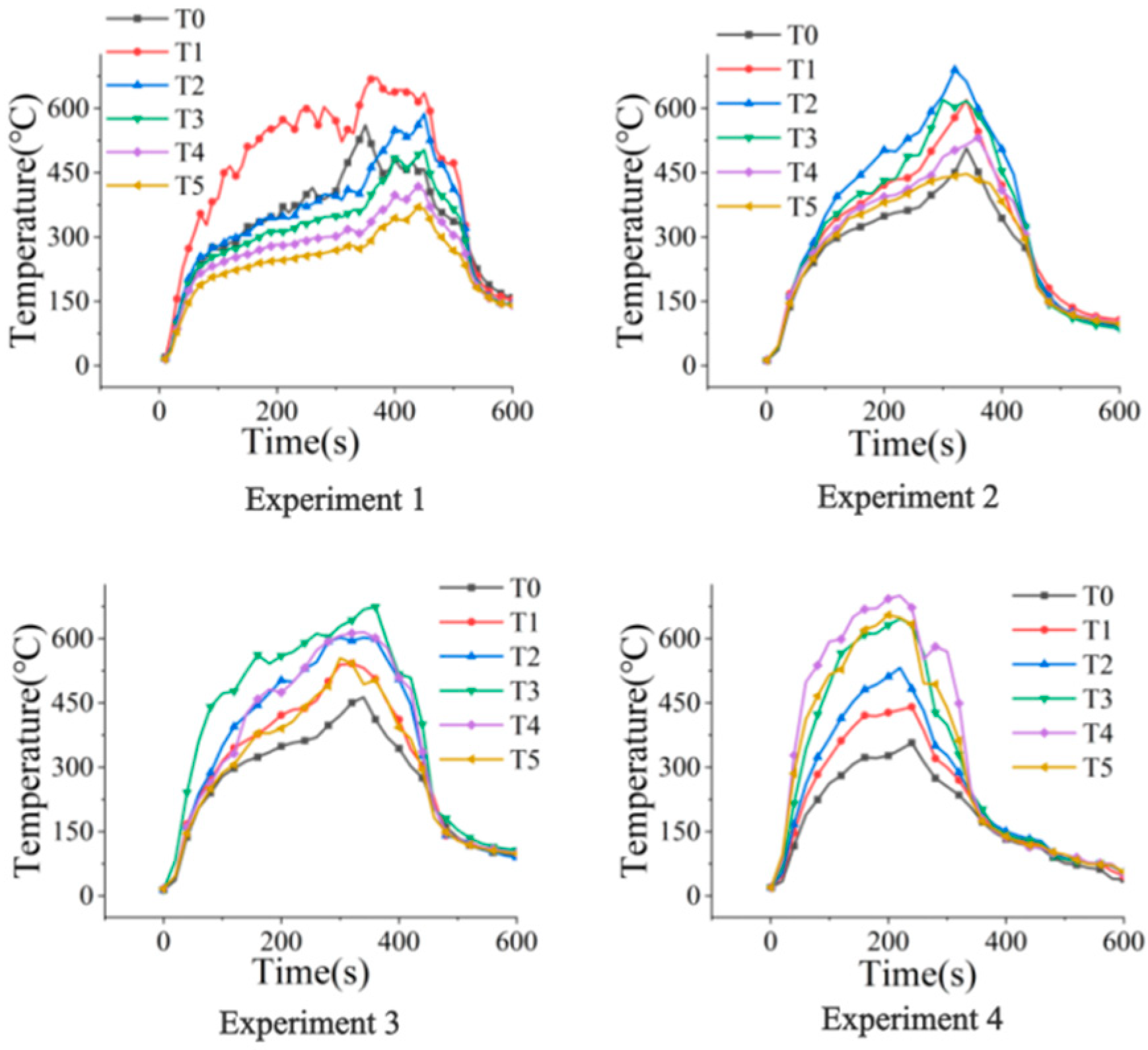
| Experiment Number | Parameter | X = 0 m | X = 1 m | X = 2 m | X = 3 m | X = 4 m | X = 5 m |
|---|---|---|---|---|---|---|---|
| Experiment 1 | ΔTmax | 551 | 661 | 578 | 493 | 408 | 360 |
| ΔTmax,x/ΔTmax | 0.83 | 1 | 0.87 | 0.74 | 0.62 | 0.54 | |
| d | 1 | 0 | 1 | 2 | 3 | 4 | |
| d/ΔH | 0.56 | 0 | 0.56 | 1.13 | 1.69 | 2.26 | |
| Experiment 2 | ΔTmax | 497 | 610 | 680 | 612 | 521 | 437 |
| ΔTmax,x/ΔTmax | 0.73 | 0.90 | 1 | 0.90 | 0.77 | 0.64 | |
| d | 2 | 1 | 0 | 1 | 2 | 3 | |
| d/ΔH | 1.13 | 0.56 | 0 | 0.56 | 1.13 | 1.69 | |
| Experiment 3 | ΔTmax | 453 | 531 | 592 | 678 | 605 | 521 |
| ΔTmax,x/ΔTmax | 0.67 | 0.78 | 0.87 | 1 | 0.89 | 0.77 | |
| d | 3 | 2 | 1 | 0 | 1 | 2 | |
| d/ΔH | 1.69 | 1.13 | 0.56 | 0 | 0.56 | 1.13 | |
| Experiment 4 | ΔTmax | 347 | 430 | 522 | 636 | 690 | 645 |
| ΔTmax,x/ΔTmax | 0.50 | 0.62 | 0.75 | 0.92 | 1 | 0.93 | |
| d | 4 | 3 | 2 | 1 | 0 | 1 | |
| d/ΔH | 2.26 | 1.69 | 1.13 | 0.56 | 0 | 0.56 |
| Experiment Number | Fitting Function Expression | R2 |
|---|---|---|
| 1 | ΔTmax,x/ΔTmax = 0.6424 − 0.5736 × (1 − e^(−(d/ΔH) + 1.5981)/3.3116) | 0.993 |
| 2 | ΔTmax,x/ΔTmax = 0.6796 − 1.8827 × (1 − e^(−(d/ΔH) + 1.5003)/9.1240) | 0.981 |
| 3 | ΔTmax,x/ΔTmax = 0.6574 − 1.3661 × (1 − e^(−(d/ΔH) + 1.7735)/7.9575) | 0.996 |
| 4 | ΔTmax,x/ΔTmax = 0.6864 − 1.8099 × (1 − e^(−(d/ΔH) + 1.4289)/7.9970) | 0.981 |
| Experiment Number | d1/m | d2/m | T0/°C | T5/°C | Tmax/°C | ΔTmax, x0/°C | ΔTmax, x5/°C | ΔTmax/°C |
|---|---|---|---|---|---|---|---|---|
| 5 | 1.5 | 3.5 | 577 | 399 | 709 | 567 | 389 | 699 |
| 6 | 2.5 | 2.5 | 497 | 505 | 715 | 487 | 495 | 705 |
| 7 | 3.5 | 1.5 | 411 | 565 | 706 | 401 | 555 | 696 |
| Example Number | Parameter Values | Predicting Experimental Subjects | d1 Calculation Value/m | d2 Calculation Value/m | d1 Actual Value/m | d2 Actual Value/m | Error ε/m | Accuracy |
|---|---|---|---|---|---|---|---|---|
| Example 1 | y0 = 0.6424 A = 0.5736 TD = 1.5981 Tau = 3.3116 | 5 | 1.414 | 3.586 | 1.5 | 3.5 | 0.086 | 0.975 |
| 6 | 2.261 | 2.739 | 2.5 | 2.5 | 0.239 | 0.904 | ||
| 7 | 3.452 | 1.548 | 3.5 | 1.5 | 0.048 | 0.986 | ||
| Example 2 | y0 = 0.6796 A = 1.8827 TD = 1.5003 Tau = 9.1240 | 5 | 1.402 | 3.598 | 1.5 | 3.5 | 0.098 | 0.972 |
| 6 | 2.475 | 2.525 | 2.5 | 2.5 | 0.025 | 0.990 | ||
| 7 | 3.492 | 1.508 | 3.5 | 1.5 | 0.008 | 0.998 | ||
| Example 3 | y0 = 0.6574 A = 1.3661 TD = 1.7735 Tau = 7.9575 | 5 | 1.417 | 3.583 | 1.5 | 3.5 | 0.083 | 0.976 |
| 6 | 2.700 | 2.300 | 2.5 | 2.5 | 0.200 | 0.920 | ||
| 7 | 3.343 | 1.657 | 3.5 | 1.5 | 0.157 | 0.955 | ||
| Example 4 | y0 = 0.6864 A = 1.8099 TD = 1.2890 Tau = 7.9979 | 5 | 1.402 | 3.598 | 1.5 | 3.5 | 0.092 | 0.974 |
| 6 | 2.370 | 2.830 | 2.5 | 2.5 | 0.130 | 0.948 | ||
| 7 | 3.647 | 1.353 | 3.5 | 1.5 | 0.147 | 0.958 |
| Example Number | d1/m | d2/m | ΔTmax Measurement Value/°C | ΔTmax Calculated Value/°C | Error ε/°C | Accuracy |
|---|---|---|---|---|---|---|
| Example 5 | 1.5 | 3.5 | 699 | 710 | 11 | 0.986 |
| Example 6 | 2.5 | 2.5 | 705 | 719 | 14 | 0.980 |
| Example 7 | 3.5 | 1.5 | 696 | 708 | 12 | 0.983 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Zou, L.; Yang, H.; Han, Z. Prediction of Ceiling Temperature Rise in High-Voltage Cable Trenches with Identification of Ignition Points. Fire 2024, 7, 316. https://doi.org/10.3390/fire7090316
Zhang Z, Zou L, Yang H, Han Z. Prediction of Ceiling Temperature Rise in High-Voltage Cable Trenches with Identification of Ignition Points. Fire. 2024; 7(9):316. https://doi.org/10.3390/fire7090316
Chicago/Turabian StyleZhang, Zhaochen, Liang Zou, Hongmin Yang, and Zhiyun Han. 2024. "Prediction of Ceiling Temperature Rise in High-Voltage Cable Trenches with Identification of Ignition Points" Fire 7, no. 9: 316. https://doi.org/10.3390/fire7090316
APA StyleZhang, Z., Zou, L., Yang, H., & Han, Z. (2024). Prediction of Ceiling Temperature Rise in High-Voltage Cable Trenches with Identification of Ignition Points. Fire, 7(9), 316. https://doi.org/10.3390/fire7090316