Characteristics of Hydrogen Leakage and Dissipation from Storage Tanks in an Integrated Hydrogen Production and Refueling Station
Abstract
1. Introduction
2. Numerical Modeling of Hydrogen Leakage and Dissipation
2.1. Mathematical Model
2.1.1. Governing Equations
2.1.2. Turbulence Model
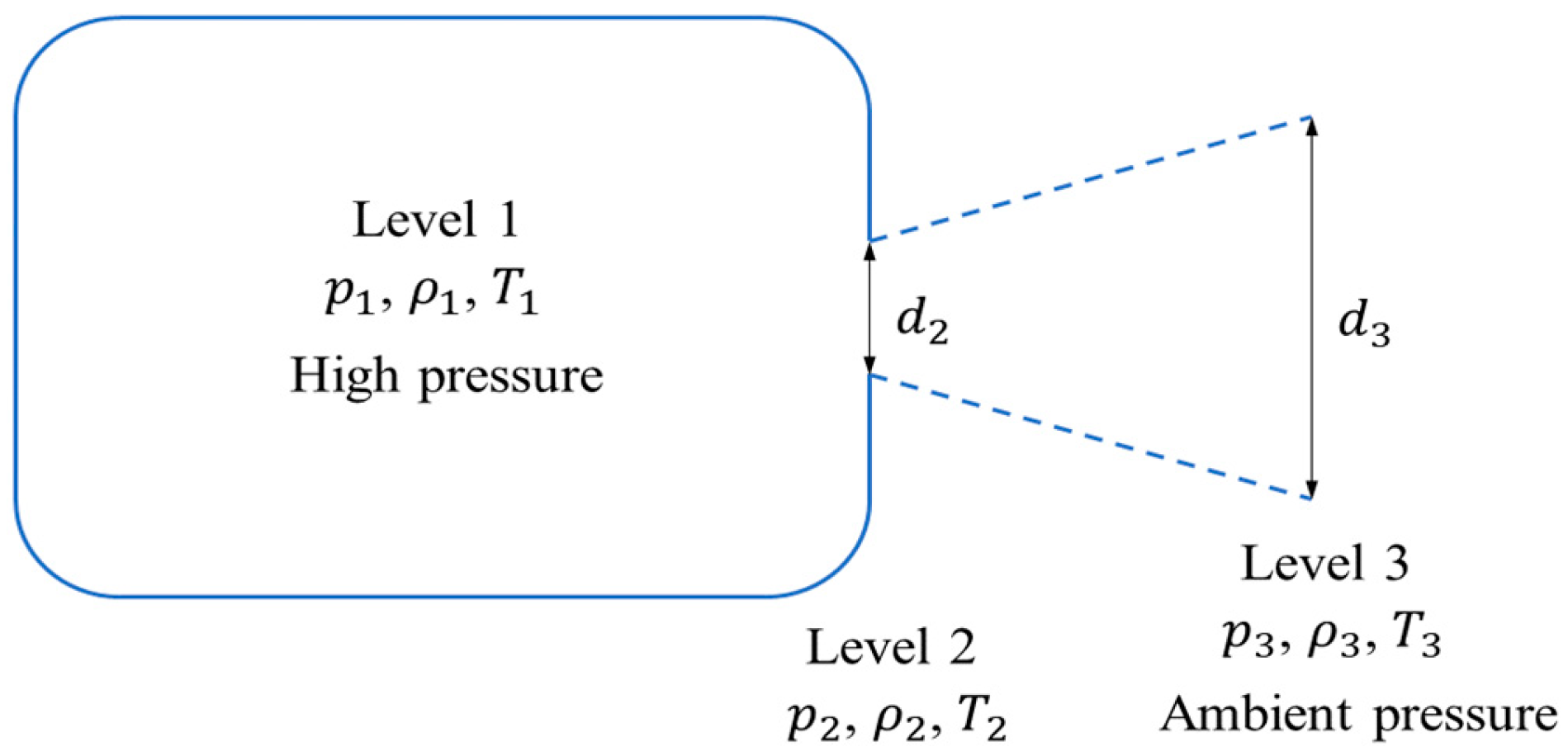
2.1.3. Virtual Nozzle Model
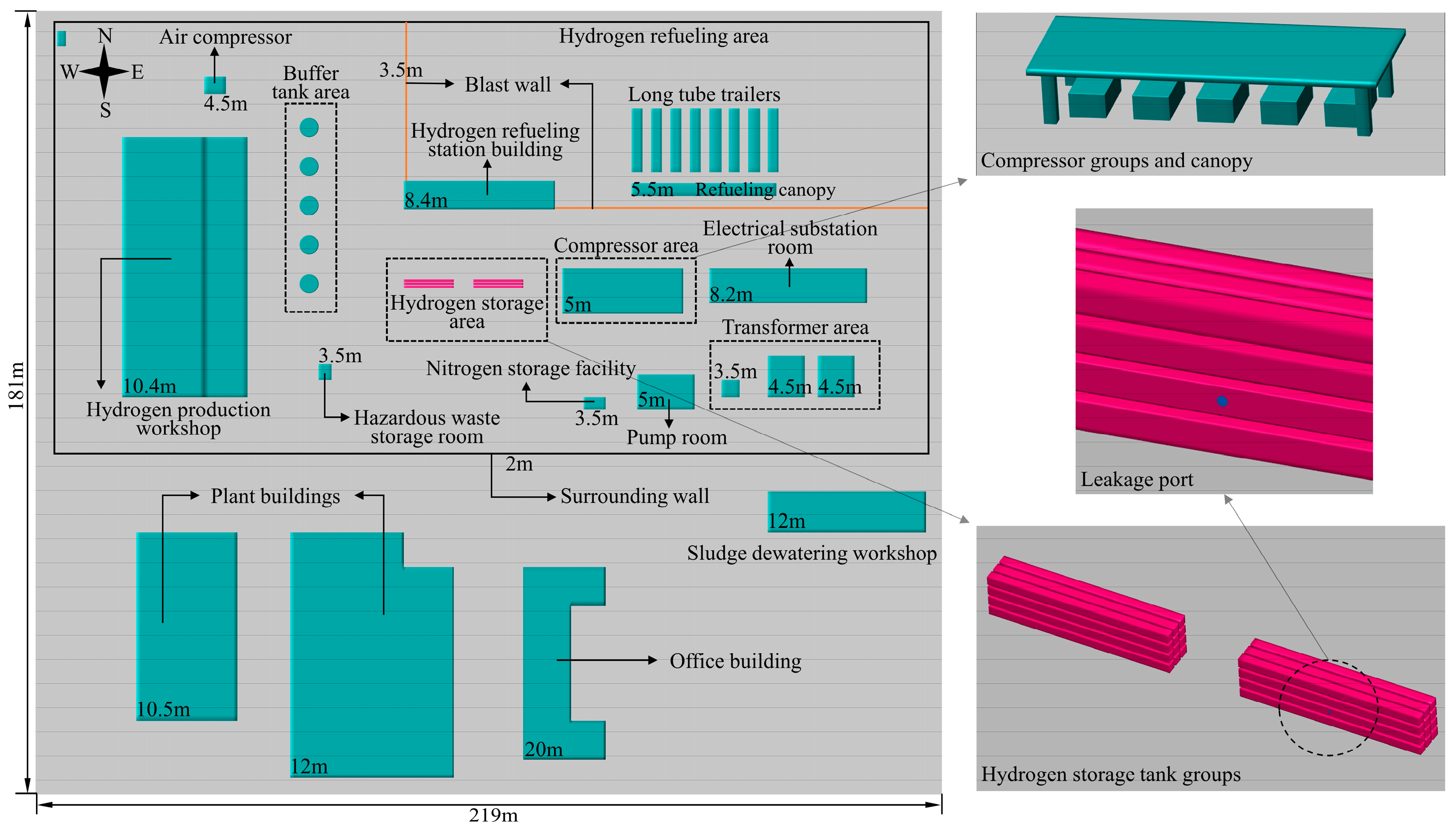
2.2. Numerical Modeling and Boundary Conditions
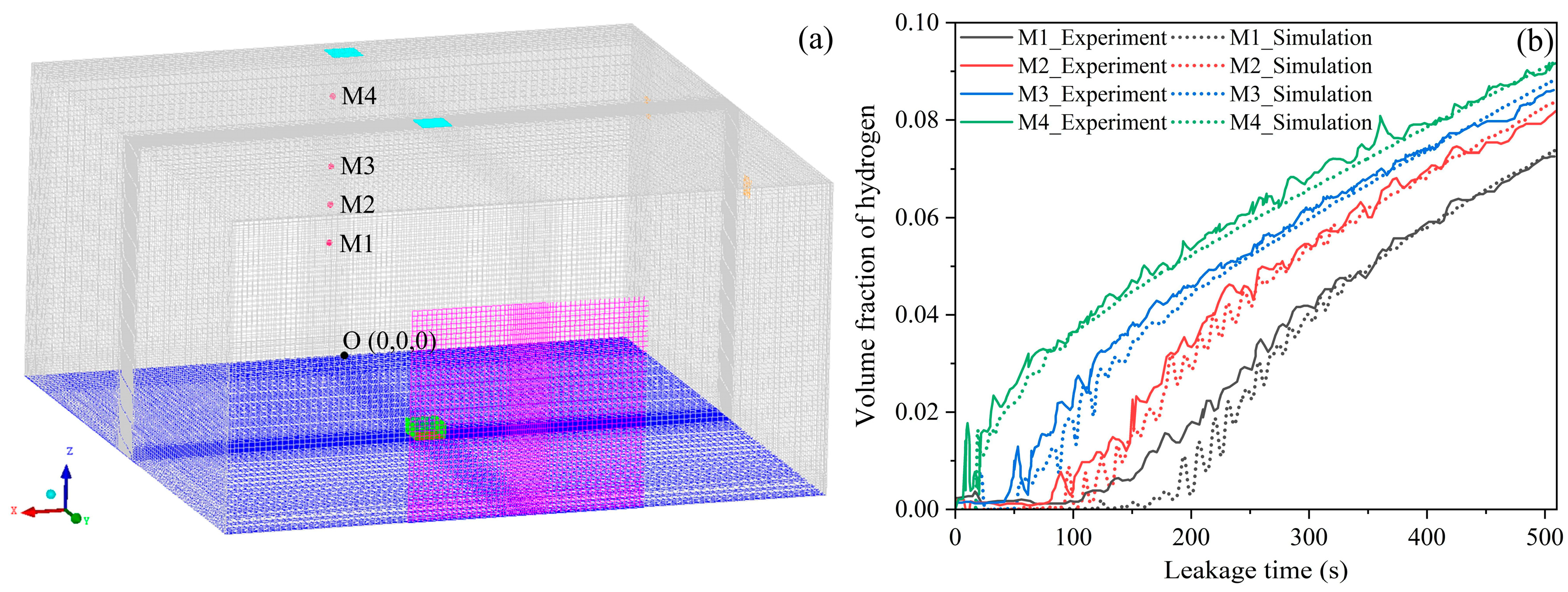
2.3. Model Validation and Mesh Independence Analysis
2.3.1. CFD Model Validation
2.3.2. Mesh Independence Analysis
3. Results and Discussion
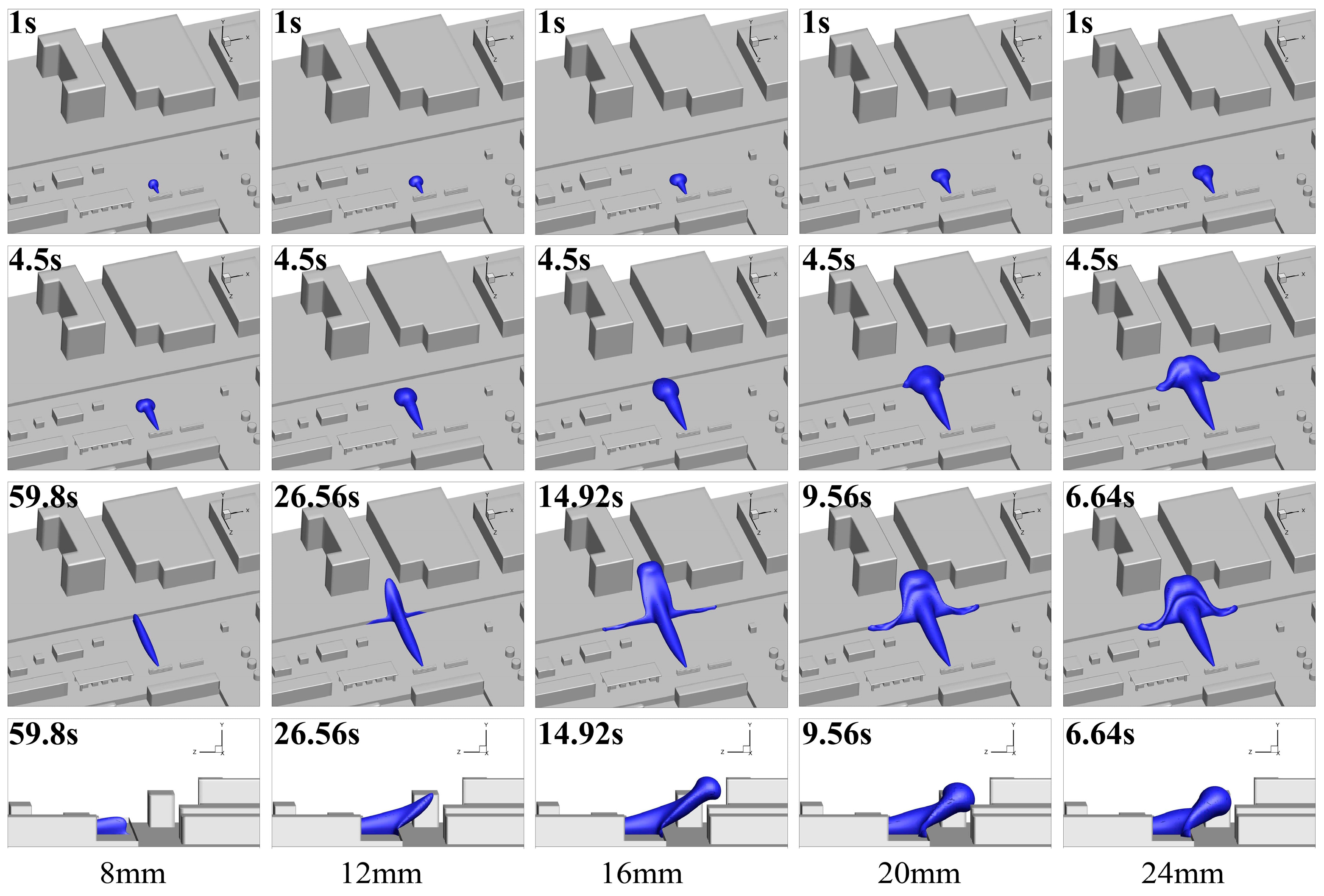
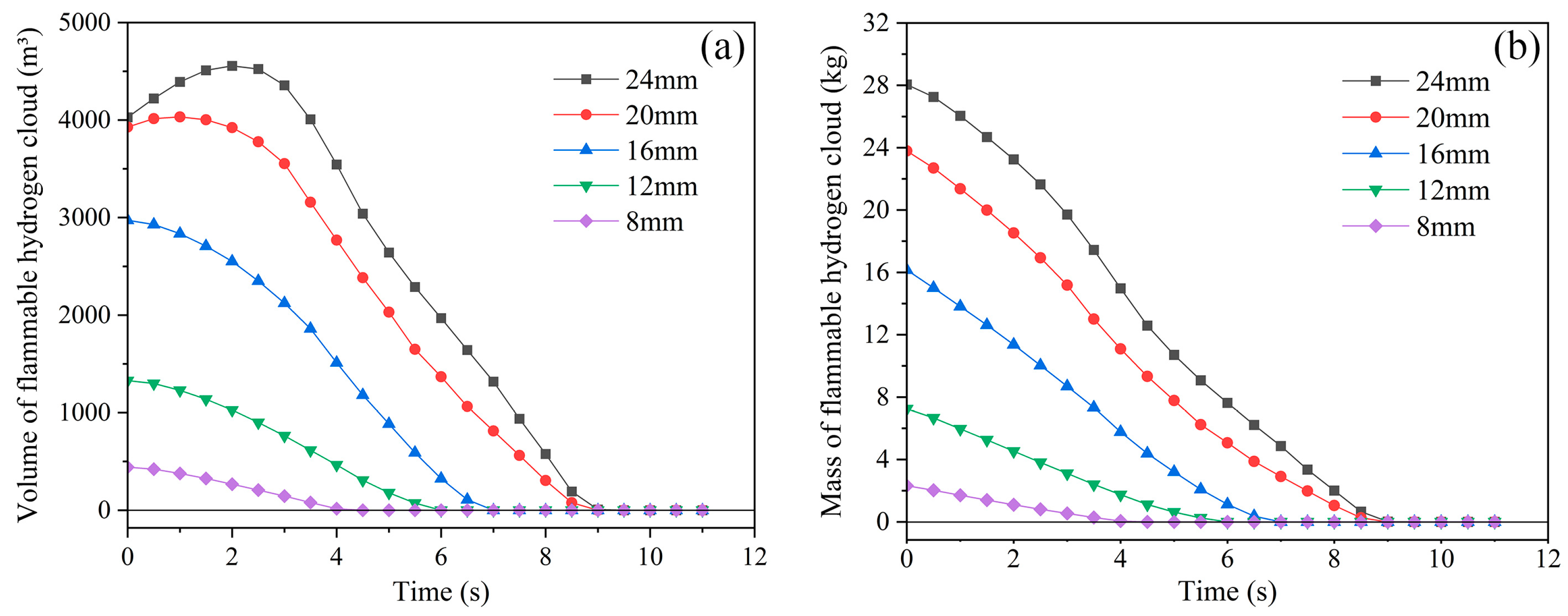
3.1. Effect of Leakage Aperture on Hydrogen Leakage and Dissipation Behavior
3.1.1. Leakage Processes at Different Leakage Apertures
3.1.2. Dissipation Processes at Different Leakage Apertures
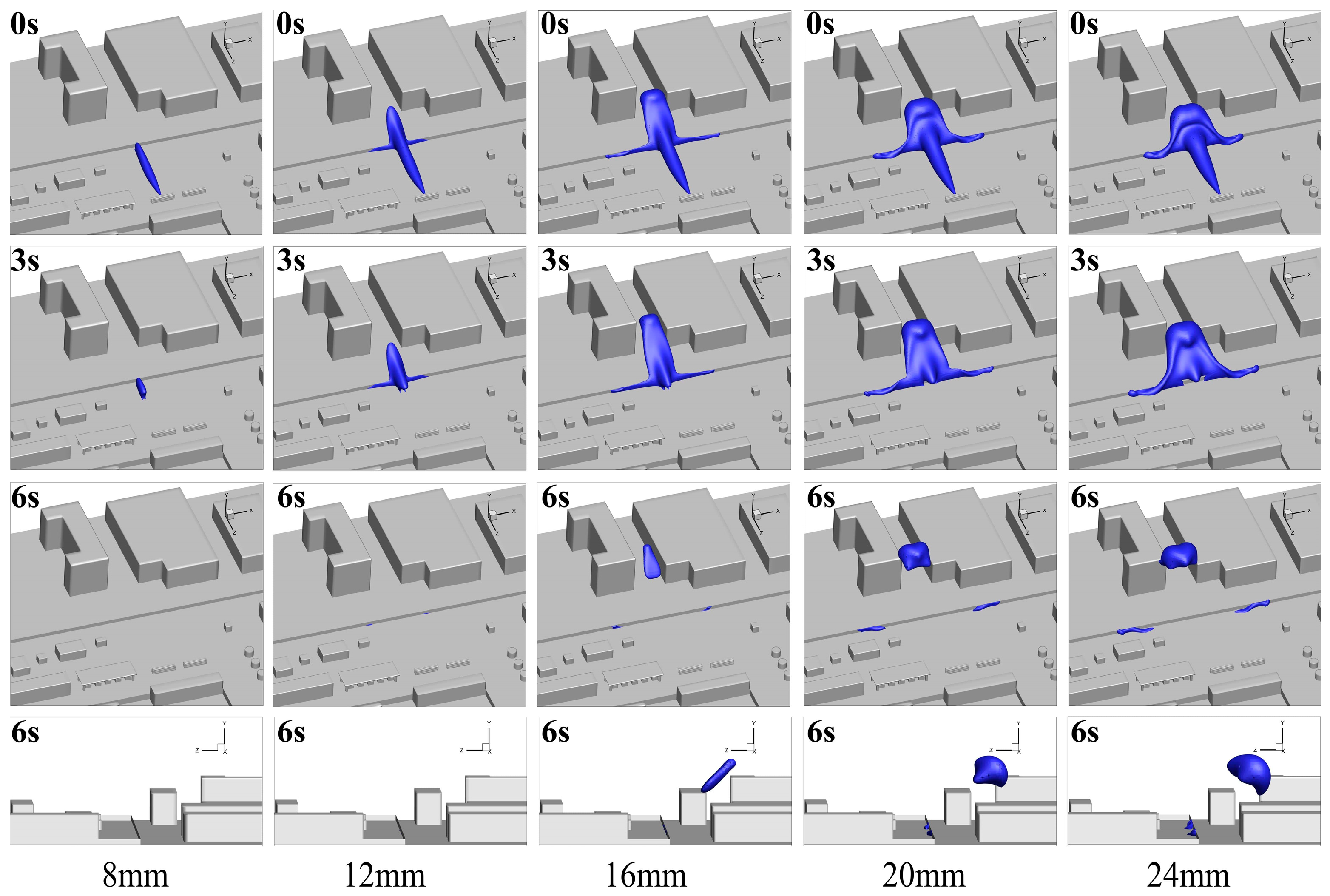
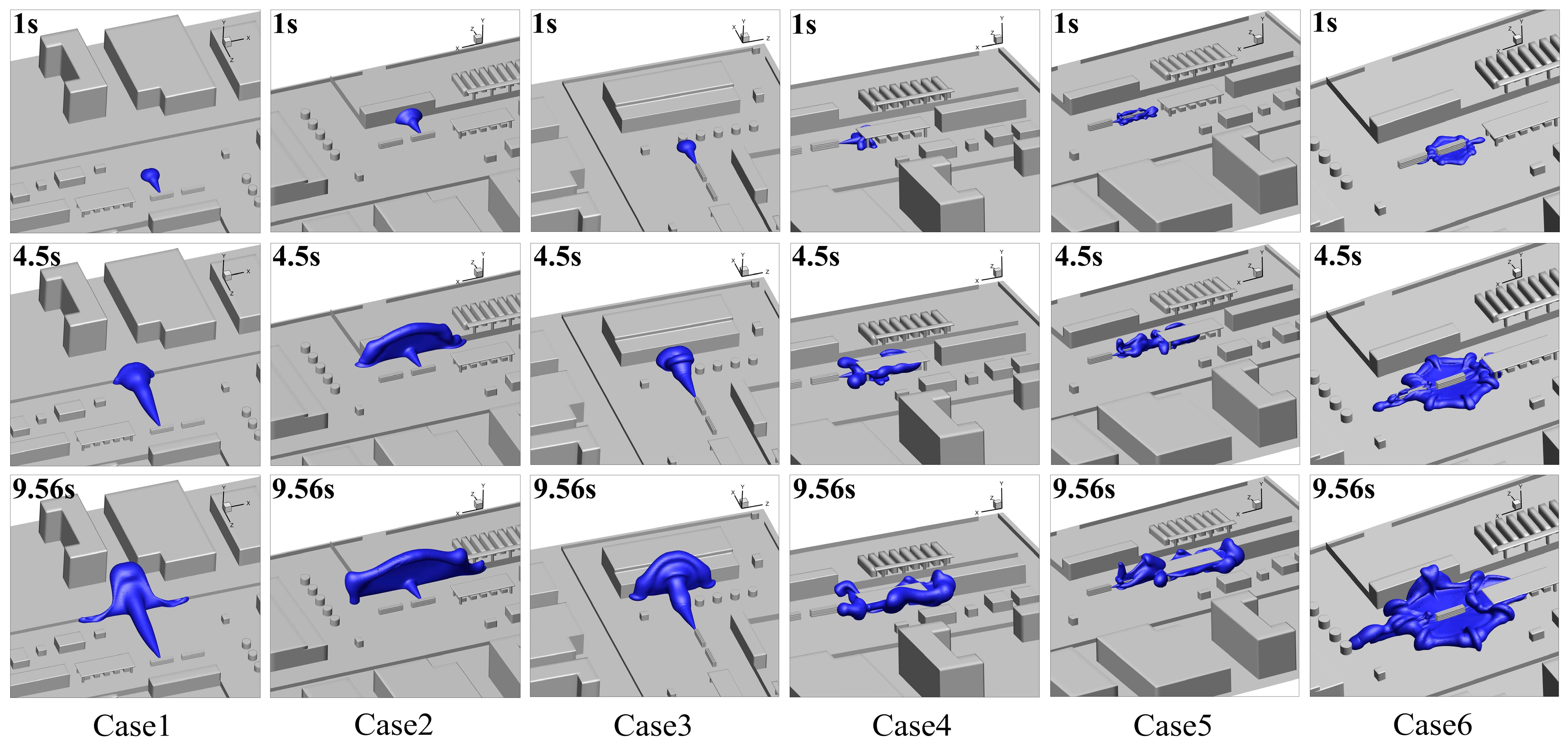
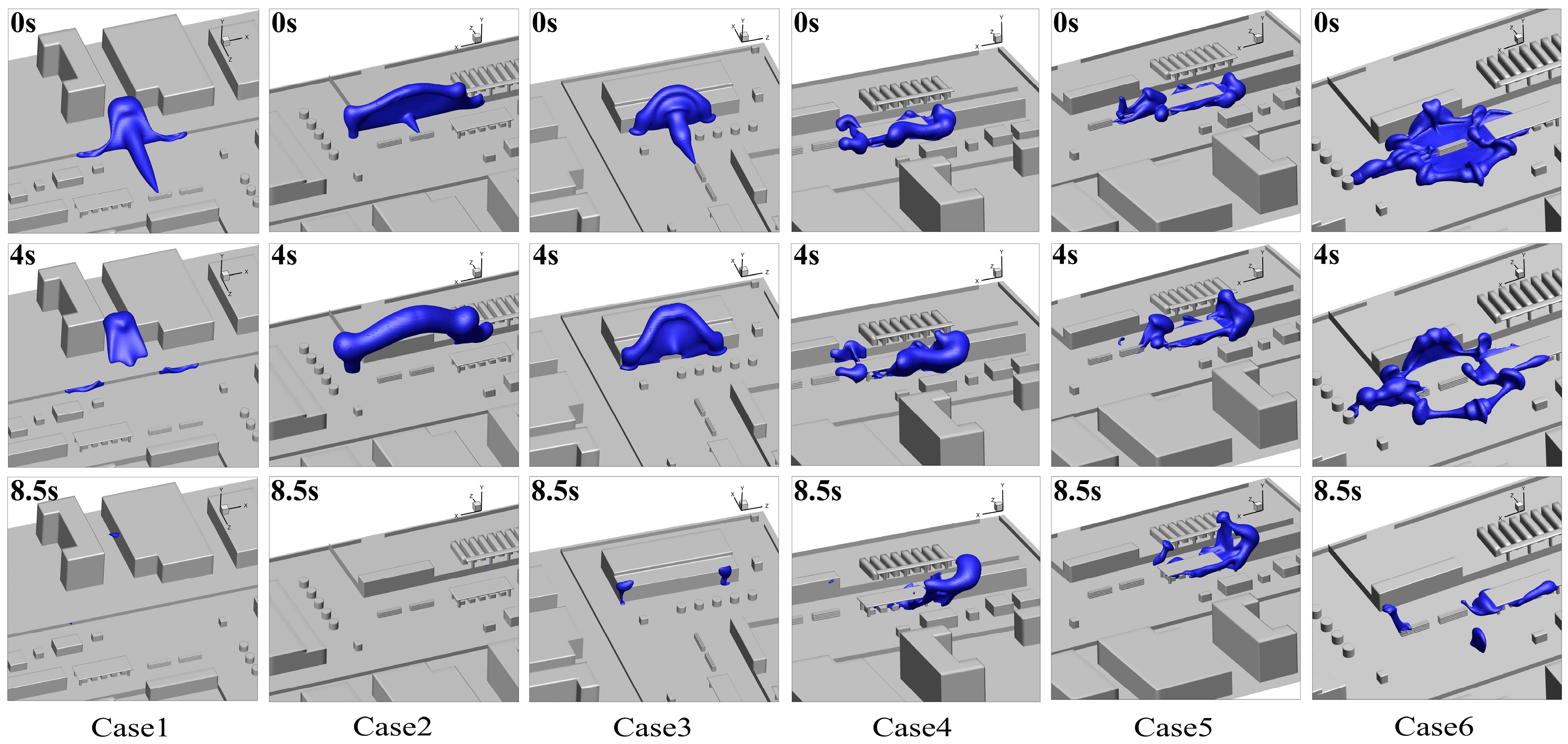
3.2. Effect of Leakage Direction on Hydrogen Leakage and Dissipation Behavior
3.2.1. Leakage Processes at Different Leakage Directions
3.2.2. Dissipation Process at Different Leakage Directions
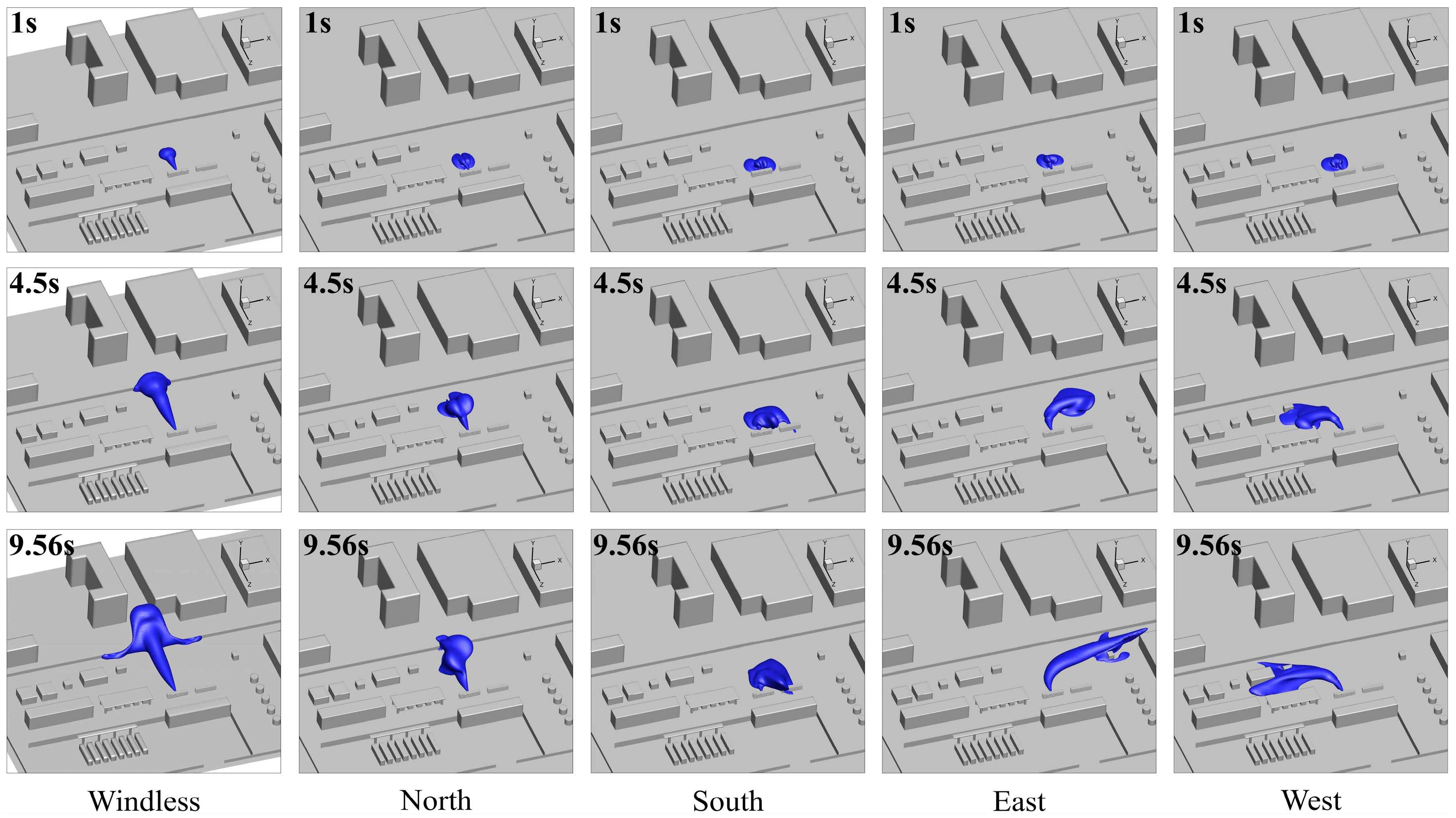
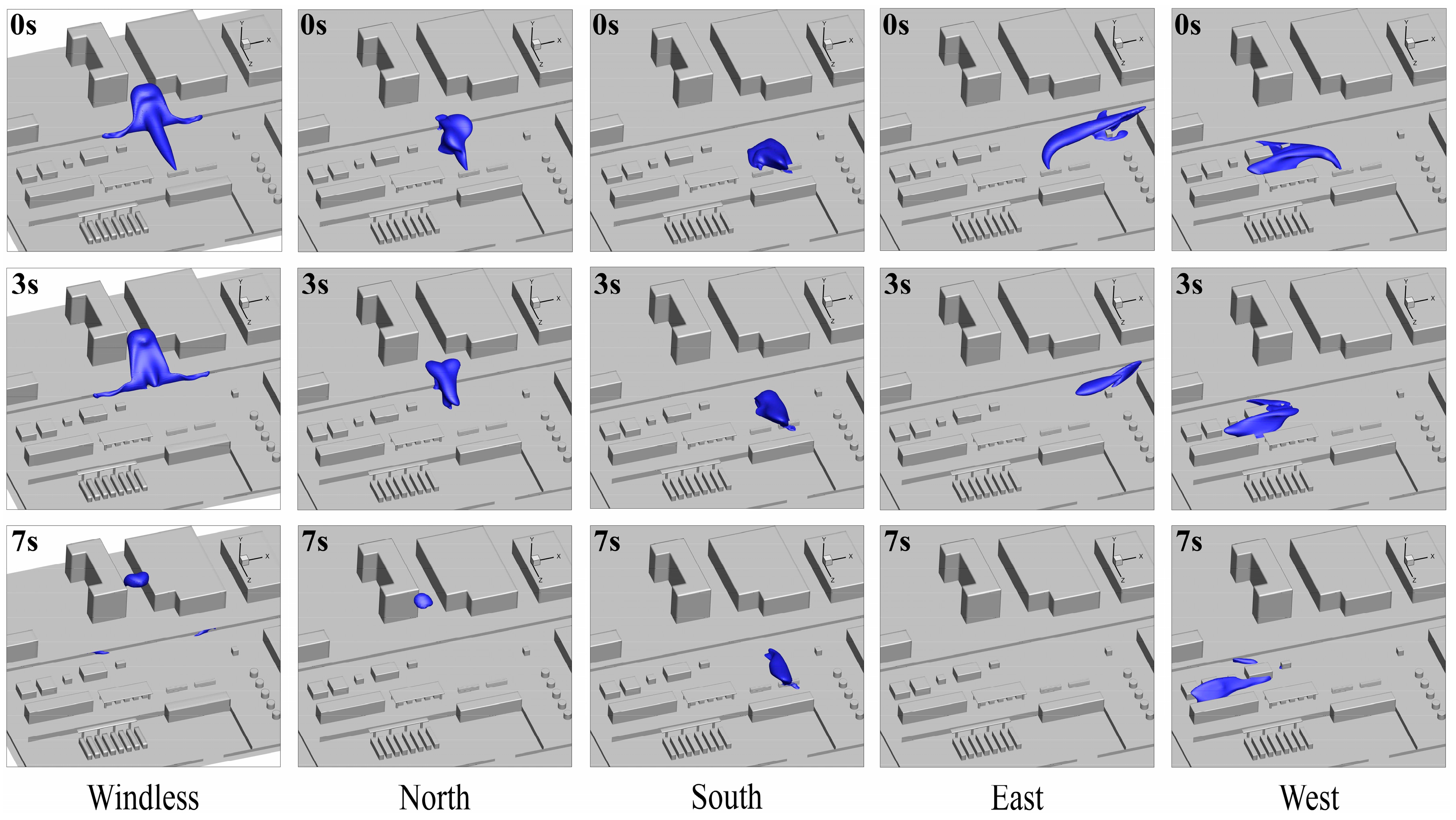
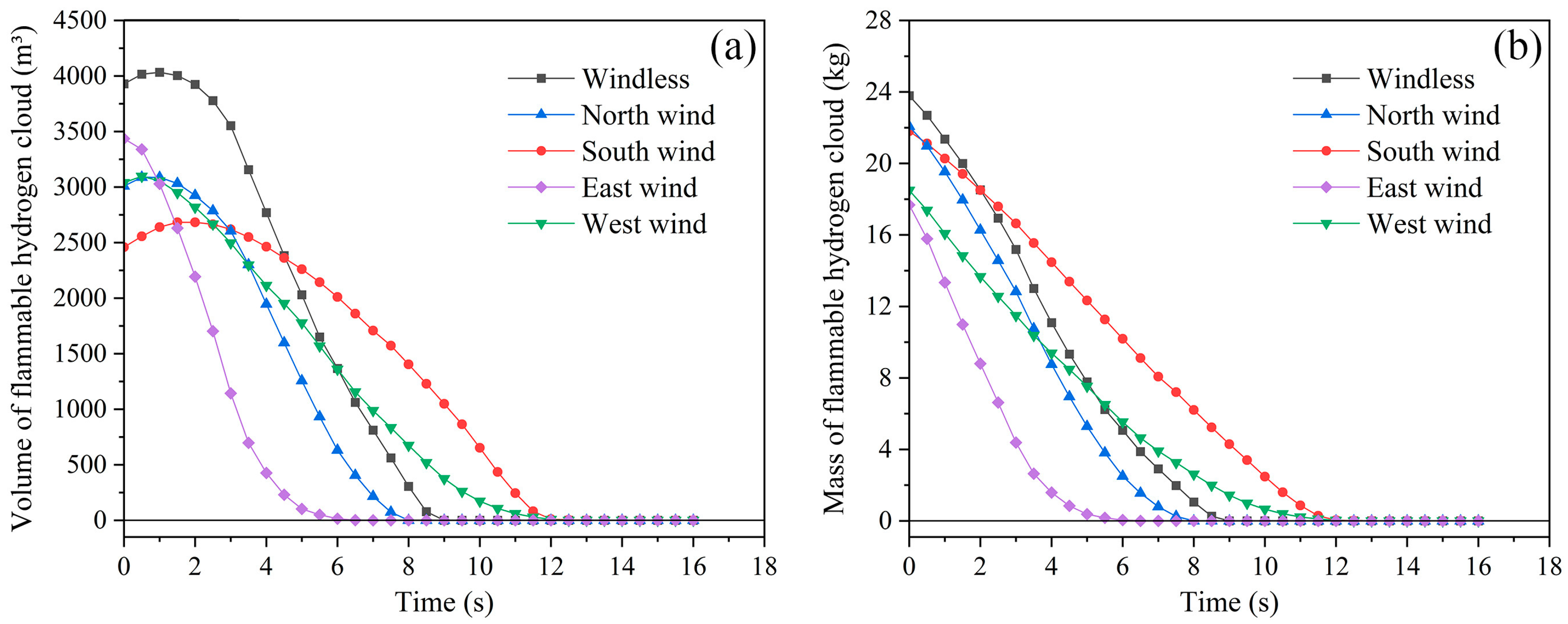
3.3. Effect of Ambient Wind Directions on Hydrogen Leakage and Dissipation Behavior
3.3.1. Leakage Processes at Different Ambient Wind Directions
3.3.2. Dissipation Processes at Different Ambient Wind Directions
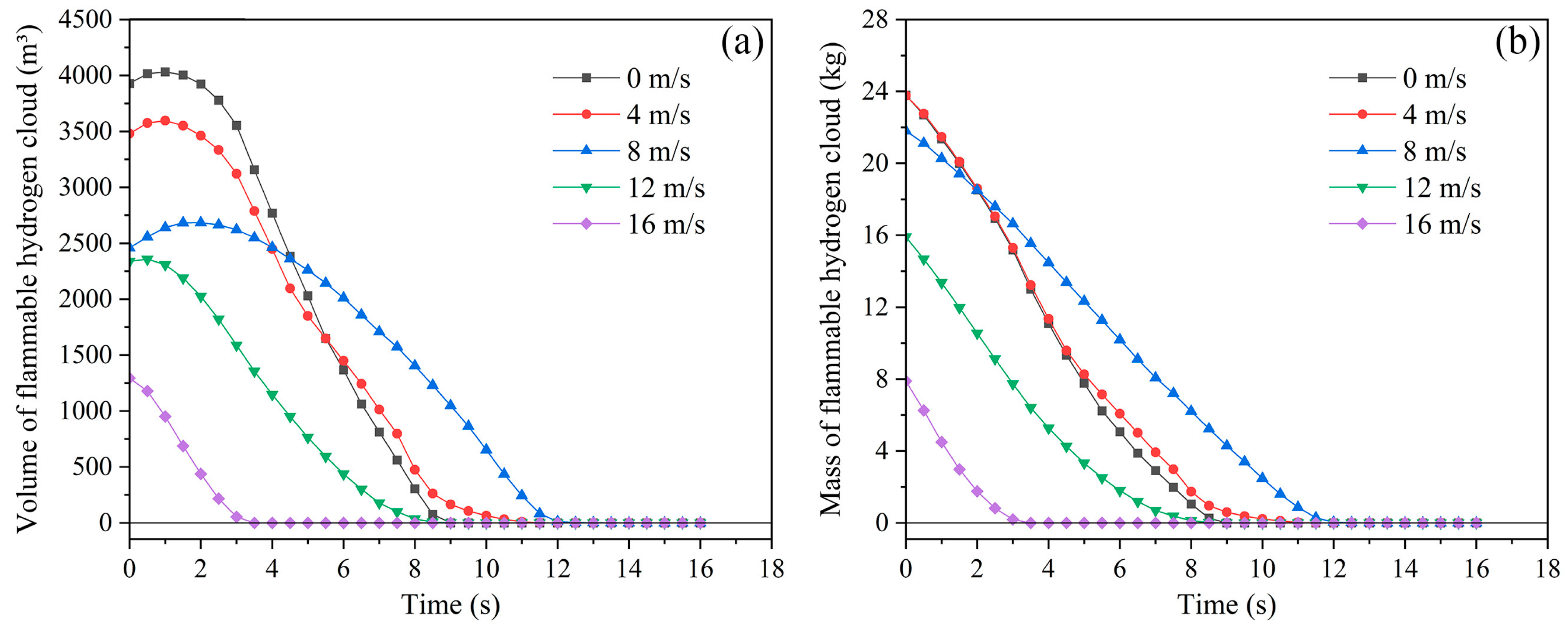
3.4. Effect of Ambient Wind Speed on Hydrogen Leakage and Dissipation Behavior
3.4.1. Leakage Processes at Different Ambient Wind Speeds
3.4.2. Dissipation Processes at Different Ambient Wind Speeds
4. Conclusions
- (1)
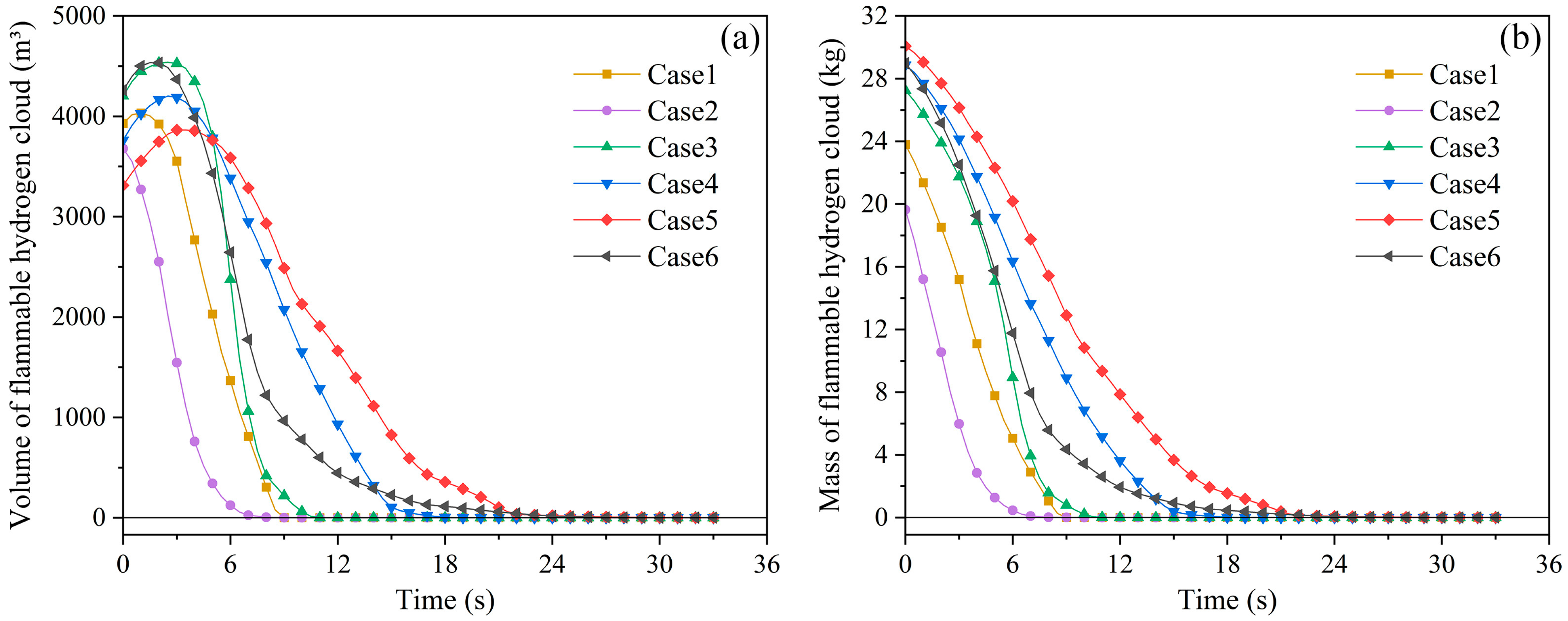
- As the leakage aperture increased, the volume and mass of the FHC increased as the hydrogen storage tank emptied. During the subsequent dissipation, the volume, mass and dissipation time of the FHC increased with an increasing leakage aperture, implying that leakage with a large aperture resulted in a larger hazard range, hazard degree and a longer hazard duration.
- (2)
- When the leakage direction was toward the ground, the leaking hydrogen formed a huge FHC on the ground level, and the hazard range was extremely large. The areas with densely packed equipment, especially in the presence of a canopy, seriously slowed down the dissipation of the FHC. Therefore, a canopy or densely packed equipment near hydrogen storage areas should be avoided.
- (3)
- Ambient winds can significantly affect the hydrogen leakage behavior. When the ambient wind direction was opposite to the leakage direction, the movement of hydrogen was hindered by air flows, which may have resulted in a highly concentrated FHC that gathered near the storage tanks and was difficult to dissipate. If the FHC ignites, it may lead to serial explosions of the storage tanks, which may seriously threaten the safety of the integrated station.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hu, D.H.; Gao, P.; Cheng, Z.X.; Shen, Y.R.; He, R.; Yi, F.Y.; Lu, M.; Wang, J.; Liu, S. Comprehensive review of hydrogen leakage in relation to fuel cell vehicles and hydrogen refueling stations: Status, challenges, and future prospects. Energy Fuels 2024, 38, 4803–4835. [Google Scholar] [CrossRef]
- Wang, C.P.; Zhao, L.C.; Qu, J.; Xiao, Y.; Deng, J.; Shu, C.M. Minireview on the leakage ignition and flame propagation characteristics of hydrogen: Advances and perspectives. Energy Fuels 2023, 37, 5653–5666. [Google Scholar] [CrossRef]
- Lyu, S.; Huang, X.M.; Peng, S.N.; Sun, M.X.; Qi, Q.; Aimaieraili, D. A novel method for analyzing the leakage and diffusion of hydrogen: First arrival time distribution. Renew. Sustain. Energy Rev. 2024, 198, 114451. [Google Scholar] [CrossRef]
- Zhao, Q.S.; Li, Y.; Cao, W.H.; Li, Y.B. Risk analysis of high-pressure hydrogen leakage in confined space with tube skid container for cylinder. Int. J. Hydrogen Energy 2024, 60, 581–592. [Google Scholar] [CrossRef]
- Yan, M.H.; Wang, W.; Tian, S.X.; Liu, J.; Jiang, Z.B.; Dai, Z.Y. Study of the influence of different ignition times on detonation generation and shock wave propagation in high-pressure hydrogen leakage. Case Stud. Therm. Eng. 2024, 57, 104318. [Google Scholar] [CrossRef]
- Liu, J.; Zheng, S.Y.; Zhang, Z.X.; Zheng, J.Y.; Zhao, Y.Z. Numerical study on the fast filling of on-bus gaseous hydrogen storage cylinder. Int. J. Hydrogen Energy 2020, 45, 9241–9251. [Google Scholar] [CrossRef]
- Jiang, Y.M.; Pan, X.H.; Cai, Q.; Klymenko, O.V.; Hua, M.; Zhang, T.; Wang, Z.L.; Wang, Q.Y.; Yu, A.D.; Jiang, J.C. Effects of the partially open inlet on shock waves and spontaneous ignition during the leakage of hydrogen. Process Saf. Environ. Prot. 2022, 168, 1089–1100. [Google Scholar] [CrossRef]
- Jorgensen, S.W. Hydrogen storage tanks for vehicles: Recent progress and current status. Curr. Opin. Solid State Mater. Sci. 2011, 15, 39–43. [Google Scholar] [CrossRef]
- Acar, C.; Dincer, I. Review and evaluation of hydrogen production options for better environment. J. Clean. Prod. 2019, 218, 835–849. [Google Scholar] [CrossRef]
- Bi, Y.B.; Wu, Q.L.; Wang, S.L.; Shi, J.H.; Cong, H.Y.; Ye, L.L.; Gao, W.; Bi, M.S. Hydrogen leakage location prediction at hydrogen refueling stations based on deep learning. Energy 2023, 284, 209–220. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, X.Y.; Shan, M.M.; Qi, M.; Shu, C.M.; Li, B.; Liu, Y. Methodology for optimally designing firewalls in hydrogen refueling stations. Int. J. Hydrogen Energy 2024, 49, 1196–1209. [Google Scholar] [CrossRef]
- Yang, N.N.; Deng, J.; Wang, C.P.; Bai, Z.J.; Qu, J. High pressure hydrogen leakage diffusion: Research progress. Int. J. Hydrogen Energy 2024, 50, 1029–1046. [Google Scholar] [CrossRef]
- Lai, Q.; Sun, Y.; Wang, T.; Modi, P.; Cazorla, C.; Demirci, U.B.; Ares Fernandez, J.R.; Leardini, F.; Aguey Zinsou, K.F. How to design hydrogen storage materials? Fundamentals, synthesis, and storage tanks. Adv. Sustain. Syst. 2019, 3, 1900043. [Google Scholar] [CrossRef]
- Omid, M.A.; Şahin, M.E.; Cora, Ö.N. Challenges and future perspectives on production, storage technologies, and transportation of hydrogen: A review. Energy Technol. 2024, 12, 2300997. [Google Scholar] [CrossRef]
- Zhang, C.Z.; Cao, X.J.; Bujlo, P.; Chen, B.; Zhang, X.; Sheng, X.F.; Liang, C. Review on the safety analysis and protection strategies of fast filling hydrogen storage system for fuel cell vehicle application. J. Energy Storage 2022, 45, 103451. [Google Scholar] [CrossRef]
- Zhou, C.L.; Yang, Z.; Chen, G.H.; Li, X. Optimizing hydrogen refueling station layout based on consequences of leakage and explosion accidents. Int. J. Hydrogen Energy 2024, 54, 817–836. [Google Scholar] [CrossRef]
- Yang, F.Y.; Wang, T.Z.; Deng, X.T.; Dang, J.; Huang, Z.Y.; Hu, S.; Li, Y.Y.; Ouyang, M.G. Review on hydrogen safety issues: Incident statistics, hydrogen diffusion, and detonation process. Int. J. Hydrogen Energy 2021, 46, 31467–31488. [Google Scholar] [CrossRef]
- Li, Y.J.; Wang, Z.R.; Shi, X.M.; Fan, R.J. Safety analysis of hydrogen leakage accident with a mobile hydrogen refueling station. Process Saf. Environ. Prot. 2023, 171, 619–629. [Google Scholar] [CrossRef]
- Kobayashi, H.; Naruo, Y.; Maru, Y.; Takesaki, Y.; Miyanabe, K. Experiment of cryo-compressed (90-mpa) hydrogen leakage diffusion. Int. J. Hydrogen Energy 2018, 43, 17928–17937. [Google Scholar] [CrossRef]
- Guo, L.; Ba, Q.X.; Zhang, S.S. Study on hydrogen dynamic leakage and flame propagation at normal-temperature and high-pressure. Int. J. Hydrogen Energy 2023, 48, 27416–27426. [Google Scholar] [CrossRef]
- Xin, J.; Duan, Q.; Jin, K.; Sun, J. A reduced-scale experimental study of dispersion characteristics of hydrogen leakage in an underground parking garage. Int. J. Hydrogen Energy 2023, 48, 16936–16948. [Google Scholar] [CrossRef]
- Xu, Q.M.; Chen, G.H.; Xie, M.L.; Li, X.F.; Zhao, Y.M.; Su, S.; Li, S.M. Experimental and numerical studies on hydrogen leakage and dispersion evolution characteristics in space with large aspect ratios. J. Clean. Prod. 2024, 438, 140467. [Google Scholar] [CrossRef]
- Shu, Z.; Liang, W.; Zheng, X.; Lei, G.; Cao, P.; Dai, W.; Qian, H. Dispersion characteristics of hydrogen leakage: Comparing the prediction model with the experiment. Energy 2021, 236, 121420. [Google Scholar] [CrossRef]
- Tanaka, T.; Azuma, T.; Evans, J.A.; Cronin, P.M.; Johnson, D.M.; Cleaver, R.P. Experimental study on hydrogen explosions in a full-scale hydrogen filling station model. Int. J. Hydrogen Energy 2007, 32, 2162–2170. [Google Scholar] [CrossRef]
- Vanlaere, J.; Hendrick, P.; Blondeau, J. Indoor hydrogen dispersion with stratified filling: Can non-dimensional parameters relate dispersion characteristics across diverse applications? Int. J. Hydrogen Energy 2024, 81, 1216–1223. [Google Scholar] [CrossRef]
- Chang, Y.; Zhang, C.; Shi, J.; Li, J.; Zhang, S.; Chen, G. Dynamic bayesian network based approach for risk analysis of hydrogen generation unit leakage. Int. J. Hydrogen Energy 2019, 44, 26665–26678. [Google Scholar] [CrossRef]
- He, X.; Kong, D.; Yu, X.; Ping, P.; Wang, G.; Peng, R.; Zhang, Y.; Dai, X. Prediction model for the evolution of hydrogen concentration under leakage in hydrogen refueling station using deep neural networks. Int. J. Hydrogen Energy 2024, 51, 702–712. [Google Scholar] [CrossRef]
- Rostamzadeh, A.; Razavi, S.E.; Mirsajedi, S.M. Towards multidimensional artificially characteristic-based scheme for incompressible thermo-fluid problems. Mechanika 2017, 23, 826. [Google Scholar] [CrossRef][Green Version]
- Choi, J.; Hur, N.; Kang, S.; Lee, E.D.; Lee, K.B. A cfd simulation of hydrogen dispersion for the hydrogen leakage from a fuel cell vehicle in an underground parking garage. Int. J. Hydrogen Energy 2013, 38, 8084–8091. [Google Scholar] [CrossRef]
- Shentsov, V.; Cirrone, D.; Makarov, D. Effect of tprd diameter and direction of release on hydrogen dispersion and jet fires in underground parking. J. Energy Storage 2023, 68, 107771. [Google Scholar] [CrossRef]
- Wang, Q.; Zhai, C.; Gong, J.; Wang, Z.; Jiang, J.; Zhou, Y. Analytical and numerical predictions of hydrogen gas flow induced by wall and corner leakages in confined space. Int. J. Hydrogen Energy 2020, 45, 6848–6862. [Google Scholar] [CrossRef]
- Patel, P.; Baalisampang, T.; Arzaghi, E.; Garaniya, V.; Abbassi, R.; Salehi, F. Computational analysis of the hydrogen dispersion in semi-confined spaces. Process Saf. Environ. Prot. 2023, 176, 475–488. [Google Scholar] [CrossRef]
- Malakhov, A.A.; Avdeenkov, A.V.; du Toit, M.H.; Bessarabov, D.G. Cfd simulation and experimental study of a hydrogen leak in a semi-closed space with the purpose of risk mitigation. Int. J. Hydrogen Energy 2020, 45, 9231–9240. [Google Scholar] [CrossRef]
- Tian, Y.; Qin, C.; Yang, Z.; Hao, D. Numerical simulation study on the leakage and diffusion characteristics of high-pressure hydrogen gas in different spatial scenes. Int. J. Hydrogen Energy 2024, 50, 1335–1349. [Google Scholar] [CrossRef]
- Thomas, J.K.; Eastwood, C.; Goodrich, M. Are unconfined hydrogen vapor cloud explosions credible? Process Saf. Prog. 2015, 34, 36–43. [Google Scholar] [CrossRef]
- Kikukawa, S. Consequence analysis and safety verification of hydrogen fueling stations using cfd simulation. Int. J. Hydrogen Energy 2008, 33, 1425–1434. [Google Scholar] [CrossRef]
- Qian, J.Y.; Li, X.J.; Gao, Z.X.; Jin, Z.J. A numerical study of hydrogen leakage and diffusion in a hydrogen refueling station. Int. J. Hydrogen Energy 2020, 45, 14428–14439. [Google Scholar] [CrossRef]
- Patel, P.; Garaniya, V.; Baalisampang, T.; Arzaghi, E.; Abbassi, R.; Salehi, F. Enhancing safety in hydrogen refuelling stations: Computational analysis of hydrogen explosion hazards. Can. J. Chem. Eng. 2024, 2024, 1–16. [Google Scholar] [CrossRef]
- Wang, F.; Xiao, J.; Kuznetsov, M.; Breitung, W.; He, B.; Rui, S.; Zhou, S.; Jordan, T.; Song, K.; Zhang, L. Deterministic risk assessment of hydrogen leak from a fuel cell truck in a real-scale hydrogen refueling station. Int. J. Hydrogen Energy 2024, 50, 1103–1118. [Google Scholar] [CrossRef]
- Gao, Q.; Wang, L.; Peng, W.; Zhang, P.; Chen, S. Safety analysis of leakage in a nuclear hydrogen production system. Int. J. Hydrogen Energy 2022, 47, 4916–4931. [Google Scholar] [CrossRef]
- Han, U.; Oh, J.; Lee, H. Safety investigation of hydrogen charging platform package with cfd simulation. Int. J. Hydrogen Energy 2018, 43, 13687–13699. [Google Scholar] [CrossRef]
- Xiao, J.; Xu, N.; Li, Y.; Li, G.; Liu, M.; Tong, L.; Yuan, C.; Li, X.; Yang, T. CFD Simulation and ANN Prediction of Hydrogen Leakage and Diffusion Behavior in a Hydrogen Refuelling Station. Int. J. Energy Res. 2024, 2024, 8910533. [Google Scholar] [CrossRef]
- Cui, W.Y.; Yuan, Y.P.; Tong, L.; Shen, B.Y. Numerical simulation of hydrogen leakage diffusion in seaport hydrogen refueling station. Int. J. Hydrogen Energy 2023, 48, 24521–24535. [Google Scholar] [CrossRef]
- Lateb, M.; Masson, C.; Stathopoulos, T.; Bédard, C. Comparison of various types of k–ε models for pollutant emissions around a two-building configuration. J. Wind Eng. Ind. Aerodyn. 2013, 115, 9–21. [Google Scholar] [CrossRef]
- Lee, J.; Cho, S.; Cho, H.; Cho, S.; Lee, I.; Moon, I.; Kim, J. Cfd modeling on natural and forced ventilation during hydrogen leaks in a pressure regulator process of a residential area. Process Saf. Environ. Prot. 2022, 161, 436–446. [Google Scholar] [CrossRef]
- Molkov, V.; Makarov, D.; Bragin, M. Physics and Modelling of Under-Expanded Jets and Hydrogen Dispersion in Atmosphere. Phys. Extrem. States Matter 2009, 11, 143–145. [Google Scholar]
- Chenoweth, D.R.; Paolucci, S. Compressible flow of a two-phase fluid between finite vessels—II. Abel-noble carrier gas. Int. J. Multiph. Flow 1992, 18, 669–689. [Google Scholar] [CrossRef]
- ANSYS®. Available online: https://www.ansys.com (accessed on 23 August 2024).
- Nouroozi, M.; Pasandidehfard, M.; Djavareshkian, M.H. Simulation of partial and supercavitating flows around axisymmetric and quasi-3d bodies by boundary element method using simple and reentrant jet models at the closure zone of cavity. Math. Probl. Eng. 2016, 2016, 1593849. [Google Scholar] [CrossRef]
- Pitts, W.M.; Yang, J.C.; Prasad, K.; Fernandez, M. Dispersion and burning behavior of hydrogen released in a full-scale residential garage in the presence and absence of conventional automobiles. Int. J. Hydrogen Energy 2012, 37, 17457–17469. [Google Scholar] [CrossRef]



| Property | Value | Unit |
|---|---|---|
| Hydrogen storage tank type | III | / |
| Operating pressure | 20 | MPa |
| Outer diameter | 0.559 | m |
| Thickness of the tank wall | 0.0184 | m |
| Length | 11.58 | m |
| Volume | 2.36 | m3 |
| Monitoring Point | Experimental Value | Simulated Value | Relative Error (%) |
|---|---|---|---|
| M1 | 0.07311 | 0.07396 | 1.163 |
| M2 | 0.08203 | 0.08392 | 2.304 |
| M3 | 0.08658 | 0.08845 | 2.160 |
| M4 | 0.09174 | 0.09205 | 0.3379 |
| Leakage Aperture | Simplified Leakage Port Boundary Conditions for Virtual Nozzles | Leakage Duration |
|---|---|---|
| 8 mm | = 1187.6 m/s = 78.6 mm; T = 244.3 K | 59.80 s |
| 12 mm | = 1187.6 m/s = 117.9 mm; T = 244.3 K | 26.56 s |
| 16 mm | = 1187.6 m/s = 157.2 mm; T = 244.3 K | 14.92 s |
| 20 mm | = 1187.6 m/s = 196.5 mm; T = 244.3 K | 9.56 s |
| 24 mm | = 1187.6 m/s = 235.8 mm; T = 244.3 K | 6.64 s |
| Leakage Aperture (mm) | Diffusion Distance in Each Direction (m) | ||
|---|---|---|---|
| X | Y | Z | |
| 8 | 4.23 | 6.61 | 39.15 |
| 12 | 31.56 | 15.31 | 53.36 |
| 16 | 58.72 | 21.37 | 62.17 |
| 20 | 57.26 | 19.18 | 58.56 |
| 24 | 51.27 | 17.72 | 55.70 |
| Cases | Leakage Directions |
|---|---|
| Case 1 | Leakage toward the plant buildings and office building |
| Case 2 | Leakage toward the HRS building |
| Case 3 | Leakage toward the buffer tank and hydrogen production workshop |
| Case 4 | Leakage toward the compressor area |
| Case 5 | Leakage toward the adjacent hydrogen storage tank group |
| Case 6 | Leakage toward the ground |
| Cases | Diffusion Distance in Each Direction (m) | ||
|---|---|---|---|
| X | Y | Z | |
| Case 1 | 57.26 | 19.18 | 58.56 |
| Case 2 | 70.90 | 22.54 | 18.49 |
| Case 3 | 40.66 | 21.56 | 44.12 |
| Case 4 | 51.96 | 11.97 | 34.63 |
| Case 5 | 63.82 | 13.24 | 23.03 |
| Case 6 | 73.46 | 12.06 | 43.10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, T.; Xiao, Z.; Zeng, S.; Zhao, Y.; Xu, L.; Chen, S.; Song, C.; Yan, X.; Li, X.; Luo, H.; et al. Characteristics of Hydrogen Leakage and Dissipation from Storage Tanks in an Integrated Hydrogen Production and Refueling Station. Fire 2024, 7, 306. https://doi.org/10.3390/fire7090306
Yang T, Xiao Z, Zeng S, Zhao Y, Xu L, Chen S, Song C, Yan X, Li X, Luo H, et al. Characteristics of Hydrogen Leakage and Dissipation from Storage Tanks in an Integrated Hydrogen Production and Refueling Station. Fire. 2024; 7(9):306. https://doi.org/10.3390/fire7090306
Chicago/Turabian StyleYang, Tianqi, Zhili Xiao, Shiyan Zeng, Yingjiang Zhao, Linzhi Xu, Shiyu Chen, Chunyan Song, Xianglin Yan, Xuefang Li, Hao Luo, and et al. 2024. "Characteristics of Hydrogen Leakage and Dissipation from Storage Tanks in an Integrated Hydrogen Production and Refueling Station" Fire 7, no. 9: 306. https://doi.org/10.3390/fire7090306
APA StyleYang, T., Xiao, Z., Zeng, S., Zhao, Y., Xu, L., Chen, S., Song, C., Yan, X., Li, X., Luo, H., Xu, N., & Xiao, J. (2024). Characteristics of Hydrogen Leakage and Dissipation from Storage Tanks in an Integrated Hydrogen Production and Refueling Station. Fire, 7(9), 306. https://doi.org/10.3390/fire7090306







