Thermal Characteristics of Multiple Blockages with Various Sizes in Longitudinal Ventilated Tunnel Fire
Abstract
1. Introduction
2. Numerical Model
2.1. Physical Model
2.2. Grid Independence Analysis
2.3. Dependability Verification
3. Results and Discussion
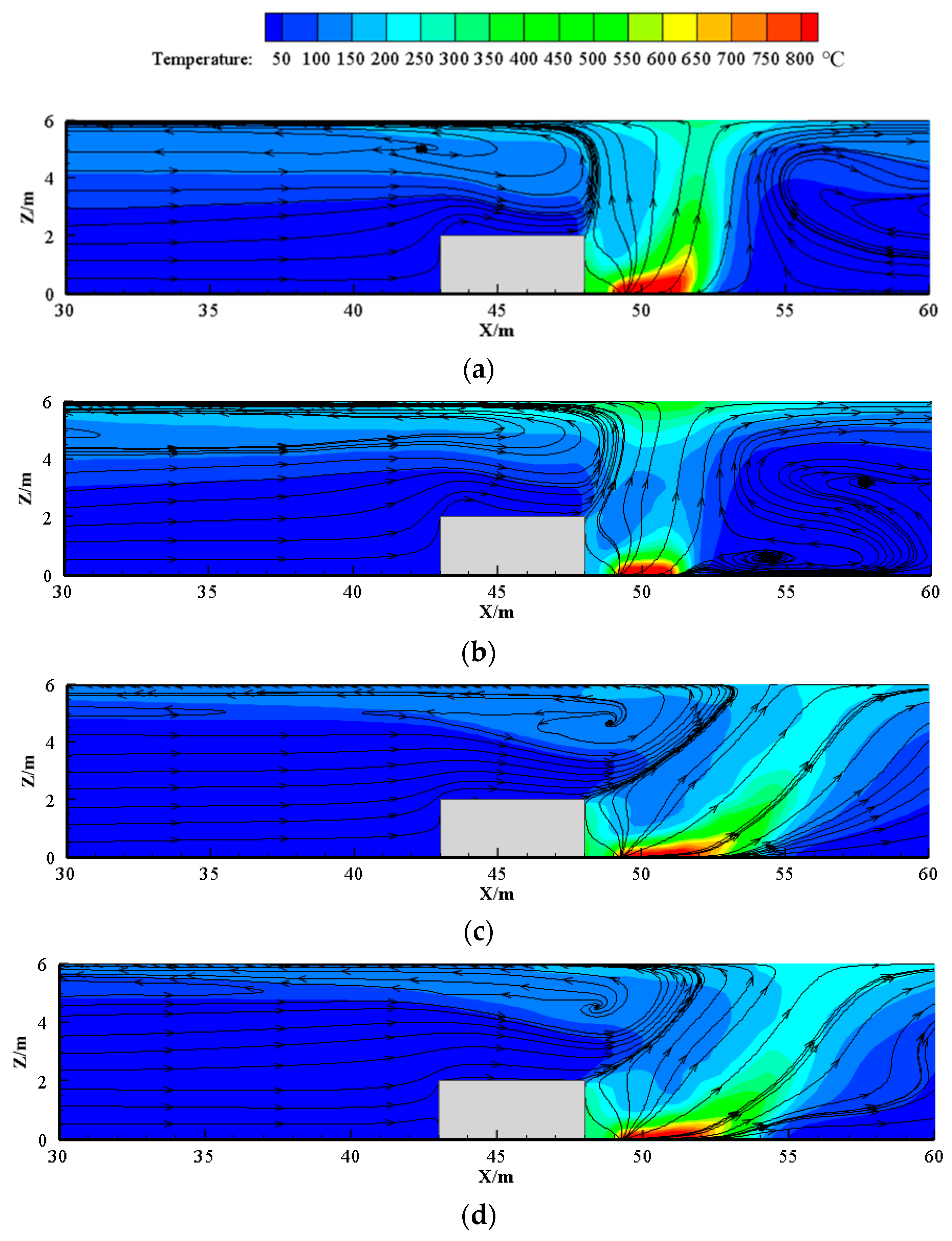
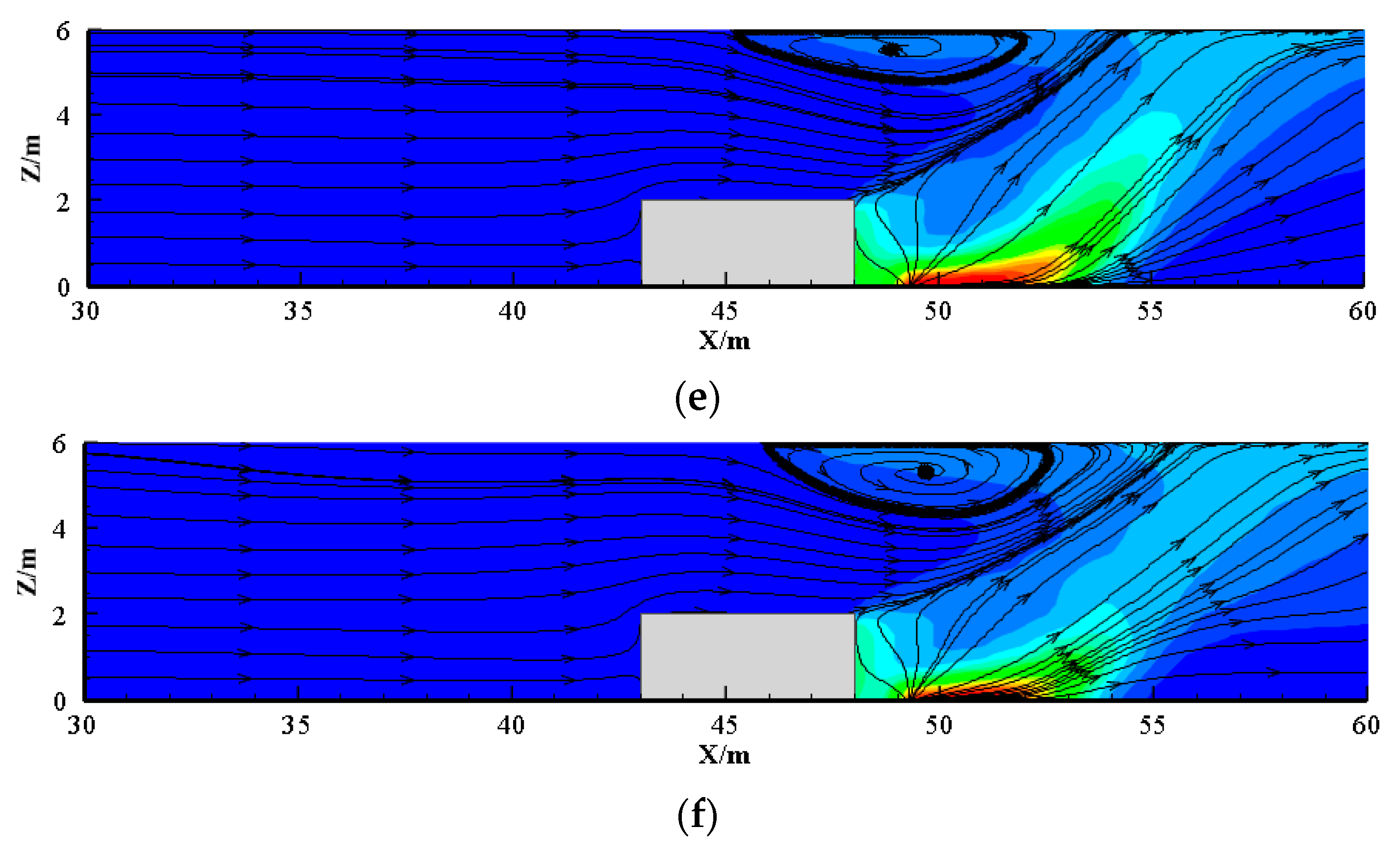
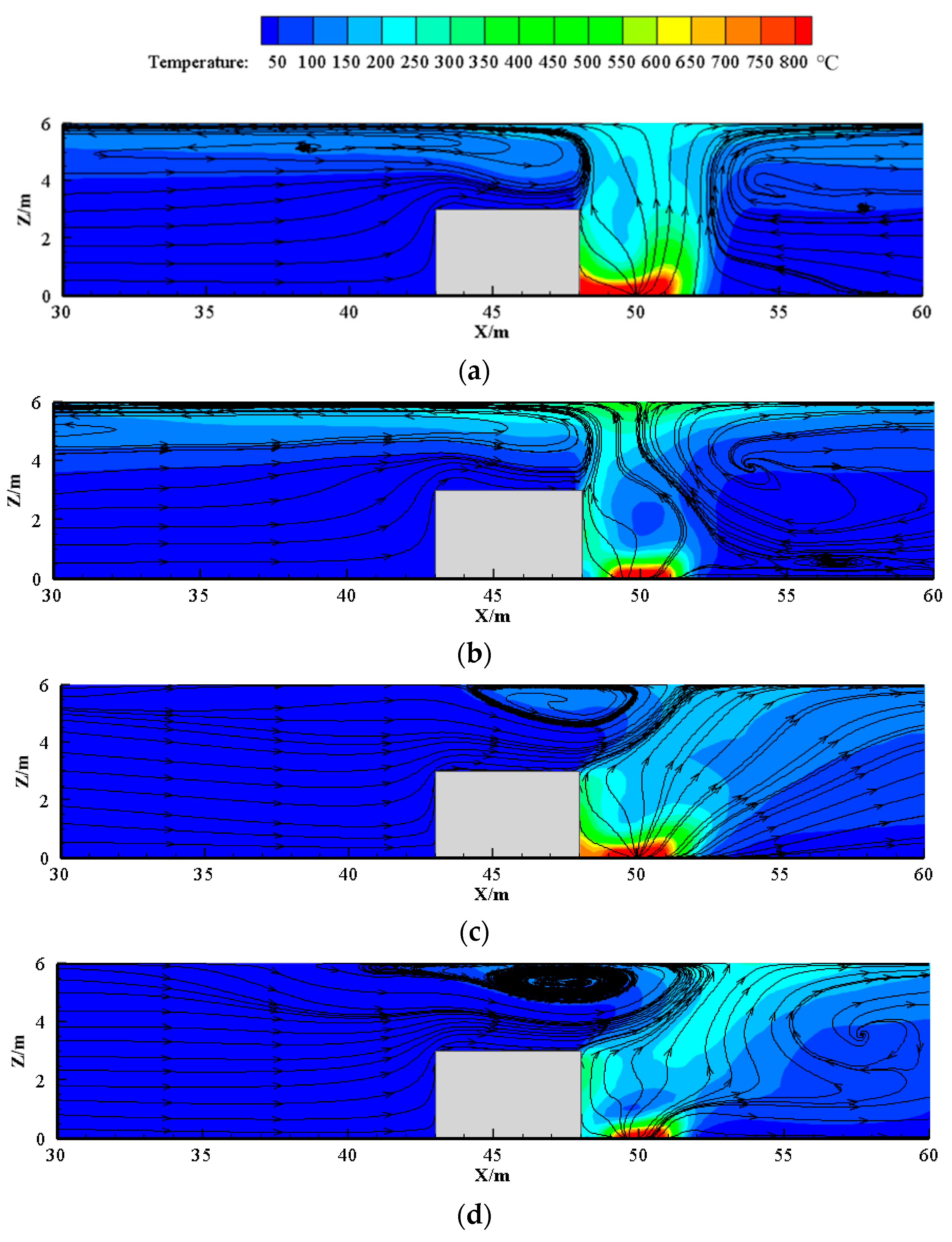
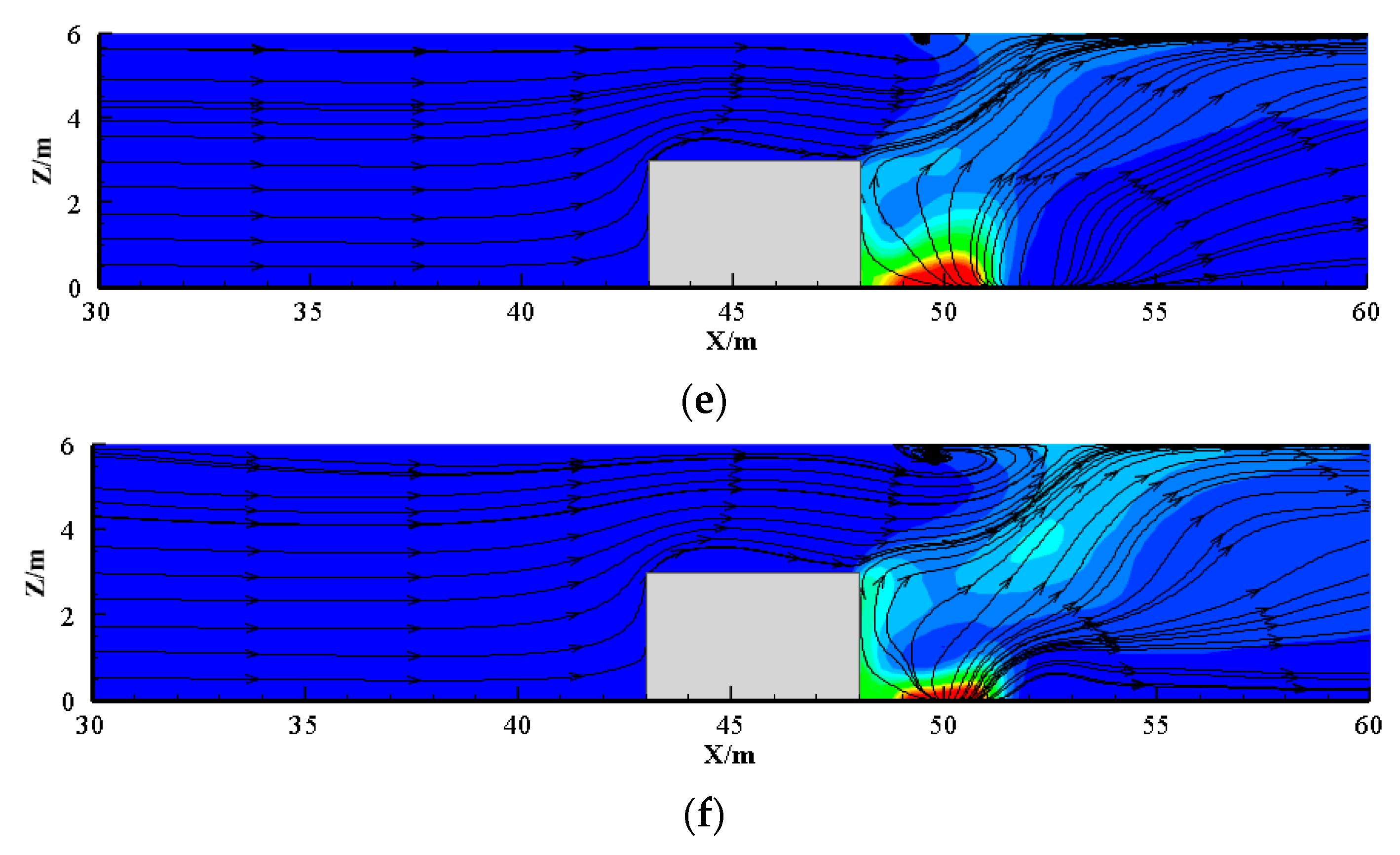
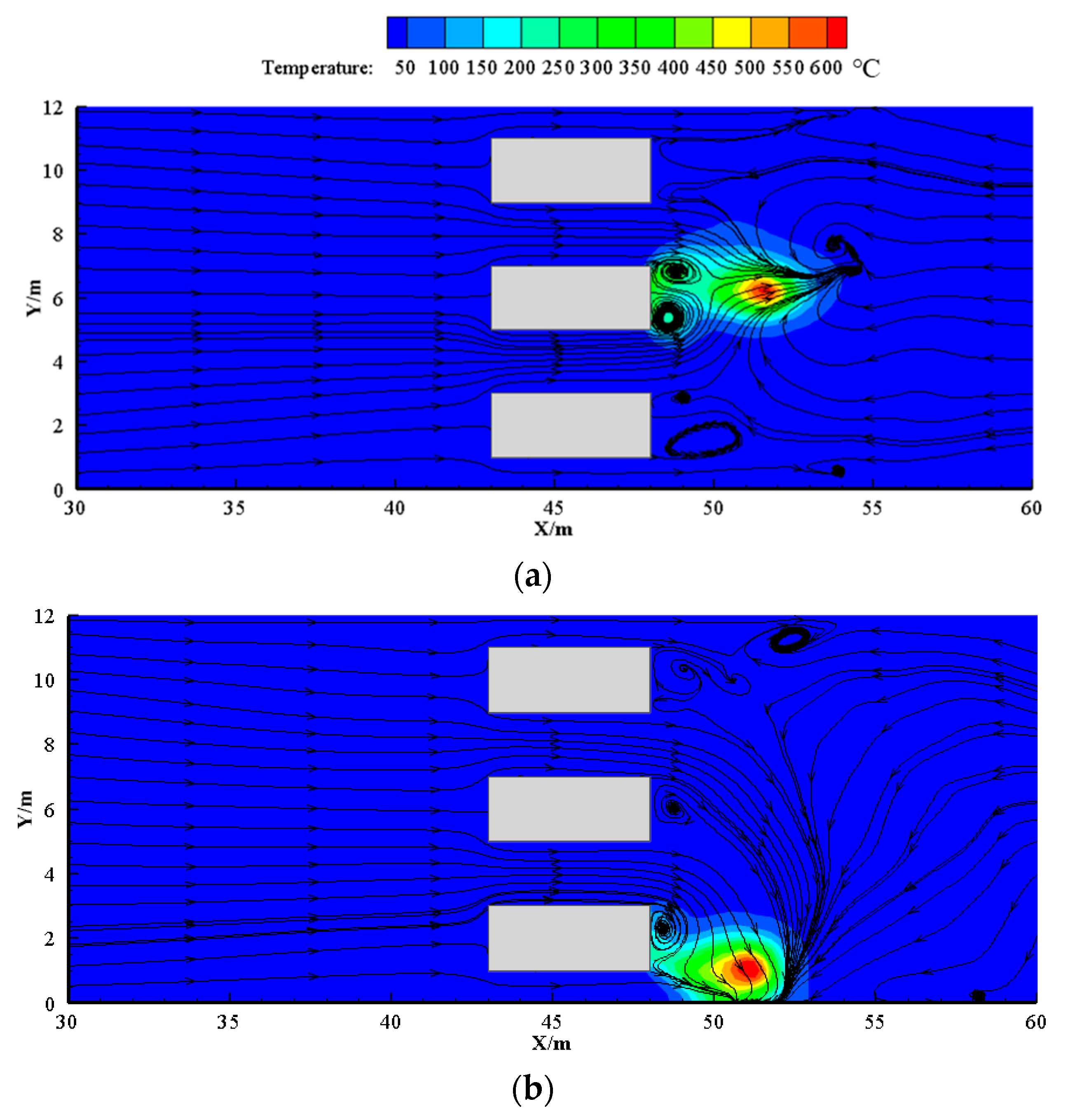
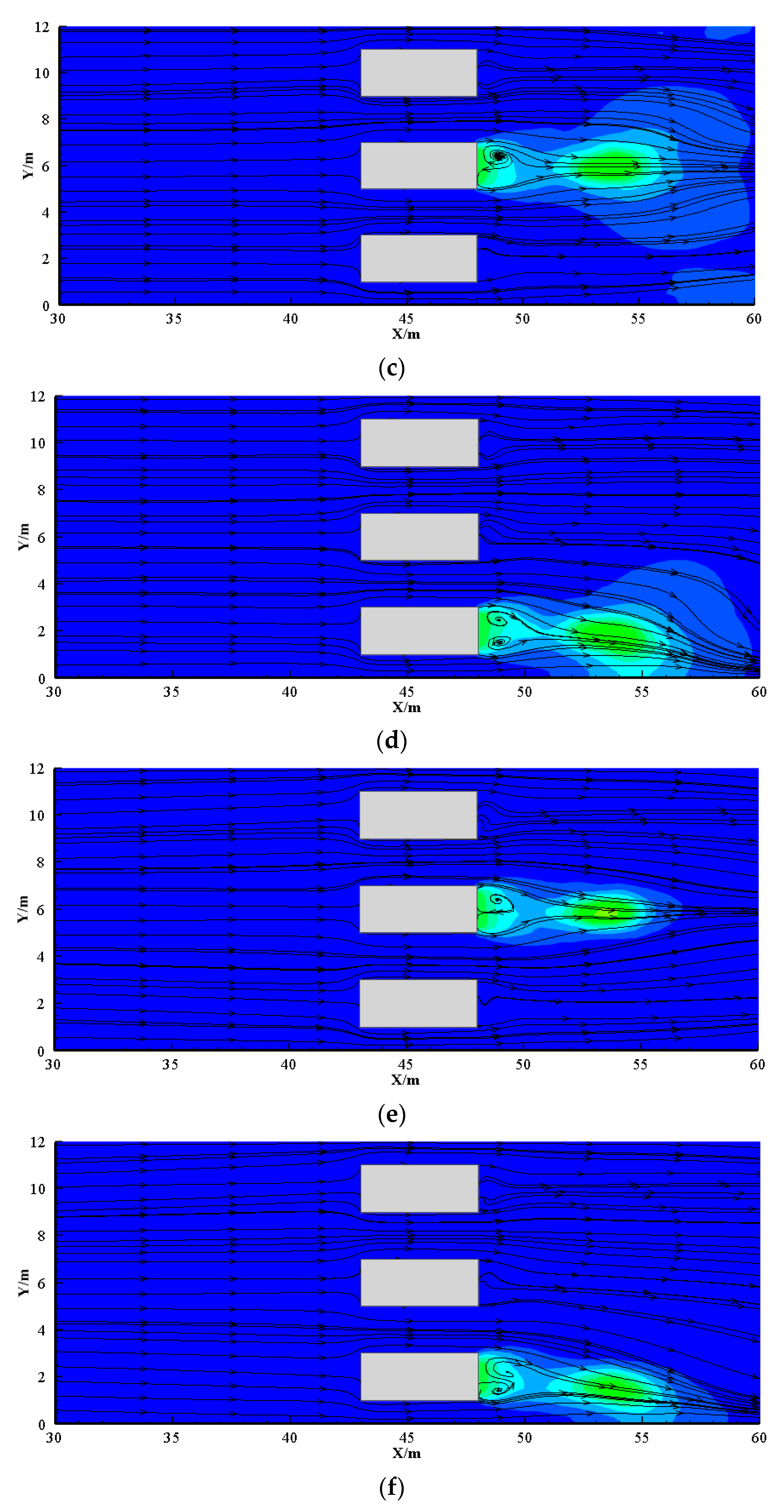
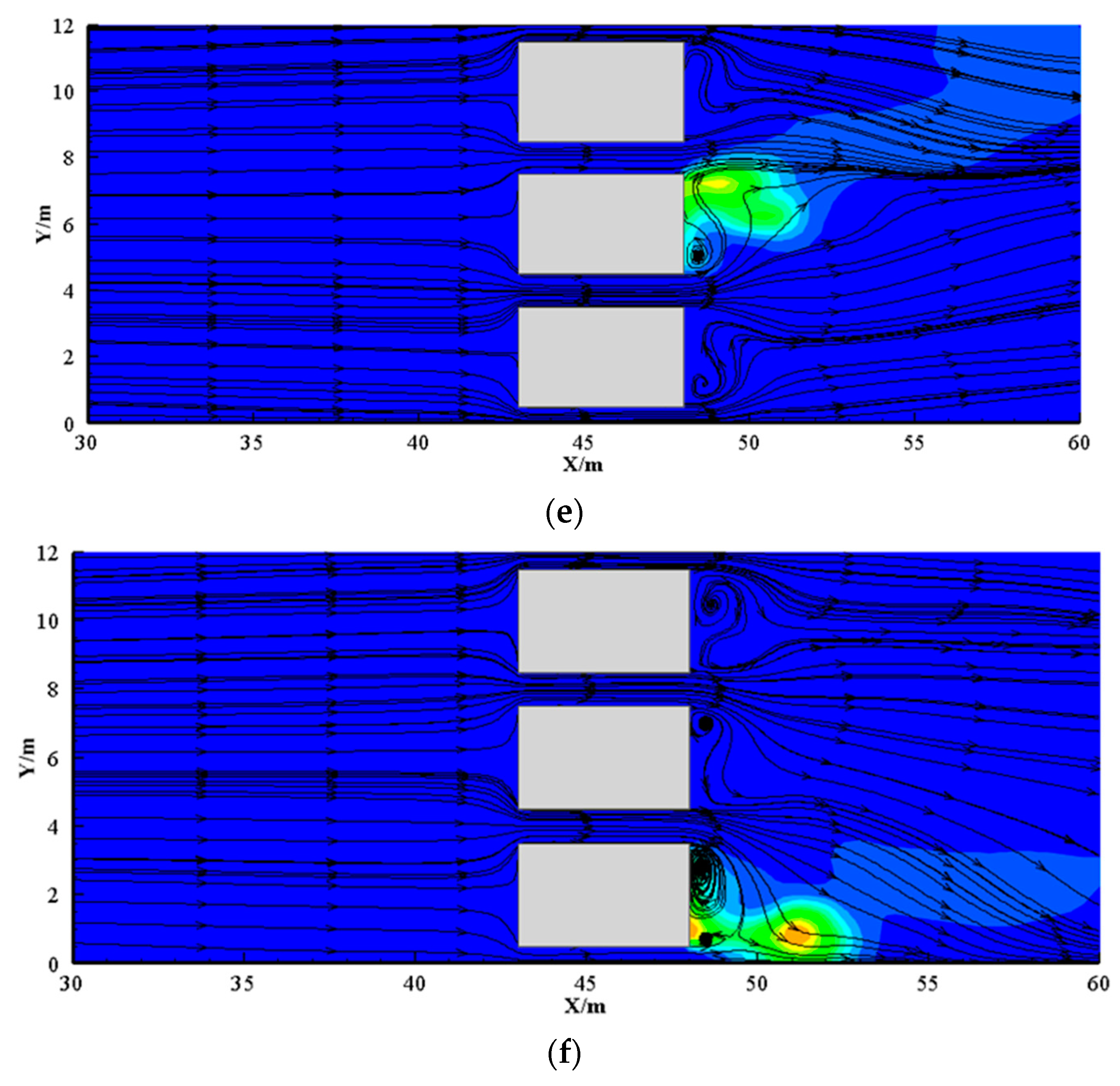
3.1. Flow Field and Flame Behavior
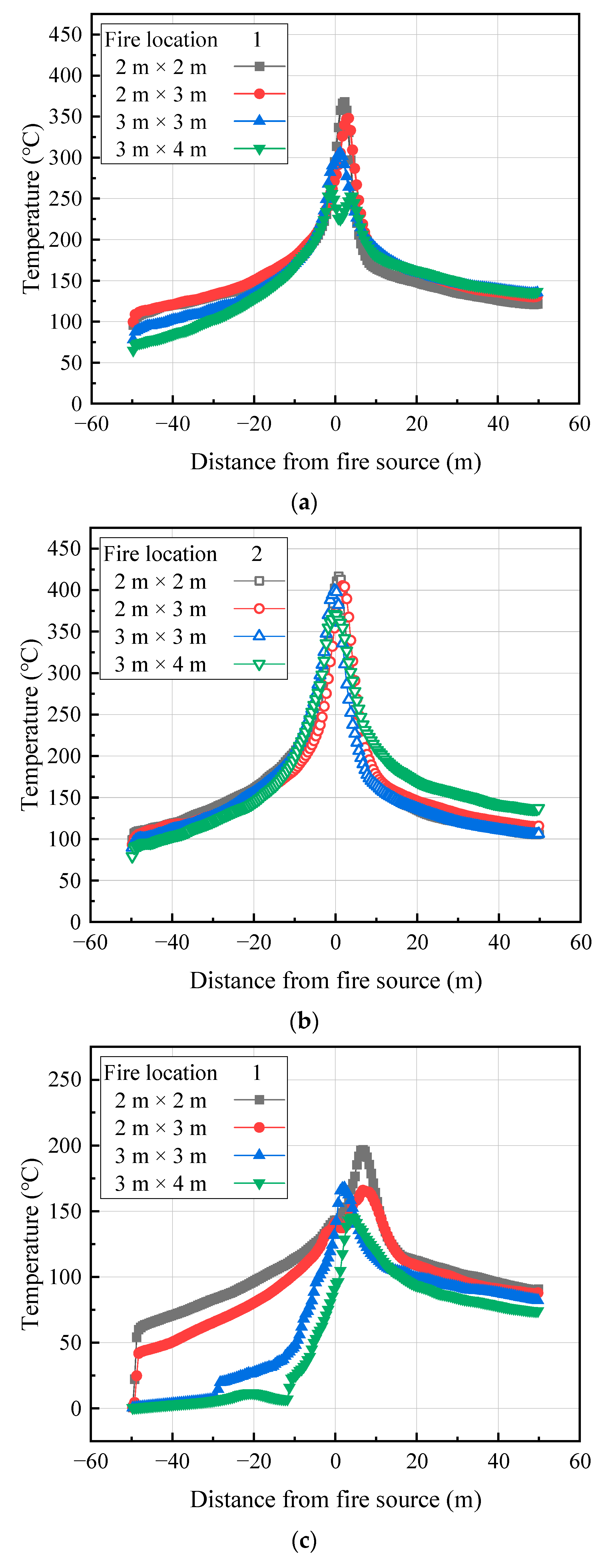
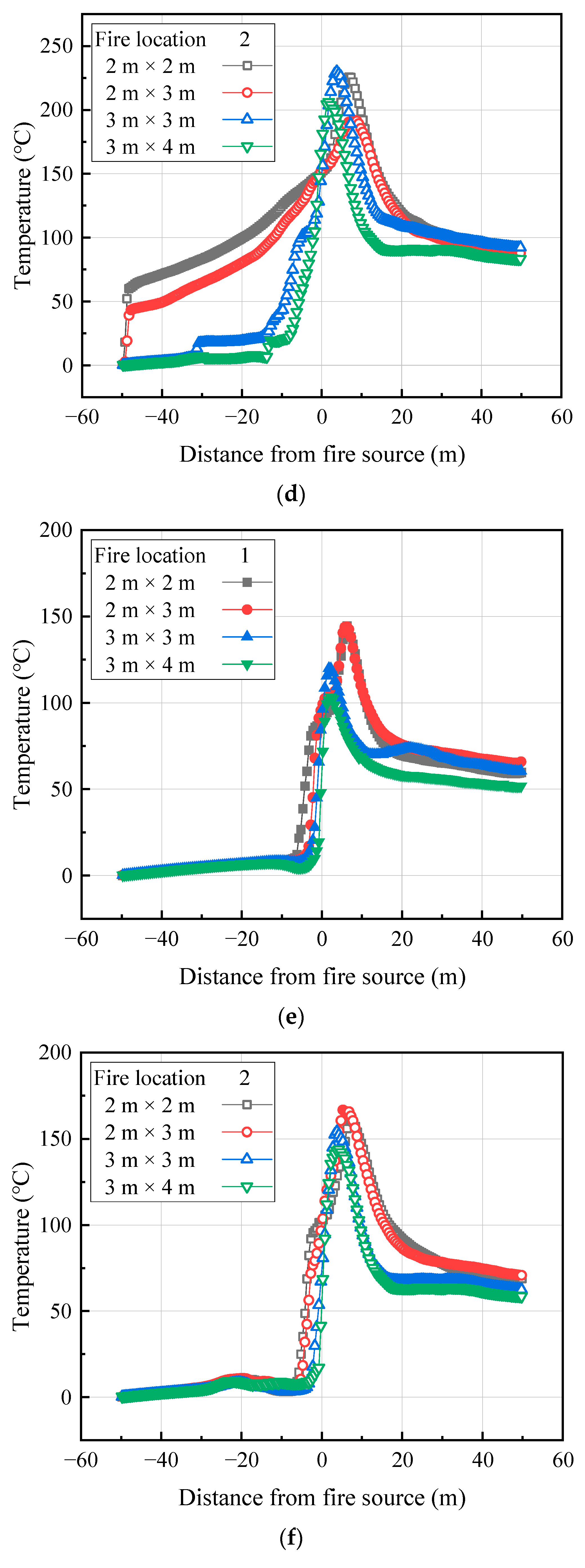
3.2. Temperature Distribution
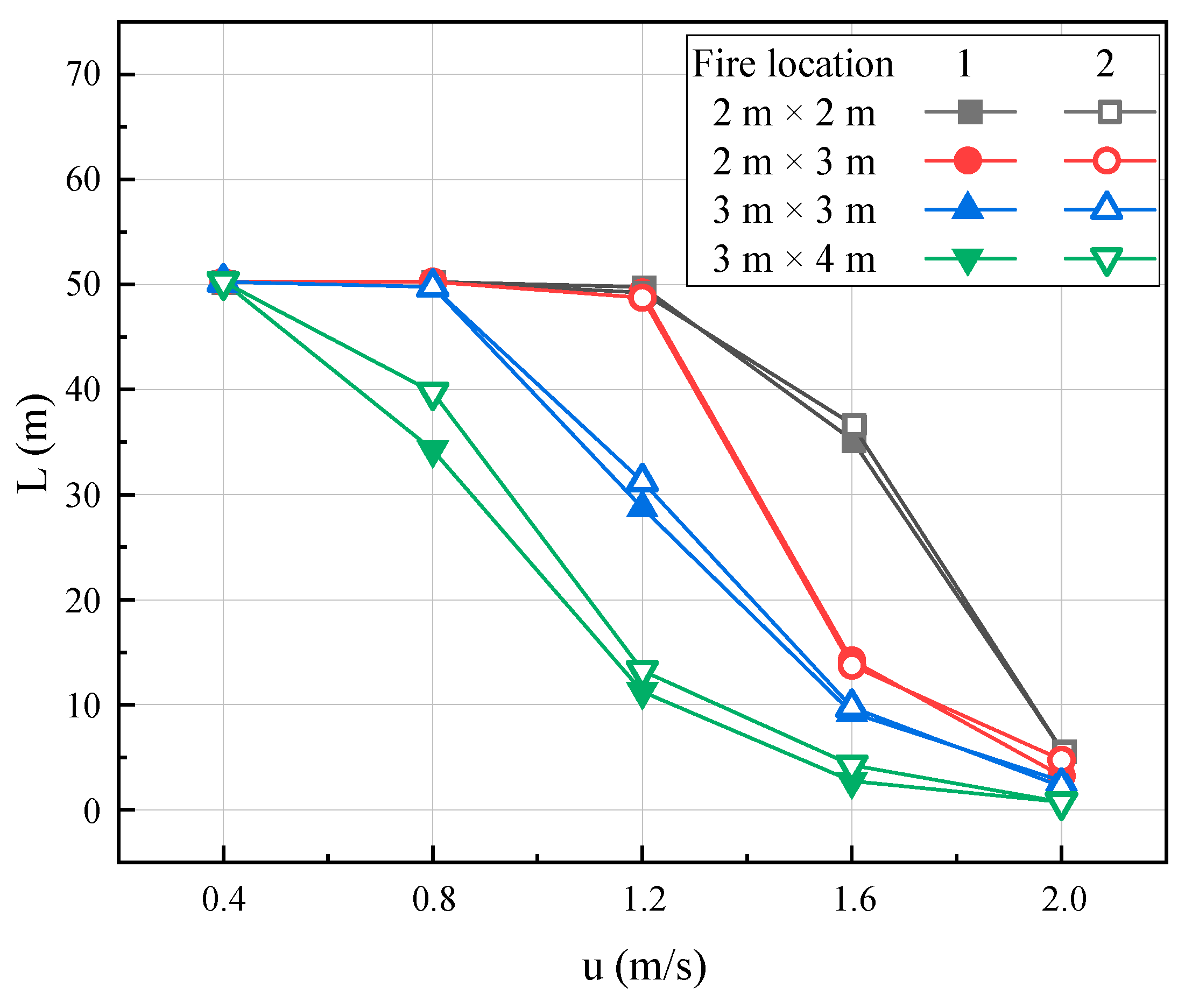
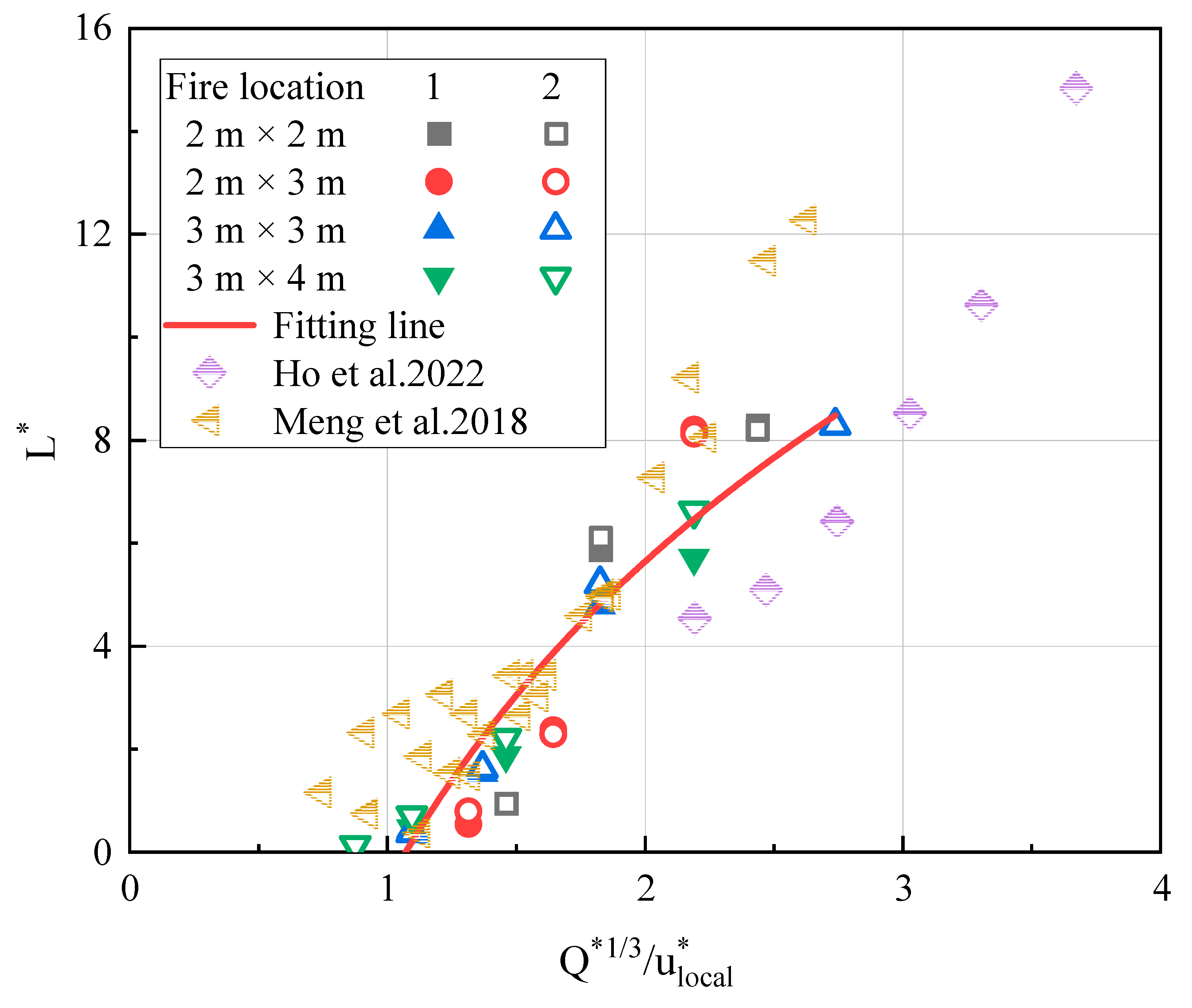
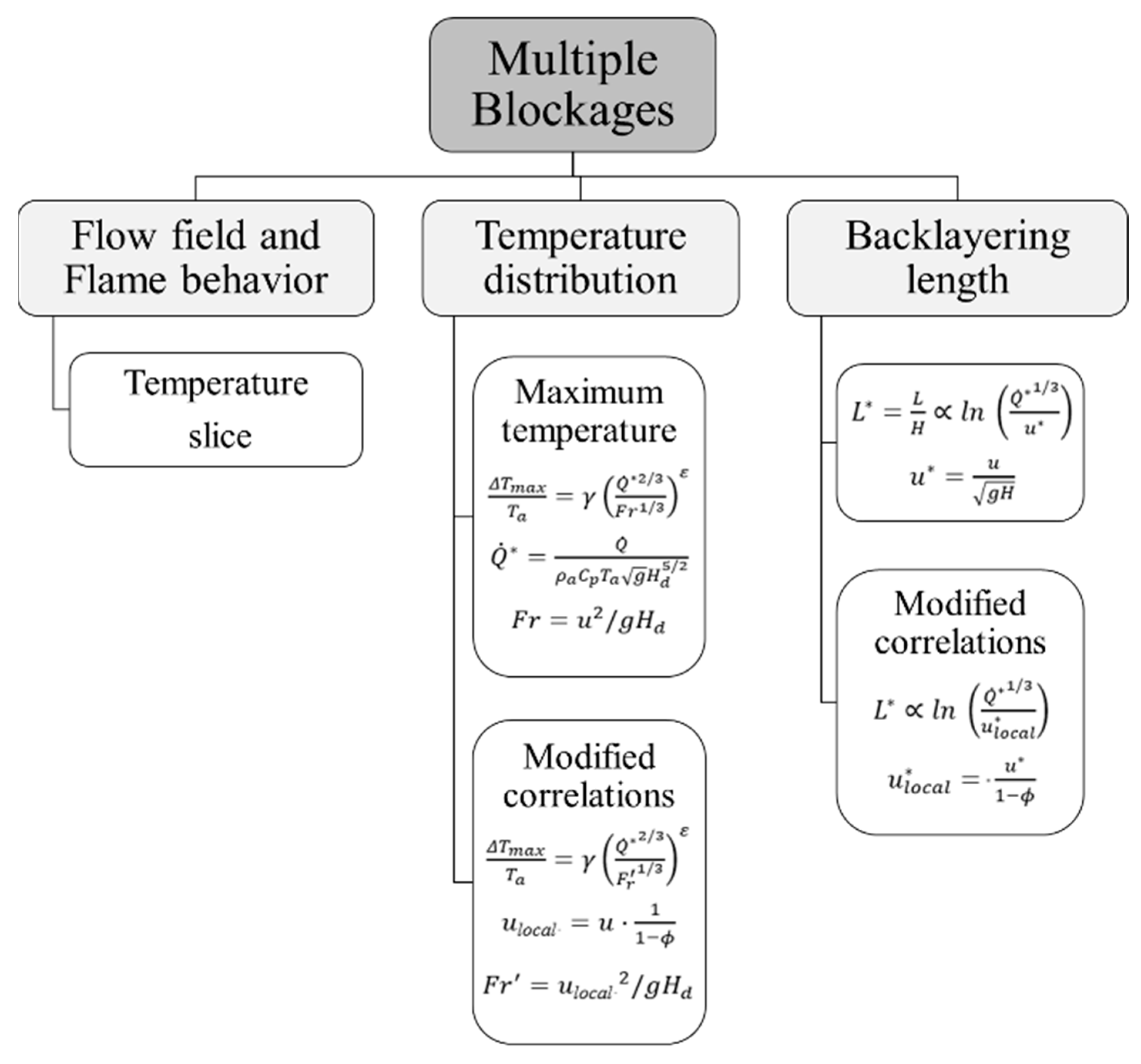
3.3. Back-Layering Length
4. Conclusions
- As the ventilation velocity increases, the bifurcation angle of the flame increases and the back-layering length decreases. Meanwhile, the recirculation region expands with the increase in the blockage ratio. It is important to note that the flame in the side lane leans towards the sidewall due to lower pressure.
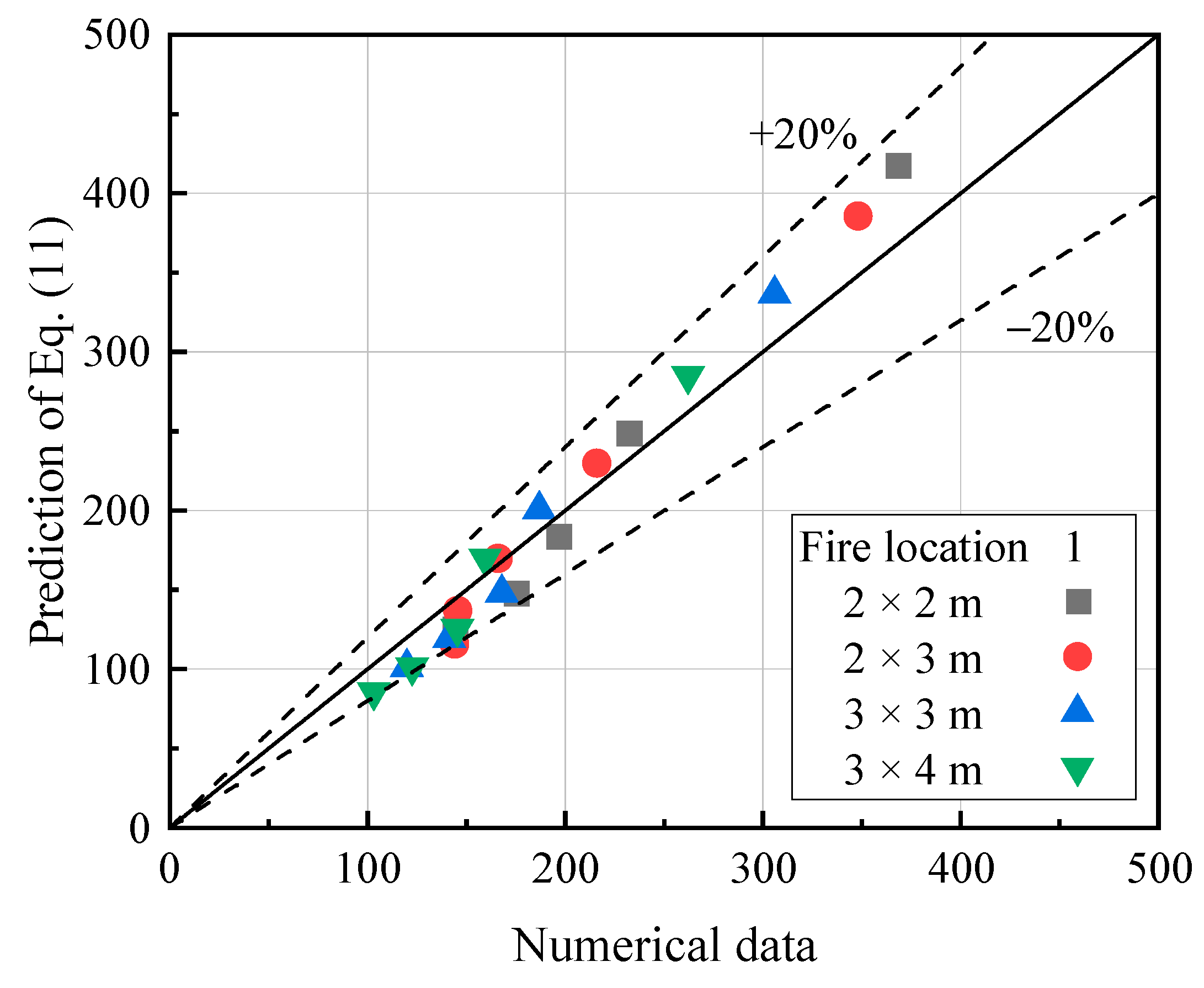
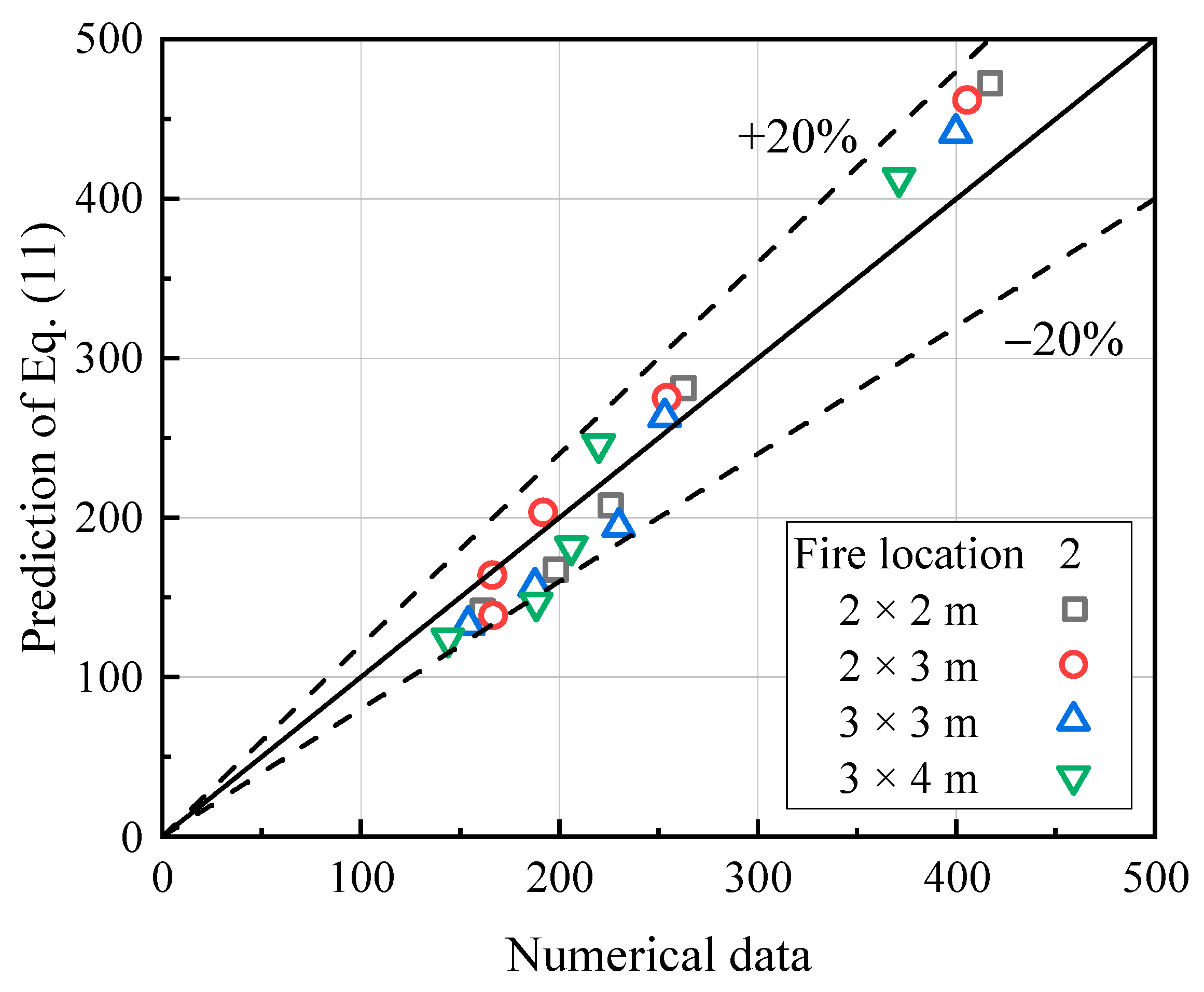
- The fires in the side lane have higher maximum temperatures compared to those in the middle lane. Furthermore, the temperature distribution under the tunnel ceiling for both fire locations presents similar patterns, excluding the near-fire region. A new formula for the prediction of the maximum temperature rise of middle-lane vehicle fires was proposed and its correlation with the side-lane case was analyzed.
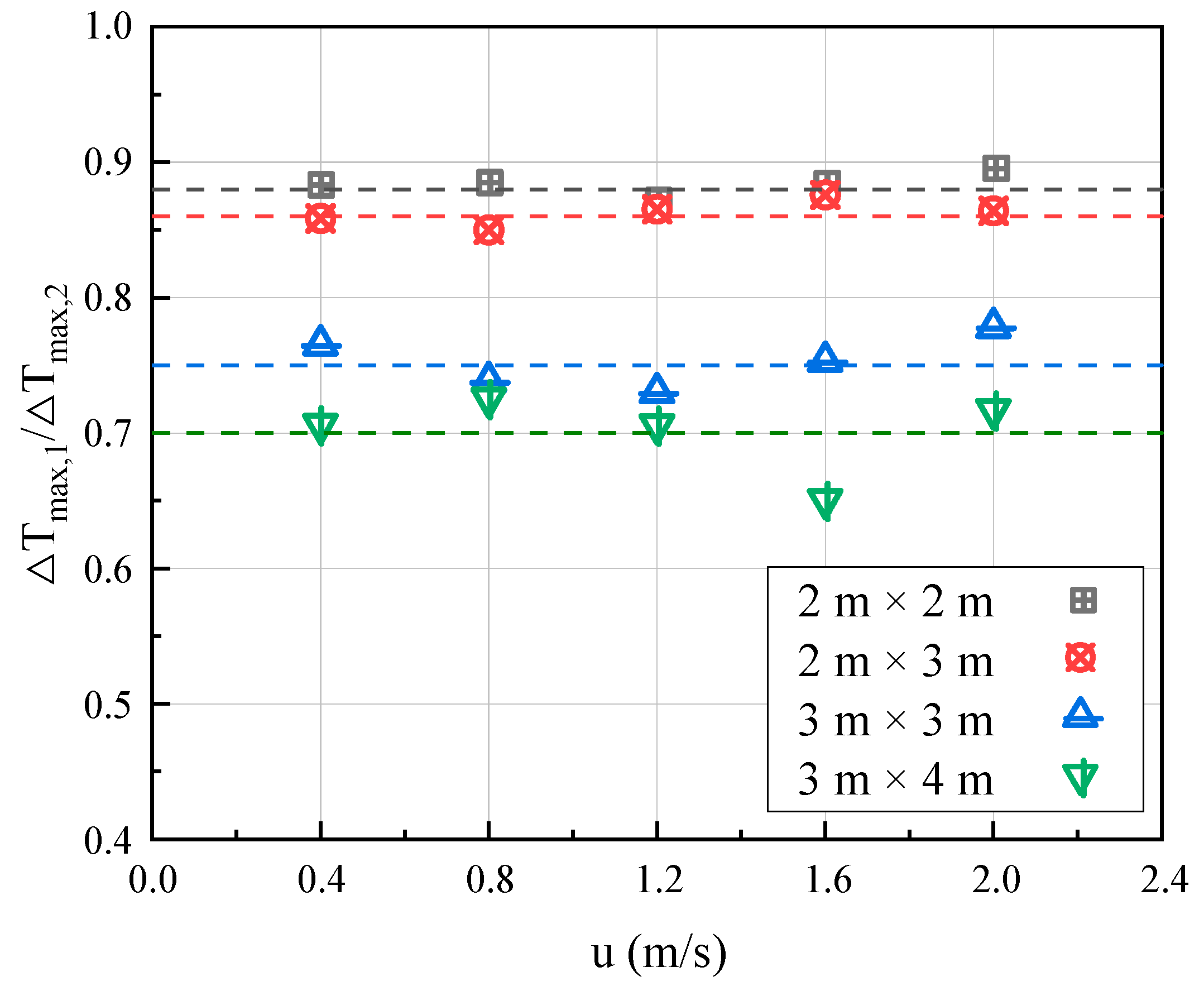
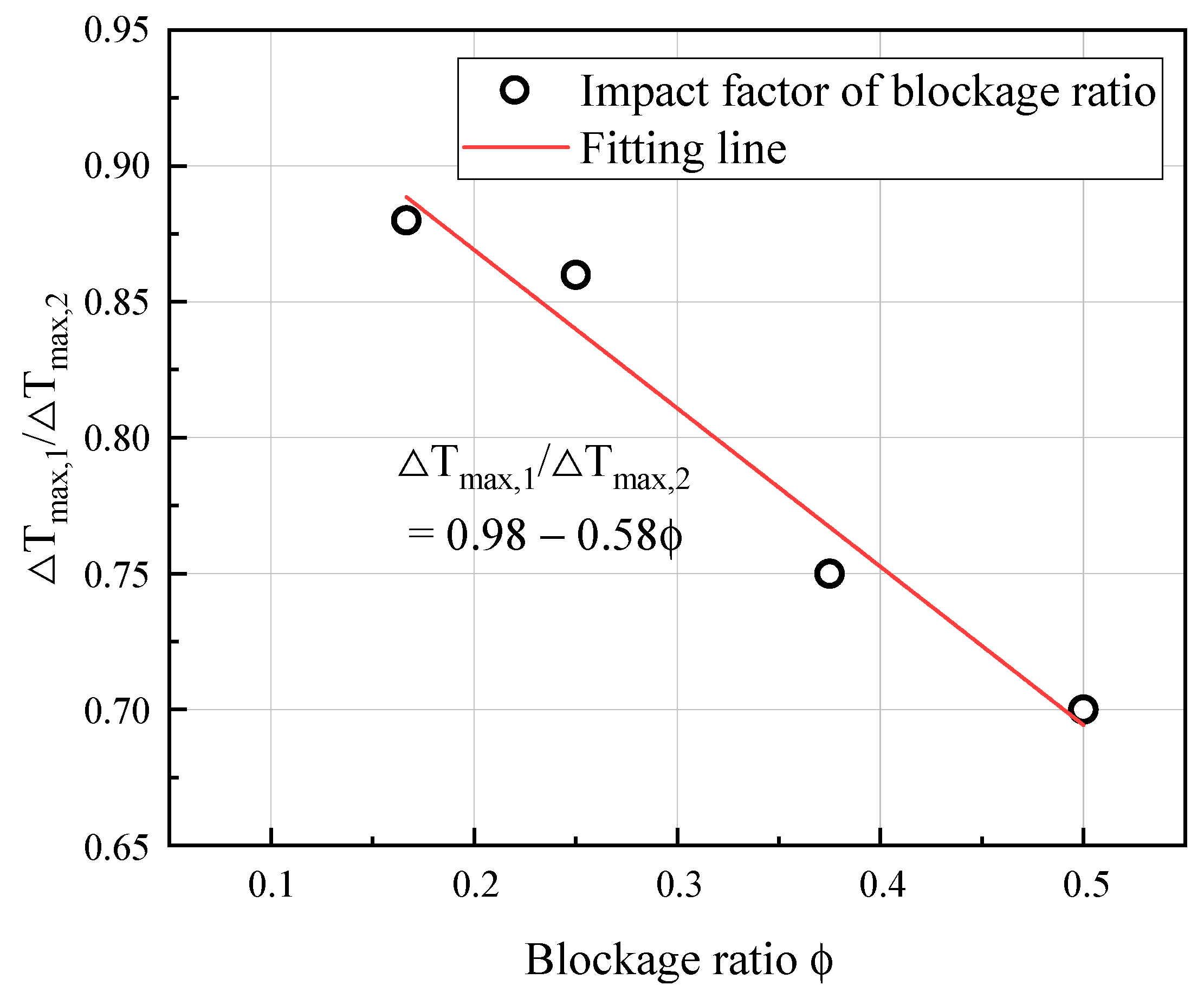
- A modified correlation for the smoke back-layering length in three-blockage longitudinal ventilated tunnels was established, which is closely related to the local ventilation velocity (blockage ratio). Further research is required to explore cases with various heat release rates and longer back-layering lengths.
- It is worth noting that we only considered three-lane road tunnel fires in this study. For tunnel fire scenarios with more lanes and more complex blockages, further research is needed in the future.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jeon, G.; Hong, W. Characteristic Features of the Behavior and Perception of Evacuees from the Daegu Subway Fire and Safety Measures in an Underground Fire. J. Asian Archit. Build. Eng. 2009, 8, 415–422. [Google Scholar] [CrossRef]
- Vuilleumier, F.; Weatherill, A.; Crausaz, B. Safety aspects of railway and road tunnel: Example of the Lötschberg railway tunnel and Mont-Blanc road tunnel. Tunn. Undergr. Space Technol. 2002, 17, 153–158. [Google Scholar] [CrossRef]
- Leitner, A. The fire catastrophe in the Tauern Tunnel: Experience and conclusions for the Austrian guidelines. Tunn. Undergr. Space Technol. 2001, 16, 217–223. [Google Scholar] [CrossRef]
- Ingason, H.; Li, Y.Z.; Lönnermark, A. Tunnel Fire Dynamics; Springer: New York, NY, USA, 2015; ISBN 978-1-4939-2198-0. [Google Scholar]
- Beard, A.; Carvel, R. The Handbook of Tunnel Fire Safety; Thomas Telford Publishing: London, UK, 2005; ISBN 978-0-7277-3875-2. [Google Scholar]
- aofst_6.pdf. Available online: https://publications.iafss.org/publications/aofst/6/s-5/view/aofst_6.pdf (accessed on 31 October 2023).
- Li, Y.Z.; Ingason, H. Overview of research on fire safety in underground road and railway tunnels. Tunn. Undergr. Space Technol. 2018, 81, 568–589. [Google Scholar] [CrossRef]
- Hietaniemi, J.; Kallonen, R.; Mikkola, E. Burning characteristics of selected substances: Production of heat, smoke and chemical species. Fire Mater. 1999, 23, 171–185. [Google Scholar] [CrossRef]
- Hu, L.H.; Tang, F.; Yang, D.; Liu, S.; Huo, R. Longitudinal distributions of CO concentration and difference with temperature field in a tunnel fire smoke flow. Int. J. Heat Mass Transf. 2010, 53, 2844–2855. [Google Scholar] [CrossRef]
- Ji, J.; Fan, C.G.; Zhong, W.; Shen, X.B.; Sun, J.H. Experimental investigation on influence of different transverse fire locations on maximum smoke temperature under the tunnel ceiling. Int. J. Heat Mass Transf. 2012, 55, 4817–4826. [Google Scholar] [CrossRef]
- Gao, Z.H.; Liu, Z.X.; Wan, H.X.; Zhu, J.P. Experimental study on longitudinal and transverse temperature distribution of sidewall confined ceiling jet plume. Appl. Therm. Eng. 2016, 107, 583–590. [Google Scholar] [CrossRef]
- Hu, L.H.; Chen, L.F.; Wu, L.; Li, Y.F.; Zhang, J.Y.; Meng, N. An experimental investigation and correlation on buoyant gas temperature below ceiling in a slopping tunnel fire. Appl. Therm. Eng. 2013, 51, 246–254. [Google Scholar] [CrossRef]
- Yao, Y.; He, K.; Peng, M.; Shi, L.; Cheng, X. The maximum gas temperature rises beneath the ceiling in a longitudinal ventilated tunnel fire. Tunn. Undergr. Space Technol. 2021, 108, 103672. [Google Scholar] [CrossRef]
- Peng, M.; Cheng, X.; He, K.; Cong, W.; Shi, L.; Yuen, R. Experimental study on ceiling smoke temperature distributions in near field of pool fires in the subway train. J. Wind Eng. Ind. Aerodyn. 2020, 199, 104135. [Google Scholar] [CrossRef]
- Tang, F.; Cao, Z.; Palacios, A.; Wang, Q. A study on the maximum temperature of ceiling jet induced by rectangular-source fires in a tunnel using ceiling smoke extraction. Int. J. Therm. Sci. 2018, 127, 329–334. [Google Scholar] [CrossRef]
- Li, Y.Z.; Lei, B.; Ingason, H. The maximum temperature of buoyancy-driven smoke flow beneath the ceiling in tunnel fires. Fire Saf. J. 2011, 46, 204–210. [Google Scholar] [CrossRef]
- Li, Y.Z.; Ingason, H. The maximum ceiling gas temperature in a large tunnel fire. Fire Saf. J. 2012, 48, 38–48. [Google Scholar] [CrossRef]
- Wang, H.F.; Zhou, Y. The finite-length square cylinder near wake. J. Fluid Mech. 2009, 638, 453–490. [Google Scholar] [CrossRef]
- Yen, S.C.; Liu, J.H. Wake flow behind two side-by-side square cylinders. Int. J. Heat Fluid Flow 2011, 32, 41–51. [Google Scholar] [CrossRef]
- Shanbhogue, S.J.; Husain, S.; Lieuwen, T. Lean blowoff of bluff body stabilized flames: Scaling and dynamics. Prog. Energy Combust. Sci. 2009, 35, 98–120. [Google Scholar] [CrossRef]
- Sohankar, A.; Norberg, C.; Davidson, L. Simulation of three-dimensional flow around a square cylinder at moderate Reynolds numbers. Phys. Fluids 1999, 11, 288–306. [Google Scholar] [CrossRef]
- Lyn, D.A.; Einav, S.; Rodi, W.; Park, J.-H. A laser-Doppler velocimetry study of ensemble-averaged characteristics of the turbulent near wake of a square cylinder. J. Fluid Mech. 1995, 304, 285–319. [Google Scholar] [CrossRef]
- Hu, L.H.; Zhao, X.Y.; Zhu, W.; Tang, F. An experimental investigation and characterization on flame bifurcation and leaning transition behavior of a pool fire in near wake of a square cylinder. Int. J. Heat Mass Transf. 2012, 55, 7024–7035. [Google Scholar] [CrossRef]
- Okaa, Y.; Atkinson, G.T. Control of Smoke Flow in Tunnel Fires. Fire Saf. J. 1995, 25, 305–322. [Google Scholar] [CrossRef]
- Li, L.; Cheng, X.; Cui, Y.; Li, S.; Zhang, H. Effect of blockage ratio on critical velocity in tunnel fires. J. Fire Sci. 2012, 30, 413–427. [Google Scholar] [CrossRef]
- Li, L.; Cheng, X.; Cui, Y.; Dong, W.; Mei, Z. Effect of blockage ratio on the maximum temperature under the ceiling in tunnel fires. J. Fire Sci. 2013, 31, 245–257. [Google Scholar] [CrossRef]
- Meng, N.; Liu, X.; Li, X.; Liu, B. Effect of blockage ratio on backlayering length of thermal smoke flow in a longitudinally ventilated tunnel. Appl. Therm. Eng. 2018, 132, 1–7. [Google Scholar] [CrossRef]
- Meng, N.; Liu, B.; Li, X.; Jin, X.; Huang, Y.; Wang, Q. Effect of blockage-induced near wake flow on fire properties in a longitudinally ventilated tunnel. Int. J. Therm. Sci. 2018, 134, 1–12. [Google Scholar] [CrossRef]
- Meng, N.; Yang, W.; Xin, L.; Li, X.; Liu, B.; Jin, X. Experimental study on backlayering length of thermal smoke flow in a longitudinally ventilated tunnel with blockage at upstream of fire source. Tunn. Undergr. Space Technol. 2018, 82, 315–324. [Google Scholar] [CrossRef]
- Wang, Z.; Han, J.; Wang, J.; Geng, P.; Weng, M.; Liu, F. Temperature distribution in a blocked tunnel with one closed portal under natural ventilation. Tunn. Undergr. Space Technol. 2021, 109, 103752. [Google Scholar] [CrossRef]
- Han, J. The effect of blockage and tunnel slope on smoke spread and ceiling temperature distribution in a natural-ventilated metro depot. Energy Build. 2021, 253, 111540. [Google Scholar] [CrossRef]
- Wang, J. Effect of the blockage ratio on the smoke extraction efficiency in tunnel fires with natural ventilation. Tunn. Undergr. Space Technol. 2021, 117, 10416. [Google Scholar] [CrossRef]
- Hu, L.H.; Tang, W.; Chen, L.F.; Yi, L. A non-dimensional global correlation of maximum gas temperature beneath ceiling with different blockage–fire distance in a longitudinal ventilated tunnel. Appl. Therm. Eng. 2013, 56, 77–82. [Google Scholar] [CrossRef]
- Tang, W.; Hu, L.H.; Chen, L.F. Effect of blockage-fire distance on buoyancy driven back-layering length and critical velocity in a tunnel: An experimental investigation and global correlations. Appl. Therm. Eng. 2013, 60, 7–14. [Google Scholar] [CrossRef]
- Zhang, S.; Shi, L.; Li, X.; Huang, Y.; He, K.; Wang, J. Critical ventilation velocity under the blockage of different metro train in a long metro tunnel. Fire Mater. 2020, 44, 497–505. [Google Scholar] [CrossRef]
- Zhang, S.; Yao, Y.; Zhu, K.; Li, K.; Zhang, R.; Lu, S.; Cheng, X. Prediction of smoke back-layering length under different longitudinal ventilations in the subway tunnel with metro train. Tunn. Undergr. Space Technol. 2016, 53, 13–21. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Z.; Tao, H. A numerical study on critical velocity and back-layering length with trains’ blockage in longitudinally ventilated tunnel fires. Tunn. Undergr. Space Technol. 2021, 116, 104093. [Google Scholar] [CrossRef]
- Zhang, S.; Cheng, X.; Yao, Y.; Zhu, K.; Li, K.; Lu, S.; Zhang, R.; Zhang, H. An experimental investigation on blockage effect of metro train on the smoke back-layering in subway tunnel fires. Appl. Therm. Eng. 2016, 99, 214–223. [Google Scholar] [CrossRef]
- Jiang, X.; Zhang, H.; Jing, A. Effect of blockage ratio on critical velocity in tunnel model fire tests. Tunn. Undergr. Space Technol. 2018, 82, 584–591. [Google Scholar] [CrossRef]
- Altay, M.; Surmen, A. Effect of the relative positions of vehicular blockage on the smoke flow behaviour in a scaled tunnel. Fuel 2019, 255, 115694. [Google Scholar] [CrossRef]
- Meng, N.; Hu, X.; Tian, M. Effect of blockage on critical ventilation velocity in longitudinally ventilated tunnel fires. Tunn. Undergr. Space Technol. 2020, 106, 103580. [Google Scholar] [CrossRef]
- Tang, F.; Cao, Z.L.; Chen, Q.; Meng, N.; Wang, Q.; Fan, C.G. Effect of blockage-heat source distance on maximum temperature of buoyancy-induced smoke flow beneath ceiling in a longitudinal ventilated tunnel. Int. J. Heat Mass Transf. 2017, 109, 683–688. [Google Scholar] [CrossRef]
- Gannouni, S.; Maad, R.B. Numerical study of the effect of blockage on critical velocity and backlayering length in longitudinally ventilated tunnel fires. Tunn. Undergr. Space Technol. 2015, 48, 147–155. [Google Scholar] [CrossRef]
- Kunikane, Y.; Kawabata, N.; Yamada, T.; Shimoda, A. Influence of Stationary Vehicles on Backlayering Characteristics of Fire Plume in a Large Cross Section Tunnel. JSME Int. J. Ser. B 2006, 49, 594–600. [Google Scholar] [CrossRef]
- Lee, Y.-P.; Tsai, K.-C. Effect of vehicular blockage on critical ventilation velocity and tunnel fire behavior in longitudinally ventilated tunnels. Fire Saf. J. 2012, 53, 35–42. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, Z.; Liu, Q.; Ren, J.; Fu, Z. Impact of block transportation on buoyancy flows during fires in a shallow urban road tunnel. Procedia Eng. 2017, 205, 1850–1857. [Google Scholar] [CrossRef]
- Ho, Y.-T.; Kawabata, N.; Seike, M.; Hasegawa, M.; Chien, S.-W.; Shen, T.-S. Scale Model Experiments and Simulations to Investigate the Effect of Vehicular Blockage on Backlayering Length in Tunnel Fire. Buildings 2022, 12, 1006. [Google Scholar] [CrossRef]
- Rojas Alva, W.U.; Jomaas, G.; Dederichs, A.S. The influence of vehicular obstacles on longitudinal ventilation control in tunnel fires. Fire Saf. J. 2017, 87, 25–36. [Google Scholar] [CrossRef]
- Ming, Y.; Zhu, G.; He, L.; Zhou, Y.; Liu, X.; Wang, X.; Wang, G.; Wu, L. Effect of different configurations of multi-blockages on the fire characteristics in tunnel fires with longitudinal ventilation. Therm. Sci. Eng. Prog. 2023, 45, 102113. [Google Scholar] [CrossRef]
- Luo, J. Effect of vehicular blocking scene on smoke spread in the longitudinal ventilated tunnel fire. Case Stud. Therm. Eng. 2019, 14, 100495. [Google Scholar] [CrossRef]
- Caliendo, C.; Genovese, G.; Russo, I. Risk Analysis of Road Tunnels: A Computational Fluid Dynamic Model for Assessing the Effects of Natural Ventilation. Appl. Sci. 2020, 11, 32. [Google Scholar] [CrossRef]
- Chow, W.K.; Gao, Y.; Zou, J.F.; Liu, Q.K.; Chow, C.L.; Miao, L. Numerical Studies on Thermally-Induced Air Flow in Sloping Tunnels with Experimental Scale Modelling Justifications. Fire Technol. 2018, 54, 867–892. [Google Scholar] [CrossRef]
- Ji, J.; Guo, F.; Gao, Z.; Zhu, J.; Sun, J. Numerical investigation on the effect of ambient pressure on smoke movement and temperature distribution in tunnel fires. Appl. Therm. Eng. 2017, 118, 663–669. [Google Scholar] [CrossRef]
- Ji, J.; Tan, T.; Gao, Z.; Wan, H.; Zhu, J.; Ding, L. Numerical Investigation on the Influence of Length–Width Ratio of Fire Source on the Smoke Movement and Temperature Distribution in Tunnel Fires. Fire Technol. 2019, 55, 963–979. [Google Scholar] [CrossRef]
- Huang, Y.; Li, Y.; Dong, B.; Li, J.; Liang, Q. Numerical investigation on the maximum ceiling temperature and longitudinal decay in a sealing tunnel fire. Tunn. Undergr. Space Technol. 2018, 72, 120–130. [Google Scholar] [CrossRef]
- Li, Q.; Kang, J.; Wu, Y.; Luo, J. Theoretical and Numerical Study of Smoke Back-Layering Length for an Inclined Tunnel under Longitudinal Ventilation. Fire Technol. 2022, 58, 2143–2166. [Google Scholar] [CrossRef]
- Ko, J.; Yoon, C.; Yoon, S.; Kim, J. Determination of the applicable exhaust airflow rate through a ventilation shaft in the case of road tunnel fires. Saf. Sci. 2010, 48, 722–728. [Google Scholar] [CrossRef]
- McGrattan, K.B.; Forney, G.P. Fire Dynamics Simulator (Version 4): User’s Guide; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2004. [CrossRef]
- Kurioka, H.; Oka, Y.; Satoh, H.; Sugawa, O. Fire properties in near field of square fire source with longitudinal ventilation in tunnels. Fire Saf. J. 2003, 38, 319–340. [Google Scholar] [CrossRef]
- Han, J.; Wang, F.; Wen, J.; Liu, F.; Ma, W.; Wang, Z.; Ma, Z. Investigation on the characteristics of fire burning and smoke spreading in longitudinal-ventilated tunnels with blockages. Tunn. Undergr. Space Technol. 2023, 131, 104790. [Google Scholar] [CrossRef]
- Li, Y.Z.; Lei, B. Ingason, Study of critical velocity and backlayering length in longitudinally ventilated tunnel fires. Fire Saf. J. 2010, 45, 361–370. [Google Scholar] [CrossRef]

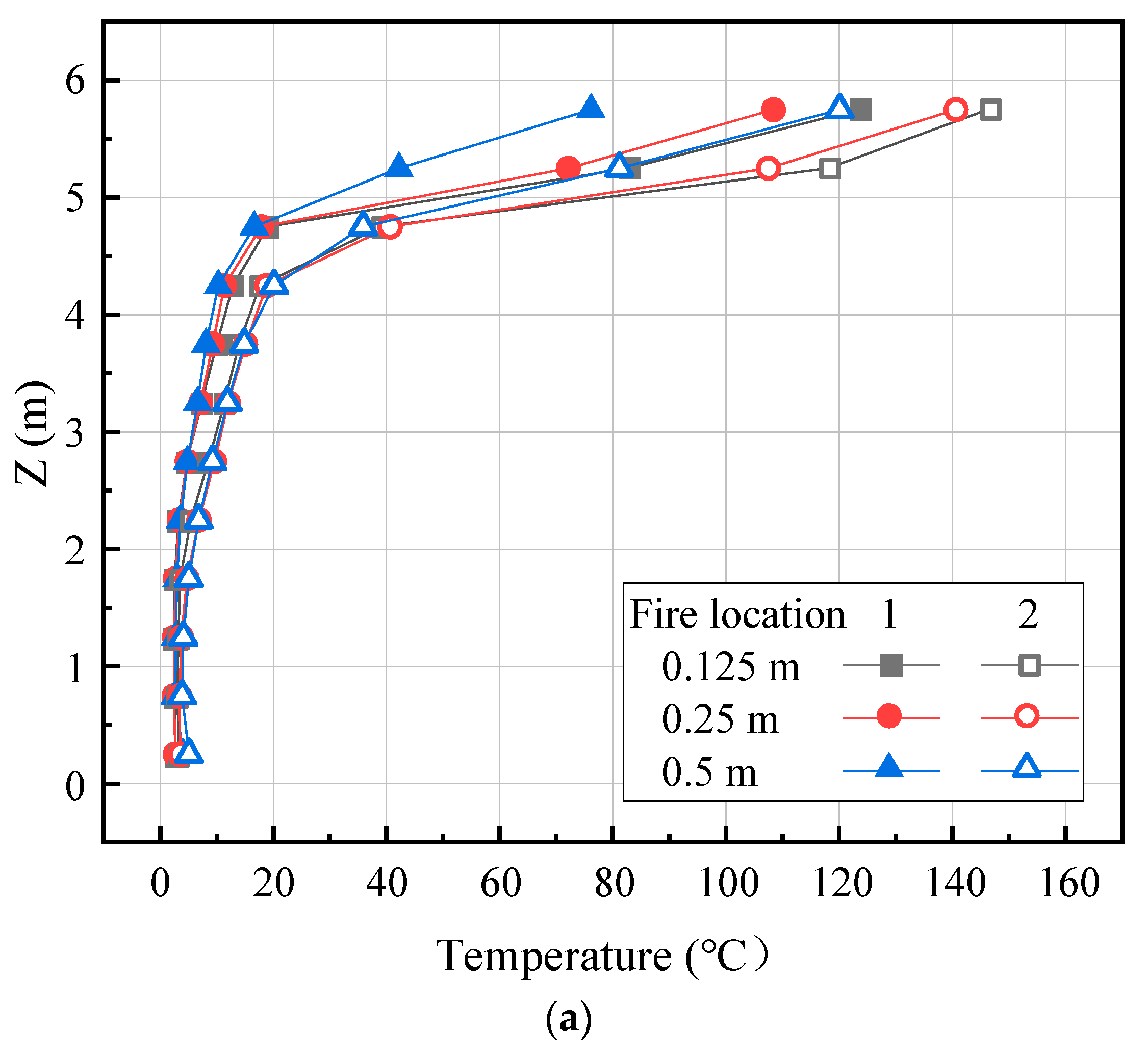
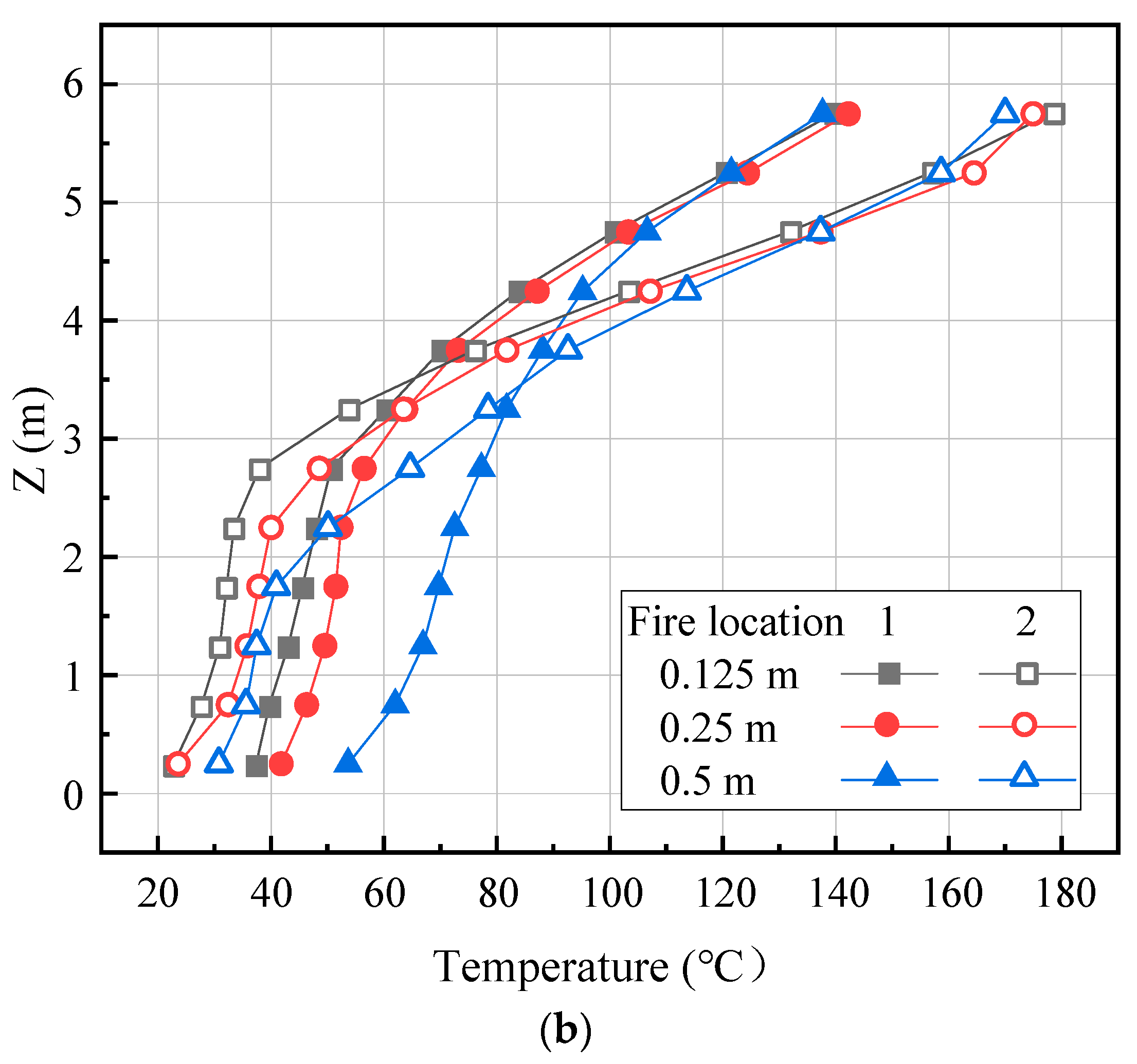
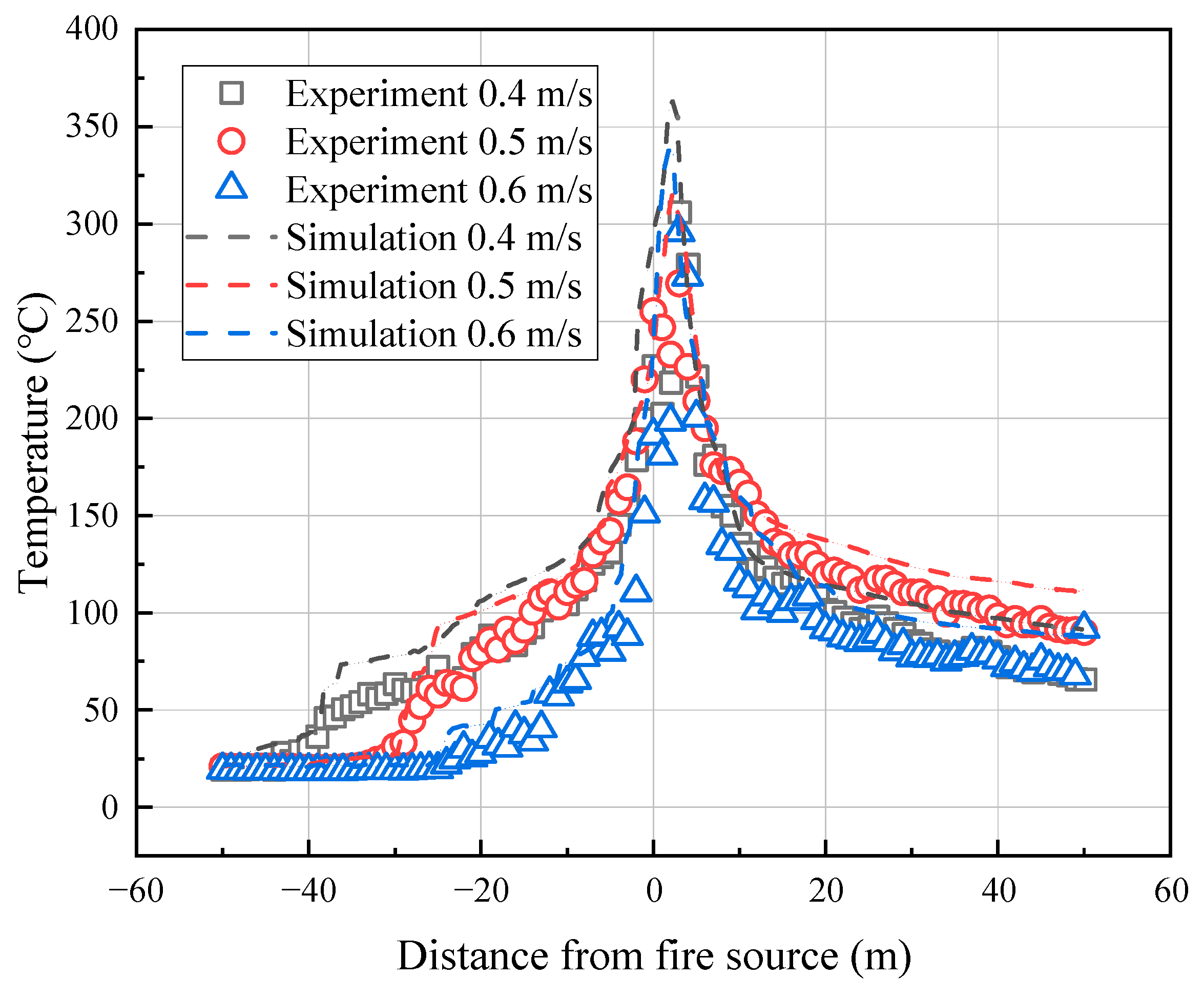

| No. | Fire Location | Cross-Section of Blockage (m × m) | (m/s) |
|---|---|---|---|
| 1~5 | 1 | 2 × 2 | 0.4 m/s, 0.8 m/s, 1.2 m/s, 1.6 m/s, 2 m/s |
| 6~10 | 1 | 2 × 3 | 0.4 m/s, 0.8 m/s, 1.2 m/s, 1.6 m/s, 2 m/s |
| 11~15 | 1 | 3 × 3 | 0.4 m/s, 0.8 m/s, 1.2 m/s, 1.6 m/s, 2 m/s |
| 16~20 | 1 | 3 × 4 | 0.4 m/s, 0.8 m/s, 1.2 m/s, 1.6 m/s, 2 m/s |
| 21~25 | 2 | 2 × 2 | 0.4 m/s, 0.8 m/s, 1.2 m/s, 1.6 m/s, 2 m/s |
| 26~30 | 2 | 2 × 3 | 0.4 m/s, 0.8 m/s, 1.2 m/s, 1.6 m/s, 2 m/s |
| 31~35 | 2 | 3 × 3 | 0.4 m/s, 0.8 m/s, 1.2 m/s, 1.6 m/s, 2 m/s |
| 36~40 | 2 | 3 × 4 | 0.4 m/s, 0.8 m/s, 1.2 m/s, 1.6 m/s, 2 m/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Dai, F.; Miao, B.; Wu, Z.; Ou, J. Thermal Characteristics of Multiple Blockages with Various Sizes in Longitudinal Ventilated Tunnel Fire. Fire 2024, 7, 269. https://doi.org/10.3390/fire7080269
Zhang H, Dai F, Miao B, Wu Z, Ou J. Thermal Characteristics of Multiple Blockages with Various Sizes in Longitudinal Ventilated Tunnel Fire. Fire. 2024; 7(8):269. https://doi.org/10.3390/fire7080269
Chicago/Turabian StyleZhang, Herui, Fengqiang Dai, Bin Miao, Zhengfei Wu, and Jianchun Ou. 2024. "Thermal Characteristics of Multiple Blockages with Various Sizes in Longitudinal Ventilated Tunnel Fire" Fire 7, no. 8: 269. https://doi.org/10.3390/fire7080269
APA StyleZhang, H., Dai, F., Miao, B., Wu, Z., & Ou, J. (2024). Thermal Characteristics of Multiple Blockages with Various Sizes in Longitudinal Ventilated Tunnel Fire. Fire, 7(8), 269. https://doi.org/10.3390/fire7080269






