The Progress of Autoignition of High-Pressure Hydrogen Gas Leakage: A Comprehensive Review
Abstract
1. Introduction
2. Mechanism of Autoignition of High-Pressure Hydrogen Gas Leakage
2.1. Reverse Joule–Thomson Effect
2.2. Electrostatic Ignition
2.3. Sudden Adiabatic Compression
2.4. Hot Surface Ignition
2.5. Mechanical Friction and Impact
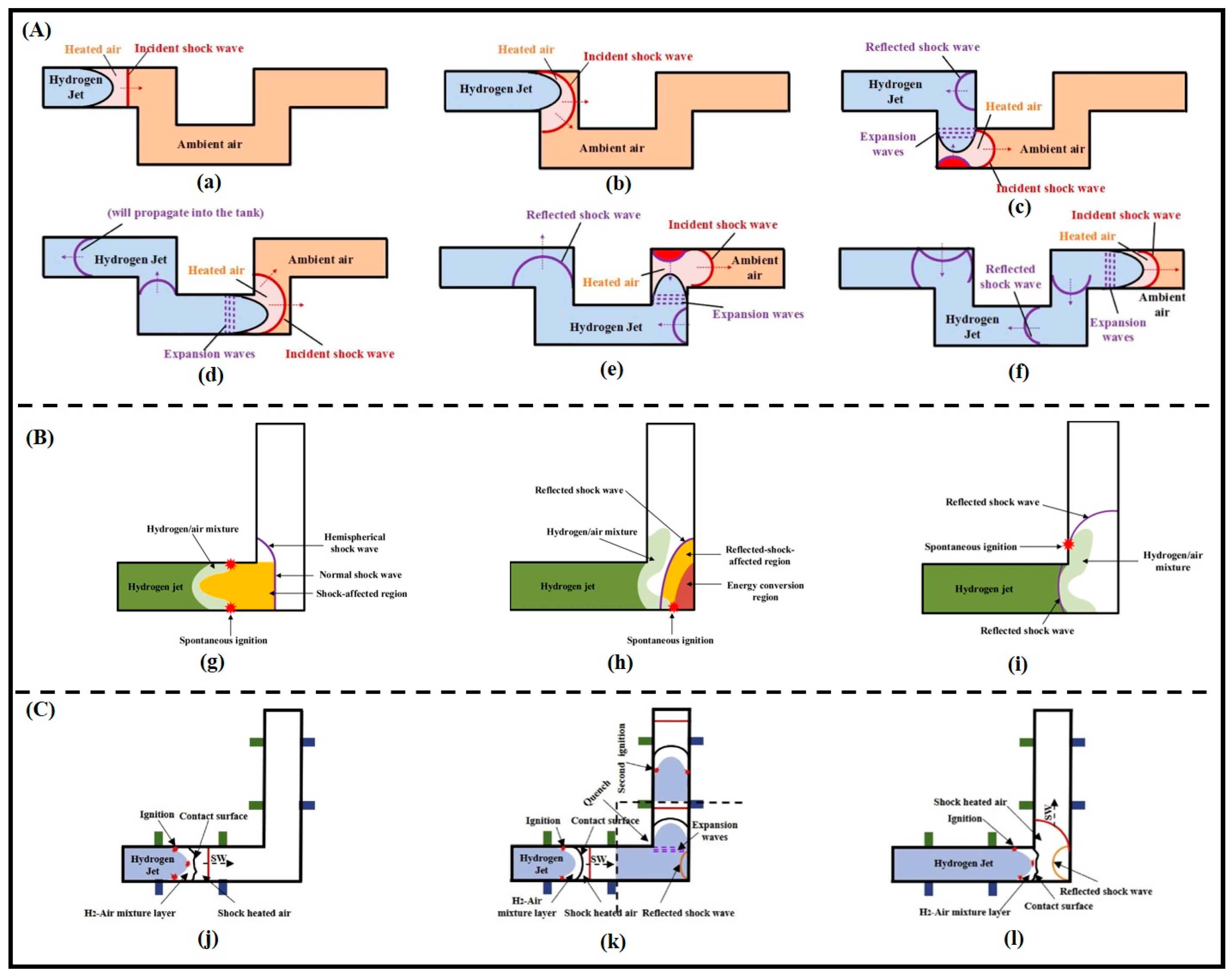
2.6. Diffusion Ignition
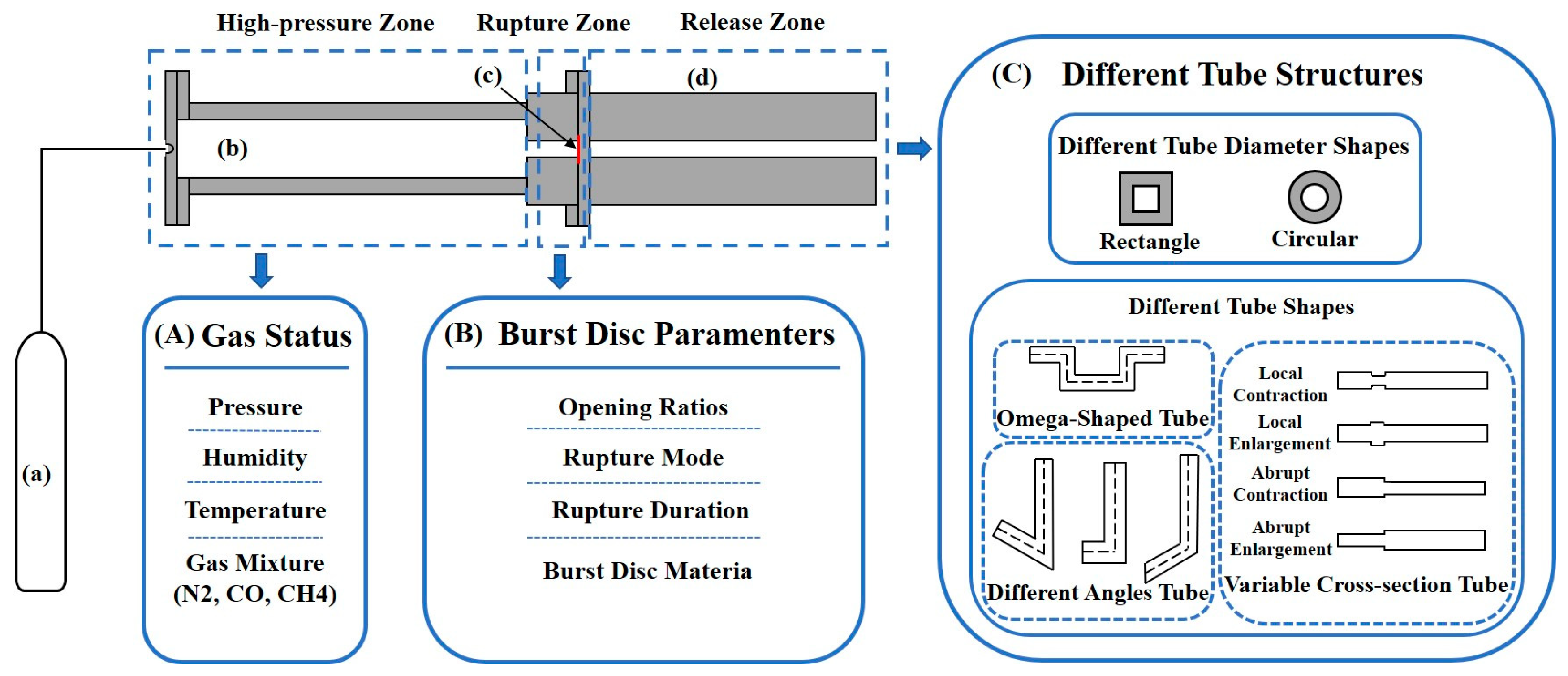
3. Factors Influencing Autoignition of High-Pressure Hydrogen Gas Leakage
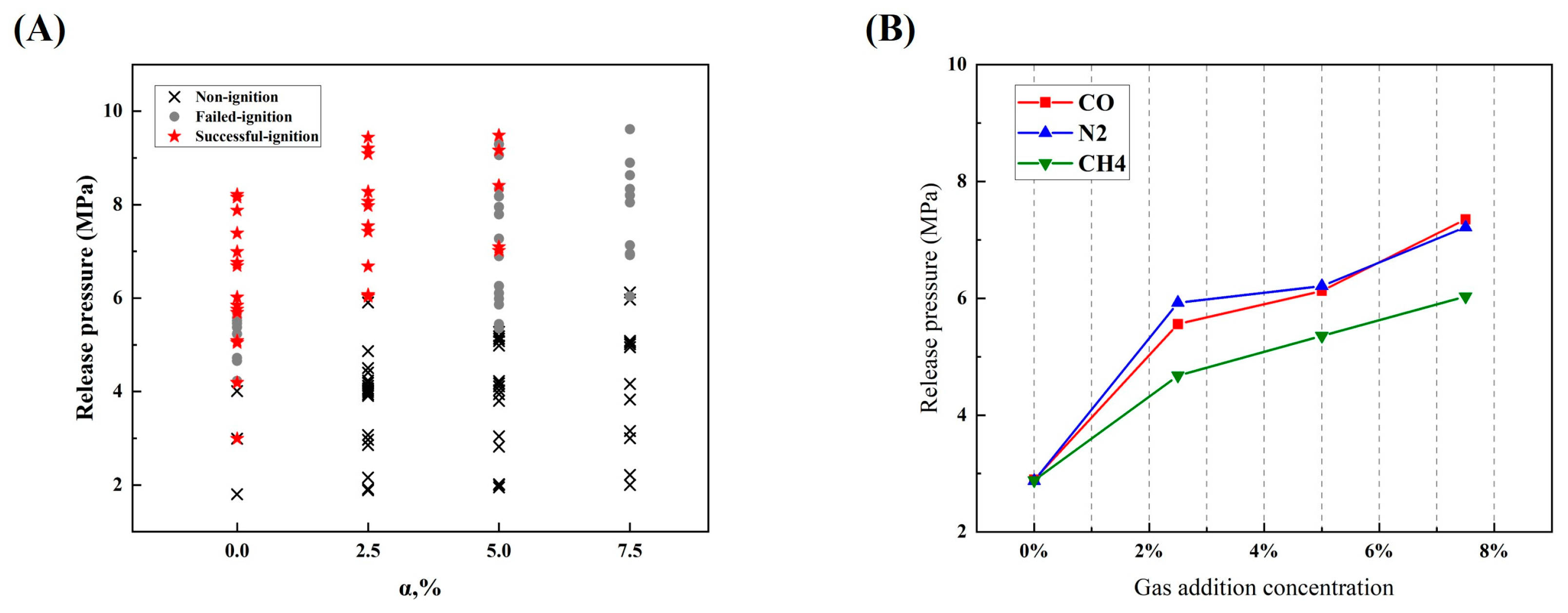
3.1. Study on the Effect of Gas State on Autoignition
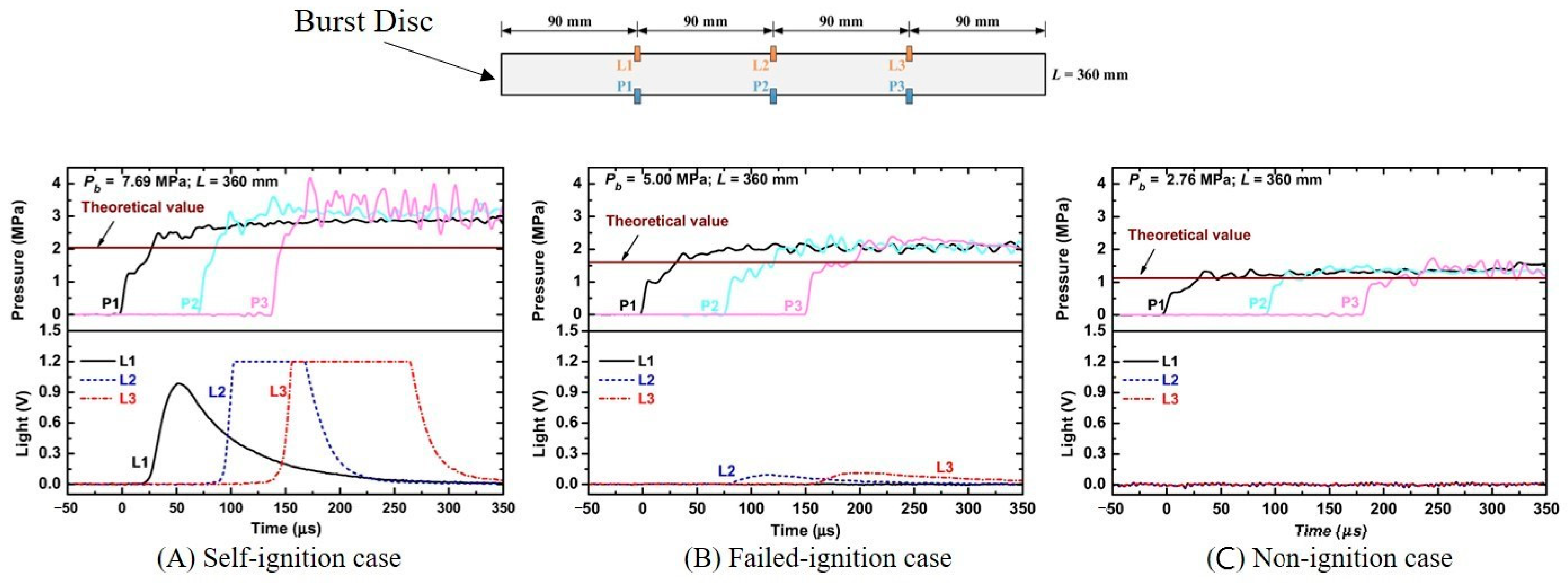
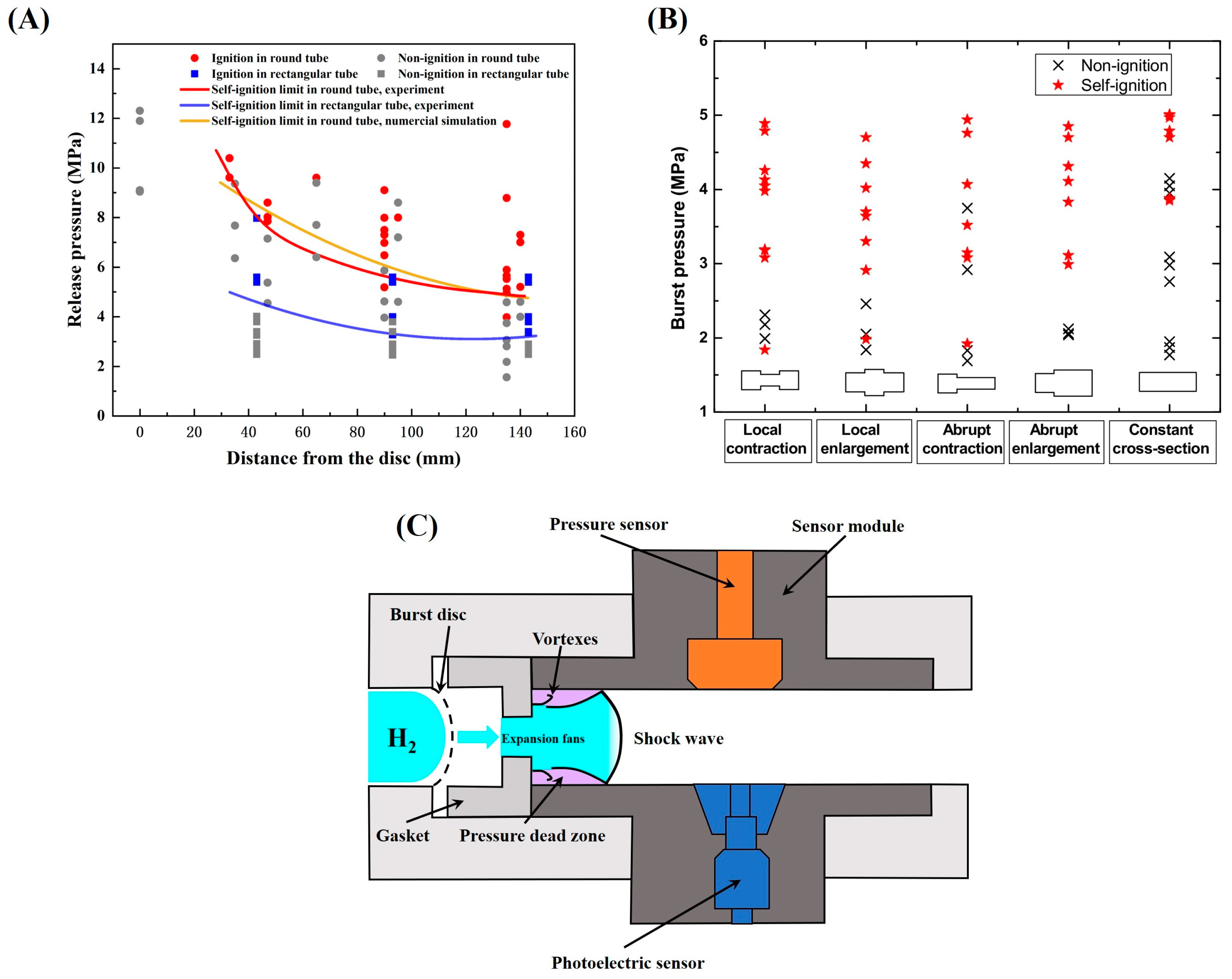
3.2. Study on the Effect of Burst Disc on Autoignition
3.3. Study of the Effect of Tube Geometry on Autoignition
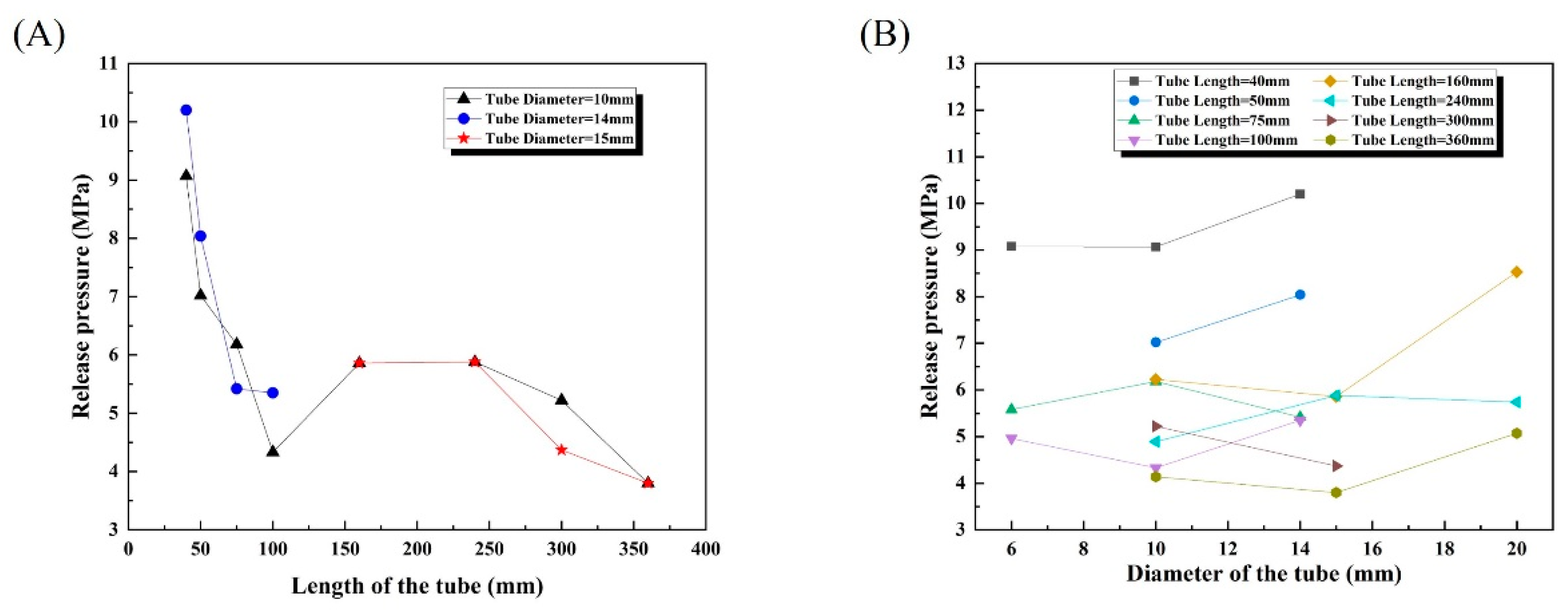
3.3.1. The Effect of Tube Length and Diameter on Autoignition

| Tube Diameter (mm) | Tube Length (mm) | Rupture Pressure (MPa) | Author | Tube Diameter (mm) | Tube Length (mm) | Rupture Pressure (MPa) | Author | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| S-Ignition | F-Ignition | N-Ignition | S-Ignition | F-Ignition | N-Ignition | ||||||
| 4 | 30 | 20.03 | 19.88 | Grune [78] | 5 | 185 | 8.77 | 11.71 | Mogi [74] | ||
| 42 | 4.99 | 4.82 | 7.05 | 11.11 | |||||||
| 58 | 2.45 | 1.69 | 300 | 19.17 | 13.33 | Mogi [75] | |||||
| 77 | 2.66 | 2.33 | 400 | 11.55 | |||||||
| 120 | 4.23 | 4.06 | 500 | 12.85 | |||||||
| 5 | 0 | 12.30 | Golub [39] | 6 | 10 | 15.65 | Rudy [79] | ||||
| 20 | 20.52 | Mogi [75] | 25 | 16.19 | |||||||
| 18.95 | Mogi [74] | 40 | 9.38 | 9.36 | |||||||
| 50 | 18.74 | 15.20 | Mogi [75] | 9.08 | 9.11 | ||||||
| 65 | 9.60 | 9.60 | Golub [39] | 8.67 | |||||||
| 7.70 | 50 | 10.79 | 9.19 | ||||||||
| 70 | 7.51 | Mogi [74] | 8.79 | 8.76 | |||||||
| 85 | 15.56 | 11.78 | 11.50 | Mogi [75] | 7.73 | 8.32 | |||||
| 15.64 | 21.69 | 13.11 | Mogi [74] | 8.14 | |||||||
| 20.67 | 7.75 | ||||||||||
| 18.48 | 7.45 | ||||||||||
| 14.79 | 75 | 6.37 | 6.25 | ||||||||
| 95 | 8.60 | 8.60 | Golub [39] | 6.20 | 5.85 | ||||||
| 8.00 | 7.20 | 5.78 | 5.63 | ||||||||
| 100 | 7.46 | Mogi [74] | 5.58 | 5.33 | |||||||
| 135 | 11.73 | 8.38 | Mogi [75] | 5.28 | |||||||
| 140 | 5.20 | 4.60 | Golub [39] | 5.21 | |||||||
| 185 | 11.85 | 18.46 | 10.79 | Mogi [75] | 4.99 | ||||||
| 13.26 | 100 | 7.11 | 4.79 | ||||||||
| 10.55 | 6.94 | 5.28 | |||||||||
| 9.38 | 5.68 | 5.95 | |||||||||
| 4.00 | 3.80 | Golub [39] | 4.96 | ||||||||
| 16.56 | 21.51 | 10.07 | Mogi [74] | 6.6 | 660 | 8.00 | 7.01 | Zhang [80] | |||
| 14.52 | 19.32 | 6.58 | |||||||||
| 10 | 5 | 20.24 | Mogi [74] | 10 | 25 | 17.21 | Rudy [79] | ||||
| 10 | 18.19 | 40 | 10.73 | 10.51 | |||||||
| 15.51 | Rudy [79] | 9.07 | 10.46 | ||||||||
| 10 | 40 | 10.39 | Rudy [79] | 10 | 300 | 5.50 | 4.50 | Kitabayashi [76] | |||
| 10.33 | 7.00 | 5.97 | Wang [48] | ||||||||
| 10.16 | 5.97 | 4.97 | |||||||||
| 9.59 | 350 | 3.91 | 4.10 | Kaneko [41] | |||||||
| 9.52 | 3.70 | ||||||||||
| 9.42 | 360 | 4.14 | 4.16 | Duan [73] | |||||||
| 9.34 | 2.84 | ||||||||||
| 50 | 7.02 | 9.05 | 400 | 9.36 | 11.73 | 11.14 | Mogi [75] | ||||
| 7.47 | 8.36 | ||||||||||
| 7.32 | 4.80 | Kitabayashi [76] | |||||||||
| 6.82 | 500 | 10.66 | 11.67 | Mogi [75] | |||||||
| 75 | 6.18 | 8.01 | 10.84 | ||||||||
| 7.05 | 8.66 | ||||||||||
| 6.82 | 640 | 6.25 | 5.04 | Zhang [80] | |||||||
| 6.03 | 700 | 5.93 | 5.84 | Wang [48] | |||||||
| 80 | 9.11 | Kaneko [41] | 6.04 | 4.86 | Xu [49] | ||||||
| 13.31 | 10.66 | Mogi [75] | 977 | 5.00 | 4.00 | Jiang [81] | |||||
| 100 | 4.33 | 8.51 | Rudy [79] | 1200 | 4.80 | Kitabayashi [76] | |||||
| 4.37 | 4.99 | 4.05 | Wang [48] | ||||||||
| 135 | 5.68 | 6.21 | Kaneko [41] | 1700 | 4.80 | Kitabayashi [76] | |||||
| 5.59 | 4.99 | 4.13 | Wang [48] | ||||||||
| 160 | 6.23 | 9.94 | Duan [73] | 4.14 | 2.99 | ||||||
| 7.09 | 2200 | 6.94 | 5.91 | ||||||||
| 5.27 | 5.92 | 4.97 | |||||||||
| 185 | 10.78 | 11.07 | 9.07 | Mogi [75] | 3000 | 9.04 | 8.84 | ||||
| 190 | 5.22 | 5.96 | Kaneko [41] | 7.91 | 7.92 | ||||||
| 190 | 5.82 | 7.06 | |||||||||
| 240 | 4.89 | 3.91 | Duan [73] | 3200 | 4.80 | Kitabayashi [76] | |||||
| 245 | 4.84 | 4.43 | Kaneko [41] | 14 | 10 | 15.84 | Rudy [79] | ||||
| 300 | 9.26 | 10.96 | Mogi [75] | 25 | 16.34 | ||||||
| 7.47 | 40 | 10.20 | 13.28 | ||||||||
| 5.22 | 4.96 | Kaneko [41] | 11.19 | ||||||||
| 4.77 | 11.12 | ||||||||||
| 4.67 | 10.37 | ||||||||||
| 4.34 | 10.12 | ||||||||||
| 3.70 | 9.82 | ||||||||||
| 14 | 50 | 8.04 | 9.50 | Rudy [79] | 15 | 240 | 5.88 | 5.42 | Duan [32] | ||
| 8.36 | 5.20 | ||||||||||
| 8.23 | 4.71 | ||||||||||
| 7.99 | 4.40 | ||||||||||
| 75 | 5.42 | 5.30 | 4.05 | ||||||||
| 5.60 | 4.13 | 4.08 | Duan [73] | ||||||||
| 5.75 | 3.81 | ||||||||||
| 6.17 | 300 | 5.00 | 4.78 | Wang [35] | |||||||
| 6.99 | 4.89 | 41.02 | 4.28 | Gong [83] | |||||||
| 100 | 5.35 | 4.88 | 4.37 | 3.30 | Gong [43] | ||||||
| 3.33 | 4.75 | 5.88 | 5.38 | 4.12 | Duan [32] | ||||||
| 4.73 | 4.98 | 4.98 | 3.90 | ||||||||
| 4.58 | 4.65 | 4.74 | 3.02 | ||||||||
| 4.11 | 3.83 | ||||||||||
| 4.06 | 360 | 3.80 | 4.14 | Duan [73] | |||||||
| 3.49 | 3.87 | ||||||||||
| 3.41 | 3.09 | ||||||||||
| 3.21 | 9.50 | 9.00 | Zhu [47] | ||||||||
| 15 | 80 | 8.90 | 7.89 | Duan [32] | 700 | 4.76 | 4.53 | Wang [35] | |||
| 120 | 8.84 | 7.80 | 7.84 | 6.02 | 4.97 | Xu [49] | |||||
| 7.10 | 1200 | 3.83 | 3.09 | Wang [35] | |||||||
| 160 | 6.85 | 6.09 | 1700 | 3.91 | 2.79 | ||||||
| 5.93 | 5.31 | 2200 | 4.92 | 4.06 | |||||||
| 5.86 | 3000 | 5.15 | 4.30 | ||||||||
| 5.47 | 20 | 160 | 8.53 | 6.89 | Duan [73] | ||||||
| 5.55 | 6.14 | Duan [73] | 240 | 5.74 | 5.38 | ||||||
| 5.35 | 360 | 5.07 | 5.14 | ||||||||
| 240 | 6.99 | 6.65 | 3.77 | Duan [32] | 4.72 | ||||||
3.3.2. The Effect of Tube Structure on Autoignition
4. Combustion Characteristics of High-Pressure Hydrogen Gas Leakage Autoignition Flame
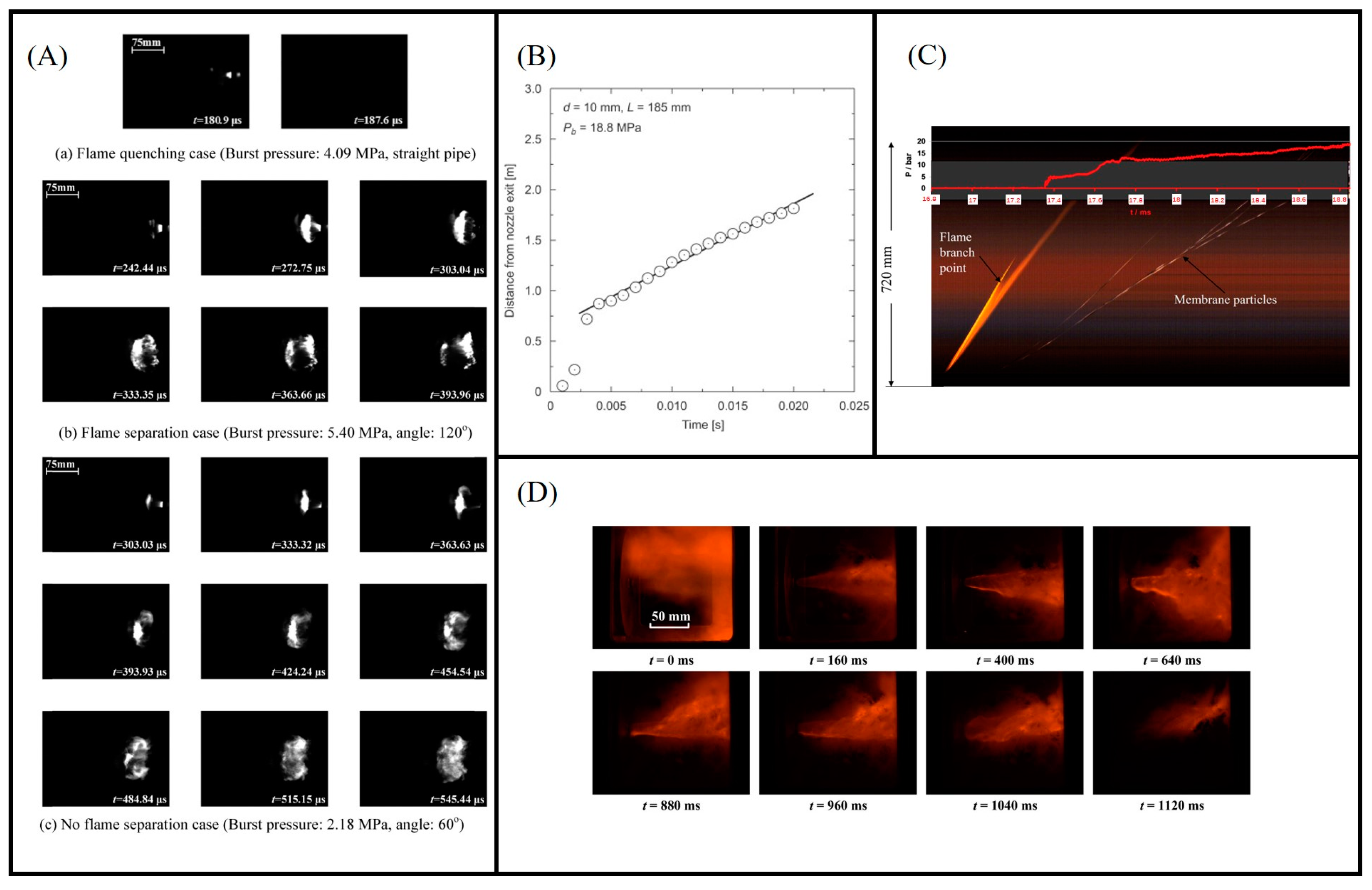
4.1. Study of the Evolution Characteristics of the Autoignition Flame in the Tube
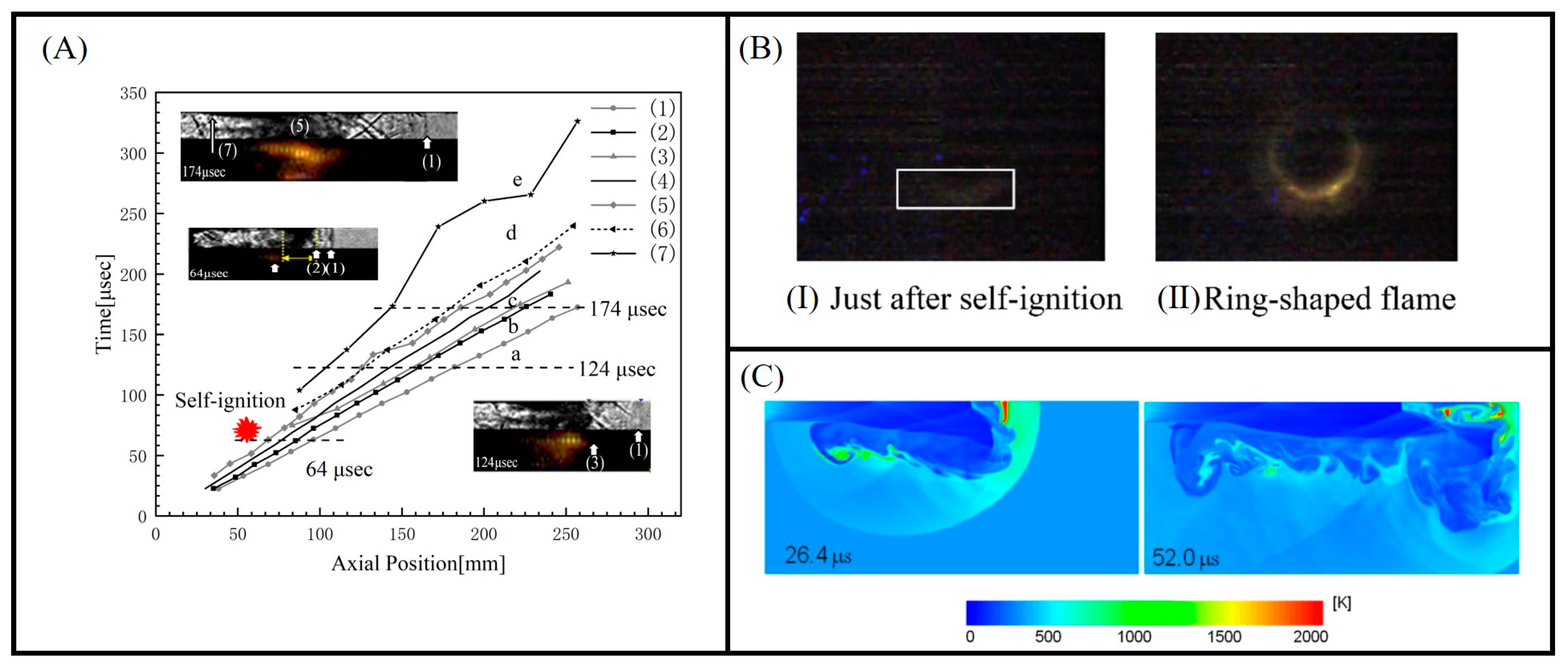
4.2. Study of the Propagation Characteristics of Jet Flame outside the Tube
5. Conclusions
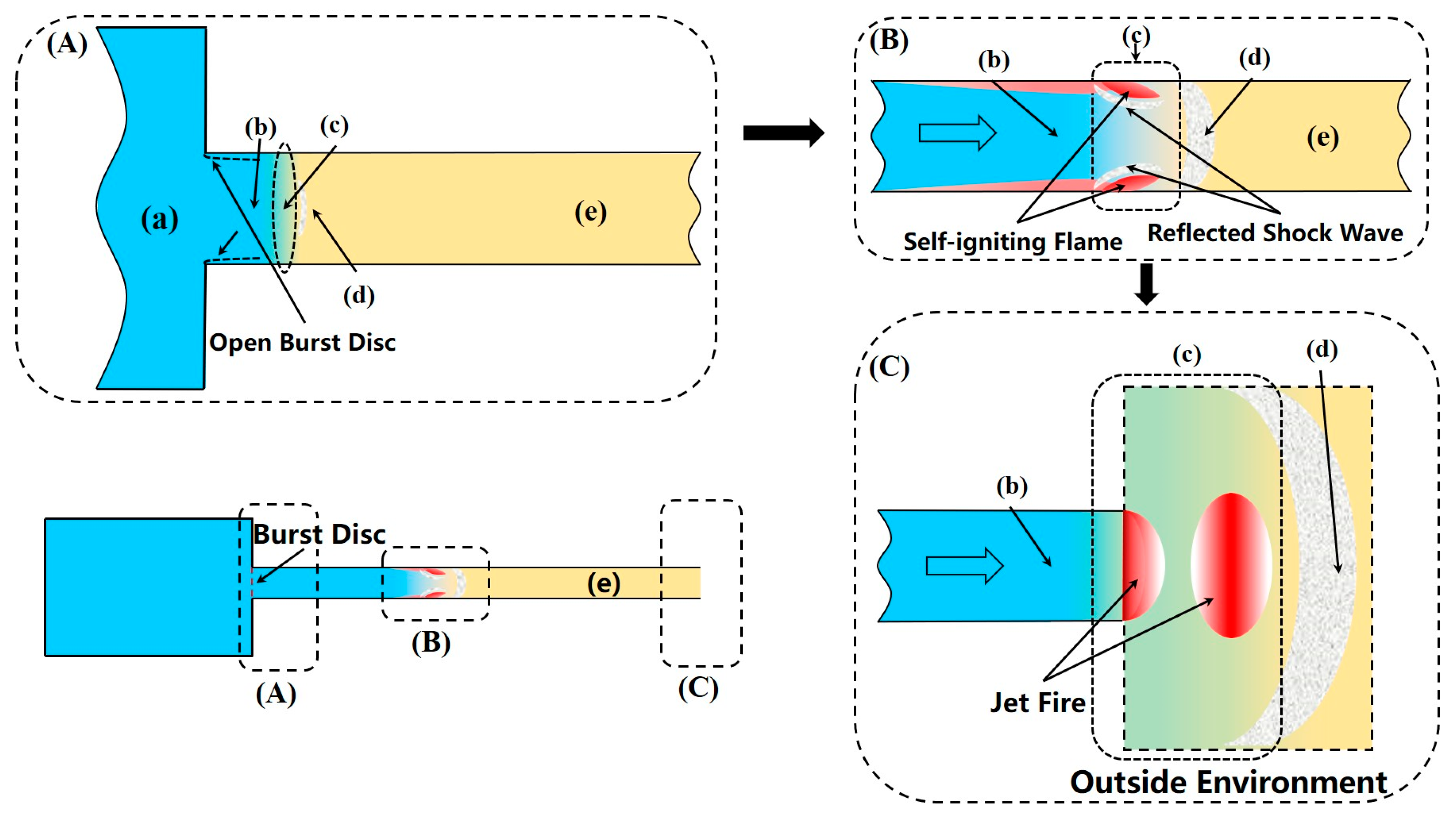
- Various factors within the high-pressure and rupture zones influence shock wave generation, while factors within the release zone affect shock wave propagation. Differences in gas properties, burst disc rupture conditions, tube geometric structure, and obstacles lead to variations in shock wave growth patterns. These factors combine to determine the occurrence of spontaneous combustion, and as long as one of these factors is above or below the threshold, spontaneous combustion cannot occur. For instance, even with a burst pressure of 100 bar, a sufficient shock wave intensity to ignite hydrogen cannot be generated when the aperture area is 1/4.
- When the tube length is shorter, the diameter has a significant impact on the minimum release pressure required for autoignition, resulting in a broader range of experimentally measured minimum release pressures. However, as the tube length increases, the minimum release pressure required for autoignition gradually becomes more concentrated, leading to a narrower range of experimental data.
- The ignition of the “diffusion ignition” mechanism occurs within the most reactive hydrogen–air mixture, with hydrogen concentrations ranging from 19% to 36% by volume. After the kernel of autoignition is generated, it gradually develops into a premixed flame under the interaction of a large number of shock waves. Once a complete flame spanning the entire cross-section of the tube is formed internally, the flame transitions to an external jet. The development of an external flame differs from autoignition, primarily influenced by release pressure and external conditions rather than tube geometric structure. The intrinsic factor affecting flame development is the vortex, and therefore the study of the vortex can help understand the propagation of a jet flame outside a tube.
6. Outlook
- Currently, research on the spontaneous combustion of high-pressure hydrogen leaks often relies on shock tube models, with tube cross-sections typically being rectangular or circular. However, in practical engineering, the rupture shapes of high-pressure tanks or pipelines are often irregular, and the presence of obstacles in the leak environment complicates shock wave propagation. To enhance the effective application of research outcomes in hydrogen safety engineering, further studies should be conducted based on existing research foundations, focusing on various release scenarios. For instance, conditions involving metal mesh inside tubes and slit conditions should be considered.
- Current research predominantly focuses on the impact of individual factors on high-pressure hydrogen leakage and autoignition, with limited depth in studying the characteristics underlying the coupled effects of multiple factors. Future research should investigate the growth patterns of shock waves under different influencing factors to comprehensively understand the autoignition characteristics under coupled multi-factor conditions.
- The current study only focuses on shock waves’ macroscopic effects on the boundary layer. There is a lack of in-depth exploration into how shock wave intensity affects the distribution of hydrogen concentration gradients and temperature rise rates within the boundary layer. The mechanisms by which shock waves enhance hydrogen–air diffusion mixing and boundary layer heating are also inadequately understood. Future research should delve deeper into how shock waves influence gas properties (such as temperature and mixing levels) within the boundary layer and investigate the relationship between gas characteristics and the generation of autoignition ignition kernels.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Noussan, M.; Raimondi, P.P.; Scita, R.; Hafner, M. The Role of Green and Blue Hydrogen in the Energy Transition—A Technological and Geopolitical Perspective. Sustainability 2020, 13, 298. [Google Scholar] [CrossRef]
- Penner, S.S. Steps toward the hydrogen economy. Energy 2006, 31, 33–43. [Google Scholar] [CrossRef]
- Dincer, I. Green methods for hydrogen production. Int. J. Hydrogen Energy 2012, 37, 1954–1971. [Google Scholar] [CrossRef]
- Sarkar, A.; Banerjee, R. Net energy analysis of hydrogen storage options. Int. J. Hydrogen Energy 2005, 30, 867–877. [Google Scholar] [CrossRef]
- Elberry, A.M.; Thakur, J.; Santasalo-Aarnio, A.; Larmi, M. Large-scale compressed hydrogen storage as part of renewable electricity storage systems. Int. J. Hydrogen Energy 2021, 46, 15671–15690. [Google Scholar] [CrossRef]
- Yang, F.; Wang, T.; Deng, X.; Dang, J.; Huang, Z.; Hu, S.; Li, Y.; Ouyang, M. Review on hydrogen safety issues: Incident statistics, hydrogen diffusion, and detonation process. Int. J. Hydrogen Energy 2021, 46, 31467–31488. [Google Scholar] [CrossRef]
- Ono, R.; Nifuku, M.; Fujiwara, S.; Horiguchi, S.; Oda, T. Minimum ignition energy of hydrogen–air mixture: Effects of humidity and spark duration. J. Electrost. 2007, 65, 87–93. [Google Scholar] [CrossRef]
- Crowl, D.A.; Jo, Y.-D. The hazards and risks of hydrogen. J. Loss Prev. Process Ind. 2007, 20, 158–164. [Google Scholar] [CrossRef]
- Green, M.A. Hydrogen safety issues compared to safety issues with methane and propane. AIP Conf. Proc. 2006, 823, 319–326. [Google Scholar]
- Duan, Q.; Xiao, H.; Gao, W.; Shen, X.; Wang, Q.; Sun, J. Experimental investigation on shock waves generated by pressurized gas release through a tube. J. Loss Prev. Process Ind. 2015, 36, 39–44. [Google Scholar] [CrossRef]
- Najjar, Y.S.H. Hydrogen safety: The road toward green technology. Int. J. Hydrogen Energy 2013, 38, 10716–10728. [Google Scholar] [CrossRef]
- Kotchourko, A.; Baraldi, D.; Bénard, P.; Jordan, T.; Keßler, A.; LaChance, J.; Steen, M.; Tchouvelev, A.V.; Wen, J.X. Stare of the Art and Research Priorities in Hydrogen Safety; Publications Office of the European Union: Luxembourg, 2014. [Google Scholar]
- Meda, U.S.; Bhat, N.; Pandey, A.; Subramanya, K.N.; Raj, M.A.L.A. Challenges associated with hydrogen storage systems due to the hydrogen embrittlement of high strength steels. Int. J. Hydrogen Energy 2023, 48, 17894–17913. [Google Scholar] [CrossRef]
- Astbury, G.; Hawksworth, S. Spontaneous ignition of hydrogen leaks: A review of postulated mechanisms. Int. J. Hydrogen Energy 2007, 32, 2178–2185. [Google Scholar] [CrossRef]
- Xu, B.P.; Wen, J.X.; Dembele, S.; Tam, V.H.Y.; Hawksworth, S.J. The effect of pressure boundary rupture rate on spontaneous ignition of pressurized hydrogen release. J. Loss Prev. Process Ind. 2009, 22, 279–287. [Google Scholar] [CrossRef]
- Wolanski, P.; Wojcicki, S. Investigation into the Mechanism of the Diffusion Ignition of a Combustible Gas Flowing into an Oxidizing Atmosphere. In Proceedings of the 14th International Symposium on Combustion, University Park, PA, USA, 20–25 August 1972. [Google Scholar]
- National Aeronautics and Space Administration Report. Safety Standard for Hydrogen and Hydrogen Systems; Report NSS 1740.16; Office of Safety and Mission Assurance: Washington, DC, USA, 1997; p. A-16.
- Michels, A.; de Graaff, W.; Wolkers, G.J. Thermodynamic properties of hydrogen and deuterium at temperatures between −175°C and 150°C and at densities up to 840 amagat. Physica 1959, 25, 1097–1124. [Google Scholar] [CrossRef]
- Camp, P.R. Charge, morphology, and pH of natural snow. J. Geophys. Res. 1976, 81, 1589–1592. [Google Scholar] [CrossRef]
- Molkov, V. Hydrogen safety research: State-of-the-art. In Proceedings of the 5th International Seminar on Fire and Explosion Hazards, Edinburgh, UK, 23–27 April 2007; pp. 28–43. [Google Scholar]
- Cain, T.M. Autoignition of hydrogen at high pressure. Combust. Flame 1997, 111, 124–132. [Google Scholar] [CrossRef]
- Powell, F. Ignition of gases and vapours by hot surfaces and particles—A review. In Proceedings of the 9th International Symposium on the Prevention of Occupational Accidents and Diseases in the Chemical Industry, Lucerne, Switzerland, 5–7 June 1984. [Google Scholar]
- Cho, P.; Law, C.K. Catalytic ignition of fuel/oxygen/nitrogen mixtures over platinum. Combust. Flame 1986, 66, 159–170. [Google Scholar] [CrossRef]
- Powell, F. Ignition of flammable gases and vapours by friction between footwear and flooring materials. J. Hazard. Mater. 1977, 2, 309–319. [Google Scholar] [CrossRef]
- Pan, L.; Fisher, S.A.; Jayanti, S.; Hewitt, G.F. Measurement and prediction of temperature rise following sudden compression in a high-pressure pipeline. Process Saf. Environ. Prot. 1995, 73, 18–20. [Google Scholar]
- Duan, Q.; Xiao, H.; Gong, L.; Li, P.; Zeng, Q.; Gao, W.; Sun, J. Experimental study of shock wave propagation and its influence on the spontaneous ignition during high-pressure hydrogen release through a tube. Int. J. Hydrogen Energy 2019, 44, 22598–22607. [Google Scholar] [CrossRef]
- Golovastov, S.V.; Bocharnikov, V.M.; Samoilova, A.A. Experimental investigation of influence of methane additions on spontaneous self-ignition of pulsed jet of hydrogen. Int. J. Hydrogen Energy 2016, 41, 13322–13328. [Google Scholar] [CrossRef]
- Golovastov, S.; Bocharnikov, V. The influence of diaphragm rupture rate on spontaneous self-ignition of pressurized hydrogen: Experimental investigation. Int. J. Hydrogen Energy 2012, 37, 10956–10962. [Google Scholar] [CrossRef]
- Gong, L.; Zheng, X.; Yang, S.; Yao, Y.; Xie, Y.; Mo, T.; Zhang, Y. Numerical study on the shock evolution and the spontaneous ignition of high-pressure hydrogen during its sudden release into the tubes with different angles. Fuel 2023, 331, 125940. [Google Scholar] [CrossRef]
- Jin, K.; Yang, S.; Gong, L.; Mo, T.; Gao, Y.; Zhang, Y. Mechanism of spontaneous ignition of high-pressure hydrogen during its release through a tube with local contraction: A numerical study. Int. J. Hydrogen Energy 2022, 47, 6421–6436. [Google Scholar] [CrossRef]
- Lee, H.J.; Lee, S.Y.; Park, J.H.; Jeung, I.-S. Effects of opening conditions on the self-ignition of high pressurized hydrogen released through a tube. In Proceedings of the 25th International Colloquium on the Dynamics of Explosions and Reactive Systems, Leeds, UK, 2–7 August 2015. [Google Scholar]
- Duan, Q.; Xiao, H.; Gao, W.; Gong, L.; Wang, Q.; Sun, J. Experimental study on spontaneous ignition and flame propagation of high-pressure hydrogen release via a tube into air. Fuel 2016, 181, 811–819. [Google Scholar] [CrossRef]
- Baev, V.K.; Shumskii, V.V.; Yaroslavtsev, M.I. Self-ignition of a fuel gas escaping into an oxidizing medium. Combust. Explos. Shock Waves 1983, 19, 600–605. [Google Scholar] [CrossRef]
- Baev, V.K.; Buzukov, A.A.; Shumskii, V.V. Conditions of self-ignition upon pulsed high-pressure injection of combustible gases into a bounded space. Combust. Explos. Shock Waves 2000, 36, 3–10. [Google Scholar] [CrossRef]
- Wang, Z.; Pan, X.; Jiang, Y.; Wang, Q.; Yan, W.; Xiao, J.; Jordan, T.; Jiang, J. Experiment study on the pressure and flame characteristics induced by high-pressure hydrogen spontaneous ignition. Int. J. Hydrogen Energy 2020, 45, 18042–18056. [Google Scholar] [CrossRef]
- Yamada, E.; Watanabe, S.; Hayashi, A.K.; Tsuboi, N. Numerical analysis on auto-ignition of a high pressure hydrogen jet spouting from a tube. Proc. Combust. Inst. 2009, 32, 2363–2369. [Google Scholar] [CrossRef]
- Kim, Y.R.; Lee, H.J.; Kim, S.; Jeung, I.-S. A flow visualization study on self-ignition of high pressure hydrogen gas released into a tube. Proc. Combust. Inst. 2013, 34, 2057–2064. [Google Scholar] [CrossRef]
- Duan, Q.; Tang, J.; Jin, K.; Zeng, Q.; Wu, Y.; Zhang, S.; Wang, Q.; Sun, J. Experimental investigation of shock wave propagation, spontaneous ignition, and flame development of high-pressure hydrogen release through tubes with different obstacles arrangements. Int. J. Hydrogen Energy 2022, 47, 38075–38086. [Google Scholar] [CrossRef]
- Golub, V.V.; Baklanov, D.I.; Golovastov, S.V.; Ivanov, M.F.; Laskin, I.N.; Saveliev, A.S.; Semin, N.V.; Volodin, V.V. Mechanisms of high-pressure hydrogen gas self-ignition in tubes. J. Loss Prev. Process Ind. 2008, 21, 185–198. [Google Scholar] [CrossRef]
- Bazhenova, T.V.; Bragin, M.V.; Golub, V.V.; Ivanov, M.F. Self-ignition of a fuel gas upon pulsed efflux into an oxidative medium. Tech. Phys. Lett. 2006, 32, 269–271. [Google Scholar] [CrossRef]
- Kaneko, W.; Ishii, K. Effects of diaphragm rupturing conditions on self-ignition of high-pressure hydrogen. Int. J. Hydrogen Energy 2016, 41, 10969–10975. [Google Scholar] [CrossRef]
- Gong, L.; Jin, K.; Zheng, X.; Han, Y.; Yao, Y.; Duan, Q.; Zhang, Y.; Sun, J. Effect of Al-made burst disk on the shock wave and the spontaneous ignition of high-pressure hydrogen during its sudden discharge. J. Energy Storage 2023, 72, 108371. [Google Scholar] [CrossRef]
- Gong, L.; Duan, Q.; Liu, J.; Li, M.; Jin, K.; Sun, J. Effect of burst disk parameters on the release of high-pressure hydrogen. Fuel 2019, 235, 485–494. [Google Scholar] [CrossRef]
- Rudy, W.; Teodorczyk, A.; Wen, J. Self-ignition of hydrogen–nitrogen mixtures during high-pressure release into air. Int. J. Hydrogen Energy 2017, 42, 7340–7352. [Google Scholar] [CrossRef]
- Golub, V.V.; Baklanov, D.I.; Bazhenova, T.V.; Bragin, M.V.; Golovastov, S.V.; Ivanov, M.F.; Volodin, V.V. Shock-induced ignition of hydrogen gas during accidental or technical opening of high-pressure tanks. J. Loss Prev. Process Ind. 2007, 20, 439–446. [Google Scholar] [CrossRef]
- Golub, V.V.; Baklanov, D.I.; Bazhenova, T.V.; Golovastov, S.V.; Ivanov, M.F.; Laskin, I.N.; Semin, N.V.; Volodin, V.V. Experimental and numerical investigation of hydrogen gas auto-ignition. Int. J. Hydrogen Energy 2009, 34, 5946–5953. [Google Scholar] [CrossRef]
- Zhu, M.; Jin, K.; Duan, Q.; Zeng, Q.; Sun, J. Numerical simulation on the spontaneous ignition of high-pressure hydrogen release through a tube at different burst pressures. Int. J. Hydrogen Energy 2022, 47, 10431–10440. [Google Scholar] [CrossRef]
- Wang, Z.; Pan, X.; Wang, Q.; Jiang, Y.; Xu, X.; Yan, W.; Jiang, J. Experimental study on spontaneous ignition and flame propagation of high-pressure hydrogen release through tubes. Int. J. Hydrogen Energy 2019, 44, 22584–22597. [Google Scholar] [CrossRef]
- Xu, X.; Jiang, J.; Jiang, Y.; Wang, Z.; Wang, Q.; Yan, W.; Pan, X. Spontaneous ignition of high-pressure hydrogen and boundary layer characteristics in tubes. Int. J. Hydrogen Energy 2020, 45, 20515–20524. [Google Scholar] [CrossRef]
- Kaneko, W.; Ishii, K. An experimental study on the mechanism of self-ignition of high-pressure hydrogen. Int. J. Hydrogen Energy 2017, 42, 7374–7379. [Google Scholar] [CrossRef]
- Dryer, F.L.; Chaos, M.; Zhao, Z.; Stein, J.N.; Alpert, J.Y.; Homer, C.J. Spontaneous Ignition of Pressurized Releases of Hydrogen and Natural Gas into Air. Combust. Sci. Technol. 2007, 179, 663–694. [Google Scholar] [CrossRef]
- Yamashita, K.; Saburi, T.; Wada, Y.; Asahara, M.; Mogi, T.; Hayashi, A.K. Visualization of spontaneous ignition under controlled burst pressure. Int. J. Hydrogen Energy 2017, 42, 7755–7760. [Google Scholar] [CrossRef]
- Bragin, M.V.; Makarov, D.V.; Molkov, V.V. Pressure limit of hydrogen spontaneous ignition in a T-shaped channel. Int. J. Hydrogen Energy 2013, 38, 8039–8052. [Google Scholar] [CrossRef]
- Radulescu, M.I.; Law, C.K. The transient start of supersonic jets. J. Fluid Mech. 2007, 578, 331–369. [Google Scholar] [CrossRef]
- Zeng, Q.; Duan, Q.; Sun, D.; Li, P.; Zhu, M.; Wang, Q.; Sun, J. Experimental study of methane addition effect on shock wave propagation, self-ignition and flame development during high-pressure hydrogen sudden discharge from a tube. Fuel 2020, 277, 118217. [Google Scholar] [CrossRef]
- Asahara, M.; Saburi, T.; Ando, T.; Takahashi, Y.; Miyasaka, T.; Kubota, S. Self-ignited flame behavior of high-pressure hydrogen release by rupture disk through a long tube. Int. J. Hydrogen Energy 2021, 46, 13484–13500. [Google Scholar] [CrossRef]
- Cirrone, D.; Makarov, D.; Proust, C.; Molkov, V. Minimum ignition energy of hydrogen-air mixtures at ambient and cryogenic temperatures. Int. J. Hydrogen Energy 2023, 48, 16530–16544. [Google Scholar] [CrossRef]
- Zhou, S.; Luo, Z.; Wang, T.; He, M.; Li, R.; Su, B. Research progress on the self-ignition of high-pressure hydrogen discharge: A review. Int. J. Hydrogen Energy 2022, 47, 9460–9476. [Google Scholar] [CrossRef]
- Sun, L.; Jia, C.; Miao, Y. Visualization of hydrogen leak for electro-hydrogen coupled system based on Background Oriented Schlieren. Process Saf. Environ. Prot. 2023, 175, 437–446. [Google Scholar] [CrossRef]
- Zhang, K.; Luo, T.; Li, Y.; Zhang, T.; Li, X.; Zhang, Z.; Shang, S.; Zhou, Y.; Zhang, C.; Chen, X.; et al. Effect of ignition, initial pressure and temperature on the lower flammability limit of hydrogen/air mixture. Int. J. Hydrogen Energy 2022, 47, 15107–15119. [Google Scholar] [CrossRef]
- Ghosh, A.; Munoz-Munoz, N.M.; Lacoste, D.A. Minimum ignition energy of hydrogen-air and methane-air mixtures at temperatures as low as 200 K. Int. J. Hydrogen Energy 2022, 47, 30653–30659. [Google Scholar] [CrossRef]
- Zeng, Q.; Duan, Q.; Li, P.; Zhu, H.; Sun, D.; Sun, J. An experimental study of the effect of 2.5% methane addition on self-ignition and flame propagation during high-pressure hydrogen release through a tube. Int. J. Hydrogen Energy 2020, 45, 3381–3390. [Google Scholar] [CrossRef]
- Ivanov, M.F.; Kiverin, A.D.; Smygalina, A.E.; Golub, V.V.; Golovastov, S.V. Mechanism of self-ignition of pressurized hydrogen flowing into the channel through rupturing diaphragm. Int. J. Hydrogen Energy 2017, 42, 11902–11910. [Google Scholar] [CrossRef]
- Zeng, Q.; Jin, K.; Duan, Q.; Zhu, M.; Gong, L.; Wang, Q.; Sun, J. Effects of CO addition on shock wave propagation, self-ignition, and flame development of high-pressure hydrogen release into air. Int. J. Hydrogen Energy 2022, 47, 14714–14724. [Google Scholar] [CrossRef]
- Zeng, Q.; Duan, Q.; Jin, K.; Zhu, M.; Sun, J. Effects of nitrogen addition on the shock-induced ignition of high-pressure hydrogen release through a rectangular tube of 400 mm in length. Fuel 2022, 308, 122016. [Google Scholar] [CrossRef]
- Tanaka, K.; Urano, Y.; Iwasaka, M.; Hashiguchi, Y. The ignition of a compressed hydrogen by the discharge from a rupture disc. J. High Press. Gas Saf. Inst. Jpn. 1978, 15, 355–358. [Google Scholar]
- Maxwell, B.M.; Radulescu, M.I. Ignition limits of rapidly expanding diffusion layers: Application to unsteady hydrogen jets. Combust. Flame 2011, 158, 1946–1959. [Google Scholar] [CrossRef]
- Pan, X.; Lu, L.; Zhang, T.; Jiang, Y.; Li, Y.; Wang, Z.; Hua, M.; Jiang, J. Effect of the leak port area and tube length on suppression of spontaneous ignition of high-pressure hydrogen. J. Energy Storage 2023, 74, 109396. [Google Scholar] [CrossRef]
- Cha, S.-W.; Roh, T.-S.; Lee, H.J. Effect of opening area on the suppression of self-ignition of high-pressure hydrogen gas leaking in the air by an extension tube. Int. J. Hydrogen Energy 2021, 46, 5904–5915. [Google Scholar] [CrossRef]
- Golovastov, S.V.; Baklanov, D.I.; Volodin, V.V.; Golub, V.V.; Ivanov, K.V. An experimental study of the diffusion-controlled self-ignition of hydrogen in a channel. Russ. J. Phys. Chem. B 2009, 3, 348–355. [Google Scholar] [CrossRef]
- Xu, B.P.; El Hima, L.; Wen, J.X.; Tam, V.H.Y. Numerical study of spontaneous ignition of pressurized hydrogen release into air. Int. J. Hydrog. Energy 2009, 34, 5954–5960. [Google Scholar] [CrossRef]
- Liu, Y.F.; Tsuboi, N.; Sato, H.; Higashino, F.; Hayashi, A.K.; Gakuin, A. Direct numerical simulation on hydrogen fuel jetting from high pressure tank. In Proceedings of the 20th International Colloquium on the Dynamics of Explosion and Reactive Systems, Montreal, Canada, 31 July–5 August 2005. [Google Scholar]
- Duan, Q.; Xiao, H.; Gong, L.; Jin, K.; Gao, W.; Chai, H.; Sun, J. Experimental study on spontaneous ignition and subsequent flame development caused by high-pressure hydrogen release: Coupled effects of tube dimensions and burst pressure. Fire Saf. J. 2018, 97, 44–53. [Google Scholar] [CrossRef]
- Mogi, T.; Kim, D.; Shiina, H.; Horiguchi, S. Self-ignition and explosion during discharge of high-pressure hydrogen. J. Loss Prev. Process Ind. 2008, 21, 199–204. [Google Scholar] [CrossRef]
- Mogi, T.; Wada, Y.; Ogata, Y.; Hayashi, A.K. Self-ignition and flame propagation of high-pressure hydrogen jet during sudden discharge from a pipe. Int. J. Hydrogen Energy 2009, 34, 5810–5816. [Google Scholar] [CrossRef]
- Kitabayashi, N.; Wada, Y.; Mogi, T.; Saburi, T.; Hayashi, A.K. Experimental study on high pressure hydrogen jets coming out of tubes of 0.1–4.2 m in length. Int. J. Hydrogen Energy 2013, 38, 8100–8107. [Google Scholar] [CrossRef]
- Chen, J.R.; Tsai, H.Y.; Ku, C.W.; Lin, Y.C. Effect of Channel Width on the Shock and Ignition of High-Pressure Hydrogen Release. In Proceedings of the Seventh International Seminar Fire and Explosion Hazards, Providence, RI, USA, 5–10 May 2013; pp. 951–958. [Google Scholar]
- Grune, J.; Sempert, K.; Kuznetsov, M.; Jordan, T. Experimental study of ignited unsteady hydrogen releases from a high pressure reservoir. Int. J. Hydrogen Energy 2014, 39, 6176–6183. [Google Scholar] [CrossRef]
- Rudy, W.; Dabkowski, A.; Teodorczyk, A. Experimental and numerical study on spontaneous ignition of hydrogen and hydrogen-methane jets in air. Int. J. Hydrogen Energy 2014, 39, 20388–20395. [Google Scholar] [CrossRef]
- Zhang, T.; Jiang, Y.; Pan, X.; Wang, Z.; Wang, Q.; Li, Y.; Ta, L.; Hua, M.; Jiang, J. Effects of tubes with different inlet shapes on the shock wave and self-ignition induced by accidental release of pressurized hydrogen. Fuel 2022, 317, 123554. [Google Scholar] [CrossRef]
- Jiang, Y.; Pan, X.; Hua, M.; Wang, Z.; Zhang, T.; Wang, Q.; Li, Y.; Yu, A.; Jiang, J. Effect of flow directions in the T-shaped tubes on the shock wave and spontaneous ignition of pressurized hydrogen. Fuel 2023, 332, 126054. [Google Scholar] [CrossRef]
- Oleszczak, P.; Wolanski, P. Ignition during hydrogen release from high pressure into the atmosphere. Shock Waves 2010, 20, 539–550. [Google Scholar] [CrossRef]
- Gong, L.; Duan, Q.; Sun, Q.; Jin, K.; Sun, J. Effects of the geometry of downstream pipes with different angles on the shock ignition of high-pressure hydrogen during its sudden expansion. Int. J. Hydrogen Energy 2017, 42, 8382–8391. [Google Scholar] [CrossRef]
- Asahara, M.; Yokoyama, A.; Tsuboi, N.; Hayashi, A.K. Influence of tube cross-section geometry on high-pressure hydrogen-flow-induced self-ignition. Int. J. Hydrogen Energy 2023, 48, 7909–7926. [Google Scholar] [CrossRef]
- Duan, Q.; Xiao, H.; Gao, W.; Gong, L.; Sun, J. Experimental investigation of spontaneous ignition and flame propagation at pressurized hydrogen release through tubes with varying cross-section. J. Hazard. Mater. 2016, 320, 18–26. [Google Scholar] [CrossRef] [PubMed]
- Gong, L.; Duan, Q.; Jiang, L.; Jin, K.; Sun, J. Experimental study on flow characteristics and spontaneous ignition produced by pressurized hydrogen release through an Omega-shaped tube into atmosphere. Fuel 2016, 184, 770–779. [Google Scholar] [CrossRef]
- Gong, L.; Jin, K.; Yang, S.; Yang, Z.; Li, Z.; Gao, Y.; Zhang, Y. Numerical study on the mechanism of spontaneous ignition of high-pressure hydrogen in the L-shaped tube. Int. J. Hydrogen Energy 2020, 45, 32730–32742. [Google Scholar] [CrossRef]
- Pan, X.; Wang, Q.; Yan, W.; Jiang, Y.; Wang, Z.; Xu, X.; Hua, M.; Jiang, J. Experimental study on pressure dynamics and self-ignition of pressurized hydrogen flowing into the L-shaped tubes. Int. J. Hydrogen Energy 2020, 45, 5028–5038. [Google Scholar] [CrossRef]
- Li, Y.; Jiang, Y.; Pan, X.; Wang, Z.; Hua, M.; Wang, Q.; Ta, L.; Jiang, J. Effects of the arc-shaped corner on the shock wave and self-ignition induced by sudden release of pressurized hydrogen. Fuel 2021, 303, 121294. [Google Scholar] [CrossRef]
- Morii, Y.; Terashima, H.; Koshi, M.; Shimizu, T. Numerical study of the effect of obstacles on the spontaneous ignition of high-pressure hydrogen. J. Loss Prev. Process Ind. 2015, 34, 92–99. [Google Scholar] [CrossRef]
- Smygalina, A.E.; Kiverin, A.D. Self-ignition of hydrogen jet due to interaction with obstacle in the obstructed space. Int. J. Hydrogen Energy 2022, 47, 35877–35885. [Google Scholar] [CrossRef]
- Li, P.; Duan, Q.; Gong, L.; Jin, K.; Chen, J.; Sun, J. Effects of obstacles inside the tube on the shock wave propagation and spontaneous ignition of high-pressure hydrogen. Fuel 2019, 236, 1586–1594. [Google Scholar] [CrossRef]
- Li, P.; Duan, Q.; Jin, K.; Zeng, Q.; Sun, J. Experimental study on shock waves, spontaneous ignition, and flame propagation produced by pressurized hydrogen release through tubes with varying obstacle location. Fuel 2021, 290, 120093. [Google Scholar] [CrossRef]
- Li, P.; Zeng, Q.; Duan, Q.; Chen, X.; Sun, J. Effects of obstacles inside the tube on initial self-ignition of high-pressure hydrogen release through a tube. Fuel 2023, 339, 127354. [Google Scholar] [CrossRef]
- Li, P.; Zeng, Q.; Duan, Q.; Sun, J. Visualization of spontaneous ignition and flame behavior in tubes with and without obstacles during the high-pressure hydrogen release. Process Saf. Environ. Prot. 2021, 153, 354–362. [Google Scholar] [CrossRef]
- Li, X.; Teng, L.; Li, W.; Huang, X.; Li, J.; Luo, Y.; Jiang, L. Numerical simulation of the effect of multiple obstacles inside the tube on the spontaneous ignition of high-pressure hydrogen release. Int. J. Hydrogen Energy 2022, 47, 33135–33152. [Google Scholar] [CrossRef]
- Liu, Z.; Li, Z.; Luan, X.; Xu, W.; Zhao, S.; Zhang, B. Numerical study on the effects of the obstacle shapes on the spontaneous ignition of high-pressure hydrogen in a tube. Int. J. Hydrogen Energy 2024, 56, 1067–1078. [Google Scholar] [CrossRef]
- Lee, B.J.; Jeung, I.-S. Numerical study of spontaneous ignition of pressurized hydrogen released by the failure of a rupture disk into a tube. Int. J. Hydrogen Energy 2009, 34, 8763–8769. [Google Scholar] [CrossRef]
- Chang, X.; Bai, C.; Zhang, B.; Sun, B. The effect of ignition delay time on the explosion behavior in non-uniform hydrogen-air mixtures. Int. J. Hydrogen Energy 2022, 47, 9810–9818. [Google Scholar] [CrossRef]
- Lee, H.J.; Kim, Y.R.; Kim, S.-H.; Jeung, I.-S. Experimental investigation on the self-ignition of pressurized hydrogen released by the failure of a rupture disk through tubes. Proc. Combust. Inst. 2011, 33, 2351–2358. [Google Scholar] [CrossRef]
- Asahara, M.; Saburi, T.; Kubota, S.; Kubota, T.; Ando, T.; Miyasaka, T. Self-ignition and flame development of high-pressure hydrogen flow in a rectangular tube by simultaneous shadowgraph and direct photograph. In Proceedings of the Selected Papers from the 31st International Congress on High-Speed Imaging and Photonics, Osaka, Japan, 7–10 November 2016. [Google Scholar]
- Lee, H.J.; Park, J.H.; Kim, S.D.; Kim, S.; Jeung, I.-S. Numerical study on the spontaneous-ignition features of high-pressure hydrogen released through a tube with burst conditions. Proc. Combust. Inst. 2015, 35, 2173–2180. [Google Scholar] [CrossRef]
- Yokoyama, A.; Asahara, M.; Tsuboi, N.; Hayashi, A.K. Numerical study on three-dimensional flow effect of self-ignition induced by high pressure hydrogen jet in a rectangular tube. Sci. Technol. Energetic Mater. 2016, 77, 7–12. [Google Scholar]
- Gavrilakis, S. Numerical simulation of low-Reynolds-number turbulent flow through a straight square duct. J. Fluid Mech. 1992, 244, 101–129. [Google Scholar] [CrossRef]
- Huser, A.; Biringen, S. Direct numerical simulation of turbulent flow in a square duct. J. Fluid Mech. 1993, 257, 65–95. [Google Scholar] [CrossRef]
- Grune, J.; Kuznetsov, M.; Jordan, T. Spontaneous ignition process due to high-pressure hydrogen release in air. In Proceedings of the 4th International Conference of Hydrogen Safety, San Francisco, CA, USA, 12–14 September 2011. [Google Scholar]
- Kaneko, W.; Hayashi, K.; Ishii, K. Self-ignition of high-pressure hydrogen released by reproducible rupture of diaphragm. In Proceedings of the 25th International Colloquium on the Dynamics of Explosions and Reactive Systems, Leeds, UK, 2–7 August 2015. [Google Scholar]
- Wen, J.X.; Xu, B.P.; Tam, V.H.Y. Numerical study on spontaneous ignition of pressurized hydrogen release through a length of tube. Combust. Flame 2009, 156, 2173–2189. [Google Scholar] [CrossRef]
- Grune, J.; Sempert, K.; Kuznetsov, M.; Jordan, T. Experimental investigation of flame and pressure dynamics after spontaneous ignition in tube geometry. Int. J. Hydrogen Energy 2014, 39, 20396–20403. [Google Scholar] [CrossRef]
- Xu, B.P.; Wen, J.X. The effect of tube internal geometry on the propensity to spontaneous ignition in pressurized hydrogen release. Int. J. Hydrogen Energy 2014, 39, 20503–20508. [Google Scholar] [CrossRef]
- Xu, B.P.; Wen, J.X. Numerical study of spontaneous ignition in pressurized hydrogen release through a length of tube with local contraction. Int. J. Hydrogen Energy 2012, 37, 17571–17579. [Google Scholar] [CrossRef]
- Bragin, M.V.; Molkov, V.V. Physics of spontaneous ignition of high-pressure hydrogen release and transition to jet fire. Int. J. Hydrogen Energy 2011, 36, 2589–2596. [Google Scholar] [CrossRef]
- Imamura, T.; Hamada, S.; Mogi, T.; Wada, Y.; Horiguchi, S.; Miyake, A.; Ogawa, T. Experimental investigation on the thermal properties of hydrogen jet flame and hot currents in the downstream region. Int. J. Hydrogen Energy 2008, 33, 3426–3435. [Google Scholar] [CrossRef]
- Mogi, T.; Horiguchi, S. Experimental study on the hazards of high-pressure hydrogen jet diffusion flames. J. Loss Prev. Process Ind. 2009, 22, 45–51. [Google Scholar] [CrossRef]
- Gautam, T. Lift-off Heights and Visible Lengths of Vertical Turbulent Jet Diffusion Flames in Still Air. Combust. Sci. Technol. 2010, 41, 17–29. [Google Scholar]
- Proust, C.; Jamois, D.; Studer, E. High pressure hydrogen fires. Int. J. Hydrogen Energy 2011, 36, 2367–2373. [Google Scholar] [CrossRef]
- Ruggles, A.J.; Ekoto, I.W. Experimental investigation of nozzle aspect ratio effects on underexpanded hydrogen jet release characteristics. Int. J. Hydrogen Energy 2014, 39, 20331–20338. [Google Scholar] [CrossRef]
- Li, X.; Chen, M.; Wang, Y.; Hu, J.; Sun, Z.; Christopher, D.M.; Cheng, L. Measurements of concentration decays in underexpanded jets through rectangular slot nozzles. Int. J. Hydrogen Energy 2018, 43, 9884–9893. [Google Scholar] [CrossRef]
- Li, X.; Chen, Q.; Chen, M.; He, Q.; Christopher, D.M.; Cheng, X.; Chowdhury, B.R.; Hecht, E.S. Modeling of underexpanded hydrogen jets through square and rectangular slot nozzles. Int. J. Hydrogen Energy 2019, 44, 6353–6365. [Google Scholar] [CrossRef]
- Kim, S.; Lee, H.J.; Park, J.H.; Jeung, I.-S. Effects of a wall on the self-ignition patterns and flame propagation of high-pressure hydrogen release through a tube. Proc. Combust. Inst. 2013, 34, 2049–2056. [Google Scholar] [CrossRef]
- Xu, B.P.; Wen, J.X.; Tam, V.H.Y. The effect of an obstacle plate on the spontaneous ignition in pressurized hydrogen release: A numerical study. Int. J. Hydrogen Energy 2011, 36, 2637–2644. [Google Scholar] [CrossRef]
- Wang, J.; Luan, X.; Huo, J.; Jing, M.; Huffman, M.; Wang, Q.; Zhang, B. Numerical study on the effect of complex structural barrier walls on high-pressure hydrogen horizontal jet flames. Process Saf. Environ. Prot. 2023, 175, 632–643. [Google Scholar] [CrossRef]
- Gelfand, B.E.; Silnikov, M.V.; Medvedev, S.P.; Khomik, S.V. Thermo-Gas Dynamics of Hydrogen Combustion and Explosion; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Luo, X.; Wang, C.; Rui, S.; Wan, Y.; Zhang, Z.; Li, Q. Effects of ignition location, obstacles, and vent location on the vented hydrogen-air deflagrations with low vent burst pressure in a 20-foot container. Fuel 2020, 280, 118677. [Google Scholar] [CrossRef]
- Wang, L.-Q.; Ma, H.-H.; Shen, Z.-W. Effects of vessel height and ignition position upon explosion dynamics of hydrogen-air mixtures in vessels with low asymmetry ratios. Fuel 2021, 289, 119926. [Google Scholar] [CrossRef]
- Mironov, V.N.; Penyazkov, O.G.; Ignatenko, D.G. Self-ignition and explosion of a 13-MPa pressurized unsteady hydrogen jet under atmospheric conditions. Int. J. Hydrogen Energy 2015, 40, 5749–5762. [Google Scholar] [CrossRef]



| Compressed Tank | Cryogenic Tank | Fe-Ti Hydride | Mg Hydride | |
|---|---|---|---|---|
| H2 consumption (gms) | 6.24 | 6.4 | 8.04 | 9.7 |
| Direct energy required to travel (kJ) | 749 [0 (Base) | 768 19 | 965.4 216.4 | 1164 415] |
| Energy required to produce and store H2 (kJ) | 1260.7 | 2172.7 | 1473.7 | 1777 |
| Energy required to produce tank (kJ) | 34.2 [18.6 | 15.6 0 (Base) | 177.3 161.7 | 60 44.4] |
| Total energy required (kJ) | 2043.9 | 2956.3 | 2616.4 | 3001.5 |
| Ignition Source | Astbury [14] | Kingston University [15] | ||
|---|---|---|---|---|
| Number | % | Number | % | |
| Arson | 0 | 0 | 3 | 0.44 |
| Collision | 2 | 2.5 | 29 | 4.29 |
| Flame | 3 | 3.7 | 58 | 8.58 |
| Hot surface | 2 | 2.5 | 57 | 8.43 |
| Electric | 2 | 2.5 | 44 | 6.51 |
| Friction spark | 2 | 2.5 | 0 | 0 |
| Not identified | 70 | 86.3 | 419 | 61.98 |
| Non-ignition | 0 | 0 | 66 | 9.76 |
| Total | 81 | 100 | 676 | 100 |
| Author | Year | Cross-Sectional Shape and Size | Extension Tube | Burst Disc Material | Opening Ratio |
|---|---|---|---|---|---|
| Lee [31] | 2015 | Rectangle: 11 mm × 11 mm | 200 mm | Mylar polyester film | 1/4, 1/2, 3/4, 1 |
| Gong [43] | 2019 | Circle: d = 15 mm | 360 mm | Nickel 201 | 1/3, 1/2, 2/3, 1 |
| Cha [69] | 2021 | Rectangle: 10 mm × 10 mm | 300 mm | Mylar polyester film | 1/8, 1/4, 1/2, 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, G.; Li, Y.; Wu, D.; Li, H.; Liu, H.; Xing, X.; Liu, J. The Progress of Autoignition of High-Pressure Hydrogen Gas Leakage: A Comprehensive Review. Fire 2024, 7, 268. https://doi.org/10.3390/fire7080268
Cui G, Li Y, Wu D, Li H, Liu H, Xing X, Liu J. The Progress of Autoignition of High-Pressure Hydrogen Gas Leakage: A Comprehensive Review. Fire. 2024; 7(8):268. https://doi.org/10.3390/fire7080268
Chicago/Turabian StyleCui, Gan, Yixuan Li, Di Wu, Hongwei Li, Huan Liu, Xiao Xing, and Jianguo Liu. 2024. "The Progress of Autoignition of High-Pressure Hydrogen Gas Leakage: A Comprehensive Review" Fire 7, no. 8: 268. https://doi.org/10.3390/fire7080268
APA StyleCui, G., Li, Y., Wu, D., Li, H., Liu, H., Xing, X., & Liu, J. (2024). The Progress of Autoignition of High-Pressure Hydrogen Gas Leakage: A Comprehensive Review. Fire, 7(8), 268. https://doi.org/10.3390/fire7080268






