Probabilistic Path Planning for UAVs in Forest Fire Monitoring: Enhancing Patrol Efficiency through Risk Assessment

Abstract

Forest fire is a significant global natural disaster, and unmanned aerial vehicles (UAVs) have gained attention in wildfire prevention for their efficient and flexible monitoring capabilities. Proper UAV patrol path planning can enhance fire-monitoring accuracy and response speed. This paper proposes a probabilistic path planning (PPP) module that plans UAV patrol paths by combining real-time fire occurrence probabilities at different points. Initially, a forest fire risk logistic regression model is established to compute the fire probabilities at different patrol points. Subsequently, a patrol point filter is applied to remove points with low fire probabilities. Finally, combining fire probabilities with distances between patrol points, a dynamic programming (DP) algorithm is employed to generate an optimal UAV patrol route. Compared with conventional approaches, the experimental results demonstrate that the PPP module effectively improves the timeliness of fire monitoring and containment, and the introduction of DP, considering that the fire probabilities and the patrol point filter both contribute positively to the experimental outcomes. Different combinations of patrol point coordinates and their fire probabilities are further studied to summarize the applicability of this method, contributing to UAV applications in forest fire monitoring and prevention.

1. Introduction

Forest fires, as severe natural disasters, pose extreme threats to the environment, ecosystems, and socio-economic stability. Extensive burning releases large quantities of toxic gases and particulate matter, disrupting the ecological balance, causing significant economic losses, and even threatening the lives of nearby residents [1,2,3].

Effective monitoring of forest fires can substantially reduce their spread [4]. The advent of UAV technology has garnered considerable attention and is increasingly being used in various aspects of forest fire detection and prevention [5,6]. With computer vision technology, UAVs can gather information mid-flight, quickly identifying fire sources and reacting promptly [7,8]. However, this approach necessitates continuous image acquisition for fire detection and may be inefficient in large forest areas due to the lack of effective path planning. Additionally, this approach is less sensitive to detecting small flames, being more suitable for visible fires over larger areas. Furthermore, the absence of additional information types, such as temperature and humidity, may limit its ability to predict potential fire areas [9]. Recently, wireless sensors have become a common tool for forest fire prediction, quickly forecasting fires across different forest regions [10,11]. However, due to the complex terrain of forested areas, sensors can only make effective predictions but cannot conduct efficient searches. Thus, constructing effective monitoring routes after fire prediction becomes crucial for forest fire prevention [12].

Therefore, finding a suitable patrol route for UAVs in vast forest areas—and prioritizing regions with higher fire risk during patrols—remains a subject requiring further research. Current UAV path planning methods predominantly use distance as the sole criterion, such as dynamic programming, heuristic algorithms like A*, D*, and simulated annealing for path planning, which effectively shorten the search paths of UAVs during flight detection [13,14,15]. While these methods can guide UAVs to avoid dynamic obstacles along their flight paths, effectively shortening their patrol routes, they often fail to comprehensively consider complex environmental factors closely linked to the occurrence of fires. Such environmental data are crucial for fire prediction and prevention. Through data analysis, potential fire risk areas can be identified in advance, enabling the development of more scientifically informed patrol paths and fire prevention strategies. Consequently, these methods may overlook incorporating the probability of fire occurrence in different regions into path planning considerations. This oversight could result in delayed UAV responses to high-fire-probability areas, where UAVs may not prioritize reaching locations with higher fire occurrence probabilities, leading to greater fire spread and associated losses.

Given that different forest areas have varying fire probabilities, to apply tailored strategies for different areas, a comprehensive analysis of factors such as climate, vegetation, and historical fire points is necessary [16]. Predicting the probability of fire occurrence in each area at the beginning of path planning helps in formulating more targeted fire prevention plans, enhancing the effectiveness of fire prevention. Therefore, this paper proposes a probabilistic path planning (PPP) module, as shown in Figure 1. Based on sensor data from monitoring points, it calculates the fire risk within a certain range of each point, and combines the distances between monitoring points to achieve optimal UAV patrol path planning. Unlike previous studies, our method does not require traversing all locations; by balancing the distance and probability within each area, it filters out low-risk locations and prioritizes patrols in high-risk areas to improve patrol efficiency. This indicates that the proposed method has the ability to respond more promptly, enabling quick and accurate responses to effectively control the fire, significantly reducing the potential for fire spread and thereby minimizing fire damage.

The module integrates distances and fire risk probabilities, suitable for optimal UAV patrol path planning in large, dispersed forest fire scenarios. First, a logistic regression model analyzes and weighs data from multiple sensors, predicting the fire probability for each area as the basis for UAV path planning. Then, a dynamic programming algorithm [17] plans the UAV’s patrol path, ultimately generating an optimal search route that combines probability and distance, thereby improving the UAV’s search efficiency in forest fires. This paper conducts comparative experiments on whether to consider probabilities in path planning and whether to filter out low-probability fire points before planning. The results show that our proposed method reduces the patrol time by 18.5% and the spread area of fires by 23% compared to traditional methods, verifying the feasibility and superiority of this path planning method. This algorithm ensures earlier arrival at higher fire probability areas and, by considering distance, avoids excessive patrol distance, thereby enhancing forest fire prevention capabilities.

2. Related Work

2.1. Forest Fire Prediction

2.1.1. Objectives and Methods of Fire Prediction

The supervised image classification algorithm using deep learning can process the relevant images collected by UAVs with high accuracy [18,19]. This method can be used to efficiently identify fires that have already occurred. But timely fire prevention by prediction is also very important. The aim of forest fire prediction is to provide a scientific foundation for monitoring, managing, and preventing fires to minimize the adverse effects on forest ecosystems and human communities. Various environmental parameters, such as climate and vegetation, play a crucial role in predicting forest fires. Recent studies have explored the integration of remote sensing, GIS structures, and machine learning (ML) models to predict the probability of forest fires [16]. These studies utilize historical fire data and meteorological variables to construct prediction models through methods like logistic regression [20] and Bayesian networks. Machine learning [16] enhances models’ generalization and accuracy by learning from extensive datasets and fine-tuning the model parameters [21]. Accurately predicting fire probabilities requires including various parameters to quantify the impact factors of forest fires [22].

2.1.2. Influencing Factors of Forest Fires

Accurate forest fire prediction requires understanding the relative importance of multiple influencing factors [23]. Natural and anthropogenic elements, such as terrain, weather conditions, fuel types, and human activities, affect fire occurrences. Terrain, climate, and vegetation are considered primary factors affecting fire occurrence. Predicting forest fires requires a comprehensive understanding of the relative importance of the factors influencing fire occurrence. Different regions exhibit varying vegetation types and climate changes, leading to varying fire occurrence patterns; for instance, areas covered with deciduous broadleaf forests are more prone to fires [24]. Thus, besides the typical climatic variables, such as temperature, humidity, and precipitation obtained via sensors, integrating additional data types like DMC (Duff Moisture Code) and ISI (Initial Spread Index) enhances the understanding of fire risks and the analysis of complex fire scenarios. This paper uses a logistic regression model, incorporating forest-specific and climatic factors along with other influencing parameters, to predict forest fires.

2.2. UAV Path Planning for Forest Fire Monitoring

Early detection is key to preventing large-scale damage from fires and safeguarding forest resources and the ecological environment [25]. Traditional ground patrols are limited by terrain and manpower, whereas UAV patrols can cover a much larger area with higher efficiency. UAVs can fly over dense forests and complex terrains, offering comprehensive and uninterrupted monitoring views. Equipped with high-resolution cameras and other devices, UAVs can monitor vast areas in real time, quickly detect fire sources in the early stages, and relay critical information, such as a fire’s location, intensity, and spread direction [26]. This provides the command center with crucial decision-making data, enabling faster and more accurate fire warnings compared to traditional ground patrols and satellite monitoring. Additionally, UAVs can carry fire-extinguishing bombs, fire retardants, and other equipment to provide initial control during the early stages of a fire [27], preventing its spread. UAVs can also operate in extreme environments, filling in gaps where human intervention is not possible.

2.2.1. Path Planning Considering Spatial Factors

Spatial factors encompass distance, terrain, and obstacles. The rapid advancement of UAV technology has garnered significant attention [28,29]. Due to their flexibility and low cost, UAVs are increasingly utilized in various aspects of forest fire monitoring [30]. Compared to ground patrol tools, UAVs offer shorter response times, allowing for quick deployment to fire sites for real-time monitoring and data transmission [31]. In complex and variable terrains, UAVs can fly freely, unaffected by terrain limitations. In contrast to satellite monitoring [21,32], UAVs can operate closer to the ground [33], enhancing monitoring efficiency and accuracy. Therefore, the application of UAVs in forest fire monitoring can effectively search for and detect potential or ongoing fires. A crucial aspect of this application is path planning [30], aiming to design cost-effective patrol paths for specific targets. Researchers have investigated various intelligent algorithms for UAV path planning, such as genetic algorithms, heuristic algorithms [34,35], and optimization algorithms [36,37]. For example, Affiani Machmudah et al. [38] researched the maneuver planning problem of fixed-wing UAVs in environments with obstacles. In the fields of path planning and flight trajectory planning, the particle swarm optimization algorithm demonstrated superior performance in finding optimal solutions compared to the genetic algorithm and grey wolf optimization algorithm [38]. When patrolling limited areas, these algorithms can determine the shortest path when considering various spatial factors. However, they often neglect to incorporate diverse forest fire factors into the planning process, which could limit the system’s ability to predict fires and focus on high-risk areas. This omission may lead to delays in identifying high-probability fire locations, resulting in greater fire spread and associated damages.

2.2.2. Path Planning Considering Fire Risk Factors

Currently, some researchers are focusing on UAV path planning for forest fires by considering fire risk factors [39,40]. Yiqing Xu et al. [40] analyzed the relationship between factors such as terrain and historical fire locations to generate a forest fire risk map, clustering fire risk areas into smaller sections for individual UAV patrols. Path planning algorithms are then applied to the points with similar fire risk to determine the shortest path for UAVs within each section. Finally, multiple sections patrolled by individual UAVs are combined into a comprehensive patrol plan for the entire area. This method is well-suited for fine-grained patrols of large forest areas but demands high resource allocation. Our approach differs from that of Yiqing Xu et al. [40], our PPP module is more general and does not require the number of patrol UAVs to be adjusted based on the number of sections. By considering probabilities and optionally utilizing a filtering mechanism, UAVs can flexibly adapt to the area’s size. Recognizing the significant impact of climatic factors on fire risk [41], we employ more diverse and detailed sensor data to swiftly and accurately calculate fire probabilities at specific points.

3. PPP Module

3.1. Design

In large forest areas, path planning based solely on spatial factors is inadequate to address the complex and volatile nature of wildfires. The current path planning that incorporates fire risk factors often demands high levels of resource allocation and encounters challenges with the timeliness and diversity of data. Thus, this paper presents a general-purpose UAV-based forest fire risk patrolling solution. By utilizing real-time sensor data to determine the fire probabilities, a single UAV can flexibly balance these probabilities with point distances to generate optimal routes. This approach can adapt to various forest sizes by filtering out low-risk areas when necessary. The core of this solution is the PPP module, which ensures that regions with different fire probabilities are prioritized appropriately during the search process while also considering distance.

The module takes point coordinates and various sensor data as inputs and outputs the UAV’s patrol path. It comprises three linear units as follows: probability calculation, filtering mechanism, and path planning, with the filtering mechanism being optional. Sensor data from each point are used to compute the fire probabilities, which are then mapped to the corresponding coordinates. When the filtering unit is activated, the low-probability points are removed from the dataset and excluded from the UAV’s patrol path. Finally, the path planning unit processes the remaining points and probabilities to produce the final route.

3.2. Implementation

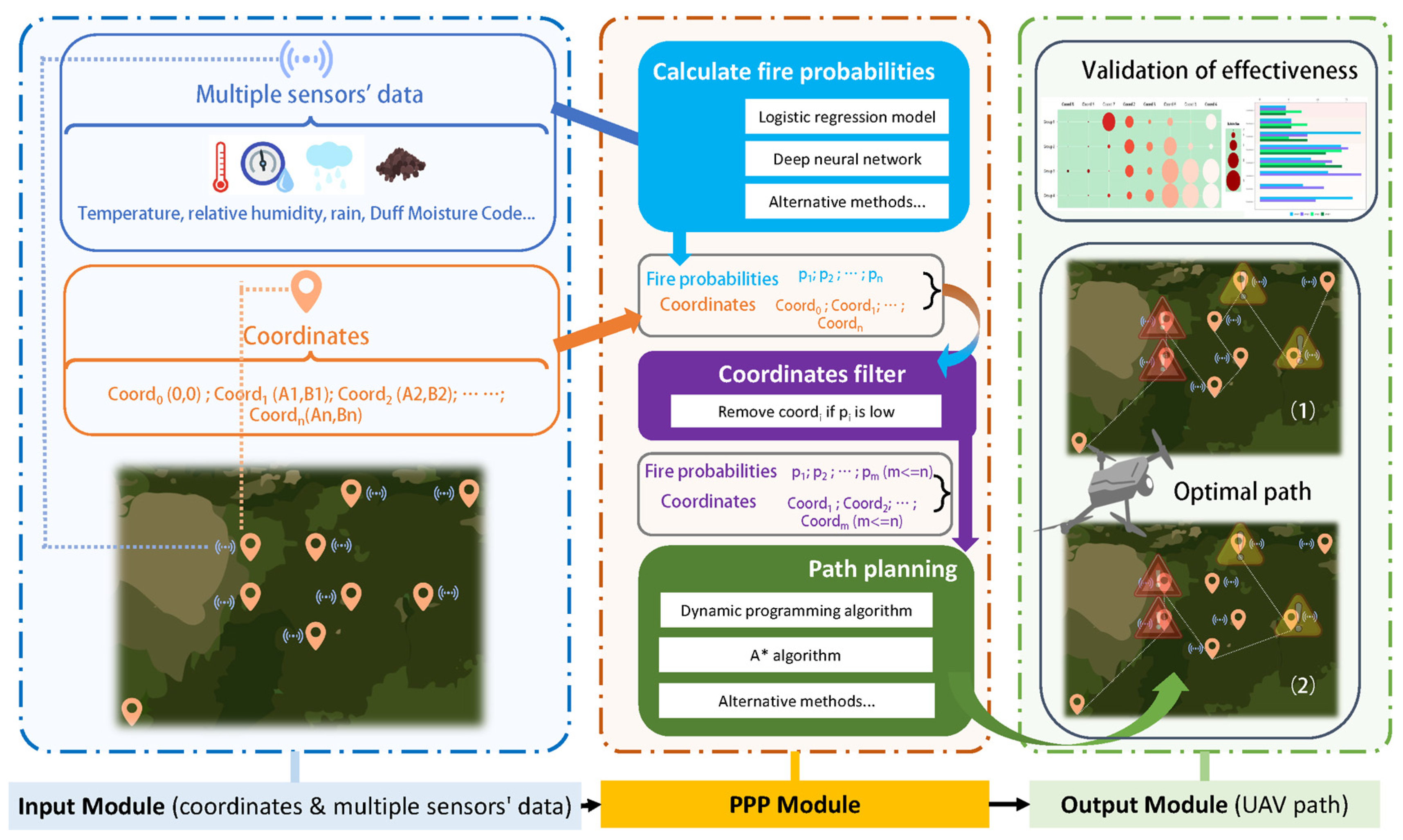
The module’s generality means it can accommodate various methods for probability calculations and path planning. For the system, this paper implemented logistic regression and dynamic programming, both classic algorithms. This paper utilizes these two algorithms primarily because they are easy to implement and broadly applicable. Both logistic regression and dynamic programming have low implementation difficulty and wide applicability, supported by many open-source libraries and tools providing their implementations and optimization algorithms. This enables a quick setup and adjustment. For example, logistic regression models have fewer parameters compared to deep learning models, simplifying the tuning process and facilitating the rapid identification of the optimal model. Additionally, logistic regression requires less data, making it suitable for cases with small sample sizes. This is particularly crucial for forest fire prediction in areas where data are scarce or challenging to obtain. The regression coefficients in logistic regression are clearly interpretable, with each coefficient representing the direction and magnitude of the effect of the corresponding independent variable (like temperature, humidity, etc.) on the probability of fire occurrence. It can also test the parameter’s significance, which cannot be tested by artificial neural networks [42]. Furthermore, logistic regression is a stable and robust model that can handle various data types, including continuous and categorical data. It also shows good tolerance to missing and outlier values, ensuring reliable predictions, even in complex and incomplete data environments. Optimal resource scheduling and routing are frequently required in fire prediction and control. Dynamic programming can address these optimal routing issues, ensuring the efficient allocation and use of resources, thus enhancing fire response efficiency. Dynamic programming is highly flexible and scalable, allowing model structures and parameters to be adjusted according to real-world needs. For example, the state space and transition rules of a dynamic programming model can be adjusted based on different distance and probability weight factors, improving the model’s adaptability and generalization abilities.

By combining dynamic programming with wildfire occurrence probabilities, the system provides an optimal path for the UAV in complex environments, considering both point distances and fire probabilities, thus improving the effectiveness of forest fire searches.

3.2.1. Establishing the Logistic Regression Model

Logistic regression is a statistical learning method designed for classification tasks. In the context of the forest fire prevention discussed in this paper, it involves a binary classification problem: determining whether a fire will occur in a specific area. The logistic regression model transforms a linear combination of input features into a probability value between 0 and 1 using the logistic function. The mathematical formula is as follows.

$$\mathrm{P}={\displaystyle \frac{1}{1+{\mathrm{e}}^{-\mathrm{z}}}}$$

(1)

where P is the probability of the event, e is the base of the natural logarithm, and z is the linear combination. The linear combination is given by:

$$\mathrm{z}=\mathrm{w}·\mathrm{x}+\mathrm{b}$$

(2)

Here, x is the input feature vector, x = (x1, x2, …, xn) is the corresponding weight vector w = (w1, w2, …, wn), and b is a bias term. Thus, the relationship between P and x can be expressed as:

$$\ln \left({\displaystyle \frac{\mathrm{P}}{1-\mathrm{P}}}\right)={\mathrm{w}}_1·{\mathrm{x}}_1+{\mathrm{w}}_2·{\mathrm{x}}_2+\dots +{\mathrm{w}}_{\mathrm{n}}·{\mathrm{x}}_{\mathrm{n}}+\mathrm{b}$$

(3)

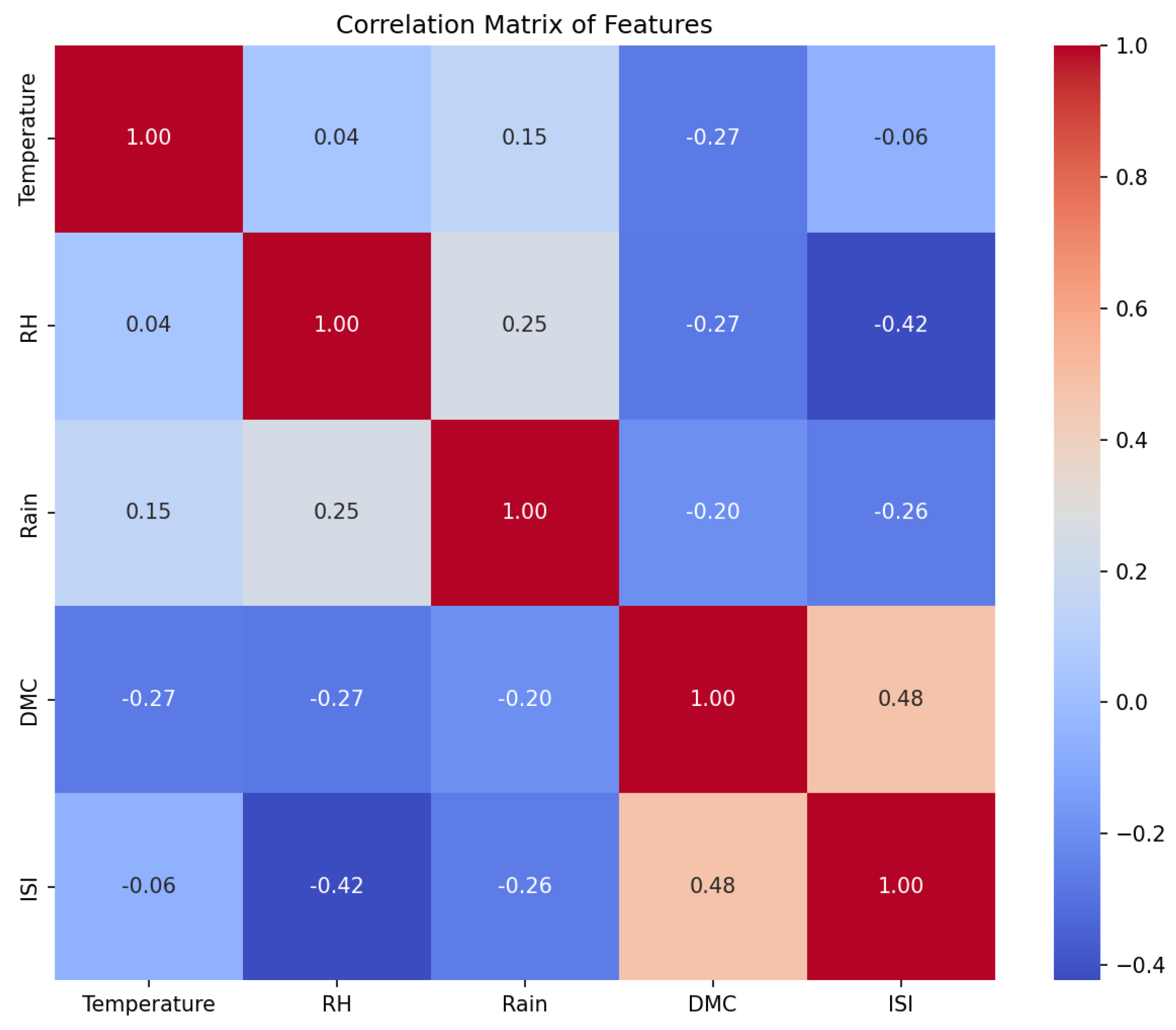
This paper uses data from publicly available datasets [43,44]. The original dataset comprises the following eight features: temperature, relative humidity, wind, rain, FFMC (fine fuel moisture code), DMC, DC (drought code), and ISI. To ensure the stability of the model and the accuracy of the parameter estimates, this paper performed a correlation analysis of the data. A correlation-based feature selection method was used during the feature selection process. Initially, the correlation matrix of the features was calculated to identify potential multicollinearity issues. Severe multicollinearity can result in unstable parameter estimates, model overfitting, and reduced interpretability. Consequently, by combining correlation analysis with domain knowledge, features with high correlations and redundancy were removed: wind (with an average correlation of 0.53 with other features), FFMC (with an average correlation of 0.50 with other features), and DC (with an average correlation of 0.50 with other features). After the feature selection process, five features were retained: temperature, relative humidity, rain, DMC, and ISI. The average correlation value of these features with other features is less than 0.50. These features were chosen based on their importance in predicting fire probability while mitigating the issues caused by strong correlations. Specifically, in the final retained features, the highest correlation is between ISI and DMC at 0.48, with weaker correlations among the other variables. These features can be obtained from sensors positioned at specific points, with the parameters and their descriptions provided in

Table 1. Forest fire impacting factors.

Symbol	Abbreviation	Full Name
x1	T	Temperature
x2	RH	Relative humidity
x3	R	Rain
x4	DMC	Duff Moisture Code
x5	ISI	Initial Spread Index

. This feature selection strategy reduces unnecessary, redundant information, enhancing the model’s interpretability and generalization ability. The correlation heatmap of the features, shown in Figure 2, demonstrates that there are no highly correlated features among the retained ones, making them relatively suitable for model training.

L1 regularization is a technique used in machine learning and statistical modeling to control model complexity and prevent overfitting [45]. It works by incorporating the L1 norm of the parameters into the loss function. The L1 norm is the sum of the absolute values of the parameter vector elements, where λ is the regularization parameter, and w is the weight vector of the model. The primary effect of L1 regularization is to sparsify the model by reducing the importance of irrelevant or redundant features, thereby improving the model’s generalization ability.

$$\mathrm{Loss}={\mathrm{Loss}}_{\mathrm{original}}+\mathsf{\lambda }\sum _{\mathrm{i}=1}^{\mathrm{n}}\left|{\mathrm{w}}_{\mathrm{i}}\right|$$

(4)

Based on the variables from the aforementioned dataset, a logistic regression model for predicting fire probability can be accurately trained by incorporating L1 regularization. This model calculates the probability of fire occurrence within the vicinity of a given point, which serves as a reference for subsequent path planning. The model parameters are shown in

Table 2. Logistic regression model fitting results.

Model Variable	Coefficient	Standard Error	Wald Test	Significance	Degree of Freedom	Exp(B)
x1	0.3517	0.091	15.063	0.000	1	1.4215
x2	−0.0168	0.096	0.031	0.861	1	0.9834
x3	−0.8861	0.289	9.396	0.002	1	0.4123
x4	−0.0702	0.099	0.502	0.479	1	0.9322
x5	0.3286	0.118	7.768	0.005	1	1.3890
constant	0.0466	0.093	0.249	0.618	1	1.0477

below.

The table indicates that the temperature, rain, and ISI significantly impact the fire probability (significance values ≤ 0.005), while the constant term and other variables do not have a significant influence. Specifically, increases in the temperature and ISI are positively correlated with the fire probability, whereas RH, rain, and DMC negatively impact fire occurrence. In the logistic regression model, Exp(B) is used to measure the impact of each independent variable on the dependent variable [46]. The x1(temperature) has the highest Exp(B) value among variables with values greater than 1, indicating its strong positive effect on fire probability. The x3(rain) has the lowest Exp(B) value among variables with values less than 1, indicating its strong inhibitory effect on fire probability.

Based on the fitting results, the logistic regression model is formulated as follows.

$$\ln \left({\displaystyle \frac{\mathrm{P}}{1-\mathrm{P}}}\right)=0.3517{\mathrm{x}}_1-0.0168{\mathrm{x}}_2-0.8861{\mathrm{x}}_3-0.0702{\mathrm{x}}_4-0.3286{\mathrm{x}}_5-0.0466$$

(5)

The performance of logistic regression models is typically assessed using metrics such as accuracy, precision, recall, F1 score, ROC curve, and AUC value. The confusion matrix, a 2 × 2 matrix summarizing the model’s predictions, underpins these metrics. It includes the following key indicators.

• True Positive (TP): Number of positive samples correctly predicted as positive.
• True Negative (TN): Number of negative samples correctly predicted as negative.
• False Positive (FP): Number of negative samples incorrectly predicted as positive (Type I error).
• False Negative (FN): Number of positive samples incorrectly predicted as negative (Type II error).

Accuracy reflects the proportion of correct predictions but may not be reliable for imbalanced datasets. Precision indicates the ratio of true positives to the sum of true and false positives, showing the proportion of true positives among all positive predictions. Recall indicates the proportion of true positives correctly identified by the model out of all the actual positives, measuring the model’s ability to capture true positives. The F1 score, a harmonic mean of precision and recall, balances the two and is more reliable for imbalanced datasets.

$$\mathrm{Accuracy}={\displaystyle \frac{\mathrm{TP}+\mathrm{TN}}{\mathrm{TP}+\mathrm{TN}+\mathrm{FP}+\mathrm{FN}}}$$

(6)

$$\mathrm{Precision}={\displaystyle \frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FP}}}$$

(7)

$$\mathrm{Recall}={\displaystyle \frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}}}$$

(8)

$$\mathrm{F}1=2\times {\displaystyle \frac{\mathrm{Precision}\times \mathrm{Recall}}{\mathrm{Precision}+\mathrm{Recall}}}$$

(9)

The accuracy of the logistic regression model is 0.73. The specific precision, recall, F1 score, and support values are shown in

Table 3. Model analysis results.

	Precision	Recall	F1 Score	Support
0	0.69	0.70	0.70	67
1	0.76	0.76	0.76	86
Macro Avg	0.73	0.73	0.73	153
Weighted Avg	0.73	0.73	0.73	153

. This paper focuses on predicting the probability of forest fires using a logistic regression model, emphasizing the precision, recall, and F1 scores for class 1. The model performs well for class 1, with high precision, recall, and F1 scores, indicating its ability to effectively capture positive cases. For class 0, the metrics are slightly lower, indicating some false negatives, which minimally affect the paper’s objectives.

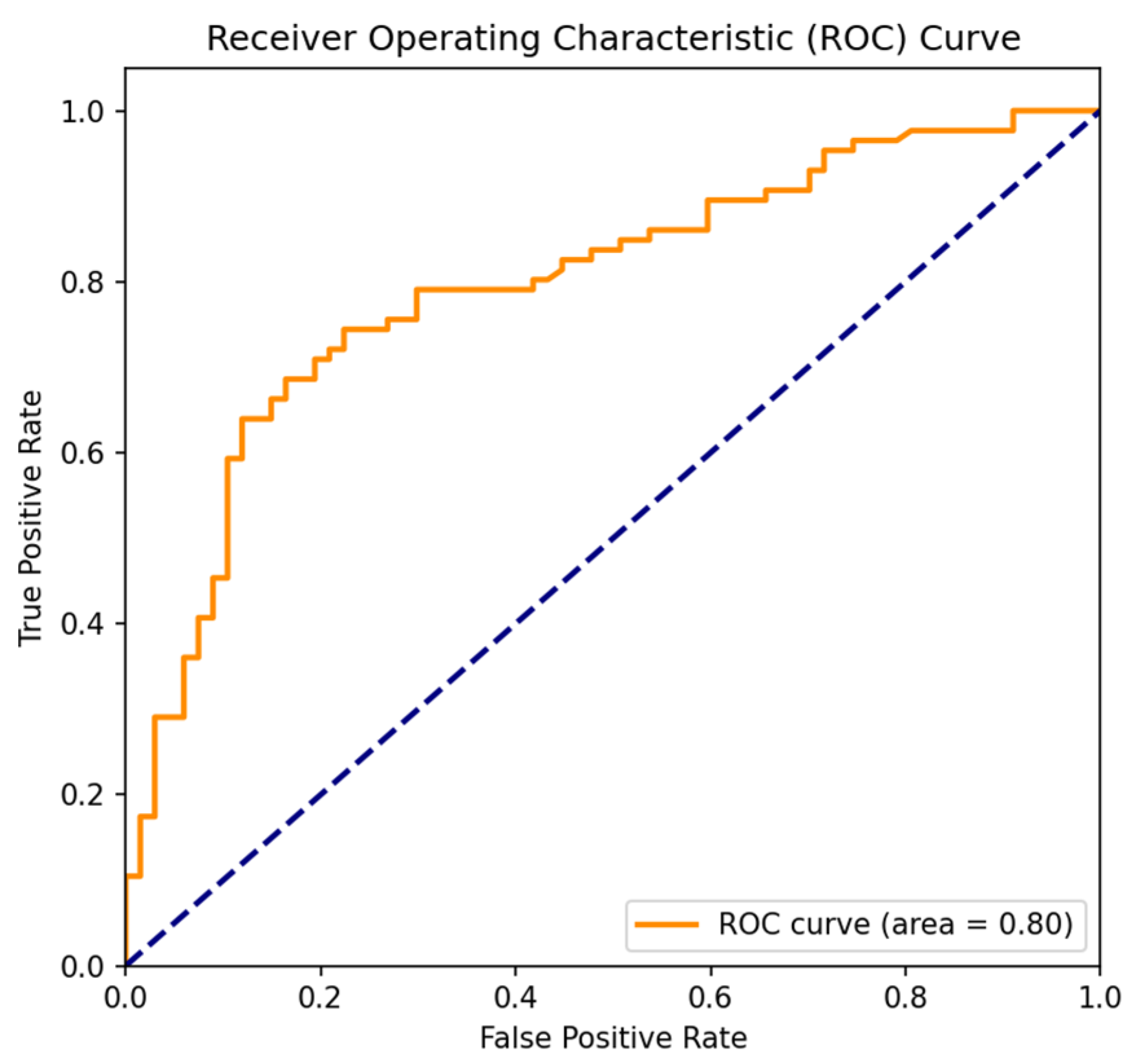
The receiver operating characteristic (ROC) curve plots the false-positive rate on the x-axis and the true-positive rate (i.e., recall) on the y-axis. The area under the curve (AUC) measures the model’s classification performance, with higher values indicating a better performance. As shown in Figure 3, the ROC curve approaches the (0, 1) point and deviates significantly from the 45-degree diagonal line, demonstrating that the model’s predictors have strong explanatory power. The AUC is 0.80, much greater than 0.5, demonstrating that the model fits well. Therefore, the probability values output by the model are suitable for use as a basis for path planning research.

3.2.2. Dynamic Programming Algorithm

Dynamic programming is an algorithmic technique for solving multi-stage decision problems [17]. Its core idea is to break down the original problem into smaller sub-problems, solve these sub-problems, and store the intermediate results to avoid redundant calculations, thus optimizing efficiency.

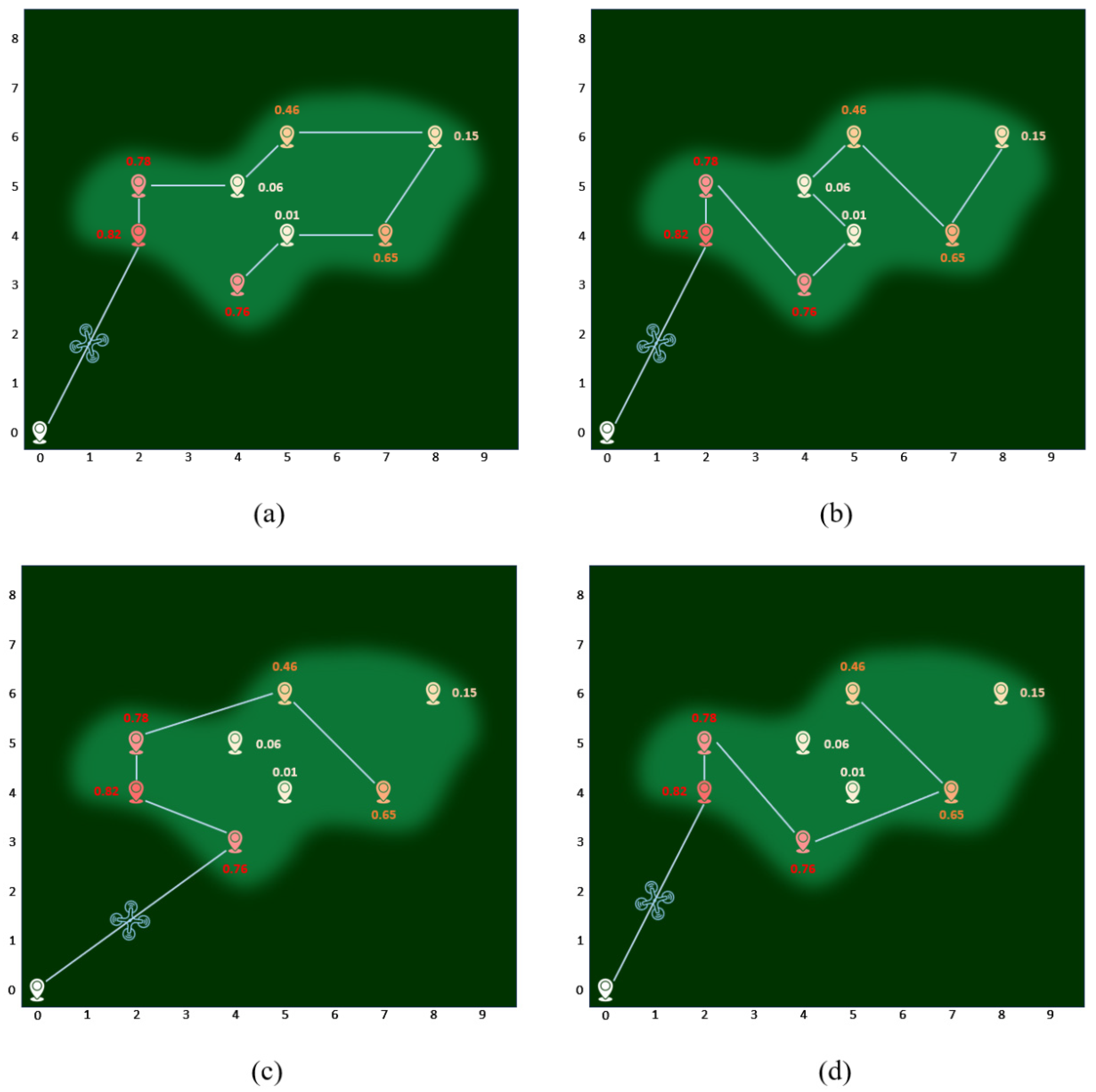
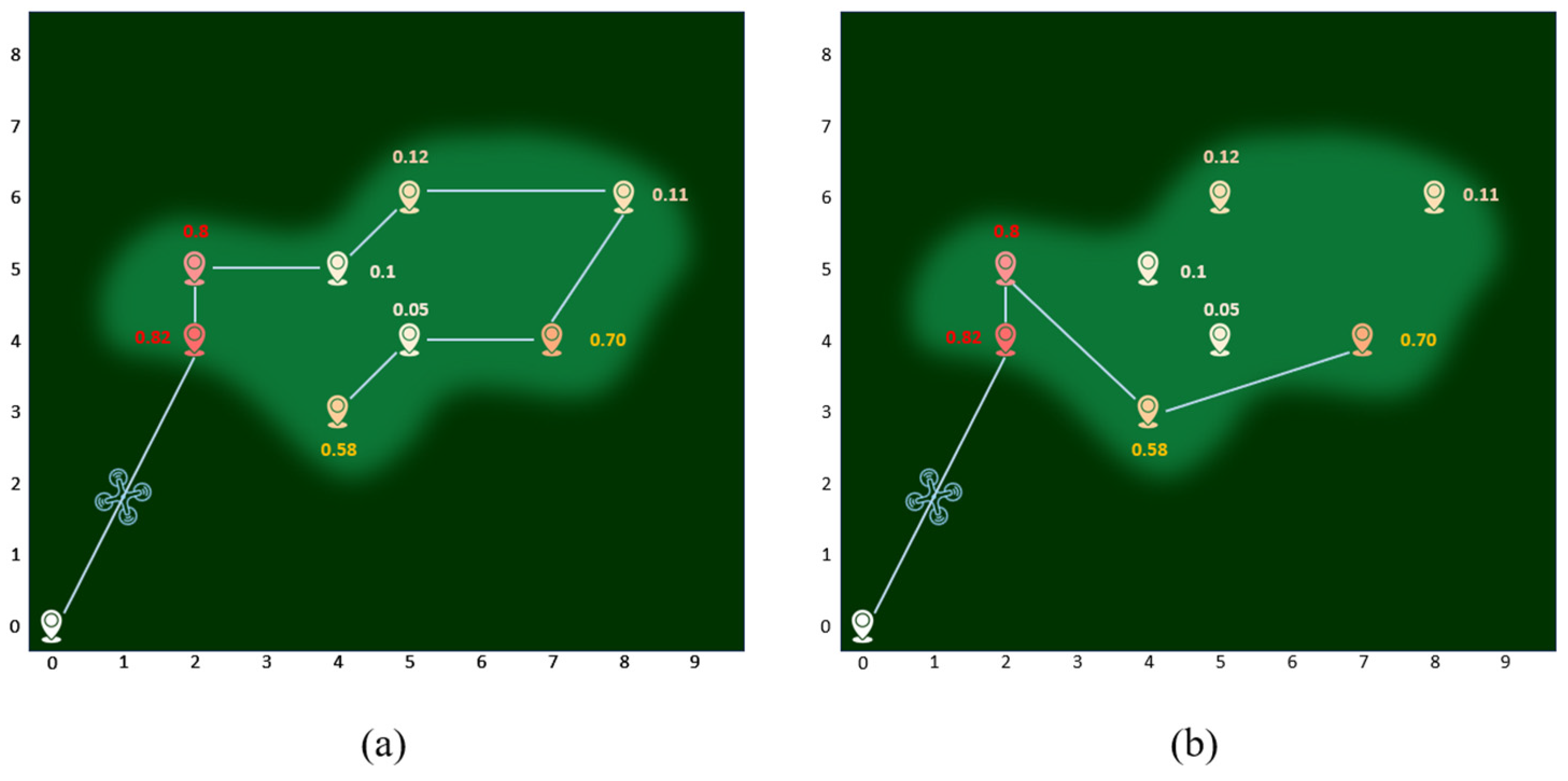
The objective of this paper is to find a UAV patrol route that allows the UAV to complete its search task while minimizing the cost of reaching areas with higher fire probabilities to make the UAV efficiently complete the forest fire search task.

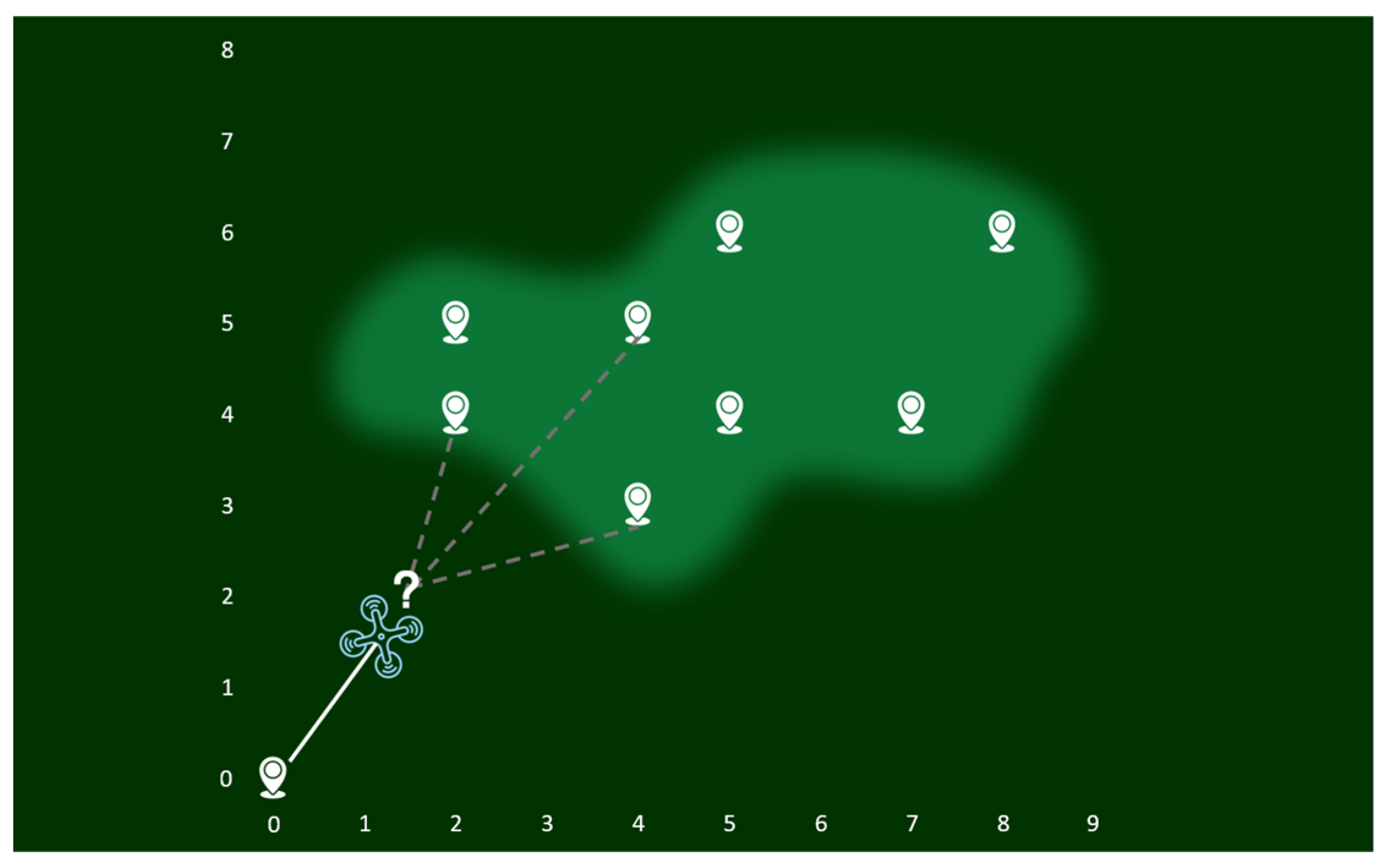
First, a logistic regression model is used to obtain the probability of fire occurrence at each point, which serves as a reference for path planning. Each coordinate with a fire probability represents a potential location. The task area is represented by nine discrete nodes, as shown in Figure 4. The UAV starts from the origin, and the cost at each node is related to the distance between nodes and the fire probability.

To solve this problem, we decompose the overall task into multiple sub-tasks, requiring the UAV to minimize the cost at each node by considering both distance and probability. The path that connects nodes with a minimal cost represents the desired path. Using an improved DP algorithm, we integrate both probability and distance. Let C_i,j represent the cost from point_i to point_j, where dp_mask,i is the minimal cost from the starting point to point_i, dist_i,j is the spatial distance between point_i and point_j, (xi, yi) and (xj, yj) are the coordinates of point_i and point_j, respectively, and p_j is the fire probability at point_j. The cost to reach each point is given by:

$${\mathrm{C}}_{\mathrm{i},\mathrm{j}}={\mathrm{dp}}_{\mathrm{mask},\mathrm{i}}+{\displaystyle \frac{{\mathrm{dist}}_{\mathrm{i},\mathrm{j}}}{{\mathrm{p}}_{\mathrm{j}}+1}}$$

(10)

$$\mathrm{dis}{\mathrm{t}}_{\mathrm{i},\mathrm{j}}=\sqrt{{\left({\mathrm{x}}_{\mathrm{i}}-{\mathrm{x}}_{\mathrm{j}}\right)}^2+{\left({\mathrm{y}}_{\mathrm{i}} -{\mathrm{y}}_{\mathrm{j}}\right)}^2}$$

(11)

Assuming the optimal path passes through coordinates point₀, point₁, point₂, …, point_n, where point₀ is the starting point, and point_n is the endpoint, the cost for each segment from point_i-1 to point_i (for i = 1, 2, …, n) can be calculated using the above formulas. Thus, the total cost of the optimal route is:

$$Min\sum _{i=1}^n{\displaystyle \frac{\sqrt{{\left(x_i-x_{i-1}\right)}^2+{\left(y_i-y_{i-1}\right)}^2}}{p_i+1}}$$

(12)

This approach enables optimal decision-making at each node, ultimately resulting in an efficient UAV search route.

4. Experiments and Results

4.1. Experimental Setup

The primary objective of the PPP module is to optimize the search efforts in future forest fire scenarios by prioritizing closer locations with higher probabilities of fire occurrence. This approach aims to mitigate the spread of forest fires. In this paper, the effectiveness of the proposed PPP module is evaluated against conventional methods through a series of experiments. The fire risk levels are categorized into four grades: low, medium, high, and very high. A probability threshold of 0.25 is set to filter out the low-risk points. In methods incorporating this filtering mechanism, points with probabilities below this threshold are removed before the DP algorithm generates the path for the remaining points. The experimental setup consists of the following groups:

• Group 1 (Conventional Method): Utilizes the DP algorithm, considering only the distances between locations without accounting for fire probabilities.
• Group 2: Utilizes the DP algorithm, considering both distances and fire probabilities without filtering out the low-risk points.
• Group 3: Utilizes the DP algorithm, considering only distances, with the low-risk points filtered out.
• Group 4 (Our Method): Utilizes the DP algorithm, considering both distances and fire probabilities, with the low-risk points filtered out.

The factors considered by each group are summarized in

Table 4. Factors considered by different method groups.

Group	DP Algorithm Considers Distance	DP Algorithm Considers Probability	Filters Low-Risk Points
Group 1 (conventional)	√	×	×
Group 2	√	√	×
Group 3	√	×	√
Group 4 (our method)	√	√	√

√ The group method includes the factor, × The group method does not include the factor.

:

In each experiment, a coordinate point is randomly selected based on the fire occurrence probabilities at each point, designated as the fire location. The path planning is then performed, with each path assuming that the UAV starts from the origin (0, 0) and visits all designated points. To minimize randomness in the experimental results, each method was tested 100,000 times.

4.2. Assessment Method

This paper evaluates search efficiency by using the time taken for a UAV to complete its search and assesses fire control effectiveness by the area of fire spread when the UAV arrives at the fire point. In the experiments, t represents time, with the fire starting at t = 0 when the UAV begins its search. By default, all UAVs in each group are assumed to have equal weights, sizes, and sufficient flight times to complete the longest patrol mission. The UAV’s speed is set to 1, so the time to detect the fire equals the distance traveled to the fire point.

The fire spread area over time is calculated using the following formula [47]:

$$\mathrm{A}=\mathsf{\alpha } {\mathrm{t}}^{\left(\mathrm{n}\right)}$$

(13)

Here, A represents the fire spread area, α denotes the fire spread coefficient, and n is an exponent derived from fitting data. This relationship illustrates that the fire spread area increases proportionally to the n-th power of the spread time t. For simplicity, the spread coefficient α is set to 1 for all points. Based on the literature, n typically ranges from 1.6 to 2.0 [47]; in this experiment, n is set to 2 to facilitate the calculations.

Any point can potentially catch fire (i.e., occasionally, points with high fire probability might not catch fire, while points with low probability might). Consequently, the methods using filters (groups 3 and 4) might miss the low-risk points that catch fire and are not on the UAV’s patrol path. It is assumed that a fire becomes detectable via satellite or other means once its spread area reaches 400. This threshold is notably higher than the maximum spread area of 310 observed for the points in methods without filters, and it is applied as the spread area for the fires occurring at the points not covered by the patrol path. In summary, the calculation formula for the change in fire spread area over time can be expressed as:

$$\mathrm{A}={\mathrm{t}}^2$$

(14)

4.3. Results and Evaluation

To demonstrate the performance of the PPP module, points were randomly selected and slightly adjusted for their coordinates and fire probabilities to present a diverse combination. The final selection includes nine points, detailed in

Table 5. Coordinates and fire probabilities.

Point	Coordinate	Fire Probability
Point 1	(4, 5)	0.06
Point 2	(7, 4)	0.65
Point 3	(5, 6)	0.46
Point 4	(5, 4)	0.01
Point 5	(2, 5)	0.78
Point 6	(8, 6)	0.15
Point 7	(4, 3)	0.76
Point 8	(2, 4)	0.82

. We executed four method groups using Python, resulting in the paths shown in Figure 5. It is visually apparent that the methods incorporating fire probabilities (Figure 5b,d) reach the higher-risk points more quickly than those that do not consider the probabilities (Figure 5a,c).

Subsequently, the path distances for each method were calculated. The results are depicted in Figure 6a. The path distances are: (1) Group 1—17.537, (2) Group 2—17.607, (3) Group 3—14.226, and (4) Group 4—14.291. As can be seen, the path distances obtained after the initial filtering based on probability (Groups 3 and 4) are significantly shorter than those without filtering (Groups 1 and 2). This demonstrates that the filter can substantially reduce the UAV’s patrol distance (by approximately 18.89% without considering probability and by approximately 18.83% when considering probability), thereby shortening the patrol duration. Although the paths considering probability are slightly longer than those not considering probability under the same filtering conditions, the difference is negligible (approximately 0.4%); thus, it does not affect the overall effectiveness of our method.

The results for the fire spread areas in each group are shown in Figure 6b. In over 100,000 experiments, the average fire spread areas were approximately 126 for Group 1, 101 for Group 2, 106 for Group 3, and 97 for Group 4. It is apparent that the fire spread areas for the methods with initial filtering (Groups 3 and 4) are considerably smaller than those without filtering (Groups 1 and 2). Specifically, filtering reduces the fire spread by about 15.87% without DP considering the probability and by about 3.96% with DP considering probability. This indicates that filtering methods can effectively reduce the fire spread, enhancing search efficiency and reducing the damage caused by fires.

By computing the arrival times for each point using various methods, the fire spread area can be calculated at each point when a fire occurs, as depicted in Figure 7. The points are ordered in descending fire probability from left to right. The darker red indicates a higher fire probability and a greater need for attention. In Group 1, Coord 7 shows both a high fire probability and a large spread area, highlighting the method’s weakness in controlling high-risk fire spread. Group 2, which incorporates probability into path planning, addresses this issue. Comparing Group 1 to Group 3 and Group 2 to Group 4, it is evident that the filtering methods allow the UAV to reach the high-risk fire points faster, aiding in the control of high-risk fires. Although Groups 3 and 4 do not patrol Coord 6, Coord 1, and Coord 4, these points have very low fire probabilities. The saved time allows the UAV to arrive more quickly at high-risk locations.

With technological advancements, UAV patrol durations have significantly improved. Promptly containing a fire spread remains a higher priority than extending the UAV’s patrol durations. Our findings indicate that without filtering, probability-based DP methods can reduce the fire spread area by approximately 19.8% while increasing the patrol time by only about 0.4%. This highlights the importance of incorporating probability into the PPP module. Additionally, the PPP module method that incorporates both probability and filtering (Group 4) reduces the route distance by 18.51% and the fire spread area by 23.02% compared to the conventional method (Group 1). This confirms the effectiveness of the PPP module in reducing the patrol time and containing fire spread.

To investigate the applicability of our module further, we conducted various experiments with different points and probabilities. Three representative outcomes were identified as follows: (1) significantly better results with probability consideration/filtering, (2) identical results with and without probability consideration in DP, and (3) no significant advantage or even a disadvantage with probability consideration/filtering. The first scenario was noted in the previous section before filtering. This paper maintained the same nine coordinate points but updated the probabilities, as shown in

Table 6. Different coordinates and fire probabilities.

Point	Coordinate	Fire Probability
Point 1	(4, 5)	0.1
Point 2	(7, 4)	0.7
Point 3	(5, 6)	0.12
Point 4	(5, 4)	0.05
Point 5	(2, 5)	0.8
Point 6	(8, 6)	0.11
Point 7	(4, 3)	0.58
Point 8	(2, 4)	0.82

, illustrating a case where the DP results are identical with or without probability consideration.

The calculated path distances using different methods reveal that Group 1 has a path distance of 17.537, while after filtering, Groups 3 and 4 both have path distances of 11.463. The average fire spread area is 122 for Group 1 and approximately 98 for Groups 3 and 4.

It is visually apparent that, as before, the path distances obtained after an initial filtering are significantly shorter than those obtained without filtering (Figure 8). Additionally, the fire spread areas show a substantial decrease. However, in terms of paths, the routes obtained for this set of points are identical, whether or not probability is considered after filtering.

4.4. Analysis

The coordinates and probabilities provided in the previous section are analyzed mathematically to interpret the experimental results. Figure 9 illustrates the time required for the UAV to reach each point using different methods, which corresponds to the fire spread time at each point if a fire occurs. The points in Figure 9 are sorted in descending order of fire probability.

Initially, all fire probabilities are normalized for random fire sampling. Based on the times needed for the UAV to reach different points, the fire spread area A_i is calculated at the moment the UAV arrives at Coord_i in the event of a fire ignition there. Using the normalized probabilities as weights, the statistical fire spread area SA_i for each point is then computed.

$${\mathrm{p}}_{\mathrm{i}}^{\prime }={\displaystyle \frac{{\mathrm{p}}_{\mathrm{i}}}{{\sum }_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{p}}_{\mathrm{i}}}}$$

(15)

$$\mathrm{S}{\mathrm{A}}_{\mathrm{i}}={\mathrm{A}}_{\mathrm{i}}\times {\mathrm{p}}_{\mathrm{i}}^{\prime }$$

(16)

Next, the effectiveness of incorporating probability is analyzed.

Table 7. Mathematical analysis of probability consideration in DP.

Point Number	1	2	3	4	5	6	7	8
Probability	0.06	0.65	0.46	0.01	0.78	0.15	0.76	0.82
Normalized Probability	0.015	0.165	0.117	0.003	0.198	0.038	0.193	0.208
A(w/o P)	55.833	199.443	78.967	259.932	29.944	141.285	307.533	20
A(w/P)	123.854	236.287	157.332	94.377	29.944	310.031	68.899	20
SA(w/o P)	0.85	32.903	9.22	0.66	5.928	5.379	59.321	4.162
SA(w/P)	1.886	38.981	18.369	0.24	5.928	11.803	13.29	4.162

presents A_i and SA_i for each point Coord_i using the DP methods that consider and do not consider probability.

The values of A_i and SA_i for each point Coord_i are plotted for both methods (Figure 10). It is evident that DP considering only distance and DP incorporating both probability and distance reach C5 and C8 in the same order. The method, without the probability consideration, reaches points C1, C2, C3, and C6 earlier, thereby aiding fire control at these points. Since the time difference to reach C2 (probability 0.65) is minimal (about 1.25), and the time difference to reach C6 (probability 0.15) is significant (5.72), the impact on fire spread statistics is less substantial for C6. The DP method incorporating probability reaches points C4 and C7 earlier. Point C7 has a high fire probability (0.78) and a significant time difference (9.24), resulting in a notable difference in statistical fire spread area (highlighted in green). Conversely, the minimal probability at C4 (0.01) has little impact on the method differences.

Overall, the DP method that considers probability reaches the high-probability fire points earlier. Due to the simultaneous consideration of distance, the time difference for the points reached later than the distance-only method is minimal, balancing probability and distance for improved forest fire control.

The A_i and SA_i values for each point Coord_i were plotted to compare the methods that consider probabilities with those that do not (

Table 8. Mathematical analysis of filtering consideration in DP.

Point Number	1	2	3	4	5	6	7	8
Probability	0.06	0.65	0.46	0.01	0.78	0.15	0.76	0.82
Normalized probability	0.015	0.165	0.117	0.003	0.198	0.038	0.193	0.208
A(w/o P)	123.854	236.287	157.332	94.377	29.944	310.031	68.899	20
A(w/P)	400	131.397	204.24	400	29.944	400	68.899	20
SA(w/o P)	1.886	38.981	18.369	0.24	5.928	11.803	13.29	4.162
SA(w/P)	6.091	21.677	23.845	1.015	5.928	15.228	13.29	4.162

and Figure 11). The green highlighted sections reveal that points with low fire probabilities significantly reduce the SA increase for the filtered method versus the non-filtered method. Points C5, C7, and C8 show equal statistical fire spread areas for both methods. The filtering method skips points C1, C4, and C6, leading to a fire spread area of 400 at these points (the smallest area detectable by satellites or other means, as specified in this paper), which is larger than the non-filtered method. Nonetheless, the fire likelihood at these points is very low, resulting in a small difference in statistical areas. The filtering method reaches C2 faster due to ignoring the low-probability points. The spread area difference at C2 is substantial (approximately 92), and with its high probability (0.65), the combined probability and filtering method marginally outperforms the probability-only method. This comparison holds when probability is considered; without it, the filtering method’s advantage is more pronounced, as it naturally ignores the low-probability fire points.

5. Discussion and Future Work

5.1. Discussion

Overall, the methods considering probability and filtering can significantly improve patrol efficiency and control fire spread. The use of these methods should be comprehensively balanced based on the spatial distribution and probability of each point.

First, the points filtered out still have a slight possibility of catching fire. Since they are not included in the UAV patrol route, the fire spread area for these points is set at 400. Although this value is relatively large compared to the current maximum fire spread area of 310 without filtering, it may seem that undetected fires at these points will lead to a significant spread in the short term. However, repeated experiments have shown that, in the long term, the filtering method can significantly control the overall fire spread. By removing points with low probabilities, the UAVs can reach more fire-prone locations more quickly, thus responding to fires more promptly.

Secondly, taking probability into account usually leads to a better performance for DP, though there are instances where the planned paths are the same, and in rare cases, the probability-based method performs slightly worse. This may be because, in most situations, the fire probability distribution shows that most points have low probabilities and only a few have high probabilities. In these cases, the UAV achieves an optimal balance between distance and probability, reaching higher probability points with shorter distances and effectively controlling the fire spread. However, when all points have very low probabilities, or when the differences in probabilities are much smaller than the differences in distances, the influence of probability in DP is significantly reduced, making our module similar to a distance-only DP algorithm. Lastly, when there are differences in fire probabilities, but they are generally close, our method may perform slightly worse. This happens because the path planning tends to prioritize points with higher fire probabilities, but our fire simulation assumes only one point catches fire at a time, making the fire sampling almost random and impacting the simulation results. However, this situation is rare, as it is uncommon for multiple points to have high probabilities with slight differences. Furthermore, in such cases, multiple points are more likely to catch fire simultaneously, requiring more complex simulation methods.

In summary, our proposed module can adapt to forest fire occurrences in most situations. By considering probabilities during the search process, it increases the effectiveness of the search and shortens the patrol path through filtering. For areas where fires have already started, our method can promptly contain the spread. This is crucial for forest fire prevention and the efficient allocation of firefighting resources.

5.2. Future Work

This paper has some limitations in the path planning process. It did not consider the UAV’s endurance affected by its weight, fuel, or battery capacity, nor did it address the changes in flight speed due to the wind or other factors. The flight requirements of a UAV are directly influenced by its weight, impacting both the lift needed and energy consumption. The fuel or battery capacity determines the total energy stored by the UAV, directly influencing its endurance. Larger capacities lead to extended UAV flight times, but they may also increase its size and weight, creating a trade-off [48]. External conditions such as wind speed and temperature also affect a UAV’s endurance; for instance, strong winds may complicate stability control and increase energy usage.

The probability analysis was limited to individual locations’ fire probabilities without considering the correlations between locations, thus missing the probability of simultaneous fires at multiple points. Strong winds, for instance, act as a potential correlating factor between different fire-prone locations, speeding up the spread of fires and potentially carrying sparks to farther areas, igniting new fire spots [49]. As a result, the experiments did not include scenarios where multiple points caught fire at the same time. For experimental simplicity, the UAV was only required to start from an origin point and detect fire locations without needing to return to the origin or define a new endpoint. Future research will consider UAV endurance, multiple fire scenarios, and other complex factors.

6. Conclusions

This paper introduces a PPP module that integrates forest fire occurrence probability and point distance for UAV patrol path planning. The aim is to address the issue in conventional path planning, where the planning criteria are primarily based on distance, failing to prioritize areas with higher fire probabilities. To this end, we developed a UAV fire patrol path planning system that combines logistic regression and DP algorithms. Firstly, a logistic regression model is applied to predict the probability of forest fires in the region. Then, a DP algorithm is used to plan the path by considering both distance and probability. Given the low likelihood of fires at low-probability points, a patrol point filter is implemented to exclude these points from the search path. This enables the UAV to reach areas with higher fire probabilities more swiftly, minimizing potential damage. Four sets of comparative experiments were conducted to verify the module’s effectiveness. The baseline was path planning based solely on the point locations. This paper then evaluated the performance of the models, considering probability and applying filtering. The experimental results demonstrate that during forest fire monitoring, the method proposed in this paper reduced the path time by 18.5% compared to traditional methods that do not consider probabilities or apply filtering, resulting in a 23% decrease in fire spread area when fires occur. The results indicate that our approach prioritizes high-risk areas, shortens the total patrol time, and effectively controls the spread of fires in a region.