Abstract
Carbon stocks provide information that is essential for analyzing the role of forests in global climate mitigation, yet they are highly vulnerable to wildfires in Mediterranean ecosystems. These carbon stocks’ exposure to fire is usually estimated from specific allometric equations relating tree height and diameter to the overall amount of aboveground carbon storage. Assessments of vulnerability to fire additionally allow for specific fire resistance (bark thickness, crown basal height) and post-fire recovery traits (cone mass for regeneration, and fine branches or leaves mass for flammability) to be accounted for. These traits are usually considered as static, and their temporal dynamic is rarely assessed, thus preventing a full assessment of carbon stocks’ vulnerability and subsequent cascading effects. This study aimed to measure the pools of carbon stocks of individual trees varying between 30 and 96 years old in the Djbel Mansour Aleppo pine (Pinus halepensis) forest in semi-arid central Tunisia in the southern range of its distribution to fit a sigmoid equation of the carbon pools and traits recovery according to age as a vulnerability framework. Allometric equations were then developed to establish the relationships between fire vulnerability traits and dendrometric independent variables (diameter at breast height, height, and live crown length) for further use in regional vulnerability assessments. The total carbon stocks in trees varied from 29.05 Mg C ha−1 to 92.47 Mg C ha−1. The soil organic carbon stock (SOC) at a maximum soil depth of 0–40 cm varied from 31.67 Mg C ha−1 to 115.67 Mg C ha−1 at a soil depth of 0–70 cm. We could identify an increasing resistance related to increasing bark thickness and basal crown height with age, and enhanced regeneration capacity after 25 years of age with increasing cone biomass, converging toward increasing vulnerability and potential cascading effects under shorter interval fires. These results should be considered for rigorous forest carbon sequestration assessment under increasing fire hazards due to climate and social changes in the region.
1. Introduction
Forests have been identified as the primary terrestrial carbon sink and pool, sequestering more carbon than any other terrestrial ecosystem [1]. As a result, they are expected to play a key role in the global carbon cycle [2]. Aleppo pine (Pinus halepensis) has garnered significant interest in the Mediterranean basin due to its ecological and conservation properties. Its wide distribution and ability to protect soils make it important in regions where other species struggle to survive or adapt to drought and fire [3]. Moreover, this species plays a significant role as a carbon sink, particularly in stands with low site quality in the Mediterranean region [4]. In addition, Aleppo pine forests are among the species most affected by wildfires in the Mediterranean basin [5], with increasing concerns due to climate changes prolonging drought and increasing heat waves [6]. In turn, wildfires may actually jeopardize the carbon sink provided by these pine forests by combusting litter and fine fuel located in the aboveground part of the ecosystem, as well as producing dead biomass in the form of unburned trunks and roots, which decompose after the fire and emit CO2 to the atmosphere by heterotrophic respiration [7]. Potential carbon sinks in the form of forests must then not only be seen in terms of their carbon stocks and productivity, but also through the lens of their susceptibility to burn, be affected by, and recover from wildfires.
From the conceptual framework of ecological vulnerability to wildfires developed for Europe [8], carbon stocks’ vulnerability can be defined by their potential loss (how much carbon is actually on site), their resistance (how much of the available carbon stock was not affected by the fire), and their recovery rate (how fast the carbon stock can be reconstructed after a fire) (Figure 1). In addition, fire intensity affecting trees is driven by flammability traits [9] such as the amount of fine fuel, bulk density, and crown height, which can propagate a surface fire to a crown fire. Recovery is driven by seed amount (or a resprouting strategy, but this is not the case for Pinus halepensis, which is an obligate seeder species [10]), and carbon accumulation across time is usually assessed through trunk biomass. Belowground root biomass development and pre-fire root carbon stocks being decomposed are hardly ever quantified. They are, however, related to the concept of absorbance, defined as post-disturbance losses that are not directly due to the disturbance but occur afterwards, according to Linkov and Trump [11]. These species-specific traits are assumed to determine their vulnerability and are considered to be static over time. Little attention has been devoted to intraspecific trait variations within tree aging other than the tree age maturity threshold which represents when individuals are able to produce seeds [12]. These time varying trait values could, however, be a keystone aspect [13] potentially leading to cascading effects when one fire event promotes a second one [14], and potentially prolonging the recovery period and enhancing vulnerability.
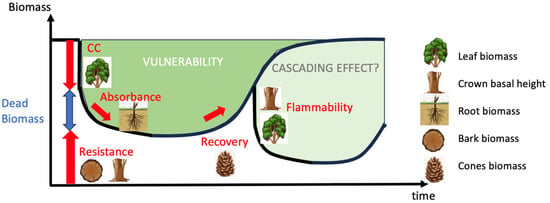
Figure 1.
Conceptual scheme of carbon stock vulnerability to fire. Carbon stock (black line) is affected by fire over time according to combustion completeness (CC) and resistance (fraction of individual surviving the fire). Dead material C stock, not lost to the atmosphere during combustion, is then decomposed after the fire and constitutes the absorption phase [11] followed by a recovery phase according to plant growth and regeneration strategy. Aboveground fine fuel (Canopy) is fully combusted, while trunk and root systems are killed but not combusted. Increased severity (through canopy biomass and climate) can impact resistance and CC. Availability of fruits (cones) can delay regeneration, and low crown base height can increase new crown fire likelihood.
Although fine resolution remote sensing now allows for large scale biomass potential loss assessments [15], some key aspects of the amount of biomass within organs and resistance/regeneration potentials based on bark thickness or seed mass are hardly ever assessed or are only derived from generic allometric equations. Numerous studies have been conducted to estimate the pine aboveground biomass in Mediterranean countries, such as Pinus pinea in Italy [16], Pinus brutia in Turkey [17], or Pinus halepensis and Pinus nigra in Spain [18], among others. Accurate assessments of forest biomass then became the fundamental basis for evaluating ecosystem productivity and carbon stocks. Various methods have been utilized by foresters to obtain such estimates [19], including tree-level allometric equations aimed to be generic enough to be applied over large areas, but still reliable for various species and site conditions [20,21]. These equations typically utilize diameter at breast height (DBH) as a key parameter for estimating tree biomass [22], while total height can be incorporated as an additional covariate to enhance accuracy [23]. In Tunisia, previous studies on the genus Pinus have mainly focused on tree biomass [24,25], without considering litter and soil organic carbon stocks. To fully cover the vulnerability assessment framework, plant traits related to fire resistance (bark biomass), regeneration (cone biomass), and flammability (crown height, fine fuel fraction, bulk density, combined with landscape level assumptions on canopy cover continuity) [26] should be investigated, but are rarely performed due to time-consuming and destructive methods.
With the recent increase in the number of fires Tunisia (North Africa) since the political collapse in 2011 [27], the important coverage of Pinus halepensis forests in this country with many human and forestry applications [28], and the high fire susceptibility to Saharan heatwaves controlling fire events [29], we proposed here to investigate the carbon stock vulnerability of this species through all these aspects of potential loss, resistance, and recovery. We then constructed our study on a thorough field sampling of above and belowground carbon pools and keystone compartments on tree pines of different ages to capture the maximum potential loss and recovery rate near a recently burned area in the central Tunisian (Southern Mediterranean basin, North Africa) pine forests. We aimed to (1) capture the growth rate of all carbon pools in Pinus halepensis trees, (2) to assess the time course of resistance, regeneration and fire susceptibility traits across time as a time-since-last-fire-varying vulnerability assessment, and (3) to produce non-linear allometric equations for estimating the aboveground and belowground biomass and fire-related plant traits for regional applications.
2. Materials and Methods
2.1. Study Area
This study was conducted in the Djebel Mansour forest (36°16′0″ N, 9°42′0″ E), situated in the semi-arid region of central Tunisia in North Africa (Figure 2). The area of the Djebel Mansour forest covers 5800 hectares, predominantly occupied by Aleppo pine (Pinus halepensis). Soils vary from shallow to deep (Table 1). The overstory is primarily composed of Aleppo pine, while prominent shrubs include rosemary (Rosmarinus officinalis L.), phillyrea (Phillyrea latifolia L.), mastic tree (Pistacia lentiscus L.), or a sparse shrub layer of prickly juniper (Juniperus oxycedrus). In the study area, the soil type was generally represented by carbonate soils (calcic-magnesic) covering calcareous parent material [30]. The Djebel Mansour forest, located in the upper semi-arid region, exhibits a typical Mediterranean climate with distinct wet and dry seasons. During the study period (2020–2021), the average temperature ranged from 11.60 °C in January to 29.68 °C in August. The annual precipitation reached 438.2 mm.
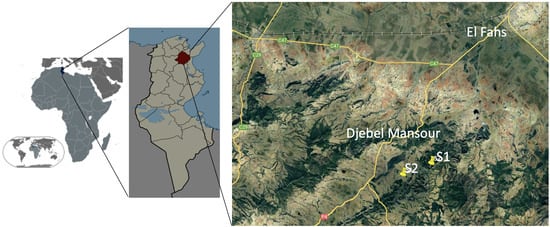
Figure 2.
Location of Tunisia in the Mediterranean basin, and the study sites: (S1, 9.8136 N, 36.2353 N) young stand and (S2, 9.7823 E, 36.2249 N) old stand.

Table 1.
Stand parameters and characteristics of the research sites. (Means ± SE).
The soil water holding capacity (WHC) was 77.55 mm and 41.03 mm, respectively, in two of the stands, S1 and S2 (Table 1), chosen for their tree height and age difference. The soil physicochemical properties of the two sites are presented in Table 2. In the upper 10 cm layer, and the clay content is higher in S2 (16%) compared to S1 (10%). However, S1 had a greater percentage of coarse fragments (65%) than S2 (35%).

Table 2.
Chemical and physical properties of soil in various layers of Aleppo pine forests in Djebel Mansour, NE Tunisia.
2.2. Sampling Design and Tree Biomass Data Collection
Six plots measuring 25 × 25 m were randomly selected to cover young (S1) and old (S2) stand conditions. Within each plot, measurements were taken for Aleppo pine trees including tree height (H), stem diameter at breast height (DBH) and live crown length (LCL). A total of fifteen trees from various diameter classes and ages were selected and harvested. Prior to tree felling, the DBH, LCL, and H of all sampled trees were measured. The trees were then harvested by cutting them from the stump. Each tree’s stem was divided into 0.5 m sections and weighted fresh. The branches were separated from the needles and their total fresh weight was measured. The bark was also separated from the wood of each stem section and branch. The weights of the stem and branches of each tree were measured fresh in the field, using a mechanical platform weighing scale for samples > 1 kg and a balance (Kern 440-47N, 0.1 g accuracy) for samples < 1 kg, with or without bark to calculate the weight of the wood and bark. After felling the trees, an elliptical area was determined on the ground, taking into account the projection of the tree crowns and the half-distance from neighboring trees. The entire area of the ellipse was excavated to estimate root biomass [31]. The complete root system was removed using an excavator, and any remaining parts were carefully lifted out with a hand digger. Fresh belowground samples were weighed in the field after cleaning.
For each tree compartment, five subsamples of plant material, including wood, bark, needles, cones, and roots, were collected, dried at 70 °C for 48 h, crushed, and then sieved to determine the dry weight (laboratory electronic precision balance at 0.01 g accuracy) and the carbon concentration using CHN(O)S elemental analysis in the Laboratory of Chemical Metrology at National Research Institute of Physical chemical Analysis (INRAP) of Tunisia. Tree compartment dry weights and carbon masses were then deduced from these ratios to their fresh weight collected in the field, thus assembling the whole tree weight exhaustively.
2.3. Litter, Soil Sampling and Analysis
In each site, litter samples were collected from five 25 × 25 cm squares to estimate litter stock. The collected samples were then taken to the laboratory and dried in an oven at 70 °C for 48 h. The same method used for analyzing plant samples was applied to determine the organic carbon content of the litter.
To gather soil samples for physical and chemical analyses, pits were excavated at each site. The particle size distribution was determined using the international pipette method [32] and the proportion of the stone fraction was determined through sieving. Organic carbon content was analyzed following the method described by [33]. Total organic nitrogen was measured using the Kjeldahl method according to [34]. Soil bulk density was determined by collecting five pseudo replicates of soil samples at each soil profile and within each soil layer, using 100 cm3 stainless steel rings. Water content was measured using a pressure plate. The soil organic carbon stock (SOCs) in the mineral soil was calculated using the following equation:
where SOCs is the soil organic carbon stock (kg C m−2), Dbi is the bulk density (g cm−3) of layer i, Ci is the soil organic carbon concentration (%) in layer i, Di is the thickness of this layer (cm), and CE is the percentage of coarse elements [35].
SOCs = Σ (Dbi × Ci × Di) × (1 − CE),
2.4. Statistical Analysis and Allometric Model Fitting
Modeling of biomass Y in relation to dendrometric variable Xj was carried out using the general nonlinear structural form:
where Π denotes the product mathematical operator, Xj is dendrometric variable with index j, β0 and βj are model parameters; βj is specific coefficient to variable Xj in the allometric model. This model structure was previously applied to estimate tree biomass components from the dendrometric variables DBH, H, and CR (Crown Ratio = LCL/H) [36], LCL, Life Crown Length. In our study, we applied this model to the nine biomass components Y (kg) provided by the analytic equations depending on two or three dendrometric variables including DBH, H, and CR:
where β0, β1, β2 are regression parameters. Model (3) provided the best fitting for five of the biomass components including total tree, aboveground, stem wood, stem bark, and root. Bi et al. [37] mentioned a significant improvement in the performance of DBH-based biomass equations after addition of tree height (H). Model (4) fitted four of the biomass components the best including branch wood, branch bark, needles, and pine cones. LCL (directly associated with CR) has been proven to be one of the best predictor variables for crown length [38]. Allometric equations were evaluated based on the following goodness-of-fit statistics: high coefficient of determination (R2) vs. low root mean square error (RMSE), mean absolute error (MAE), and significance levels of parameter estimators (p < 0.05). The equations with the highest adjusted R2 values were selected and proposed for biomass estimation. Normal distributions of residuals were checked by the Shapiro–Wilk test. Homogeneity of variances was checked by the White (W) and Breuch–Pagnan (B-P) tests referring to a Chi-square distribution (χ2). Nonlinear allometric equations were performed using JMP statistical software, version 8.0. The effects of categorical soil depth (shallow soil vs. deep soil) on soil characteristics were tested using a one-way ANOVA. The SPSS statistical software 23.0 (IBM Corp., Armonk, NY, USA) was used. Descriptive results were provided as variation ranges of mean values ± standard error (SE).
Y = β0 Πj(Χj)βj,
Y = β0DBHβ1Hβ2,
Y = β0DBHβ1CRβ2,
2.5. Recovery Model Fitting
Carbon stock dynamics across tree age were fitted to a sigmoid function (Equation (5), using nls_gls function of the glsnsl v1.3.2 package in R cran v4.4.1), as a standard equation for ecosystem resilience assessments [39].
where Cstock is the carbon stock of a given pool, K is the maximum value of this carbon stock reached by the sigmoid function, and a and R are the growth parameters according to time (t in years).
Cstock = K/(1 + a · exp (−R . t))
We finally used this temporal dynamic of traits to readjust the static vulnerability conceptual framework (Figure 1), by extracting trait values for tree ages 20, 50, and 80 years old and deduced their adjusted resistance and recovery dynamics during and after a fire according to age. We then combined this result with the variations in flammability traits throughout time to assess any potential cascading effects when a first fire promoted a second fire in young stands with lower fire tolerance capacities.
3. Results
3.1. Carbon Stock Dynamic
3.1.1. Litter and Soil Carbon Stocks
We obtained the litter and SOC stocks from the S1 and S2 sites, with average ages of 57.12 ± 10.76 years and 76 ± 10.08 years, respectively. The litter carbon stock in S2 was 6.90 Mg C ha−1 vs. 4.25 Mg C ha−1 in S1 (Table 3). Regarding soil organic carbon stocks (SOC stocks), S2 had a higher value of 115.67 Mg C ha−1 (0–70 cm) compared to S1 with 31.67 Mg C ha−1 (0–40 cm, Table 3). The SOC content in the upper layer in S2 was approximately four times higher than that in S1, being 45.28 Mg C ha−1 in S2 and 10.36 Mg C ha−1 in S1.

Table 3.
Biomass of the total tree and its various components and carbon (C) pools of Aleppo pine forests in Djebel Mansour, NE Tunisia. (Means ± SE). For each parameter, different letters (a and b) indicate statistically significant differences at p-values < 0.05 (one-way ANOVA) between the two stands. Bold numbers represent total tree and soil, both summing up to the ecosystem carbon stock.
3.1.2. Aboveground Biomass
From the field measurements, it was seen that the whole tree aboveground biomass reached a maximum value of 856 kg.DW at the age of 96 years. When fitting this to a logistic curve, we reached a K value of 3762 kg.DW, much higher than the observed maximum value which was theoretically reached at an age of 421 years when prolonging the curve. Among the different modules composing the tree, trunk biomass reached 256 kg.DW at age 96 years, with a K value of 313 kg.DW which was reached at the age of 117 years. The trunk biomass remained below 50 kg.DW until a tree age of 50 years, before sharply increasing until it reached an asymptotic value at a recovery age of around 100 years old. The fine fuel pool recovery (leaves and branches) was a little bit delayed, reaching 100 kg DW at 82 years of age. A value of 626 kg.DW was observed at 96 years of age, which is much higher than the trunk biomass at the same age (250 kg.DW) (Figure 3).
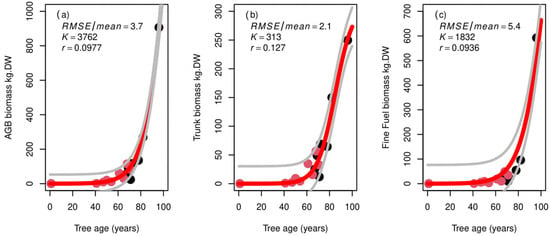
Figure 3.
(a) Total aboveground biomass (AGB), (b) trunk biomass, and (c) fine fuel biomass (leaves & branches) (in kg.DW) according to tree age (X axis, in years). Red line represents the fitted sigmoid curve, with its 95% confidence interval (grey lines). K: carrying capacity, r: growth rate, RMSE: root mean squared error. Red dots represent tree individuals from the young stand S1 and black dots from the old stand S2.
The belowground root biomass reached a maximum value of 150 kg.DW at 96 years of age, with a K value of 186 kg.DW which was reached at 112 years of age. The root biomass followed the same pattern as the trunk biomass recovery but with a decreasing root/shoot ratio from 1.5 at age 30 years which stabilized at a value of 0.6 at an age of 90 years, meaning that root development seems to happen faster than trunk development in the earliest growing period (Figure 4).
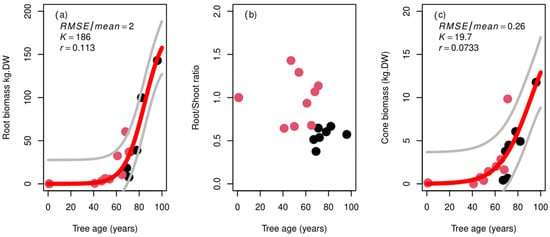
Figure 4.
(a) Root biomass (in kg.DW), (b) root/shoot ratio, and (c) cone biomass (in kg.DW) according to tree age (X axis, in years). Red line represents the fitted sigmoid curve, with its 95% confidence interval (grey line). K: carrying capacity, r: growth rate, RMSE: root mean squared error. Red dots represent tree individuals from the young stand S1 and black dots from the old stand S2.
3.1.3. Combustibility
Leaf biomass, the most combustible part of the tree, reached a maximum value of 59 kg.DW, at an age of 78 years, and followed a logistic curve (r = 1.2) with K= 55.2 kg.DW being reached at 100 years of age. The branches alone reached 58 kg.DW at age 80, and increased further up to 500 kg.DW at age 96 years, an extreme value obtained for one tree. When converting the leaf biomass into the bulk density (crown height) we observed a stable value around 0.15 (SD = 0.19), which did not significantly vary across time. Canopy combustibility then tends to increase across time (Figure 5).
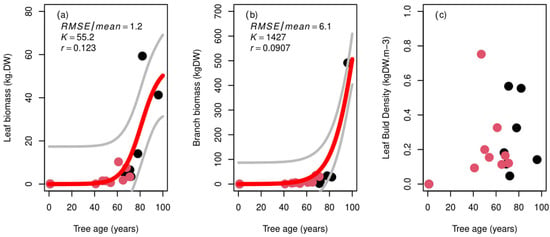
Figure 5.
(a) Leaf biomass, (b) branch biomass (in kg.DW), and (c) leaf bulk density (in kg.DW.m−3) according to tree age (X axis, in years). Red line represents the fitted sigmoid curve, with its 95% confidence interval (grey line). K: carrying capacity, r: growth rate, RMSE: root mean squared error. Red dots represent tree individuals from the young stand S1 and black dots represent trees from the old stand S2.
Tree height was the fastest recovering parameter with a highest value of 12 m which was reached at 78 years of age, and a K value of 11.4 m which was reached at 87 years of age as the recovery time. The crown base height reached a maximum value of 5 m and a maximum K value of 3.45 m, reached at the same age of 87 years. The mean crown base height was 0 m before 40 years of age when the tree height was below 3 m, and then maintained a constant proportion of the tree morphology representing 30% of the total tree height (Figure 6)
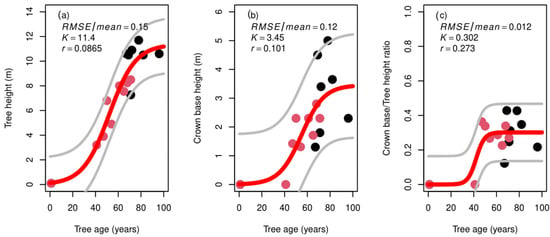
Figure 6.
(a) Tree height (m), (b) crown base height (m), and (c) crown base height/tree height ratio according to tree age (X axis, in years). Red line represents the fitted sigmoid curve, with its 95% confidence interval (grey line). K: carrying capacity, r: growth rate, RMSE: root mean squared error. Red dots represent tree individuals from the young stand S1 and black dots represent individuals from the old stand S2.
3.1.4. Resistance and Regeneration
Bark biomass reached a maximum value of 58 kg.DW at an age of 96 years, with a K value of 127 kg.DW which was reached at 130 years of age. Bark biomass remains a constant fraction of trunk biomass across time. When converting it to bark thickness, we obtained an increasing value with age, reaching a maximum value of 4 kg.DW.m−2 (Figure 7).
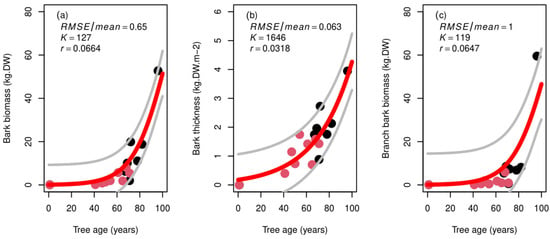
Figure 7.
(a) Bark biomass (kg.DW), (b) bark thickness (kg.DW.m2), and (c) branch bark biomass (kg.DW) according to tree age (X axis, in years). Red line represents the fitted sigmoid curve, with its 95% confidence interval (grey line). K: carrying capacity; r: growth rate; RMSE: root mean squared error. Red dots represent tree individuals from the young stand S1 and black dots represent individuals from the old stand S2.
For branches, bark biomass reached 10 kg.DW at 82 years of age with a maximum value of 80 kg DW at 96 years of age. Bark represents 24% of the total branch biomass with an increasing proportion across the years (Figure 7).
Regeneration ability, seen through cone biomass, varied between 1 kg.DW at 40 years andto 15 kg.DW at 96 years (Figure 4), with no cones being present below age 20.
3.2. Allometric Biomass Equations for Regional Applications
In order to provide traits and biomass estimates based on simple morphology measurements, we computed allometric equations. Table 4 provides estimated coefficients estimates and goodness of fit statistics (R2, RMSE, Adj. R2, MAE) for all of the biomass models for the two sites S1 and S2. These statistics were significant with p-value < 0.05, indicating that the fitted biomass equations performed well. The most reliable model fitting was obtained for total (Yt), aboveground (Ya), belowground (Yr), and stem biomass (Ysb, Ysw), while the needle (Yn) and branch biomass (Ybb, Ybw) models showed less reliable fittings with relatively lower R2 (0.77 ≤ R2 ≤ 0.82) and higher RMSE values. The pine cones particularly showed a minimal model fitting aspect with R2 = 0.51.

Table 4.
Best fitting biomass equations and their statistics for tree components of Aleppo pine forests in Djebel Mansour, NE Tunisia. Yt: total biomass, Ya: aboveground biomass; Ysw: stem wood biomass; Ybw: branch wood biomass; Ysb: stem bark biomass; Ybb: branch bark biomass; Yn: needle biomass; Yc: cone; Yr: belowground biomass. W, white test; B-P, Breush–Pagnan test. RMSE: root mean squared error. MAE: mean absolute error.
The adjusted R2 values indicated that fitted models explained between 47% and 99% of the biomass variance per tree component, explaining 75%, 79%, 97%, and 99% of the variance in needles, branch wood, aboveground, and stem wood biomass, respectively. The stem bark and belowground biomass equation explained, on average, 95% of the total observed variance. The total, stem wood, stem bark, above, and belowground biomasses (Yt, Ysw, Ysb, Ya, and Yr) were better estimated using DBH and H. However, for the biomass of branches, needles, and cones (Ybw, Ybb, Yn, and Yc) better estimations were provided using DBH and the Crown Ratio (CR) as predictive variables. The best fitting biomass equations are presented in Table 4.
3.3. Adjusted Vulnerability Framework
Based on the time course of fire-related traits (3.1), we could obtain the resistance trait values at 20, 50 (mean age of young stand S1), and 80 (mean age of old stand S2) years of age. Bark thickness (resistance trait) varied, respectively, between 0.25, 0.8, and 2.0 kg.DW.m−2, thus increasing resistance during fire in older stands and leading to a lower biomass decrease (Figure 8a). Root biomass (not affected by fires but decomposing after the fire as an index of absorbance) varied between 3.1, 11.2, and 73.5 kg.DW for 20-, 50-, and 80-year-old trees, respectively, thus increasing absorbance in older stands (Figure 8b). Cone biomass (regeneration trait) varied between 0, 2.5, and 7.1 kg.DW, thus suggesting a more efficient start to the recovery and enhanced regeneration in older stands (Figure 8c). An example of the potential cascading effect is the occurrence of an early second fire leading to no recovery when the cones are not sufficient in very young stands (Figure 8e).
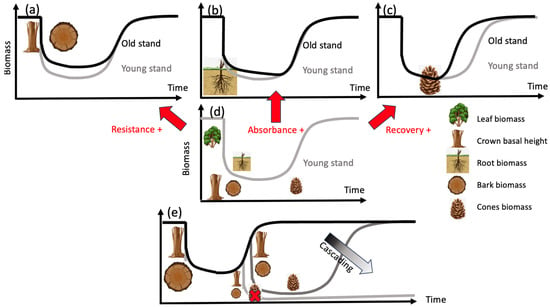
Figure 8.
Vulnerability curves of carbon stock in Pinus halepensis forest (young stand, grey line (d)) adjusted to increasing resistance (a), absorbance (b), and recovery (c) traits in old growth stands (black line). Potential cascading effect to second early fire is also shown (e).
4. Discussion
4.1. Allometric Equations and Regional Applications
Site- and species-specific allometric equations provide an efficient way to estimate both biomass and carbon stocks in forests. Nonlinear equations were developed to predict above and belowground biomass (stem and branch wood, stem and branch bark, needle and root) of Aleppo pine trees from dendrometric independent variables including DBH, H, and the Crown Ratio (CR). DBH represents keystone information, since it is easily measured in the field compared with the tree height and other variables. Previous studies revealed a significant relationship between DBH and aboveground biomass worldwide [40]. In the present study, the interaction between height and squared diameter significantly improved the stem wood and stem bark biomass predictions with adjusted R2 values of 0.99 and 0.97, respectively (Table 3). The R2 values were very high indicating the performance of the models in predicting the biomasses of all of the tree compartments. The predictive ability of (DBH2H) was reported in a Brazilian ecosystem study [41]. The inclusion of tree height (H) in the regression model may increase the potential applicability of the equation to different sites since the height is often used as an index of site growing conditions [42] and together with DBH it can be used to define the main structural patterns of forest systems. Here, we assumed homogeneous site conditions, although deeper soils and more nitrogen were measured in the older S2 stand (Table 2). For branches and needles, it is important to add a parameter that describes the shape and architecture of the crown and branching patterns to accurately estimate the biomass at the tree canopy level. In our study, for branches and needles, the combined effect of DBH and the Crown Ratio (CR = LCL/H) as independent variables resulted in higher R2 values (Table 4). Here, we here independent allometric relationships for each compartment, which cannot ensure an accurate additivity to the total biomass estimate. Using an additive system of equations where parameters are estimated with seemingly unrelated regression (SUR) would ensure this additivity [21].
Tree morphology-based relationships were shown to be able to capture the amount of biomass in different tree compartments, with each of these compartments being related to the total biomass (or potential loss) affected by fires but also the resistance, absorbance, and resilience of the trees. With the increased resolution of and precision in measuring tree height [43] and the tree crown area [44] at the regional scale with remote sensing, local allometric relationships will allow for landscape-scale applications of tree compartment assessments [45]. From this information, at a fine resolution and over extended areas, regional impacts [15] and ecosystem vulnerabilities to fires could then be easily evaluated to drive post-fire management and restoration plans.
4.2. Forest Biomass Stocks in Mediterranean Pine Forests
Based on the allometric equations developed in this study, the estimated aboveground biomass of the Aleppo pine (46.02–148.08 Mg ha−1) was in the range reported in other studies examining Pinus species in Tunisia (80 Mg ha−1, [46], 93–113 Mg ha−1, [24]) and in Portugal (63 Mg ha−1, [47]). Similar variations were reported for mixed forests containing Pinus nigra in Turkey (29.4 Mg C ha−1, [48] and Pinus pinea stands in Spain (30–63 Mg C ha−1, [49]).
Similarly, the estimated belowground biomass (15.58–47.35 Mg ha−1) falls within the range of values reported for Aleppo pine forests in Tunisia (21.8 Mg ha−1, [46]). The carbon stocks in the belowground biomass (roots), ranging from 7.05 Mg C ha−1 to 21.43 Mg C ha−1 (Table 3), aligns with the reported range for analogous forest types in Turkey (14.8 Mg C ha−1, [50]).
Moreover, the root/shoot ratios observed in this study (S2, 0.32, and S1, 0.34) align with the findings for Portuguese pine stands (0.30, [47]). However, it is higher than the ratios previously reported for Aleppo pines in Tunisia (0.26, [46]), conifer forests in Turkey (0.18, [50]), and stone pines in Spain (0.24, [51]). The variation in root/shoot ratios may be attributed to differences in root excavation methods and potential differences in site fertility. Furthermore, these discrepancies could be explained by the plants’ strategies to mitigate water deficiency episodes, such as the development of a taproot system to avoid water stress and competition from understory vegetation [52].
In forest ecosystems, the deposition of litter fall is the primary mechanism for returning organic matter and nutrients to the soil [53]. The rates of litter input in forest soils are influenced by vegetation types, composition, and site conditions [54]. In the present study, the estimated carbon stocks of litter ranged from 4 to 7 Mg C ha−1. These findings align with the reported range for the same forest type in Turkey (2–7 Mg C ha−1, [55]). The quantity of litter carbon varies according to the age and density of trees [56] making older forests more prone to lose carbon stocks during fires. Forest litter is indeed flammable and combusted during fires [57], particularly in Pinus halepensis forests [58].
The soil organic carbon (SOCs) content in the deep soil S2 (0–70 cm) was higher (115.67 Mg C ha−1) compared to that reported for the same soil depth in conifer forests in Spain (76 Mg C ha−1, [59]). However, in the shallow soil S1 (0–40 cm), the SOC content (31.67 Mg C ha−1) was closer to values reported for Aleppo pine forests at the same depth in Spain (37.32 Mg ha−1, [18]). These results, in conjunction with the carbon stocks of different biomass components, emphasize the significant role of soil depth. Several factors, including tree species, stand age, soil fertility, stand management practices, previous land use, and climate, can contribute to the observed differences in carbon stocks among forest ecosystems [60]. The amount of SOC is also influenced by the rate of organic matter inputs and accumulation as well as the rate of mineralization in different organic carbon pools [61]. The SOC’s contribution to the total forest carbon stock was found to be 48.74% to 53.79% (Table 4). The total carbon stocks (64.97–215.04 Mg C ha−1) in the studied ecosystem, including living aboveground biomass, belowground tree biomass, litter, and soil, are comparable to those reported in other pine forests across the Mediterranean region. It has been shown that forested ecosystems with shallow soils often exhibit lower carbon stocking. Another study reported carbon stocks of 23.96 Mg C ha−1 for Pinus halepensis and 58.09 Mg C ha−1 for Pinus nigra at a soil depth of 40 cm in a conifer forest in south-eastern Spain [18]. On the other hand, the estimated total carbon stock in the deep site was in the range of higher values observed in Mediterranean pine forests, such as those reported for conifers in Turkey (265.7 Mg C ha−1, [40] and Pinus sylvestris in Spain (252 Mg C ha−1, [62]).
4.3. Implication of Carbon Pools Dynamic on Vulnerability Assessment to Fire and Cascading Effects
Our results could capture the time course of functional traits related to Pinus halepensis’ vulnerability to fire, including resistance, absorbance, and recovery, as a contribution to the understanding of tree traits in relation to resistance and resilience to fires [63], as well as potential cascading effects in promoting a new fire through flammability traits [14]. We must deplore here the few very old (>70 years) and very young (<30 years) individuals used for our analysis which might induce more uncertainties at these early and late stages of forest development.
As a first result, we showed that Pinus halepensis resistance related to the bark thicknesses [26] of the trunk and branches increases over time, making older forests more resistant (Figure 8), as has been observed for most species [64]. During fires, leaf and branches carbon stocks are usually fully combusted and emitted to the atmosphere. The trunk carbon stock is only partly affected depending on resistance traits and flame intensity, and either survives the fire or is killed and submitted to decomposition. Additionally, carbon can remain on site as black pyrogenic carbon after wood smoldering combustion and could constitute a long-standing form of carbon storage [65]. However, smoldering is a rare event within Mediterranean climate conditions [66].
At the same time, root biomass, which is hardly affected by direct combustion, also increases with time, as is the case for most tree species [67], so that the post-fire absorbance time taken for the root carbon stock to fully decompose in an old growth forest would be more important than that in the young stands [68]. With regard to this root C stock, old growth forests would then be less vulnerable (Figure 8). For Mediterranean species, root biomass takes between 5 and 15 years to fully decompose [69,70] with exponential decay. We limited our study to root biomass within the first 50 cm, below which the root system might take longer to decompose [71], so that older trees might have even a longer absorbance time and a lower vulnerability.
Regarding the regeneration potential of seeds, we were able to quantify the increasing cone biomass with age, but this started at 25 years old, before which no cones were observed in our area. This maturity threshold is higher than that previously reported for this species which was around 15 years old [72], but fire frequency has been shown to stimulate earlier maturity [73,74] and more cone biomass [10]. A relationship between cone biomass and DBH was previously demonstrated [75], so that older forests have an increased ability to regenerate as a consequence of there being more cones to germinate [76], although seed number was also not always considered as a limiting factor once the trees had passed the maturity threshold [77]. We should note here that there is a potential tipping point at this age of maturity, below which the trees would not be able to regenerate (and would take a lot of time from seed dispersal), a vital attribute related to fire as identified by Noble and Slatyer [12]. Recurrent fires with a return interval below this maturity threshold would result in a cascading effect which significantly increase the vulnerability of carbon stocks.
Finally, the dynamics of crown basal height revealed that Pinus halepensis trees experience vertical fuel continuity in their first 30 years with a crown basal height of 0 m, thus favoring crown fires during the early stages of tree development [78]. Then, the crown basal height followed a fixed ratio with tree height, a feature implemented in tree height/crown basal area models [79,80,81,82] which has an impact on flammability [83]. However, the dynamics of horizontal fuel continuity and litter amount, as major drivers of ignition and fire spread, which were not assessed in our study, may reduce this crown fire probability during the very early stages of forest development through horizontal discontinuity [84]. We assumed here a continuous canopy cover as observed in the study area, but fuel discontinuity in the canopy layer and reduced bulk density at the landscape level could locally reduce fire spread and should be accounted for in a full flammability assessment. Nevertheless, our results could contribute to the conceptual framework of carbon stock vulnerability to fires in Mediterranean Pinus halepensis forests (summarized in Figure 8), revealing an increasing vulnerability under short-interval reburning as observed in other coniferous forests [85], and causing potential cascading effects in the face of successive fires [85,86,87], which are becoming more frequent in the country with increasingly frequent and intense heatwaves [6] such as that during the summer 2023, and recent social troubles [88].
5. Conclusions
The present study has developed nine allometric models that estimate the aboveground and belowground biomasses of Pinus halepensis based on the tree’s diameter at breast height (DBH), height (H), and Live Crown Length (LCL) as independent variables. These equations can be utilized as a valuable resource for assessing the carbon stocks in various carbon pools in Mediterranean Aleppo pines. In particular, we provided detailed information on the different carbon pools, including root biomass, a rarely assessed tree compartment due to methodological constraints [89]. We also showed the value of the information provided by these different pools in an evaluation of the fire-related traits that contribute to resistance, absorbance, and recovery for a dynamic vulnerability assessment according to the time since last fire (TSLF). From this information, we can conclude that the carbon stock in young forests has a higher vulnerability to fire, because of its reduced resistance and regeneration potential. This pattern was coupled with higher flammability in the young stands, thus enhancing crown fire danger and cascading effects and reducing the forests’ ability to recover, making protecting these young forests from fire a priority. Landscape assessments of tree height could provide additional fruitful information for a regional assessment of forests’ vulnerability to fire, driving fire management policies to their secure carbon sequestration abilities and the other ecological values of these forests.
Author Contributions
All authors designed and carried out the experiment. N.S. and F.M. performed the statistical analysis. F.R. wrote the manuscript with the support of F.M., L.Z., N.S. and F.G., A.K. and Z.N. helped with the critical discussion. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the Tunisian National Institute for Agricultural Research, Rural Engineering, Water and Forestry.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
The authors would like to express their gratitude to the staff of the Djebel Mansour station for their valuable contributions during the fieldwork. The authors also would like to thank the staff of the Tunisian meteorological service station for their assistance.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Harris, N.L.; Gibbs, D.A.; Baccini, A.; Birdsey, R.A.; De Bruin, S.; Farina, M. Global maps of twenty-first century forest carbon fluxes. Nat. Clim. Change 2021, 11, 234–240. [Google Scholar] [CrossRef]
- Rodríguez-Veiga, P.; Wheeler, J.; Louis, V.; Tansey, K.; Balzter, H. Quantifying forest biomass carbon stocks from space. Curr. Oncol. Rep. 2017, 3, 1–18. [Google Scholar] [CrossRef]
- Salvatore, R.; Moya, D.; Pulido, L.; Lovreglio, R.; López-Serrano, F.R.; De las Heras, J.; Leone, V. Morphological and anatomical differences in Aleppo pine seeds from serotinous and non-serotinous cones. New For. 2010, 39, 329–341. [Google Scholar] [CrossRef]
- Montero, G.; Cañellas, I.; Ruiz-Peinado, R. Growth and yield models for Pinus halepensis mill. For. Syst. 2001, 10, 179–201. [Google Scholar] [CrossRef]
- Quézel, P. Taxonomy and biogeography of Mediterranean pines (Pinus halepensis and P. brutia). In Ecology, Biogeography and Management of Pinus halepensis and Pinus brutia Forest Ecosystems in the Mediterranean Basin; Néeman, G., Trabaud, L., Eds.; Backhuys Publishers: Leiden, The Netherlands, 2000; pp. 1–12. [Google Scholar]
- Ruffault, J.; Curt, T.; Moron, V.; Trigo, R.M.; Mouillot, F.; Koutsias, N.; Pimont, F.; Martin-StPaul, N.; Barbero, R.; Dupuy, J.L.; et al. Increased likelihood of heat-induced large wildfires in the Mediterranean Basin. Sci. Rep. 2020, 10, 13790. [Google Scholar] [CrossRef] [PubMed]
- Van der Werf, G.R.; Randerson, J.T.; Giglio, L.; Van Leeuwen, T.T.; Chen, Y.; Rogers, B.M.; Mu, M.; van Marle, M.J.; Morton, D.C.; Collatz, G.J.; et al. Global fire emissions estimates during 1997–2016. Earth Syst. Sci. Data 2017, 9, 697–720. [Google Scholar] [CrossRef]
- Chuvieco, E.; Yebra, M.; Martino, S.; Thonicke, K.; Gomez-Gimenez, M.; San-Miguel, J.; Oom, D.; Velea, R.; Mouillot, F.; Molina, J.R.; et al. Towards an integrated approach to wild re risk assessment: When, where, what and how may the landscapes burn. Fire 2023, 6, 215. [Google Scholar] [CrossRef]
- Popovic, Z.; Bojovic, S.; Markovic, M.; Cerda, A. Tree species flammability based on plant traits: A synthesis. Sci. Total Environ. 2021, 800, 149625. [Google Scholar] [CrossRef] [PubMed]
- Ne’eman, G.; Goubitz, S.; Nathan, R. Reproductive traits of Pinus halepensis in the light of fire—A critical Review. Plant Ecol. 2004, 171, 69–79. [Google Scholar] [CrossRef]
- Linkov, I.; Trump, B.D. Resilience as function of space and time. In The Science and Practice of Resilience. Risk, Systems and Decisions; Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Noble, I.R.; Slatyer, R.O. The use of vital attributes to predict successional changes in plant communities subject to recurrent disturbances. Vegetatio 1980, 43, 5–21. [Google Scholar] [CrossRef]
- Chiminazzo, M.A.; Charles-Dominique, T.; Rossatto, D.R.; Bombo, A.B.; Fidelis, A. Why woody plant modularity through time and space must be integrated in fire research? AoB Plants 2023, 15, plad029. [Google Scholar] [CrossRef] [PubMed]
- Ibanez, T.; Platt, W.J.; Bellingham, P.J.; Vieilledent, G.; Franklin, J.; Martin, P.H.; Menkes, C.; Perez-Salicrup, D.R.; Russell-Smith, J.; Keppel, G. Altered cyclone-fire interactions are changing ecosystems. Trends Plant Sci. 2022, 27, 1218–1230. [Google Scholar] [CrossRef] [PubMed]
- Vallet, L.; Schwartz, M.; Ciais, P.; van Wees, D.; Truchis, A.; Mouillot, F. High-resolution data reveal a surge of biomass loss from temperate and Atlantic pine forests, contextualizing the 2022 fire season distinctiveness in France. Biogeosciences 2023, 20, 3803–3825. [Google Scholar] [CrossRef]
- Cutini, A.; Bongi, P.; Chianucci, F.; Pagon, N.; Grignolio, S.; Amorini, E.; Apollonio, M. Roe deer (Capreolus capreolus L.) browsing effects and use of chestnut and Turkey oak coppiced areas. Ann. For. Sci. 2011, 68, 667–674. [Google Scholar] [CrossRef]
- Sonmez, T.; Kahriman, A.; Şahin, A.; Yavuz, M. Biomass equations for Calabrian pine in the Mediterranean region of Turkey. Šumarski List 2016, 11–12, 567–576. [Google Scholar] [CrossRef]
- Navarrete-Poyatos, M.A.; Navarro-Cerrillo, R.M.; Lara-Gómez, M.A.; Duque-Lazo, J.; de los Angeles Varo, M.; Palacios Rodriguez, G. Assessment of the Carbon Stock in Pine Plantations in Southern Spain through ALS Data and K-Nearest Neighbor Algorithm Based Models. Geosciences 2019, 9, 442. [Google Scholar] [CrossRef]
- Basuki, T.M.; Van Lake, P.E.; Skidmore, A.K.; Hussin, Y.A. Allometric equations for estimating the aboveground biomass in the tropical lowland Dipterocarp forests. For. Ecol. Manag. 2009, 257, 1684–1694. [Google Scholar] [CrossRef]
- Paul, K.I.; England, J.; Roxburgh, S.H.; Ritson, P.S.; Hobbs, T.; Brooksbank, K.; Raison, R.J.; Larmour, J.S.; Murphy, S.; Norris, J.; et al. Development and testing of generic allometric equations for estimating aboveground biomass of mixed-species environmental plantings. For. Ecol. Manag. 2013, 310, 483–494. [Google Scholar] [CrossRef]
- Jorge, C.; Tomé, M.; Ruiz-Peinado, R.; Zribi, L.; Paulo, J.A. Quercus suber Allometry in the West Mediterranean Basin. Forests 2023, 14, 649. [Google Scholar] [CrossRef]
- Avendano-Hernandez, D.M.; Acosta-Mireles, M.; Carrillo-Anzures, F.; Etchevers-Barra, J.D. Biomass and carbon estimation in a forest of Abies religiosa. Rev. Fitotec. Mex. 2009, 32, 233–238. [Google Scholar] [CrossRef]
- Rodrıguez-Ortiz, G.; Garcıa-Aguilar, J.A.; Leyva-Lopez, J.C.; Ruiz-Dıaz, C.; Enrıquez-del Valle, J.R.; Santiago-Garcıa, W. Structural biomass and by compartments of Pinus patula regeneration in clearcutting sites. Madera Bosques 2019, 25, e2511713. [Google Scholar] [CrossRef]
- Shaiek, O.; Loustau, D.; Garchi, S.; Bachtobji, B.; El Aouni, M.H. Estimation allométrique de la biomasse du pin maritime en dune littorale: Cas de la forêt de Rimel (Tunisie). Forêt Méditerranéenne 2010, 31, 231–242. [Google Scholar]
- Ennajah, A.; Kachout-Sai, S.; Khaldi, A.; Elaoui, M.; Laamouri, A.; Fezzani, T.; Cherni, T.; Eleuch, S.; Nasr, Z. Interactive Effects of Ecosystem Managements on Gas Exchange, Water Use Efficiency and Carbon Stock in Pinus pinea Forests. J. Chem. Biol. Phys. Sci. 2016, 63, 1044–1059. [Google Scholar] [CrossRef]
- Pausas, J.G. Bark thickness and fire regime. Funct. Ecol. 2015, 29, 315–327. [Google Scholar] [CrossRef]
- Belhadj-Khedher, C.; Koutsias, N.; Karamitsou, A.; EI-Melki, T.; Ouelhazi, B.; Hamdi, A.; Nouri, H.; Mouillot, F. A Revised Historical Fire Regime Analysis in Tunisia (1985–2010) from a Critical Analysis of the National Fire Database and Remote Sensing. Forests 2018, 9, 59. [Google Scholar] [CrossRef]
- Sghaier, T.; Ammari, Y. Croissance et production du Pin d’Alep (Pinus halepensis mill.) en Tunisie. Ecol. Mediterr. 2012, 38, 39–57. [Google Scholar] [CrossRef]
- Belhadj-Khedher, C.; El-Melki, T.; Mouillot, F. Saharan hot and dry sirocco winds drive extreme fire events in Mediterranean Tunisia (North Africa). Atmosphere 2020, 11, 590. [Google Scholar] [CrossRef]
- Mtimet, A. Atlas Des Sols Tunisiens; Ministère de l’Agriculture, Direction des Sols: Tunis, Tunisia, 1999; p. 165. [Google Scholar]
- Addo-Danso, D.; Prescott, C.E.; Smith, A.R. Methods for estimating root biomass and production in forest and woodland ecosystems carbon studies: A review. For. Ecol. Manag. 2016, 359, 332–351. [Google Scholar] [CrossRef]
- Burt, R. Soil Survey Laboratory Methods Manual; Report No. 42 Version 4.0; United States Department of Agriculture, Natural Re-Sources Conservation Service, Soil Survey Investigations: Lincoln, NE, USA, 2004. [Google Scholar]
- Nelson, D.W.; Sommers, L.E. Total carbon, organic carbon and organic matter. In Methods of Soil Analysis; Page, A.L., Miller, R.H., Keeny, D.R., Eds.; American Society of Agronomy and Soil Science Society of America: Madison, WI, ASA, 1996; pp. 1119–1123. [Google Scholar] [CrossRef]
- Bremner, J.M.; Mulvaney, C.S. Nitrogen-Total. In Methods of Soil Analysis; Part 2. Chemical and Microbiological, Properties; Page, A.L., Miller, R.H., Keeney, D.R., Eds.; American Society of Agronomy, Soil Science Society of America: Madison, WI, ASA, 1982; pp. 595–624. [Google Scholar]
- Martin, M.P.; Wattenbach, M.; Smith, P.; Meersmans, J.; Jolivet, C.; Boulonne, L.; Arrouays, D. Spatial distribution of soil organic carbon stocks in France. Biogeosciences 2011, 8, 1053–1065. [Google Scholar] [CrossRef]
- Parresol, B.R. Assessing tree and stand biomass: A review with examples and critical comparisons. For. Sci. 1999, 45, 573–593. [Google Scholar] [CrossRef]
- Bi, H.; Turner, J.; Lambert, M.J. Additive biomass equations for native eucalypt forest trees of temperate Australia. Trees 2004, 18, 467–479. [Google Scholar] [CrossRef]
- Zribi, L.; Chaar, H.; Khaldi, A.; Hanchi, B.; Mouillot, F.; Gharbi, F. Estimate of biomass and carbon pools in disturbed and undisturbed oak forests in Tunisia. For. Syst. 2016, 25, e060. [Google Scholar] [CrossRef]
- Amani, B.H.; N’Guessan, A.E.; Van der Meersch, V.; Derroire, G.; Piponiot, C.; Elogne, A.G.; Traoré, K.; N’Dja, J.K.; Hérault, B. Lessons from a regional analysis of forest recovery trajectories in West Africa. Environ. Res. Lett. 2022, 17, 115005. [Google Scholar] [CrossRef]
- Medeiros, T.C.C.; Sampaio, E. Allometry of aboveground biomasses in mangrove species in Itamaracá, Pernambuco, Brazil. Wetl. Ecol. Manag. 2008, 16, 323–330. [Google Scholar] [CrossRef]
- Ribeiro, C.S.; Fehrmann, L.; Boechat Soares, C.P.; Gonçalves Jacovine, L.A.; Kleinn, C.; de Oliveira Gaspar, R. Above- and belowground biomass in a Brazilian Cerrado. For. Ecol. Manag. 2011, 262, 491–499. [Google Scholar] [CrossRef]
- Navar, J. Allometric equations for tree species and carbon stocks for forests of northwestern Mexico. For. Ecol. Manag. 2009, 257, 427–434. [Google Scholar] [CrossRef]
- Schwartz, M.; Ciais, P.; De Truchis, A.; Chave, J.; Ottlé, C.; Vega, C.; Wigneron, J.P.; Nicolas, M.; Jouaber, S.; Liu, S.; et al. FORMS: Forest Multiple Source height, wood volume, and biomass maps in France at 10 to 30 m resolution based on Sentinel-1, Sentinel-2, and GEDI data with a deep learning approach. Earth Syst. Sci. Data 2023, 15, 4927–4945. [Google Scholar] [CrossRef]
- Weinstein, B.G.; Marconi, S.; Bohlman, S.A.; Zare, A.; Singh, A.; Graves, S.J.; White, E.P. A remote sensing derived data set of 100 million individual tree crowns for the National Ecological Observatory Network. eLife 2021, 10, e62922. [Google Scholar] [CrossRef] [PubMed]
- Williams, V.L.; Witkowski, E.T.F.; Balkwill, K. Relationship between bark thickness and diameter at breast height for six tree species used medicinally in South Africa. S. Afr. J. Bot. 2007, 73, 449–465. [Google Scholar] [CrossRef][Green Version]
- Gallalou, C. Etude des caractéristiques dendrométriques du pin d’Alep (Pinus halepensis Mill.) dans la forêt de Bouhertma (Région de Fernana) (Tunisie). Master’s Thesis, Université 7 Novembre à Carthage, Tunis, Tunisie, 2006. [Google Scholar]
- Correia, A.C.; Tomé, M.; Carlos, P.; Sónia, F.; Dias, A.; Freire, J.; Carvalho, P.O.; Pereira, J.S. Biomass allometry and carbon factors for a Mediterranean pine (Pinus pinea L.) in Portugal. For. Syst. 2010, 19, 418–433. [Google Scholar] [CrossRef]
- Dinc, M.; Vatandaslar, C. Analyzing carbon stocks in a mediterranean forest enterprise: A case study from kizildag, Turkey. Cerne 2019, 25, 402–414. [Google Scholar] [CrossRef]
- Del Río, M.; Barbeito, I.; Bravo-Oviedo, A.; Calama, C.; Cañellas, I.; Herrero, C.; Montero, G.; Moreno-Fernández, D.; Ruiz-Peinado, R.; Bravo, F. Forest Carbon Sequestration: The Impact of Forest Management. In Managing Forest Ecosystems: The Challenge of Climate Change; Bravo, F., Le May, V., Jandl, R., Eds.; Springer International Publishing: Cham, Switzerland, 2017; Volume 34, pp. 301–327. [Google Scholar] [CrossRef]
- Evrendilek, F.; Berberoglu, S.; Taskinsu-Meydan, S.; Yilmaz, E. Quantifying carbon budgets of conifer Mediterranean forest ecosystems, Turkey. Environ. Monit. Assess. 2006, 119, 527–543. [Google Scholar] [CrossRef]
- Ruiz-Peinado, R.; Del Rio, M.; Montero, G. New models for estimating the carbon sink capacity of Spanish soft-wood species. For. Syst. 2011, 20, 176–188. [Google Scholar] [CrossRef]
- Frattegiani, M.; Mercurio, M.; Mencuccini, M.; Profili, W. Quantitative analysis of stone pine (Pinus pinea L.) root systems morphology and its relationship with water table and soil characters. Investig. Agrar. Sist. Recur. For. 1993, 3, 405–416. [Google Scholar]
- Demessie, A.; Singh, B.R.; Lal, R.; Strand, T. Leaf litterfall and litter decomposition under Eucalyptus and coniferous plantations in Gambo District, southern Ethiopia. Acta Agric. Scand. B Soil Plant Sci. 2012, 62, 467–476. [Google Scholar] [CrossRef]
- Jhariya, M.K. Influences of Forest Fire on Forest Floor and Litterfall in Bhoramdeo Wildlife Sanctuary (C.G.), India. J. Environ. Sci. 2017, 33, 330–341. [Google Scholar] [CrossRef]
- Misir, M.N.; Bayburtlu, S.; Bilgili, F. The yield of natural trembling aspen (Populus tremula L.) stands (Northern and Eastern Anatolia). Pak. J. Agric. Sci. 2013, 50, 537–547. [Google Scholar]
- Yue, J.; Guan, J.; Deng, L.; Zhang, J.; Li, G.; Du, S. Allocation pattern and accumulation potential of carbon stock in natural spruce forests in Northwest China. PeerJ 2018, 6, e4859. [Google Scholar] [CrossRef] [PubMed]
- Varner, J.M.; Kane, J.M.; Kreye, J.K.; Engber, E. The flammability of forest and woodland litter: A synthesis. Curr. For. Rep. 2015, 1, 91–99. [Google Scholar] [CrossRef]
- Xifré-Salvadó, M.À.; Prat-Guitart, N.; Francos, M.; Úbeda, X.; Castellnou, M. Smouldering Combustion Dynamics of a Soil from a Pinus halepensis Mill. Forest. A Case Study of the Rocallaura Fires in Northeastern Spain. Appl. Sci. 2020, 10, 3449. [Google Scholar] [CrossRef]
- Rodrıguez-Murillo, J. Organic carbon content under different types of land use and soil in peninsular Spain. Biol. Fertil. Soils 2001, 33, 53–61. [Google Scholar] [CrossRef]
- Peng, S.S.; Piao, S.l.; Zeng, Z.Z.; Ciais, P.; Zhou, L.M.; Liu, L.Z.X. Afforestation in China cools local land surface temperature. Proc. Natl. Acad. Sci. USA 2014, 111, 2915–2919. [Google Scholar] [CrossRef] [PubMed]
- Post, W.M.; Kwon, K.C. Soil carbon sequestration and land use change: Processes and potential. Glob. Change Biol. 2000, 6, 317–327. [Google Scholar] [CrossRef]
- Ruíz-Peinado, R.; Bravo-Oviedo, A.; Montero, G.; Río, M. Carbon stocks in a Scots pine afforestation under different thinning intensities management. Mitig Adapt. Strateg. Glob. Change 2014, 21, 1059–1072. [Google Scholar] [CrossRef]
- Rodman, K.C.; Veblen, T.T.; Andrus, R.A. A trait-based approach to assessing resistance and resilience to wildfire in two iconic North American conifers. J. Ecol. 2021, 109, 313–326. [Google Scholar] [CrossRef]
- Konôpka, B.; Pajtík, J.; Šebeň, V.; Merganičová, K. Modeling Bark Thickness and Bark Biomass on Stems of Four Broadleaved Tree Species. Plants 2022, 11, 1148. [Google Scholar] [CrossRef]
- Jones, M.W.; Santín, C.; van der Werf, G.R.; Doerr, S.H. Global fire emissions buffered by the production of pyrogenic carbon. Nat. Geosci. 2019, 12, 742–747. [Google Scholar] [CrossRef]
- Vallet, L.; Abdallah, C.; Lauvaux, T.; Joly, L.; Ramonet, M.; Ciais, P.; Lopez, M.; Xueref-Remy, I.; and Mouillot, F. Soil smoldering in temperate forests: A neglected contributor to fire carbon emissions revealed by atmospheric mixing ratios. Biogeosciences Discuss. 2023, 2421, Preprint. [Google Scholar] [CrossRef]
- Uri, V.; Kukumagi, M.; Aosaar, J.; Varik, M.; Becker, H.; Aun, K.; Lohmus, K.; Soosaar, K.; Astover, A.; Uri, M.; et al. The dynamics of the carbon storage and fluxes in scots pine (Pinus sylvestris) chronosequence. Sci. Total Environ. 2022, 817, 152973. [Google Scholar] [CrossRef]
- Campbell, J.L.; Fontaine, J.B.; Donato, C. Carbon emissions from decomposition of fire-killed trees following a large wildfire in Oregon, United States. J. Geophys. Res. Biogeosci. 2016, 121, 718–730. [Google Scholar] [CrossRef]
- Molinas-González, C.R.; Castro, J.; Leverkus, A.B. Deadwood Decay in a Burnt Mediterranean Pine Reforestation. Forests 2017, 8, 158. [Google Scholar] [CrossRef]
- Deng, X.; Liang, X.; Shen, L.; Liu, H.; Yang, M.; Zeng, M.; Liang, M.; Cheng, F. Decomposition and nutrient dynamics of stumps and coarse roots of Eucalyptus plantations in southern China. Ann. For. Sci. 2023, 80, 30. [Google Scholar] [CrossRef]
- Anderson, P.H.; Johnsen, K.H.; Butnor, J.R.; Gonzalez-Benecke, C.A.; Samuelson, L.J. Predicting longleaf pine coarse root decomposition in the southwestern US. For. Ecol. Manag. 2018, 425, 1–8. [Google Scholar] [CrossRef]
- Guiote, C.; Pausas, J.G. Fire favors sexual precocity in a Mediterranean pine. Oikos 2023, e09373. [Google Scholar] [CrossRef]
- Saracino, A.; Bellino, A.; Allevato, E.; Mingo, A.; Conti, S.; Rossi, S.; Bonanomi, G.; Carputo, D.; Mazzoleni, S. Repeated stand-replacing crown fires affect seed morphology and germination in Aleppo pine. Front. Plant Sci. 2017, 8, 1160. [Google Scholar] [CrossRef]
- Romero, B.; Ganteaume, A. Does recent fire activity impact fire-related traits of Pinus halepensis Mill. and Pinus sylvestris L. in the French Mediterranean area? Ann. For. Sci. 2020, 77, 106. [Google Scholar] [CrossRef]
- Ayari, A.; Zubizarreta-Gerendiain, A.; Tome, M.; Tome, J.; Garchi, S.; Henchi, B. Stand, tree and crown variables affecting cone crop and seed yield of Aleppo pine forests in different bioclimatic regions of Tunisia. For. Syst. 2012, 21, 128–140. [Google Scholar] [CrossRef]
- García-Jiménez, R.; Palmero-Iniesta, M.; Espelta, J.M. Contrasting effects of fire severity on the regeneration of Pinus halepensis Mill. and resprouter species in recently thinned thickets. Forests 2017, 8, 55. [Google Scholar] [CrossRef]
- Moya, D.; Espelta, J.; Verkaik, I.; López-Serrano, F.; Heras, J. Tree density and site quality influence on Pinus halepensis Mill. reproductive characteristics after large fires. Ann. For. Sci. 2007, 64, 649–656. [Google Scholar] [CrossRef]
- Mitsopoulos, I.D.; Dimitrakopoulos, A.P. Canopy fuel characteristics and potential crown fire behavior in Aleppo pine (Pinus halepensis Mill.) forests. Ann. For. Sci. 2007, 64, 287–299. [Google Scholar] [CrossRef]
- Valentine, H.T.; Amateis, R.L.; Gove, J.H.; Mäkelä, A. Crown-rise and crown-length dynamics: Application to loblolly pine. J. For. Res. 2013, 86, 371–375. [Google Scholar] [CrossRef]
- Allensworth, E.; Temesgen, H.; Frank, B.; Gray, A. Imputation to predict height to crown base for trees with predicted heights. For. Ecol. Manag. 2021, 498, 119574. [Google Scholar] [CrossRef]
- Zhu, W.; Liu, Z.; Jia, W.; Li, D. Modelling the Tree Height, Crown base height, and effective crown height of Pinus koraiensis plantations based on knot analysis. Forests 2021, 12, 1778. [Google Scholar] [CrossRef]
- Li, Y.; Wang, W.; Zeng, W.; Wang, J.; Meng, J. Development of crown ratio and height to crown base models for masson pine in Southern China. Forests 2020, 11, 1216. [Google Scholar] [CrossRef]
- Álvarez, E.; Duque, Á.; Saldarriaga, J.G.; Cabrera, K.R.; Salas, G.D.; Valle, I.D.; Lema, Á.; Moreno, F.; Orrego, S.A.; Rodriguez, L.C. Tree above-ground biomass allometries for carbon stocks estimation in the natural forests of Colombia. For. Ecol. Manag. 2012, 267, 297–308. [Google Scholar] [CrossRef]
- Hoy, E.E.; Turestsky, M.; Kasischke, E.S. More frequent burning increases vulnerability of Alaskan boreal black spruce forests. Environ. Res. Lett. 2016, 11, 095001. [Google Scholar] [CrossRef]
- Moghli, A.; Santana, V.M.; Baeza, M.J.; Pastor, E.; Soliveres, S. Fire recurrence and time since last fire interact to determine the supply of multiple ecosystem services by Mediterranean forests. Ecosystems 2022, 25, 1358–1370. [Google Scholar] [CrossRef]
- Turner, M.G.; Braziunas, K.H.; Hansen, W.D.; Harvey, B.J. Short-interval severe fire erodes the resilience of subalpine lodgepole pine forests. Proc. Natl. Acad. Sci. USA 2019, 116, 11319–11328. [Google Scholar] [CrossRef] [PubMed]
- Steel, Z.L.; Foster, D.; Coppoletta, M.; Lydersen, J.M.; Stephens, S.L.; Paudel, A.; Markwith, S.H.; Merriam, K.; Collins, B.M. Ecological resilience and vegetation transition in the face of two successive large wildfires. J. Ecol. 2021, 109, 3340–3355. [Google Scholar] [CrossRef]
- Chriha, S.; Sghari, A. Forest fires in Tunisia, irreversible sequelae of the revolution of 2011. J. Mediterr. Geogr. 2013, 121, 87–93. [Google Scholar] [CrossRef]
- Huang, Y.; Ciais, P.; Santoro, M.; Makowski, D.; Chave, J.; Schepaschenko, D.; Abramoff, R.Z.; Goll, D.S.; Yang, H.; Chen, Y.; et al. A global map of root biomass across the world’s forests. Earth Syst. Sci. Data 2021, 13, 4263–4274. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).