Predicting Wildfire Ember Hot-Spots on Gable Roofs via Deep Learning
Abstract
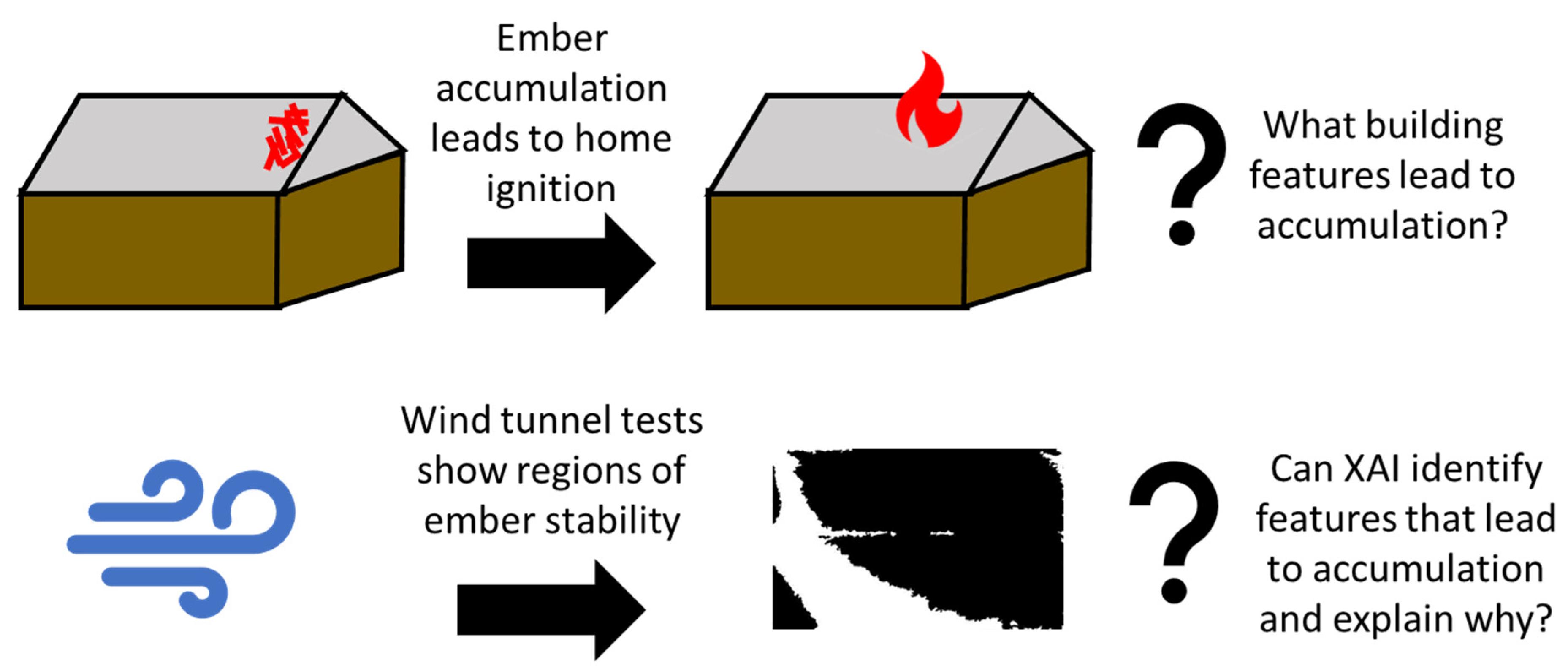
1. Introduction
- The DL model is capable of accurately predicting the fraction of the roof that retains embers as a function of the building geometry and wind conditions;
- The XAI tools can identify the nature of the relationship between the ember coverage and the building and wind parameters;
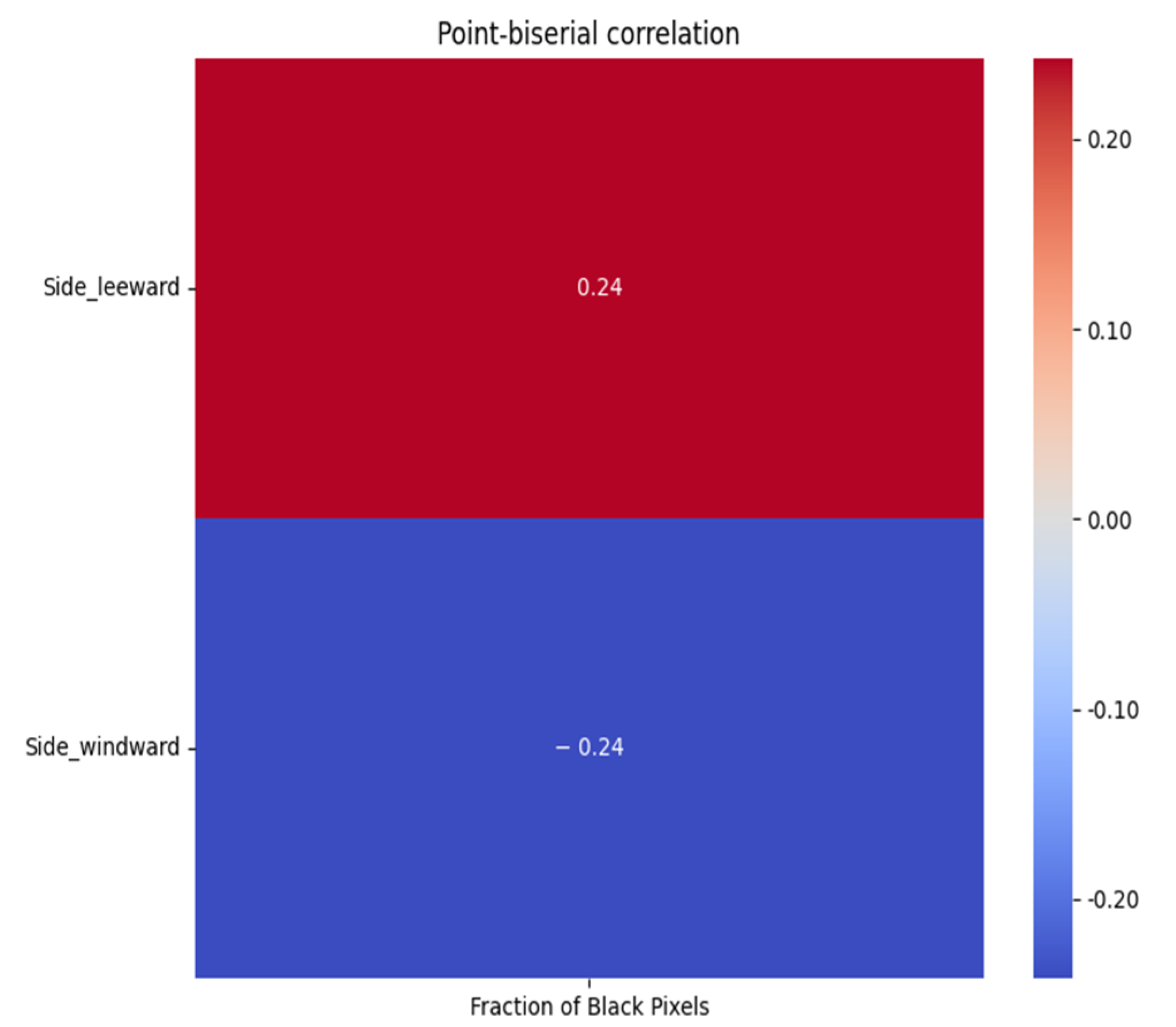
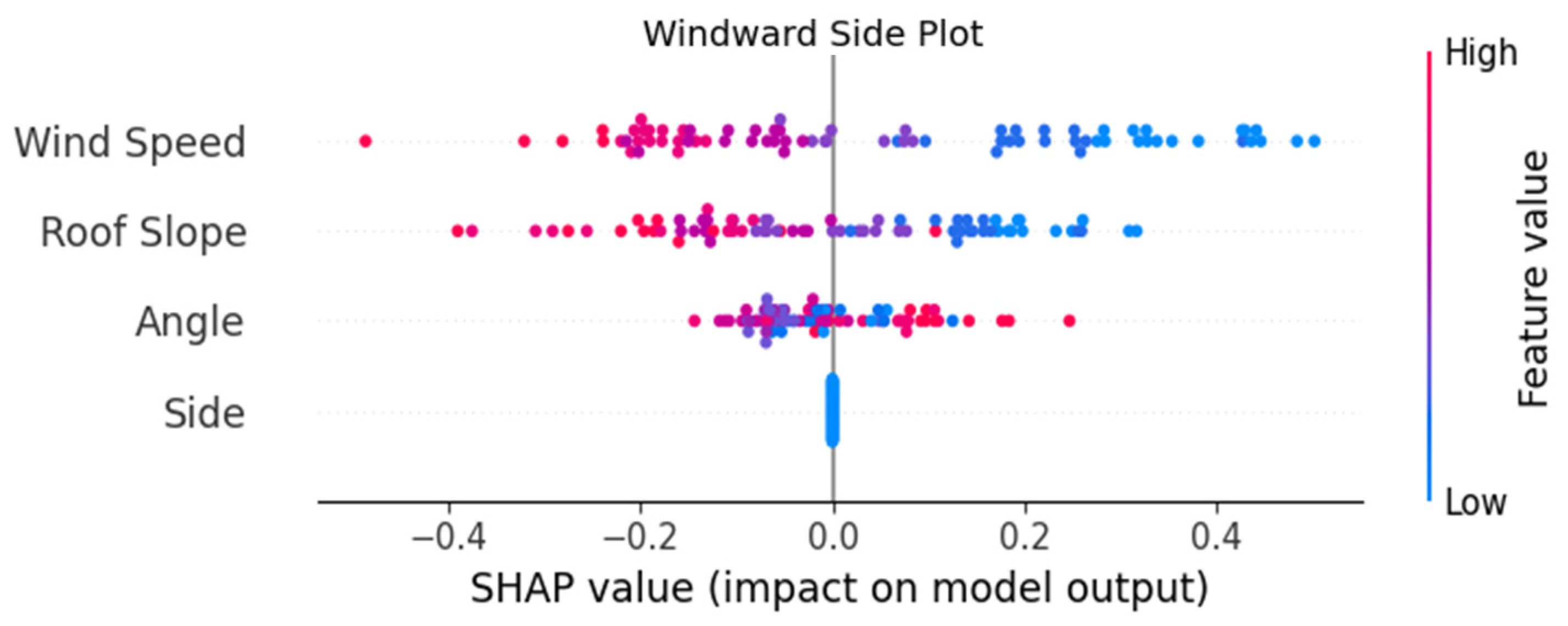
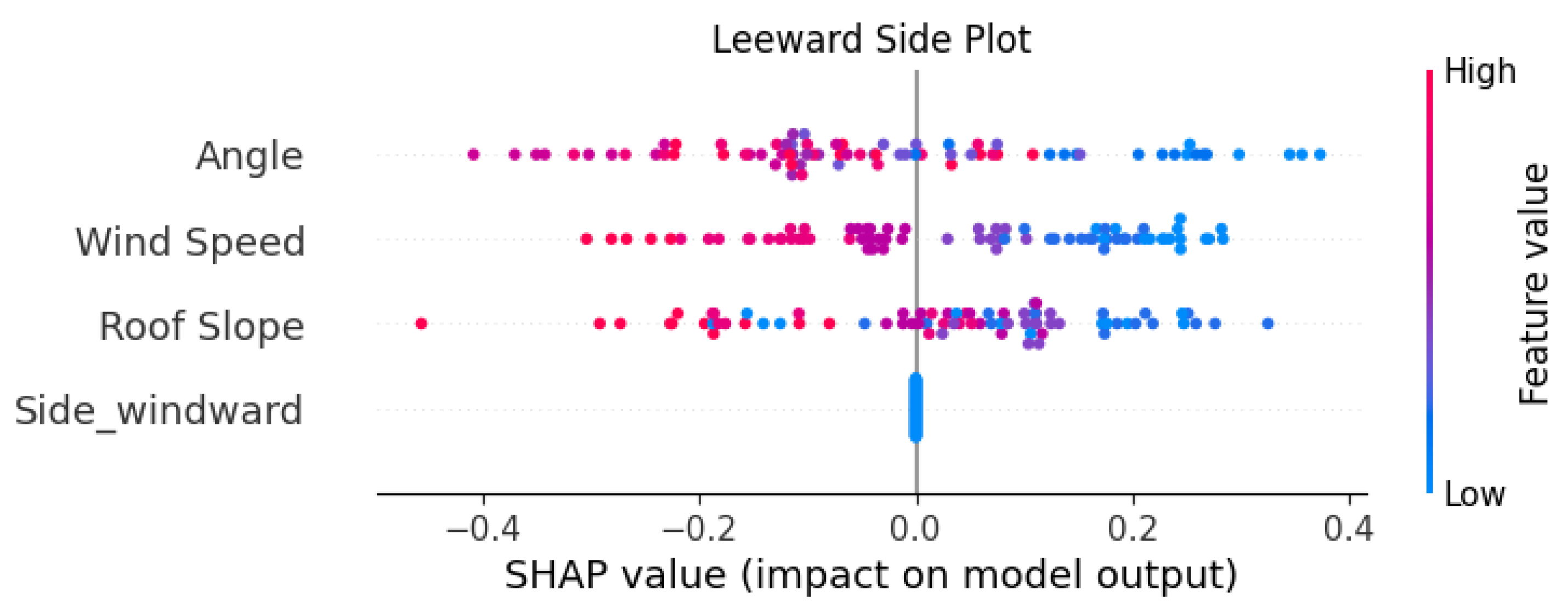
- There is a distinct difference between the behavior on the windward and leeward retention processes that was elucidated by the XAI data.
2. Experimental Methods
2.1. Experimental Conditions
2.2. Summary of Test Conditions
2.3. Image Analysis
2.4. Qualitative Result
3. Deep Learning (DL)
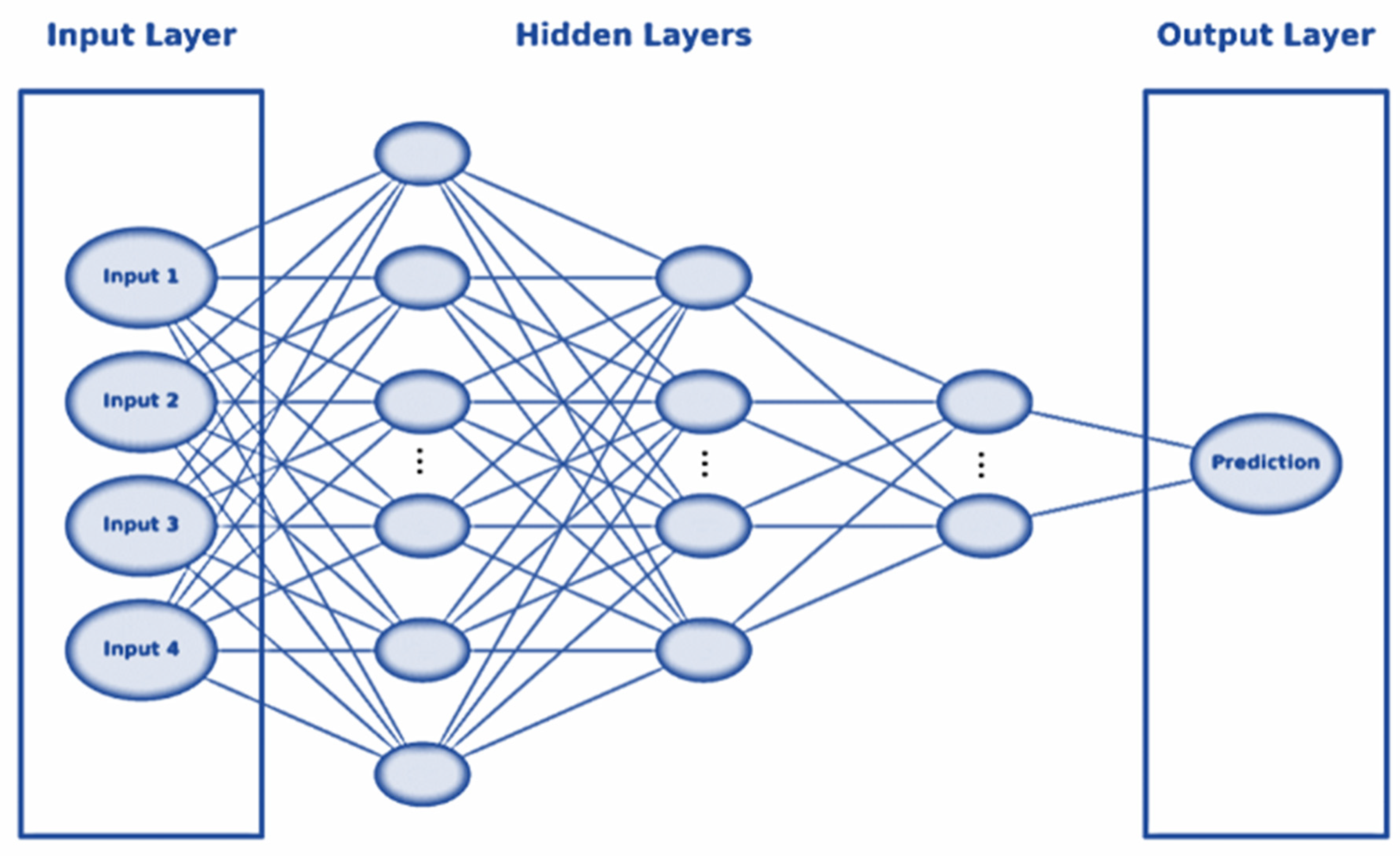
3.1. Deep Learning Model Description
- Using the complete ‘Full’ database of roof images, including leeward and windward sections;
- The database is segmented into two datasets based on the side feature;
- Lastly, the third segment of the windward dataset is selected for further examination.
3.2. Database Preprocessing
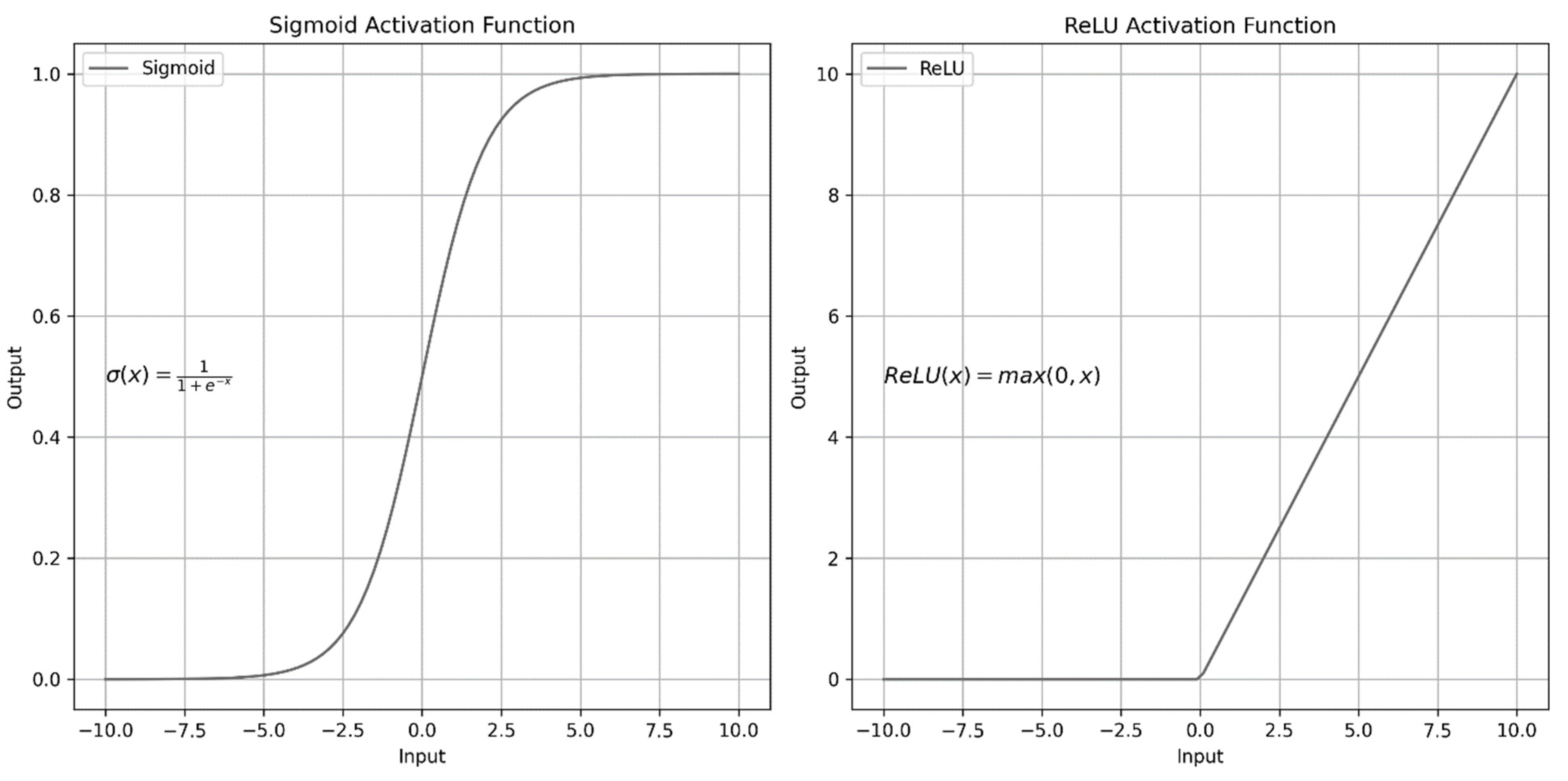
3.3. Model Architecture
3.4. Dataset Partitioning and Model Training and Evaluation
4. Results and Discussion
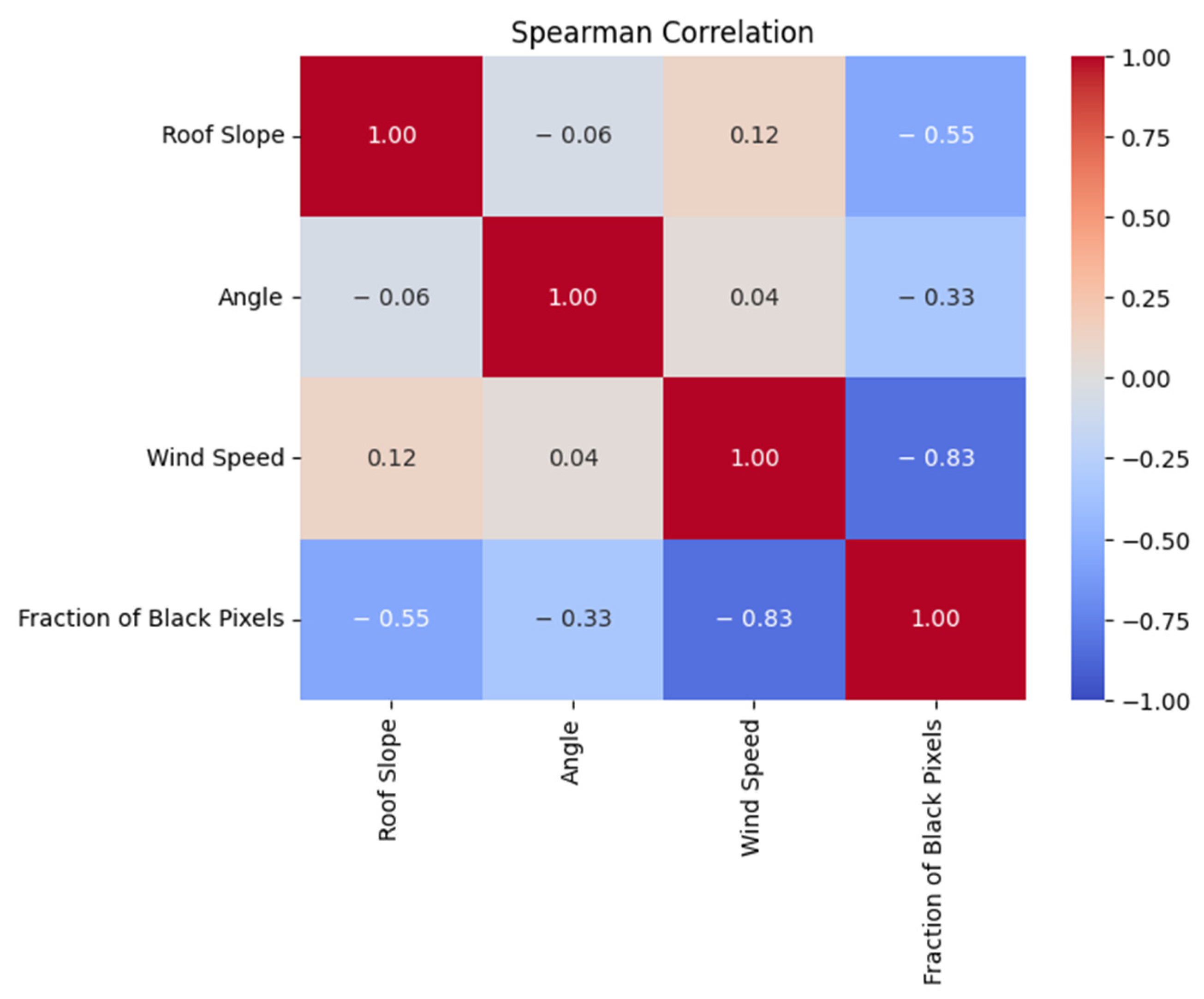
4.1. Correlations
4.2. Model Evaluation
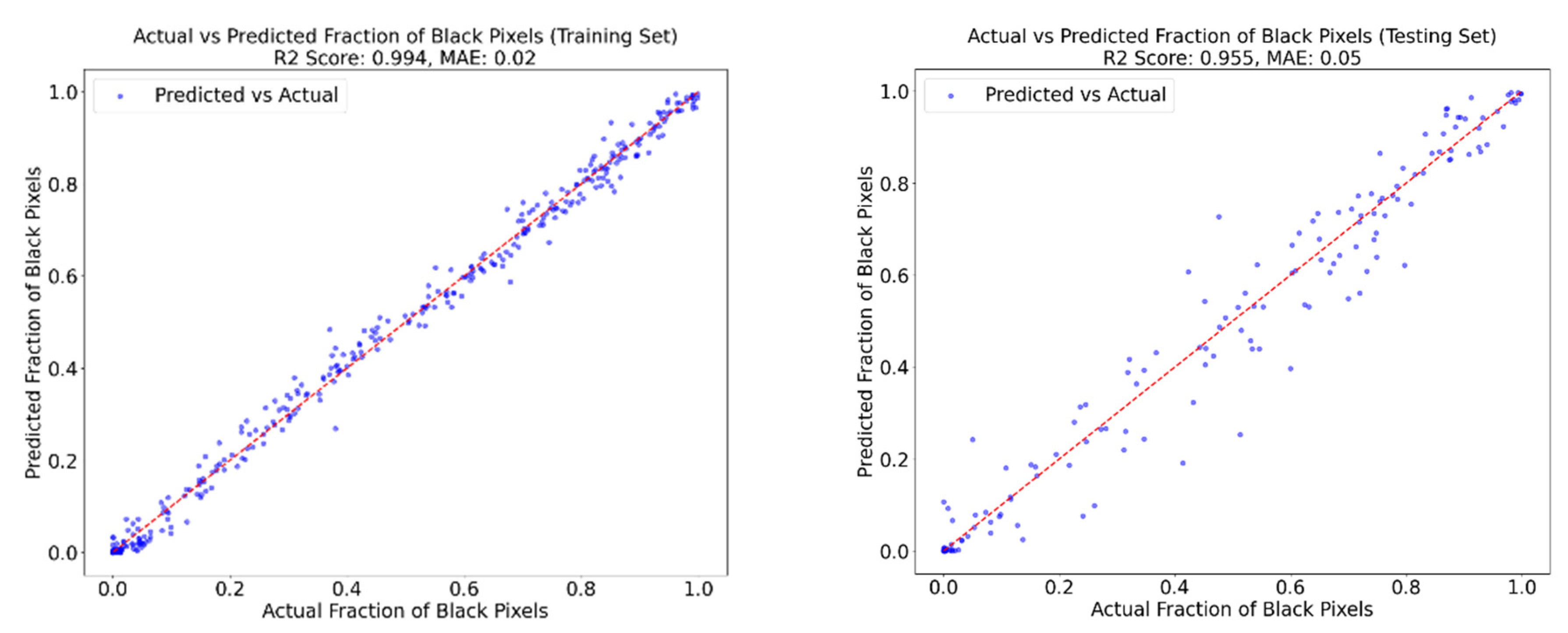
4.2.1. Full Database Model Performance
4.2.2. Leeward and Windward Datasets
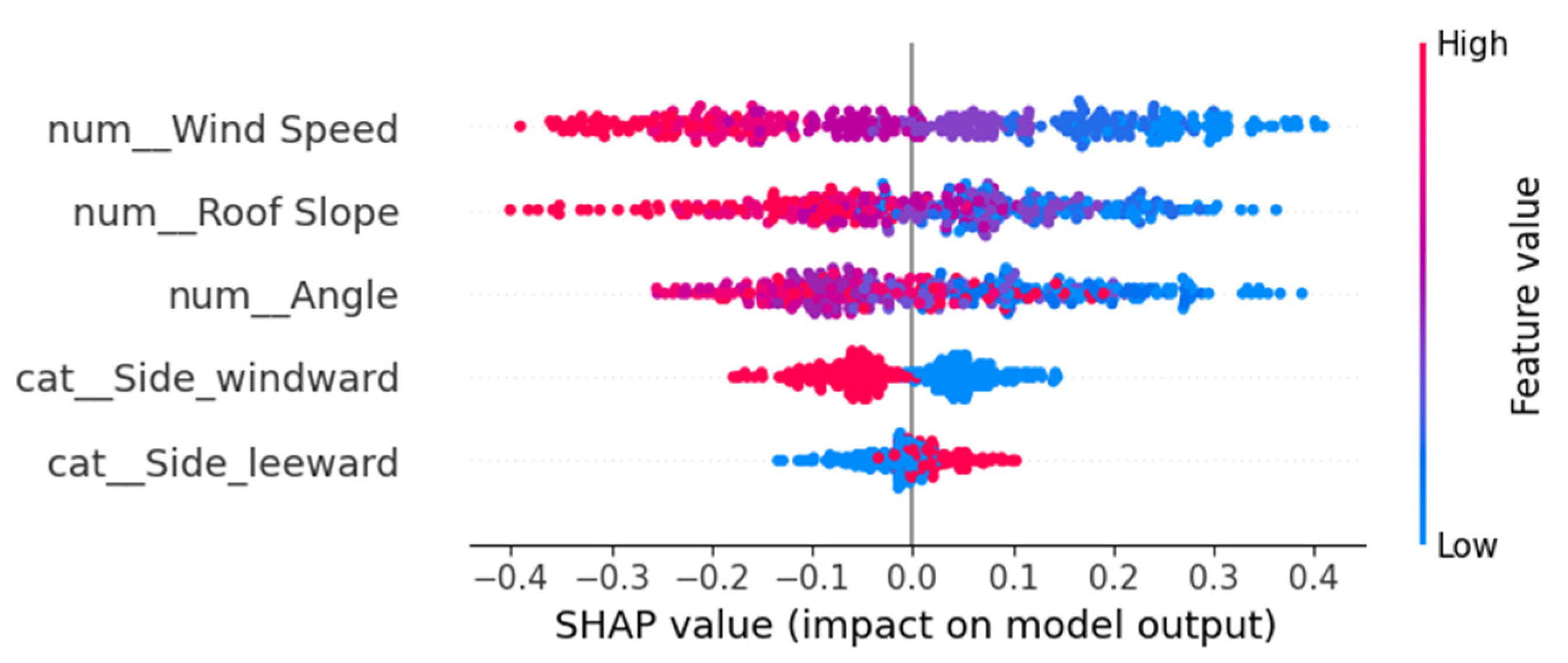
4.2.3. SHAP Explainability Tools
- This work is limited to rectangular floor plan buildings with sloped gable end roofs and does not account for complex roof shapes. This is due, in part, to the lack of experimental data for non-rectangular roof buildings. Once building shapes beyond rectangular are considered, there is a significant increase in the number of parameters. For example, simply adding a T-shaped building introduces internal and external roof corners. There are geometric features that have only one dimension (length) and so much more work would need to be done to assess the influence area of such features. This would require a much larger dataset of non-rectangular buildings than is currently unavailable;
- In general, complicating the roof types/shapes will increase the complexity of the DL model, which will dramatically increase the already significant computational resources required for training and testing;
- Although some explainability tools can be implemented in ANN to extract qualitative insights and verify domain knowledge, quantified interpretability remains a challenge. That is, the XAI data must still be interpreted with a domain expert to gain the full benefit of the analysis.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mckenzie, D.; Littell, J.S. Climate change and the eco-hydrology of fire: Will area burned increase in a warming western USA? Ecol. Appl. 2017, 27, 26–36. [Google Scholar] [CrossRef] [PubMed]
- Abatzoglou, J.T.; Kolden, C.A. Climate Change in Western US Deserts: Potential for Increased Wildfire and Invasive Annual Grasses. Rangel. Ecol. Manag. 2011, 64, 471–478. [Google Scholar] [CrossRef]
- Pinol, J.; Terradas, J.; Lloret, F. Climate warming, wildfire hazard, and wildfire occurrence in coastal eastern Spain. Clim. Change 1998, 38, 345–357. [Google Scholar] [CrossRef]
- Cal Fire. Top 20 Deadliest California Wildfires. Available online: https://www.fire.ca.gov/our-impact/statistics (accessed on 12 December 2023).
- National Museum of Australia, National Museum of Australia—Black Saturday Bushfires. Available online: https://www.nma.gov.au/defining-moments/resources/black-saturday-bushfires (accessed on 12 December 2023).
- Unprecedented season breaks all records. Bush Fire Bull. 2020, 42, 2–4. Available online: https://www.rfs.nsw.gov.au/__data/assets/pdf_file/0007/174823/Bush-Fire-Bulletin-Vol-42-No1.pdf (accessed on 12 December 2023).
- Mell, W.E.; Manzello, S.L.; Maranghides, A.; Butry, D.; Rehm, R.G. The wildland–urban interface fire problem—Current approaches and research needs. Int. J. Wildland Fire 2010, 19, 238–251. [Google Scholar] [CrossRef]
- Manzello, S.L.; Suzuki, S.; Gollner, M.J.; Fernandez-Pello, A.C. Role of firebrand combustion in large outdoor fire spread. Prog. Energy Combust. Sci. 2020, 76, 100801. [Google Scholar] [CrossRef] [PubMed]
- Koo, E.; Pagni, P.J.; Weise, D.R.; Woycheese, J.P. Firebrands and spotting ignition in large-scale fires. Int. J. Wildland Fire 2010, 19, 818–843. [Google Scholar] [CrossRef]
- Manzello, S.L.; Maranghides, A.; Mell, W.E. Firebrand generation from burning vegetation. Int. J. Wildland Fire 2007, 16, 458–462. [Google Scholar] [CrossRef]
- Mell, W.; Maranghides, A.; McDermott, R.; Manzello, S.L. Numerical simulation and experiments of burning Douglas fir trees. Combust. Flame 2009, 156, 2023–2041. [Google Scholar] [CrossRef]
- Sayaka, S.; Manzello, S.L. Firebrand production from building components fitted with siding treatments. Fire Saf. J. 2016, 80, 64–70. [Google Scholar]
- Manzello, S.L.; Suzuki, S. Generating wind-driven firebrand showers characteristic of burning structures. Proc. Combust. Inst. 2017, 36, 3247–3252. [Google Scholar] [CrossRef] [PubMed]
- Tohidi, A.; Kaye, N.B.; Bridges, W. Statistical description of firebrand size and shape distribution from coniferous trees for use in Metropolis Monte Carlo simulations of firebrand flight distance. Fire Saf. J. 2015, 77, 21–35. [Google Scholar] [CrossRef]
- Albini, F.A. Transport of firebrands by line thermals. Combust. Sci. Technol. 1983, 32, 277–288. [Google Scholar] [CrossRef]
- Anthenien, R.A.; Tse, S.D.; Fernandez-Pello, A.C. On the trajectories of embers initially elevated or lofted by small scale ground fire plumes in high winds. Fire Saf. J. 2006, 41, 349–363. [Google Scholar] [CrossRef]
- Bhutia, S.; Jenkins, M.A.; Sun, R. Comparison of firebrand propagation prediction by a plume model and a coupled-fire/atmosphere large-eddy simulator. J. Adv. Model. Earth Syst. 2010, 2, 4. [Google Scholar] [CrossRef]
- Tohidi, A.; Kaye, N.B. Stochastic modeling of firebrand shower scenarios. Fire Saf. J. 2017, 91, 91–102. [Google Scholar] [CrossRef]
- Tohidi, A.; Kaye, N.B. Comprehensive wind tunnel experiments of lofting and downwind transport of non-combusting rod-like model firebrands during firebrand shower scenarios. Fire Saf. J. 2017, 90, 95–111. [Google Scholar] [CrossRef]
- Wadhwani, R.; Sutherland, D.; Ooi, A.; Moinuddin, K. Firebrand transport from a novel firebrand generator: Numerical simulation of laboratory experiments. Int. J. Wildland Fire 2022, 31, 634–648. [Google Scholar] [CrossRef]
- Standohar-Alfano, C.D.; Estes, H.; Johnston, T.; Morrison, M.J.; Brown-Giammanco, T.M. Reducing Losses from Wind-Related Natural Perils: Research at the IBHS Research Center. Front. Built Environ. 2017, 3, 9. [Google Scholar] [CrossRef]
- Suzuki, S.; Manzello, S.L. Experimental investigation of firebrand accumulation zones in front of obstacles. Fire Saf. J. 2017, 94, 1–7. [Google Scholar] [CrossRef]
- Suzuki, S.; Johnsson, E.; Maranghides, A.; Manzello, S. Ignition of wood fencing assemblies exposed to continuous wind-driven firebrand showers. Fire Technol. 2016, 52, 1051–1067. [Google Scholar] [CrossRef]
- Manzello, S.; Suzuki, S.; Nii, D. Full-scale experimental investigation to quantify building component ignition vulnerability from mulch beds attacked by firebrand showers. Fire Technol. 2017, 53, 535–551. [Google Scholar] [CrossRef] [PubMed]
- Stephen, L.Q.; Christine, S.-A.; Faraz, H.; Daniel, J.G. Factors influencing ember accumulation near a building. Int. J. Wildland Fire 2023, 32, 80–387. [Google Scholar]
- Nguyen, D.; Kaye, N.B. Quantification of ember accumulation on the rooftops of isolated buildings in an ember storm. Fire Saf. J. 2022, 128, 103525. [Google Scholar] [CrossRef]
- Nguyen, D.; Kaye, N.B. The role of surrounding buildings on the accumulation of embers on rooftops during an ember storm. Fire Saf. J. 2022, 131, 103624. [Google Scholar] [CrossRef]
- Nguyen, D.; Kaye, N.B. Experimental investigation of rooftop hotspots during wildfire ember storms. Fire Saf. J. 2021, 125, 103445. [Google Scholar] [CrossRef]
- Jain, P.; Coogan, S.C.P.; Subramanian, S.G.; Crowley, M.; Taylor, S.; Flannigan, M.D. A review of machine learning applications in wildfire science and management. Environ. Rev. 2020, 28, 478–505. [Google Scholar] [CrossRef]
- Aikaterini-Eleni, L. Wildfire Prediction Using Machine Learning; University of West Attica Institutional Repository: Athens, Greece, 2022. [Google Scholar] [CrossRef]
- Storer, J.; Green, R. PSO Trained Neural Networks for predicting forest fire size: A comparison of implementation and performance. In Proceedings of the International Joint Conference on Neural Networks, Vancouver, Canada, 24–29 July 2016; pp. 676–683. [Google Scholar] [CrossRef]
- Lall, S.; Mathibela, B. The Application of Artificial Neural Networks for Wildfire Risk Prediction. In Proceedings of the International Conference on Robotics and Automation, Stockholm, Sweden, 16–21 May 2016; Available online: https://ieeexplore.ieee.org/abstract/document/7931880/ (accessed on 23 February 2024).
- Li, L.-M.; Song, W.-G.; Ma, J.; Satoh, K. Artificial neural network approach for modeling the impact of population density and weather parameters on forest fire risk. Int. J. Wildland Fire 2009, 18, 640–647. [Google Scholar] [CrossRef]
- Xiong, Y.; Wu, J.; Chen, Z. Machine Learning Wildfire Prediction Based on Climate Data. Available online: http://noiselab.ucsd.edu/ECE228-2020/projects/Report/75Report.pdf (accessed on 23 February 2024).
- Sakr, G.; Elhajj, I.; Mitri, G. Efficient forest fire occurrence prediction for developing countries using two weather parameters. Eng. Appl. Artif. Intell. 2011, 24, 888–894. [Google Scholar] [CrossRef]
- Vecín-Arias, D.; Castedo-Dorado, F.; Ordóñez, C.; Rodríguez-Pérez, J.R. Biophysical and lightning characteristics drive lightning-induced fire occurrence in the central plateau of the Iberian Peninsula. Agric. For. Meteorol. 2016, 225, 36–47. [Google Scholar] [CrossRef]
- Preeti, T.; Kanakaraddi, S.; Beelagi, A.; Malagi, S.; Sudi, A. Forest Fire Prediction Using Machine Learning Techniques. In Proceedings of the 2021 International Conference on Intelligent Technologies, CONIT 2021, Hubli, India, 25–27 June 2021. [Google Scholar] [CrossRef]
- Aldersley, A.; Murray, S.; Cornell, S. Global and regional analysis of climate and human drivers of wildfire. Sci. Total. Environ. 2011, 409, 3472–3481. [Google Scholar] [CrossRef] [PubMed]
- Cortez, P.; Morais, A. A Data Mining Approach to Predict Forest Fires Using Meteorological Data. 2007. Available online: https://repositorium.sdum.uminho.pt/handle/1822/8039 (accessed on 23 February 2024).
- Guo, F.; Zhang, L.; Jin, S.; Tigabu, M.; Su, Z.; Wang, W. Modeling Anthropogenic Fire Occurrence in the Boreal Forest of China Using Logistic Regression and Random Forests. Forests 2016, 7, 250. [Google Scholar] [CrossRef]
- Xie, Y.; Peng, M. Forest fire forecasting using ensemble learning approaches. Neural Comput. Appl. 2019, 31, 4541–4550. [Google Scholar] [CrossRef]
- Lundberg, S.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 4768–4777. [Google Scholar]
- American Society of Civil Engineers. Wind Tunnel Testing for Buildings and Other Structures: ASCE/SEI 49-12; American Society of Civil Engineers: Reston, VA, USA, 2012. [Google Scholar]
- Meroney, R.N.; Pavageau, M.; Rafailidis, S.; Schatzmann, M. Study of line source characteristics for 2-D physical modelling of pollutant dispersion in street canyons. J. Wind. Eng. Ind. Aerodyn. 1996, 62, 37–56. [Google Scholar] [CrossRef]
- Hoerner, S.F. Fluid-Dynamic Drag: Practical Information on Aerodynamic Drag and Hydrodynamic Resistance; Liselotte A. Hoerner: Bakersfield, CA, USA, 1965. [Google Scholar]
- Knudsen, J.G.; Katz, D.L. Fluid Dynamics and Heat Transfer; McGraw-Hill: New York, NY, USA, 1958. [Google Scholar]
- Holmes, H.D.; Baker, C.J.; Tamura, Y. Tachikawa number: A proposal. J. Wind. Eng. Ind. Aerodyn. 2006, 94, 41–47. [Google Scholar] [CrossRef]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Lau, M.M.; Lim, K.H. Review of Adaptive Activation Function in Deep Neural Network. In Proceedings of the 2018 IEEE-EMBS Conference on Biomedical Engineering and Sciences (IECBES), Sarawak, Malaysia, 3–6 December 2018; pp. 686–690. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2024, 15, 1929–1958. [Google Scholar]
- Pratiwi, H.; Windarto, A.P.; Susliansyah, S.; Aria, R.R.; Susilowati, S.; Rahayu, L.K.; Fitriani, Y.; Merdekawati, A.; Rahadjeng, I.R. Sigmoid Activation Function in Selecting the Best Model of Artificial Neural Networks. J. Phys. Conf. Ser. 2020, 1471, 012010. [Google Scholar] [CrossRef]
- Adam. Available online: https://keras.io/api/optimizers/adam/ (accessed on 25 February 2024).
- Sumera, S.; Sirisha, R.; Anjum, N.; Vaidehi, K. Implementation of CNN and ANN for Fashion-MNIST-Dataset using Different Optimizers. Indian J. Sci. Technol. 2022, 15, 2639–2645. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Pahlavani, P.; Raei, A.; Bigdeli, B.; Ghorbanzadeh, O. Identifying Influential Spatial Drivers of Forest Fires through Geographically and Temporally Weighted Regression Coupled with a Continuous Invasive Weed Optimization Algorithm. Fire 2024, 7, 33. [Google Scholar] [CrossRef]
- Labres dos Santos, J.F.; Kovalsyki, B.; Ferreira, T.d.S.; Batista, A.C.; Tetto, A.F. Adjustment of the Grass Fuel Moisture Code for Grasslands in Southern Brazil. Fire 2022, 5, 209. [Google Scholar] [CrossRef]
- Naser, M.Z.; Alavi, A.H. Error Metrics and Performance Fitness Indicators for Artificial Intelligence and Machine Learning in Engineering and Sciences. Archit. Struct. Constr. 2023, 3, 499–517. [Google Scholar] [CrossRef]
- Shapley, L.S. A Value for n-Person Games. In Contributions to the Theory of Games (AM-28); Princeton University Press: Princeton, NJ, USA, 2016; Volume II, pp. 307–318. [Google Scholar] [CrossRef]
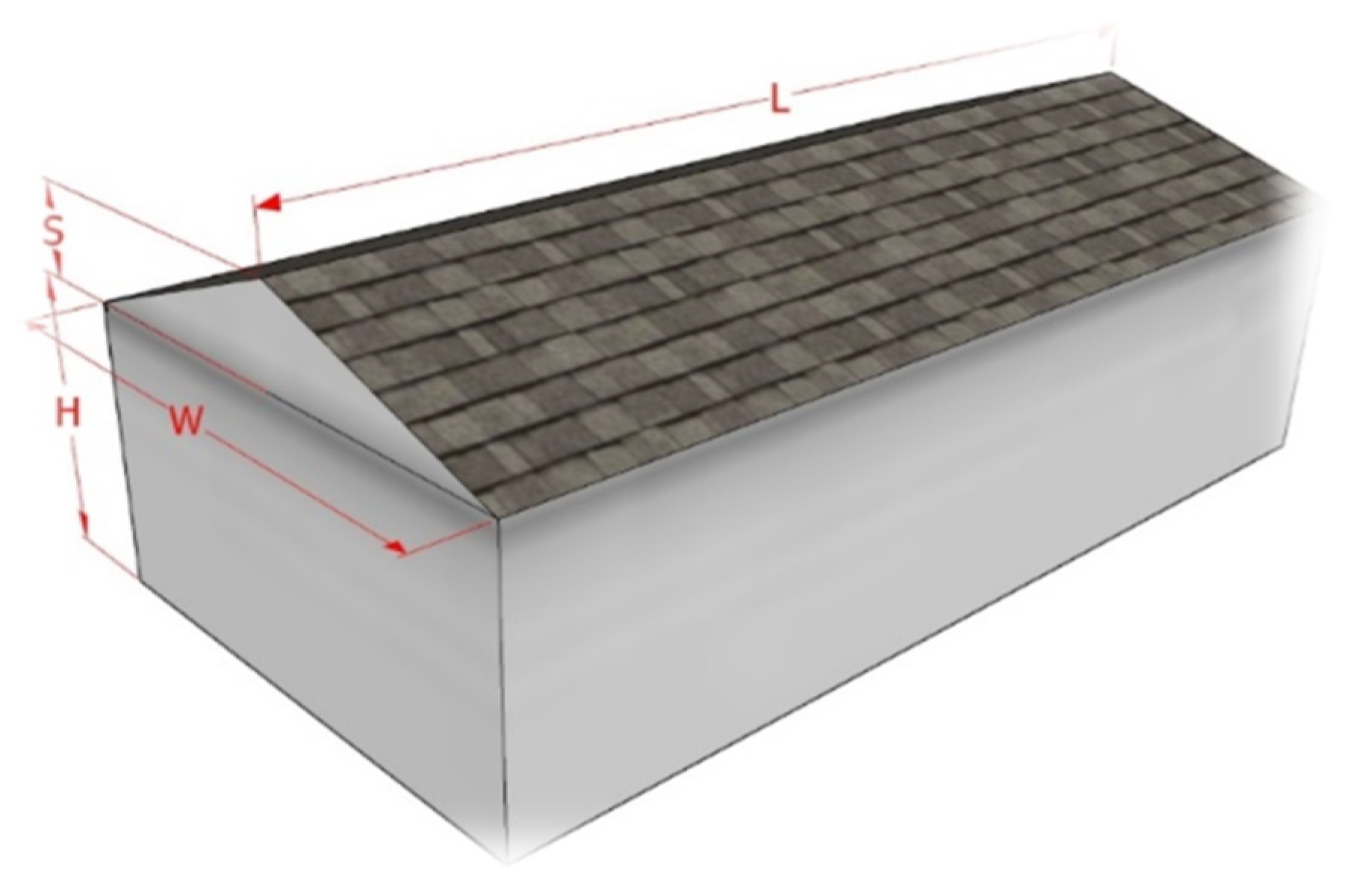


| House | cm | cm | cm | cm | Roof Pitch |
|---|---|---|---|---|---|
| A | 10.1 | 20.3 | 40.6 | 0 | 0/12 |
| B | 10.1 | 20.3 | 40.6 | 1.7 | 2/12 |
| C | 10.1 | 20.3 | 40.6 | 3.4 | 4/12 |
| D | 10.1 | 20.3 | 40.6 | 5.1 | 6/12 |
| E | 10.1 | 20.3 | 40.6 | 6.8 | 8/12 |
| F | 10.1 | 20.3 | 40.6 | 8.5 | 10/12 |
| Wind Angle (Degrees) | Wind Speed (m/s) |
|---|---|
| 0, 15, 30, 45, 60, 75, and 90 | 2.7, 3.1, 3.3, 3.5, 3.8, and 4.1 |
| Evaluation Metric | Full | Leeward | Windward | Full | Leeward | Windward |
|---|---|---|---|---|---|---|
| Training | Testing/Validation | |||||
| R2 | 98.8% | 99.2% | 99.2% | 95.5% | 93.4% | 87.7% |
| MAE | 0.025 | 0.023 | 0.02 | 0.050 | 0.056 | 0.077 |
| SHAP |
|---|
| : set of the selected features; s: the values of the input features in the set S. |S|!: the number of permutations of feature values that appear before i-th feature value. (|M| − |S| − 1)!: the number of permutations of feature values that appear after the i-th feature value. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Bashiti, M.K.; Nguyen, D.; Naser, M.Z.; Kaye, N.B. Predicting Wildfire Ember Hot-Spots on Gable Roofs via Deep Learning. Fire 2024, 7, 153. https://doi.org/10.3390/fire7050153
Al-Bashiti MK, Nguyen D, Naser MZ, Kaye NB. Predicting Wildfire Ember Hot-Spots on Gable Roofs via Deep Learning. Fire. 2024; 7(5):153. https://doi.org/10.3390/fire7050153
Chicago/Turabian StyleAl-Bashiti, Mohammad Khaled, Dac Nguyen, M. Z. Naser, and Nigel B. Kaye. 2024. "Predicting Wildfire Ember Hot-Spots on Gable Roofs via Deep Learning" Fire 7, no. 5: 153. https://doi.org/10.3390/fire7050153
APA StyleAl-Bashiti, M. K., Nguyen, D., Naser, M. Z., & Kaye, N. B. (2024). Predicting Wildfire Ember Hot-Spots on Gable Roofs via Deep Learning. Fire, 7(5), 153. https://doi.org/10.3390/fire7050153






