Temperature Evolution inside Hollow Core Wood Elements and Fire Resistance
Abstract
1. Introduction
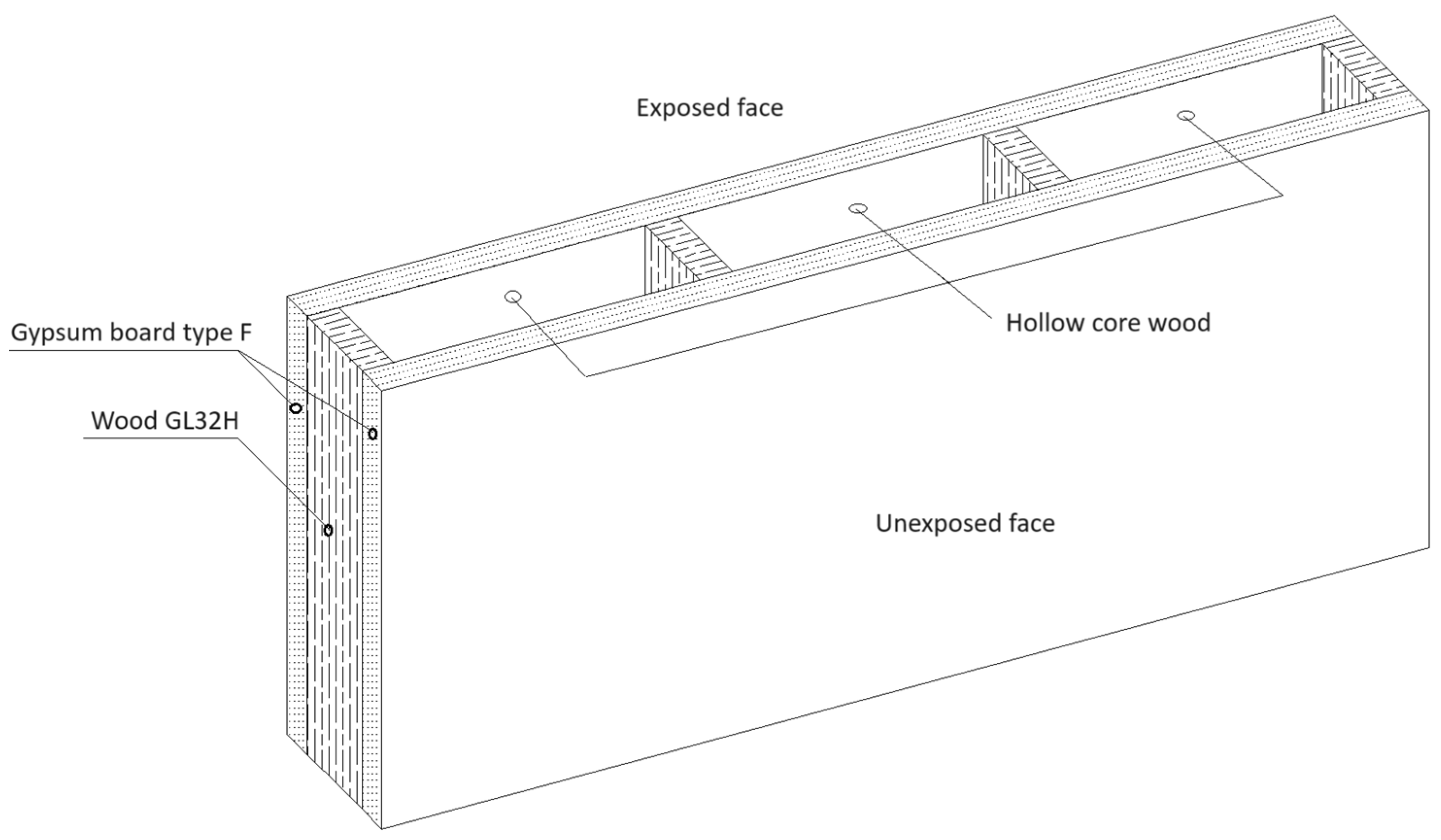
2. Model Description
3. Thermal and Numerical Model
- -
- Radiation and convection on the surface exposed to fire, with the effect of increasing temperature through the standard fire curve ISO 834 [16];
- -
- Only convection on the unexposed face;
- -
- Adiabatic conditions at the lateral edges;
- -
- The initial condition of the model corresponds to an ambient temperature of 20 °C.
4. Results and Discussion of the Studied Hollow Core Wood Elements
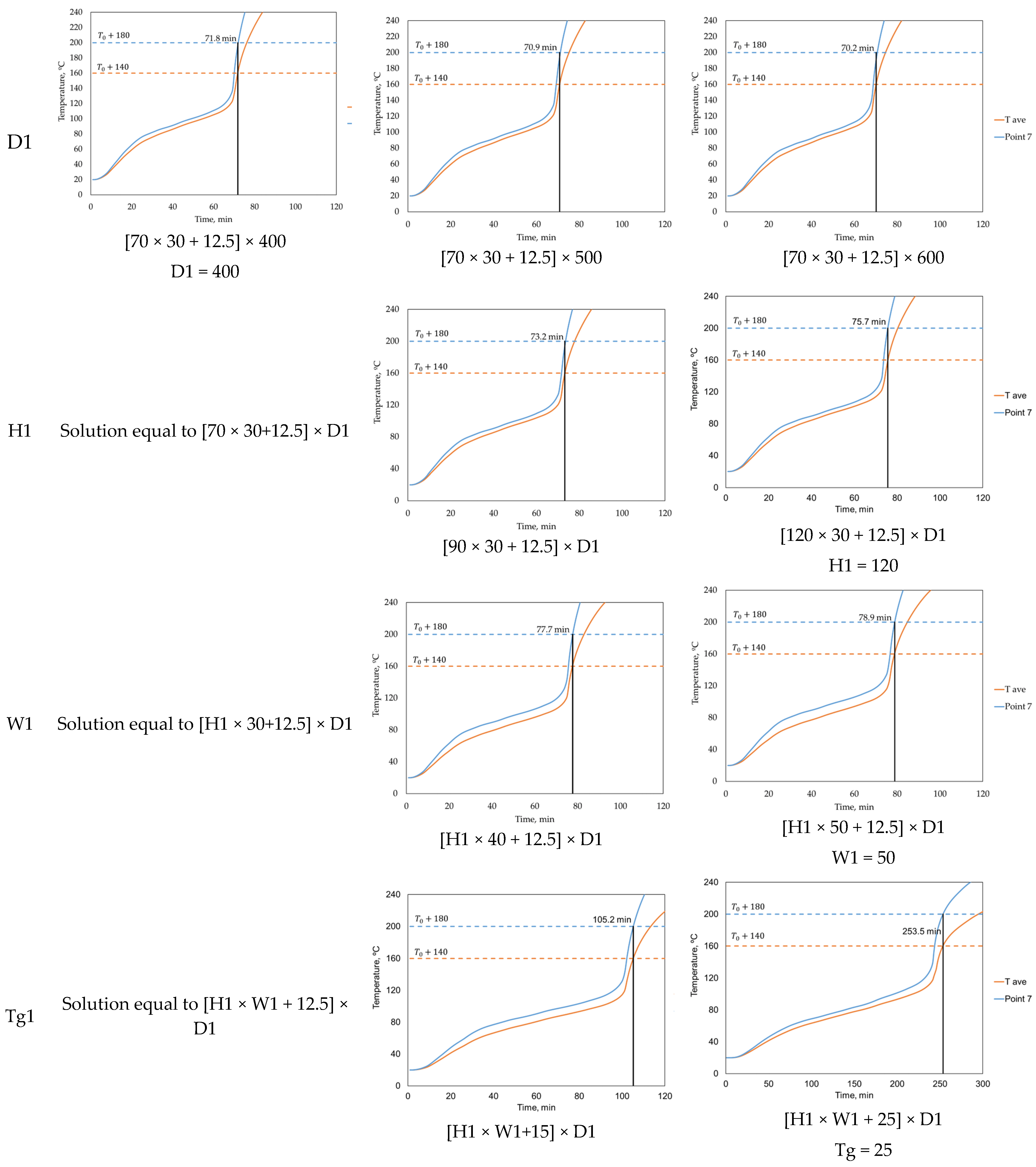
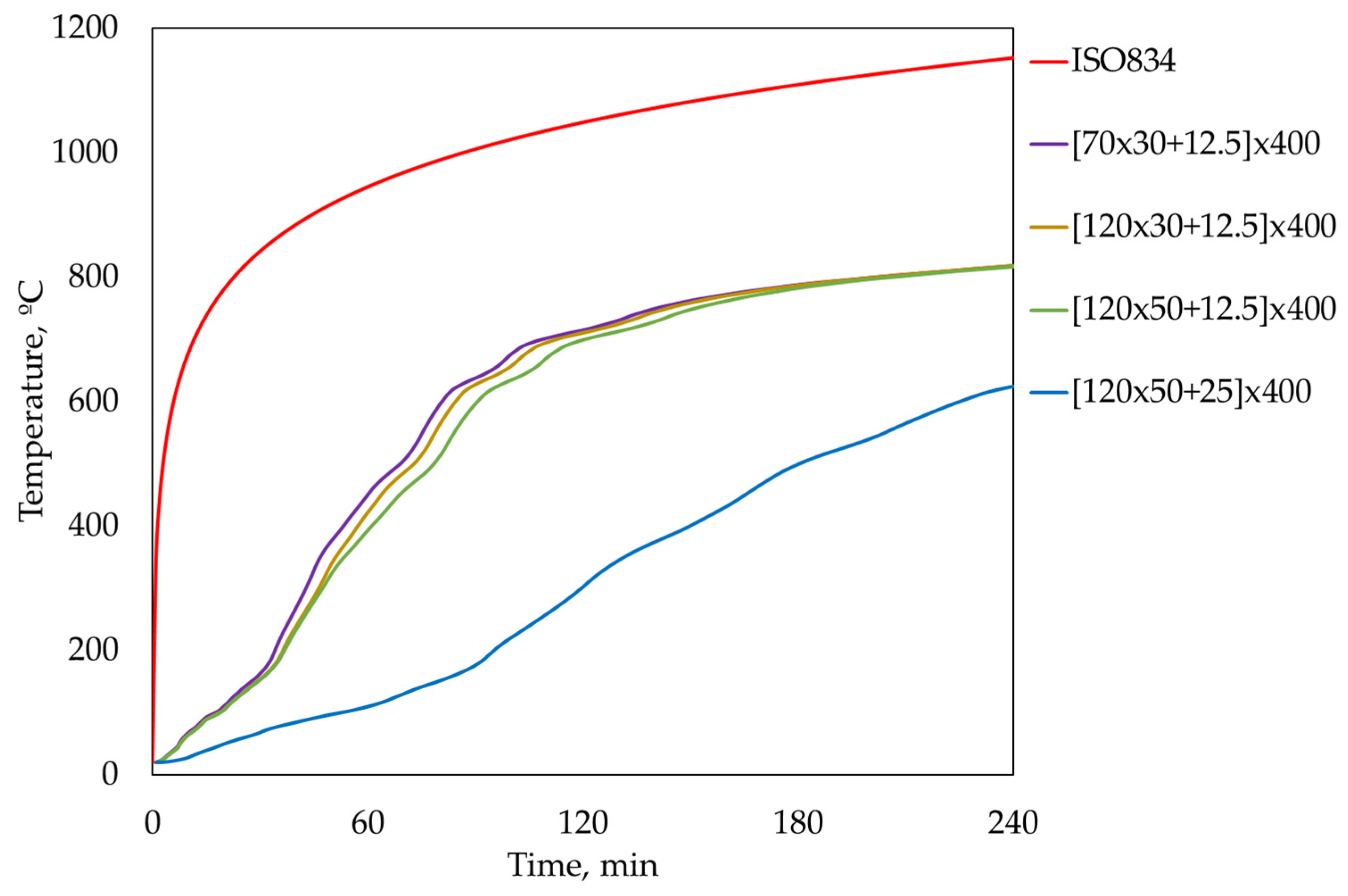
4.1. Fire Resistance: Thermal Insulation Criterion
4.2. Temperature Evolution Inside the Hollow Core Element
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Barber, D.; Gerard, R. Summary of the fire protection foundation report—Fire safety challenges of tall wood buildings. Fire Sci. Rev. 2005, 4, 5. [Google Scholar] [CrossRef]
- Voth, C.; White, N.; Yadama, V.; Cofer, W. Design and Evaluation of Thin-Walled Hollow-Core Wood-Strand Sandwich Panels. J. Renew. Mater. 2015, 3, 234–243. [Google Scholar] [CrossRef]
- Wisconsin Enrolled Commercial Building Code; Fire-Resistance-Rated Construction; Department of Safety and Professional Services: Madison, WI, USA, 2002; B-75:178.
- Žajdlík, T.; Šuhajda, K.; Průša, D. Medium-Scale Fire Resistance Testing of Timber Structures with Composite Cement Fibre Materials. Buildings 2023, 13, 527. [Google Scholar] [CrossRef]
- CEN. EN 1363-1; Fire Resistance Tests Part 1: General Requirements. CEN: Brussels, Belgium, 2020.
- CEN. EN 1364-1; Fire Resistance Tests for Non-Loadbearing Elements. Part 1: Walls. CEN: Brussels, Belgium, 2015.
- ANSYS, Inc. ANSYS Mechanical APD 2022 R2; Release 2; ANSYS, Inc.: Southpointe, PA, USA, 2022. [Google Scholar]
- Pereira, D. Análise Computacional para a Avaliação da Resistência ao fogo em Elementos Construtivos de Suporte em aglomerado de Madeira com Proteção. Master’s Thesis, ISEP, IPP, Porto, Portugal, 2023. [Google Scholar]
- Fonseca, E.M.M.; Gomes, C. FEM Analysis of 3D Timber Connections Subjected to Fire: The Effect of Using Different Densities of Wood Combined with Steel. Fire 2023, 6, 193. [Google Scholar] [CrossRef]
- Piloto, P.A.G.; Fonseca, E.M.M. Timber framed walls lined with gypsum plates under fire. In Proceedings of the IRF2020: 7th International Conference Integrity-Reliability-Failure, INEGI-FEUP, Funchal, Portugal, 6–10 September 2020; Gomes, J.F.S., Meguid, S.A., Eds.; pp. 547–556. [Google Scholar]
- Takeda, H.; Mehaffey, J.R. WALL2D: A Model for Predicting Heat Transfer through Wood-Stud Walls Exposed to Fire. Fire Mater. 1998, 22, 133–140. [Google Scholar] [CrossRef]
- Yang, T.-H.; Wang, S.-Y.; Tsai, M.-J.; Lin, C.-Y. The charring depth and charring rate of glued laminated timber after a standard fire exposure test. Build. Environ. 2009, 44, 231–236. [Google Scholar] [CrossRef]
- CEN. EN1995-1-2; Eurocode 5: Design of Timber Structures. Part 1–2: General Structural Fire Design. BSI: Brussels, Belgium, 2004.
- Frangi, A.; Schleifer, V.; Fontana, M.; Hugi, E. Experimental and Numerical Analysis of Gypsum Plasterboards in Fire. Fire Technol. 2010, 46, 149–167. [Google Scholar] [CrossRef]
- CEN. EN1991-1-2; Eurocode 1: Actions on Structures. Part 1–2: Structural Fire Design. BSI: Brussels, Belgium, 2010.
- ISO 834-1; Fire Resistance Tests-Elements of Building Construction—Part 1: General Requirement. International Organization for Standardization: Geneva, Switzerland, 1999. Available online: https://www.iso.org/standard/2576.html (accessed on 20 November 2023).
- C04 Partitions, Non-Loadbearing Timber Stud. Traditional Stud Partitions. White Book S11, 275–286, Ireland. Available online: https://www.gyproc.ie/sites/default/files/Non-loadbearing%20timber%20stud.pdf (accessed on 20 November 2023).
- Pang, S.J.; Ahn, K.S.; Oh, J.W.; Lee, H.S.; Kang, S.G.; Oh, J.K. Fire Resistance of Structural Wooden Walls Covered by Gypsum and Diatomite Board. BioResouces 2023, 18, 991–1007. [Google Scholar] [CrossRef]



| Temperature, °C | Density, kg/m3 | Temperature, °C | Specific Heat, kJ/KgK | Temperature, °C | Thermal Conductivity, W/mK |
|---|---|---|---|---|---|
| 20 | 889.00 | 20 | 0.95 | 20 | 0.190 |
| 100 | 889.00 | 100 | 0.95 | 195 | 0.190 |
| 170 | 737.87 | 135 | 25.00 | 155 | 0.100 |
| 600 | 737.87 | 170 | 0.95 | 200 | 0.103 |
| 750 | 700.98 | 650 | 0.95 | 400 | 0.113 |
| 1200 | 700.98 | 675 | 10.00 | 600 | 0.127 |
| 700 | 0.95 | 800 | 0.145 | ||
| 1200 | 0.95 | 1200 | 0.165 |
| Temperature, °C | Density, kg/m3 | Temperature, °C | Specific Heat, kJ/KgK | Temperature, °C | Thermal Conductivity, W/mK |
|---|---|---|---|---|---|
| 20 | (1 + w) * 537.6 | 20 | 1.53 | 20 | 0.12 |
| 99 | (1 + w) * 537.6 | 99 | 1.77 | 200 | 0.15 |
| 120 | (1.0) * 480.0 | 100 | 13.60 | 350 | 0.07 |
| 200 | (1.0) * 480.0 | 120 | 13.50 | 500 | 0.09 |
| 250 | (0.93) * 446.4 | 121 | 2.12 | 800 | 0.35 |
| 300 | (0.76) * 364.8 | 200 | 2.00 | 1200 | 1.50 |
| 350 | (0.52) * 249.6 | 250 | 1.62 | ||
| 400 | (0.38) * 182.4 | 300 | 0.71 | ||
| 600 | (0.28) * 134.4 | 350 | 0.85 | ||
| 800 | (0.26) * 124.8 | 400 | 1.00 | ||
| 1200 | (0) * 0 | 600 | 1.40 | ||
| * Density ratio | 800 | 1.65 | |||
| w moisture content | 1200 | 1.65 | |||
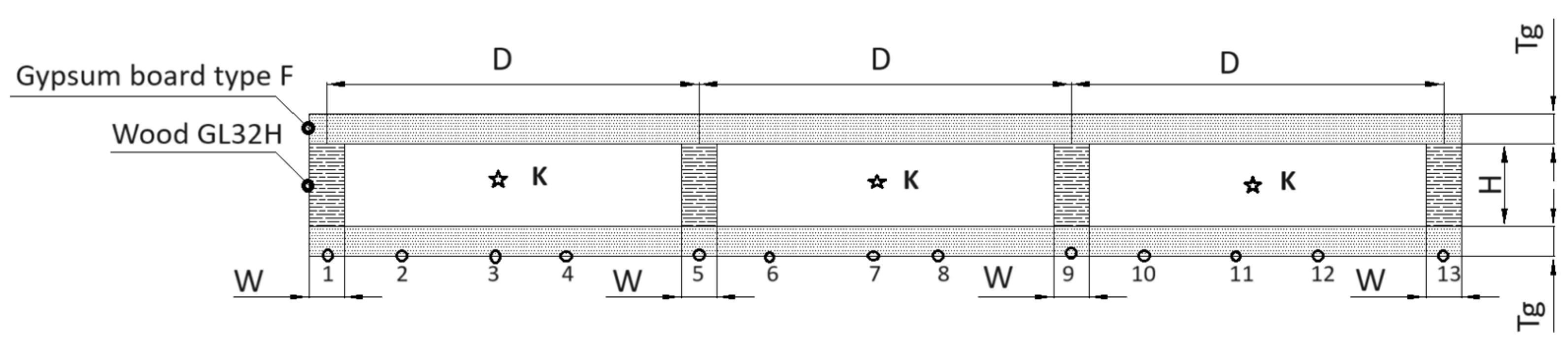
| Geometric Parameters in the Study | Dimension [H × W + Tg] × D | ||
|---|---|---|---|
| D1 | [70 × 30 + 12.5] × 400 | [70 × 30 + 12.5] × 500 | [70 × 30 + 12.5] × 600 |
| H1 | [70 × 30 + 12.5] × D1 | [90 × 30 + 12.5] × D1 | [120 × 30 + 12.5] × D1 |
| W1 | [H1 × 30 + 12.5] × D1 | [H1 × 40 + 12.5] × D1 | [H1 × 50 + 12.5] × D1 |
| Tg1 | [H1 × W1 + 12.5] × D1 | [H1 × W1 + 15] × D1 | [H1 × W1 + 25] × D1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pereira, D.; Fonseca, E.M.M.; Osório, M. Temperature Evolution inside Hollow Core Wood Elements and Fire Resistance. Fire 2024, 7, 57. https://doi.org/10.3390/fire7020057
Pereira D, Fonseca EMM, Osório M. Temperature Evolution inside Hollow Core Wood Elements and Fire Resistance. Fire. 2024; 7(2):57. https://doi.org/10.3390/fire7020057
Chicago/Turabian StylePereira, Domingos, Elza M. M. Fonseca, and Miguel Osório. 2024. "Temperature Evolution inside Hollow Core Wood Elements and Fire Resistance" Fire 7, no. 2: 57. https://doi.org/10.3390/fire7020057
APA StylePereira, D., Fonseca, E. M. M., & Osório, M. (2024). Temperature Evolution inside Hollow Core Wood Elements and Fire Resistance. Fire, 7(2), 57. https://doi.org/10.3390/fire7020057







