Next Article in Journal
Application End Evaluation of Electrostatic Precipitation for Control PM and NOx Emissions from Small-Scale Combustions
Previous Article in Journal
Advances in Detection and Monitoring of Coal Spontaneous Combustion: Techniques, Challenges, and Future Directions
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Fire
Volume 7
Issue 10
10.3390/fire7100355
fire-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Active Fire Clustering and Spatiotemporal Dynamic Models for Forest Fire Management

by
Hatef Dastour
1,†,
Hanif Bhuian
1,†,
M. Razu Ahmed
2 and
Quazi K. Hassan
1,*
1
Department of Geomatics Engineering, University of Calgary, Calgary, AB T2N 1N4, Canada
2
Western Arctic Centre for Geomatics, Government of Northwest Territories, Inuvik, NT X0E 0T0, Canada
*
Author to whom correspondence should be addressed.
†
These authors contributed equally to this work.
Fire 2024, 7(10), 355; https://doi.org/10.3390/fire7100355
Submission received: 14 September 2024 / Revised: 1 October 2024 / Accepted: 4 October 2024 / Published: 6 October 2024
(This article belongs to the Topic Application of Remote Sensing in Forest Fire)
Browse Figures
Versions Notes

Abstract

:
Forest fires are increasingly destructive, contributing to significant ecological damage, carbon emissions, and economic losses. Monitoring these fires promptly and accurately, particularly by delineating fire perimeters, is critical for mitigating their impact. Satellite-based remote sensing, especially using active fire products from VIIRS and MODIS, has proven indispensable for real-time forest fire monitoring. Despite advancements, challenges remain in accurately clustering and delineating fire perimeters in a timely manner, as many existing methods rely on manual processing, resulting in delays. Active fire perimeter (AFP) and Timely Active Fire Progression (TAFP) models were developed which aim to be an automated approach for clustering active fire data points and delineating perimeters. The results demonstrated that the combined dataset achieved the highest matching rate of 85.13% for fire perimeters across all size classes, with a 95.95% clustering accuracy for fires ≥100 ha. However, the accuracy decreased for smaller fires. Overall, 1500 m radii with alpha values of 0.1 were found to be the most effective for fire perimeter delineation, particularly when applied at larger radii. The proposed models can play a critical role in improving operational responses by fire management agencies, helping to mitigate the destructive impact of forest fires more effectively.

1. Introduction

Forest fires globally inflict catastrophic damage on the Earth’s surface, significantly affecting ecosystems, human life, and property [1,2]. The frequency and intensity of forest fires have markedly increased from the past to the present [3,4]. Recent data indicate that forest fires now cause an average of three million more hectares of tree cover loss annually compared to 2001 [5], contributing to an average of over 420 million hectares of forest damage worldwide between 1990 and 2020 [6]. Although forests cover 31% of the Earth’s land area, they are increasingly vulnerable, with 36% of forested land impacted by wildfires globally [7]. Climate change, particularly global warming, along with anthropogenic activities, are major contributors to this alarming increase [8,9], while only a small proportion of fires are naturally caused [10]. The consequences are severe, resulting in irreversible environmental damage, the release of 30% of global carbon dioxide emissions [11,12], and significant economic losses estimated at USD 2.4 billion [13]. Moreover, the smoke and air pollution from these forest fires have resulted in tragic human casualties, contributing to over 33,000 deaths annually in 749 cities across 43 countries [14].
In 2023, the Canadian Interagency Forest Fire Centre (CIFFC) reported a record-breaking year, with around 17.2 million hectares of forest impacted by 7131 fire incidents, exceeding the previous record set in 1989 [15]. As of 22 July 2024, Alberta has experienced 932 fires, resulting in 522,545 ha burned, while the Northwest Territories (NT) recorded 143 fires, burning 199,258 ha [16]. Given the severity and scale of the damage, it is crucial to monitor and measure forest fire spots and extents, including fire perimeters, accurately and promptly [17,18]. A significant challenge remains the availability of official data, such as high-accuracy fire perimeter polygons [19,20,21]. Typically, these data are released to the public by the government only at the end of the year or shortly before the next fire season [22]. This delay could hinder early preparedness and mitigation efforts [23]. Therefore, there is a critical need for further research into the timely assessment of active forest fire perimeters. Developing improved methods or new models for evaluating these perimeters could significantly enhance fire management strategies, thereby reducing the risks and impact of forest fires [23,24,25].
Satellite-based remote sensing has transformed forest fire monitoring, providing unparalleled capabilities ranging from coarse to high spatial resolution, coupled with rapid temporal frequency [26,27,28,29,30]. However, integrating and interpreting these diverse data sources remains challenging, especially in real-time fire management scenarios. Active fire or thermal anomaly products have become essential tools for rapid response, resource allocation, and evacuation during forest fires [28,31,32]. While these products are operationally crucial for fire management and firefighting agencies [33,34], their effectiveness in mitigating fire impacts varies significantly due to factors such as data latency, spatial resolution, and local environmental conditions. The Visible Infrared Imaging Radiometer Suite (VIIRS) [35] and Moderate Resolution Imaging Spectroradiometer (MODIS) satellites [36,37,38] have significantly reduced data latency while offering comprehensive global and regional coverage. However, the cause–effect relationship between improved data availability and enhanced fire management outcomes remains understudied, particularly in the United States and Canada [34]. VIIRS, equipped with three instruments (SNPP, NOAA-20, and NOAA-21), offers a spatial resolution of 375 m and twice-daily observations [39]. MODIS satellites (Aqua and Terra) provide 1 km resolution with four daily observations [40,41,42]. While the combined capabilities of these systems enable at least ten daily observations for active fire detection, the challenge remains in optimally integrating these diverse data streams to support real-time decision-making. The classification of fire detection products into ultra real-time (URT), real-time (RT), and near real-time (NRT) based on data latency presents both advantages and challenges [43]. URT products, available within 60 s of satellite observation, offer unparalleled immediacy but may compromise accuracy [34]. RT data, delivered within 20–60 min for the U.S. and Canada, and NRT data, available globally within 3 h, strike a balance between timeliness and reliability [43]. However, the trade-offs between these product types across various fire management scenarios remain largely unexplored. This study aims to address these gaps by developing new approaches to integrate and analyze multi-source satellite data for enhanced fire detection and management.
Given the constraints of data availability and latency, advancing research in early fire monitoring and automatic fire perimeter delineation is crucial. Current research reveals significant gaps, particularly in the accuracy and methodologies used for delineating forest fire perimeters. Most studies have focused on evaluating individual algorithms [22,24,44,45,46,47,48], with a few conducting comparative analyses of multiple algorithms [19]. Typically, these studies have employed either the buffer [45,47,48] or convex hull [22,44,46] algorithms, with only one study exploring the α-shape concave hull algorithm [49].
Few studies have utilized both MODIS and VIIRS [22,24,44] or combined MODIS, VIIRS, and AVHRR [45] active fire data to delineate forest fire perimeters, with some using either MODIS [47] or VIIRS [46,48,49] data points exclusively. Notably, only one study has applied both MODIS and VIIRS active fire data points, assessing individual and combined approaches to evaluate existing algorithms, including buffer (round and square shapes), convex hull, and α-shape concave hull [19]. This study found the α-shape concave hull algorithm to be the most effective, followed by the round buffer algorithm. However, Bhuian et al. [19] manually clustered individual fire data points before generating perimeters, which increased analysis latency. For operational use, particularly in real-time forest fire monitoring and accurate perimeter delineation, minimizing data processing and analysis latency is essential. This underscores the need for automated approaches that integrate both clustering and perimeter delineation.
To mitigate analytical latency, it is essential to develop automated models for clustering individual fires and delineating fire perimeters [22]. Clustering methods can be broadly categorized into partitioning, hierarchical, density-based, and model-based approaches [50,51]. Commonly used algorithms include K-means clustering [52], Gaussian mixture models [53], Density-Based Spatial Clustering of Applications with Noise (DBSCAN) [54], Ball-tree [55], and aggregated data points [22]. Among these, two studies applied Ball-tree [49] and aggregated data points [22] for fire perimeter delineation, while a significant number of studies have successfully employed DBSCAN in fire ecology. For example, Artés et al. [56] used DBSCAN to cluster hotspot data, Kristianto et al. [57] and Sheng et al. [58] used it to recognize fire stages based on flame and smoke, Vatresia et al. [59] clustered hotspot data, and Usman et al. [60] analyzed the distribution patterns of hotspot data. However, the objectives and study regions of these works differ significantly from the current research focus.
DBSCAN is specifically designed for identifying clusters and detecting noise (outliers) in spatial databases [54]. It identifies core points—those with a high density of neighboring points within a given radius—and forms clusters around them [61]. Points that do not meet this density criterion are classified as noise. DBSCAN links core points and their surrounding neighbors to form dense clusters. Unlike other clustering algorithms, DBSCAN does not require the pre-definition of the number of clusters [51,62,63] and can accommodate clusters of various shapes and sizes [51]. This flexibility makes DBSCAN highly effective for large datasets, such as active fire data points, offering advantages over other clustering algorithms [63].
The goal of this study is to develop the Timely Active Fire Progression (TAFP) model for rapid and accurate forest fire monitoring and perimeter delineation through automated approaches. Additionally, the study evaluates the performance of active fire clustering and perimeter delineation models. To the best of our knowledge, this research builds on the work of Bhuian et al. [19] and represents the first application of the TAFP model for clustering active fire data points and consistently delineating fire perimeters in an automated manner. For operational purposes, this model is critical for forest fire management authorities, including fire agencies and firefighters.

2. Study Area and Data Requirements

2.1. Study Region

The study area covers a significant portion of Alberta (AB), particularly focusing on the northern region, the southern part of the Northwest Territories (NT), and small sections of both northeastern British Columbia (BC) and northwestern Saskatchewan (SK) (Figure 1) which are predominantly forested and feature a wide range of climatic conditions. This study selected 30 forest fires between the years 2015 and 2021, ranging in size from small to large (>200 ha). Many of these fires were located in Alberta, with fewer in the NT, while some larger fires extended across provincial boundaries into the NT, BC, and SK (see Figure 1).
Alberta’s diverse landscape encompasses a variety of climatic zones and vegetation types, reflecting the province’s complex geography. It is divided into six natural regions: Boreal Forest, Canadian Shield, Foothills, Parkland, Rocky Mountains, and Grassland, which are further subdivided into 21 natural subregions [9,64]. Southern Alberta features short-grass and mixed-grass prairies, characterized by drought-resistant grasses like blue grama, while the central regions are dominated by aspen parkland, with tall grasses and aspen trees [65,66]. Northern Alberta is covered by boreal forest, including species such as aspen, white birch, white spruce, larch, and black spruce. The Rocky Mountains host alpine fir, white spruce, and lodgepole pine at lower elevations, transitioning to alpine meadows with scattered black spruce and alpine larch at higher altitudes [65,66]. This diverse vegetation is influenced by varying precipitation patterns across the province, with southern Alberta experiencing chronic water deficits, ranging from moderate in the parkland region to severe in the short-grass prairie area, while northern regions generally receive more precipitation [67,68]. The variety of climatic conditions and vegetation types across Alberta contributes to its rich biodiversity and complex ecosystem dynamics while also presenting challenges in terms of natural resource management and wildfire risk mitigation [69,70].
Table 1 provides detailed information on the selected fire occurrences for this study, including unique fire identification numbers, fire start and end dates, and the regions affected. Information in this table was collected from the AB historical wildfire database [71] including the Canadian National Fire Database (CNFDB) and the National Burned Area Composite (NBAC) database [72]. Where available, the table also includes the names of individual fires as aliases. Among the 30 fires selected, 20 fires were chosen annually between 2015 and 2018, eight in 2019, and two in 2021, based on their size and intensity. Within this group, four fires took two weeks to one month to be fully extinguished, six fires required over a month, and the remaining twenty fires took between two to over six months to be completely extinguished. Notably, two significant fires, the Horse River Wildfire in 2016 and the Chuckegg Creek Fire in 2019, burned over 490,000 ha [19] and 350,000 ha [17], respectively.

2.2. Datasets

2.2.1. Active Fire Data

This study utilized active fire and thermal anomaly data from two satellite sources: the VIIRS sensor aboard the Suomi National Polar-orbiting Partnership (SNPP), with a spatial resolution of 375 m [35], and the MODIS sensors on Aqua and Terra, with a 1 km resolution [73]. Specifically, the VIIRS (SNPP) 375 m Active Fire NRT Product (VNP14IMGTDL_NRT) [35] and the MODIS (Aqua and Terra) 1 km thermal anomalies NRT Product (MCD14DL-NRT v0061) [73] were employed. These datasets are part of the Fire Information for Resource Management System (FIRMS) initiated by the University of Maryland in 2007 [74]. FIRMS provides near real-time fire data, including fire locations and thermal anomalies, at a daily temporal frequency. VIIRS collects observations twice daily, while MODIS (Aqua and Terra) offers four daily crossings, including both day and night [19]. While up to six to eight observations could be captured per day, this study focused on annual data points from both satellites, available in CSV format [75], covering the years 2015 to 2021.

2.2.2. Ground Data

Two types of ground data were utilized: the National Burn Area Composite (NBAC) and the Canadian National Fire Database (CNFDB), both sourced from the Natural Resources Canada’s fire history database [72]. NBAC fire polygons were used to evaluate the accuracy of the estimated fire perimeters from 2015 to 2021. Conversely, CNFDB fire point data were used to assess the accuracy of fire clusters between 2015 and 2019. The CNFDB fire points offer information on fire locations, sizes, and additional details, such as reporting and fire end dates.

2.2.3. Land Use Land Cover Data

The MODIS Land Cover product (MCD12Q1 v061), a global annual dataset with a spatial resolution of 500 m [76], was used to remove water-covered areas from the estimated fire perimeters to improve the accuracy of the analysis.

3. Methods

Figure 2 provides an overview of this study’s methods, including processing data and generating the final output of active fire perimeters, along with their accuracy assessments. A detailed explanation of each stage of the method will be provided in the following subsections.

3.1. Active Fire Perimeter Calculations

The data processing involved four main steps, starting with pre-processing. In this step, active fire data from the VIIRS and MODIS satellite sensors were extracted for the study area, covering the annual fire seasons. For our study, this period is from 2015 to 2021.
In the next step, the extracted fire data points were grouped into individual fire events using the DBSCAN (Density-Based Spatial Clustering of Applications with Noise) algorithm [61], which relies on two key parameters. The first is the neighborhood radius, which defines the maximum distance between points within a cluster. The second is the minimum number of points required to form a cluster, where anything with fewer points is treated as noise or an outlier. Several neighborhood radii were tested to optimize clustering, including 750 m, 1000 m, 1125 m, and 1500 m for both VIIRS and MODIS data and 2000 m, 2500 m, and 3000 m for MODIS specifically. These distances were selected based on the spatial resolutions of VIIRS (375 m) and MODIS (1000 m). Additionally, clusters were tested with minimum point thresholds of three and four to enhance accuracy.
To assess the accuracy of the fire clusters, we use the following metrics:
  • Matching hotspots (HSs): This measures how well the fire occurrences detected by the generated fire polygons align with the actual fire occurrences recorded in the ground data. It is calculated by dividing the number of matching fire occurrences (fires that were correctly identified) by the total number of fire occurrences in the ground data:
    Matching   HSs = Number   of   Matching   Fire   Occurrences Total   Number   of   Fire   Occurrences ,
  • Point commission error (CE): This measures the extent of overestimation by calculating the number of generated fire polygons that did not match any ground data fire occurrences, divided by the total number of generated fire polygons:
    Point   CE   = Number   of   Unmatched   Polygons   Total   number   of   Generated   Fire   Polygons .
  • Point omission error (OE): This identifies the proportion of fire occurrences that were missed by the generated fire polygons. It is calculated as follows:
    Point   OE   = 1 − Matching   HS ,
     Once the fire clusters were formed, active fire perimeter (AFP) polygons were generated using buffering and concave methods applied to datasets sourced from MODIS, VIIRS, and a combination of both [19]. This study evaluated the performance of these post-processed active fire perimeters by analyzing both the estimated number of active fires (represented as polygons) and their areas (measured as perimeters). Fire counts, derived through clustering, were compared with fire occurrence data from the Canadian National Fire Database (CNFDB) for the period 2015 to 2019. The evaluation focused on four fire size categories: ≥100 ha, ≥50 to <100 ha, ≥25 to <50 ha, and ≥10 to <25 ha.
     Additionally, the study evaluated the accuracy of the calculated fire perimeter areas using confusion matrix-based metrics such as area matching, commission error (CE), and omission error (OE). These metrics were applied to compare the calculated fire perimeters with ground data from 30 selected NBAC fire polygons.
  • Area matching measures how closely the calculated perimeters match the actual ground data and is calculated by comparing the overlap between the calculated and ground fire areas:
    Area   Matching   = Overlap   of   Calculated   and   Ground   Area Total   Ground   Area × 100 % ,
  • Area commission error (CE) indicates overestimation by calculating the proportion of the calculated fire perimeter area that did not match the ground data:
    Area   CE   = Calculated   Area   −   Overlap   Area Total   Calculated   Area × 100 %
  • Area omission error (OE) represents the proportion of the ground area missed by the calculated perimeters and can be expressed as follows:
    Area   OE   = 100 % − Area   Matching

3.2. Timely Active Fire Progression Model

The Timely Active Fire Progression (TAFP) uses an iterative process to map active fire perimeters and monitor their changes, including areas that remain stable, become contained, or expand. Current Fire Progression measures the overall expansion of the fire perimeter by continuously adding newly detected fire areas to the existing perimeter from previous iterations:
Current Fire Progression = Previous Fire Progression + New Fire Perimeter

4. Results

4.1. Performance of Active Fire Clustering and Perimeter Calculation

Table 2 presents the results of fire clustering performance for identifying individual fires. The combined dataset (VIIRS and MODIS) demonstrated the highest matching rate across all fire size classes compared to VIIRS and MODIS datasets individually. For fires ≥100 ha, the combined dataset achieved a matching rate of 95.95%, with a gradual decline as fire sizes decreased: 72.73% for fires ≥50 to <100 ha, 54.84% for fires ≥25 to <50 ha, and 42.86% for fires ≥10 to <25 ha. The number of matching fire polygons also decreased with smaller fire sizes, from 166 out of 173 for fires ≥100 ha to 42 out of 98 for fires ≥10 to <25 ha.
The VIIRS dataset followed a similar trend, with a matching rate of 94.22% for fires ≥100 ha, dropping to 38.78% for fires ≥10 to <25 ha. The highest match for VIIRS was 163 out of 173 polygons for fires ≥100 ha, and the lowest was 38 out of 98 polygons for fires ≥10 to <25 ha. The MODIS dataset exhibited a lower matching rate overall, ranging from 87.86% for fires ≥100 ha to 35.71% for fires ≥10 to <25 ha, with 152 out of 173 matches for the ≥100 ha class and 35 out of 98 for the ≥10 to <25 ha class.
In terms of commission error (CE), the combined dataset exhibited a CE rate ranging from 13.95% for fires ≥100 ha to 60.92% for fires ≥25 to <50 ha. The CE rate increased with smaller fire sizes, reaching 57.58% for fires ≥10 to <25 ha. For VIIRS, the CE rate ranged from 8.59% for fires ≥100 ha to 63.46% for fires ≥10 to <25 ha. The MODIS dataset had the lowest CE rates, from 10.46% for fires ≥100 ha to 28.57% for fires ≥10 to <25 ha, indicating a more consistent but lower accuracy.
Cumulatively, the combined dataset performed the best across fire size classes. For fires ≥50 ha, the matching rate was 90.35%, with 206 out of 228 polygons matched. However, for smaller fires (≥10 ha), the matching rate decreased to 72.68%. VIIRS achieved a cumulative matching rate of 87.72% for fires ≥50 ha, dropping to 69.07% for fires ≥10 ha. MODIS, while showing lower matching rates (81.15% for fires ≥50 ha and 62.88% for fires ≥10 ha), exhibited more consistent CE rates, with the cumulative CE for MODIS increasing from 10.46% to 20.33% as fire sizes decreased.
Table 3 presents the matching and commission error (CE) percentages for VIIRS and MODIS active fire datasets from 2015 to 2021, across different concave alpha (α) values (ranging from 0.1 to 0.5) and radius distances (750 m to 3000 m). The matching percentage represents the alignment between the calculated fire area and ground-truth data (NBAC), while the CE reflects the degree of overestimation in the calculated fire area. The table highlights how the changes in α values and radius distances influence both the matching rate and CE for the VIIRS and MODIS datasets.
For the VIIRS dataset, the analysis shows that increasing the α values leads to a consistent improvement in the matching rate across different radii. At a 750 m radius, for example, the matching rate increased from 72.22% to 76.99% as the α values rose from 0.1 to 0.5. However, this improvement was accompanied by an increase in the CE from 21% to 26.64%, indicating a rise in overestimation. Similarly, at a 1125m radius, the matching rate improved from 77.83% to 81.34%, while the CE increased from 22.43% to 27.62%.
The 1500 m radius showed the most significant improvement, where matching rates increased from 79.43% to 84.66% as the α values rose. However, the CE also increased from 22.22% to 28.80%. For MODIS, the matching rate at a 1000 m radius improved from 59.86% to 63.89% with increasing α values, but the CE remained high, ranging from 35.39% to 36.58%. Similar trends were observed for larger radii (2000 m to 3000 m), where MODIS matching rates improved but were accompanied by rising CE values, indicating consistent overestimation as α values and radii increased.
Table 4 expands on the findings from Table 3 by presenting the matching and CE percentages for the combined VIIRS and MODIS datasets. This combination is aimed at reducing gaps in active fire detection. The table evaluates how matching and CE change across varying α values (0.1 to 0.5) and radii (750 m to 1500 m), while also considering the impact of different minimum sample sizes (three and four) for calculating active fire perimeters.
At a 750 m radius, the matching rate for the combined datasets improved from 81.02% to 84.20% as α values increased from 0.1 to 0.5. However, this improvement was coupled with a rise in the CE from 30.98% to 34.76%, indicating overestimation. Larger radii, such as 1000 m and 1125 m, showed further improvement in matching rates, reaching 86.30% and 87.19%, respectively. The CE also increased, with values rising from 28.58% to 33.49% at 1000 m and from 28.27% to 33.64% at 1125 m.
The most significant improvement was observed at a 1500 m radius, where the matching rate increased from 85.13% to 89.29% as α values rose. However, this came with a corresponding rise in the CE from 27.96% to 34.35%, reflecting increased overestimation. Interestingly, when a minimum sample size of four was applied, the matching rate remained consistent at 85.12% for an α value of 0.1, but the CE slightly increased to 28.05%.

4.2. Analysis of Active Fire Progression

Figure 3 presents an example case study illustrating the application of the Timely Active Fire Progression (TAFP) model, which integrates VIIRS and MODIS active fire data points. This case study demonstrates the model’s capability to track fire progression over a specific 5-day period for a single fire event (Fire ID: HWF-042-2019, Chuckegg Creek Fire, as referenced in Figure 1 and Table 1). It is important to note that this figure represents the application of the TAFP model to a specific fire event and is not intended to compare fire occurrences across multiple years.
The figure shows the overall progression of the fire perimeter from Day 1 through Day 5. Each day’s fire progression is represented by distinct colors and dashed lines, while the total fire progression over the five days is delineated by a solid boundary line.
The optimal algorithm parameters for this model were determined through a combination of settings: a minimum sample size of three and a radius of 1500 m, an alpha value of 0.1 for the concave hull (CC) algorithm, and buffer distances of 375 m for VIIRS and 1000 m for MODIS. These parameters were used for the TAFP model to delineate active fire progression based on the performance of calculated AFP with ground data.
On Day 1, the deep green color illustrates a fire perimeter formed solely by the concave hull algorithm. The area affected on Day 1 was 42 ha. On Day 2, the fire perimeter extends to include additional round shapes generated by the buffer algorithm, reflecting the incorporation of outliers or noise points. The area affected on Day 2 was 785 ha, bringing the cumulative area to 827 ha. In contrast, Days 3 to 5 depict a continuous extension of the active fire front, moving from the southeast (SE) towards the northwest (NW). The area affected on Day 3 was 14,127 ha, with a cumulative area of 14,954 ha. On Day 4, the area affected was 39,527 ha, bringing the cumulative area to 54,481 ha. Finally, on Day 5, the area affected was 27,982 ha, with a cumulative area of 82,463 ha.

5. Discussion

5.1. Fire Point Clustering

The analysis of the accuracy results demonstrated that the fire clustering achieved its highest matching performance between ground data and clusters for fire sizes ≥ 100 ha, particularly with the combined VIIRS and MODIS data points, as well as VIIRS alone. In contrast, the fire clustering accuracy consistently decreased as fire sizes were reduced, both for individual datasets and their combinations. While the algorithm maintained a matching rate of approximately 67% to 72% for fires ≥50 ha, the rate dropped below 55% for smaller fire sizes. Notably, higher point CEs were predominantly associated with the combination of VIIRS and MODIS data, as well as the VIIRS dataset alone, compared to MODIS. The lower point CE in MODIS was attributed to its fewer detections of fire hotspots, primarily large fires, resulting in a smaller number of clusters compared to VIIRS [77].
Furthermore, many false detections of fire clusters, which did not match ground data, were found in built-up and grass-covered areas, whereas the ground data identified actual forest fire occurrences. Smaller fire sizes, particularly those <100 ha, exhibited higher point CEs, with the error rate increasing consistently as fire sizes decreased for both individual and combined satellite datasets. It was evident that the DBSCAN clustering algorithm performed best, with fewer point CEs, for fires ≥100 ha compared to smaller fire sizes. For fires that persisted over a longer period, smaller fire clusters might have merged into larger ones, potentially affecting the accuracy of fire clustering. Additionally, fire management agencies might not have mapped small and short-duration fires, leading to fewer detected clusters compared to satellite observations. Moreover, fire point and polygon data from national parks were not publicly available. Consequently, without reference data to compare the estimated fire clusters, these clusters were excluded from the accuracy calculations.
Several factors could contribute to these limitations in fire detection and clustering accuracy. Spatial resolution constraints mean that a 1 km2 hotspot pixel may represent a fire as small as 100 m2, potentially leading to overestimation of fire size, especially for smaller fires. Cloud cover and smoke can obscure fires, causing them to go undetected for several days or miss small fires entirely. This interference particularly affects the accuracy of fire clustering for smaller or short-duration fires. Temporal resolution constraints, with satellite observations occurring up to 10 times daily, may limit the ability to accurately detect and cluster rapidly changing fire environments. [35,73,78,79,80,81].
Despite conservative tests in fire detection algorithms, false alarms can occur, particularly over bright surfaces like metallic rooftops, contributing to the higher point CEs observed in built-up areas. Understory fires beneath tree canopies are unlikely to be detected due to obstruction, partly explaining the lower detection rates for smaller fires in forested areas. Fire-clustering algorithms that rely on spatial and temporal proximity of fire pixels may struggle to separate individual fires within large burn patches containing multiple ignition points, a frequent phenomenon in grassland biomes [35,73,78,79,80,81].
Spatial accuracy is another concern, as the exact location of a fire may differ from the reported coordinates, with offsets typically ranging from tens to hundreds of meters, depending on the satellite data used. This could affect the accuracy of fire clustering, especially for smaller fires [79,80]. Lastly, fire pixels detected over mountain ranges and steep terrain can show larger locational errors due to terrain correction procedures, potentially impacting clustering accuracy in these areas [35,73,78,79,80,81].

5.2. Active Fire Premiter

The AFP was determined with area CEs of less than 25.50% for VIIRS and less than 30.50% for MODIS (or combination) active fire datasets. Within these area CE limits, a 1500 m radius with a minimum of three samples in the clustering algorithm provided the best accuracy for the AFP calculation using VIIRS data points, while MODIS achieved optimal results with a 3000 m radius. Additionally, both datasets performed better with an alpha value of 0.2 (area matching rate: 82.89% for VIIRS and 72.22% for MODIS), whereas MODIS required a 0.3 alpha value in a previous study [19]. This difference may be attributed to the previous use of a single CC algorithm, whereas the AFP model was developed using a combination of the CC and buffer algorithms. Although the matching rate improved with increasing radius and alpha values, this also introduced a risk of overestimation, leading to higher area CEs. Considering the area CE limits, the highest matching performance was observed for VIIRS compared to MODIS active fire data points, likely due to VIIRS’s higher spatial resolution, which allows for the detection of smaller fires. Conversely, a lower clustering radius for both datasets resulted in the opposite trend for area CE, with a consistent decrease in the matching area rate or an increase in area OE.
Single-source data points, such as those from MODIS, sometimes missed detecting specific fires due to limitations in spatial resolution and temporal coverage. However, the combination of multiple satellite data points, such as VIIRS and MODIS, was able to fill these detection gaps and provide more comprehensive results. Consequently, the AFP found that the combined VIIRS and MODIS datasets performed better compared to using individual datasets. The combination dataset achieved the best matching performance with a 0.1 alpha value (area matching rate: 85.13%), while it was found to be 83.19% for the previous study [19]. However, an increased risk of overestimation of AFP was observed when higher alpha values were used to achieve a greater matching rate. Similarly, altering the radius—either by increasing or decreasing it—carried the risk of a higher area OE, similar to what was observed with the individual datasets. A previous study that used a convex hull algorithm achieved optimal performance at a distance of 1125 m with combination datasets [22]. In contrast, this study found a 1500 m radius to be more effective, highlighting the differences between the convex hull algorithm (from [22]) and the AFP model employed in this research.
This study also explored increasing the sample size to four, which resulted in a similar matching rate but with an overestimated CE. This suggests that increasing the minimum sample size for clustering poses the risk of excluding small fire hotspots and leads to an overestimation of CE. Potential reasons for this outcome include the exclusion of small fire hotspots, overestimation of cluster extent (CE), reduced sensitivity of the clustering algorithm, and algorithmic limitations when dealing with larger sample sizes.

5.3. Timely Active Fire Progression

The fire progression tracked through the TAFP model may initially show moderate or lower performance at first detection, primarily due to the availability of multiple satellite datasets and the time lag between a fire’s start and its detection. For instance, initial detections sometimes include only three or four active fire data points, which often form a triangular shape, whereas the actual ground fire might have a different shape. In some cases, the TAFP model has generated a linear-shaped polygon because the initial data points were aligned linearly (only three or four points) at the time of first detection. Although increasing the minimum sample size to four or more could potentially address this issue, it also increases the risk of overestimating CE and OE. However, this issue was observed only in a few instances, particularly during the initial detection and when using individual data sources (i.e., data points from either MODIS or VIIRS). Generally, the issue is resolved in subsequent detections as new data points are added. Moreover, this problem was not observed when using a combination of satellite datasets, where more than three or four data points were typically available for a particular fire at first detection.

5.4. Considerations and Future Research

Future research should aim to refine the AFP model to reduce errors, particularly for smaller fire sizes (<100 ha) and in early detection scenarios. Exploring alternative algorithms or enhancing the current model with advanced data fusion and machine learning techniques could further improve accuracy.
While this study employs MODIS and VIIRS near real-time (NRT) active fire data points, the TAFP model is specifically designed to process ultra real-time (URT) data, enabling the generation of active fire perimeters shortly after satellite observations. The methods and models developed in this research will assist forest fire agencies in making accurate and timely assessments of fires, thereby enhancing emergency response and mitigation efforts.

6. Concluding Remarks

This study demonstrates the effectiveness of integrating VIIRS and MODIS datasets to improve the detection and delineation of active fire perimeters, particularly across different fire size classes. The combined dataset consistently outperformed the individual datasets, with higher clustering matching rates observed for larger fires. For fires ≥100 ha, the combined dataset achieved a matching rate of 95.95% for clustering, gradually decreasing for smaller fire sizes, reaching 42.86% for fires between 10 and 25 ha. This trend was consistent for both the VIIRS and MODIS datasets, although the combined dataset maintained better overall accuracy. The high performance of the combined dataset for larger fires suggests that merging data from multiple satellite sources provides a more reliable and comprehensive view of fire clustering.
The commission error (CE) rates further highlight the challenges in accurately determining smaller fire clusters. For both VIIRS and the combined dataset, CE rates increased significantly for smaller fires, with the combined dataset exhibiting a CE as high as 57.58% for fires between 10 and 25 ha. In contrast, MODIS showed lower CE rates across all size classes, albeit at the expense of lower matching rates, indicating that while MODIS may be more conservative in fire clustering, it tends to under-detect individual fire clusters compared to VIIRS and the combined dataset.
The analysis of different concave alpha (α) values and radii revealed a trade-off between improving the matching rate and increasing the commission error (CE) for active fire perimeter delineation. For the VIIRS dataset, higher α values consistently led to improved matching rates across radii, with the most notable increase observed at a 1500 m radius, where the rate rose from 79.43% to 84.66%. However, this improvement came with a rise in the CE from 22.22% to 28.80%. A similar trend was seen in the MODIS dataset, where higher α values improved matching but at the cost of greater CE rates. The combined dataset followed this pattern, where larger radii and higher α values improved matching rates but increased perimeter overestimation. Notably, the combined use of VIIRS and MODIS datasets consistently yielded higher matching accuracy between calculated AFP and ground data, highlighting the advantage of leveraging multiple datasets. The AFP model achieved matching rates of 82.89% for VIIRS, 72.22% for MODIS, and an impressive 85.13% when both datasets were combined, underscoring the superiority of combined datasets in achieving higher accuracy.
The results also highlight the importance of parameter optimization for timely fire detection. The Timely Active Fire Progression (TAFP) model, which integrates VIIRS and MODIS data points, demonstrated how optimal algorithm parameters—such as a 1500 m radius, an α value of 0.1, and specific buffer distances—can be used to track fire progression accurately. The case study illustrated how fire perimeters extended over time, with the fire front progressing from Day 1 to Day 5, eventually covering a total area of 82,463 ha. The ability to monitor the continuous growth of fire perimeters in near real-time is critical for fire management and response, particularly in large-scale fire events.

Author Contributions

Conceptualization, H.B., H.D., M.R.A. and Q.K.H.; methodology, H.B., H.D. and Q.K.H.; software, H.B.; validation, H.B., H.D. and Q.K.H.; formal analysis, H.B., H.D. and Q.K.H.; investigation, H.B., H.D. and Q.K.H.; resources, Q.K.H.; data curation, H.B.; writing—original draft preparation, H.B. and H.D.; writing—review and editing, H.B. and H.D.; visualization, H.B. and H.D.; supervision, H.D. and Q.K.H.; project administration, H.D., M.R.A. and Q.K.H.; funding acquisition, Q.K.H. All authors have read and agreed to the published version of the manuscript.

Funding

This study was partially funded through (i) an NSERC Discovery Grant and (ii) an Alberta Innovates ‘NSERC Alliance—Alberta Innovates Advance Program’ Grant.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data used in this research are available in the public domain.

Acknowledgments

The authors would like to express their gratitude to the Fire Information for Resource Management System (FIRMS), a component of NASA’s Earth Observing System Data and Information System (EOSDIS), for providing active fire and land cover data. Additionally, the authors would like to thank Natural Resources Canada (NRCan) for the annual burn area polygon data utilized in this research.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
Active fire perimeterAFP
Advanced Very High-Resolution RadiometerAVHRR
Concave hull algorithmCC
Commission errorCE
Canadian Interagency Forest Fire CentreCIFFC
Canadian National Fire DatabaseCNFDB
Canadian Wildland Fire Information SystemCWFIS
Convex hull algorithmCX
Density-Based Spatial Clustering of Applications with NoiseDBSCAN
Earth Observing System Data and Information SystemEOSDIS
Food and Agriculture OrganizationFAO
Fire Information for Resource Management SystemFIRMS
HotspotsHSs
Hectaresha
Moderate Resolution Imaging SpectroradiometerMODIS
National Aeronautics and Space AdministrationNASA
National Burn Area CompositeNBAC
Natural Resources CanadaNRC
Near real-timeNRT
Northwest TerritoriesNT
Omission errorOE
Real-timeRT
Suomi National Polar-orbiting PartnershipSNPP
Timely Active Fire ProgressionTAFP

References

  1. Bowman, D.M.J.S.; Balch, J.; Artaxo, P.; Bond, W.J.; Cochrane, M.A.; D’Antonio, C.M.; DeFries, R.; Johnston, F.H.; Keeley, J.E.; Krawchuk, M.A.; et al. The Human Dimension of Fire Regimes on Earth. J. Biogeogr. 2011, 38, 2223–2236. [Google Scholar] [CrossRef]
  2. van Lierop, P.; Lindquist, E.; Sathyapala, S.; Franceschini, G. Global Forest Area Disturbance from Fire, Insect Pests, Diseases and Severe Weather Events. For. Ecol. Manag. 2015, 352, 78–88. [Google Scholar] [CrossRef]
  3. Zumbrunnen, T.; Pezzatti, G.B.; Menéndez, P.; Bugmann, H.; Bürgi, M.; Conedera, M. Weather and Human Impacts on Forest Fires: 100 Years of Fire History in Two Climatic Regions of Switzerland. For. Ecol. Manag. 2011, 261, 2188–2199. [Google Scholar] [CrossRef]
  4. Saleh, A.; Zulkifley, M.A.; Harun, H.H.; Gaudreault, F.; Davison, I.; Spraggon, M. Forest Fire Surveillance Systems: A Review of Deep Learning Methods. Heliyon 2024, 10, e23127. [Google Scholar] [CrossRef]
  5. Tyukavina, A.; Potapov, P.; Hansen, M.C.; Pickens, A.H.; Stehman, S.V.; Turubanova, S.; Parker, D.; Zalles, V.; Lima, A.; Kommareddy, I.; et al. Global Trends of Forest Loss Due to Fire from 2001 to 2019. Front. Remote Sens. 2022, 3, 825190. [Google Scholar] [CrossRef]
  6. FAO and UNEP. The State of the World’s Forests 2020: Forests, Biodiversity and People; FAO and UNEP: Rome, Italy, 2020; ISBN 978-92-5-132419-6. [Google Scholar]
  7. Kala, C.P. Environmental and Socioeconomic Impacts of Forest Fires: A Call for Multilateral Cooperation and Management Interventions. Nat. Hazards Res. 2023, 3, 286–294. [Google Scholar] [CrossRef]
  8. Ahmed, M.R.; Hassan, Q.K. Occurrence, Area Burned, and Seasonality Trends of Forest Fires in the Natural Subregions of Alberta over 1959–2021. Fire 2023, 6, 96. [Google Scholar] [CrossRef]
  9. Dastour, H.; Ahmed, M.R.; Hassan, Q.K. Analysis of Forest Fire Patterns and Their Relationship with Climate Variables in Alberta’s Natural Subregions. Ecol. Inform. 2024, 80, 102531. [Google Scholar] [CrossRef]
  10. Agbeshie, A.A.; Abugre, S.; Atta-Darkwa, T.; Awuah, R. A Review of the Effects of Forest Fire on Soil Properties. J. For. Res. 2022, 33, 1419–1441. [Google Scholar] [CrossRef]
  11. Abatzoglou, J.T.; Battisti, D.S.; Williams, A.P.; Hansen, W.D.; Harvey, B.J.; Kolden, C.A. Projected Increases in Western US Forest Fire despite Growing Fuel Constraints. Commun. Earth Environ. 2021, 2, 227. [Google Scholar] [CrossRef]
  12. Boudinot, F.G.; Sepúlveda, J. Marine Organic Carbon Burial Increased Forest Fire Frequency during Oceanic Anoxic Event 2. Nat. Geosci. 2020, 13, 693–698. [Google Scholar] [CrossRef]
  13. Chatenoux, B.; Peduzzi, P. Biomass Fires: Preliminary Estimation of Ecosystems Global Economic Losses; UNEP/GRID-Geneva: Geneva, Switzerland, 2012. [Google Scholar]
  14. Akdis, C.A.; Nadeau, K.C. Human and Planetary Health on Fire. Nat. Rev. Immunol. 2022, 22, 651–652. [Google Scholar] [CrossRef] [PubMed]
  15. CIFFC. Canada Report: 2023 Fire Season; Canadian Interagency Forest Fire Centre: Winnipeg, MB, Canada, 2024. [Google Scholar]
  16. CIFFC. Situation Report 22 July 2024. Available online: https://ciffc.net/situation/ (accessed on 23 July 2024).
  17. Ban, Y.; Zhang, P.; Nascetti, A.; Bevington, A.R.; Wulder, M.A. Near Real-Time Wildfire Progression Monitoring with Sentinel-1 SAR Time Series and Deep Learning. Sci. Rep. 2020, 10, 1322. [Google Scholar] [CrossRef] [PubMed]
  18. Kurbanov, E.; Vorobev, O.; Lezhnin, S.; Sha, J.; Wang, J.; Li, X.; Cole, J.; Dergunov, D.; Wang, Y. Remote Sensing of Forest Burnt Area, Burn Severity, and Post-Fire Recovery: A Review. Remote Sens. 2022, 14, 4714. [Google Scholar] [CrossRef]
  19. Bhuian, H.; Dastour, H.; Ahmed, M.R.; Hassan, Q.K. Comparison of Perimeter Delineation Methods for Remote Sensing Fire Spot Data in Near/Ultra-Real-Time Applications. Fire 2024, 7, 226. [Google Scholar] [CrossRef]
  20. Dixon, D.J.; Callow, J.N.; Duncan, J.M.A.; Setterfield, S.A.; Pauli, N. Regional-Scale Fire Severity Mapping of Eucalyptus Forests with the Landsat Archive. Remote Sens. Environ. 2022, 270, 112863. [Google Scholar] [CrossRef]
  21. Skakun, R.; Castilla, G.; Metsaranta, J.; Whitman, E.; Rodrigue, S.; Little, J.; Groenewegen, K.; Coyle, M. Extending the National Burned Area Composite Time Series of Wildfires in Canada. Remote Sens. 2022, 14, 3050. [Google Scholar] [CrossRef]
  22. Briones-Herrera, C.I.; Vega-Nieva, D.J.; Monjarás-Vega, N.A.; Briseño-Reyes, J.; López-Serrano, P.M.; Corral-Rivas, J.J.; Alvarado-Celestino, E.; Arellano-Pérez, S.; Álvarez-González, J.G.; Ruiz-González, A.D.; et al. Near Real-Time Automated Early Mapping of the Perimeter of Large Forest Fires from the Aggregation of VIIRS and MODIS Active Fires in Mexico. Remote Sens. 2020, 12, 2061. [Google Scholar] [CrossRef]
  23. Chuvieco, E.; Mouillot, F.; van der Werf, G.R.; San Miguel, J.; Tanase, M.; Koutsias, N.; García, M.; Yebra, M.; Padilla, M.; Gitas, I.; et al. Historical Background and Current Developments for Mapping Burned Area from Satellite Earth Observation. Remote Sens. Environ. 2019, 225, 45–64. [Google Scholar] [CrossRef]
  24. Briones-Herrera, C.I.; Vega-Nieva, D.J.; Briseño-Reyes, J.; Monjarás-Vega, N.A.; López-Serrano, P.M.; Corral-Rivas, J.J.; Alvarado, E.; Arellano-Pérez, S.; Jardel Peláez, E.J.; Pérez Salicrup, D.R.; et al. Fuel-Specific Aggregation of Active Fire Detections for Rapid Mapping of Forest Fire Perimeters in Mexico. Forests 2022, 13, 124. [Google Scholar] [CrossRef]
  25. Scaduto, E.; Chen, B.; Jin, Y. Satellite-Based Fire Progression Mapping: A Comprehensive Assessment for Large Fires in Northern California. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 5102–5114. [Google Scholar] [CrossRef]
  26. Dastour, H.; Hassan, Q.K. Utilizing MODIS Remote Sensing and Integrated Data for Forest Fire Spread Modeling in the Southwest Region of Canada. Environ. Res. Commun. 2024, 6, 025007. [Google Scholar] [CrossRef]
  27. Ray, T.; Malasiya, D.; Verma, A.; Purswani, E.; Qureshi, A.; Khan, M.L.; Verma, S. Characterization of Spatial–Temporal Distribution of Forest Fire in Chhattisgarh, India, Using MODIS-Based Active Fire Data. Sustainability 2023, 15, 7046. [Google Scholar] [CrossRef]
  28. Tian, Y.; Wu, Z.; Li, M.; Wang, B.; Zhang, X. Forest Fire Spread Monitoring and Vegetation Dynamics Detection Based on Multi-Source Remote Sensing Images. Remote Sens. 2022, 14, 4431. [Google Scholar] [CrossRef]
  29. Hassan, Q.K.; Bourque, C.P.A.; Meng, F.-R. Application of Landsat-7 ETM+ and MODIS Products in Mapping Seasonal Accumulation of Growing Degree Days at an Enhanced Resolution. J. Appl. Remote Sens. 2007, 1, 013539. [Google Scholar] [CrossRef]
  30. Chen, R.; He, B.; Li, Y.; Zhang, Y.; Liao, Z.; Fan, C.; Yin, J.; Zhang, H. Incorporating Fire Spread Simulation and Machine Learning Algorithms to Estimate Crown Fire Potential for Pine Forests in Sichuan, China. Int. J. Appl. Earth Obs. Geoinf. 2024, 132, 104080. [Google Scholar] [CrossRef]
  31. Liangrocapart, S.; Khetkeeree, S.; Petchthaweetham, B. Thermal Anomaly Level Algorithm for Active Fire Mapping by Means of Sentinel-2 Data. In Proceedings of the 2020 17th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), Phuket, Thailand, 24–27 June 2020; pp. 687–690. [Google Scholar]
  32. Seydi, S.T.; Saeidi, V.; Kalantar, B.; Ueda, N.; Halin, A.A. Fire-Net: A Deep Learning Framework for Active Forest Fire Detection. J. Sens. 2022, 2022, 8044390. [Google Scholar] [CrossRef]
  33. Çolak, E.; Sunar, F. The Importance of Ground-Truth and Crowdsourcing Data for the Statistical and Spatial Analyses of the NASA FIRMS Active Fires in the Mediterranean Turkish Forests. Remote Sens. Appl. Soc. Environ. 2020, 19, 100327. [Google Scholar] [CrossRef]
  34. Smith, J.M. FIRMS Adds Ultra Real-Time Data from MODIS and VIIRS | Earthdata. Available online: https://www.earthdata.nasa.gov/learn/articles/firms-urt-data (accessed on 18 May 2024).
  35. Giglio, L. VIIRS/SNPP Active Fires 6-Min L2 Swath 375m V002; Distributed by NASA EOSDIS Land Processes; Distributed Active Archive Center: Sioux Falls, SD, USA, 2024. [Google Scholar]
  36. Giglio, L.; Descloitres, J.; Justice, C.O.; Kaufman, Y.J. An Enhanced Contextual Fire Detection Algorithm for MODIS. Remote Sens. Environ. 2003, 87, 273–282. [Google Scholar] [CrossRef]
  37. Giglio, L.; Schroeder, W.; Justice, C.O. The Collection 6 MODIS Active Fire Detection Algorithm and Fire Products. Remote Sens. Environ. 2016, 178, 31–41. [Google Scholar] [CrossRef] [PubMed]
  38. Giglio, L.; Csiszar, I.; Justice, C.O. Global Distribution and Seasonality of Active Fires as Observed with the Terra and Aqua Moderate Resolution Imaging Spectroradiometer (MODIS) Sensors. J. Geophys. Res. Biogeosciences 2006, 111, G02016. [Google Scholar] [CrossRef]
  39. Choi, T.; Cao, C.; Blonski, S.; Shao, X.; Wang, W.; Ahmad, K. Preliminary Assessment of On-Orbit Radiometric Calibration Challenges in NOAA-21 VIIRS Reflective Solar Bands (RSBs). Remote Sens. 2024, 16, 2737. [Google Scholar] [CrossRef]
  40. Gupta, P.; Remer, L.A.; Patadia, F.; Levy, R.C.; Christopher, S.A. High-Resolution Gridded Level 3 Aerosol Optical Depth Data from MODIS. Remote Sens. 2020, 12, 2847. [Google Scholar] [CrossRef]
  41. Román, M.O.; Justice, C.; Paynter, I.; Boucher, P.B.; Devadiga, S.; Endsley, A.; Erb, A.; Friedl, M.; Gao, H.; Giglio, L.; et al. Continuity between NASA MODIS Collection 6.1 and VIIRS Collection 2 Land Products. Remote Sens. Environ. 2024, 302, 113963. [Google Scholar] [CrossRef]
  42. Xiong, X.; Wu, A.; Chang, T.; Wilson, T.M.; Li, Y.; Chen, N.; Shrestha, A.; Díaz, C.L.P. On-Orbit Calibration and Performance Assessments of Terra and Aqua MODIS Thermal Emissive Bands. J. Appl. Remote Sens. 2021, 15, 014520. [Google Scholar] [CrossRef]
  43. Davies, D. Wildfire Detection in the US and Canada within a Minute of Satellite Observation. Available online: https://wiki.earthdata.nasa.gov/display/FIRMS/2022/07/14/Wildfire+detection+in+the+US+and+Canada+within+a+minute+of+satellite+observation (accessed on 21 May 2024).
  44. Artés, T.; Boca, R.; Liberta, G.; San-Miguel, J. Non-Supervised Method for Early Forest Fire Detection and Rapid Mapping. In Proceedings of the Fifth International Conference on Remote Sensing and Geoinformation of the Environment (RSCy2017), Paphos, Cyprus, 20–23 March 2017; SPIE: Bellingham, WA, USA, 2017; Volume 10444, pp. 224–233. [Google Scholar]
  45. Canadian Forest Service; Canadian Wildland Fire Information System (CWFIS); Natural Resources Canada; Canadian Forest Service; Northern Forestry Centre. Fire M3 Season-to-Date Buffered Hotspots—Fire Perimeter Estimates. Available online: https://cwfis.cfs.nrcan.gc.ca/datamart/metadata/fm3buffered (accessed on 21 May 2024).
  46. Cardil, A.; Monedero, S.; Ramírez, J.; Silva, C.A. Assessing and Reinitializing Wildland Fire Simulations through Satellite Active Fire Data. J. Environ. Manage. 2019, 231, 996–1003. [Google Scholar] [CrossRef]
  47. Henderson, S.B.; Ichoku, C.; Burkholder, B.J.; Brauer, M.; Jackson, P.L. The Validity and Utility of MODIS Data for Simple Estimation of Area Burned and Aerosols Emitted by Wildfire Events. Int. J. Wildland Fire 2010, 19, 844–852. [Google Scholar] [CrossRef]
  48. Oliva, P.; Schroeder, W. Assessment of VIIRS 375m Active Fire Detection Product for Direct Burned Area Mapping. Remote Sens. Environ. 2015, 160, 144–155. [Google Scholar] [CrossRef]
  49. Chen, Y.; Hantson, S.; Andela, N.; Coffield, S.R.; Graff, C.A.; Morton, D.C.; Ott, L.E.; Foufoula-Georgiou, E.; Smyth, P.; Goulden, M.L.; et al. California Wildfire Spread Derived Using VIIRS Satellite Observations and an Object-Based Tracking System. Sci. Data 2022, 9, 249. [Google Scholar] [CrossRef] [PubMed]
  50. Han, J.; Kamber, M.; Pei, J. (Eds.) 10—Cluster Analysis: Basic Concepts and Methods. In Data Mining, 3rd ed.; The Morgan Kaufmann Series in Data Management Systems; Morgan Kaufmann: Boston, UK, 2012; pp. 443–495. ISBN 978-0-12-381479-1. [Google Scholar]
  51. Li, W.; Dodwell, E.; Cook, D. A Clustering Algorithm to Organize Satellite Hotspot Data for the Purpose of Tracking Bushfires Remotely. R J. 2023, 15, 17–33. [Google Scholar] [CrossRef]
  52. Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A K-Means Clustering Algorithm. J. R. Stat. Soc. Ser. C Appl. Stat. 1979, 28, 100–108. [Google Scholar] [CrossRef]
  53. Reynolds, D. Gaussian Mixture Models. In Encyclopedia of Biometrics; Li, S.Z., Jain, A., Eds.; Springer US: Boston, MA, USA, 2009; pp. 659–663. ISBN 978-0-387-73003-5. [Google Scholar]
  54. Ester, M.; Kriegel, H.-P.; Sander, J.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996; AAAI Press: Portland, OR, USA, 1996; pp. 226–231. [Google Scholar]
  55. Huang, Q.; Tung, A.K.H. Lightweight-Yet-Efficient: Revitalizing Ball-Tree for Point-to-Hyperplane Nearest Neighbor Search. In Proceedings of the 2023 IEEE 39th International Conference on Data Engineering (ICDE), Anaheim, CA, USA, 3–7 April 2023; pp. 436–449. [Google Scholar]
  56. Artés, T.; Oom, D.; de Rigo, D.; Durrant, T.H.; Maianti, P.; Libertà, G.; San-Miguel-Ayanz, J. A Global Wildfire Dataset for the Analysis of Fire Regimes and Fire Behaviour. Sci. Data 2019, 6, 296. [Google Scholar] [CrossRef] [PubMed]
  57. Kristianto, A.; Sediyono, E.; Hartomo, K.D. Implementation DBSCAN Algorithm to Clustering Satellite Surface Temperature Data in Indonesia. Regist. J. Ilm. Teknol. Sist. Inf. 2020, 6, 109–118. [Google Scholar] [CrossRef]
  58. Sheng, D.; Deng, J.; Xiang, J. Automatic Smoke Detection Based on SLIC-DBSCAN Enhanced Convolutional Neural Network. IEEE Access 2021, 9, 63933–63942. [Google Scholar] [CrossRef]
  59. Vatresia, A.; Rais, R.R.; Miliana, R.S. Spatio-Temporal Clustering for Fire Hot Spots Occurrence Over Sulawesi Island. In Proceedings of the 2020 FORTEI-International Conference on Electrical Engineering (FORTEI-ICEE), Bandung, Indonesia, 23–24 September 2020; pp. 156–161. [Google Scholar]
  60. Usman, M.; Sitanggang, I.S.; Syaufina, L. Hotspot Distribution Analyses Based on Peat Characteristics Using Density-Based Spatial Clustering. Procedia Environ. Sci. 2015, 24, 132–140. [Google Scholar] [CrossRef]
  61. Creţulescu, R.G.; Morariu, D.I.; Breazu, M.; Volovici, D. DBSCAN Algorithm for Document Clustering. Int. J. Adv. Stat. ITC Econ. Life Sci. 2019, 9, 58–66. [Google Scholar] [CrossRef]
  62. Fitrianah, D.; Fahmi, H.; Kemala, A.P.; Syahputra, M.E. Indonesian Forest Fire Data Clustering Using Spatiotemporal Data Using Grid Density-Based Clustering Algorithm. In Proceedings of the Knowledge Management and Acquisition for Intelligent Systems, Jakarta, Indonesia, 15–16 November 2023; Wu, S., Yang, W., Amin, M.B., Kang, B.-H., Xu, G., Eds.; Springer Nature: Singapore, 2023; pp. 124–133. [Google Scholar]
  63. Hanafi, N.; Saadatfar, H. A Fast DBSCAN Algorithm for Big Data Based on Efficient Density Calculation. Expert Syst. Appl. 2022, 203, 117501. [Google Scholar] [CrossRef]
  64. Downing, D.J.; Pettapiece, W.W. Natural Regions and Subregions of Alberta; Natural Regions Committee: Alberta, GA, USA, 2006. [Google Scholar]
  65. McNew, L.B.; Dahlgren, D.K.; Beck, J.L. (Eds.) Rangeland Wildlife Ecology and Conservation; Springer International Publishing: Cham, Switzerland, 2023; ISBN 978-3-031-34036-9. [Google Scholar]
  66. Peh, K.S.-H.; Corlett, R.T.; Bergeron, Y. (Eds.) Routledge Handbook of Forest Ecology; Routledge: New York, NY, USA, 2015; ISBN 978-1-317-81644-7. [Google Scholar]
  67. Lyseng, M.P.; Bork, E.W.; Hewins, D.B.; Alexander, M.J.; Carlyle, C.N.; Chang, S.X.; Willms, W.D. Long-Term Grazing Impacts on Vegetation Diversity, Composition, and Exotic Species Presence across an Aridity Gradient in Northern Temperate Grasslands. Plant Ecol. 2018, 219, 649–663. [Google Scholar] [CrossRef]
  68. Dastour, H.; Hassan, Q.K. Quantifying the Influence of Climate Variables on Vegetation Through Remote Sensing and Multi-Dimensional Data Analysis. Earth Syst. Environ. 2024, 8, 165–180. [Google Scholar] [CrossRef]
  69. Brandt, J.P.; Flannigan, M.D.; Maynard, D.G.; Thompson, I.D.; Volney, W.J.A. An Introduction to Canada’s Boreal Zone: Ecosystem Processes, Health, Sustainability, and Environmental Issues. Environ. Rev. 2013, 21, 207–226. [Google Scholar] [CrossRef]
  70. Venier, L.A.; Thompson, I.D.; Fleming, R.; Malcolm, J.; Aubin, I.; Trofymow, J.A.; Langor, D.; Sturrock, R.; Patry, C.; Outerbridge, R.O.; et al. Effects of Natural Resource Development on the Terrestrial Biodiversity of Canadian Boreal Forests. Environ. Rev. 2014, 22, 457–490. [Google Scholar] [CrossRef]
  71. Alberta Government Wildfire Data: 2006–2023. Available online: https://www.alberta.ca/wildfire-maps-and-data (accessed on 11 September 2024).
  72. CWFIS Canadian Wildland Fire Information System (CWFIS) Datamart. Available online: https://cwfis.cfs.nrcan.gc.ca/datamart (accessed on 19 August 2024).
  73. Giglio, L.; Justice, C. MODIS/Terra Thermal Anomalies/Fire 5-Min L2 Swath 1km V061; Distributed by NASA EOSDIS Land Processes; DAAC: Sioux Falls, SD, USA, 2021. [Google Scholar]
  74. Jiao, L.; Bo, Y. Near Real-Time Mapping of Burned Area by Synergizing Multiple Satellites Remote-Sensing Data. GIScience Remote Sens. 2022, 59, 1956–1977. [Google Scholar] [CrossRef]
  75. NASA-FIRMS Archive Download. Available online: https://firms.modaps.eosdis.nasa.gov/download/ (accessed on 22 August 2024).
  76. Sulla-Menashe, D.; Gray, J.M.; Abercrombie, S.P.; Friedl, M.A. Hierarchical Mapping of Annual Global Land Cover 2001 to Present: The MODIS Collection 6 Land Cover Product. Remote Sens. Environ. 2019, 222, 183–194. [Google Scholar] [CrossRef]
  77. Vadrevu, K.; Lasko, K. Intercomparison of MODIS AQUA and VIIRS I-Band Fires and Emissions in an Agricultural Landscape—Implications for Air Pollution Research. Remote Sens. 2018, 10, 978. [Google Scholar] [CrossRef] [PubMed]
  78. Earthdata Forum What Caveats Should Be Considered When Using Active Fire Data from FIRMS? Available online: https://forum.earthdata.nasa.gov/viewtopic.php?t=5188 (accessed on 29 September 2024).
  79. EFFIS Active Fire Detection. Available online: https://forest-fire.emergency.copernicus.eu/about-effis/technical-background/active-fire-detection (accessed on 29 September 2024).
  80. Small, C. Spatiotemporal Characterization of VIIRS Night Light. Front. Remote Sens. 2021, 2, 775399. [Google Scholar] [CrossRef]
  81. Chen, Z.; Yu, B.; Yang, C.; Zhou, Y.; Yao, S.; Qian, X.; Wang, C.; Wu, B.; Wu, J. An Extended Time Series (2000–2018) of Global NPP-VIIRS-like Nighttime Light Data from a Cross-Sensor Calibration. Earth Syst. Sci. Data 2021, 13, 889–906. [Google Scholar] [CrossRef]
Fire 07 00355 g001
Figure 1. Study region. (a) Forest fire burn areas (red polygons), lakes (blue polygons), and rivers (blue lines). Numbers 1–30 correspond to Table 1. (b) Inset map showing the study region’s location within Canada.
Figure 1. Study region. (a) Forest fire burn areas (red polygons), lakes (blue polygons), and rivers (blue lines). Numbers 1–30 correspond to Table 1. (b) Inset map showing the study region’s location within Canada.
Fire 07 00355 g001
Fire 07 00355 g002
Figure 2. Workflow diagram illustrating the processes of data acquisition, processing, and accuracy assessment for (a) active fire perimeter (AFP) calculation and (b) Timely Active Fire Progression (TAFP) models.
Figure 2. Workflow diagram illustrating the processes of data acquisition, processing, and accuracy assessment for (a) active fire perimeter (AFP) calculation and (b) Timely Active Fire Progression (TAFP) models.
Fire 07 00355 g002
Fire 07 00355 g003
Figure 3. A case study of the TAFP model for 5 days (Fire ID: HWF-042-2019, Chuckegg Creek Fire, as in Figure 1 and Table 1). Panel (a) illustrates the fire progression using the TAFP model, while panel (b) shows the individual and cumulative fire perimeter sizes (ha) for each day of progression. The figure includes two types of shapes in the fire perimeter: contour shapes and round shapes. The contour shapes are derived from the concave hull algorithm applied to clusters of data points, while the round shapes result from the buffer algorithm, which addresses outliers or noise points (less than 3 points).
Figure 3. A case study of the TAFP model for 5 days (Fire ID: HWF-042-2019, Chuckegg Creek Fire, as in Figure 1 and Table 1). Panel (a) illustrates the fire progression using the TAFP model, while panel (b) shows the individual and cumulative fire perimeter sizes (ha) for each day of progression. The figure includes two types of shapes in the fire perimeter: contour shapes and round shapes. The contour shapes are derived from the concave hull algorithm applied to clusters of data points, while the round shapes result from the buffer algorithm, which addresses outliers or noise points (less than 3 points).
Fire 07 00355 g003
Table 1. Summary of selected forest fires in the study regions from 2015 to 2021. The table includes the following columns: fire number (unique ID), area (the burned area in ha), start date (the day the fire started or was discovered), end date (the day the fire was extinguished), affected regions (e.g., AB for Alberta, NT for the Northwest Territories, BC for British Columbia, and SK for Saskatchewan), and alias (common name, if available).
Table 1. Summary of selected forest fires in the study regions from 2015 to 2021. The table includes the following columns: fire number (unique ID), area (the burned area in ha), start date (the day the fire started or was discovered), end date (the day the fire was extinguished), affected regions (e.g., AB for Alberta, NT for the Northwest Territories, BC for British Columbia, and SK for Saskatchewan), and alias (common name, if available).
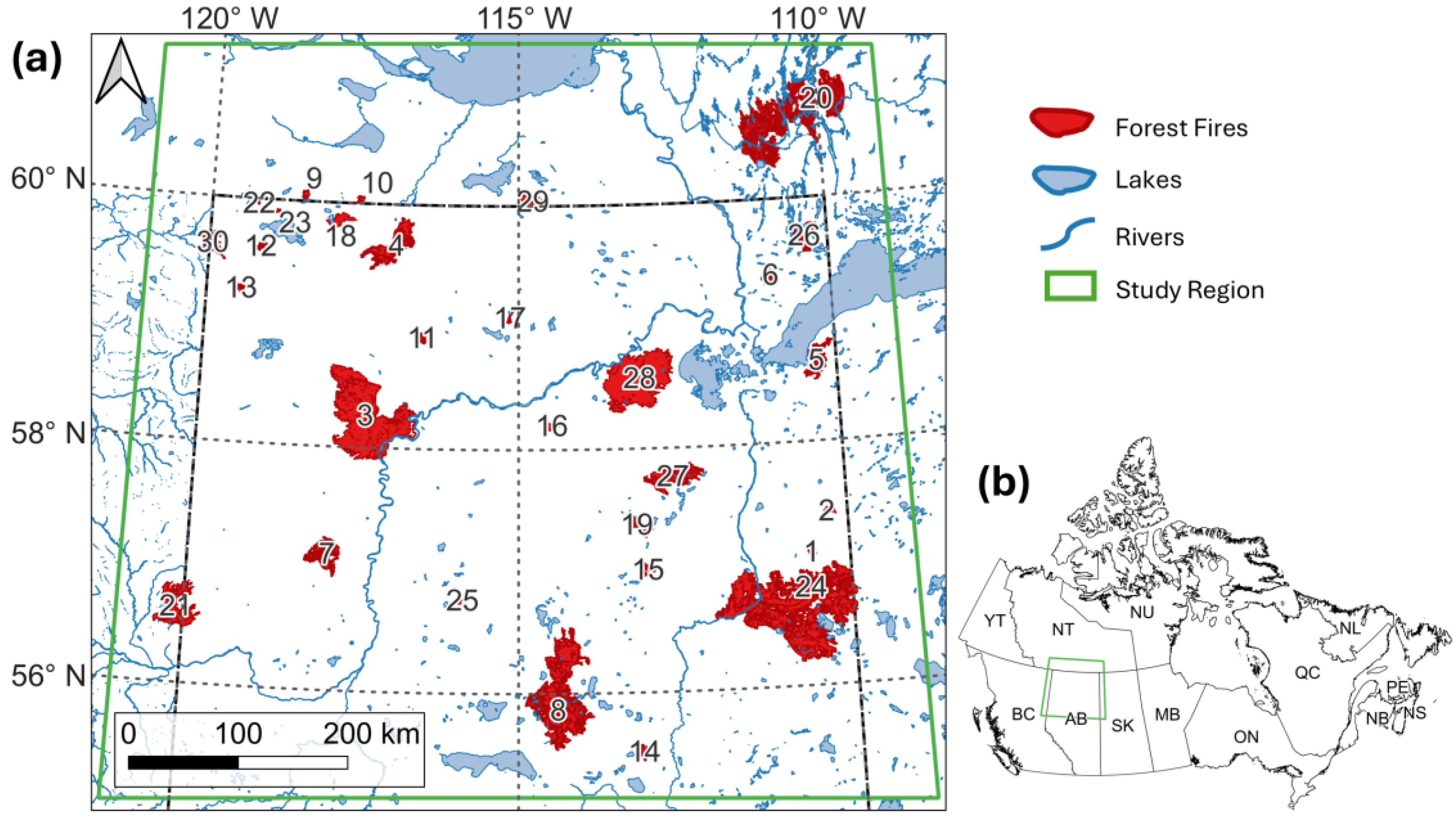
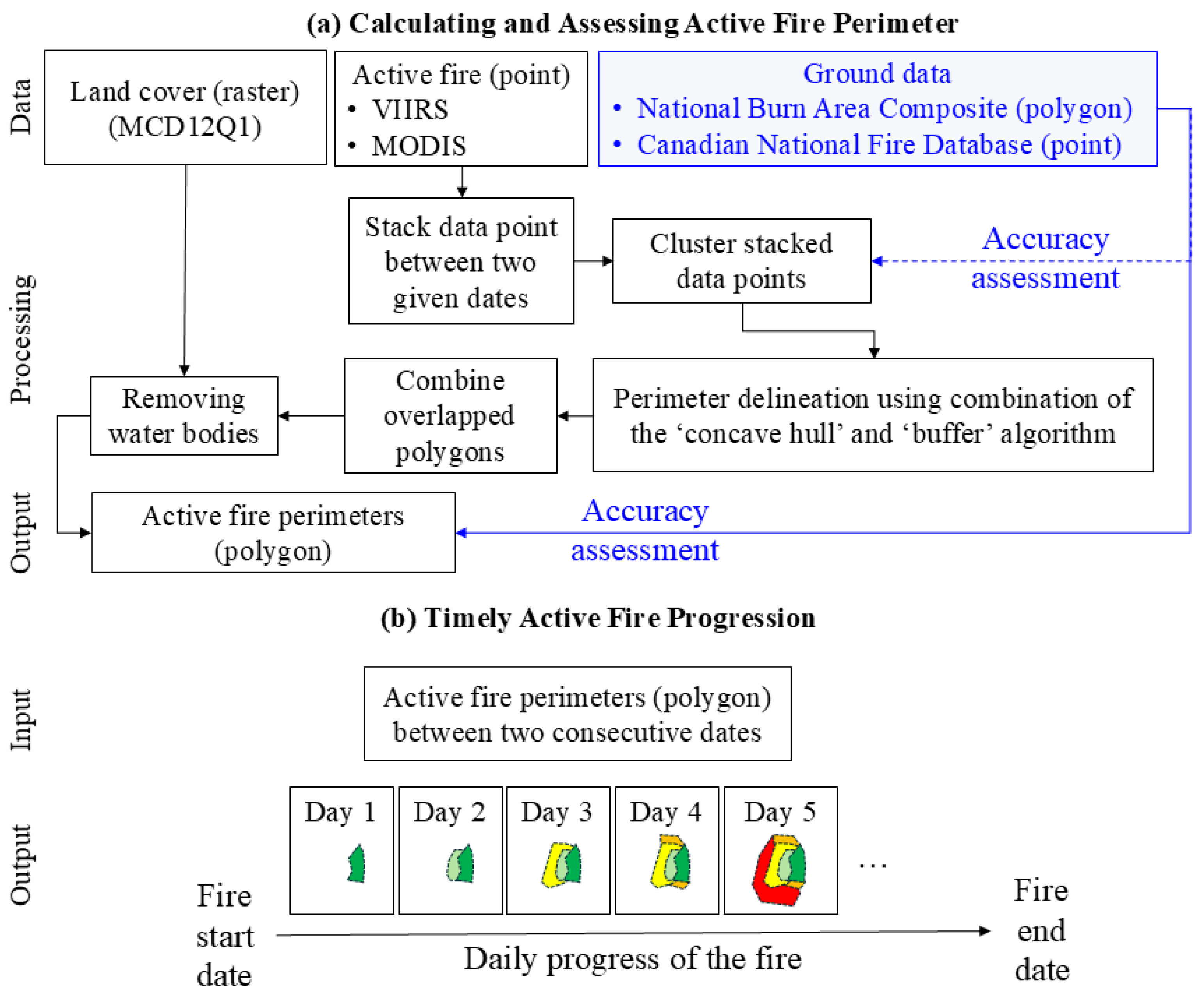
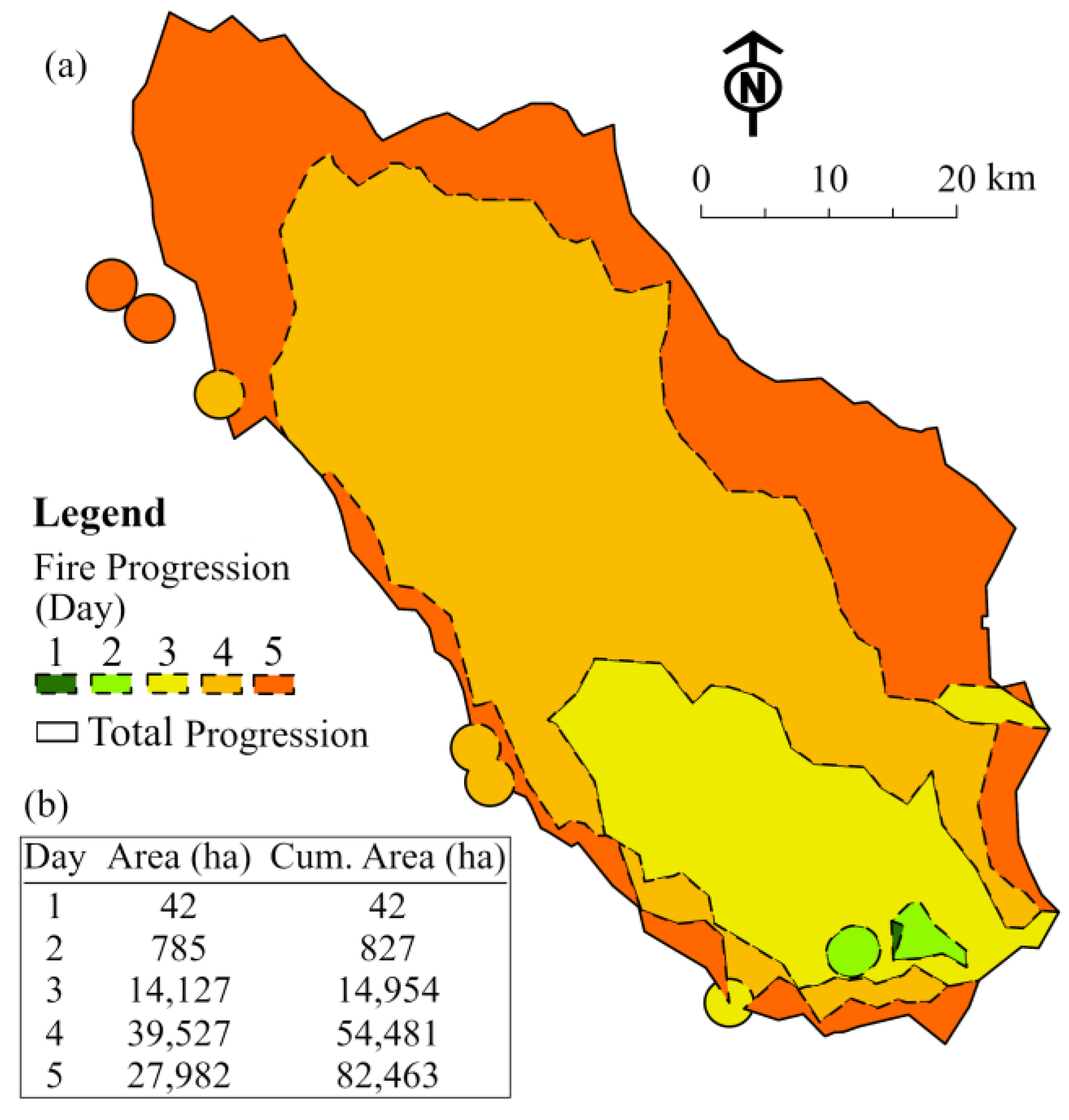
#Fire NumberArea (ha)Start DateEnd DateAffected RegionsAlias
1MWF-059-20213605.3610-Jul-202103-Aug-2021ABMuskeg Complex
2MWF-079-20213263.4910-Jul-202109-Dec-2021AB-
3HWF-042-2019335,032.5612-May-201913-Oct-2020ABChuckegg Creek
4HWF-066-201964,711.0427-May-201908-May-2020ABJackpot Creek
5MWF-051-201924,040.2017-Jul-201930-Aug-2019ABOld Fort Complex
6MWF-054-20198213.2617-Jul-201930-Aug-2019ABBocquene Complex
7PWF-052-201936,520.7611-May-201916-Oct-2020ABBattle–Battle Complex
8SWF-049-2019222,869.0518-May-201919-Oct-2020ABMcMillan Complex
9SS-010-20193715.3916-Jun-201920-Aug-2019NT-
10SS-021-20193045.5717-Jul-201903-Aug-2019AB–NT-
11HWF-083-20184117.3424-May-201815-Jul-2018ABLittle Rapids
12HWF-137-20183600.4022-Jun-201807-Sep-2018AB-
13HWF-177-20182633.7526-Jul-201807-Dec-2018AB-
14LWF-099-20187278.6321-May-201819-Jul-2018ABRock Island Complex
15SWF-094-20185028.9723-Jun-201828-Nov-2018ABRabbit Lake
16HWF-221-20174709.0005-Aug-201717-Nov-2017AB-
17HWF-252-20171703.3714-Aug-201717-Nov-2017AB-
18HWF-280-201713,638.2701-Sep-201717-Nov-2017AB-
19SWF-107-201712,729.1409-Aug-201720-May-2018ABMuskrat Lake
20SS-019-2017269,583.5513-Jul-201725-Sep-2017NT-
21ABC-001-201672,527.4718-Apr-201629-Jul-2016AB–BCSweeney Creek
22HWF-100-2016229.6607-Jun-201620-Jun-2016AB
23HWF-193-2016553.5313-Jul-201603-May-2017AB-
24MWF-009-2016490,964.7901-May-201602-Aug-2017ABHorse River
25SWF-030-20161671.4830-Apr-201613-Jun-2016AB-
26MWF-052-201522,356.6522-Jun-201512-Nov-2015AB-
27MWF-101-201557,674.0823-Jun-201512-Nov-2015AB-
28WB-004-2015223,766.9628-May-201501-Oct-2015AB-
29WB-039-201518,572.7627-Jun-201512-Aug-2015AB–NT-
30HBZ-001-201517,932.2825-Jun-201507-Jul-2015AB–BC-
Table 2. Accuracy assessment of fire clustering for detecting individual fires. The table compares calculated fire polygons from VIIRS, MODIS, and the combined datasets against CNFDB fire occurrence data (2015–2019). Matching hotspots (HSs), point omission error (OE), and point commission error (CE) were computed using Equations (1)–(3). For each fire size class, the table provides the fraction (actual/total), percentage (%), cumulative fraction (Cum. Frac.), and cumulative percentage (cum. %).
Table 2. Accuracy assessment of fire clustering for detecting individual fires. The table compares calculated fire polygons from VIIRS, MODIS, and the combined datasets against CNFDB fire occurrence data (2015–2019). Matching hotspots (HSs), point omission error (OE), and point commission error (CE) were computed using Equations (1)–(3). For each fire size class, the table provides the fraction (actual/total), percentage (%), cumulative fraction (Cum. Frac.), and cumulative percentage (cum. %).
Data SourceVIIRSMODISCombination
Class
(ha)		CalculationMatching
HSs		Point
OE		Point
CE		Matching
HSs		Point
OE		Point
CE		Matching
HSs		Point
OE		Point
CE
≥100 Fraction163/17310/17314/163152/17321/17316/153166/1737/17324/172
%94.225.788.5987.8612.1410.4695.954.0513.95
50 ≥ Area < 100 Fraction37/5518/5522/5933/5522/559/4240/5515/5525/65
%67.2732.7337.2960.0040.0021.4372.7327.2738.46
Cum. Frac.200/22828/22836/222185/22843/22825/195206/22822/22829/237
Cum.
%		87.7212.2816.2281.1518.8512.8290.359.6512.23
25 ≥ Area < 50 Fraction30/6232/6247/7724/6238/6221/5134/6228/6253/87
%48.3951.6161.0438.7161.2941.1854.8445.1660.92
Cum. Frac.230/29060/29083/299209/29081/29046/246240/29050/29082/324
Cum.
%		79.3120.6927.7672.0627.9418.7082.7617.2425.30
10 ≥ Area < 25 Fraction38/9860/9866/10435/9863/9814/4942/9856/9857/99
%38.7861.2263.4635.7164.2928.5742.8657.1457.58
Cum. Frac.268/388120/388149/403244/388144/38860/295282/388106/388139/423
Cum.
%		69.0730.9336.9762.8837.1220.3372.6827.3232.86
Table 3. Matching and commission error (CE) percentages for VIIRS and MODIS active fire datasets (2015–2021) across varying concave alpha (α) values (0.1 to 0.5) and radius distances (750 m to 3000 m). Matching values represent the alignment between the calculated fire area and ground-truth data (NBAC), while the CE reflects the degree of overestimation in the calculated area. Higher α values and larger radii lead to improved matching rates but are consistently accompanied by an increase in CE, indicating potential overestimation, particularly at larger radii.
Table 3. Matching and commission error (CE) percentages for VIIRS and MODIS active fire datasets (2015–2021) across varying concave alpha (α) values (0.1 to 0.5) and radius distances (750 m to 3000 m). Matching values represent the alignment between the calculated fire area and ground-truth data (NBAC), while the CE reflects the degree of overestimation in the calculated area. Higher α values and larger radii lead to improved matching rates but are consistently accompanied by an increase in CE, indicating potential overestimation, particularly at larger radii.
Radius (m)α ValuesVIIRS (%)MODIS (%)
0.10.20.30.40.50.10.20.30.40.5
750Area matching72.2274.7775.9576.6176.99*****
Area CE21.0023.5124.9325.9226.64*****
1000Area matching*****59.8662.1763.0063.6163.89
Area CE*****35.3936.1536.3336.4936.58
1125Area matching77.8379.7280.5881.0881.34*****
Area CE22.4324.6226.0127.0927.62*****
1500Area matching79.43 82.89 83.8384.3484.6662.2066.4767.8968.6869.14
Area CE22.22 25.38 26.8228.0528.8028.2230.3931.4031.8832.53
2000Area matching*****63.8669.2470.8171.8172.19
Area CE*****27.4729.8231.1031.9432.67
2500Area matching*****64.4871.3473.0573.8874.23
Area CE*****26.8229.7831.5232.4133.30
3000Area matching*****64.60 72.22 73.9374.6475.03
Area CE*****26.69 29.63 31.4732.4233.25
* These tests were not assessed due to inconsistencies in the spatial resolution of data points from MODIS and VIIRS, as well as the overestimation of commission error limits.
Table 4. Matching and commission error (CE) percentages for the combined VIIRS and MODIS active fire datasets (2015–2021), assessed across varying concave alpha (α) values (0.1 to 0.5) and radius distances (750 m to 1500 m), with additional analysis for minimum sample sizes of 3 and 4 for active fire perimeter calculations. Matching rates improved with increasing α values and radii, though the CE consistently increased, indicating overestimation. The best balance between matching and CE was achieved at a 1500 m radius with an α value of 0.1.
Table 4. Matching and commission error (CE) percentages for the combined VIIRS and MODIS active fire datasets (2015–2021), assessed across varying concave alpha (α) values (0.1 to 0.5) and radius distances (750 m to 1500 m), with additional analysis for minimum sample sizes of 3 and 4 for active fire perimeter calculations. Matching rates improved with increasing α values and radii, though the CE consistently increased, indicating overestimation. The best balance between matching and CE was achieved at a 1500 m radius with an α value of 0.1.
Radius (m)α Values0.10.20.30.40.5
750Area matching81.0282.6983.4083.9384.20
Area CE30.9832.5533.5734.5034.76
1000Area matching82.8084.2385.6586.1486.30
Area CE28.5830.1931.9932.9733.49
1125Area matching83.4285.8286.6787.0387.19
Area CE28.2730.5931.9533.0633.64
1500Area matching85.1387.7088.7389.0989.29
Area CE27.9630.9332.4133.5434.35
1500
(sample size: ≥4)		Area matching85.1287.71***
Area CE28.0531.01***
* These tests were not assessed due to inconsistencies in the spatial resolution of data points from MODIS and VIIRS, as well as the overestimation of commission error limits.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Dastour, H.; Bhuian, H.; Ahmed, M.R.; Hassan, Q.K. Active Fire Clustering and Spatiotemporal Dynamic Models for Forest Fire Management. Fire 2024, 7, 355. https://doi.org/10.3390/fire7100355

AMA Style

Dastour H, Bhuian H, Ahmed MR, Hassan QK. Active Fire Clustering and Spatiotemporal Dynamic Models for Forest Fire Management. Fire. 2024; 7(10):355. https://doi.org/10.3390/fire7100355

Chicago/Turabian Style

Dastour, Hatef, Hanif Bhuian, M. Razu Ahmed, and Quazi K. Hassan. 2024. "Active Fire Clustering and Spatiotemporal Dynamic Models for Forest Fire Management" Fire 7, no. 10: 355. https://doi.org/10.3390/fire7100355

APA Style

Dastour, H., Bhuian, H., Ahmed, M. R., & Hassan, Q. K. (2024). Active Fire Clustering and Spatiotemporal Dynamic Models for Forest Fire Management. Fire, 7(10), 355. https://doi.org/10.3390/fire7100355

Article Metrics

Back to TopTop