An Experimental Study of Pool Fire Characteristics under the Effects of Cross Winds and Baffles
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. Numerical Analysis
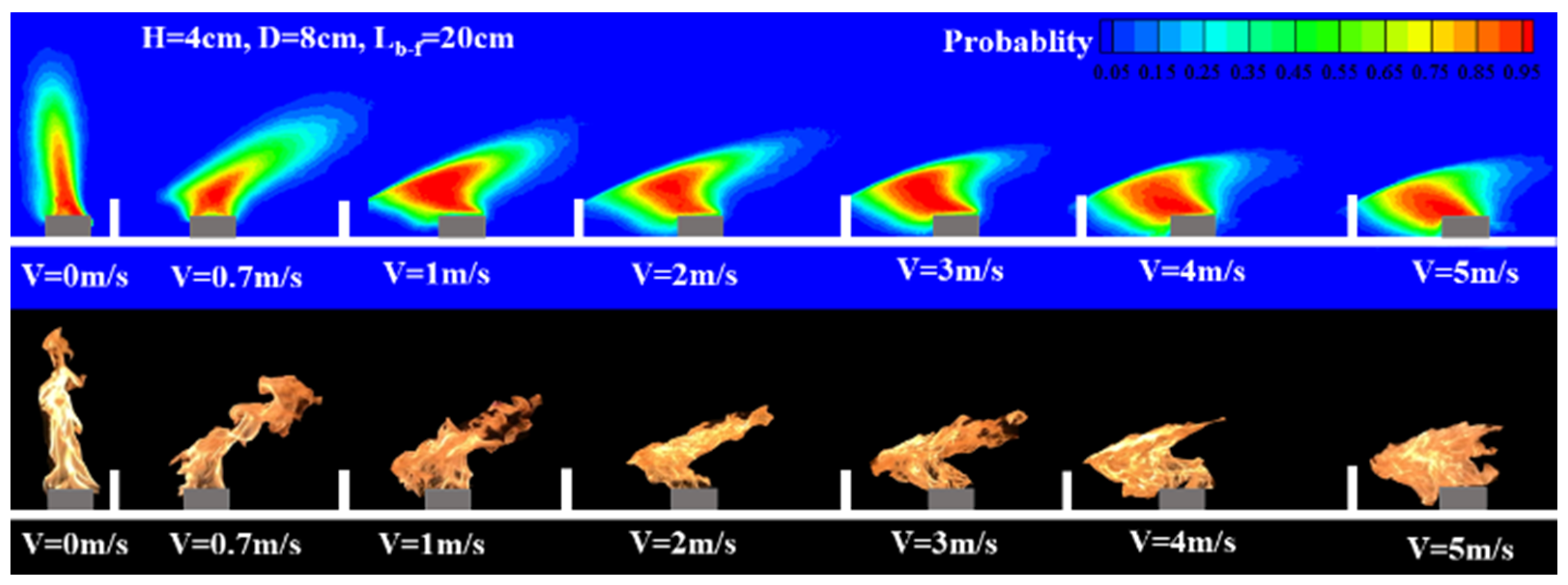
3.2. Typical Flame Images
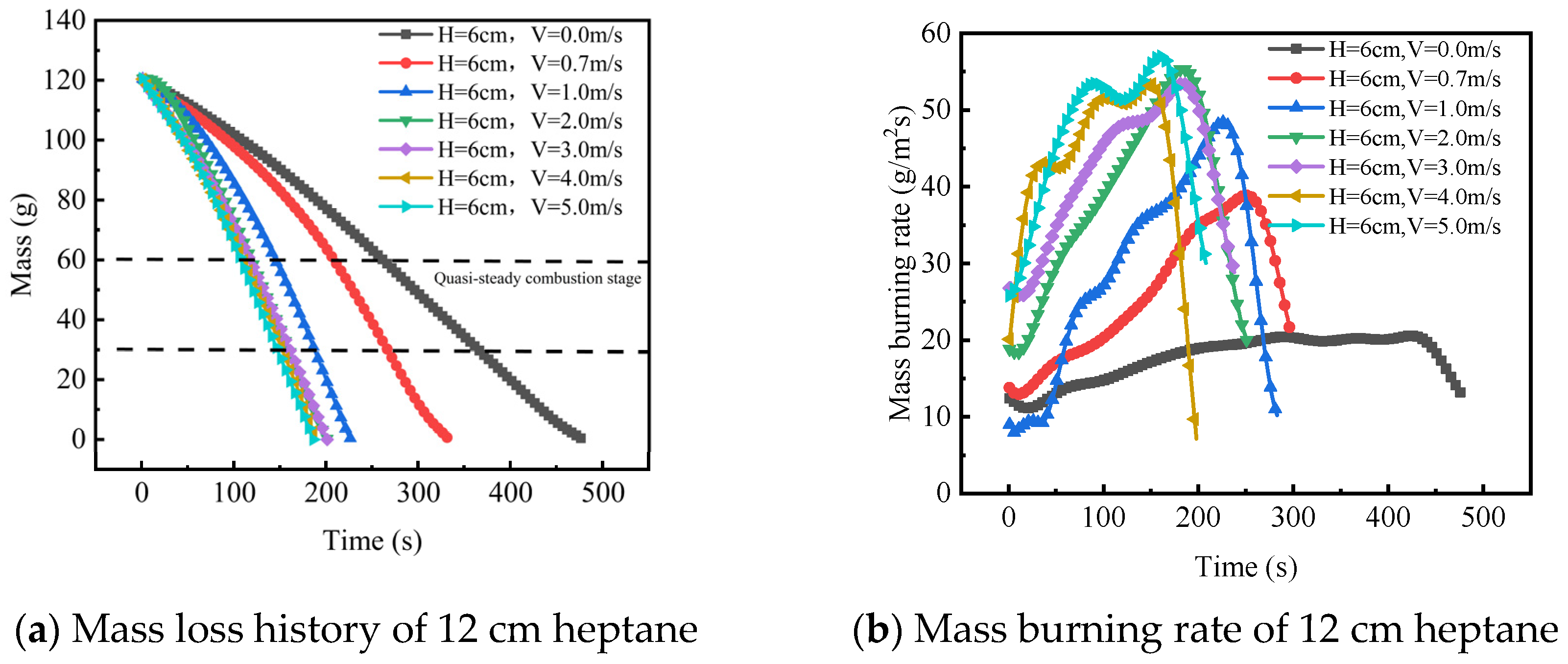
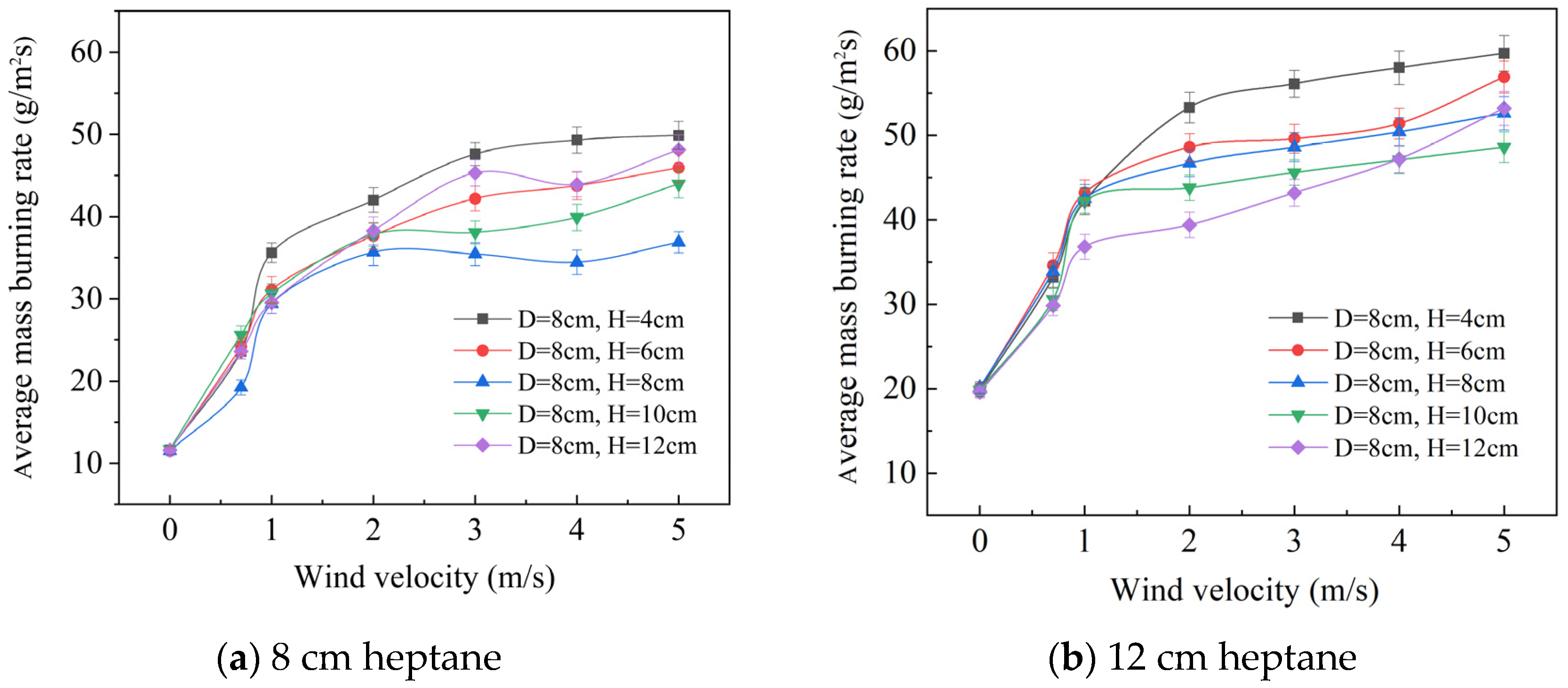
3.3. Mass Burning Rate
3.4. Flame Length and Tilt Angle
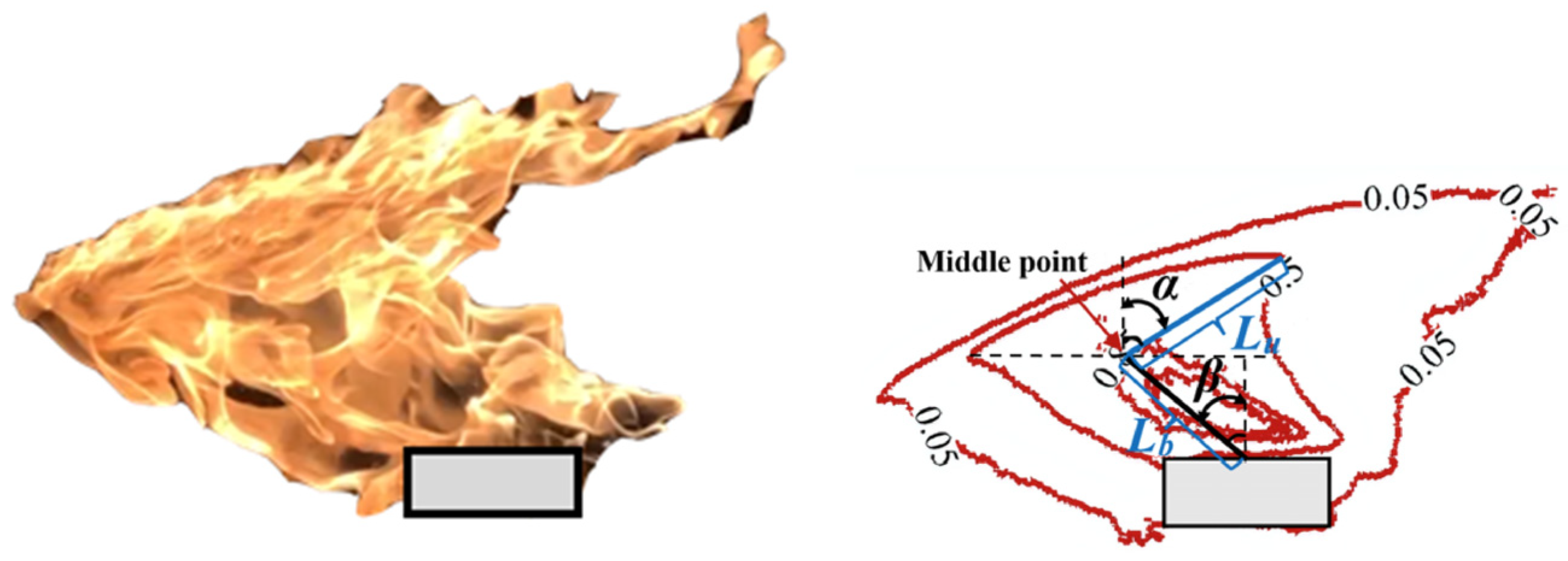
3.4.1. Definitions
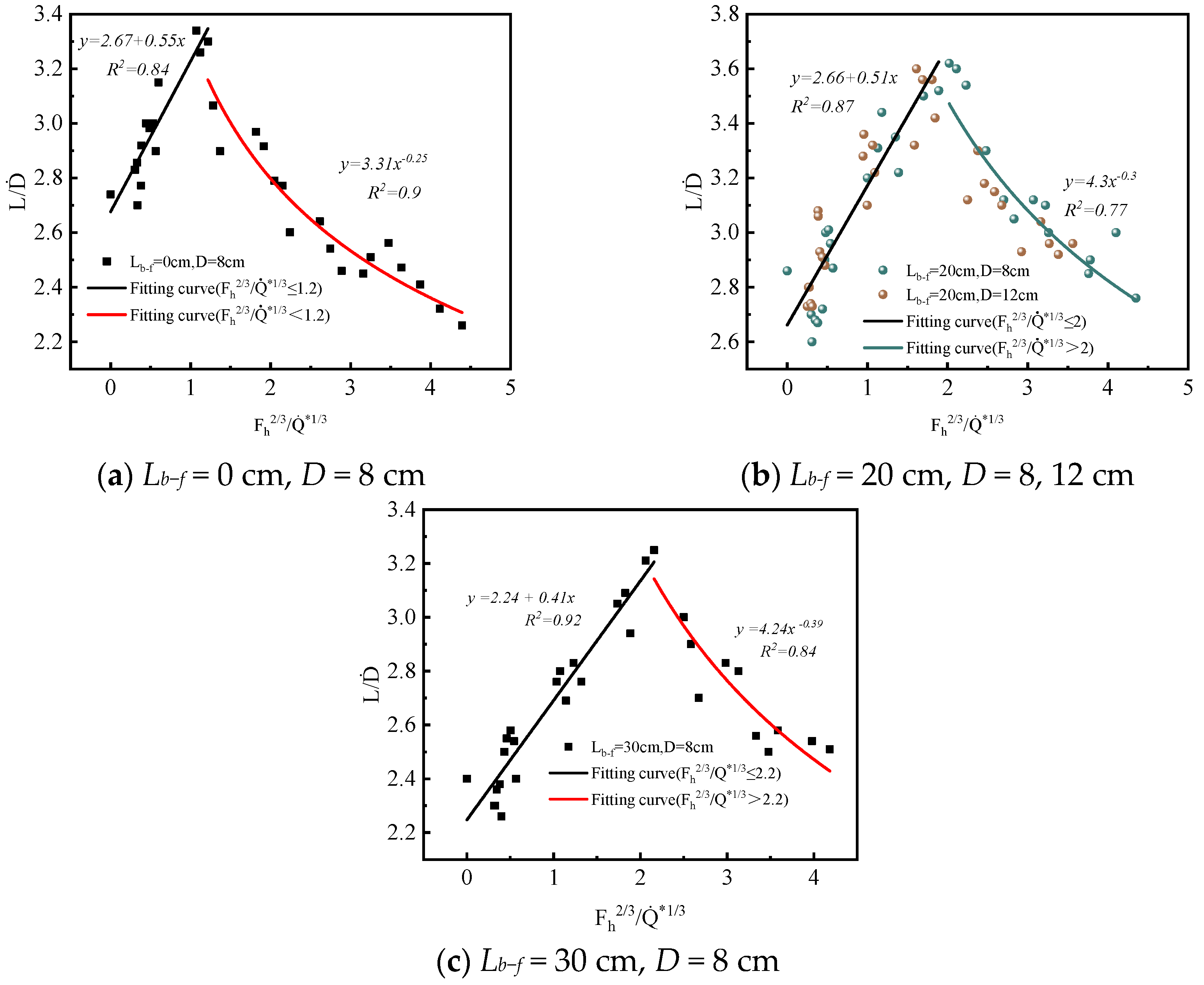
3.4.2. Flame Length
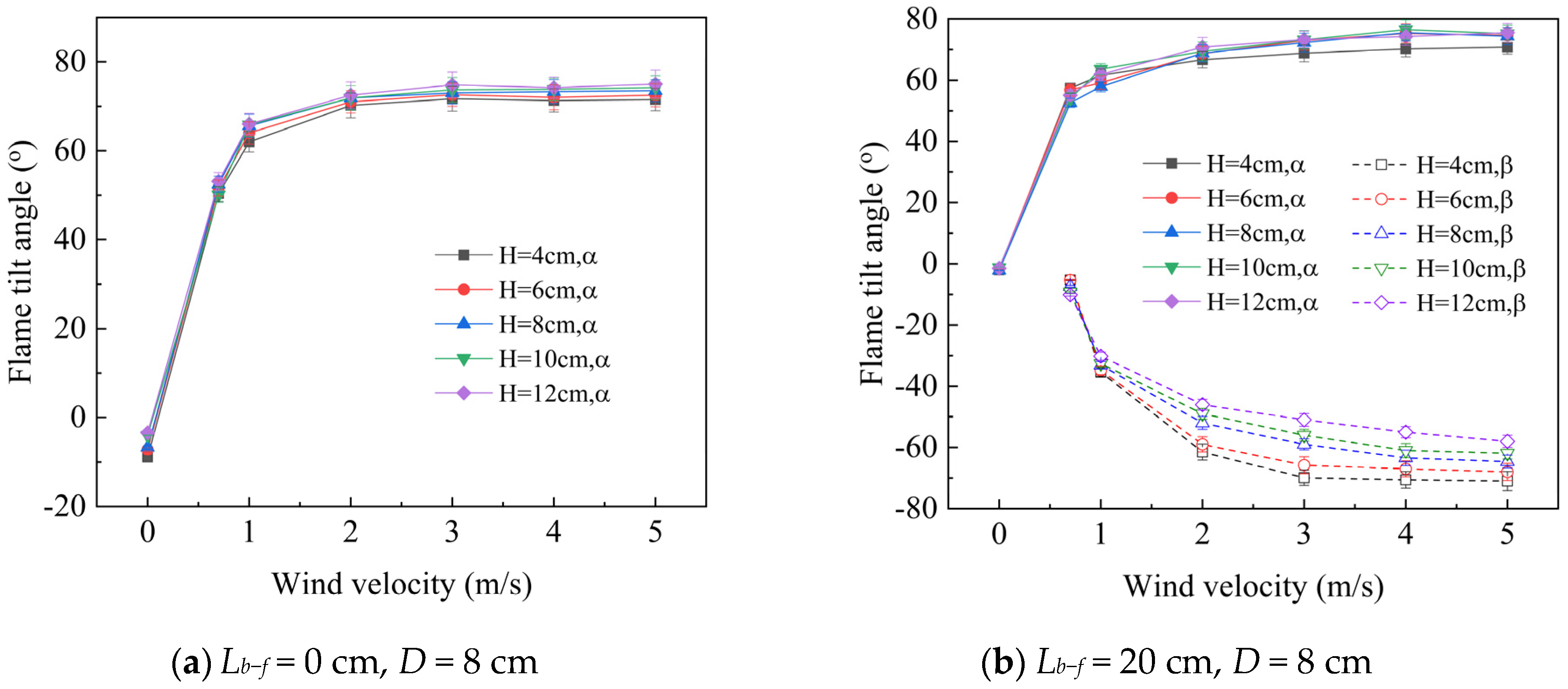
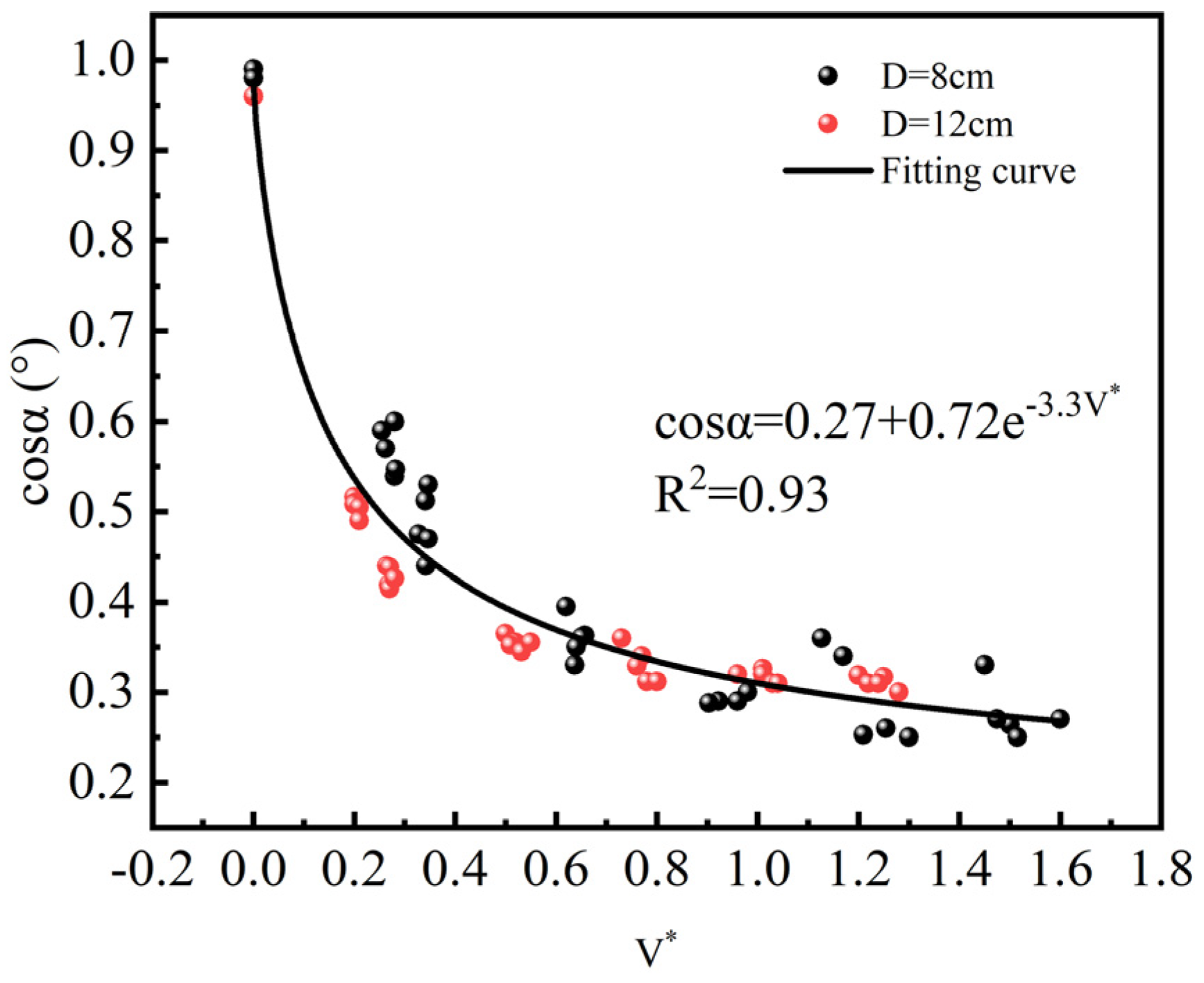
3.4.3. Flame Tilt Angle
4. Conclusions
- The flame behind the baffle bends due to the pulling forces in two opposite directions. The bottom flame below the baffle is pulled towards the baffle by the momentum of the recirculation flow behind it. The upper flame above the baffle is fanned and extends downstream by the cross wind in the mainstream zone.
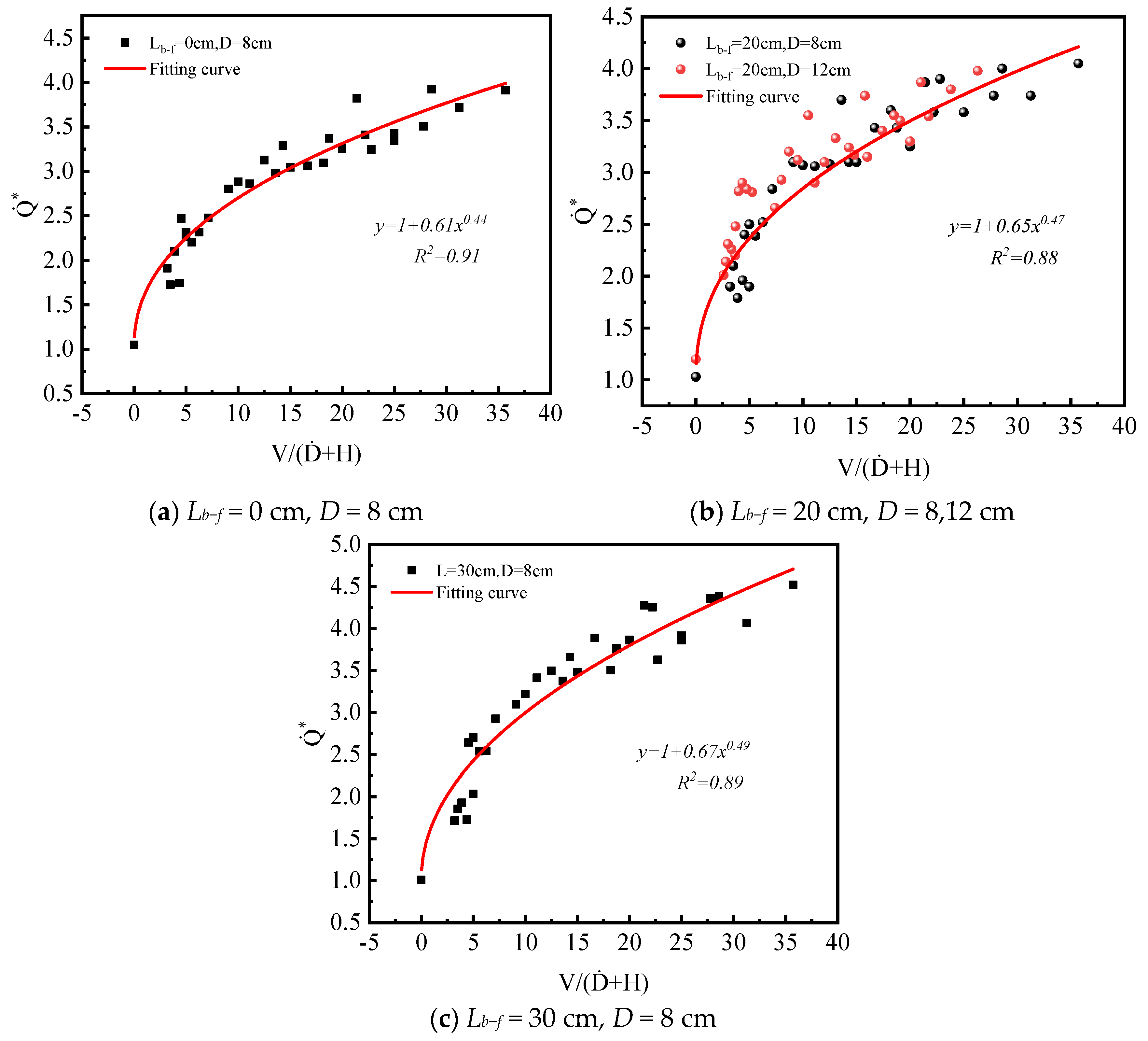
- The burning rate of the pool fire increases and the fire size enlarges as the cross wind velocity increases. With an increase in baffle height, the burning rate initially decreases and then gradually increases. Empirical correlations have been proposed to predict the dimensionless heat release rate in relation to the baffle height and cross wind velocity with different distances between the baffle and flame.
- The flame length increases at first and then decreases as the wind velocity increases due to the combined effects of the baffle and cross wind. To quantify the relationship between the flame length, baffle height, and cross wind velocity, a dimensionless coefficient, Fh, has been introduced.
- The tilt angle α of the upper flame is primarily influenced by cross wind, which increases rapidly when the ventilation velocity is below 1 m/s and then remains constant. The tilt angle β of the bottom flame is affected by three factors. When the cross wind velocity or the distance between the baffle and fire increases, the tilt angle β becomes larger. Conversely, when the baffle height increases, the tilt angle β becomes smaller.
- Based on the experimental results, it can be predicted that the presence of ventilation and obstacles within the aircraft engine nacelle will increase the intensity of oil leakage fires and tilt the flame, therefore increasing the likelihood of the flame spreading. To decrease the intensity of the flames and slow down the rate of spreading, it is recommended to lower the ventilation intensity within the aircraft engine nacelle in the event of a fire, and to avoid placing combustible materials such as cables near obstacles. This study only focused on specific conditions involving particular wind speeds and obstacle heights. Further research is needed, including scaled and full-scale fire experiments, to achieve a deeper understanding of the characteristics of aircraft engine fires.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gann, R.G. Advanced Technology for Fire Suppression in Aircraft; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2007.
- Wild, T.W. Aircraft: Powerplants, 9th ed.; McGraw-Hill Education: New York, NY, USA, 2018. [Google Scholar]
- Gann, R.G. Guidance for advanced fire suppression in aircraft. Fire Technol. 2008, 44, 263–282. [Google Scholar] [CrossRef]
- Hradecky, S. Incident: Aerostan B742 at Macau on Nov 23rd 2022, Engine Shut Down in Flight, The Aviation Herald. 2022. Available online: https://avherald.com/h?article=5017f4ef (accessed on 24 November 2022).
- Takahashi, F.; Schmoll, W.; Belovich, V. Suppression of bluff-body stabilized diffusion flames. In Proceedings of the 34th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Cleveland, OH, USA, 13–15 July 1998. [Google Scholar] [CrossRef]
- Takahashi, F.; Schmoll, W.; Strader, E.A. Suppression behavior of obstruction-stabilized pool flames. Combust. Sci. Technol. 2001, 163, 107–130. [Google Scholar] [CrossRef]
- Hirst, R.; Farenden, P.J.; Simmons, R.F. The extinction of fires in aircraft jet engines—Part I, small-scale simulation of fires. Fire Technol. 1976, 12, 266–275. [Google Scholar] [CrossRef]
- Hirst, R.; Farenden, P.J.; Simmons, R.F. The extinction of fires in aircraft jet engines—Part II, full-scale fire tests. Fire Technol. 1977, 13, 59–67. [Google Scholar] [CrossRef]
- Hu, L.; Liu, S.; Xu, Y.; Li, D. A wind tunnel experimental study on burning rate enhancement behavior of gasoline pool fires by cross air flow. Combust. Flame 2011, 158, 586–591. [Google Scholar] [CrossRef]
- Tang, F.; Li, L.J.; Zhu, K.J.; Qiu, Z.W.; Tao, C.F. Experimental study and global correlation on burning rates and flame tilt characteristics of acetone pool fires under cross air flow. Int. J. Heat Mass Transf. 2015, 87, 369–375. [Google Scholar] [CrossRef]
- Oka, Y.; Sugawa, O.; Imamura, T.; Matsubara, Y. Effect of cross-winds to apparent flame height and tilt angle from several kinds of fire source. Fire Saf. Sci. 2003, 7, 915–926. [Google Scholar] [CrossRef]
- Ouyang, R.; Zhao, W.; Yang, L.; Jiao, A.; Xu, Z.; Fan, C. An experimental investigation of burning rate and flame geometric parameters of tunnel fires under canyon cross wind and longitudinal ventilation. Fire Saf. J. 2021, 126, 103474. [Google Scholar] [CrossRef]
- Mao, S.; Liu, S.; Yu, S.; Li, B.; Hao, W.; Chen, H. Experimental investigation of the burning characteristics of aviation fuel under atmospheric crosswind conditions. Fuel 2023, 332, 125981. [Google Scholar] [CrossRef]
- Ji, J.; Li, F.; Lu, W.; Sun, R.; Wang, K.; Cao, Y. An experimental study on flame geometry in wind-blown pool fires and a new dimensionless parameter. Case Stud. Therm. Eng. 2022, 30, 101782. [Google Scholar] [CrossRef]
- Ingason, H.; Li, Y.Z. Model scale tunnel fire tests with longitudinal ventilation. Fire Saf. J. 2010, 45, 371–384. [Google Scholar] [CrossRef]
- Shafee, S.; Yozgatligil, A. An analysis of tunnel fire characteristics under the effects of vehicular blockage and tunnel inclination. Tunn. Undergr. Space Technol. 2018, 79, 274–285. [Google Scholar] [CrossRef]
- Cong, W.; He, K.; Yang, H.; Peng, M.; Nan, T.; Shi, L.; Cheng, X. Effects of blockage on the flame morphologic characteristics in a ventilated tunnel. Tunn. Undergr. Space Technol. 2022, 123, 104410. [Google Scholar] [CrossRef]
- Chen, X.; Ding, Z.; Lu, S. Investigation of sidewall height effect on the burning rate and flame tilt characteristics of pool fire in cross wind. Fire Saf. J. 2021, 120, 103111. [Google Scholar] [CrossRef]
- Meng, N.; Liu, B.; Li, X.; Jin, X.; Huang, Y.; Wang, Q. Effect of blockage-induced near wake flow on fire properties in a longitudinally ventilated tunnel. Int. J. Therm. Sci. 2018, 134, 1–12. [Google Scholar] [CrossRef]
- Yu, Z.; Huang, X. Study of baffle height and wind velocity effect on the characteristics of pool fires in a wind tunnel. Appl. Sci. 2023, 13, 1920. [Google Scholar] [CrossRef]
- McGrattan, K.; Hostikka, S.; Floyd, J.; Vanella, M.; Craig, W.; Overholt, K. Fire Dynamics Simulator, User’s Guide; NIST Special Publication 1019, 6th ed.; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2017.
- McGrattan, K.; Baum, H.; Rehm, R. Large eddy simulation of smoke movement. Fire Saf. J. 1998, 30, 161–178. [Google Scholar] [CrossRef]
- Hill, K.; Dreisbach, J.; Joglar, F.; Najafi, B.; McGrattan, K.; Peacock, R.; Hamins, A. Verification and Validation of Selected Fire Models for Nuclear Power Plant Applications; United States Nuclear Regulatory Commission: Washington, DC, USA, 2007.
- Raghunandan, B.N.; Yogesh, G.P. Recirculating flow over a burning surface—Flame structure and heat transfer augmentation. Symp. Int. Combust. 1989, 22, 1501–1507. [Google Scholar] [CrossRef]
- Siller, H.A.; Fernholz, H.H. Separation behaviour in front of a two-dimensional fence. Eur. J. Mech.-B/Fluids 2001, 20, 727–740. [Google Scholar] [CrossRef]
- Counihan, J.J.C.R.; Hunt, J.C.R.; Jackson, P.S. Wakes behind two-dimensional surface obstacles in turbulent boundary layers. J. Fluid Mech. 1974, 64, 529–564. [Google Scholar] [CrossRef]
- Schofield, W.H.; Logan, E. Turbulent shear flow over surface mounted obstacles. Transactions of the ASME. J. Fluids Eng. 1990, 112, 376–385. [Google Scholar] [CrossRef]
- Hu, L.H.; Liu, S.; Peng, W.; Huo, R. Experimental study on burning rates of square/rectangular gasoline and methanol pool fires under longitudinal air flow in a wind tunnel. J. Hazard. Mater. 2009, 169, 972–979. [Google Scholar] [CrossRef] [PubMed]
- Blinov, V.I.; Khudyakov, G.N. Diffusion Burning of Liquids; Army Engineer Research and Development Labs: Fort Belvoir, VA, USA, 1961. [Google Scholar]
- Hurley, M.J.; Gottuk, D.T.; Hall, J.R., Jr.; Harada, K.; Kuligowski, E.D.; Puchovsky, M.; Wieczorek, C.J. SFPE Handbook of Fire Protection Engineering; Springer: Cham, Switzerlands, 2015. [Google Scholar] [CrossRef]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Hu, L. A review of physics and correlations of pool fire behaviour in wind and future challenges. Fire Saf. J. 2017, 91, 41–55. [Google Scholar] [CrossRef]
- Oka, Y.; Kurioka, H.; Satoh, H.; Sugawa, O. Modelling of unconfined flame tilt in cross-winds. Fire Saf. Sci. 2000, 6, 1101–1112. [Google Scholar] [CrossRef]
- Gao, W.; Liu, N.; Jiao, Y.; Xie, X.; Pan, Y.; Li, Z.; Tu, R. Flame length of buoyant turbulent slot flame. Proc. Combust. Inst. 2019, 37, 3851–3858. [Google Scholar] [CrossRef]
- Zhou, B.; Yoshioka, H.; Noguchi, T.; Ando, T. Experimental study on vertical temperature profile of buoyant window spill plume from intermediate-scale compartments. Fire Mater. 2020, 44, 516–529. [Google Scholar] [CrossRef]
- Thomas, P.H. The size of flames from natural fires. Symp. Int. Combust. 1963, 9, 844–859. [Google Scholar] [CrossRef]
- Zhou, B.; Yoshioka, H.; Noguchi, T.; Wang, K.; Huang, X. Upward fire spread rate over real-scale EPS ETICS Facades. Fire Technol. 2021, 57, 2007–2024. [Google Scholar] [CrossRef]
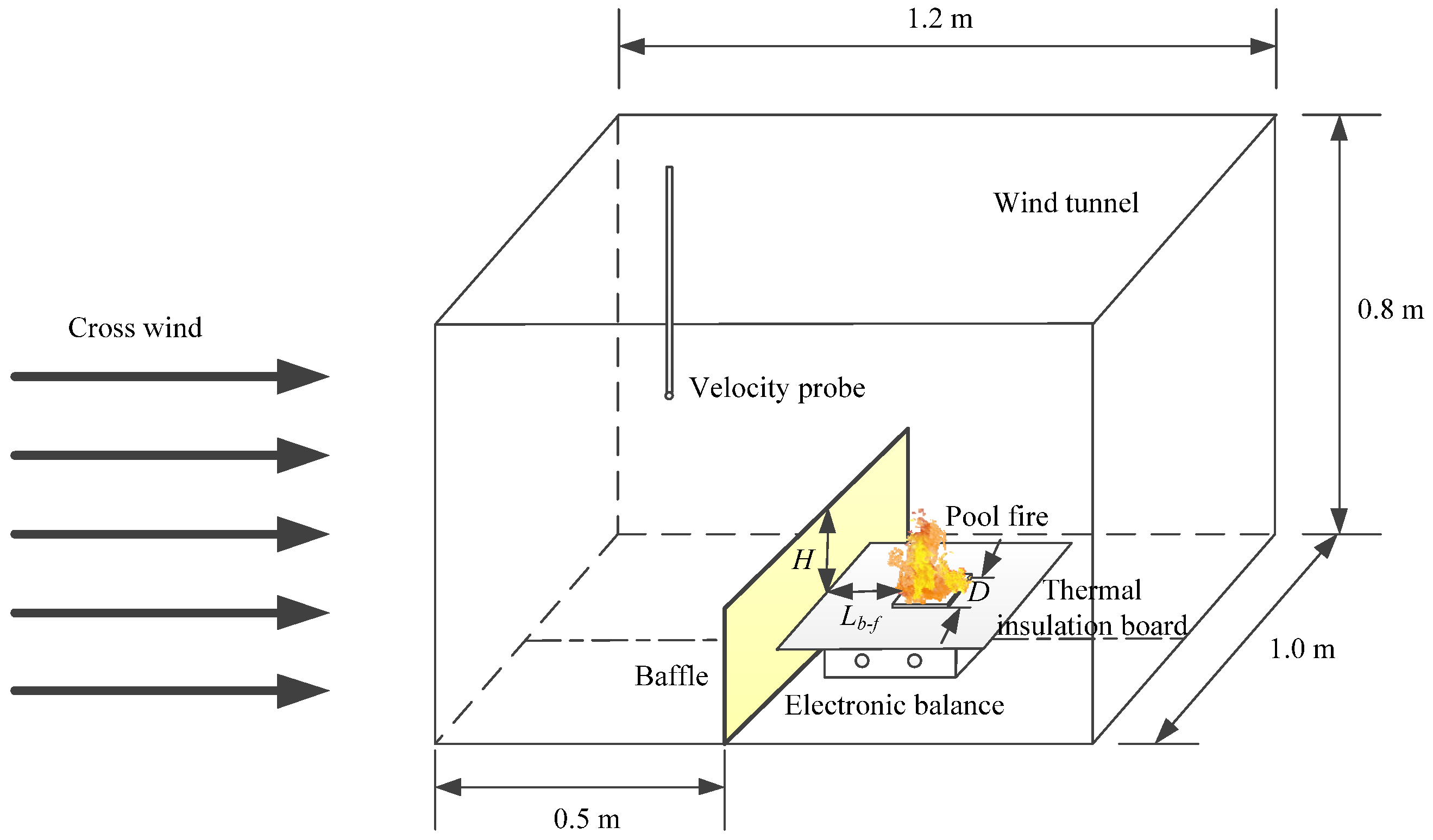
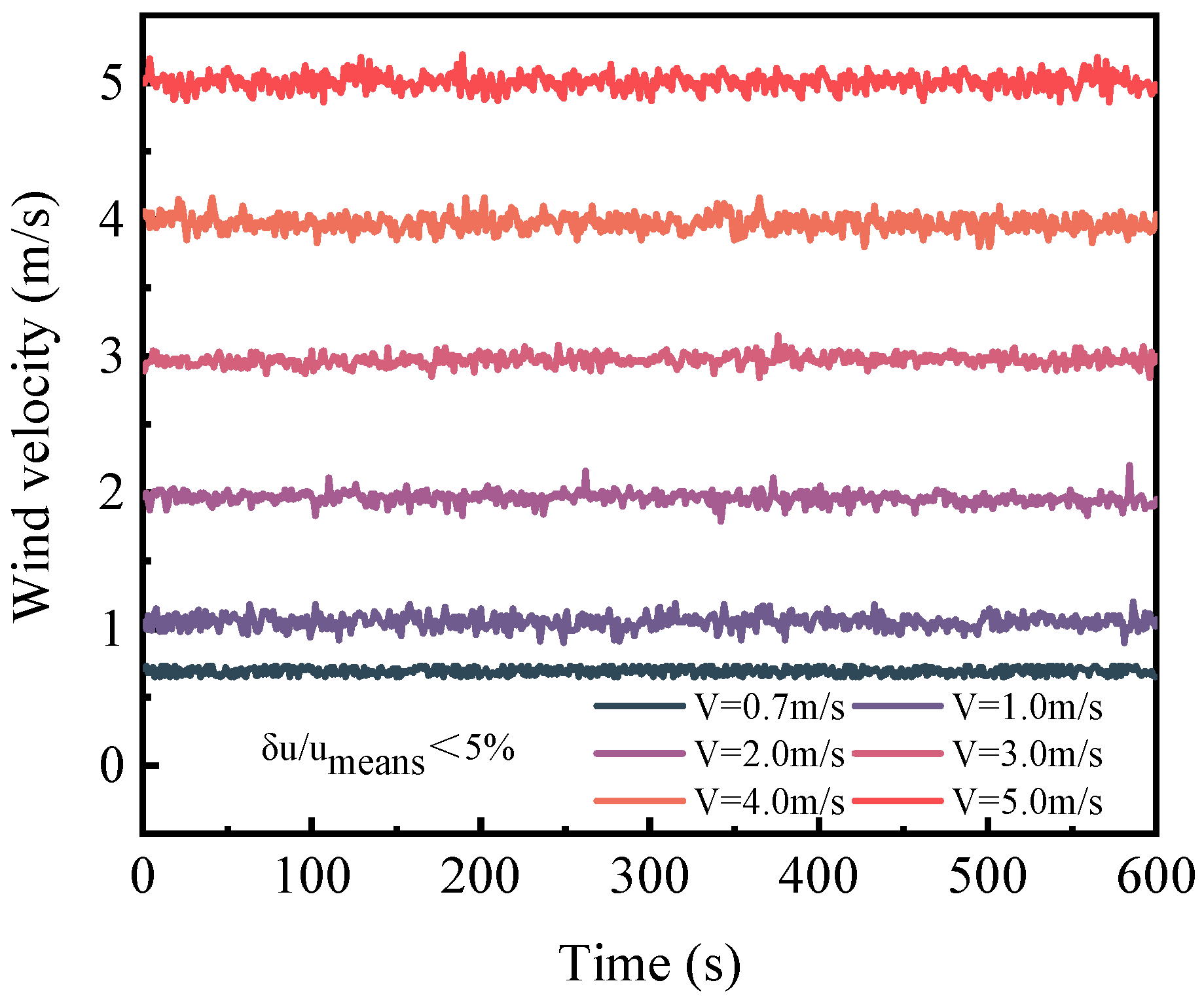


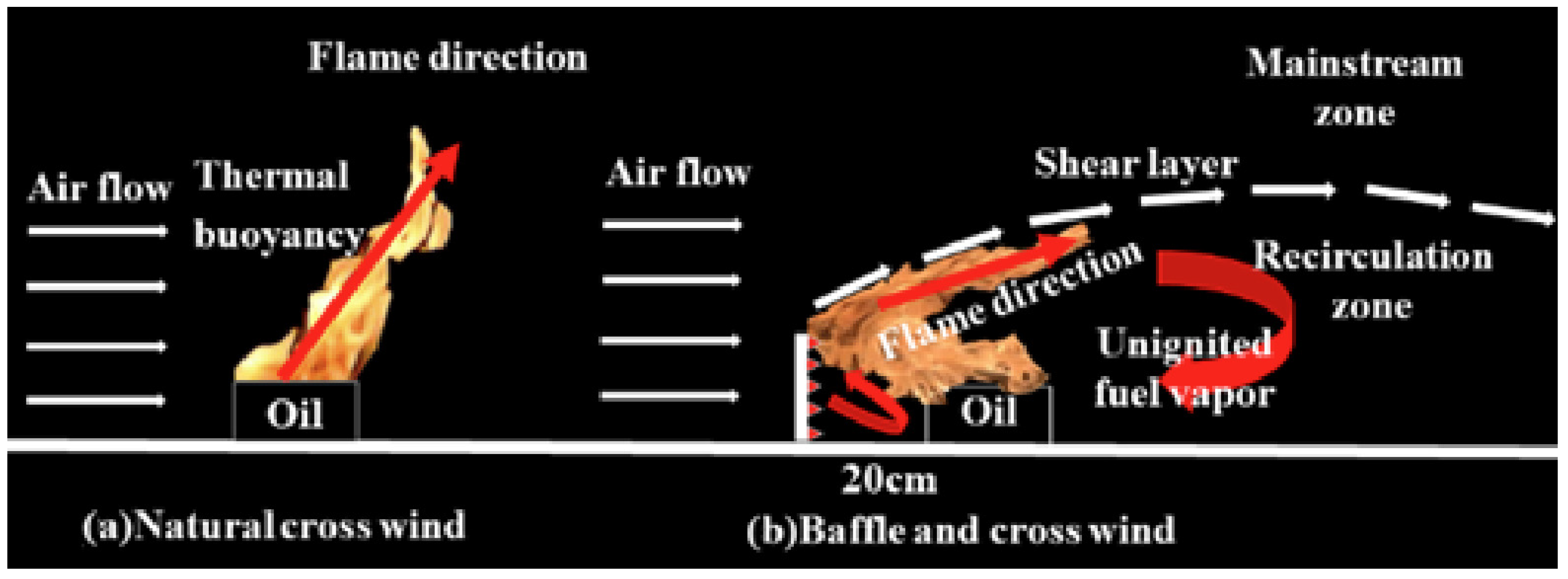
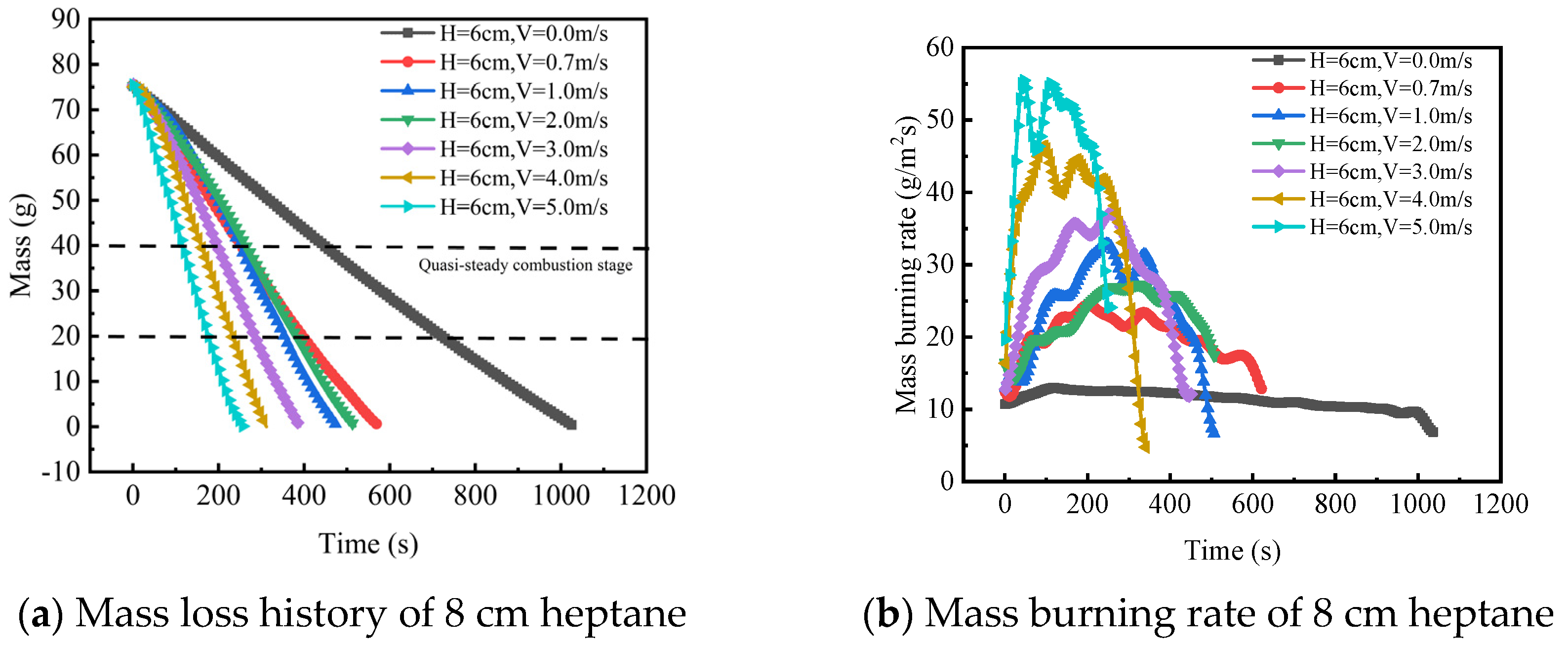

| Test No. | D (cm) | Lb−f (cm) | V (m/s) | H (cm) |
|---|---|---|---|---|
| 1–35 | 8 | 0 | 0, 0.7, 1, 2, 3, 4, 5 | 4, 6, 8, 10, 12 |
| 36–70 | 8 | 20 | 0, 0.7, 1, 2, 3, 4, 5 | 4, 6, 8, 10, 12 |
| 71–105 | 12 | 20 | 0, 0.7, 1, 2, 3, 4, 5 | 4, 6, 8, 10, 12 |
| 105–140 | 8 | 30 | 0, 0.7, 1, 2, 3, 4, 5 | 4, 6, 8, 10, 12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, X.; Yu, Z.; Zhan, Z. An Experimental Study of Pool Fire Characteristics under the Effects of Cross Winds and Baffles. Fire 2024, 7, 4. https://doi.org/10.3390/fire7010004
Huang X, Yu Z, Zhan Z. An Experimental Study of Pool Fire Characteristics under the Effects of Cross Winds and Baffles. Fire. 2024; 7(1):4. https://doi.org/10.3390/fire7010004
Chicago/Turabian StyleHuang, Xin, Zhilei Yu, and Zhiming Zhan. 2024. "An Experimental Study of Pool Fire Characteristics under the Effects of Cross Winds and Baffles" Fire 7, no. 1: 4. https://doi.org/10.3390/fire7010004
APA StyleHuang, X., Yu, Z., & Zhan, Z. (2024). An Experimental Study of Pool Fire Characteristics under the Effects of Cross Winds and Baffles. Fire, 7(1), 4. https://doi.org/10.3390/fire7010004






