Experimental Study on the Effect of Sub-Flash Point Fuel Temperature on the Spread Characteristics of Spill Fire
Abstract
1. Introduction
2. Experimental Setup
3. Results and Discussion
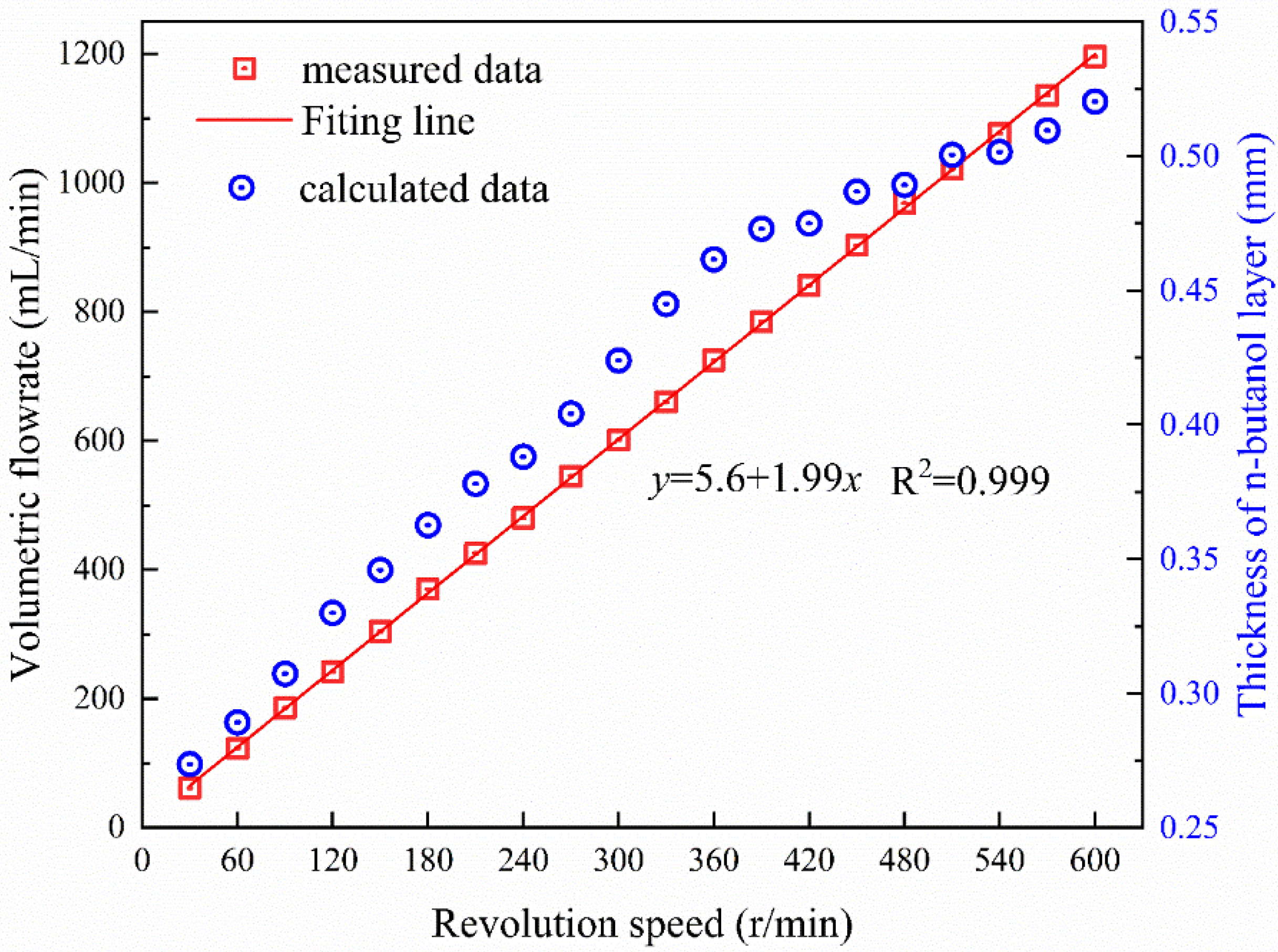
3.1. Fluid Dynamic Analysis of Continuously Spill Fuel
| Temperature (°C) | Density (g/cm3) | Surface Tension (N/m) | Specific Heat Capacity [J/(g·°C)] | Thermal Conductivity [W/(m·°C)] | Vapor Pressure (kPa) |
|---|---|---|---|---|---|
| 15 | 0.8136 | 25.1 | 2.345 | 0.1677 | 0.40 |
| 20 | 0.8100 | 24.7 | 2.372 | 0.1670 | 0.56 |
| 25 | 0.8625 | 24.3 | 2.404 | 0.1663 | 0.87 |
| 30 | 0.8025 | 23.9 | 2.436 | 0.1656 | 1.19 |
3.2. Flame Spread Appearance
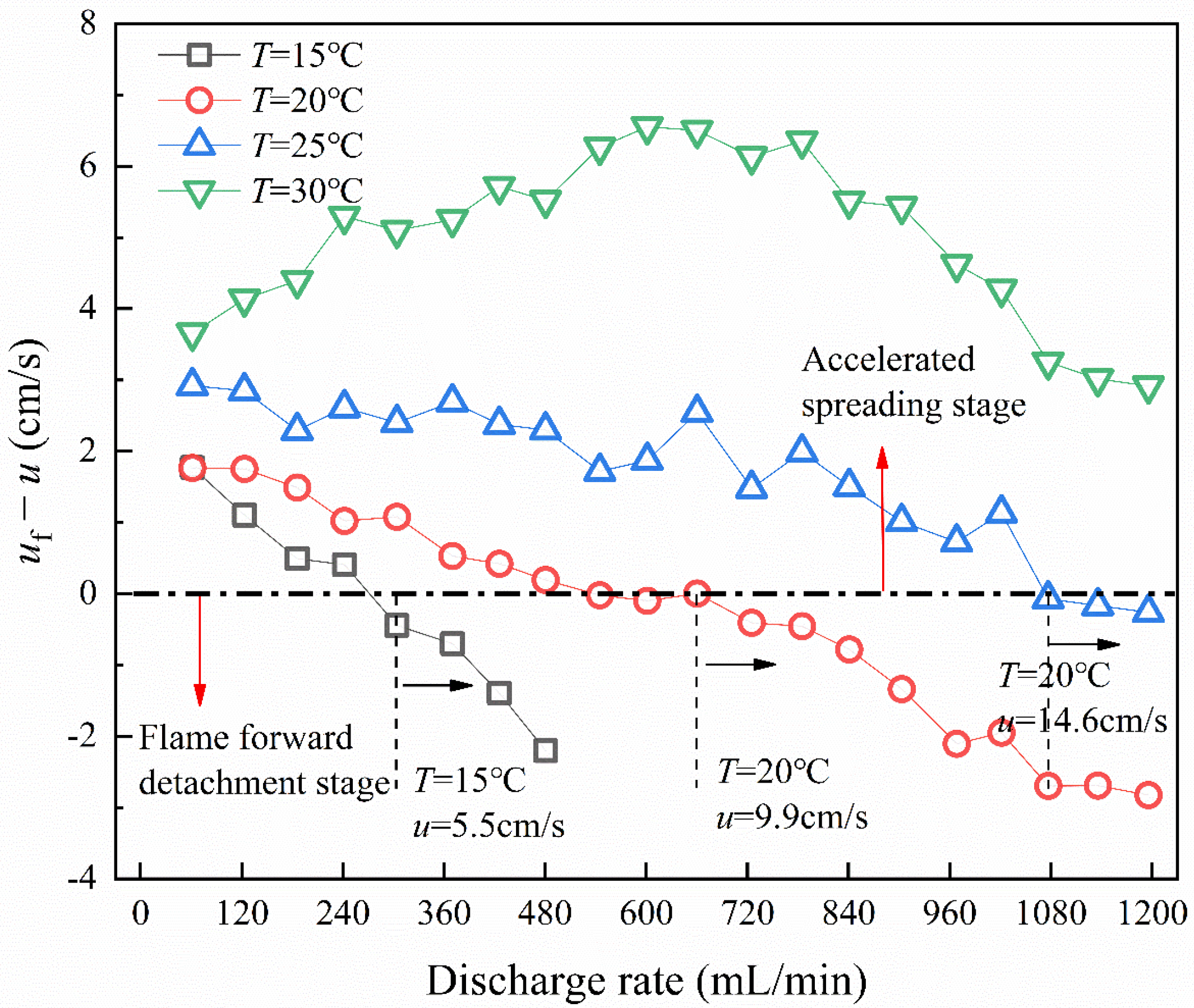
3.3. Flame Spread Rate
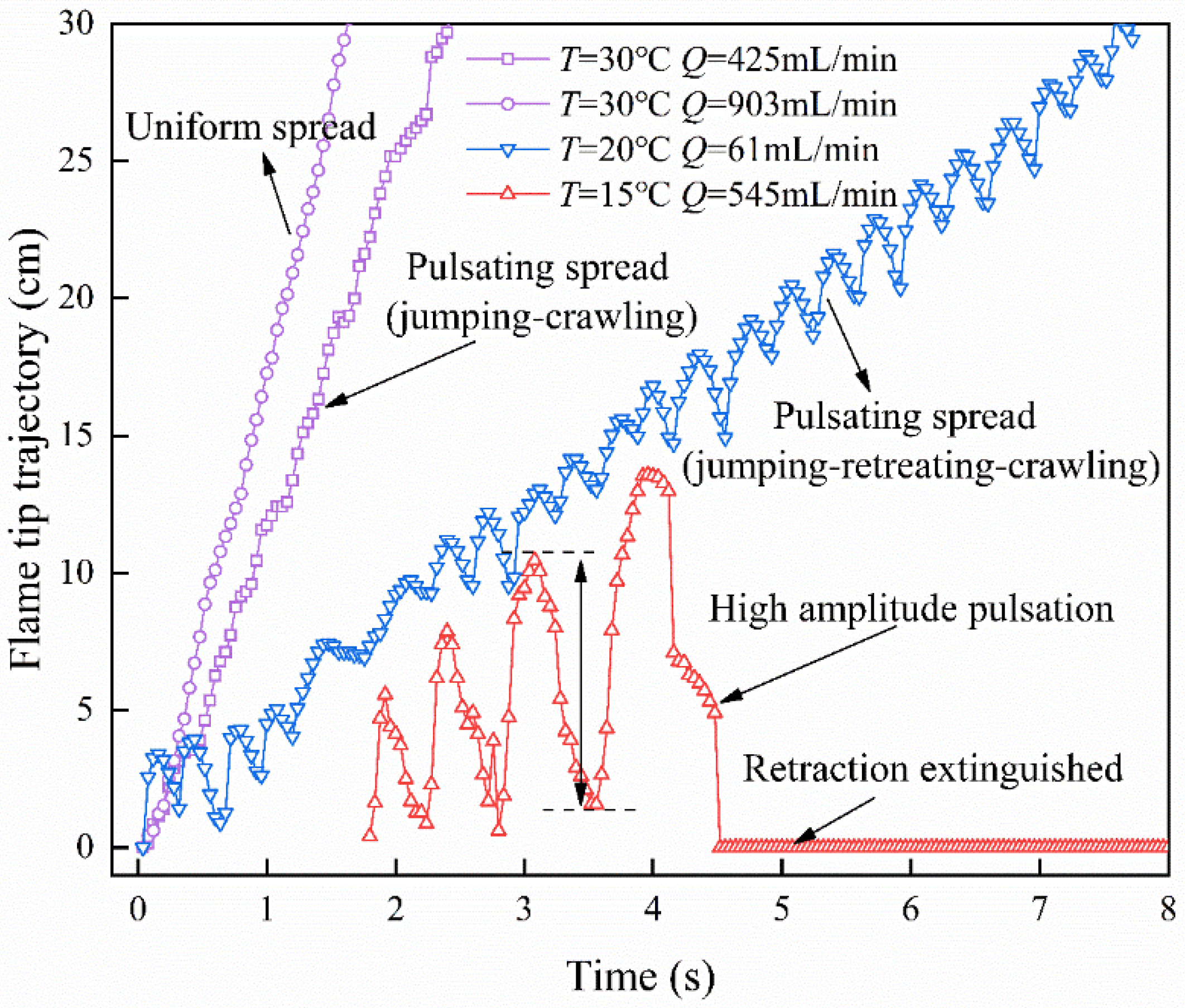
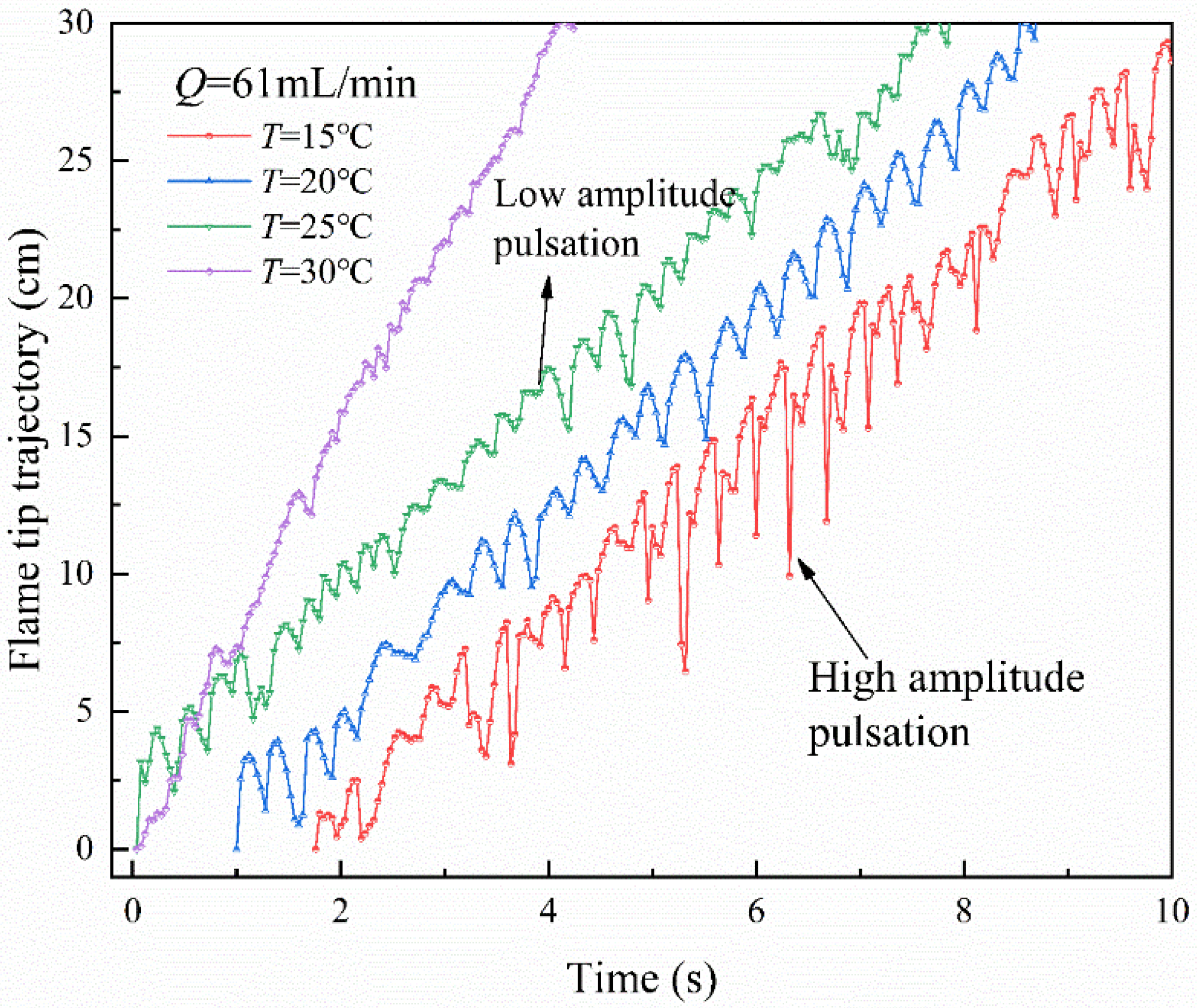
3.4. Flame Front Pulsation
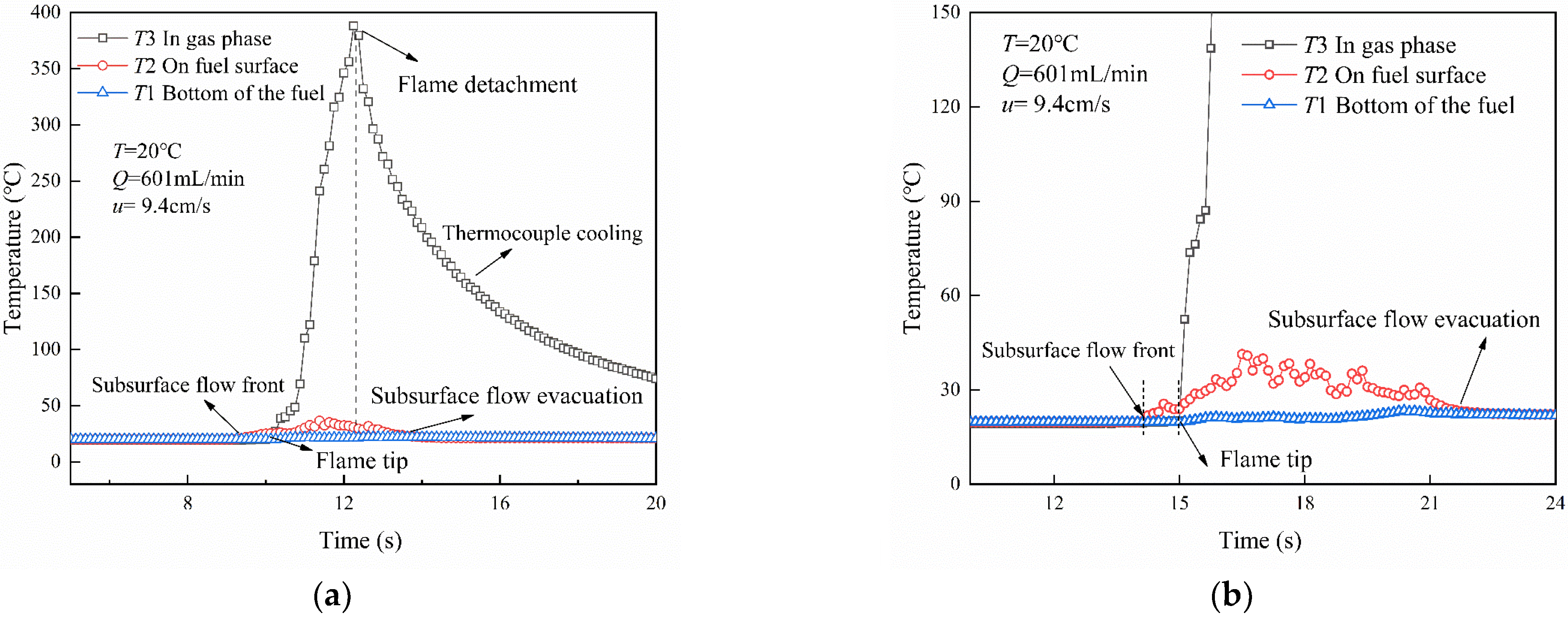
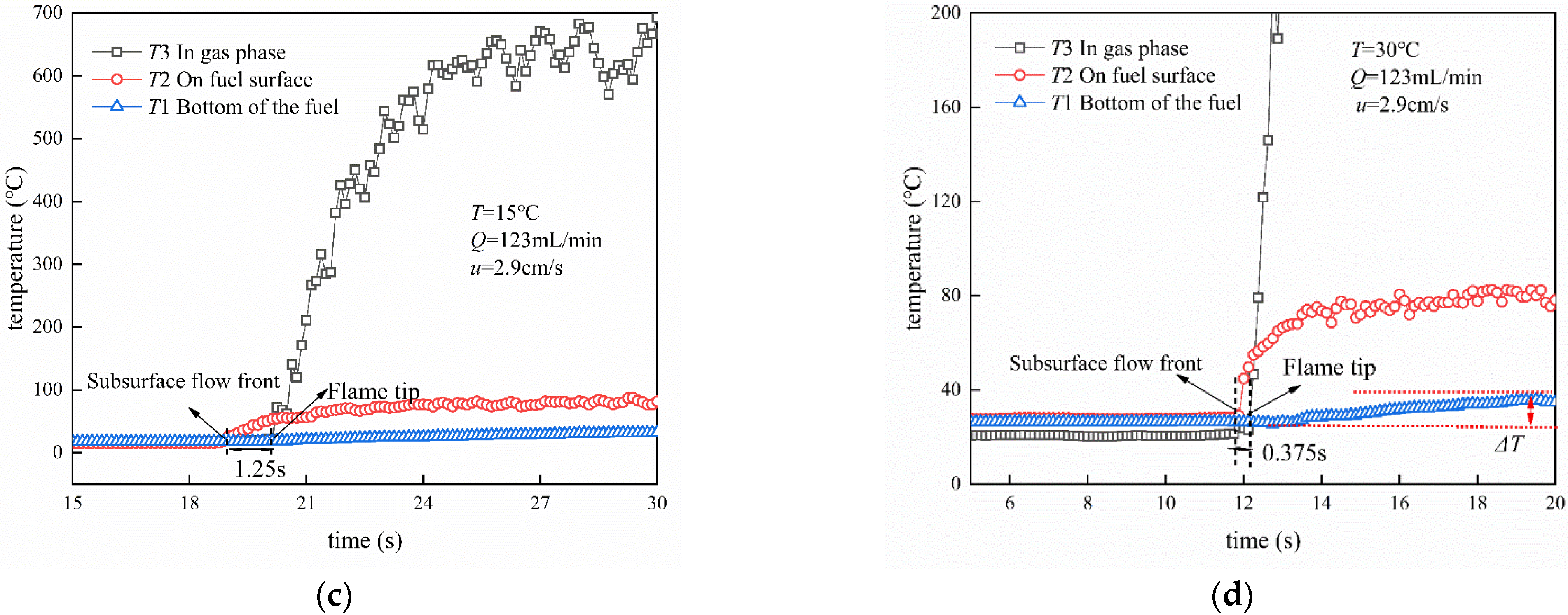
3.5. Temperature Distribution
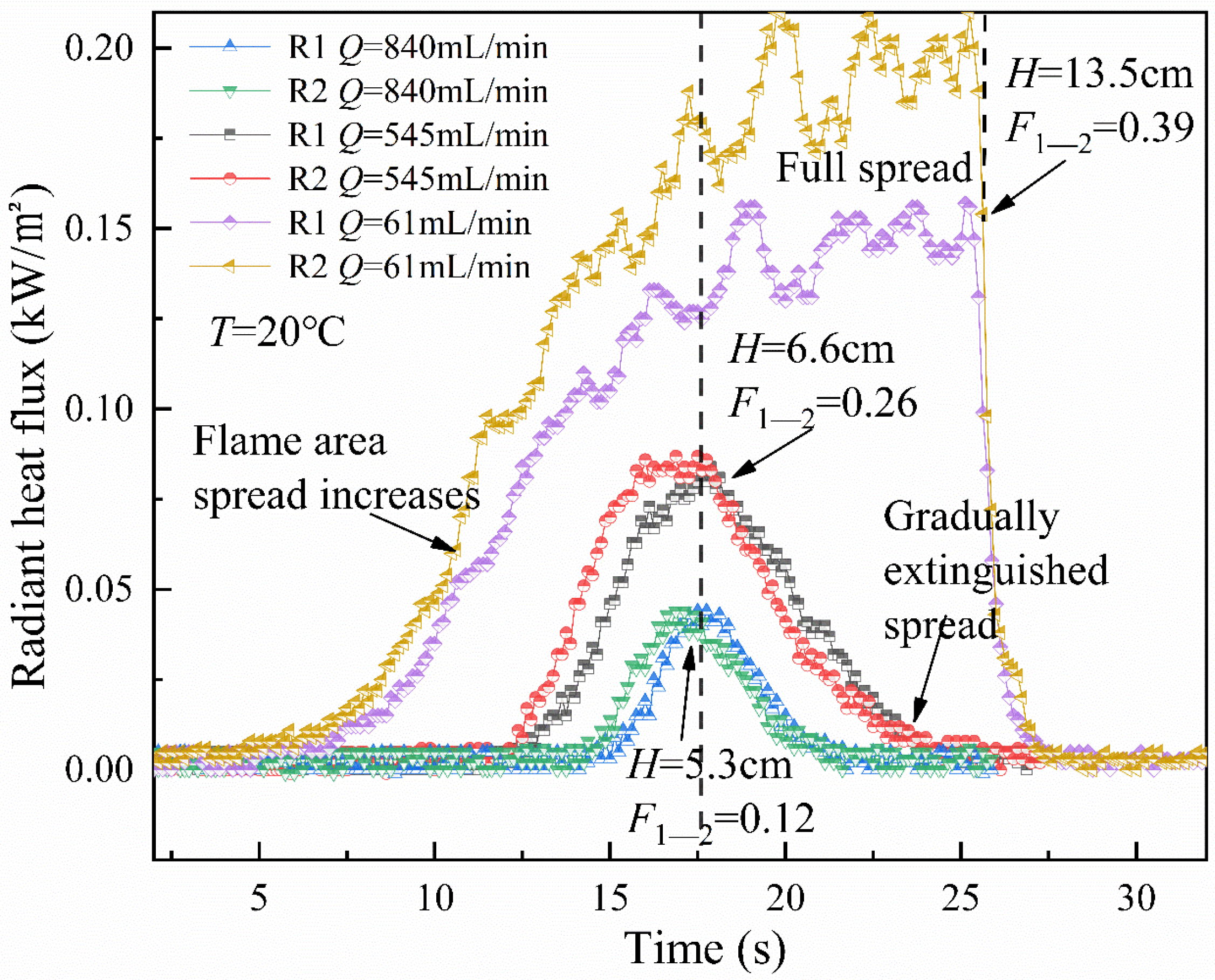
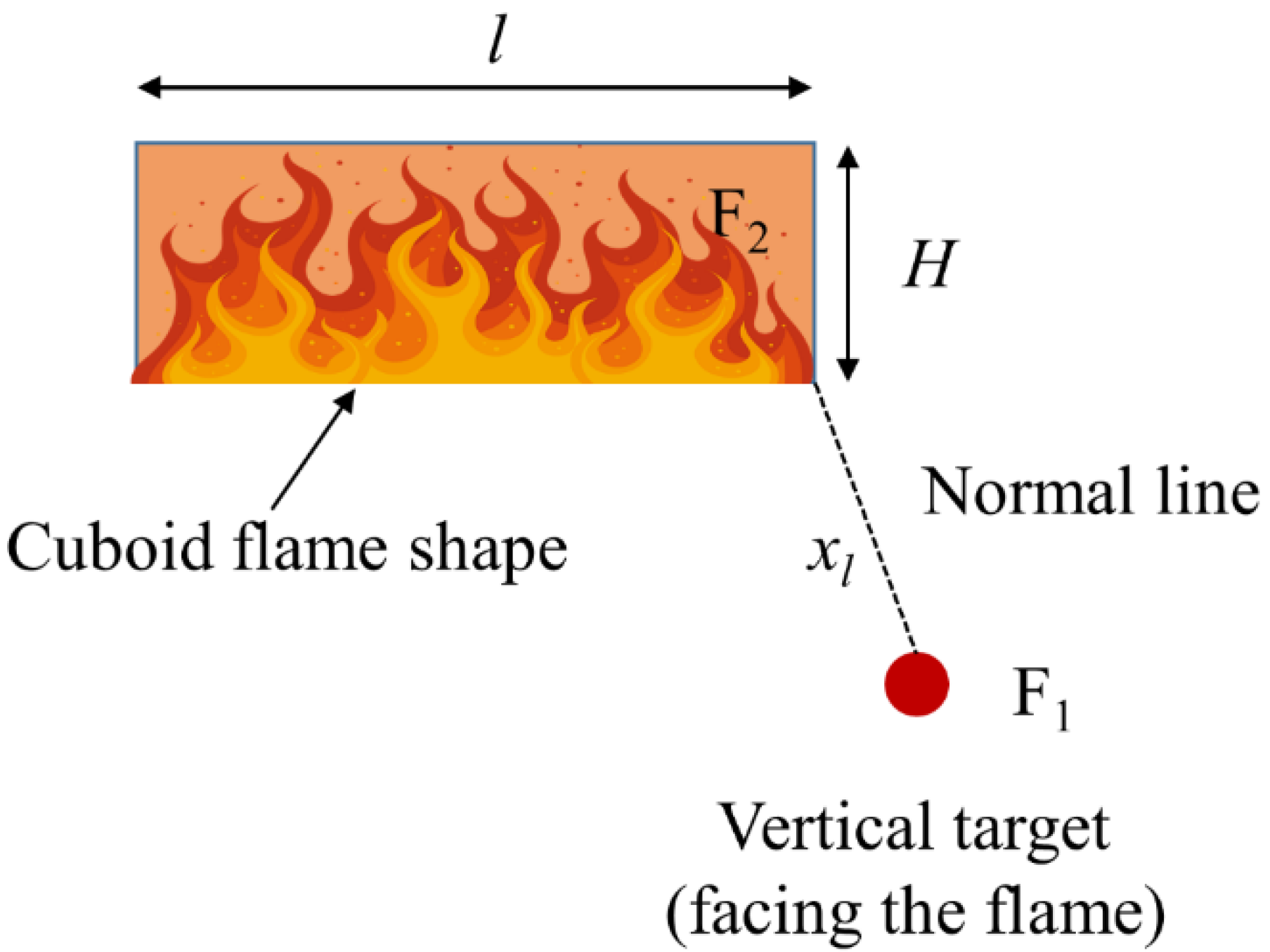
3.6. Radiant Heat Flow
4. Conclusions
- (1)
- The experimental fuel flow is in the laminar state, and the maximum thickness of the fuel layer is 0.52 cm; the influence of the fuel layer thickness on the flame spread is not negligible. The flame spread state is affected by temperature and discharge rate in three stages, (I) full spread, (II) gradually extinguished spread, and (III) unable to spread.
- (2)
- The spreading rate of spill fire reduces with the decrease in temperature and fuel liquid flow rate; when the temperature T = 15 °C, Q > 545 mL/min, the flame cannot spread, and the detachment rate of flame spread enlarges with the increase in temperature.
- (3)
- Flame front pulsation trajectory is gradually transitioned to uniform spreading by the dragging force of the liquid surface flow rate. The temperature increases, and the flame pulsation amplitude and subsurface flow preheating time decrease.
- (4)
- Radiant heat flow first increases at the full spread and then stabilizes, with a maximum view coefficient of 0.39; however, there is a tendency for a single peak change in gradually extinguishing the spread.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, M.; Lu, S.; Guo, J.; Chen, R.; Tsui, K.L. Flame spread over n-butanol at sub-flash temperature in normal and elevated altitude environments. J. Therm. Anal. Calorim. 2015, 119, 401–409. [Google Scholar] [CrossRef]
- Lehr, W.; Simecek-Beatty, D. Comparison of hypothetical LNG and fuel oil fires on water. J. Hazard. Mater. 2004, 107, 3–9. [Google Scholar] [CrossRef]
- Oka, H.; Ota, S. Evaluation of consequence assessment methods for pool fires on water involving large spills from liquefied natural gas carriers. J. Mar. Sci. Tech. 2008, 13, 178. [Google Scholar] [CrossRef]
- Webber, D.M. Source terms. J. Loss Prev. Process Ind. 1991, 4, 5–15. [Google Scholar] [CrossRef]
- Webber, D.M. On models of spreading pools. J. Loss Prev. Process Ind. 2012, 25, 923–926. [Google Scholar] [CrossRef]
- Chebbi, R. Dynamics of unidirectional gravity-inertial spreading of oil on water. Chem. Eng. Sci. 2005, 60, 6806–6813. [Google Scholar] [CrossRef]
- Grimaz, S.; Allen, S.; Stewart, J.; Dolcetti, G. Predictive evaluation of surface spreading extent for the case of accidental spillage of oil on the ground. AIDIC Chem. Eng. Trans. 2007, 11, 389–394. [Google Scholar]
- Gottuk, D.T.; White, D.A. Liquid fuel fires. In SFPE Handbook of Fire Protection Engineering; Springer: New York, NY, USA, 2015; pp. 2552–2590. [Google Scholar]
- Pan, Y.; Li, M.; Wang, C.; Luo, X.; Luo, Q. Experimental investigation of spilling fire spread over steady flow n-butanol fuel: Effects of flow speed and spreading direction. Process Saf. Prog. 2020, 39, e12131. [Google Scholar] [CrossRef]
- Pan, Y.; Li, M.; Luo, X.; Wang, C.; Luo, Q.; Li, J. Analysis of heat transfer of spilling fire spread over steady flow of n-butanol fuel. Int. Commun. Heat Mass Transf. 2020, 116, 104685. [Google Scholar] [CrossRef]
- Li, M.; Xu, Z.; Luo, Q.; Wang, C. Oscillation behavior and heat transfer involving opposed spilling fire spread over n-butanol with various slope angles. Int. Commun. Heat Mass Transf. 2023, 140, 106512. [Google Scholar] [CrossRef]
- Sirignano, W.A.; Glassman, I. Flame Spreading Above Liquid Fuels: Surface-Tension-Driven Flows. Combust. Sci. Technol. 1970, 1, 307–312. [Google Scholar] [CrossRef]
- Degroote, E.; García Ybarra, P.L. Flame propagation over liquid alcohols: Part I. Experimental results. J. Therm. Anal. Calorim. 2005, 80, 541–548. [Google Scholar] [CrossRef]
- Degroote, E.; García Ybarra, P.L. Flame propagation over liquid alcohols: Part III. Pulsating regime. J. Therm. Anal. Calorim. 2005, 80, 555–558. [Google Scholar] [CrossRef]
- Degroote, E.; García Ybarra, P.L. Flame propagation over liquid alcohols: Part II. Steady propagation regimes. J. Therm. Anal. Calorim. 2005, 80, 549–553. [Google Scholar] [CrossRef]
- Miller, F.J.; Ross, H.D. Liquid-phase velocity and temperature fields during uniform flame spread over 1-propanol. In Proceedings of the 8th International Symposium on transport phenomena in Combustion, San Francisco, CA, USA, 16–20 July 1995; pp. 736–744. [Google Scholar]
- Schiller, D.; Ross, H.; Sirignano, W. Computational predictions of flame spread over alcohol pools. In Proceedings of the 31st Aerospace Sciences Meeting, Reno, NV, USA, 11–14 January 1993; p. 825. [Google Scholar]
- Yaws, C.L. Chemical Properties Handbook, 1st ed.; McGraw-Hill Education: New York, NY, USA, 1999; pp. 19–154. [Google Scholar]
- Li, Y.; Huang, H.; Shuai, J.; Zhao, J.; Su, B. Experimental study of continuously released liquid fuel spill fires on land and water in a channel. J. Loss Prev. Process Ind. 2018, 52, 21–28. [Google Scholar] [CrossRef]
- White, D.; Beyler, C.L.; Fulper, C.; Leonard, J. Flame spread on aviation fuels. Fire Saf. J. 1997, 28, 1–31. [Google Scholar] [CrossRef]
- Li, M.; Wang, C.; Yang, S.; Zhang, J. Precursor flame characteristics of flame spread over aviation fuel. Appl. Therm. Eng. 2017, 117, 178–184. [Google Scholar] [CrossRef]
- Takahashi, K.; Ito, A.; Kudo, Y.; Konishi, T.; Saito, K. Scaling analysis on pulsating flame spread over liquids. Int. J. Chem. Eng. 2008, 2008, 178292. [Google Scholar] [CrossRef]
- Li, M.; Wang, C.; Li, Z.; Yang, S.; Fukumoto, K.; Fan, C. Combustion and flame spreading characteristics of diesel fuel with forced air flows. Fuel 2018, 216, 390–397. [Google Scholar] [CrossRef]
- Li, M.; Luo, Q.; Ji, J.; Wang, C. Hydrodynamic analysis and flame pulsation of continuously spilling fire spread over n-butanol fuel under different slope angles. Fire Saf. J. 2021, 126, 103467. [Google Scholar] [CrossRef]
- Guo, J.; Lu, S.; Wang, C. Study on the subsurface flow induced by flame spread over aviation kerosene. J. Therm. Anal. Calorim. 2014, 116, 455–460. [Google Scholar] [CrossRef]
- Kim, I.; Schiller, D.N.; Sirignano, W.A. Axisymmetric flame spread across propanol pools in normal and zero gravities. Combust. Sci. Technol. 1998, 139, 249–275. [Google Scholar] [CrossRef]
- Glassman, I.; Dryer, F.L. Flame spreading across liquid fuels. Fire Saf. J. 1981, 3, 123–138. [Google Scholar] [CrossRef]
- Ji, J.; Lin, S.; Zhao, C.; Li, K.; Gao, Z. Experimental study on initial temperature influence on flame spread characteristics of diesel and gasoline–diesel blends. Fuel 2016, 178, 283–289. [Google Scholar] [CrossRef]
- Ji, J.; Gong, C.; Wan, H.; Gao, Z.; Ding, L. Prediction of thermal radiation received by vertical targets based on two-dimensional flame shape from rectangular n-heptane pool fires with different aspect ratios. Energy 2019, 185, 644–652. [Google Scholar] [CrossRef]
- Ingason, H.; Li, Y.Z.; Lönnermark, A. Heat flux and thermal resistance. In Tunnel Fire Dynamics; Springer: New York, NY, USA, 2015; pp. 249–290. [Google Scholar]
- Muñoz, M.; Planas, E.; Ferrero, F.; Casal, J. Predicting the emissive power of hydrocarbon pool fires. J. Hazard. Mater. 2007, 144, 725–729. [Google Scholar] [CrossRef] [PubMed]


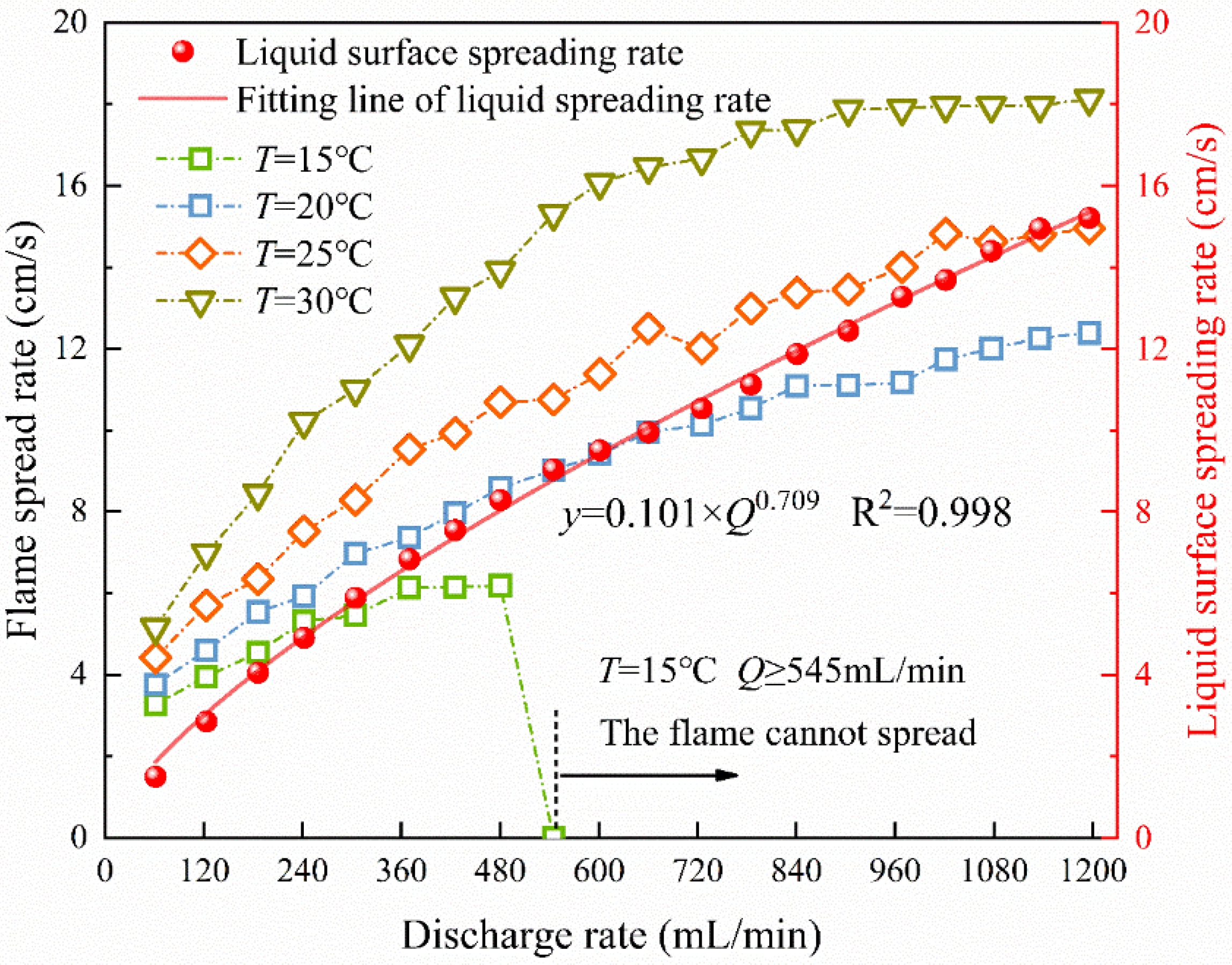
| Temperature °C | Discharge Rate mL/min | Flame Spread State |
|---|---|---|
| 15 | Q ≤ 123 | Full Spread |
| 186 < Q ≤ 481 | Gradually extinguish the spread | |
| 545 ≤ Q | Unable to spread | |
| 20 | Q ≤ 185 | Full Spread |
| 241 < Q ≤ 1195 | Gradually extinguish the spread | |
| 25 | Q ≤ 370 | Full Spread |
| 426 < Q ≤ 1195 | Gradually extinguish the spread | |
| 30 | Q ≤ 545 | Full Spread |
| 660 < Q ≤ 1195 | Gradually extinguish the spread |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, C.; Ma, S.; Yan, Z.; He, L.; Li, Y.; Fang, T.; Jiao, Y. Experimental Study on the Effect of Sub-Flash Point Fuel Temperature on the Spread Characteristics of Spill Fire. Fire 2023, 6, 284. https://doi.org/10.3390/fire6080284
Ding C, Ma S, Yan Z, He L, Li Y, Fang T, Jiao Y. Experimental Study on the Effect of Sub-Flash Point Fuel Temperature on the Spread Characteristics of Spill Fire. Fire. 2023; 6(8):284. https://doi.org/10.3390/fire6080284
Chicago/Turabian StyleDing, Chao, Shuangyang Ma, Zijian Yan, Lingfeng He, Yuyao Li, Tingyong Fang, and Yan Jiao. 2023. "Experimental Study on the Effect of Sub-Flash Point Fuel Temperature on the Spread Characteristics of Spill Fire" Fire 6, no. 8: 284. https://doi.org/10.3390/fire6080284
APA StyleDing, C., Ma, S., Yan, Z., He, L., Li, Y., Fang, T., & Jiao, Y. (2023). Experimental Study on the Effect of Sub-Flash Point Fuel Temperature on the Spread Characteristics of Spill Fire. Fire, 6(8), 284. https://doi.org/10.3390/fire6080284







