Abstract
The unfixed flame propagation velocity of a gas explosion and the fixed response time of explosion suppression devices are the important reasons for the poor protective effect of active explosion suppression. A flexible explosion suppression method based on buffer energy absorption is detailed in this study. The explosion suppression system consists of an explosive characteristic monitoring system, an explosion suppression agent system, and an explosion suppression airbag. An empty pipe experiment and an explosion suppression experiment with a flexible-airbag gas-explosion suppression device were conducted in a 20.5 m-long pipe with an inner diameter of 180 mm. The flame propagation velocity and maximum overpressure values were compared between the two groups of experiments. The experimental results show that the flame wave propagation can be completely suppressed by the explosion suppression device under certain pressure. The occurrence time of maximum overpressure at each pressure measuring point is also analyzed. P3 is generally later than P4, which verifies the existence of energy absorption and explosion suppression effect of airbag. Finally, the energy absorption effect of the airbag is analyzed theoretically. The shock wave overpressure calculated in the sealing limit state of the airbag is 0.3432 MPa, and the maximum error is 7.8%, which provides reliable guidance and prediction for the experimental process in the future.
1. Introduction
A gas explosion is among the most hazardous industrial disasters, especially in coal mining. Moreover, high temperature, high pressure, and toxic gases are the main factors causing casualties and property loss due to gas explosions [1,2]. However, if the explosion can be suppressed or even extinguished, at the initial stage, the harmful consequences can be greatly reduced or eliminated.
Characteristics of methane flame deflagration can be used to predict fires and explosions. Mohammed et al. [3,4,5] studied the influence of mixed methane, coal powder, and suspended coal dust on methane deflagration through a new large straight pipe (LSDT), designed by themselves. It has also been proven the influence on fire and explosions of the main driving parameters, such as pressure rise, flame propagation speed, and vent location, on different methane flame-detonation concentrations [6]. Chunhua Bai et al. [7] studied the explosion overpressure and flame of methane/air and methane/coal dust/air in a 10 m3 container. The experiment showed that the maximum overpressure of the methane/air mixture appeared at 0.75 m away from the ignition point. When the methane concentration is 9.5%, the thickness of the flame is about 10 mm, and the propagation velocity fluctuates around 2.5 m/s, while the maximum overpressure of the methane/coal dust/air mixture occurs at 0.5 m.
In their research of gas explosion suppression technology, Li et al. [8,9,10] investigated inert gas suppression approaches to restrain the continuous spread of explosive gas, such as the use of nitrogen, among other suppressants, as an inhibitor to prevent the flame from spreading, finding that the suppression is a result of inertia isolation rather than inert gas dilution. Ya Lisochkin et al. [11] studied the inertness of a methane–air mixture based on the composition of carbon dioxide and nitrogen, combined with halogenated carbon (CF3Br, C2F4Br2, and CF3). When the concentration of CF3I increased to more than 15% in volume, it would increase sharply to higher than the minimum inert concentration of pure nitrogen. In addition, Maria Mitu et al. [12] studied the characteristic indices of mixtures with different methane concentrations (6–12%) and inert concentrations (5–40%) in two spherical containers of different volumes. Among inert additives, CO2 had the highest efficiency, followed by N2, Ar, and He. On the other hand, Song et al. [13,14,15] studied the inhibition effect of inert dust and solid particle inhibitors [16] on gas explosions, finding that particle size has a great influence on inert rock dust to inhibit gas explosions. In addition, Chen et al. [17,18] studied metal foam and found that it can reduce the overpressure generated, but it has little effect on the flame tip speed and shape. Wang et al. [19,20] studied the combinations of inert gas and solid inhibitors to better suppress methane explosions.
This explosion experiment is expensive and time-consuming, and the explosion data can be predicted efficiently by numerical simulation based on calculation. Pawel Wawrzyniak et al. [21,22] simulated the dust explosion in the countercurrent spray drying tower. In the case of six different safety vent configurations at the top and side walls of the dryer, the results show that the maximum pressure of all the safety vent spatial configurations obtained by CFD simulation is close to the decompression pressure calculated according to EN 14991:2006. Under the condition of uniform gas concentration and variable gas concentration, the (CFD) calculation results show that the dust explosion mainly develops from the ignition point to the upper part of the tower, and the temperature, velocity, and reaction curves all follow the same rising pattern. For shock wave propagation simulation, Arif S. M. Sohaim et al. [23] adopted two different explosion analysis methods, carried out a CFD simulation of free field explosion and explosion load under the capsule model, and used ANSYS FLUENT software to carry out free field wind blasting and blast loading on a certain structure. By comparison, ANSYS FLUENT is more efficient in predicting explosion wave propagation. C. Diaz-Ovalle et al. [24] compared the prediction results of overpressure based on CFD method with those based on the TNO method, and the results show that the physical characteristics adopted by the CFD model can produce satisfactory prediction results in open areas. Eisenreich et al. [25] carried out an experimental study in a 100 mm-diameter pipeline with an internal pressure of their airbags between 1.1 and 6.1 MPa, where the impact pressure generated by the shock tube was 0.2–5 MPa. Determining that the shockwave velocity was low, 57 m/s to 170 m/s, far from the velocity of a gas explosion of several hundred kilometers per second, provides an interesting reference for flexible explosion suppression systems. In this regard, to make the gas explosion suppression effect of an airbag better [26,27], it is important to study the influence of airbag energy absorption on gas explosion suppression. Khan and Moatamedi [28,29] explain the early developments of airbag modeling and discuss the initial mathematical models [30] that were created, which, in turn, lead to the development of the control volume (CV) methods applied to simulate airbag deployment. Results show that the internal pressure of the airbag is greater than the impact pressure. Consequently, the airbag cannot be compressed and deformed.
Previous studies mainly focus on the rigid explosion barrier, rarely analyzing the influence of airbag flexibility on gas explosions. As a kind of flexible explosion suppression material, the airbag has the property of absorbing impact energy. It can also plug the explosion pipeline and block the impact pressure and flame propagation. This work aims to verify the suppression effect of airbag on the methane/air explosion shock wave and flame through a flexible explosion suppression system and analyze the suppression mechanism of airbag shrinkage and deformation energy absorption on shock wave.
2. Experimental System and Method
2.1. Flexible-Airbag Gas-Explosion Suppression System
A flexible-airbag gas-explosion suppression system is composed of a detection system, a gas generator, a powder storage tank, and a closed diaphragm. The gas generator is the key component of the explosion suppressor agent system. The upper part is connected to the starting power supply through the wire harness plug, while the lower part is vented to the powder storage tank for six vents. The final gas composition of the selected gas-producing mixture was 85% N2, 10% CO2, less than 5% H2O, and a trace of NOX. The gas generator is connected to the powder storage tank by a thread. The powder storage tank is made of steel, with 500 g of ultra-fine ABC dry powder inside. The bottom of the powder storage tank is a 70 mm-diameter opening, closed with a certain diaphragm. The whole flexible-airbag gas-explosion suppression system is shown in Figure 1a. When the gas generator is stimulated, a large amount of inert gas is produced in the powder storage tank, resulting in a rapid increase of pressure in the tank. After reaching the condition of film rupture, the membrane is opened. The dry powder injection is shown in Figure 1b, and the dry powder quickly fills the explosion suppression airbag, shown in Figure 1c.
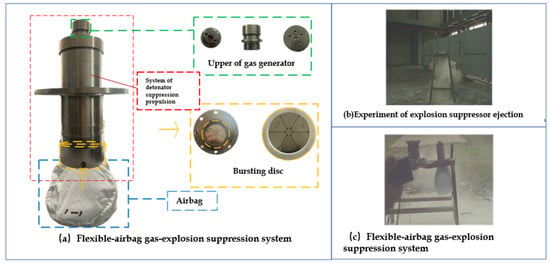
Figure 1.
Flexible-airbag gas-explosion suppression system and methodology applied.
2.2. Gas Explosion Experiment System
It is composed of a pipeline, a gas distribution, an ignition system, and a data acquisition system. The piping system used in the experiment in Figure 2. The inner diameter of the pipeline is 180 mm, with a total length of 20.5 m. The pipeline is open during the experiment. The detection probe for explosion characteristic signals is set 1.5 m away from the ignition end and 15 m away from the assembly of the airbag explosion-suppression device. The gas distribution system adopts negative pressure inflation and the Dalton partial pressure principle configuration. The gas used in the experiment is replaced by 99.99% loading purity. During the experiment, the distribution pressure is set as −50 KPa, and when the negative pressure in the blast chamber reaches the set pressure, methane gas is filled to 0 KPa, and then methane–air premixed gas with different concentrations is prepared. The concentration of methane in the experiment was 9.5%, which was in the range of chemical equivalent and easy to ignite. The ignition system is composed of a fuse, electrode, conductor, and power supply. The ignition pressure is set to 0 Kpa. The valve hysteresis time is set to 1 s, and the electrostatic ignition delay is set to 60 ms. The ignition voltage is set at 200 V. The model of pressure sensor in the data acquisition system is CYG1401F (0~3 MPa), and the model of the flame sensor is CKG100. Each quantity is 5, and the layout is shown in Figure 3a. The TST6300 high-speed data acquisition system is adopted for data acquisition, and the acquisition software is DAP7.2.
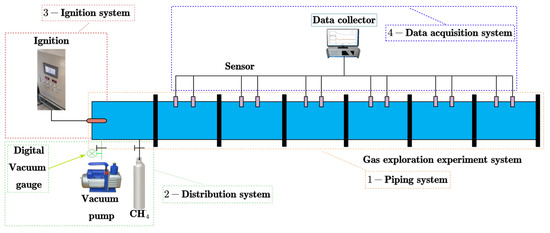
Figure 2.
Gas explosion experiment system.
2.3. Experimental Process
The explosion suppressor is set 16.5 m away from the ignition end and 15 m away from the pressure sensor (P1). After debugging the system, the empty pipe experiment is carried out first in Figure 2. After the completion of the gas distribution work, the ignition system is connected and start the information acquisition system for the ignition experiment. Then, the explosion suppressor is installed for the explosion suppression test. Figure 3a shows the setting of the sensor and explosion suppression device in the pipeline, while Figure 3b,c show the actual pipeline setting status.
In the experiment, the material used to suppress the explosion airbag is PA66, namely polyhexamethylene adipamide, which has a droplet structure. The diameter of the cross-sectional area of the air bag is 180 mm, and the length of the air bag in the pipeline is 180 mm. The actual volume of the airbag deployed in the pipeline is 3.81 L.
The experiment verifies that the deployment time of the explosion suppression airbag can be controlled within 20 ms, and the time required by the explosion suppression agent system and the execution system is 22.8 ms. Considering a certain safety factor, the overall corresponding time of the system is calculated as 25 ms [31].
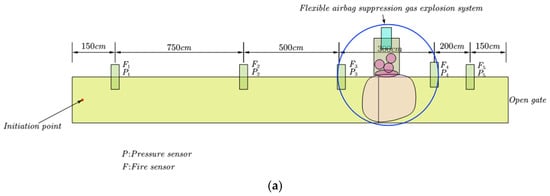

Figure 3.
Experimental pipe and explosion suppression device. (a) Layout diagram of sensor and explosion suppressor. (b) Experiment used 20.5 m-long pipe. (c) Assembled explosion suppression device.
The flame velocity shown in the experimental data is the average flame propagation velocity between the two flame sensors, following Equation (1).
where i is the number of each flame measuring point from the ignition end (1–5); Vi is the average propagation speed between flame measuring point F (i-1) and Fi; Si is the distance between flame measuring point F (i-1) and Fi; Ti is the difference of signal occurrence time between flame measuring point F (i-1) and Fi.
3. Results and Discussion
The distribution curves of flame propagation velocity and maximum overpressure, along the pipe in the 20.5 m empty pipe experiment, and the results of three parallel experiments are shown in Figure 4. From the empty pipe experiment, it can be seen in Figure 4a that the flame propagation velocity keeps increasing and reaches the maximum value at measurement point 5, at which time the value is 593.3 m/s. It also shows that the flame propagation speed is constantly rising under the condition of the empty pipe experiment. On the other hand, Figure 4b displays that the pressure reaches the maximum at measuring point 3, where the overpressure value is 1.607 MPa. This is due to the longer pipe. The second half of the gas concentration is slightly lower, and the overpressure is 0.973 MPa at the pipe opening, point 5. This indicates that the overpressure value is in the process of increasing and only slightly decreases at the outlet.
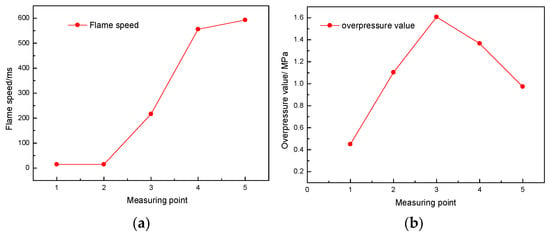
Figure 4.
Flame propagation velocity and overpressure distribution before explosion suppression. (a) Flame propagation velocity. (b) Overpressure value.
Install the flexible-airbag gas-explosion suppression system as shown in Figure 1a to the upper part of the 0.5 long tee pipe, and then replace the same long tube at the explosive pipe 16.5 m away from the ignition end, after it is installed in Figure 3c to carry out the explosion suppression experiment. Results of three parallel experiments are shown in Figure 5, where it is shown the distribution curves of flame propagation velocity and maximum overpressure along the pipe after detonation suppression.
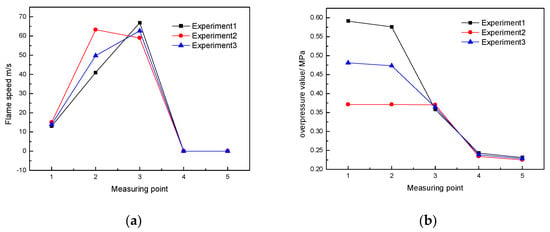
Figure 5.
Flame propagation velocity and overpressure distribution after explosion suppression. (a) Sampling curve of flame signal after explosion suppression. (b) Sampling curve of pressure signal after explosion suppression.
Figure 6 shows that the behavior of the flame propagation velocity and maximum overpressure value is significantly different from that of a conventional explosion after the detonation of the suppression airbag is started in the pipeline. During this process, the maximum overpressure occurred at P3, where the maximum overpressure was 0.358–0.37 MPa, while the maximum overpressure at five pressure measuring points was in the range of 0.225–0.231 MPa and the average flame velocity at F3 was in the range of 58.96–66.90 m/s. The pressure and flame velocity decreased by at least 34.86% and 73.10%, respectively, compared with the empty pipe experiment. However, no flame signal was detected at F4 and F5, indicating that flame propagation was completely suppressed under this condition due to the existence of the explosion suppression balloon. In this experimental condition, no damage occurred to the explosion suppression airbag. Dry powder may only escape a small amount at the position of airbag sewing line, and it is the influence of this small amount of dry powder that leads to the reduction of explosion pressure, so that the airbag cannot reach the failure condition.
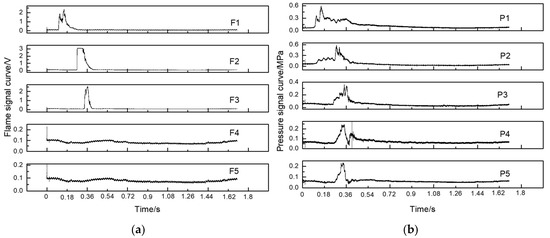
Figure 6.
Sampling curve of flame and pressure signals, after explosion suppression. (a) Sampling curve of flame signal after explosion suppression. (b) Sampling curve of pressure signal after explosion suppression.
3.1. Deformation and Energy Absorption of the Airbag
In the explosion suppression experiment, the occurrence time of maximum overpressure at each pressure measuring point was analyzed under the condition of no airbag damage. The occurrence time of maximum overpressure at P3 was generally later than that at P4, with a time difference of 1.47–39 ms, as shown in Table 1. This is extremely abnormal under open conditions. The reason is that during the propagation of the explosion inside the pipeline, due to the obstruction and blockage of the deployed airbag, the shock wave pressure decreases due to the shrinkage and deformation of the airbag until the shock wave pressure and the airbag friction reach an equilibrium state at some point. In addition, a small amount of dry powder escapes in the process of the airbag extinguishing the flame wave, resulting in the occurrence time of maximum overpressure P3 is generally later than P4.

Table 1.
The moment of maximum overpressure value after explosion suppression.
3.2. Analysis of the Energy Absorption Effect
For this study, a two-dimensional model [32,33,34,35,36,37] is established to analyze the force and deformation energy absorption characteristics of the airbag in the pipe. Because the calculation of the two-dimensional model is simple and the result is on the safe side, the two-dimensional model is used to study the force and change of the energy absorption process of the airbag.
3.2.1. Two-Dimensional Model Assumptions
The inflatable generator produces inert gas, which fills the airbag in a full state (hereinafter referred to as inflatable airbag) in the pipeline explosion suppression shape and force situation. To analyze its energy absorption effect, the following analytical assumptions are made: (1) airbag shape, the deformation after the force is considered as two-dimensional strain; (2) airbag is made of a homogeneous material, without considering the airbag material thickness; (3) there is an explosion shock wave in the pipeline for the uniform load; (4) for an airbag that is completely sealed, its two ends are regarded as part of the standard circle; (5) for an inflatable airbag with an internal blast suppressant uniform diffusion distribution, internal parameters meet the ideal gas equation of state.
where P0, V0 and P1, V1 are the internal pressure (kPa) and volume (m3) of the inflatable airbag before and after the shock wave, respectively.
3.2.2. Airbag Initial State Analysis
The initial state of the airbag is considered before the shock wave. At this moment, the airbag is filled with inert gas produced by the inflatable generator. The straight section is attached to the inner side of the pipe wall. The two ends are not in contact with the pipe wall, and the dry powder is evenly diffused inside the airbag, in Figure 7a. Without considering the effect of air on the air pressure inside the airbag, the pressure inside the airbag is equal everywhere. Before being subjected to the impact pressure, the airbag is at rest, and the friction force, Fm is equal to 0. To analyze the shape and force of the airbag after being subjected to the impact wave, the length L of the straight section of the airbag against the wall, the radius R corresponding to the curve at both ends, and the angle θ of the circle center, corresponding to the angle of radian as α, are calculated first. In the calculation process, the volume unit of the airbag is the liter (l), and the length unit is the decimeter (dm).
where L is the length of the straight section of the airbag against the wall; h is the length of zone I, and are the volume of zones I and II, respectively.
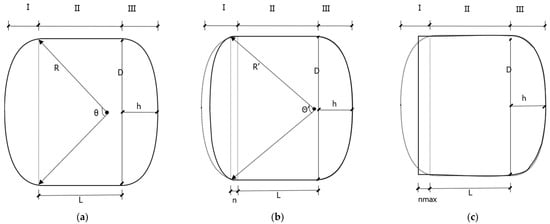
Figure 7.
Airbag deformation process under shock wave pressure. (a) Airbag initial state. (b) The shape of the airbag when subjected to shock waves. (c) Airbag blocking limit state.
3.2.3. Airbag Shape and Force Analysis after Being Subjected to a Shock Wave
The airbag of the I zone is studied. When one end of the airbag (hereinafter referred to as head-on end) starts to be subjected to the shock wave pressure, at this moment, the airbag is subjected to the shock external pressure Pw, internal pressure, a pipe wall support force, and pipe wall friction force, and the airbag produces a shape change under the action of these forces. Under the action of shock external pressure, the pressure difference between the inside and outside of the airbag decreases, which means that the I area, where the head-on end is located, is in the process of energy absorption.
The change in the shape of the shock wave pressure curve at the head-on end of the airbag, as shown in Figure 7b, is due to the increase in the shock wave pressure. Supposing the airbag volume changes continuously from the initial V0 to the stable state V1, the corresponding internal pressure from P0 to P1, the length of the arc is l’. The angle of the center of the circle is θ’, and the radius of the arc is R’. According to the analysis, at this time, the curve section is a part of the arc, the initial airbag head-on end curve deformation before the length L arc into this time the arc l’ and the straight-line section n. The airbag is not subjected to the shock wave end and free end, and its shape does not change during the internal pressure process (P0 to P1). The shape of the free end remains an arc with a central angle of θ.
After the head-on end of the airbag is subjected to the shock wave pressure, it is assumed that the material of the airbag cannot be elongated, so the head-on end is deformed, while the wall section is not deformed under the action of the internal pressure and the support force of the pipe wall, and the free end only increases the material tension under the action of the internal pressure, which does not affect the shape. Therefore, as long as the shape parameters n and the corresponding radian angle α ‘of the head-on end (mainly I area) are confirmed, the corresponding energy absorption shape of the airbag can be determined under the condition of known internal pressure, before and after the deformation of the airbag. It can be determined by two equations: the total length of the airbag before and after deformation, which is equal, and the ideal state equation.
a. The total length of the airbag before and after deformation is equal
The initial length of area I is Larc, determined by the radian angle α and the corresponding radii R at both ends. As follows:
The length of area Ⅰ, after deformation, is composed of an arc and two straight segments n. According to the geometric relation in Figure 7b, the length L’arc after deformation can be seen as:
In Equation (10), Larc is the length of zone I before the airbag is subjected to shock wave, m.
L’arc is the length of zone I of the airbag after shock wave, m. Larc = L’arc.
b. The ideal gas phase equation is satisfied inside the airbag before and after shock wave.
The area of zone I of the airbag, before the shock wave is blown, can be obtained by the difference of sector area and triangle area (Equation (11)).
The area of region I after the shock wave is composed of a bow and rectangle, in Equation (12).
Moreover, Equation (13) displays how the area of region Ⅱ and region Ⅲ of airbag did not change before and after the shock wave.
Therefore,
Before and after the airbag deformation, the gas state equation Equation (2) is satisfied. By substituting the above calculation results, we can obtain:
In the formula, SI and S’I are the area of zone I before and after deformation, m2; SII and S’II are the area of zone Ⅱ before and after deformation, m2; SⅢ and S’Ⅲ are the area of zone Ⅲ before and after deformation, m2. S0 is the total area of the airbag before shock wave, m2; S1 is the total area after the airbag after shock wave, m2.
Given the internal pressure, before and after the shock wave, shape parameters n and α’ before and after the shock wave can be calculated by combining (10) and (17), obtaining the specific shape of the airbag after the shock wave pressure. For a fixed initial internal pressure P0, given any deformed internal pressure P1, a specific shape of airbag deformation can be obtained. According to the analysis of airbag deformation, when the internal pressure of airbag increases from the initial internal pressure to P1, the arc center angle corresponding to the arc of the head-on end gradually decreases from α to zero, and the value of n gradually increases from zero.
3.2.4. Analysis of Airbag Deformation Limit State
With the increase of the impacted external pressure, the internal pressure also increases gradually. According to the above analysis, when the internal pressure increases to the extreme value P2, the curve of the front end becomes a straight line; the value of the central Angle is 0; the straight-line segment attached to the wall reaches the maximum nmax, and airbag deformation in zone I reaches the limit state This is the limit state of the airbag blocking shock wave air flow deformation, as shown in Figure 6c. The airbag is about to slip, and the straight-line section is fitted to the pipe.
The total length of the airbag before and after deformation is equal. In the limit state, region I is a rectangle with a length of Larc, composed by a line segment D and two wall-attached line segments nmax:
The ideal gas phase equation is satisfied inside the airbag before and after the shock wave, in Equation (19) and (20). In the limit state, the area of region I is rectangular. The area of the airbag before deformation and in the limit state is as follows
The gas state equation, Equation (2), is satisfied when the airbag is in its pre-deformation and limit state. By substituting the above calculation results, we can obtain:
In the formula, S2 is the total area of airbag deformation limit state; P2 is the internal pressure of the airbag deformation e limiting state; SI” refers to the area of zone Ⅰ of airbag deformation limit state.
According to Equation (21), the internal pressure P2 of the airbag in the limit state can be obtained, which is also the maximum external impact pressure that the airbag can bear to block the airflow, providing reference data for the airbag to suppress the shock wave.
3.2.5. Equilibrium Analysis of Airbag Horizontal Force
Another important condition for the airbag to resist the shock wave pressure in the blast pipe without slipping or overturning is that the friction resistance Fs provided between the airbag and the wall of the blast pipe is greater than the external impact pressure (Equation (22)). As can be seen from the changing rule of the shape of the airbag, with the increase of the impact external pressure Pw, the length n of the straight-line segment of the airbag attached to the pipe wall is increased, and the increase of the deformation of the airbag leads to the increase of energy absorption. When the limit state of air flow blocked by the airbag is reached, the friction resistance provided is balanced with the shock wave pressure received, and the friction resistance is the maximum static friction resistance Fsmax (Equation (23)). In this state, is the maximum impact external pressure Pwmax that the airbag resists in the limit state (Equation (24)). When the impact external pressure continues to increase, greater than the maximum static friction resistance, the airbag and tube wall slide; static friction becomes dynamic friction; the airbag slips because the coefficient of dynamic friction decreases with the increase of relative motion speed. According to the conservation of energy, the airbag deformation volume will become larger until the blocking shock wave completely fails.
In the formula, Fs is the resultant frictional resistance force of the airbag without deformation, kN; Fsmax is the resultant friction resistance that the airbag can provide in the limit state, kN; Pw is the external pressure of the shock wave resisted by the air bag, kPa; Pwmax is the maximum shock wave pressure that the airbag can withstand in the limit state, kPa.
As can be seen from Equation (23), the maximum static friction resistance between the airbag and the explosive pipe is closely related to the length of the initial straight-line section of the airbag L and the friction coefficient μ.
Assuming that there is only static friction, the airbag deforms and absorbs energy, and the internal pressure rises. According to the analysis of the ability to conduct work on the medium in the explosion process, it is equivalent to a constant impulse wave external force Fw compressing the length of the airbag h. In this case, the work to be conducted on the airbag is shown in Equation (25).
The impact pressure generating this constant force is Pw, which can be calculated by Equation (26).
Based on this, we can calculate the impact of external pressure in contact with the head-on end of the airbag. In the above experiments, when the dosage of gas production drug in the gas generator is 10–14 g, 5.6–7.84 L of gas can be generated, respectively. Calculated according to the actual volume of the airbag (3.81 L), assuming that all the generated gas is confined in the airbag, after calculation, the internal pressure of the airbag can reach 0.15–0.2 MPa instantaneously. When the initial internal pressure of the airbag is 0.2 MPa, based on the above analysis and Equation (21) the external pressure at the head end of the airbag in the sealing limit state is calculated to be 0.3423 MPa. This is the limit state of airbag deformation. Theoretically, the critical point at which the internal pressure and external pressure of airbag can maintain balance for a long time is the moment when the static friction force is maximum. The difference between the theoretical value and the maximum overpressure at the pressure measuring point P3 (0.358–0.37 MPa) in the airbag explosion suppression experiment is 0.0148–0.0268 MPa, and the maximum error is 7.8%. Because the pressure monitoring point P3 is 1.5m away from the front of the airbag, the measured pressure value at P3 is not the pressure value when the head-on end of the airbag contacts with the shock wave. In addition, a small amount of blasting suppressor powder escapes from the airbag after the shock wave, and the pressure value at this time is affected by the detonation suppression of a small amount of escaping dry powder.
However, keep in mind that when the airbag slips, the volume of the airbag will be deformed and enlarged again. At this time, the internal pressure cannot be maintained at 0.3423 MPa, and the dynamic friction force will also become smaller. The slip of the airbag will make the internal and external pressure of the airbag become unable to maintain the balanced relationship for a long time, and the airbag will still deform and absorb energy until the sealing shock wave completely fails. If the flame is extinguished during the establishment of this equilibrium due to the interruption of energy supply or the influence of dry powder, the explosion flame wave will be completely interrupted.
From the above analysis, it can be concluded that the theoretical values are in good agreement with the actual data, which can provide reliable guidance and prediction for future airbag explosion suppression experimental.
4. Conclusions
- (1)
- A flexible detonation suppression method based on the energy absorption principle is proposed for the first time, verifying the relevance of this method through several experiments. After the suppression airbag is started in the pipeline, at 1.5 m away from the front of the suppression airbag, the maximum overpressure at P3 monitoring point is 0.358–0.37 MPa, and the average flame velocity at F3 flame detection point is between 58.96 m/s and 66.90 m/s. The pressure and flame velocity decreased at least 34.86% and 73.10%, respectively, when compared with the empty pipe experiment. After the explosion suppression airbag actuation, the explosion flame propagation is completely inhibited.
- (2)
- Moreover, by comparing the occurrence time of maximum overpressure at different pressure monitoring points in the pipeline, P3 is generally later than P4, with a time difference between 1.47 ms and 39 ms, which verifies the shrinkage and deformation process of the airbag and reflects the existence of the energy absorption process of the airbag. In the process of energy absorption by the airbag, the flame is extinguished naturally, because the methane in the pipeline cannot be replenished, which leads to the interruption of the explosion.
- (3)
- Based on the two-dimensional model, the stress and deformation theory of the explosion suppression airbag is analyzed. The law of deformation energy absorption and the relationship between internal pressure and external pressure during the process of the airbag from the initial state to the ultimate state are obtained. In the limit state of airbag deformation, the theoretical pressure of P3 is 0.3423 MPa, and the difference between P3 and the maximum overpressure value measured in the experiment is 0.0148~0.0268 MPa, with an error of only 7.8%. There is a good consistency between the theoretical data and the experimental data.
Author Contributions
Conceptualization, Y.W. and H.M.; methodology, Y.W.; formal analysis, L.H.; investigation, X.X.; data curation, H.M.; writing—review and editing, Y.W. and K.S.; supervision, M.B.; All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded the National Natural Science Foundation of China (No. 52174176) and the Natural Science Foundation of Heilongjiang Province (No. QC2015054).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This work is supported by the National Natural Science Foundation of China (No. 52174176) and the Natural Science Foundation of Heilongjiang Province (No. QC2015054).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chen, Z. Analysis on explosion of combustible gases in underground fire zone. Coal Mine Mod. 2005, 5, 17–18. [Google Scholar]
- Liu, Y.L.; Chen, H.B. Poison gases propagation rules of methane explosion in coal mine. J. China Coal Soc. 2009, 34, 788–791. [Google Scholar]
- Mohammed, J.A.; Jafar, Z.; Behdad, M. The flame deflagration of hybrid methane coal dusts in a large-scale detonation tube (LSDT). Fuel 2017, 194, 491–502. [Google Scholar]
- Mohammed, J.A.; Jafar, Z.; Behdad, M. Impact of suspended coal dusts on methane deflagration properties ina large-scale straight duct. J. Hazard. Mater. 2017, 338, 334–342. [Google Scholar]
- Mohammed, J.A.; Jafar, Z.; Behdad, M. Flame deflagration in side-on vented detonation tubes: A large scalestudy. J. Hazard. Mater. 2018, 345, 38–47. [Google Scholar]
- Mohammed, J.A.; Jafar, Z.; Behdad, M. Methane-coal dust hybrid fuel explosion properties in a largescale cylindrical explosion chamber. J. Loss Prev. Process Ind. 2016, 40, 317–328. [Google Scholar]
- Bai, C.; Gong, G.; Liu, Q.; Chen, Y.; Niu, G. The explosion overpressure field and flame propagation of methane/air and methane/coal dust/air mixtures. Saf. Sci. 2011, 49, 1349–1354. [Google Scholar] [CrossRef]
- Li, M.; Xu, J.; Wang, C.; Wang, B. Thermal and kinetics mechanism of explosion mitigation of methane-air mixture by N2/CO2 in a closed compartment. Fuel 2019, 255, 115747. [Google Scholar] [CrossRef]
- Lu, C.; Wang, H.; Pan, R.; Zhang, Y.; Yu, M. Preventing the propagation of gas explosion in ducts using spurted nitrogen. Process Saf. Environ. Prot. 2019, 123, 11–23. [Google Scholar] [CrossRef]
- Yang, H.-N.; Lin, Y.-J.; Liu, C.-H.; Chin, M.-G.; Wang, C.-C.; Tsai, H.-Y.; Chen, J.-R. Suppression of flame propagation in a long duct by inertia isolation with inert gases. J. Loss Prev. Process Ind. 2019, 59, 23–34. [Google Scholar] [CrossRef]
- Lisochkin, Y.; Poznyak, V.I. Inerting of Methane–Air Mixtures by Compositions Based on Carbon Dioxide and Nitrogen with Addition of Halocarbons. Combust. Explos. Shock Waves 2005, 41, 504–509. [Google Scholar] [CrossRef]
- Mitu, M.; Prodan, M.; Giurcan, V.; Razus, D.; Oancea, D. Influence of inert gas addition on propagation indices of methane–air deflagrations. Process Saf. Environ. Prot. 2016, 102, 513–522. [Google Scholar] [CrossRef]
- Song, Y.; Zhang, Q. The quantitative studies on gas explosion suppression by an inert rock dust deposit. J. Hazard. Mater. 2018, 353, 62–69. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Yuan, B.; Chen, X.; Li, K.; Wang, L.; Yun, Y.; Fan, A. Suppression of methane/air explosion by kaolinite-based multi-component inhibitor. Powder Technol. 2019, 343, 279–286. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, H.; Zhang, Y.; Lin, C.; Zheng, L.; Ji, W.; Han, X. Suppression Effects of Hydroxy Acid Modified Montmorillonite Powders on Methane Explosions. Energies 2019, 12, 4068. [Google Scholar] [CrossRef]
- Liu, Q.; Hu, Y.; Bai, C.; Chen, M. Methane/coal dust/air explosions and their suppression by solid particle suppressing agents in a large-scale experimental tube. J. Loss Prev. Process Ind. 2013, 26, 310–316. [Google Scholar] [CrossRef]
- Chen, P.; Huang, F.; Sun, Y.; Chen, X. Effects of metal foam meshes on premixed methane-air flame propagation in the closed duct. J. Loss Prev. Process Ind. 2017, 47, 22–28. [Google Scholar] [CrossRef]
- Dai, H.; Wang, X.; Chen, X.; Nan, X.; Hu, Y.; He, S.; Yuan, B.; Zhao, Q.; Dong, Z.; Yang, P. Suppression characteristics of double-layer wire mesh on wheat dust flame. Powder Technol. 2020, 360, 231–240. [Google Scholar] [CrossRef]
- Wang, Y.; Meng, X.; Ji, W.; Pei, B.; Lin, C.; Feng, H.; Zheng, L. The Inhibitory effect of Gas–Solid Two-Phase Inhibitors on Methane Explosion. Energies 2019, 12, 398. [Google Scholar] [CrossRef]
- Yu, M.; Liu, M.; Wen, X.; Zhao, W.; Pei, B. Experimental study on suppression of methane explosion by porous media and ultra-fine water mist. Energy Sources Part A Recovery Util. Environ. Eff. 2019, 44, 1–14. [Google Scholar] [CrossRef]
- Polanczyk, A.; Wawrzyniak, P.; Zbicinski, I. CFD Analysis of Dust Explosion Relief Systemin the Counter-Current Industrial Spray Drying Tower. Dry. Technol. 2013, 31, 881–890. [Google Scholar] [CrossRef]
- Wawrzyniak, P.; Polańczyk, A.; Zbicinski, I.; Jaskulski, M.; Podyma, M.; Rabaeva, J. Modeling of Dust Explosion in the Industrial Spray Dryer. Dry. Technol. 2012, 30, 1720–1729. [Google Scholar] [CrossRef]
- Sohaimi, A.S.; Risby, M.S.; Ishak, S.A.; Khalis, S.; Norazman, M.N.; Ariffin, I.; Yusof, M.A. Using Computational Fluid Dynamics (CFD) for Blast Wave Propagation under Structure. Procedia Comput. Sci. 2016, 80, 1202–1211. [Google Scholar] [CrossRef]
- Díaz-Ovalle, C.; López-Molina, a.; Vázquez-Románc, R. A CFD-based approach to predict explosion overpressure: A comparison to current methods. Chem. Biochem. Eng. Q. 2016, 30, 419–427. [Google Scholar] [CrossRef]
- Eisenreich, N.; Neutz, J.; Seiler, F.; Hensel, D.; Stancl, M.; Tesitel, J.; Price, R.; Rushworth, S.; Markert, F.; Marcelles, I.; et al. Airbag for the closing of pipelines on explosions and leakages. J. Loss Prev. Process Ind. 2007, 20, 589–598. [Google Scholar] [CrossRef]
- Seiler, F.; Ende, H.; Hensel, D.; Srulijes, J. Experimental simulation of airbag deployment for pipeline closing. J. Loss Prev. Process Ind. 2005, 19, 292–297. [Google Scholar] [CrossRef]
- Eduardo, M.S.; Gregory, J.T.; Ever, J.B. Testing of Full-Scale Inflatable Plug for Flood Mitigation in Tunnels. Transp. Res. Rec. 2014, 59–67. [Google Scholar]
- Khan, M.U.; Moatamedi, M. A review of airbag test and analysis. Int. J. Crashworthiness 2008, 13, 67–76. [Google Scholar] [CrossRef]
- Jiang, L.; Zhang, Y.; Huang, Z.; Gao, Y.; Zhang, Y. International Symposium on Safety Science and Technology Experimental study of fast sealing airbag in simulating tunnel. Procedia Eng. 2012, 45, 780–785. [Google Scholar] [CrossRef]
- Eduardo, M.S.; Jerry, C.S.W.; Adi, A.; Ever, J.B.; Gregory, J.T. Finite element simulation of deployment of large-scale confined inflatable structures. Thin-Walled Struct. 2016, 104, 152–167. [Google Scholar]
- Wang, Y. Study on Gas Explosion Suppression Method under Flexible Constraint Conditions and Airbag Explosion Suppression System. China Univ. Min. Technol. 2019. [Google Scholar]
- Yan, S.; Chen, J.; Yue, C.; Sun, L.; Lang, R. Analytical and Model Test Study on the Behavior of Airbags Used for Plugging Tunnel Leakage. Chin. J. Undergr. Space Eng. 2019, 15, 736–746. [Google Scholar]
- Chen, J.; Yan, S.; Sun, L.; He, X.; Lang, R. Model test on deformation characteristics of large diameter airbag in tunnel under external pressure. J. Civ. Archit. Environ. Eng. 2018, 40, 16–26. [Google Scholar]
- Yan, S.; Chen, J.; Yue, C.; Sun, L.; Lang, R. Force Analysis Model and Experimental Verification of Rubber Airbag Used for Blocking Water in Tunnel. J. Tianjin Univ. (Sci. Technol.) 2018, 51, 221–231. [Google Scholar]
- Chen, J.; Yan, S.; Zhong, X. Finite element study on the working mechanism of sealing airbag in tunnel under external pressure. Mod. Tunn. Technol. 2021, 58, 135–144, 181. [Google Scholar]
- Chen, J.; Yan, S.; Sun, L. Working mechanism and model test of plugging airbags with different diameter matching under external pressure. J. Harbin Inst. Technol. 2018, 50, 130–137. [Google Scholar]
- Chen, J.; Yan, S.; Zhong, X. Deformation characteristics and failure mechanism of double-airbag system in tunnel under uniform external pressure. Ind. Constr. 2019, 49, 111–118. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).