Abstract
Accidental flame initiation to propagation in pipes carrying flammable gases is a significant safety concern that can potentially result in loss of life and substantial damage to property. The understanding of flame propagation characteristics caused by methane–air mixtures within various extractive and associated process industries such as coal mining is critical in developing effective and safe fire prevention and mitigation countermeasures. The aim of this study is to investigate and visualise the fire and explosion properties of a methane–air mixture in a straight pipe with and without obstacles. The experimental setup included modular starting pipes, an array of sensors (flame, temperature, and pressure), a gas injection system, a gas analyser, data acquisition and a control system. The resulting observations indicated that the presence of obstacles within a straight pipe eventuated an increase in flame propagation speed and deflagration overpressure as well as a reduction in the elapsed time of flame propagation. The maximum flame propagation speed in the presence of an orifice with a 70% blockage ratio at multiple spots was increased around 1.7 times when compared to the pipe without obstacles for 10% methane concentration. The findings of this study will augment the body of scientific knowledge and assist extractive and associated process industries, including stakeholders in coal mining to develop better strategies for preventing or reducing the incidence of methane–air flame propagation caused by accidental fires.
1. Introduction
Although methane is recognised as ahigh profile and widely discussed substance due to its significant global warming potential and adverse impact on climate change, it is less researched in terms of being a major hazard in mining and the extractive industries [1,2,3]. Media coverage records that adverse incidents continue to occur in the extractive and process industries, including coal and gold mines, and that massive loss of life and damage to property have been outcomes of these incidents [4,5]. While considerable progress has been made in the development of practical prevention and mitigation measures, significant adverse incidents are still occurring. For example, 1049 lives were lost due to coal mine accidents in China alone in 2013 [6]. Even as recently as May 2020, five miners were severely injured in the Anglo-American coal mine explosion which occurred in Queensland, Australia [7].
While some studies have sought to better understand unanticipated fire and the explosion of methane–air mixtures, there is still a knowledge gap concerning the relationship between these variables and their impact on the resulting adverse incidents [8,9]. In particular, the flame propagation mechanism in the real-world geometries found in the extractive and process industries such as pipelines, tunnels, chimneys, and other enclosed and semi-enclosed structures is not well understood, and further research is required to develop the enhanced fire and explosion mitigation technologies for those industries [10,11,12].
In previously published explosion studies, the focus has typically been on understanding the effect of reactor scale on flame propagation and explosion pressure. Zhang et al. [13] determined that the explosion process of a methane–air mixture relates to the scale of the physical geometry (e.g., a duct) where the explosion occurs. The effect of scale on flame propagation gradually decreases with distance from the space containing the methane–air mixture [13]. The effect of obstacles on flame propagation properties has also been investigated by Kolahdooz et al. [14], Wang J. et al. [15], Yakush S. et al. [16], and Wang T. et al. [17]. The location of obstacles relative to each other and the ignition source significantly alters the structure and flame propagation [14,17]. The presence of obstacles or any cross-sectional changes in the flame pathway increases fuel–air turbulence [17]. This phenomenon enhances heat transfer and burning rate, which leads to a significant increase in flame propagation velocity and pressure [15,17]. Yakush et al.’s experimental study [16] in both closed and open-ended tubes indicated that the presence of obstacles in a channel where flame travels can significantly change the behaviour and shape of the flame front. Additionally, the pressure that develops due to the thermal expansion of hot combustion products is the main driving force for flame propagation and gas flow in the duct [15,16]. In this study, blockage ratio (BR) was defined as the largest cross-sectional area blocked by the obstacle divided by the inner cross-sectional area of the explosion duct or where is the hollow obstacle diameter and is the internal tube diameter. The authors investigated turbulent flame propagation for several fuels including hydrogen, acetylene, ethylene, propane and methane and noted the obstacle’s impact on explosion pressure and flame propagation speed. Phylaktou et al. also noted the phenomenon in their explosion studies on methane–air mixtures by employing a closed vertical tube with obstacles. They found that increasing the blockage ratio led to explosion pressure rise and flame propagation speed enhancement [18].
The objective of this study was to gain a better understanding of the characteristics of flame propagation in methane–air mixtures within a straight tube, and to explore how the presence of obstacles affects flame propagation properties. Additionally, this study generated experimental data that can be used to validate fire and explosion studies using computational fluid dynamics (CFD) modelling. The theoretical modelling is expected to yield a broader understanding of explosion characteristics, including flame–turbulence interaction. Single and multiple obstacles with various blockage ratios were employed in the experimental investigation. The broad objectives of this study were achieved through comprehensive experimental work using a sophisticated experimental setup designed and built for this project.
2. Experimental Setup and Methodology
The experimental setup designed and manufactured specifically for this study (shown in Figure 1 and Figure 2) consisted of a series of four modules of a clear borosilicate glass tube (75 mm internal diameter, 5 mm wall thickness and total length of about 5 m). Each module of 1 m length was connected by stainless steel flanges to another module. The 5 mm thick glass tube was sourced from Schott Duran with a temperature tolerance of above 800 °C and pressure tolerance of more than 8 bar. The concentration of methane was controlled by a mass flow controller (Bronkhorst F-201CV, Manufacturer: Bronkhorst, City: Ruurlo, Country: Netherlands) and cross-checked by an inline methane monitor. A thermocouple (K-type) was used to measure the temperature of the gas inside the tube before conducting any experiment. After initiating an experiment, a pyrometer (Impact IPE 140, Manufacturer: Advanced Energy, City: Denver, Country: USA; capable of non-contact temperature measurement and fully digital with focusable optics) was employed for measuring flame temperatures at the ignition position, based on the CO2 emission from the combustion. The maximum value obtained from the pyrometer data during an experiment was taken as the flame temperature. Pressure development in the tube was measured by three piezo-resistive pressure transducers (STS Sensor Technik Sirnach, ATM.ECO/EX with a pressure measurement range of 0–5 bar and 0.1–1 ms response time). The pressure transducers were installed on the tube in the locations of the flanges such that they were positioned 1.2, 2.4 and 3.6 m from the ignition source, as illustrated in Figure 1. A high-speed data acquisition system was employed to record pressure data. An ultra-high-speed colour video camera (Phantom V1211, 12,000 frames/second at full resolution) was used to film flame propagation during the experiment. The recorded film was then used to estimate flame propagation speeds.

Figure 1.
Schematic diagram of the experimental setup.

Figure 2.
Illustration of flame propagation inside the tube.
The system was purged (using compressed air) for five minutes prior to beginning any experiment to ensure that no burned or unburned material was left from a previous experiment. Methane was injected by closing the open end of the tube using a very thin plastic wrap. Upon completion of the methane injection, the fuel–air mixture was circulated in a closed loop line by an intrinsically safe (EX-rated) vacuum air pump (Air Dimensions Incorporated, Dia-Vac Diaphragm R252-FP-GB2). Circulation was maintained for 5 min to ensure that a homogeneous fuel–air mixture was achieved inside the tube. The mixture was then ignited by a pyrotechnic ignitor of 50 mJ energy. Figure 2 illustrates the flame propagation inside the tube from one of the experiments. Methane employed for the experimental investigation was sourced from Coregas, Australia with 99.95% purity.
With the aim of investigating the effect of obstacles, orifice plates of various blockage ratios were used at various locations along the length of the flame propagation tube. Multiple, single and no obstacle scenarios were employed in the experimental investigations. The single obstacle with 30%, 50% or 70% of the glass tube cross-sectional area was positioned at a distance of 1.2 m and 2.4 m from the ignition source. Also, two obstacles were positioned at 1.2 and 2.4 m away from the ignition source simultaneously. Figure 3 shows a schematic of a circular hollow obstacle with a 50% blockage ratio. The obstacles were installed between the flanges using 12 sealed bolts, as shown in Figure 2.
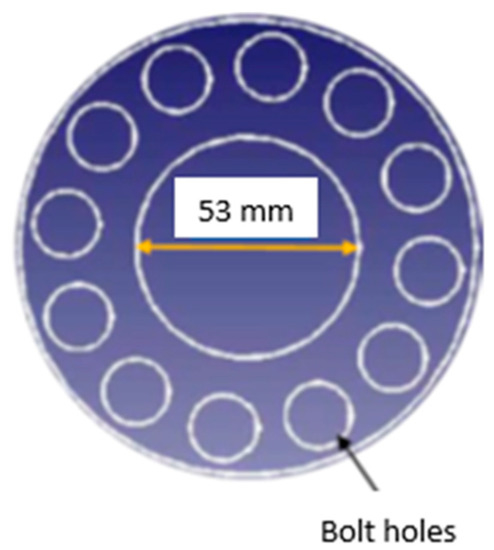
Figure 3.
Circular hollow obstacle with 50% BR.
In this study on flame propagation, measurement errors were classified into two categories: (i) systematic errors and (ii) random errors.
To mitigate and/or minimise the impact of systematic errors during the study, all sensors and analysers were accurately calibrated by skilled technicians in accordance with relevant industry standards.
The random errors were minimised through the implementation of a comprehensive experimental design and the repetition of measurements. A single, well-trained operator conducted all experiments, while the level of interaction between the operator and the experimental activities, measurements, and data collection was reduced to a negligible degree via system automation. In this setup, nearly all processes, including methane injection, ignition, and data collection, were handled by a comprehensive programmed system. The experimental work took place in a controlled laboratory environment with consistent temperature and humidity levels. All consumables, such as methane and igniters, were sourced from a single supplier to ensure consistency.
3. Flame Temperature
The adiabatic flame temperature (AFT) for methane combustion was calculated using the energy balance equation approach. For this calculation, the initial pressure of 1 atm and an initial temperature of 298 K were considered. The calculation is based on previous work and considers that the system reaches equilibrium at fixed enthalpy and pressure [19,20]. To determine the AFT the initial step was to conduct an energy balance using the heat of combustion and the specific heat capacities of the reactants and products. The calculation was performed assuming there is no heat loss to the surroundings and that all the heat released from the combustion reaction is used to heat the products.
The reaction enthalpy calculation for methane combustion can be achieved using the standard enthalpies of formation for the reactants and products. The balanced chemical equation for the complete combustion of methane is:
The standard enthalpies of formation (ΔHf°) for the substances involved in the reaction are as follows:
CH4(g) + 2 O2(g) → CO2(g) + 2 H2O(g)
ΔHf° [CH4(g)] = −74.8 kJ/mol
ΔHf° [O2(g)] = 0 kJ/mol (since it is an element in its standard state)
ΔHf° [N2(g)] = 0 kJ/mol (since it is an element in its standard state)
ΔHf° [CO2(g)] = −393.5 kJ/mol
ΔHf° [H2O(g)] = −241.8 kJ/mol
Equation (2) is used to calculate the reaction enthalpy (ΔHr°).
ΔHr° = Σ [ΔHf° (products)] − Σ [ΔHf° (reactants)]
For the methane combustion reaction:
ΔHr° = [1 × (−393.5 kJ/mol) + 2 × (−241.8 kJ/mol)] − [1 × (−74.8 kJ/mol) + 2 × (0 kJ/mol)]
ΔHr° = (−393.5 − 2 × 241.8 + 74.8) kJ/mol ≈ −802.3 kJ/mol
Therefore, the reaction enthalpy for the combustion of methane is approximately −802.3 kJ/mol.
The reaction enthalpy of methane combustion in the air (Equation (3)) follows a similar approach and achieves the same results (−802.3 kJ/mol).
CH4 + 2 (O2 + 3.76 N2) → CO2 + 2 H2O + 7.52 N2
Air is composed of about 21% O2 and 79% N2 by volume. The ATF then is calculated using the following energy balance equation
where Tref is the reference temperature (298.15 K).
ΔHr° = Σ[Cp(products) × (ATF − Tref)] − Σ[Cp(reactants) × (Tref)]
The approximate specific heat capacity (Cp) values for each species involved in the methane reaction with air, at a reference temperature (298.15 K), are [21]:
CH4: 35.7 J/mol·K O2: 29.4 J/mol·K N2: 29.1 J/mol·K CO2: 37 J/mol·K H2O: 33.6 J/mol·K.
ATF = [ΔHr° + Σ(Cp(reactants) × (ATF − Tref))]/Σ(Cp(products))
The ATF is determined by replacing the ΔHr° and Cp values in Equation (5).
ATF = [−802.3 kJ/mol × 1000 + (1 × 35.7 J/mol·K + 2 × 29.4 J/mol·K + 2 × 3.76 × 29.1 J/mol·K) × (298.15 K)]/[(1 × 37.1 J/mol·K + 2 × 33.6 J/mol·K + 7.52 × 29.1 J/mol·K)]
In addition to the calculation typically used for stoichiometric conditions, COSILAB software (version 3.3.2) was used to determine the flame temperature for the other upper and lower methane concentrations. COSILAB is a specialised software package designed for the simulation of complex chemical kinetics in combustion and reactive systems. The program includes a series of species such as CH4, CO, CO2, H2, O2, N, and N2 in the calculation. In the combustion of methane, carbon graphite does not participate directly in the reaction. It is just a reference state for calculating the enthalpies of the formation of carbon-containing compounds such as methane. The enthalpies of the formation of chemical mixtures are often reported relative to the enthalpy of the formation of the most stable allotrope of each element in its standard state, which is carbon graphite for carbon. These chemical intermediates are included in the calculation by the program based on the properties of the reactants and oxidiser [22]. The estimated adiabatic flame temperatures are directly applicable for confined vessel explosion studies with no heat loss. In the presented study, the vented geometry of the testing apparatus allows convective heat transfer and thus reduces the flame temperature. Comparing the theoretical values of adiabatic flame temperature from past studies, such as the work carried out by Movileanu [19] and Veres [22], with the present experimental results shows the deviation in flame temperature between a confined vessel and a vented vessel. This mainly happens because the adiabatic flame temperatures are directly valid for enclosed vessels where no heat is utilised or lost. Therefore, a considerable difference between the theoretical adiabatic flame temperature and experimentally measured flame temperature can be expected. The estimated values of adiabatic flame temperature are presented in the results and discussion section.
4. Results and Discussion
4.1. Flame Deflagration Overpressure and Temperature in the Straight Tube
The propagation of the flame has a significant impact on flame temperature, which is why the flame temperature was measured at the position of the ignition source. Table 1 provides a set of data to demonstrate the difference between the adiabatic flame temperature and the experimentally obtained flame temperature. The experimental setup in this study was not confined, meaning it was open at one end. Therefore, heat was transferred via convection, conduction, and radiation and/or discharged via the hot gas at the pipe’s outlet. This resulted in a considerable difference between the theoretically calculated adiabatic flame temperature and the experimentally measured flame temperature. The deviation of the flame temperature between adiabatic and experimentally obtained values suggests that the flame temperature is largely dependent on confinement. Another factor impacting the deviation of the flame temperature is the concentration of methane. The deviation of flame temperature increased as the methane concentration was increased from 6% towards the stoichiometric condition (~9.5% CH4), then decreased. At the stoichiometric condition, the flame temperature reaches a maximum; however, the convective heat transfer due to the flame propagation is also high due to the higher flame speed. Thus, the maximum deviation of the flame temperature occurs near stoichiometric methane–air mixtures.

Table 1.
Flame temperature at various methane concentrations in absence of obstacles.
Deflagration overpressure increases inside the flame propagation tube due to the partial confinement of the tube. As described in the experimental section, three pressure transducers were located at 1.2, 2.4 and 3.6 m from the ignition source. The increase of methane concentration from 6% to 10% in the absence of obstacles resulted in an increase in the maximum pressure detected (Table 2), an outcome which aligns with the results produced by previous works [8,12]. A gradual decreasing trend of maximum pressure was observed along the length of the tube, as supported by the literature [10]. The variation in pressure rise along the flame propagation tube of this geometry of interest was minimal.

Table 2.
Maximum pressure along the length of the flame propagation tube in the absence of obstacles.
The pressure values presented in Table 2 were obtained by averaging three consecutive experiments for each methane concentration. The variation of pressures for a 12% methane concentration at distances of 2.4 m and 3.6 m from the ignition source can be attributed to complete combustion of the methane, which may happen toward the end of the pipe. The 12% methane concentration falls in the upper explosion limit (rich methane region). Hence, upon combustion initiation, part of the unburned methane is pushed out toward the end of the tube where it has sufficient time to be heated by the combustion hot gases. Therefore, the remaining methane is combusted as it travels toward the outlet, resulting in a negligible pressure rise (2 pa in this study). The pressure rise associated with each methane concentration is shown in Figure 4.
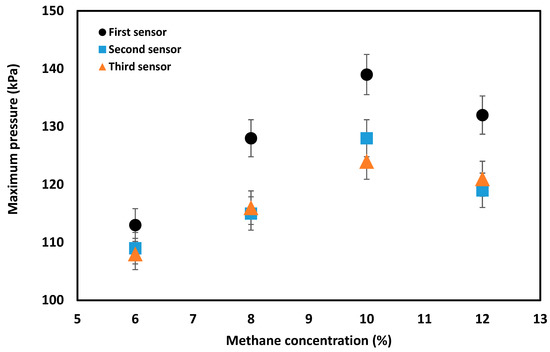
Figure 4.
Pressure verses methane concentration readings recorded by three pressure sensors at placed 1.2, 2.4 and 3.6 m from the ignition source, assuming 2.5% systematic and random errors.
4.2. Effect of Obstacles on Deflagration Overpressure
Obstacles play an important role in flame dynamics. The impact of obstacles on the generated pressure inside the flame propagation tube is reflected in Figure 5 and Figure 6. In general, deflagration overpressure increased inside the tube in the presence of obstacles.
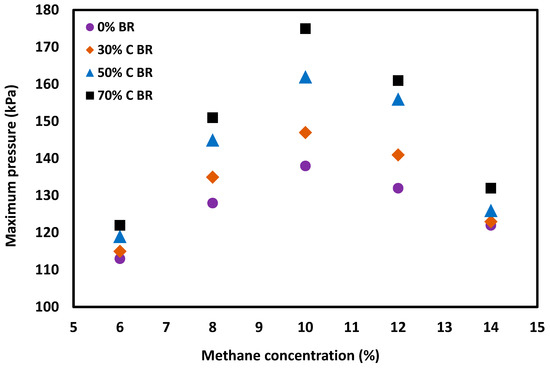
Figure 5.
Maximum pressure for different methane–air concentrations in the straight tube and when the tube included 30%, 50% or 70% blockage ratio of orifice plate positioned at 2.4 m from the ignition source.
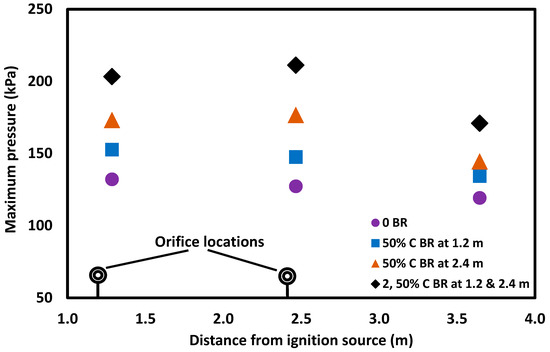
Figure 6.
Maximum pressures for 10% methane concentration recorded by three pressure sensors along the length of a straight tube and when the tube included a 50% orifice plate placed 1.2 m or 2.4 m from the ignition source, or two 50% orifice plates placed 1.2 and 2.4 m from the ignition source.
Figure 5 was developed employing the data collected from experiments for different methane concentrations, with a gradual increment of obstacle blockage ratios from 0 to 70%. In the straight tube with 0% obstacle blockage ratio (absence of obstacle), the flame propagation tube itself provides partial confinement, as described earlier. The introduction of orifice plates and the gradual increase of its blockage ratio (i.e., reducing the orifice opening) increases the confinement. Therefore, the maximum overpressure increased with the increase of the orifice’s blockage ratio, a finding that is in agreement with the relevant literature [16]. It is well known that stoichiometric methane–air mixtures (9.5% methane in air) generate the highest deflagration pressures when compared to lean and rich methane–air mixtures [23,24]. Lean and rich methane–air mixtures are those in which methane percentages are lower and higher, respectively, than they are under stoichiometric conditions. As shown in Figure 5, for the experiment with 6% and 14% methane concentrations, the influence of the orifice plates on deflagration overpressure was considerably low. However, that influence increased significantly for experiments at a 10% methane concentration (close to stoichiometry) in the employed apparatus.
The location and number of obstacles that influenced the deflagration overpressures are shown in Figure 6. Increasing the number of obstacles is expected to increase the maximum deflagration overpressure due to the increase of confinement; however, even the position of a single orifice was found to have an impact on the deflagration overpressure. For example, when an orifice plate with a 50% blockage ratio was moved from 1.2 m to 2.4 m from the ignition source along the length of tube, all pressure transducers exhibited elevated deflagration overpressures (see Figure 6). In this case, when the orifice plate was moved outward from the ignition source, the gas volume from the ignition point to the orifice plate was increased, providing a higher level of confinement. The flame area increased with this movement, causing a faster burning rate, as well as higher flame propagation speed and overpressure. Therefore, the deflagration overpressure increased when the position of the orifice plate was located further from the ignition source: in this case, located at 2.4 m instead of 1.2 m from the source of ignition.
4.3. Effect of Obstacles on the Flame Temperature
In the case of a confined vessel, the flow velocity decays to zero at the wall of the vessel [15]. Confined vessels are therefore better at preventing convection heat transfer. The introduction of an obstacle in a vented system increases the level of confinement, which results in higher turbulence and flame propagation speed and a reduction in convective heat transfer from the flame to the wall of the vessel. Therefore, the heat transfer is larger between the flame and the wall of the vessel due to the lower flame propagation speed when the vented system is without obstacles. Overall, in presence of obstacles, the heat transfer increases due to the baffle and more intensive turbulence in a vented system during a flame propagation, causing a significant rise in flame temperature. While the flame temperature was measured only at the position of the ignition source and the distance of the orifice plate location was at least 1.2 m from the ignition source, the impact of orifice plates on flame temperature was still notable (Figure 7). Increasing the obstacle blockage ratio resulted in an increase in flame temperature due to the increased confinement, and the difference between the adiabatic flame temperature and the experimentally obtained flame temperature was reduced.
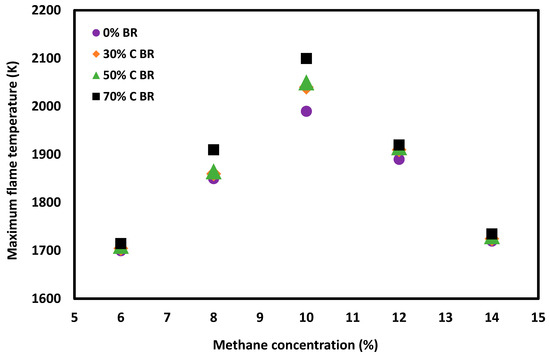
Figure 7.
Flame temperature as a function of methane concentration in the straight tube and when the tube included 30%, 50% or 70% orifice plates placed 1.2 and 2.4 m from the ignition source.
The impact of the blockage ratio, location, and number of orifice plates on the flame temperature for a 10% methane concentration is shown in Table 3. Increasing the number of obstacles from 1 to 2 was found to have an effect similar to increasing the blockage ratio of an obstacle. This is because in both cases confinement increases and heat loss is reduced. The location of an obstacle also influences the flame temperature. The flame temperature was found to increase when the orifice plate was moved from 1.2 m to 2.4 m away from the ignition source. The larger confinement caused by moving the obstacle outward caused a greater amount of flame behind the obstacle and intensive interaction with the tube wall, resulting in a higher flame temperature.

Table 3.
Maximum flame temperature (K) as a function of obstacle blockage ratio (BR%) and location (obstacle distance in metres from ignition source) for a 10% methane concentration in a straight tube.
4.4. Flame Propagation Speed
Various approaches have been employed in the literature to estimate flame propagation speed when its determination is required. In this study, the flame propagation speed was measured using a cinematography technique. The ignition source was determined as the reference point and a high-speed video camera was used to record the flame propagation behaviour and movement. This approach provides an opportunity to estimate the time required for the flame to travel from the point of origin to any point in a tunnel or pipeline, which is a very important consideration when contemplating safe fire prevention and mitigation countermeasures in extractive and process industry applications.
Figure 8 presents the flame propagation speed for 8%, 10% and 12% methane concentrations when no obstacles were applied. The 10% methane concentration showed higher flame propagation speeds along the length of the tube when compared to 8% and 12% methane concentrations (lean and rich mixtures). This finding agrees with the current literature [21].
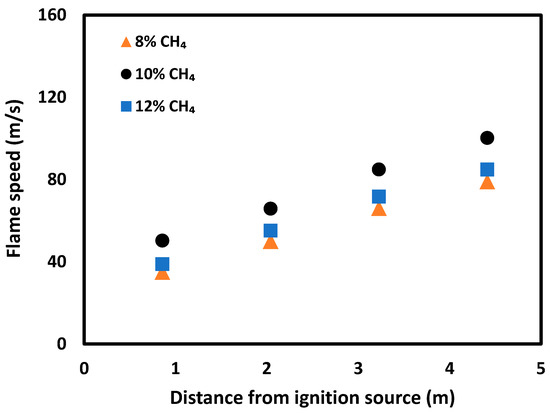
Figure 8.
Developed flame propagation speeds of 8%, 10% and 12% methane concentrations along the length of the straight tube.
The presence of obstacles in the straight tube generates vortices, as previously discussed [8]. Interaction between the tube wall and the generated vortices result in significantly enhanced turbulence. As the blockage ratio of the orifices increases, there is a further increase in the formation of vortices and wall interactions, producing a correspondingly higher level of turbulence. More turbulence leads to an increase in burning rates, which then results in an increase in flame propagation speed. The relationship between flame propagation speed and the blockage ratio of obstacles is reflected in Figure 9. The flame speed was measured at four points along the length of the glass tube, with each point representing the entrance of the flame into the flange. The time of entry was recorded by the high-speed camera. As the flame moves toward the end of the tube, the flame speed increases due to the production of higher turbulence. This phenomenon is intensified by the application of obstacles with larger blockage ratios. The variation in flame speed, shown in the error bars, is likely due to slightly different experimental conditions, or random and systematic errors.
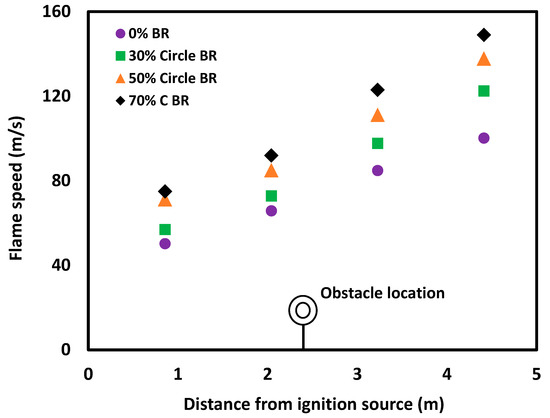
Figure 9.
Flame propagation speed for experiments with 10% methane concentration in the straight tube and when the tube included a 30%, 50% or 70% orifice plate placed 2.4 m from the ignition source.
The location and number of obstacles have similar impacts on flame propagation speed to other explosion parameters such as deflagration overpressure and flame temperature (Figure 10). Increasing the number of obstacles increases turbulence and thus enhances the formation of vortices and wall interactions, leading to a correspondingly higher flame propagation speed. The impact of the location of the obstacles on flame propagation speed is also significant. As the orifice plate was moved from 1.2 m to 2.4 m along the length of the tube, the turbulence and flame propagation speed increased, which is linked to increased tube wall interaction due to flow resistance over the longer distance between the ignition source and the obstacle.
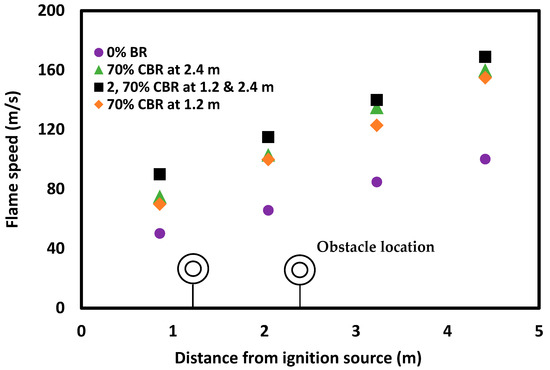
Figure 10.
Flame propagation speed for experiments with a 10% methane concentration in a straight tube; in a tube with one 70% orifice plate placed 1.2 m or 2.4 m from the ignition source; and in a tube with two 70% orifice plates placed 1.2 and 2.4 m from the ignition source.
The observed impacts of the various configurations and number of obstacles on flame propagation speed can be translated to real-world scenarios involving pipes, tunnels and other vessels. If x and y are the two equal portions of a tunnel and the flame propagates from portion x to y, the results (Figure 8, Figure 9 and Figure 10) indicate that the time required for the flame to travel portion y is smaller than that for portion x. That means the flame acceleration is higher in the second portion (y). This needs to be factored in when developing any mitigation measures which might be employed within the extractive or associated process industries.
4.5. Flame Propagation Speed in the Tube Included a 70% Obstacle
Eight sequential images have been presented in Figure 11 to illustrate 10% methane–air flame propagation in the straight tube. Figure 12 demonstrates 10% methane–air flame propagation when the tube included a 70% orifice plate positioned 1.2 m from the ignition source. In the second half of the tube, the flame front arrival time was reduced. As previously discussed, flame distortion occurs when obstacles are introduced and a higher level of turbulence is generated. The elapsed time for flame propagation is therefore reduced for experiments with obstacles when compared to experiments without obstacles. A 3 ms reduction of flame elapse time (from 40 ms to 37 ms) was observed when an obstacle was placed in the flame propagation tube at 1.2 m from the ignition source.

Figure 11.
10% methane–air flame propagation in the straight tube.

Figure 12.
10% methane–air flame propagation in the tube with a 70% circular opening obstacle positioned 1.2 m from the ignition source.
5. Conclusions
Flame propagation behaviour for methane–air mixtures was investigated in a clear borosilicate glass tube without obstacles and in the presence of single or multiple obstacles employed in various configurations. The adiabatic flame temperature was computed using COSILAB software (version 3.3.2). The difference between adiabatic flame temperature and the experimentally measured flame temperature was determined. This difference in flame temperature can be interpreted as the deviation of flame temperature from confined vessel to vented vessel.
The deflagration overpressure increased inside the flame propagation tube in the presence of obstacles. This was due to the increase in confinement when obstacles were employed. For instance, the deflagration overpressure in the 10% methane experiment was 135 kPa and 175 kPa in the straight tube and the tube with a 70% obstacle, respectively. The flame temperature also increased in the presence of obstacles. For example, for the 10% methane experiment, the flame temperature increased from about 2000 K to 2135 K when the blockage ratio of the orifice plate was increased from 0% to 70%.
Flame propagation speed increased with the introduction of orifice plates. The orifice plate increases the flame surface, causing a higher burning rate and generating a higher level of turbulence. For the 10% methane experiment, the flame propagation speed in the absence and in presence of a 70% orifice plate was around 100 m/s and 160 m/s, respectively. Flame propagation images demonstrated that the elapsed time of flame propagation in the tube was reduced in the presence of obstacles.
The results suggest that the presence of obstacles in tunnels, chimneys, pipelines and other semi-confined structures will increase the severity of explosions. Therefore, careful mitigation measures should to be adopted in order to prevent any loss of life or damage to property in these real-world applications.
Author Contributions
Conceptualization, J.Z. and B.M.; methodology, J.Z., software, M.S., validation, M.S., J.Z. and B.M.; formal analysis, M.S.; investigation, M.S.; resources, J.Z.; data curation, M.S.; writing—original draft preparation, M.S.; writing—review and editing, J.Z.; visualization, M.S.; supervision, J.Z.; project administration, J.Z.; funding acquisition, B.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Australia Coal Association Low Emissions Technologies Ltd., Australia (grant number—G1400523).
Institutional Review Board Statement
Institutional Review Board Statement and Ethical approval are not applicable as this study didn’t involve humans or animals.
Informed Consent Statement
Not applicable, the study not involving any humans or animals.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lashof, D.A.; Ahuja, D.R. Relative contributions of greenhouse gas emissions to global warming. Nature 1990, 344, 529–531. [Google Scholar] [CrossRef]
- Hansen, J.E. Sir John Houghton: Global Warming: The Complete Briefing. J. Atmospheric. Chem. 1998, 30, 409–412. [Google Scholar] [CrossRef]
- Moss, A.R.; Jouany, J.-P.; Newbold, J. Methane production by ruminants: Its contribution to global warming. In Annales de Zootechnie; EDP Sciences: Paris, France, 2000; pp. 231–253. [Google Scholar]
- Ajrash, M.J.; Zanganeh, J.; Moghtaderi, B. Experimental investigation of the minimum auto-ignition temperature (MAIT) of the coal dust layer in a hot and humid environment. Fire Saf. J. 2016, 82, 12–22. [Google Scholar] [CrossRef]
- Dhillon, B.S. Mine Safety: A Modern Approach; Springer Science & Business Media: New York, NY, USA, 2010. [Google Scholar]
- Vidal, J. Mining: Fire, Flood, Poor Health—All Part of the Job. The Guardian. 2014. Available online: https://www.theguardian.com/environment/2014/may/14/mining-fire-poor-health-flood-analysis (accessed on 8 March 2023).
- Ferrier, T.; AAP. Five Miners Burned in Underground Blast. (News.com.au Website). Available online: https://www.news.com.au/national/queensland/news/five-miners-burned-in-underground-blast/news-story/da08241740bbe4145df870f8277cfe7d (accessed on 8 March 2023).
- Kundu, S.; Zanganeh, J.; Moghtaderi, B. A review on understanding explosions from methane–air mixture. J. Loss Prev. Process. Ind. 2016, 40, 507–523. [Google Scholar] [CrossRef]
- Cheng, J.; Zhang, X.; Ghosh, A. Explosion risk assessment model for underground mine atmosphere. J. Fire Sci. 2017, 35, 21–35. [Google Scholar] [CrossRef]
- Kundu, S.K.; Zanganeh, J.; Eschebach, D.; Mahinpey, N.; Moghtaderi, B. Explosion characteristics of methane–air mixtures in a spherical vessel connected with a duct. Process Saf. Environ. Prot. 2017, 111, 85–93. [Google Scholar] [CrossRef]
- Dong, C.; Bi, M.; Zhou, Y. Effects of obstacles and deposited coal dust on characteristics of premixed methane–air explosions in a long closed pipe. Saf. Sci. 2012, 50, 1786–1791. [Google Scholar] [CrossRef]
- Masri, A.; Ibrahim, S.; Nehzat, N.; Green, A. Experimental study of premixed flame propagation over various solid obstructions. Exp. Therm. Fluid Sci. 2000, 21, 109–116. [Google Scholar] [CrossRef]
- Zhang, Q.; Pang, L.; Liang, H. Effect of scale on the explosion of methane in air and its shockwave. J. Loss Prev. Process. Ind. 2011, 24, 43–48. [Google Scholar] [CrossRef]
- Kolahdooz, H.; Nazari, M.; Kayhani, M.H.; Ebrahimi, R.; Askari, O. Effect of Obstacle Type on Methane–Air Flame Propagation in a Closed Duct: An Experimental Study. J. Energy Resour. Technol. 2019, 141, 112208. [Google Scholar] [CrossRef]
- Wang, J.; Fan, Z.; Wu, Y.; Zheng, L.; Pan, R.; Wang, Y. Effect of Abrupt Changes in the Cross-Sectional Area of a Pipe on Flame Propagation Characteristics of CH(4)/Air Mixtures. ACS Omega 2021, 6, 15126–15135. [Google Scholar] [CrossRef] [PubMed]
- Yakush, S.; Semenov, O.; Alexeev, M. Premixed Propane– Air Flame Propagation in a Narrow Channel with Obstacles. Energies 2023, 16, 1516. [Google Scholar]
- Wang, T.; Yang, P.; Yi, W.; Luo, Z.; Cheng, F.; Ding, X.; Kang, X.; Feng, Z.; Deng, J. Effect of obstacle shape on the deflagration characteristics of premixed LPG-air mixtures in a closed tube. Process Saf. Environ. Prot. 2022, 168, 248–256. [Google Scholar] [CrossRef]
- Phylaktou, H.; Andrews, G. The acceleration of flame propagation in a tube by an obstacle. Combust Flame 1991, 85, 363–379. [Google Scholar] [CrossRef]
- Movileanu, C.; Mitu, M.; Brinzea, V.; Musuc, A.; Mocanu, M.; Razus, D.; Oancea, D. Adiabatic Flame Temperature of Fuel-Air Mixtures in Isobaric and Isochoric Combustion Processes. Rev. Chim. 2011, 62, 376–379. [Google Scholar]
- National Institue of Standards and Technology, US Department of Commerce. Chemistry Webbook, SRD 69, 2023. Available online: https://webbook.nist.gov/chemistry/ (accessed on 13 March 2023).
- Wang, C.; Huang, F.; Addai, E.K.; Dong, X. Effect of concentration and obstacles on flame velocity and overpressure of methane-air mixture. J. Loss Prev. Process. Ind. 2016, 43, 302–310. [Google Scholar] [CrossRef]
- Veres, J.; Skrinsky, J. Experimental Research of Flammability and Explosion Parameters of Binary Gas Mixtures in 1 m3. Chem. Eng. Trans. 2016, 52, 1273–1278. [Google Scholar]
- Gieras, M.; Klemens, R.; Rarata, G.; Wolański, P. Determination of explosion parameters of methane-air mixtures in the chamber of 40 dm3 at normal and elevated temperature. J. Loss Prev. Process. Ind. 2006, 19, 263–270. [Google Scholar] [CrossRef]
- Vanderstraeten, B.; Tuerlinckx, D.; Berghmans, J.; Vliegen, S.; Oost, E.V.; Smit, B. Experimental study of the pressure and temperature dependence on the upper flammability limit of methane/air mixtures. J. Hazard. Mater. 1997, 56, 237–246. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).