Modern Dimensional Analysis Based on Fire-Protected Steel Members’ Analysis Using Multiple Experiments
Abstract
:1. Introduction
2. Materials and Methods
- the stand mounting, with the adequate thermal insulation;
- the mounting of the tested structural element on the lower plate ;
- checking the functioning of the test bench;
- the checking of the nominal temperature ;
- the checking of the heating regime’s steps;
- starting the test bench and monitoring all heating parameters, such as:
- the consumed electrical energy the time corresponding to the stabilised thermal regime, which was considered when the maximal temperature oscillation of was observed for a minimum period of at the upper part of the tested structural element;
- the repeating of these stages for all nominal values of .
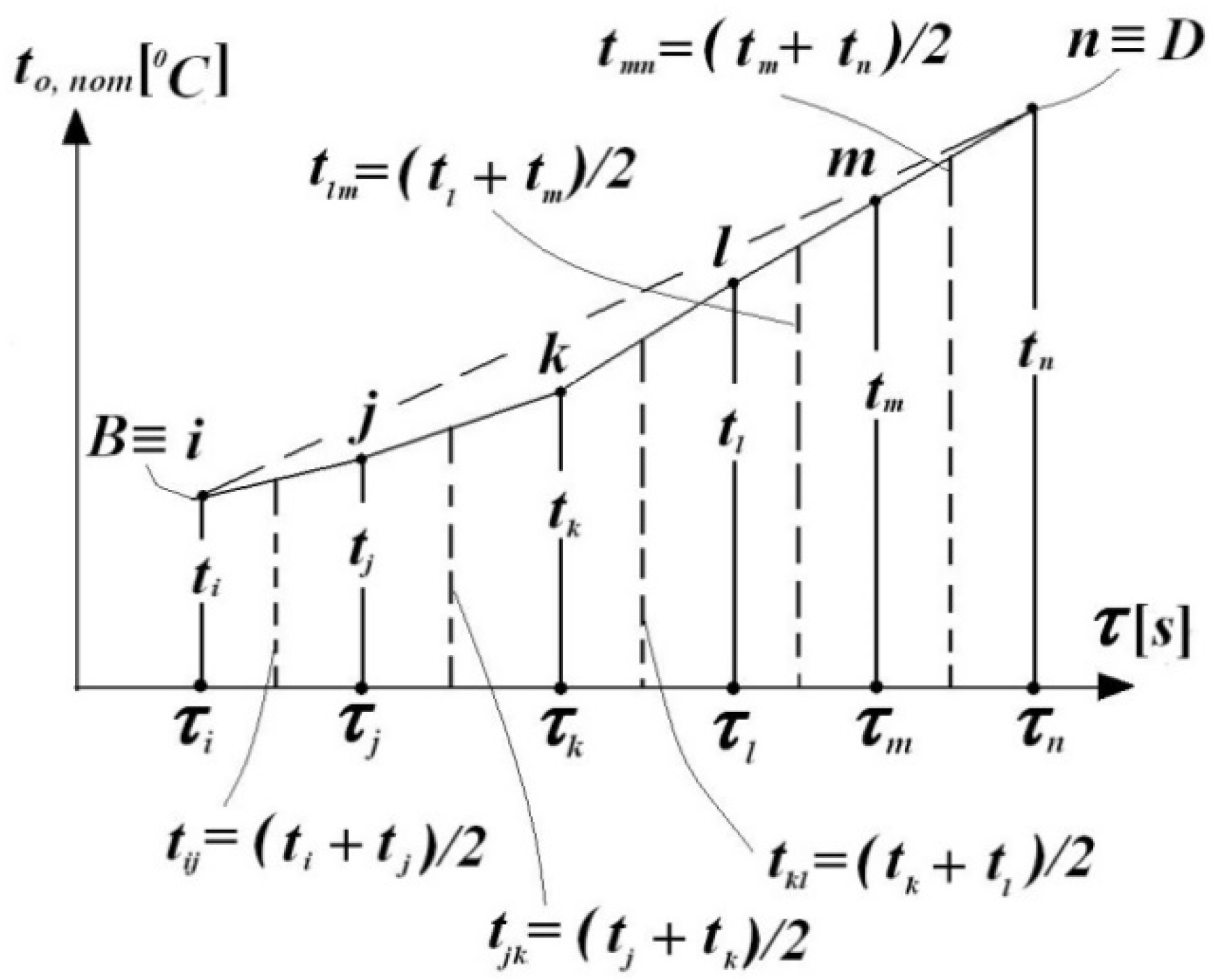
- In Equation (1) for each interval , the corresponding temperature difference [ ] will be considered and applied to the time intervals corresponding to ;
- With Equation (2), will be determined individually for each interval prior, considering the average temperature related to each interval and the temperature differences prior, respectively;
- The term will be constant; it will multiply the sum of the partial products related to these intervals.
- The quadratic section represents a particular case of the rectangular one, with the same dimensions and the same scale factors along the z and y cross-sectional coordinates;
- The MDA allows the defining of different thicknesses as well as different sizes along the z and y cross-sectional directions, which subsequently will be defined by the corresponding elements of the ML;
- When the length is considered an independent variable, i.e., freely chosen a priori for both prototype and model, the corresponding elements of ML can be ignored; one is accepted as having the same scale factor of length ;
- By selecting the shape factor as an independent variable, together with the length , MDA offers a great opportunity for the model to be freed from the geometric similarity restriction of the cross-sections for the prototype and the model (e.g., one can accept different cross-sections, not only rectangular ones, with the single condition having the foreseen shape factor );
- One has to mention that, in both cases, the independent variables are rigorously related to the actual measurements;
- Only one dependent variable represents an exception, that is the one for which one has considered having limited access to the prototype (or which will be difficult to measure) and where one has to be obtained by means of the ML. In the case of Version I, this dependent variable was considered the heat flow , while in the case of Version II, this is the amount of heat .
3. Results
- Prototype (structural element manufactured at 1:1 scale)—model (structural element at 1:2 scale), symbolised by (1:2/1:1) Model/Prototype;
- (1:4/1:2) Model/Prototype;
- (1:4/1:1) Model/Prototype;
- (1:2/1:10) Model/Prototype;
- (1:4/1:10) Model/Prototype;
- (1:4/1:10) Model/Prototype.
4. Discussion and Conclusions
- The deduced MLs by the authors in the work [57], for two experimentally significant versions I and II, were validated by rigorous experimental investigations on multiple sets of prototypes and models;
- It is also worth highlighting those simplifications related to ignoring several scale factors, involved in the following:
- existing implicit correlations (having the same material for the prototype and the model; having identical environmental and deployment conditions for both of them);
- existing over-definition of the parameters (e.g., accepting the same scale of all lengths);
- The variables of the different thicknesses (, ) can help conceive various suitable models, e.g., with different wall thicknesses along without any restriction on the geometric similarity of the prototype and model cross-sections;
- The simultaneous inclusion of both length () and shape factor in the independent variables ensures a wide generalisation of the associated model to the analysed prototype; in this case, this meant no restrictions of geometric similarity and, additionally, one can accept models having other shapes of the cross-section, imposing only the same scale factor for ;
- If is accepted as the independent variable, then another material can be chosen for the model with respect to the prototype and consequently both the manufacturing as well as the testing cost can be reduced;
- By means of or as an independent variable, one can choose a very convenient thermal stress strategy of the model with respect to the prototype;
- If is selected as an independent variable, the thermal regime can be optimised from the point of view of loading the model in relation to the prototype. By means of the exposure time as an independent variable, one can obtain some supplementary benefits in order to more efficiently follow the thermal transfer to the analysed structure on fire;
- In the authors’ opinion, based on their multiple experiences in different fields of engineering, MDA can become a useful tool for common researchers in this field of thermal transfer phenomena and, last but not least, in the analysis of the complex phenomenon of fires in metal resistance structures. The obtained ML for straight bars can be extended to structural elements formed by straight bars, having the same cross-sections, which are obviously found in all civil and industrial structures. Consequently, these MLs will become useful tools in fire simulations as well as fire prevention research;
- Taking into consideration the identity of the directly measured data with those obtained by MLs in Tables 5–8, it becomes possible to conceive high-accuracy, repetitive and very efficient thermal loading strategies for new, untested structural elements, which also represent a great/major advantage of MDA.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Munteanu (Száva), I.R. Investigation Concerning Temperature Field Propagation along Reduced Scale Modelled Metal Structures. Ph.D. Thesis, Transilvania University of Brasov, Brașov, Romania, 2018. [Google Scholar]
- Aglan, A.A.; Redwood, R.G. Strain-Hardening Analysis of Beams with 2 WEB- Rectangular Holes. Arab. J. Sci. Eng. 1987, 12, 37–45. [Google Scholar]
- Al-Homoud, M.S. Performance characteristics and practical applications of common building thermal insulation materials. Build. Environ. 2005, 40, 353–366. [Google Scholar] [CrossRef]
- Bahrami, A.; Mousavi Anijdan, S.H.; Ekrami, A. Prediction of mechanical properties of DP steels using neural network model. J. Alloy. Compd. 2005, 392, 177–182. [Google Scholar] [CrossRef]
- Bailey, C. Indicative fire tests to investigate the behaviour of cellular beams protected with intumescent coatings. Fire Saf. J. 2004, 39, 689–709. [Google Scholar] [CrossRef]
- Dai, S.J.; Zhu, B.C.; Chen, Q. Analysis of bending strength of the rectangular hole honeycomb beam. In Proceedings of the 2nd International Conference on Civil, Architectural and Hydraulic Engineering, Progress in Industrial and Civil Engineering II, Zhuhai, China, 27–28 July 2013; PTS 1-4 405-408. pp. 993–999. [Google Scholar]
- Deshwal, P.S.; Nandal, J.S. On Torsion of Rectangular Beams with Holes at the Center. Indian J. Pure Appl. Math. 1991, 22, 425–438. [Google Scholar]
- John, A.; Bakowski, H.; Száva, I.; Vlase, S. New Tribological Aspects in the Micro-Areas of the Symmetric Rolling-Sliding Contact. Symmetry 2022, 14, 1523. [Google Scholar] [CrossRef]
- Ferro, V. Assessing flow resistance law in vegetated channels by dimensional analysis and self-similarity. Flow Meas. Instrum. 2019, 69, 101610. [Google Scholar] [CrossRef]
- Fourier, J. Theorie Analytique de la Chaleur; Firmin Didot: Paris, France, 1822. (In French) [Google Scholar]
- Han, X.; Sun, X.; Li, G.; Huang, S.; Zhu, P.; Shi, C.; Zhang, T. A Repair Method for Damage in Aluminum Alloy Structures with the Cold Spray Process. Materials 2021, 14, 6957. [Google Scholar] [CrossRef]
- Khan, M.A.; Shah, I.A.; Rizvi, Z.; Ahmad, J. A numerical study on the validation of thermal formulations towards the behaviours of RC beams. Sci. Mater. Today Proc. 2019, 17, 227–234. [Google Scholar] [CrossRef]
- Lawson, R.M. Fire engineering design of steel and composite Buildings. J. Constr. Steel Res. 2001, 57, 1233–1247. [Google Scholar] [CrossRef]
- Levac, M.L.J.; Soliman, H.M.; Ormiston, S.J. Three-dimensional analysis of fluid flow and heat transfer in single- and two-layered micro-channel heat sinks. Heat Mass Transf. 2011, 47, 1375–1383. [Google Scholar] [CrossRef]
- Noack, J.; Rolfes, R.; Tessmer, J. New layerwise theories and finite elements for efficient thermal analysis of hybrid structures. Comput. Struct. 2003, 81, 2525–2538. [Google Scholar] [CrossRef]
- Papadopoulos, A.M. State of the art in thermal insulation materials and aims for future developments. Energy Build. 2005, 37, 77–86. [Google Scholar] [CrossRef]
- Quintier, G.J. Fundamentals of Fire Phenomena; John Willey & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Șova, M.; Șova, D. Thermotechnics, VL.II.; Transilvania University Press: Transylvania, Romania, 2001. [Google Scholar]
- Tafreshi, A.M.; di Marzo, M. Foams and gels as temperature protection agents. Fire Saf. J. 1999, 33, 295–305. [Google Scholar] [CrossRef]
- Vlase, S.; Năstac, C.; Marin, M.; Mihalcica, M. A Method for the Study of the Vibration of Mechanical Bars Systems with Symmetries. Acta Tech. Napoc. Ser. Appl. Math. Mech. Eng. 2017, 60, 539–544. [Google Scholar]
- Wong, M.B.; Ghojel, J.I. Sensitivity analysis of heat transfer formulations for insulated structural steel components Fire. Saf. J. 2003, 38, 187–201. [Google Scholar] [CrossRef]
- Yang, K.-C.; Chen, S.-J.; Lin, C.C.; Lee, H.H. Experimental study on local buckling of fire-resisting steel columns under fire load. J. Constr. Steel Res. 2005, 61, 553–565. [Google Scholar] [CrossRef]
- Baker, W.; Baker, W.; Westine, P.S.; Dodge, F.T. Similarity Methods in Engineering Dynamics; Elsevier: Amsterdam, The Netherlands, 1991. [Google Scholar]
- Carabogdan, G.I.; Badea, A.; Brătianu, C.; Muşatescu, V.I. Methods of Analysis of Thermal Energy Processes and Systems; Energy Processes and Systems: Ed. Tehn.: Bucharest, Romania, 1989. [Google Scholar]
- Sedov, I.L. Similarity and Dimensional Methods in Mechanics; MIR Publisher: Moscow, Russia, 1982. [Google Scholar]
- Yen, P.H.; Wang, J.C. Power generation and electrical charge density with temperature effect of alumina nanofluids using dimensional analysis. Energy Convers. Manag. 2009, 186, 546–555. [Google Scholar] [CrossRef]
- Alshqirate, A.A.Z.S.; Tarawneh, M.; Hammad, M. Dimensional Analysis and Empirical Correlations for Heat Transfer and Pressure Drop in Condensation and Evaporation Processes of Flow Inside Micropipes: Case Study with Carbon Dioxide (CO2). J. Braz. Soc. Mech. Sci. Eng. 2012, 34, 89–96. [Google Scholar] [CrossRef]
- Asgari, O.; Saidi, M. Three-dimensional analysis of fluid flow and heat transfer in the microchannel heat sink using additive-correction multigrid technique. In Proceedings of the Micro/Nanoscale Heat Transfer International Conference, PTS A AND B. 1st ASME Micro/Nanoscale Heat Transfer International Conference, Tainan, Tainan, Taiwan, 6–9 January 2008; pp. 679–689. [Google Scholar]
- Barenblatt, G.I. Dimensional Analysis; Gordon and Breach: New York, NY, USA, 1987. [Google Scholar]
- Barr, D.I.H. Consolidation of Basics of Dimensional Analysis. J. Eng. Mech. ASCE 1984, 110, 1357–1376. [Google Scholar] [CrossRef]
- Bhaskar, R.; Nigam, A. Qualitative Physics using Dimensional Analysis. Artif. Intell. 1990, 45, 73–111. [Google Scholar] [CrossRef]
- Bridgeman, P.W. Dimensional Analysis; Yale University Press: New Haven, CT, USA, 1922; (Reissued in paperbound in 1963). [Google Scholar]
- Buckingham, E. On Physically Similar Systems. Phys. Rev. 1914, 4, 345. [Google Scholar] [CrossRef]
- Canagaratna, S.G. Is dimensional analysis the best we have to offer. J. Chem. Educ. 1993, 70, 40–43. [Google Scholar] [CrossRef]
- Carinena, J.F.; Santander, M. Dimensional Analysis. Adv. Electron. Electron Phys. 1988, 72, 181–258. [Google Scholar] [CrossRef]
- Carlson, D.E. Some New Results in Dimensional Analysis. Arch. Ration. Mech. Anal. 1978, 68, 191–210. [Google Scholar] [CrossRef]
- Chen, W.K. Algebraic Theory of Dimensional Analysis. J. Frankl. Inst. 1971, 292, 403–409. [Google Scholar] [CrossRef]
- Coyle, R.G.; Ballicolay, B. Concepts and Software for Dimensional Analysis in Modeling. IEEE Trans. Syst. Man Cybern. 1984, 14, 478–487. [Google Scholar] [CrossRef]
- Gibbings, J.C. Dimensional Analysis. J. Phys. A-Math. Gen. 1980, 13, 75–89. [Google Scholar] [CrossRef]
- Gibbings, J.C. A Logic of Dimensional Analysis. J. Physiscs A-Math. Gen. 1982, 15, 1991–2002. [Google Scholar] [CrossRef]
- Illan, F.; Viedma, A. Experimental study on pressure drop and heat transfer in pipelines for brine based ice slurry Part II: Dimensional analysis and rheological Model. Int. J. Refrig. Rev. Int. Du Froid 2009, 32, 1024–1031. [Google Scholar] [CrossRef]
- Jofre, L.; del Rosario, Z.R.; Iaccarino, G. Data-driven dimensional analysis of heat transfer in irradiated particle-laden turbulent flow. Int. J. Multiph. Flow 2020, 125, 103198. [Google Scholar] [CrossRef]
- Kivade, S.B.; Murthy, C.S.N.; Vardhan, H. The use of Dimensional Analysis and Optimisation of Pneumatic Drilling Operations and Operating Parameters. J. Inst. Eng. India Ser. D 2012, 93, 31–36. [Google Scholar] [CrossRef]
- Langhaar, H.L. Dimensional Analysis and Theory of Models; John Wiley & Sons Ltd.: New York, NY, USA, 1951. [Google Scholar]
- Martins, R.D.A. The Origin of Dimensional Analysis. J. Frankl. Inst. 1981, 311, 331–337. [Google Scholar] [CrossRef]
- Nakla, M. On fluid-to-fluid modeling of film boiling heat transfer using dimensional analysis. Int. J. Multiph. Flow 2011, 37, 229–234. [Google Scholar] [CrossRef]
- Nezhad, A.H.; Shamsoddini, R. Numerical Three-Dimensional Analysis of the Mechanism of Flow and Heat Transfer in a Vortex Tube. Therm. Sci. 2009, 13, 183–196. [Google Scholar] [CrossRef]
- Pankhurst, R.C. Dimensional Analysis and Scale Factor; Chapman & Hall Ltd.: London, UK, 1964. [Google Scholar]
- Remillard, W.J. Applying Dimensional Analysis. Am. J. Phys. 1983, 51, 137–140. [Google Scholar] [CrossRef]
- Romberg, G. Contribution to Dimensional Analysis. Inginieur. Archiev. 1985, 55, 401–412. [Google Scholar] [CrossRef]
- Schnittger, J.R. Dimensional Analysis in Design. Journal of Vibration, Accoustic. Stress Reliab. Des. Trans. ASME 1988, 110, 401–407. [Google Scholar] [CrossRef]
- Szekeres, P. Mathematical Foundations of Dimensional Analysis and the Question of Fundamental Units. Int. J. Theor. Phys. 1978, 17, 957–974. [Google Scholar] [CrossRef]
- Yao, S.; Yan, K.; Lu, S.; Xu, P. Prediction and application of energy absorption characteristics of thinwalled circular tubes based on dimensional analysis. Thin-Walled Struct. 2018, 130, 505–519. [Google Scholar] [CrossRef]
- Zierep, J. Similarity Laws and Modelling; Marcel Dekker: New York, NY, USA, 1971. [Google Scholar]
- Gálfi, B.-P.; Száva, I.; Șova, D.; Vlase, S. Thermal Scaling of Transient Heat Transfer in a Round Cladded Rod with Modern Dimensional Analysis. Mathematics 2021, 9, 1875. [Google Scholar] [CrossRef]
- Száva, I.R.; Șova, D.; Dani, P.; Élesztős, P.; Száva, I.; Vlase, S. Experimental Validation of Model Heat Transfer in Rectangular Hole Beams Using Modern Dimensional Analysis. Mathematics 2022, 10, 409. [Google Scholar] [CrossRef]
- Șova, D.; Száva, I.R.; Jármai, K.; Száva, I.; Vlase, S. Modern method to analyze the Heat Transfer in a Symmetric Metallic Beam with Hole. Symmetry 2022, 14, 769. [Google Scholar] [CrossRef]
- Trif, I.; Asztalos, Z.; Kiss, I.; Élesztős, P.; Száva, I.; Popa, G. Implementation of the Modern Dimensional Analysis in Engineering Problems-Basic Theoretical Layouts. Ann. Fac. Eng. Hunedoara 2019, 17, 73–76, ISSN-L 1584-2665, Tome XVII, Fascicule 3 [August]. [Google Scholar]
- Szirtes, T. The Fine Art of Modelling, SPAR. J. Eng. Technol. 1992, 1, 37. [Google Scholar]
- Szirtes, T. Applied Dimensional Analysis and Modelling; McGraw-Hill: Toronto, ON, Canada, 1998. [Google Scholar]
- Száva, I.; Szirtes, T.; Dani, P. An Application of Dimensional Model Theory in the Determination of the Deformation of a Structure. Eng. Mech. 2006, 13, 31–39. [Google Scholar]
- Dani, P.; Száva, I.R.; Kiss, I.; Száva, I.; Popa, G. Principle schema of an original full-, and reduced-scale testing bench, destined to fire protection investigations. Ann. Fac. Eng. Hunedoara-Int. J. Eng. 2018, 16, 149–152, Tome XVI, Fascicule 2. [Google Scholar]
- Turzó, G.; Száva, I.R.; Gálfi, B.P.; Száva, I.; Vlase, S.; Hoța, H. Temperature distribution of the straight bar, fixed into a heated plane surface. Fire Mater. 2018, 42, 202–212. [Google Scholar] [CrossRef]
- Száva, R.I.; Száva, I.; Vlase, S.; Gálfi, P.B.; Jármai, K.; Gălățanu, T.; Popa, G.; Asztalos, Z. Modern Dimensional Analysis-Based Steel Column Heat Transfer Evaluation using Multiple Experiments. Symmetry 2022, 14, 1952. [Google Scholar] [CrossRef]
- Dani, P. Theoretical and Experimental Study of Heat-Field Propagation through Multi-Layer Fire-Protection on Stress-, and Strain-State of Metallic Structures. Ph.D. Thesis, Transilvania University of Brasov, Brasov, Romania, 2011. [Google Scholar]
- Turzó, G. Temperature distribution along a straight bar sticking out from a heated plane surface and the heat flow transmitted by this bar (I)-Theoretical Approach. Ann. Fac. Eng. Hunedoara-Int. J. Eng. 2016, 14, 49–53, Tome XIV, Fascicule 3, ISSN:1584-2665. [Google Scholar]
- Turzó, G.; Száva, I.R.; Dancsó, S.; Száva, I.; Vlase, S.; Munteanu, V.; Gălățanu, T.; Asztalos, Z. A New Approach in Heat Transfer Analysis: Reduced-Scale Straight Bars with Massive and Square-Tubular Cross-Sections. Mathematics 2022, 10, 3680. [Google Scholar] [CrossRef]

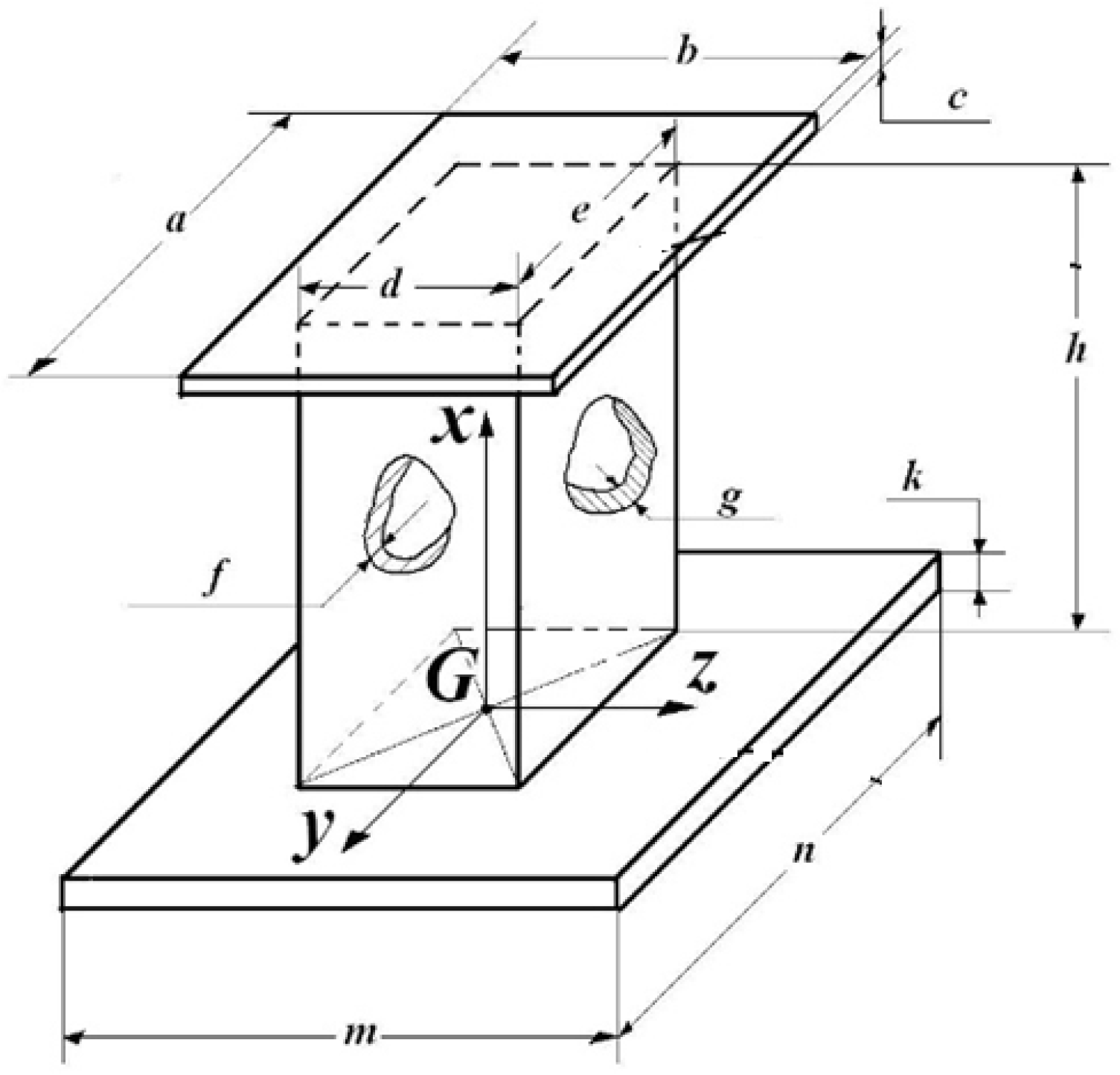
| Dimensions, in m | The Scale of the Tested Element | |||
|---|---|---|---|---|
| 1:1 | 1:2 | 1:4 | 1:10 | |
| a | 0.370 | 0.185 | 0.108 | 0.0370 |
| b | 0.370 | 0.185 | 0.108 | 0.0370 |
| c | 0.006 | 0.003 | 0.0015 | 0.0015 |
| d | 0.350 | 0.175 | 0.0875 | 0.0030 |
| e | 0.350 | 0.175 | 0.0875 | 0.0030 |
| f | 0.016 | 0.008 | 0.004 | 0.0015 |
| g | 0.016 | 0.008 | 0.004 | 0.0015 |
| h | 0.400 | 0.200 | 0.100 | 0.400 |
| k | 0.010 | 0.005 | 0.0025 | 0.0015 |
| m | 0.450 | 0.450 | 0.450 | 0.450 |
| n | 0.450 | 0.450 | 0.450 | 0.450 |
| Tested Structural Element, All Painted | KWh | |||||||
|---|---|---|---|---|---|---|---|---|
| at scale 1:10 | 23–100 | 0.7017543 | 0.4 | 1,440,000 | 77 | 20.34095 | 16,958.25002 | 1,423,041.75 |
| 100–200 | 0.7017543 | 0.7 | 2,520,000 | 100 | 20.34095 | 37,242.24536 | 2,482,757.755 | |
| 200–300 | 0.7017543 | 0.6 | 2,160,000 | 100 | 20.34095 | 15,238.33319 | 2,144,761.667 | |
| 300–400 | 0.7017543 | 0.8 | 2,880,000 | 100 | 20.34095 | 32,726.55446 | 2,847,273.446 | |
| 400–450 | 0.7017543 | 0.5 | 1,800,000 | 50 | 20.34095 | 22,656.56375 | 1,777,343.436 | |
| 450–500 | 0.7017543 | 0.5 | 1,800,000 | 50 | 20.34095 | 12,894.12821 | 1,787,105.872 | |
| at scale 1:4 | 23–100 | 0.2619760 | 0.4 | 1,440,000 | 77 | 20.07323 | 73,312.41894 | 1,366,687.581 |
| 100–200 | 0.2619760 | 1.0 | 3,600,000 | 100 | 20.07323 | 411,563.842 | 3,188,436.158 | |
| 200–300 | 0.2619760 | 1.6 | 5,760,000 | 100 | 20.07323 | 1,016,681.839 | 4,743,318.161 | |
| 300–400 | 0.2619760 | 1.0 | 3,600,000 | 100 | 20.07323 | 685,259.6097 | 2,914,740.39 | |
| 400–450 | 0.2619760 | 0.9 | 3,240,000 | 50 | 20.07323 | 706,478.8158 | 2,533,521.184 | |
| 450–500 | 0.2619760 | 2.3 | 8,280,000 | 50 | 20.07323 | 2,287,112.765 | 5,992,887.235 | |
| at scale 1:2 | 23–100 | 0.1309880 | 0.6 | 2,160,000 | 77 | 19.17165 | 35,855.38923 | 2,124,144.611 |
| 100–200 | 0.1309880 | 1.3 | 4,680,000 | 100 | 19.17165 | 329,675.8286 | 4,350,324.171 | |
| 200–300 | 0.1309880 | 1.0 | 3,600,000 | 100 | 19.17165 | 277,713.1232 | 3,322,286.877 | |
| 300–400 | 0.1309880 | 1.6 | 5,760,000 | 100 | 19.17165 | 823,809.1535 | 4,936,190.847 | |
| 400–450 | 0.1309880 | 0.7 | 2,520,000 | 50 | 19.17165 | 368,480.895 | 2,151,519.105 | |
| 450–500 | 0.1309880 | 0.8 | 2,880,000 | 50 | 19.17165 | 544,542.1814 | 2,335,457.819 | |
| at scale 1:1 | 23–100 | 0.0654940 | 1.3 | 4,680,000 | 77 | 15.55354 | 34,080.0952 | 4,645,919.905 |
| 100–200 | 0.0654940 | 2.9 | 10,440,000 | 100 | 15.55354 | 426,290.5755 | 10,013,709.42 | |
| 200–300 | 0.0654940 | 2.2 | 7,920,000 | 100 | 15.55354 | 343,502.9552 | 7,576,497.045 | |
| 300–400 | 0.0654940 | 2.0 | 7,200,000 | 100 | 15.55354 | 330,213.3152 | 6,869,786.685 | |
| 400–450 | 0.0654940 | 1.2 | 4,320,000 | 50 | 15.55354 | 242,363.0521 | 4,077,636.948 | |
| 450–500 | 0.0654940 | 1.4 | 5,040,000 | 50 | 15.55354 | 515,674.9588 | 4,524,325.041 |
| Tested Structural Element, All Painted | |||||||
|---|---|---|---|---|---|---|---|
| at scale 1:10 | 23–100 | 679,968 | 663,009.75 | 2070 | 8.192391312 | 687.4597826 | 320.2945652 |
| 100–200 | 1,189,944 | 1,152,701.755 | 2670 | 13.9484065 | 929.8718182 | 431.7235036 | |
| 200–300 | 1,019,952 | 1,004,713.667 | 1020 | 14.93954235 | 2102.707516 | 985.0133988 | |
| 300–400 | 1,359,936 | 1,327,209.446 | 1626 | 20.12703226 | 1751.09068 | 816.2419714 | |
| 400–450 | 849,960 | 827,303.4363 | 960 | 23.60058724 | 1851.399413 | 861.7744128 | |
| 450–500 | 849,960 | 837,065.8718 | 510 | 25.28260432 | 3504.12916 | 1641.305631 | |
| at scale 1:4 | 23–100 | 679,968 | 606,655.5811 | 2220 | 33.02361213 | 615.6250365 | 273.2682798 |
| 100–200 | 1,699,920 | 1,288,356.158 | 3720 | 110.6354414 | 857.1064941 | 346.3323005 | |
| 200–300 | 2,719,872 | 1,703,190.161 | 3180 | 319.7112702 | 1491.609484 | 535.5943901 | |
| 300–400 | 1,699,920 | 1,014,660.39 | 1320 | 519.1360679 | 2208.136659 | 768.6821139 | |
| 400–450 | 1,529,928 | 823,449.1842 | 1020 | 692.62629 | 2483.844298 | 807.3031218 | |
| 450–500 | 3,909,816 | 1,622,703.235 | 2700 | 847.0788018 | 2219.587865 | 601.0011982 | |
| at scale 1:2 | 23–100 | 1,019,952 | 984,096.6108 | 1260 | 28.45665812 | 1685.829056 | 781.0290562 |
| 100–200 | 2,209,896 | 1,880,220.171 | 2520 | 130.8237415 | 1726.319116 | 746.1191156 | |
| 200–300 | 1,699,920 | 1,422,206.877 | 960 | 289.2845034 | 3460.715497 | 1481.465497 | |
| 300–400 | 2,719,872 | 1,896,062.847 | 1560 | 528.0827907 | 3164.224902 | 1215.424902 | |
| 400–450 | 1,189,944 | 821,463.105 | 540 | 682.3720278 | 3984.294639 | 1521.227972 | |
| 450–500 | 1,359,936 | 815,393.8186 | 660 | 825.0639111 | 3538.572452 | 1235.44518 | |
| at scale 1:1 | 23–100 | 2,209,896 | 2,175,815.905 | 1680 | 20.28577095 | 2765.428515 | 1295.128515 |
| 100–200 | 4,929,768 | 4,503,477.425 | 3960 | 107.6491352 | 2528.714501 | 1137.241774 | |
| 200–300 | 3,739,824 | 3,396,321.045 | 1560 | 220.194202 | 4856.728875 | 2177.128875 | |
| 300–400 | 3,399,840 | 3,069,626.685 | 900 | 366.9036836 | 7633.096316 | 3410.696316 | |
| 400–450 | 2,039,904 | 1,797,540.948 | 480 | 504.9230253 | 8495.076975 | 3744.876975 | |
| 450–500 | 2,379,888 | 1,864,213.041 | 840 | 613.8987605 | 5386.10124 | 2219.30124 |
| Measured Values | |||||
|---|---|---|---|---|---|
| Model/Prototype (All Protected with Intumescent Paint) | Tmin-Tmax | ||||
| 23–100 | 2 | 0.75 | 0.457206464 | 0.452288545 | |
| 100–200 | 2 | 0.636364 | 0.434436829 | 0.417504074 | |
| 1:2/1.0 | 200–300 | 2 | 0.615385 | 0.438499066 | 0.418749246 |
| 300–400 | 2 | 1.733333 | 0.718536262 | 0.617685159 | |
| 400–450 | 2 | 1.125 | 0.527638711 | 0.456992708 | |
| 450–500 | 2 | 0.785714 | 1.026875802 | 0.437393045 | |
| 23–100 | 2 | 1.761905 | 0.643406091 | 0.616459374 | |
| 100–200 | 2 | 1.47619 | 0.732919211 | 0.685215581 | |
| 200–300 | 2 | 3.3125 | 1.427726845 | 1.197568503 | |
| 1:4/1:2 | 300–400 | 2 | 0.846154 | 0.590483731 | 0.535140695 |
| 400–450 | 2 | 1.888889 | 1.177549936 | 1.002417734 | |
| 450–500 | 2 | 4.090909 | 2.566043877 | 1.990085279 | |
| 23–100 | 4 | 1.321429 | 0.294169424 | 0.278817514 | |
| 100–200 | 4 | 0.939394 | 0.318407098 | 0.286080297 | |
| 1:4/1.0 | 200–300 | 4 | 2.038462 | 0.626056888 | 0.501480908 |
| 300–400 | 4 | 1.466667 | 0.424283973 | 0.330548465 | |
| 400–450 | 4 | 2.125 | 0.621320931 | 0.458097595 | |
| 450–500 | 4 | 3.214286 | 1.324592548 | 0.87044946 | |
| 23–100 | 10.71479 | 1.232143 | 0.306299243 | 0.304717761 | |
| 100–200 | 10.71479 | 0.674242 | 0.24793587 | 0.255958151 | |
| 1:10/1.0 | 200–300 | 10.71479 | 0.653846 | 0.283080909 | 0.295824115 |
| 300–400 | 10.71479 | 1.806667 | 0.414463152 | 0.432368357 | |
| 400–450 | 10.71479 | 2 | 0.435875842 | 0.460241775 | |
| 450–500 | 10.71479 | 0.607143 | 0.394999443 | 0.449018354 | |
| 23–100 | 5.357394 | 1.642857 | 0.669936379 | 0.673724249 | |
| 100–200 | 5.357394 | 1.059524 | 0.570706379 | 0.613067433 | |
| 1:10/1:2 | 200–300 | 5.357394 | 1.0625 | 0.645567871 | 0.706446919 |
| 300–400 | 5.357394 | 1.042308 | 0.576815916 | 0.69998178 | |
| 400–450 | 5.357394 | 1.777778 | 0.826087685 | 1.00710967 | |
| 450–500 | 5.357394 | 0.772727 | 0.765205801 | 1.026578633 | |
| 23–100 | 2.678697 | 0.932432 | 1.041234127 | 1.092893185 | |
| 100–200 | 2.678697 | 0.717742 | 0.778675699 | 0.894707374 | |
| 1:10/1:4 | 200–300 | 2.678697 | 0.320755 | 0.452164834 | 0.589901052 |
| 300–400 | 2.678697 | 1.231818 | 0.976853189 | 1.308033169 | |
| 400–450 | 2.678697 | 0.941176 | 0.701530916 | 1.004680619 | |
| 450–500 | 2.678697 | 0.188889 | 0.298204488 | 0.515846554 | |
| Values Considered to Be Reference Ones | Values Obtained with the ML | ||||||
|---|---|---|---|---|---|---|---|
| Model/Prototype (All Protected with Intumescent Paint) | Tmin-Tmax | ||||||
| 23–100 | 0.25 | 0.609609 | 0.603051 | 0.609609 | 0.603051 | 0.25 | |
| 100–200 | 0.25 | 0.682686 | 0.656078 | 0.682686 | 0.656078 | 0.25 | |
| 1:2/1.0 | 200–300 | 0.25 | 0.712561 | 0.680468 | 0.712561 | 0.680468 | 0.25 |
| 300–400 | 0.25 | 0.41454 | 0.356357 | 0.41454 | 0.356357 | 0.25 | |
| 400–450 | 0.25 | 0.469012 | 0.406216 | 0.469012 | 0.406216 | 0.25 | |
| 450–500 | 0.25 | 0.656982 | 0.556682 | 1.306933 | 0.556682 | 0.25 | |
| 23–100 | 0.25 | 0.365176 | 0.349882 | 0.365176 | 0.349882 | 0.25 | |
| 100–200 | 0.25 | 0.496494 | 0.464178 | 0.496494 | 0.464178 | 0.25 | |
| 200–300 | 0.25 | 0.431012 | 0.36153 | 0.431012 | 0.36153 | 0.25 | |
| 1:4/1:2 | 300–400 | 0.25 | 0.697844 | 0.632439 | 0.697844 | 0.632439 | 0.25 |
| 400–450 | 0.25 | 0.623409 | 0.530692 | 0.623409 | 0.530692 | 0.25 | |
| 450–500 | 0.25 | 0.627255 | 0.486465 | 0.627255 | 0.486465 | 0.25 | |
| 23–100 | 0.0625 | 0.222615 | 0.210997 | 0.222615 | 0.210997 | 0.0625 | |
| 100–200 | 0.0625 | 0.338949 | 0.304537 | 0.338949 | 0.304537 | 0.0625 | |
| 1:4/1.0 | 200–300 | 0.0625 | 0.307122 | 0.24601 | 0.307122 | 0.24601 | 0.0625 |
| 300–400 | 0.0625 | 0.289285 | 0.225374 | 0.289285 | 0.225374 | 0.0625 | |
| 400–450 | 0.0625 | 0.292386 | 0.215575 | 0.292386 | 0.215575 | 0.0625 | |
| 450–500 | 0.0625 | 0.412095 | 0.270806 | 0.412095 | 0.270806 | 0.0625 | |
| 23–100 | 0.008 | 0.248591 | 0.247307 | 0.248591 | 0.247307 | 0.008 | |
| 100–200 | 0.008 | 0.367725 | 0.379623 | 0.367725 | 0.379623 | 0.008 | |
| 1:10/1.0 | 200–300 | 0.008 | 0.432947 | 0.452437 | 0.432947 | 0.452437 | 0.008 |
| 300–400 | 0.008 | 0.229408 | 0.239318 | 0.229408 | 0.239318 | 0.008 | |
| 400–450 | 0.008 | 0.217938 | 0.230121 | 0.217938 | 0.230121 | 0.008 | |
| 450–500 | 0.008 | 0.650587 | 0.73956 | 0.650587 | 0.73956 | 0.008 | |
| 23–100 | 0.03199 | 0.407787 | 0.410093 | 0.407787 | 0.410093 | 0.0399 | |
| 100–200 | 0.03199 | 0.538644 | 0.578625 | 0.538644 | 0.578625 | 0.0319 | |
| 1:10/1:2 | 200–300 | 0.03199 | 0.607593 | 0.664891 | 0.607593 | 0.664891 | 0.0319 |
| 300–400 | 0.03199 | 0.553403 | 0.671569 | 0.553403 | 0.671569 | 0.0319 | |
| 400–450 | 0.03199 | 0.464674 | 0.566499 | 0.464674 | 0.566499 | 0.0319 | |
| 450–500 | 0.03199 | 0.990266 | 1.328514 | 0.990266 | 1.328514 | 0.0319 | |
| 23–100 | 0.12799 | 1.116686 | 1.172088 | 1.116686 | 1.172088 | 0.1279 | |
| 100–200 | 0.12799 | 1.084896 | 1.246559 | 1.084896 | 1.246559 | 0.1279 | |
| 1:10/1:4 | 200–300 | 0.12799 | 1.40969 | 1.839103 | 1.40969 | 1.839103 | 0.1279 |
| 300–400 | 0.12799 | 0.793017 | 1.061872 | 0.793017 | 1.061872 | 0.1279 | |
| 400–450 | 0.12799 | 0.745377 | 1.067473 | 0.745377 | 1.067473 | 0.1279 | |
| 450–500 | 0.12799 | 1.57873 | 2.730952 | 1,57873 | 2.730952 | 0.1279 | |
| Measured Values | |||||
|---|---|---|---|---|---|
| Model/Prototype (All Protected with Intumescent Paint) | Tmin-Tmax | ||||
| 23–100 | 2 | 0.75 | 0.609609 | 0.603051 | |
| 100–200 | 2 | 0.636364 | 0.682686 | 0.656078 | |
| 1:2/1.0 | 200–300 | 2 | 0.615385 | 0.712561 | 0.680468 |
| 300–400 | 2 | 1.733333 | 0.41454 | 0.356357 | |
| 400–450 | 2 | 1.125 | 0.469012 | 0.406216 | |
| 450–500 | 2 | 0.785714 | 0.656982 | 0.556682 | |
| 23–100 | 2 | 1.761905 | 0.365176 | 0.349882 | |
| 100–200 | 2 | 1.47619 | 0.496494 | 0.464178 | |
| 200–300 | 2 | 3.3125 | 0.431012 | 0.36153 | |
| 1:4/1:2 | 300–400 | 2 | 0.846154 | 0.697844 | 0.632439 |
| 400–450 | 2 | 1.888889 | 0.623409 | 0.530692 | |
| 450–500 | 2 | 4.090909 | 0.627255 | 0.486465 | |
| 23–100 | 4 | 1.321429 | 0.222615 | 0.210997 | |
| 100–200 | 4 | 0.939394 | 0.338949 | 0.304537 | |
| 1:4/1.0 | 200–300 | 4 | 2.038462 | 0.307122 | 0.24601 |
| 300–400 | 4 | 1.466667 | 0.289285 | 0.225374 | |
| 400–450 | 4 | 2.125 | 0.292386 | 0.215575 | |
| 450–500 | 4 | 3.214286 | 0.412095 | 0.270806 | |
| 23–100 | 10.71479 | 1.232143 | 0.248591 | 0.247307 | |
| 100–200 | 10.71479 | 0.674242 | 0.367725 | 0.379623 | |
| 1:10/1.0 | 200–300 | 10.71479 | 0.653846 | 0.432947 | 0.452437 |
| 300–400 | 10.71479 | 1.806667 | 0.229408 | 0.239318 | |
| 400–450 | 10.71479 | 2 | 0.217938 | 0.230121 | |
| 450–500 | 10.71479 | 0.607143 | 0.650587 | 0.73956 | |
| 23–100 | 5.357394 | 1.642857 | 0.407787 | 0.410093 | |
| 100–200 | 5.357394 | 1.059524 | 0.538644 | 0.578625 | |
| 1:10/1:2 | 200–300 | 5.357394 | 1.0625 | 0.607593 | 0.664891 |
| 300–400 | 5.357394 | 1.042308 | 0.553403 | 0.671569 | |
| 400–450 | 5.357394 | 1.777778 | 0.464674 | 0.566499 | |
| 450–500 | 5.357394 | 0.772727 | 0.990266 | 1.328514 | |
| 23–100 | 2.678697 | 0.932432 | 1.116686 | 1.172088 | |
| 100–200 | 2.678697 | 0.717742 | 1.084896 | 1.246559 | |
| 1:10/1:4 | 200–300 | 2.678697 | 0.320755 | 1.40969 | 1.839103 |
| 300–400 | 2.678697 | 1.231818 | 0.793017 | 1.061872 | |
| 400–450 | 2.678697 | 0.941176 | 0.745377 | 1.067473 | |
| 450–500 | 2.678697 | 0.188889 | 1.57873 | 2.730952 | |
| Model/Prototype (All Protected with Intumescent Paint) | Values Considered to Be Reference Ones | Values Obtained with the ML | ||||
|---|---|---|---|---|---|---|
| 0.25 | 0.457206 | 0.452289 | 0.457206 | 0.452289 | 0.25 | |
| 0.25 | 0.434437 | 0.417504 | 0.434437 | 0.417504 | 0.25 | |
| 1:2/1.0 | 0.25 | 0.438499 | 0.418749 | 0.438499 | 0.418749 | 0.25 |
| 0.25 | 0.718536 | 0.617685 | 0.718536 | 0.617685 | 0.25 | |
| 0.25 | 0.527639 | 0.456993 | 0.527639 | 0.456993 | 0.25 | |
| 0.25 | 0.5162 | 0.437393 | 0.5162 | 0.437393 | 0.25 | |
| 0.25 | 0.643406 | 0.616459 | 0.643406 | 0.616459 | 0.25 | |
| 0.25 | 0.732919 | 0.685216 | 0.732919 | 0.685216 | 0.25 | |
| 0.25 | 1.427727 | 1.197569 | 1.427727 | 1.197569 | 0.25 | |
| 1:4/1:2 | 0.25 | 0.590484 | 0.535141 | 0.590484 | 0.535141 | 0.25 |
| 0.25 | 1.17755 | 1.002418 | 1.17755 | 1.002418 | 0.25 | |
| 0.25 | 2.566044 | 1.990085 | 2.566044 | 1.990085 | 0.25 | |
| 0.0625 | 0.294169 | 0.278818 | 0.294169 | 0.278818 | 0.0625 | |
| 0.0625 | 0.318407 | 0.28608 | 0.318407 | 0.28608 | 0.0625 | |
| 1:4/1.0 | 0.0625 | 0.626057 | 0.501481 | 0.626057 | 0.501481 | 0.0625 |
| 0.0625 | 0.424284 | 0.330548 | 0.424284 | 0.330548 | 0.0625 | |
| 0.0625 | 0.621321 | 0.458098 | 0.621321 | 0.458098 | 0.0625 | |
| 0.0625 | 1.324593 | 0.870449 | 1.324593 | 0.870449 | 0.0625 | |
| 0.008 | 0.306299 | 0.304718 | 0.306299 | 0.304718 | 0.008 | |
| 0.008 | 0.247936 | 0.255958 | 0.247936 | 0.255958 | 0.008 | |
| 1:10/1.0 | 0.008 | 0.283081 | 0.295824 | 0.283081 | 0.295824 | 0.008 |
| 0.008 | 0.414463 | 0.432368 | 0.414463 | 0.432368 | 0.008 | |
| 0.008 | 0.435876 | 0.460242 | 0.435876 | 0.460242 | 0.008 | |
| 0.008 | 0.394999 | 0.449018 | 0.394999 | 0.449018 | 0.008 | |
| 0.031999 | 0.669936 | 0.673724 | 0.669936 | 0.673724 | 0.031998 | |
| 0.031999 | 0.570706 | 0.613067 | 0.570706 | 0.613067 | 0.031999 | |
| 1:10/1:2 | 0.031999 | 0.645568 | 0.706447 | 0.645568 | 0.706447 | 0.031999 |
| 0.031999 | 0.576816 | 0.699982 | 0.576816 | 0.699982 | 0.031999 | |
| 0.031999 | 0.826088 | 1.00711 | 0.826088 | 1.00711 | 0.031999 | |
| 0.031999 | 0.765206 | 1.026579 | 0.765206 | 1.026579 | 0.031999 | |
| 0.127994 | 1.041234 | 1.092893 | 1.041234 | 1.092893 | 0.127994 | |
| 0.127994 | 0.778676 | 0.894707 | 0.778676 | 0.894707 | 0.127994 | |
| 1:10/1:4 | 0.127994 | 0.452165 | 0.589901 | 0.452165 | 0.589901 | 0.127994 |
| 0.127994 | 0.976853 | 1.308033 | 0.976853 | 1.308033 | 0.127994 | |
| 0.127994 | 0.701531 | 1.004681 | 0.701531 | 1.004681 | 0.127994 | |
| 0.127994 | 0.298204 | 0.515847 | 0.298204 | 0.515847 | 0.127994 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gálfi, P.-B.; Száva, R.-I.; Száva, I.; Vlase, S.; Gălățanu, T.; Jármai, K.; Asztalos, Z.; Popa, G. Modern Dimensional Analysis Based on Fire-Protected Steel Members’ Analysis Using Multiple Experiments. Fire 2022, 5, 210. https://doi.org/10.3390/fire5060210
Gálfi P-B, Száva R-I, Száva I, Vlase S, Gălățanu T, Jármai K, Asztalos Z, Popa G. Modern Dimensional Analysis Based on Fire-Protected Steel Members’ Analysis Using Multiple Experiments. Fire. 2022; 5(6):210. https://doi.org/10.3390/fire5060210
Chicago/Turabian StyleGálfi, Pál-Botond, Renáta-Ildikó Száva, Ioan Száva, Sorin Vlase, Teofil Gălățanu, Károly Jármai, Zsolt Asztalos, and Gabriel Popa. 2022. "Modern Dimensional Analysis Based on Fire-Protected Steel Members’ Analysis Using Multiple Experiments" Fire 5, no. 6: 210. https://doi.org/10.3390/fire5060210
APA StyleGálfi, P.-B., Száva, R.-I., Száva, I., Vlase, S., Gălățanu, T., Jármai, K., Asztalos, Z., & Popa, G. (2022). Modern Dimensional Analysis Based on Fire-Protected Steel Members’ Analysis Using Multiple Experiments. Fire, 5(6), 210. https://doi.org/10.3390/fire5060210