Determining Firebrand Generation Rate Using Physics-Based Modelling from Experimental Studies through Inverse Analysis
Abstract
:1. Introduction
- To identify the firebrand generation rate of a single tree burning case.
- To find out the firebrand generation rate of a forest (cluster of trees) burning.
- To calibrate the firebrand generation rate as a function of wind, FMC, vegetation type.
2. Methodology
2.1. Concept of the Inverse Analysis
2.2. Governing Equations
2.3. Grid Convergence
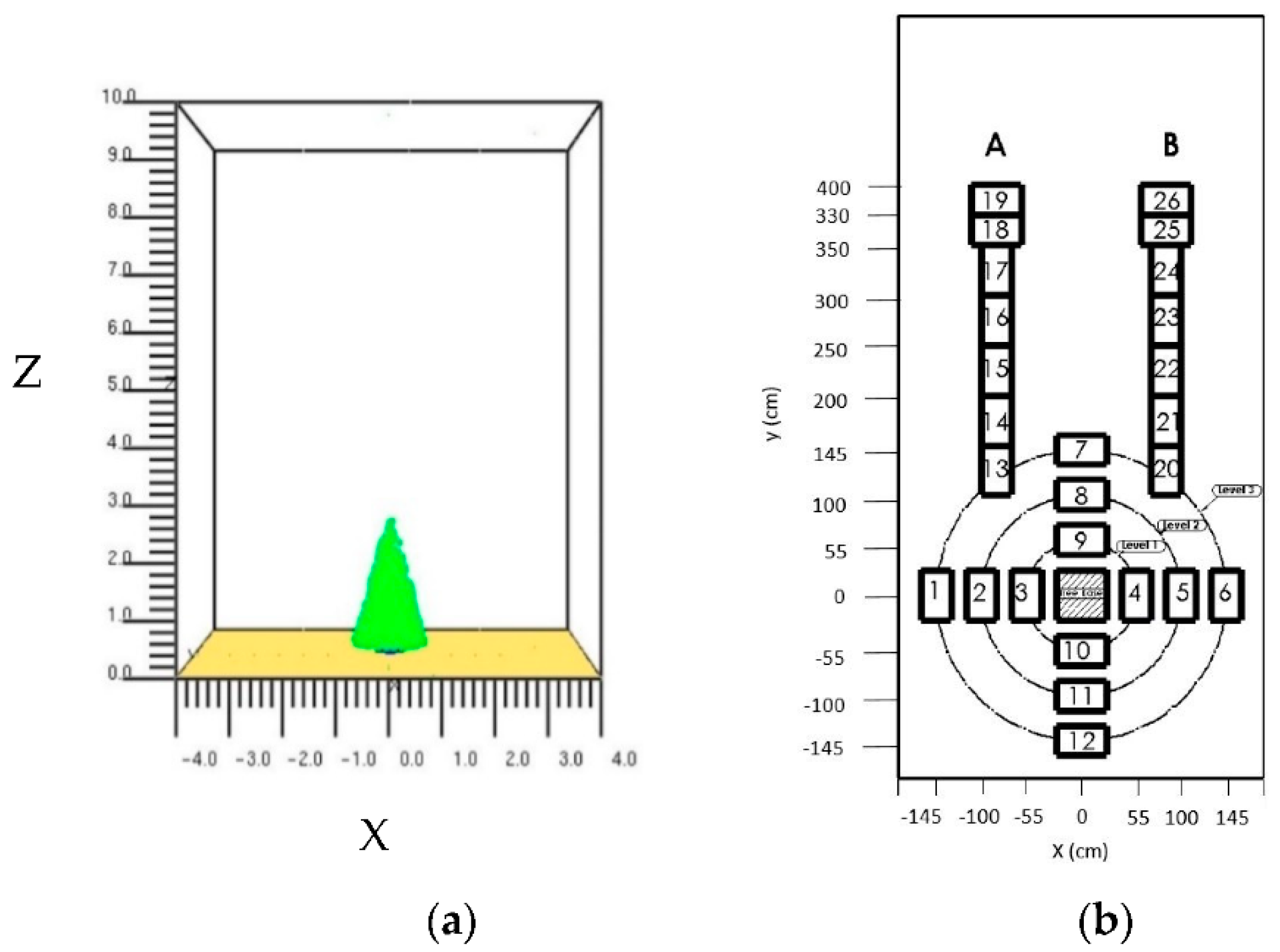
2.4. Model Set Up
2.4.1. Single Tree Burning
2.4.2. Multiple Trees (Forest) Burning
3. Results and Discussion
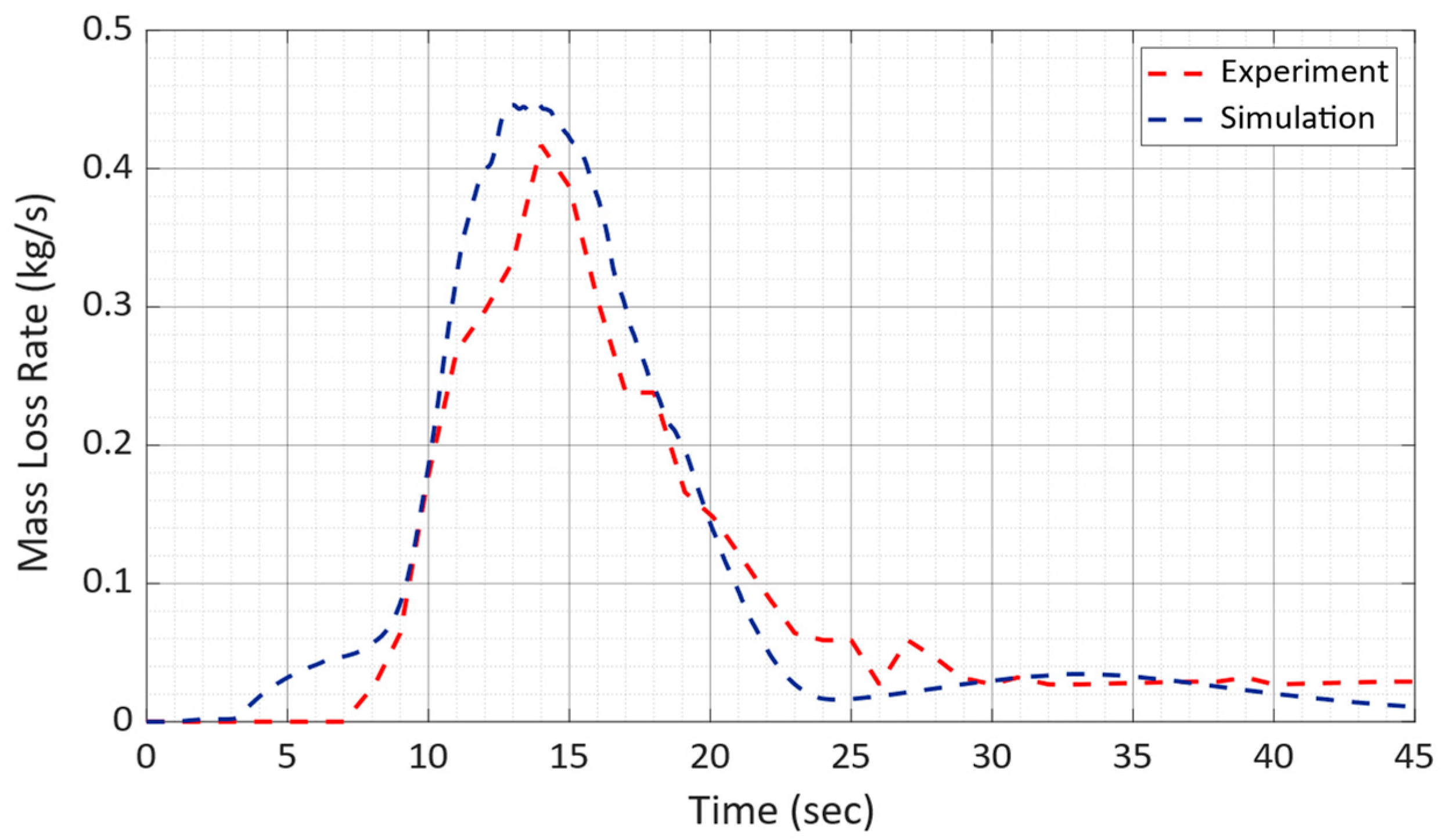
3.1. Validation of Mass Loss Data and Inverse Analysis on Firebrand Generation-Single Tree Burning
3.1.1. Validation of Mass Loss Data
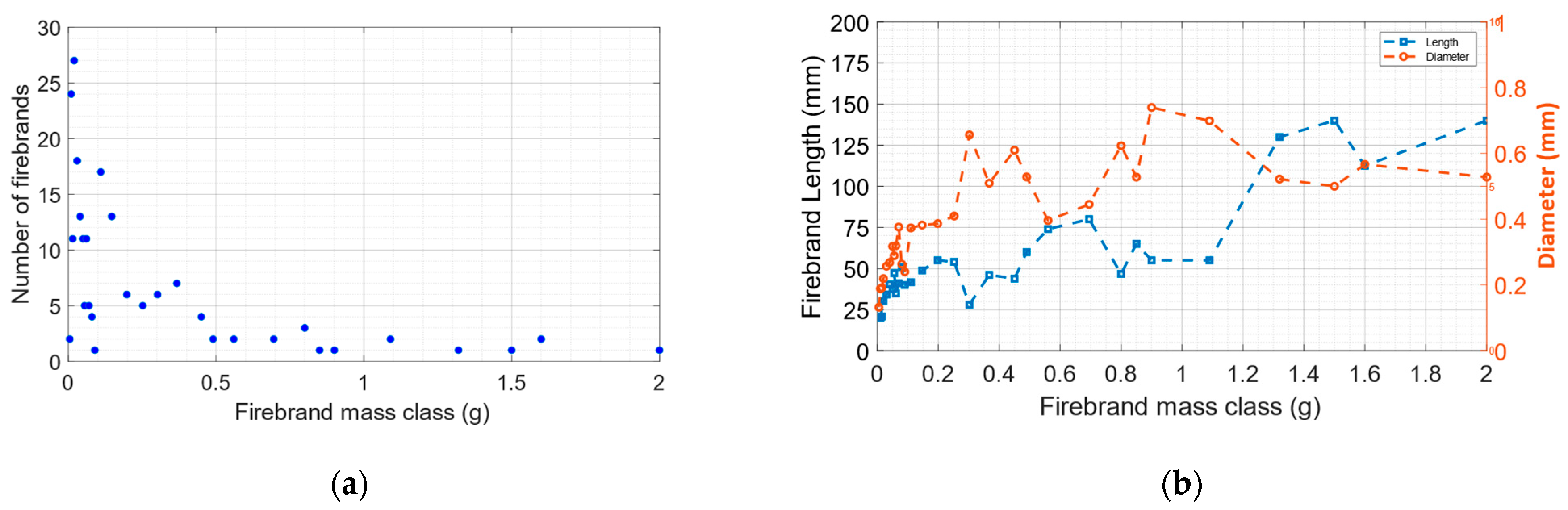
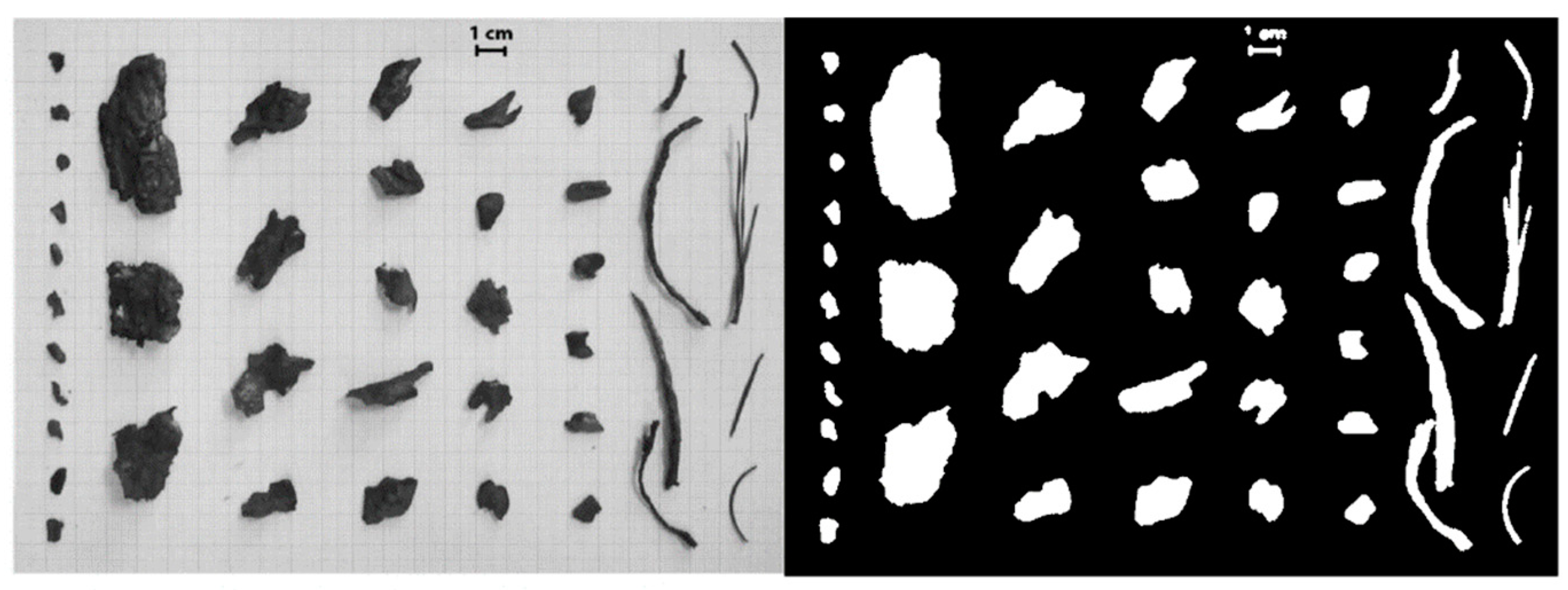
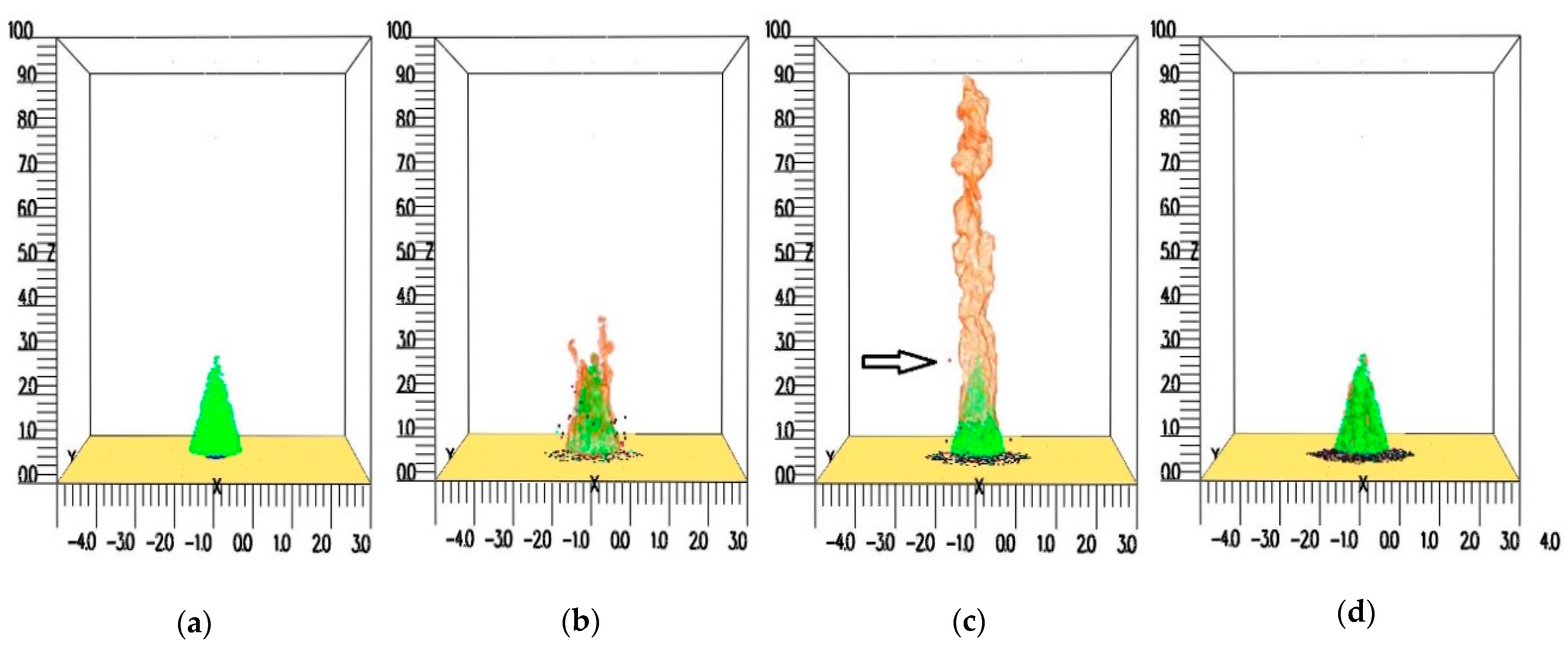
3.1.2. Finding Firebrand Generation from Single Burning Tree by Inverse Analysis
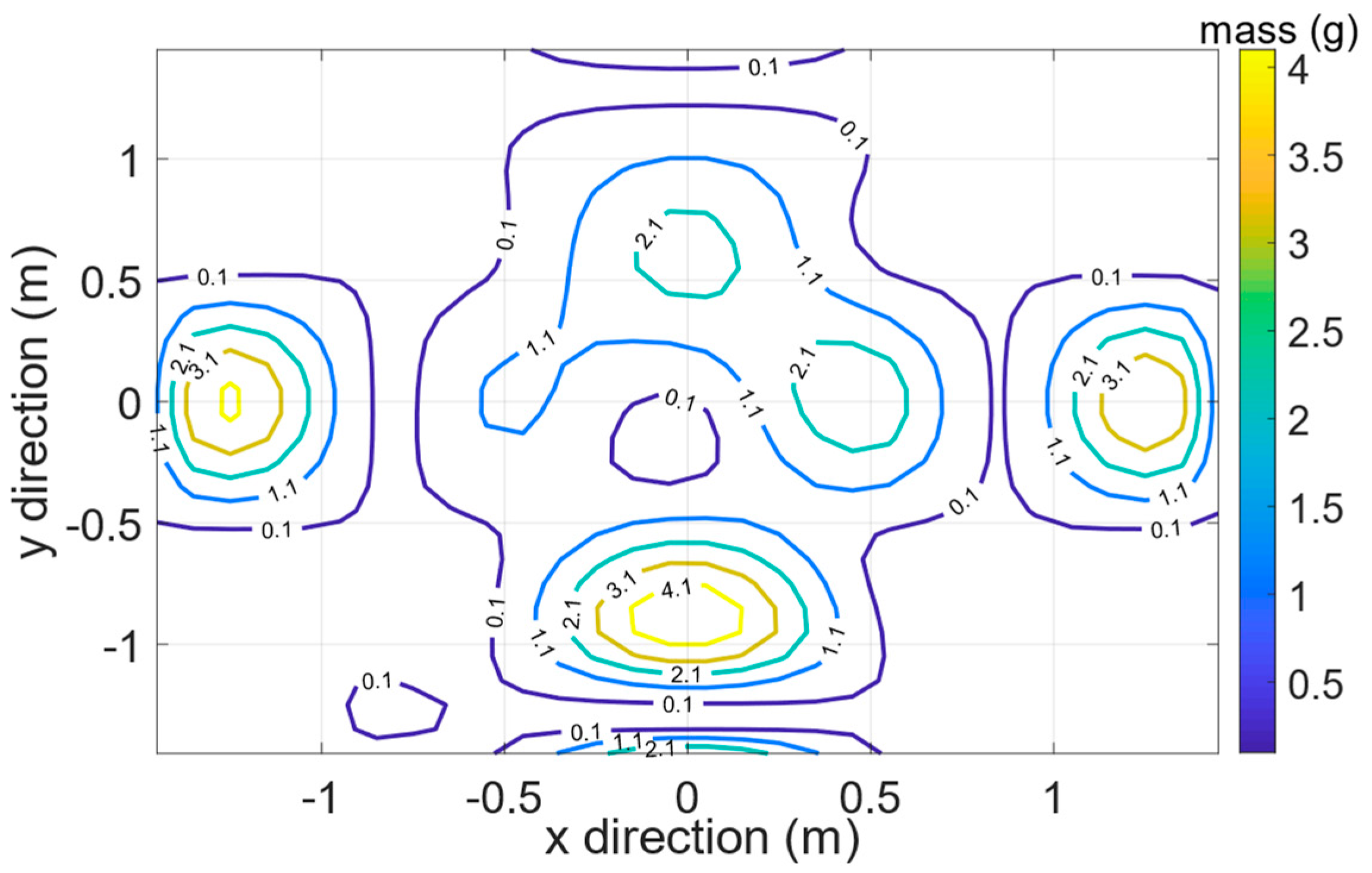
3.2. Inverse Analysis of the Prescribed Burning Experiment with Pitch Pine Forest
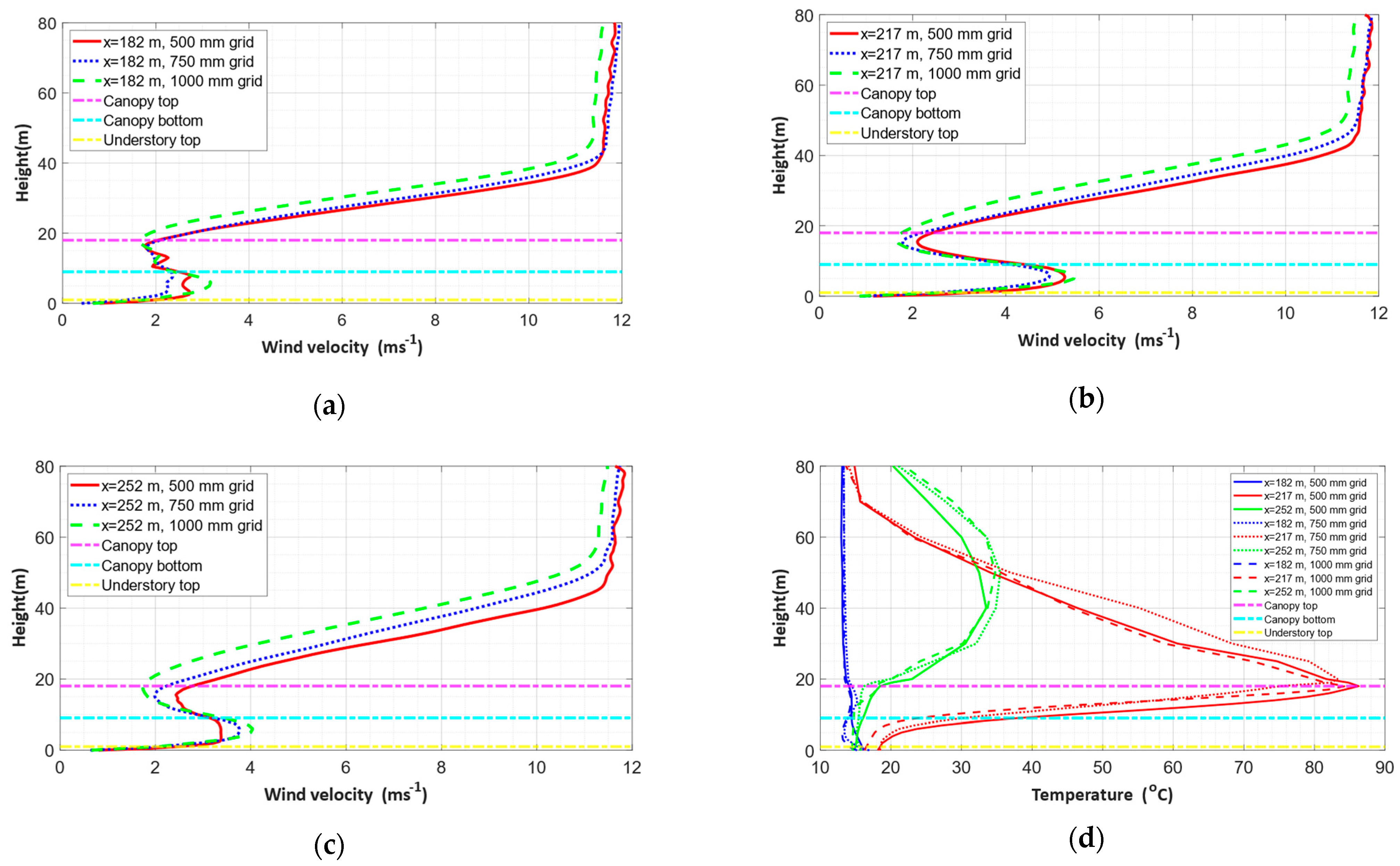
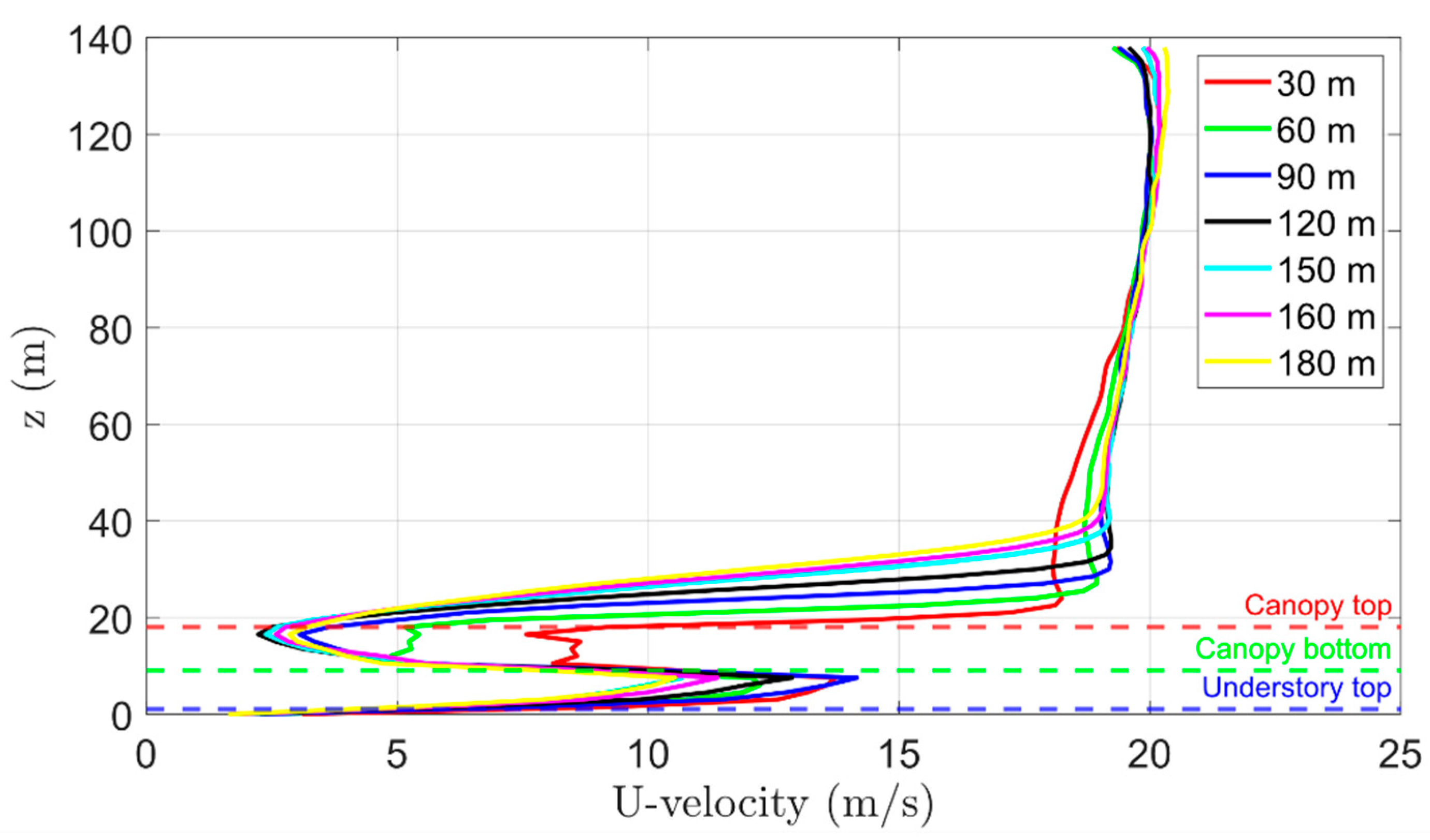
3.2.1. Grid Convergence Analysis
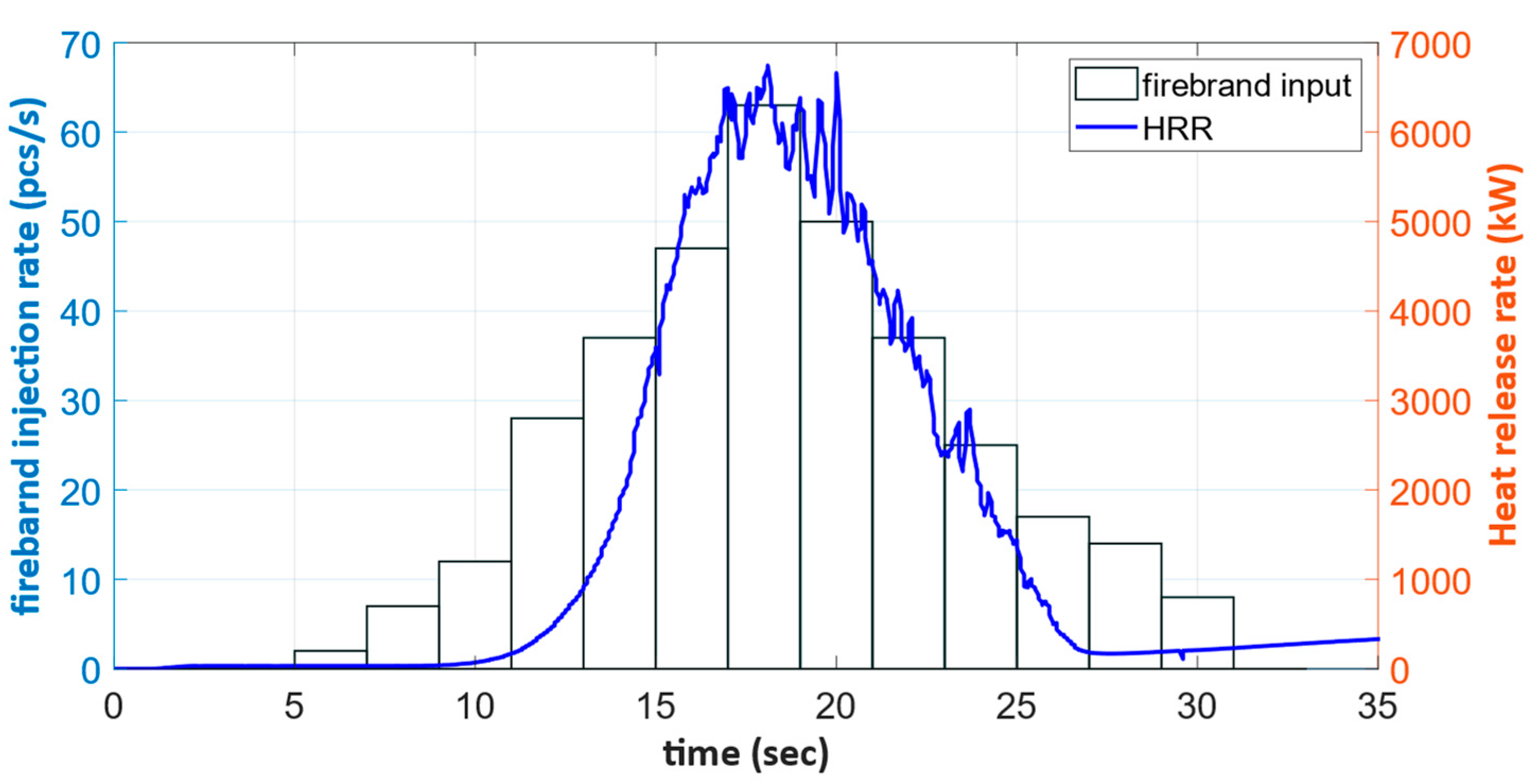
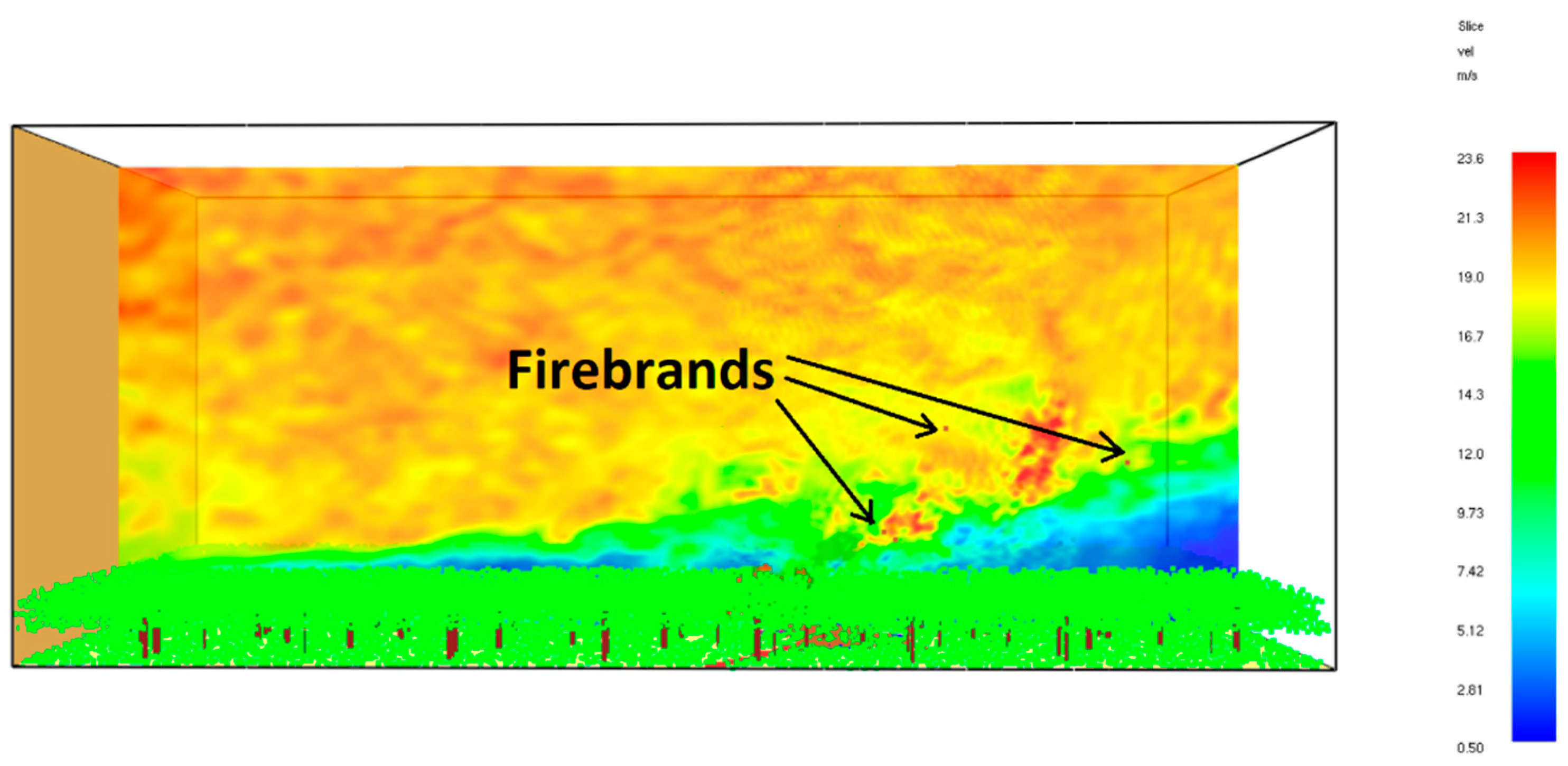
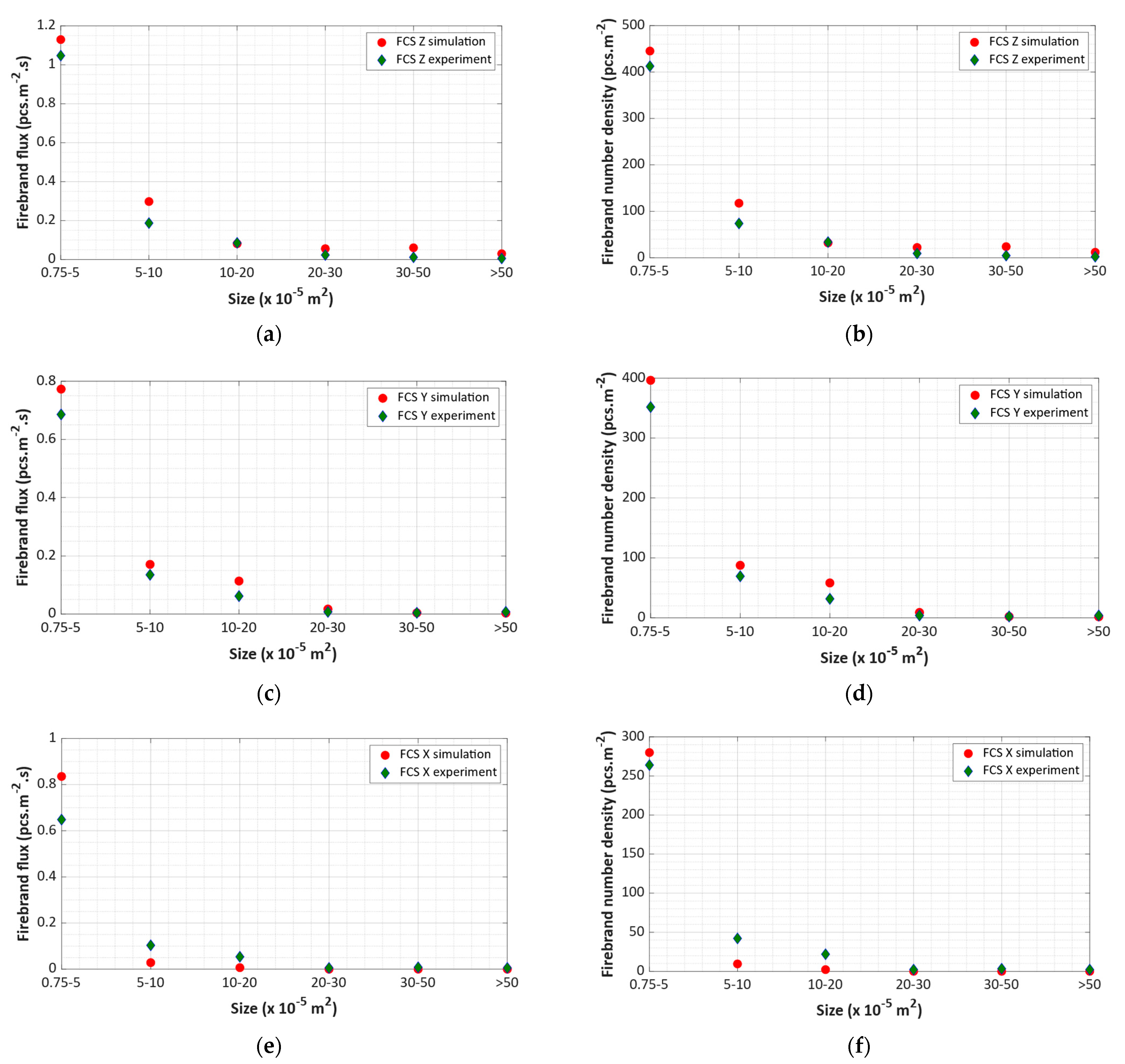
3.2.2. Finding Firebrand Generation Rate by Inverse Analysis
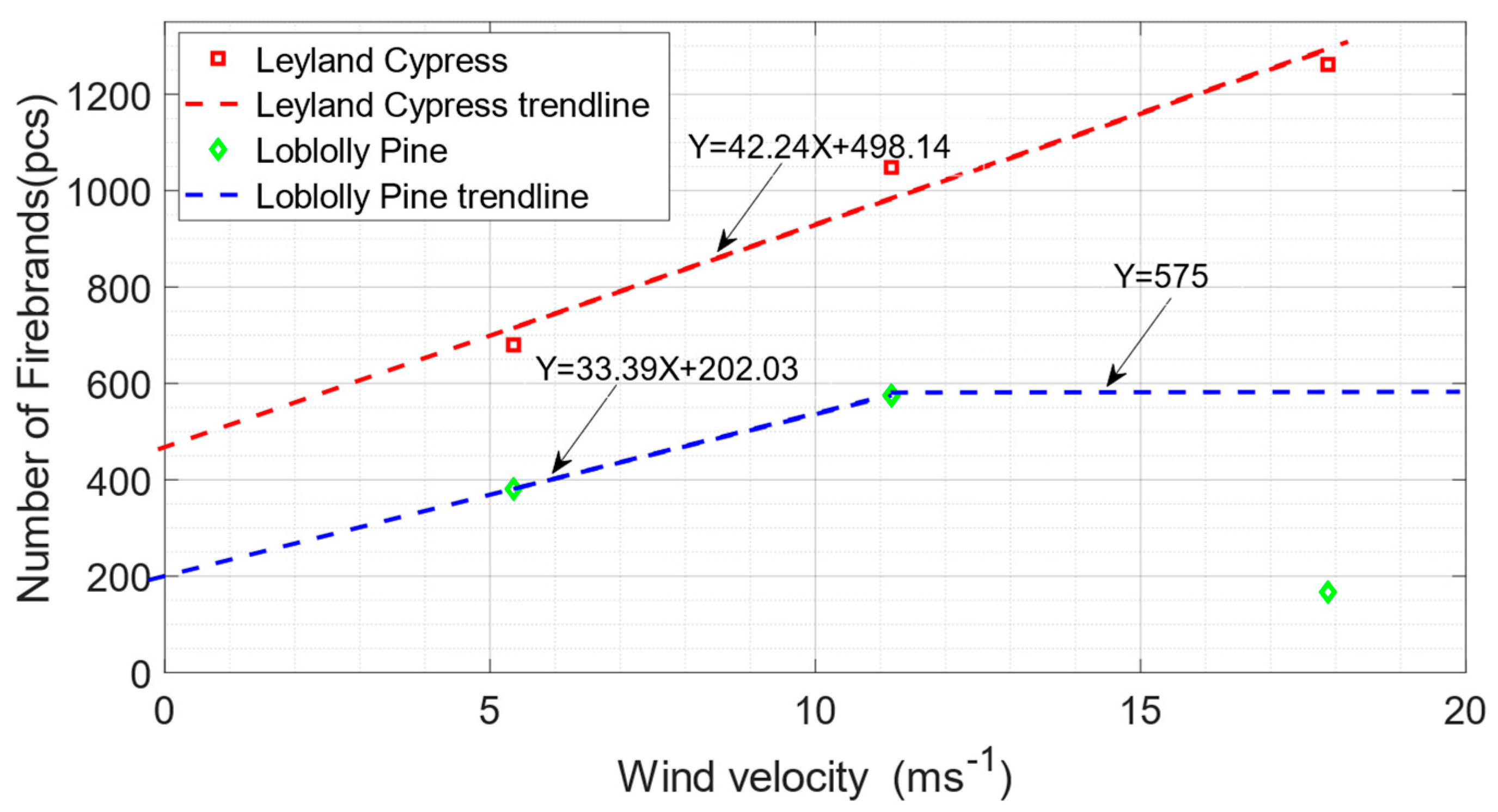
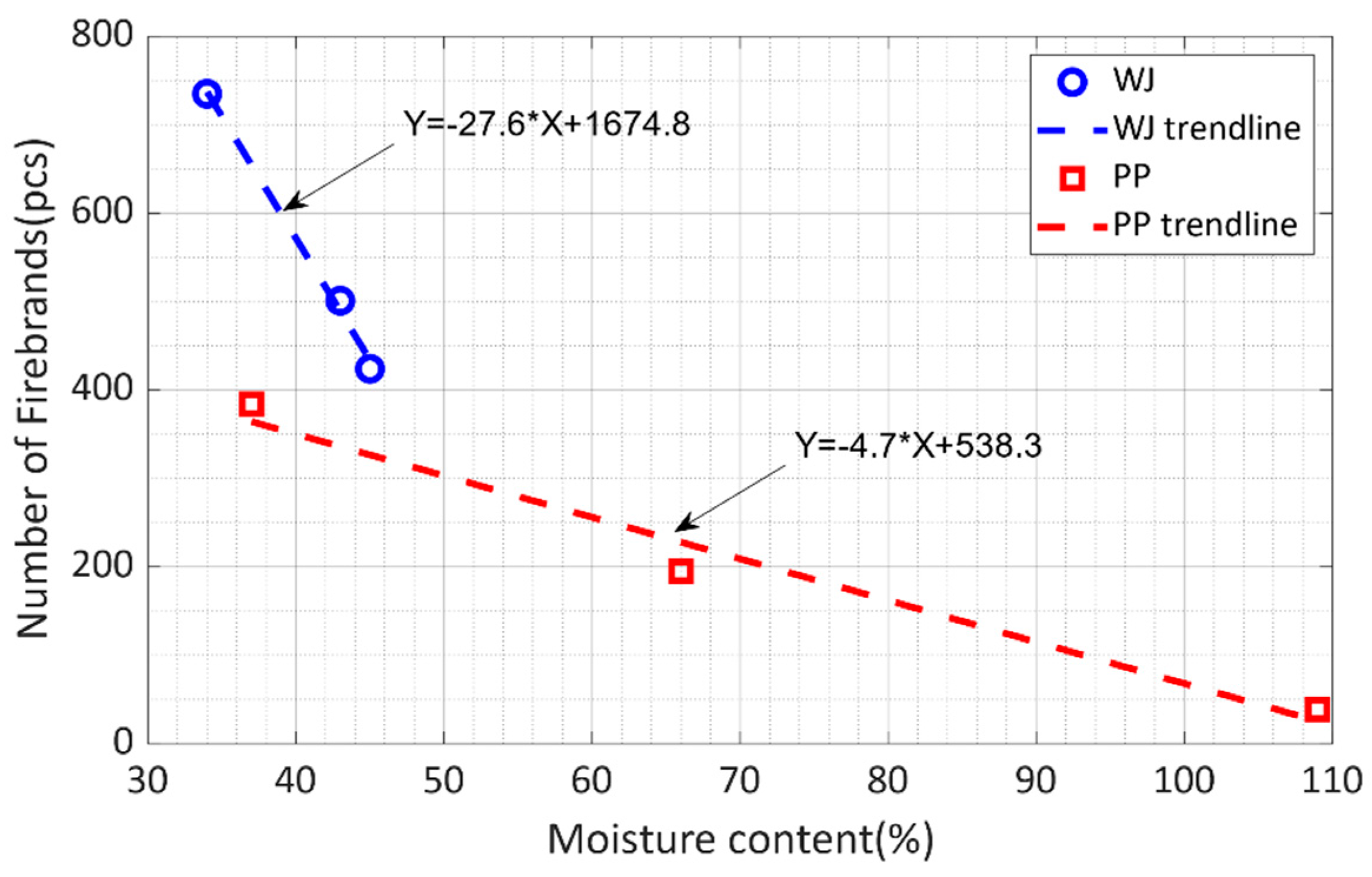
3.3. Quantifying the Effect of Wind, Vegetation Species, and Fuel Moisture Content for Firebrand Generation Rate
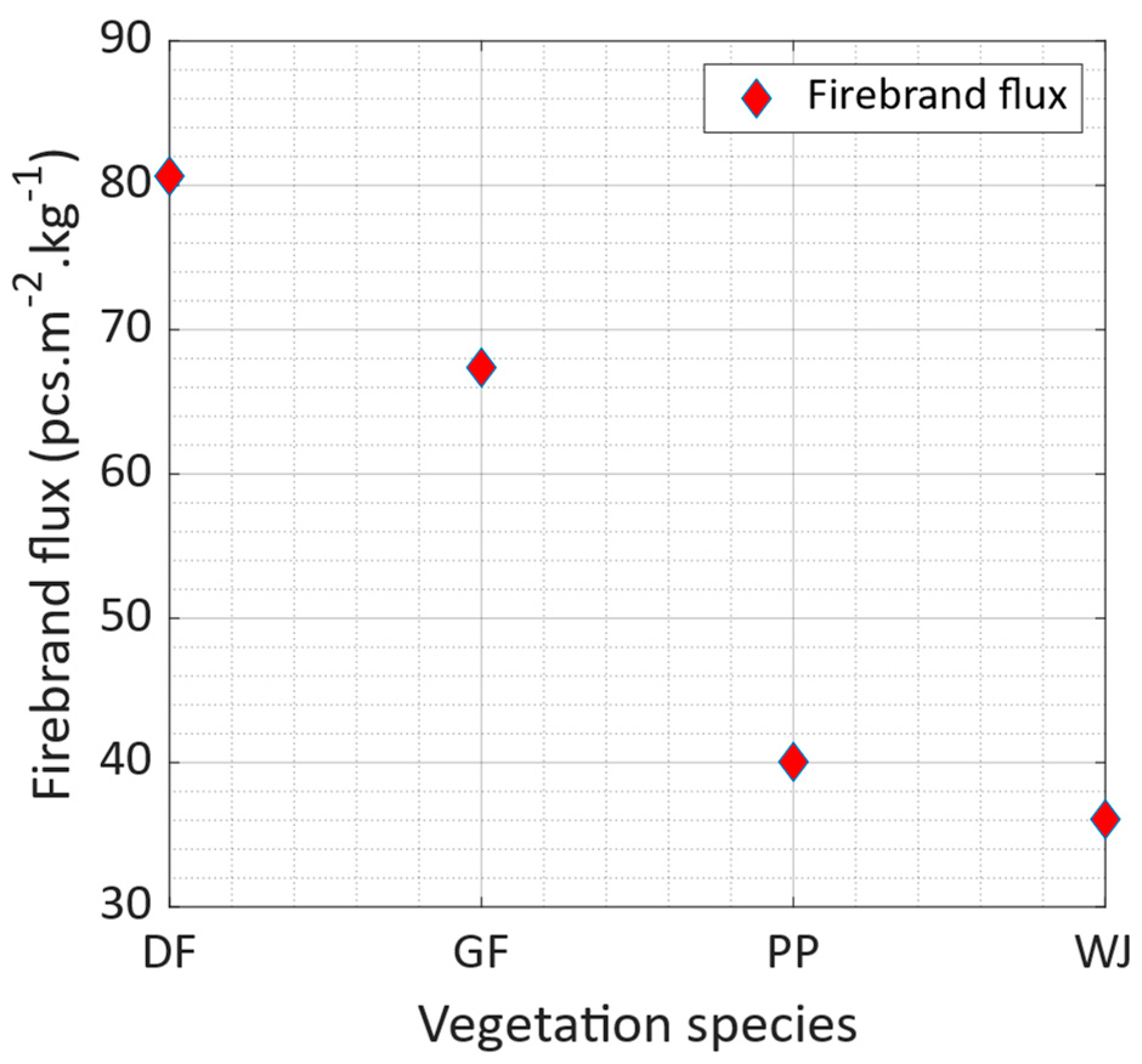
3.3.1. Effect of the Vegetation Species for Firebrand Generation
3.3.2. Effect of the Wind Speed for Firebrand Generation
3.3.3. Effect of Fuel Moisture Content for Firebrand Generation
4. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Blanchi, R.; Leonard, J.E.; Leicester, R.H. Lessons learnt from post-bushfire surveys at the urban interface in Australia. For. Ecol. Manag. 2006, 234, S139. [Google Scholar] [CrossRef]
- Muraszew, A.; Fedele, J.; Kuby, W. Investigation of Fire Whirls and Firebrands; Northern Forest Fire Laboratory, Intermountain Forest and Range Experiment: Missoula, MT, USA, 1976. [Google Scholar]
- Viegas, D.X.; Almeida, M.F.; Ribeiro, L.M. Complexo de Incendios de Pedrógão Grande e Concelhos Limítrofes Limítrofes; University of Coimbra: Coimbra, Portugal, 2017. [Google Scholar]
- Sharifian, A.; Hashempour, J. A novel ember shower simulator for assessing performance of low porosity screens at high wind speeds against firebrand attacks. J. Fire Sci. 2016, 34, 335–355. [Google Scholar] [CrossRef]
- Leonard, J.; Blanchi, R.; Bowditch, P. Bushfire impact from a house’s perspective. In Proceedings of the Earth Wind and Fire–Bushfire 2004 Conference, Adelaide, Australia, 25–28 May 2004. [Google Scholar]
- Hudson, T.R.; Bray, R.B.; Blunck, D.L.; Page, W.; Butler, B. Effects of fuel morphology on ember generation characteristics at the tree scale. Int. J. Wildland Fire 2020, 29, 1042–1051. [Google Scholar] [CrossRef]
- Adusumilli, S.; Hudson, T.; Gardner, N.; Blunck, D.L. Quantifying production of hot firebrands using a fire-resistant fabric. Int. J. Wildland Fire 2021, 30, 154–159. [Google Scholar] [CrossRef]
- Filkov, A.; Prohanov, S.; Mueller, E.; Kasymov, D.; Martynov, P.; El Houssami, M.; Thomas, J.; Skowronski, N.; Butler, B.; Gallagher, M. Investigation of firebrand production during prescribed fires conducted in a pine forest. Proc. Combust. Inst. 2017, 36, 3263–3270. [Google Scholar] [CrossRef] [Green Version]
- Manzello, S.L.; Maranghides, A.; Mell, W.E. Firebrand generation from burning vegetation. Int. J. Wildland Fire 2007, 16, 458–462. [Google Scholar] [CrossRef] [Green Version]
- El Houssami, M.; Mueller, E.; Filkov, A.; Thomas, J.C.; Skowronski, N.; Gallagher, M.R.; Clark, K.; Kremens, R.; Simeoni, A. Experimental procedures characterising firebrand generation in wildland fires. Fire Technol. 2016, 52, 731–751. [Google Scholar] [CrossRef]
- Manzello, S.L.; Maranghides, A.; Shields, J.R.; Mell, W.E.; Hayashi, Y.; Nii, D. Measurement of firebrand production and heat release rate (HRR) from burning Korean pine trees. Fire Saf. Sci. 2007, 7, 108. [Google Scholar]
- Filkov, A.; Kasymov, D.; Zima, V.; Matvienko, O. Experimental investigation of surface litter ignition by bark firebrands. In Proceedings of the AIP Conference Proceedings, Tomsk, Russia, 15 January 2016; p. 060004. [Google Scholar]
- Filkov, A.; Prohanov, S. Particle Tracking and Detection Software for Firebrands Characterization in Wildland Fires. Fire Technol. 2019, 55, 817–836. [Google Scholar] [CrossRef]
- Bahrani, B. Characterization of Firebrands Generated from Selected Vegetative Fuels in Wildland Fires; The University of North Carolina at Charlotte: Charlotte, NC, USA, 2020. [Google Scholar]
- Wadhwani, R. Physics-Based Simulation of Short-Range Spotting in Wildfires; Victoria University: Victoria, BC, Canada, 2019. [Google Scholar]
- Haider, A.; Levenspiel, O. Drag coefficient and terminal velocity of spherical and nonspherical particles. Powder Technol. 1989, 58, 63–70. [Google Scholar] [CrossRef]
- McDermott, R.; McGrattan, K.; Hostikka, S. Fire Dynamics Simulator (Version 5) Technical Reference Guide; National Institute of Standards and Technology NIST: Gaithersburg, MD, USA, 2008; Volume 1018. [Google Scholar]
- Moinuddin, K.; Sutherland, D. Modelling of tree fires and fires transitioning from the forest floor to the canopy with a physics-based model. Math. Comput. Simul. 2019, 175, 81–95. [Google Scholar] [CrossRef]
- Sarwar, M.; Cleary, M.; Moinuddin, K.; Thorpe, G.R.; Flow, F. On linking the filter width to the boundary layer thickness in explicitly filtered large eddy simulations of wall bounded flows. Int. J. Heat Fluid Flow 2017, 65, 73–89. [Google Scholar] [CrossRef] [Green Version]
- McGrattan, K.; Klein, B.; Hostikka, S.; Floyd, J. Fire Dynamics Simulator (Version 5), User’s Guide; National Institute of Standards and Technology NIST: Gaithersburg, MD, USA, 2010; Volume 1019, pp. 1–186. [Google Scholar]
- McGrattan, K.B.; Baum, H.R.; Rehm, R.G.; Hamins, A.; Forney, G.P.; Floyd, J.E.; Hostikka, S.; Prasad, K. Fire Dynamics Simulator-Technical Reference Guide; National Institute of Standards and Technology, Building and Fire Research: Gaithersburg, MD, USA, 2000. [Google Scholar]
- Ali, M.S.M.; Doolan, C.J.; Wheatley, V. Grid convergence study for a two-dimensional simulation of flow around a square cylinder at a low Reynolds number. In School of Mechanical & Mining Engineering Publications, Proceedings of the Seventh International Conference on CFD in The Minerals and Process Industries, Melbourne, Australia, 9–11 December 2009; Witt, P.J., Schwarz, M.P., Eds.; CSIRO: Melbourne, Australia, 2009; pp. 1–6. [Google Scholar]
- Roy, C.J. Grid convergence error analysis for mixed-order numerical schemes. AIAA J. 2003, 41, 595–604. [Google Scholar] [CrossRef] [Green Version]
- Mell, W.; Maranghides, A.; McDermott, R.; Manzello, S.L. Numerical simulation and experiments of burning douglas fir trees. Combust. Flame 2009, 156, 2023–2041. [Google Scholar] [CrossRef]
- Technology, NISOA. Available online: https://github.com/firemodels/fds/blob/master/Validation/NIST_Douglas_Firs/FDS_Input_Files/tree_2_m_14_pc.fds (accessed on 12 December 2019).
- Forney, G.P. Smokeview (Version 5)-A Tool for Visualizing Fire Dynamics Simulation Data, Volume I: User’s Guide; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2017. [Google Scholar]
- Manzello, S.L.; Maranghides, A.; Shields, J.R.; Mell, W.E.; Hayashi, Y.; Nii, D. Mass and size distribution of firebrands generated from burning Korean pine (Pinus koraiensis) trees. Fire Mater. 2009, 33, 21–31. [Google Scholar] [CrossRef]
- Thomas, J.C.; Mueller, E.V.; Santamaria, S.; Gallagher, M.; El Houssami, M.; Filkov, A.; Clark, K.; Skowronski, N.; Hadden, R.M.; Mell, W. Investigation of firebrand generation from an experimental fire: Development of a reliable data collection methodology. Fire Saf. J. 2017, 91, 864–871. [Google Scholar] [CrossRef] [Green Version]
- Baker, E.S. Burning Characteristics of Individual Douglas-Fir Trees in the Wildland/Urban Interface; Worcester Polytechnic Institute: Worcester, MA, USA, 2011. [Google Scholar]
- Alexander, M.E.; Cruz, M.G. Interdependencies between flame length and fireline intensity in predicting crown fire initiation and crown scorch height. Int. J. Wildland Fire 2011, 21, 95–113. [Google Scholar] [CrossRef]
- Jarrin, N.; Benhamadouche, S.; Laurence, D.; Prosser, R. A synthetic-eddy-method for generating inflow conditions for large-eddy simulations. Int. J. Heat Fluid Flow 2006, 27, 585–593. [Google Scholar] [CrossRef] [Green Version]
- Muller-Landau, H.C.; Wright, S.J.; Calderón, O.; Condit, R.; Hubbell, S.P. Interspecific variation in primary seed dispersal in a tropical forest. J. Ecol. 2008, 96, 653–667. [Google Scholar] [CrossRef]
- Mitsopoulos, I.D.; Dimitrakopoulos, A. Canopy fuel characteristics and potential crown fire behavior in Aleppo pine (Pinus halepensis Mill.) forests. Ann. For. Sci. 2007, 64, 287–299. [Google Scholar] [CrossRef] [Green Version]
- Mueller, E.V. Examination of the Underlying Physics in a Detailed Wildland Fire Behavior Model through Field-Scale Experimentation. Ph.D. Thesis, The University of Edinburgh, Edinburgh, UK, 2017. [Google Scholar]
- Menzemer, L.W. Numerical Simulations of Brand Transport in Large Outdoor Fires. Master’s Thesis, Ghent University, Ghent, Belgium, 2021. [Google Scholar]
- Khan, N.; Moinuddin, K.J.A. The Role of Heat Flux in an Idealised Firebreak Built in Surface and Crown Fires. Atmosphere 2021, 12, 1395. [Google Scholar] [CrossRef]
- Dipesh, K.; Will, R.E.; Lynch, T.B.; Heinemann, R.; Holeman, R.J.F.S. Comparison of loblolly, shortleaf, and pitch X loblolly pine plantations growing in Oklahoma. For. Sci. 2015, 61, 540–547. [Google Scholar] [CrossRef] [Green Version]
- Matthews, S.J.A.M.; Journal, O. A comparison of fire danger rating systems for use in forests. Aust. Meteorol. Oceanogr. J. 2009, 58, 41. [Google Scholar] [CrossRef]
- Moinuddin, K.; Khan, N.; Sutherland, D. Numerical study on effect of relative humidity (and fuel moisture) on modes of grassfire propagation. Fire Saf. J. 2021, 125, 103422. [Google Scholar] [CrossRef]




| Parameters | Moisture | Vegetation | Char |
|---|---|---|---|
| Thermal conductivity (W/m K) | 2.0 | 2.0 | 2.0 |
| Specific heat capacity (kJ/kg K) | 4.184 | 1.2 | 1.2 |
| Density (kg/m3) | 1000 | 514 | 300 |
| Reference temperature (°C) | 100 | 200 | - |
| Reference rate | 0.002 | 0.0005 | - |
| Heating rate (°C/min) | 1.6 | 1.6 | - |
| Heat of reaction (kJ/kg) | 2500 | 418 | - |
| Mass fraction | 0.1 | 0.9 | - |
| Fuel | Diameter (mm) | Mass Fraction (%) | MPV (kg/m3) |
|---|---|---|---|
| Needles | 0–6 | 65 | 4.208 |
| Twigs (type 1) | 0–6 | 17.5 | 1.133 |
| Twigs (type 2) | 6–10 | 17.5 | 1.133 |
| Parameter | Moisture | Needles | Twigs |
|---|---|---|---|
| Thermal conductivity (W/m K) | 2.0 | 0.1744 | 0.1737 |
| Specific heat capacity (kJ/kg K) | 4.184 | 1.691 | 1.610 |
| Density (kg/m3) | 1000 | 787 | 512 |
| Thickness (m) | - | 0.003175 | 0.0015 |
| Length (m) | - | 0.1 | 0.1 |
| Geometry | - | Cylinder | Cylinder |
| Moisture content (Wet basis %) | 100 | 55 | 24 |
| Mass per volume (kg/m3) | - | 0.2915 | 0.1783 |
| Grid | GCI (%) | % of Peak-to-Peak MLR |
|---|---|---|
| 100 mm/75 mm | 28.5 | 12.9 |
| 75 mm/50 mm | 4.0 | 3.18 |
| 50 mm/37.5 mm | 10.8 | 0.26 |
| Case | Generated/Injected Firebrands | Velocity and Directions | ||
|---|---|---|---|---|
| Number | Mass(g) | Vertical (cm/s) | Radial (cm/s) | |
| Laboratory experiment | unknown | unknown | unknown | unknown |
| Simulation 1 (50 mm grid) | 2 × 70 | 23.23 | 5 | 0 |
| 10 | 30 | |||
| 60 | 180 | |||
| 70 | 210 | |||
| Simulation 2 (50 mm grid) | 3 × 70 | 34.85 | 5 | 0 |
| 10 | 30 | |||
| 60 | 180 | |||
| 70 | 210 | |||
| Simulation 3 (50 mm grid) | 4 × 70 | 66.80 | 5 | 0 |
| 10 | 30 | |||
| 60 | 180 | |||
| 70 | 210 | |||
| Case | Number of Firebrands | Mass of Firebrands (g) | Firebrands Receiving Trays | ||
|---|---|---|---|---|---|
| Injected | Collected | Injected | Collected | ||
| 1 | 70 × 4 | 66 | 66.80 | 16.45 | 1 to 12, 13 and 14 |
| 2 | 70 × 5 | 79 | 86.92 | 18.90 | 1 to 12, 13 and 14 |
| 3 | 70 × 6 | 106 | 99.40 | 26.36 | 1 to 12, 13 and 14 |
| Grid Sizes | GCI (%) | |||||
|---|---|---|---|---|---|---|
| Velocity at | Temperature at | |||||
| 182 m | 217 m | 252 m | 182 m | 217 m | 252 m | |
| 500 mm/750 mm | 15.3 | 11.6 | 12.4 | 6.9 | 19.1 | 13.4 |
| 750 mm/1000 mm | 31.7 | 21.3 | 22.9 | 8.1 | 26.5 | 15.2 |
| Case | Wind Speed (m/s) | Firebrand | ||||
|---|---|---|---|---|---|---|
| Initial Velocity (m/s) | Injection Rate (pcs/s) | Flux (pcs/s/m2) | ||||
| FCS Z | FCS Y | FCS X | ||||
| TA | ≈1.94 | (4.2, 0.0, 2.1) | 9881 | 2.105 | 1.562 | 0.074 |
| TB | ≈2.02 | (6.2, 0.0, 2.1) | 9881 | 1.332 | 1.499 | 0.255 |
| TC | ≈1.93 | (8.3, 0.0, 2.1) | 9042 | 1.218 | 1.120 | 0.522 |
| TD | ≈1.89 | (8.3, 0.0, 5.2) | 9042 | 1.253 | 1.341 | 0.306 |
| TE | ≈1.87 | (8.3, 0.0, 6.2) | 9042 | 1.154 | 1.196 | 0.271 |
| TF | ≈1.95 | (9.3, 0.0, 4.2) | 8907 | 1.343 | 1.230 | 0.289 |
| TG | ≈1.98 | Varied on particles | 9881 | 0.738 | 1.415 | 0.214 |
| TH | ≈2.2 | (8.3, 0.0, 2.1) | 11,006 | 1.946 | 0.977 | 0.798 |
| TI | ≈2.13 | (8.3, 0.0, 2.1) | 14,436 | 2.835 | 1.355 | 0.203 |
| TJ | ≈2.17 | (8.3, 0.0, 2.1) | 12,367 | 1.625 | 1.170 | 0.641 |
| TK | ≈2.13 | (8.3, 0.0, 2.1) | 11,171 | 1.375 | 1.082 | 0.870 |
| Experiment | 2.0 | NA | NA | 1.361 | 0.902 | 0.824 |
| Location | FCS Z | FCS Y | FC X |
|---|---|---|---|
| Time span (s) | 394 | 513 | 407 |
| Firebrand density—experiment (pcs/m2) | 536 | 463 | 335 |
| Firebrand density—simulation (pcs/m2) | 652 | 555 | 292 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wickramasinghe, A.; Khan, N.; Moinuddin, K. Determining Firebrand Generation Rate Using Physics-Based Modelling from Experimental Studies through Inverse Analysis. Fire 2022, 5, 6. https://doi.org/10.3390/fire5010006
Wickramasinghe A, Khan N, Moinuddin K. Determining Firebrand Generation Rate Using Physics-Based Modelling from Experimental Studies through Inverse Analysis. Fire. 2022; 5(1):6. https://doi.org/10.3390/fire5010006
Chicago/Turabian StyleWickramasinghe, Amila, Nazmul Khan, and Khalid Moinuddin. 2022. "Determining Firebrand Generation Rate Using Physics-Based Modelling from Experimental Studies through Inverse Analysis" Fire 5, no. 1: 6. https://doi.org/10.3390/fire5010006
APA StyleWickramasinghe, A., Khan, N., & Moinuddin, K. (2022). Determining Firebrand Generation Rate Using Physics-Based Modelling from Experimental Studies through Inverse Analysis. Fire, 5(1), 6. https://doi.org/10.3390/fire5010006








