Georeferencing Oblique Aerial Wildfire Photographs: An Untapped Source of Fire Behaviour Data
Abstract
:1. Introduction
- Develop an efficient, systematic, repeatable procedure to determine the geographic coordinates of wildfire features captured in oblique photographs.
- Demonstrate the use of the procedure to obtain estimates of wildfire spread rates and validate fire behaviour models, using the FBP System models as an example.
2. Materials and Methods
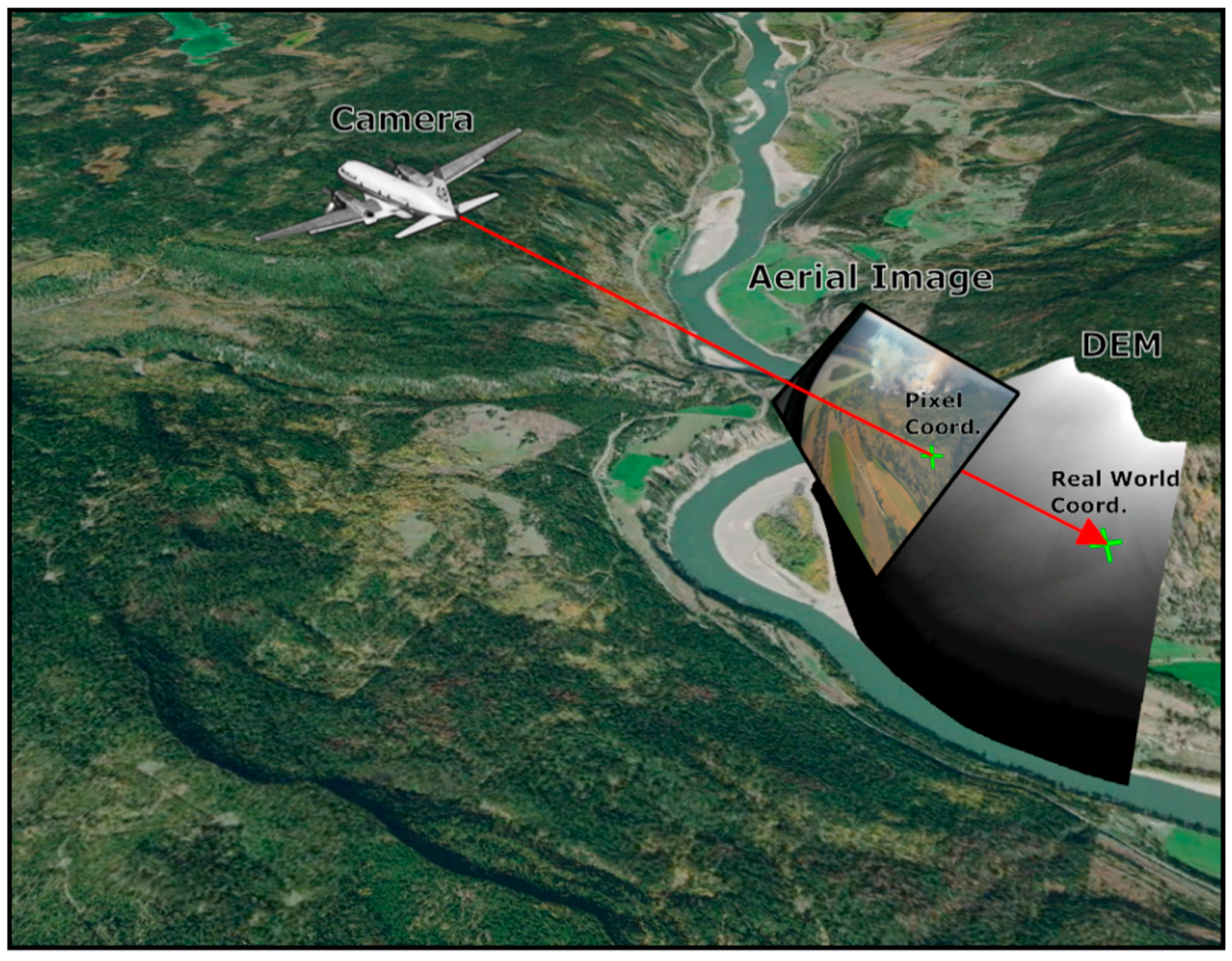
2.1. Monoplotting Process
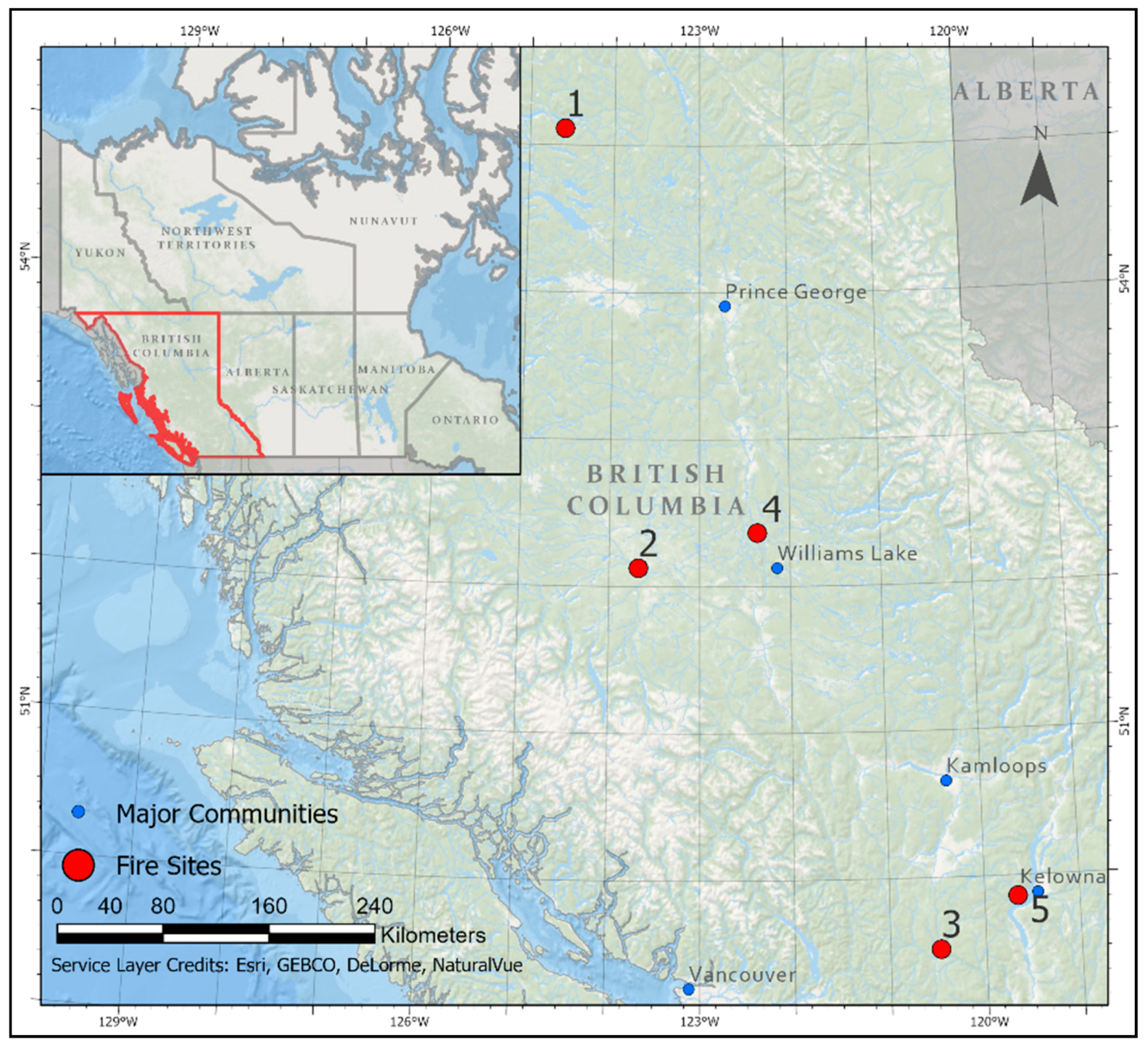
2.2. Study Area, Image Selection and Data Compilation
2.3. Georeferencing Oblique Aerial Wildfire Images Using MPT
2.4. Headfire Position Interpretation and Rate of Spread Calculation
3. Results
3.1. Fire Front Locations and Accuracy Assessment
3.2. Fire Spread Distance and Rate Estimates
4. Discussion
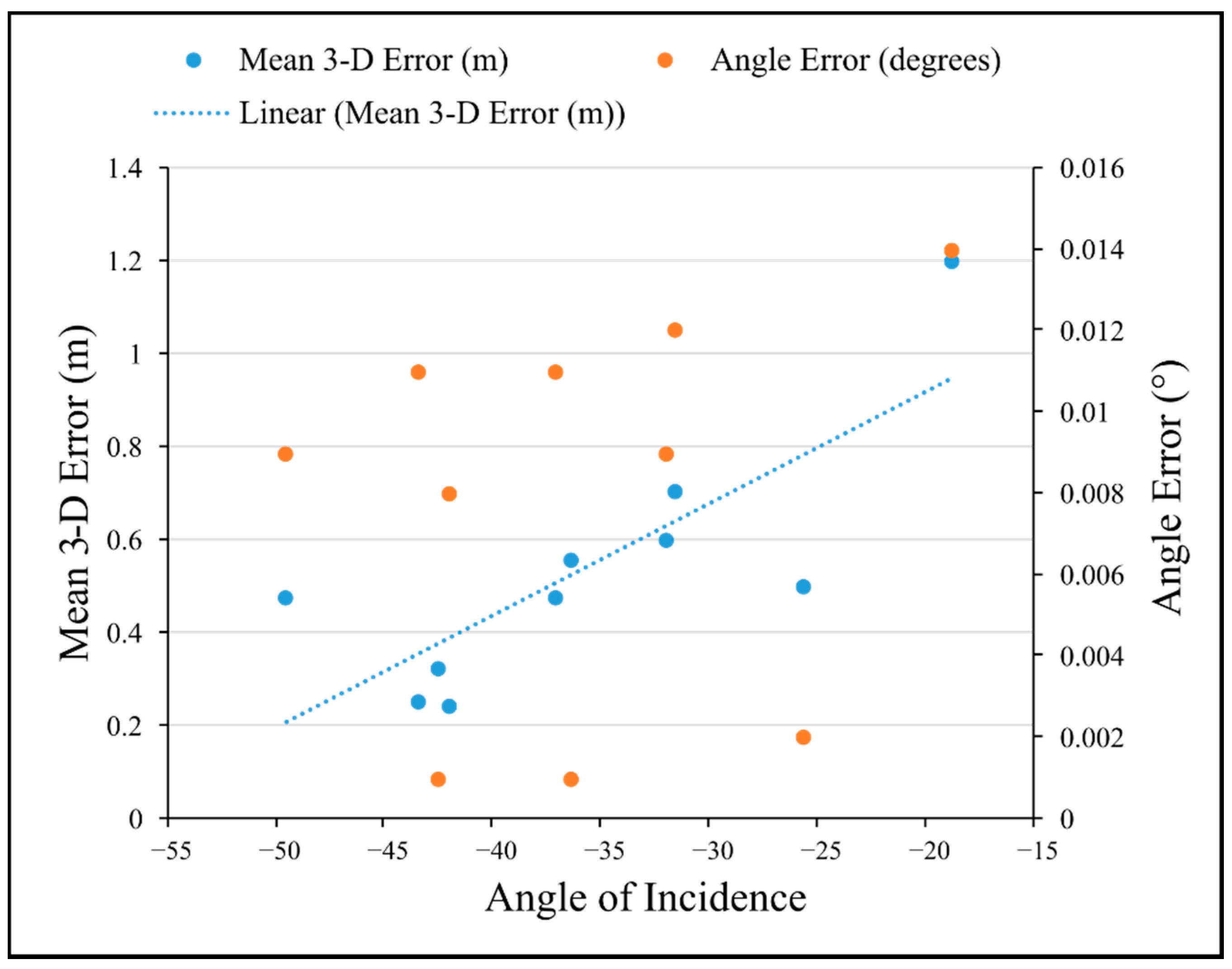
4.1. Factors Affecting MPT Accuracy
4.2. Recommendations for Future Research and Application
- When selecting wildfire images for monoplotting, the fire front position must be visible or at least interpretable with a high degree of confidence and the visible landscape and resolution of the images must permit precise location of at least five GCPs. Monoplotting to determine the position of fire features will be most successful in heterogeneous landscapes. Accuracy may be higher in mountainous terrain.
- The accuracy of georeferencing increases with the resolution of the available orthophotos and DEM as well as the distance from camera to ground and camera settings, which influence the pixel resolution. The monoplotting method will be more accurate in regions where orthophotos of half meter resolution and an underlying DEM of at least 25 m resolution are available (for very irregular terrain a DEM with higher resolution is recommended).
- Images captured from close distance to the fire and at a lower elevation allow for more precise location of GCPs. However, this also reduces the field of view and may restrict the number of GCPs. We recommend a distance range between 650 and 2500 m, and an elevation range of 350 to 1050 m to yield angles of incidence from about −30 to −50° and a good field of view and perspective of the fire front. Ideally, the view of the flaming front is unobscured by the smoke plume, although it is not always possible. Bird dog aircraft attached to air tanker groups are often in this airspace and can provide a good platform for acquiring wildfire spread imagery.
- Care must be taken in locating fire fronts in oblique photos with regard to the depth of visible flame, the shape of the fire front, the location of the smoke plume base and direction of smoke spread; this requires some training and experience. Complex fire spread patterns, particularly when fuels or terrain are highly heterogeneous or spotting is a significant factor, may be georeferenced using monoplotting, but will be much more difficult to relate to the fire environment. Such considerations are beyond the scope of this article.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BCWS | British Columbia Wildfire Service |
| BUI | Buildup Index |
| DEM | Digital Elevation Model |
| FBP | Canadian Fire Behaviour Prediction System |
| FFMC | Fine Fuel Moisture Code |
| FWI | Canadian Forest Fire Weather Index System |
| GCP | Ground Control Point |
| GIS | Geographic Information System |
| HROS | Head Fire Rate of Spread |
| ISI | Initial Spread Index |
| LST | Local Standard Time |
| MPT | WSL Monoplotting Tool |
| PATC | Provincial Air Tanker Centre |
| HSD | Geodesic Head Fire Spread Distance |
| VRI | Vegetation Resource Inventory |
Appendix A. Summary of Canadian Fire Behaviour Prediction System Calculations
| Site # | FFMC | Wind Speed (km·h−1); | Wind Observation (LST) | Distance (km) | Slope, Azimuth | ISIsw | BUI | Fuel Type | HROSp |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 89.0 | 14.5 | 1500 | 23 | <5% | 7.7 | 57 | C-2, C-3 a | 5.8 |
| 2 | 91.0 | 18.5 | 1900 | 28 | <5% | 12.6 | 42 | C-7 | 4.1 b |
| 3 | 93.6 c | 1.8 d | 1900 | 9 | <5% | 7.9 | -- | O-1b | 22.0 |
| 4 | 94.0 | 7.7 e | 1500 | 46 | 32%, 215 e | 10.0 | 94 | C-7 (O-1b) e | 3.1 |
| 5 | 95.0 | 16.1 | 1400–1500 f | 25 | <5% | 19.5 | 146 | C-7 | 9.2 |
References
- Taylor, S.W.; Woolford, D.G.; Dean, C.B.; Martell, D.L. Wildfire Prediction to Inform Fire Management: Statistical Science Challenges. Stat. Sci. 2013, 28, 586–615. [Google Scholar] [CrossRef] [Green Version]
- Forestry Canada Fire Danger Group. Development and structure of the Canadian Forest Fire Behavior Prediction System, Information Report ST-X-3; Forestry Canada, Science and Sustainable Development Directorate: Ottawa, ON, Canada, 1992. [Google Scholar]
- Johnston, L.M.; Wang, X.; Erni, S.; Taylor, S.W.; McFayden, C.B.; Oliver, J.A.; Stockdale, C.; Christianson, A.; Boulanger, Y.; Gauthier, S.; et al. Wildland fire risk research in Canada. Environ. Rev. 2020, 28, 164–186. [Google Scholar] [CrossRef]
- Parisien, M.A.; Dawe, D.A.; Miller, C.; Stockdale, C.A.; Armitage, O.B. Applications of simulation-based burn probability modelling: A review. Int. J. Wildl. Fire 2019, 28, 913. [Google Scholar] [CrossRef] [Green Version]
- Wotton, B.M.; Alexander, M.E.; Taylor, S.W. Updates and Revisions to the 1992 Canadian Forest Fire Behavior Prediction System, GLC-X-10; Natural Resources Canada, Canadian Forest Service, Great Lakes Forestry Centre: Sault St. Marie, ON, Canada, 2009. [Google Scholar]
- Plucinski, M.P.; Sullivan, A.L.; Rucinski, C.J.; Prakash, M. Improving the reliability and utility of operational bushfire behaviour predictions in Australian vegetation. Environ. Model. Softw. 2017, 91, 1–12. [Google Scholar] [CrossRef]
- Hirsch, K. Canadian Forest Fire Behavior Prediction (FBP) System: User’s Guide; Northern Forestry Centre: Edmonton, AB, Canada, 1996.
- Van Wagner, C.E. Development and Structure of the Canadian Forest Fire Weather Index System; Canadian Forestry Service: Ottawa, ON, Canada, 1987. [Google Scholar]
- Alexander, M.E.; Stocks, B.J.; Lawson, B.D. Fire Behavior in Black Spruce-Lichen Woodland: The Porter Lake project, Information Report NOR-X-310; Northern Forestry Centre, Northwest Region, Forestry Canada: Edmonton, AB, Canada, 1991. [Google Scholar]
- Stocks, B.J. Fire behavior in mature jack pine. Can. J. For. Res. 1989, 19, 783–790. [Google Scholar] [CrossRef]
- Alexander, M.E.; Thomas, D.A. Wildland fire behavior case studies and analyses: Value, approaches, and practical uses. Fire Manag. Today 2003, 63, 4–8. [Google Scholar]
- Allison, R.S.; Johnston, J.M.; Craig, G.; Jennings, S. Airborne optical and thermal remote sensing for wildfire detection and monitoring. Sensors 2016, 16, 1310. [Google Scholar] [CrossRef] [Green Version]
- Moriarty, K.; Cheng, A.S.; Hoffman, C.M.; Cottrell, S.P.; Alexander, M.E. Firefighter Observations of ‘Surprising’ Fire Behavior in Mountain Pine Beetle-Attacked Lodgepole Pine Forests. Fire 2019, 2, 34. [Google Scholar] [CrossRef] [Green Version]
- Filkov, A.; Duff, T.; Penman, T. Improving Fire Behaviour Data Obtained from Wildfires. Forests 2018, 9, 81. [Google Scholar] [CrossRef] [Green Version]
- Alexander, M.E.; Cruz, M.G. Are the applications of wildland fire behaviour models getting ahead of their evaluation again? Environ. Model. Softw. 2013, 41, 65–71. [Google Scholar] [CrossRef]
- Gould, J.; McCaw, M.; Cruz, M.; Anderson, W. How good are fire behaviour models? Validation of eucalypt forest fire spread model. In Proceedings of the Wildland Fire Conference, Sun City, South Africa, 9–13 May 2011. [Google Scholar]
- Sullivan, A.L. Wildland surface fire spread modelling, 1990–2007. 2: Empirical and quasi-empirical models. Int. J. Wildl. Fire 2009, 18, 369–386. [Google Scholar] [CrossRef] [Green Version]
- Perrakis, D.B.; Lanoville, R.A.; Taylor, S.W.; Hicks, D. Modeling wildfire spread in mountain pine beetle-affected forest stands, British Columbia, Canada. Fire Ecol. 2014, 10, 10–35. [Google Scholar] [CrossRef]
- Makarovic, B. Digital Monoplotters. ITC J. 1973, 4, 583–600. [Google Scholar]
- Bozzini, C.; Conedera, M.; Krebs, P. A New Monoplotting Tool to Extract Georeferenced Vector Data and Orthorectified Raster Data from Oblique Non-Metric Photographs. Int. J. Herit. Digit. Era 2012, 1, 499–518. [Google Scholar] [CrossRef]
- Stockdale, C.A.; Bozzini, C.; Macdonald, S.E.; Higgs, E. Extracting ecological information from oblique angle terrestrial landscape photographs: Performance evaluation of the WSL Monoplotting Tool. Appl. Geogr. 2015, 63, 315–325. [Google Scholar] [CrossRef]
- Monoplotting Tool. Available online: https://www.wsl.ch/monoplotting (accessed on 18 October 2021).
- Conedera, M.; Bozzini, C.; Ryter, U.; Bertschinger, T.; Krebs, P. Using the Monoplotting Technique for Documenting and Analyzing Natural Hazard Events. In Natural Hazards: Risk Assessment and Vulnerability Reduction; IntechOpen: London, UK, 2018; pp. 107–108. [Google Scholar] [CrossRef] [Green Version]
- Bozzini, C. WSL Monoplotting Tool: User Manual; Swiss Federal Research Institute WSL: Birmensdorf, Switzerland, 2018. [Google Scholar]
- Steiner, L. Reconstruction of Glacier States from Geo-Referenced, Historical Postcards. Master’s Thesis, Institut für Kartographie und Geoinformatik, Hannover, Germany, 2012. [Google Scholar]
- Schenk, T. Introduction to Photogrammetry; Department of Civil and Environmental Engineering and Geodetic Science, The Ohio State University: Columbus, Ohio, USA, 2005; pp. 59–61. [Google Scholar]
- Wildfire Season. 2017. Available online: https://www2.gov.bc.ca/gov/content/safety/wildfire-status/about-bcws/wildfire-history/wildfire-season-summary (accessed on 7 July 2021).
- BC Data Catalogue. Available online: https://catalogue.data.gov.bc.ca/dataset?tags=VRI (accessed on 1 January 2020).
- ESRI World Imagery (For Export). Available online: https://www.arcgis.com/home/item.html?id=226d23f076da478bba4589e7eae95952 (accessed on 1 January 2020).
- Weber, R.O. Analytical models for fire spread due to radiation. Combust. Flame. 1989, 78, 398–498. [Google Scholar] [CrossRef]
- van Wagner, C.E. A simple fire-growth model. For. Chron. 1969, 45, 103–104. [Google Scholar] [CrossRef] [Green Version]
- Cheney, N.P.; Gould, J.S. Fire Growth in grassland fuels. Int. J. Wildland Fire. 1995, 5, 237–247. [Google Scholar] [CrossRef]
- Perrakis, D.B.; Eade, G.; Hicks, D. British Columbia Wildfire Fuel Typing and Fuel Type Layer Description, Information Report BC-X-444; Pacific Forestry Centre: Victoria, BC, Canada, 2018. [Google Scholar]
- Nadeem, K.; Taylor, S.W.; Woolford, D.G.; Dean, C.B. Mesoscale spatiotemporal predictive models of daily human- and lightning-caused wildland fire occurrence in British Columbia. Int. J. Wildl. Fire 2019, 29, 11–27. [Google Scholar] [CrossRef]
- Wotton, B.M.; Gould, J.S.; McCaw, W.L.; Cheney, N.P.; Taylor, S.W. Flame temperature and residence time of fires in dry eucalypt forest. Int. J. Wildl. Fire 2012, 21, 270–281. [Google Scholar] [CrossRef]
- Werth, P.A.; Potter, B.E.; Alexander, M.E.; Clements, C.B.; Cruz, M.G.; Finney, M.A.; Forthofer, J.M.; Goodrick, S.L.; Hoffman, C.; Jolly, W.M.; et al. Synthesis of Knowledge of Extreme Fire Behavior: Volume 2 for Fire Behavior Specialists, Researchers, and Meteorologists. Gen. Tech. Rep. PNW-GTR-891; Pacific Northwest Research Station, Forest Service, U.S. Department of Agriculture: Portland, OR, USA, 2016.
- Gabellieri, N.; Watkins, C. Measuring long-term landscape change using historical photographs and the WSL Monoplotting Tool. Landsc. Hist. 2019, 40, 93–109. [Google Scholar] [CrossRef]
- Planas, E.; Cubells, M.; Pastor, E. Different approaches for the head fire perimeter definition in wildland fires. Fire. Saf. Sci. 2011, 10, 1425–1435. [Google Scholar] [CrossRef]
- Cheney, N.P.; Gould, J.S.; McCaw, W.L.; Anderson, W.R. Predicting fire behaviour in dry eucalypt forest in southern Australia. For. Ecol. Manage. 2012, 280, 120–131. [Google Scholar] [CrossRef]
- Albini, F.A.; Anderson, E.B. Predicting fire behavior in US Mediterranean ecosystems. Gen. Tech. Rep. PSW-GTR-58. In Proceedings of the Symposium on Dynamics and Management of Mediterranean-Type Ecosystems, San Diego, CA, USA, 22 June 1981; Pacific Southwest Forest and Range Experiment Station, Forest Service, U.S. Department of Agriculture: Berkeley, CA, USA, 1982; pp. 483–489. [Google Scholar]
- Finney, M. Efforts at Comparing Simulated and Observed Fire Growth Patterns. Final Report INT-95066-RJVA; USDA Forest Service, Rocky Mountain Research Station, Fire Science Laboratory: Missoula, MT, USA, 2000.
- Clark, N.A.; Martell, D.L. The use of aircraft tracking GPS data to develop models of the use of airtankers in forest fire management. INFOR 2021, 57, 535–562. [Google Scholar] [CrossRef]
- The Universal Fire Behaviour Calculator. Available online: https://redapp.org/ (accessed on 18 October 2021).
- Albini, F.A. Potential Spotting Distance from Wind-Driven Surface Fires. Res. Pap. INT-309; Intermountain Forest and Range Experiment Station, Forest Service, U.S. Department of Agriculture: Ogden, UT, USA, 1983.
- Alexander, M.E.; Cruz, M.G. Evaluating a model for predicting active crown fire rate of spread using wildfire observations. Can. J. For. Res. 2006, 36, 3015–3028. [Google Scholar] [CrossRef]
- Taylor, S.W.; Alexander, M.E. Field guide to the Canadian Forest Fire Behavior Prediction (FBP) System, 3rd ed.; Northern Forestry Centre, Canadian Forest Service: Edmonton, AB, Canada, 2018.
- Forthofer, J.M.; Butler, B.W.; Wagenbrenner, N.S. A comparison of three approaches for simulating fine-scale surface winds in support of wildland fire management. Part I. Model formulation and comparison against measurements. Int. J. Wildl. Fire 2014, 23, 969–981. [Google Scholar] [CrossRef]
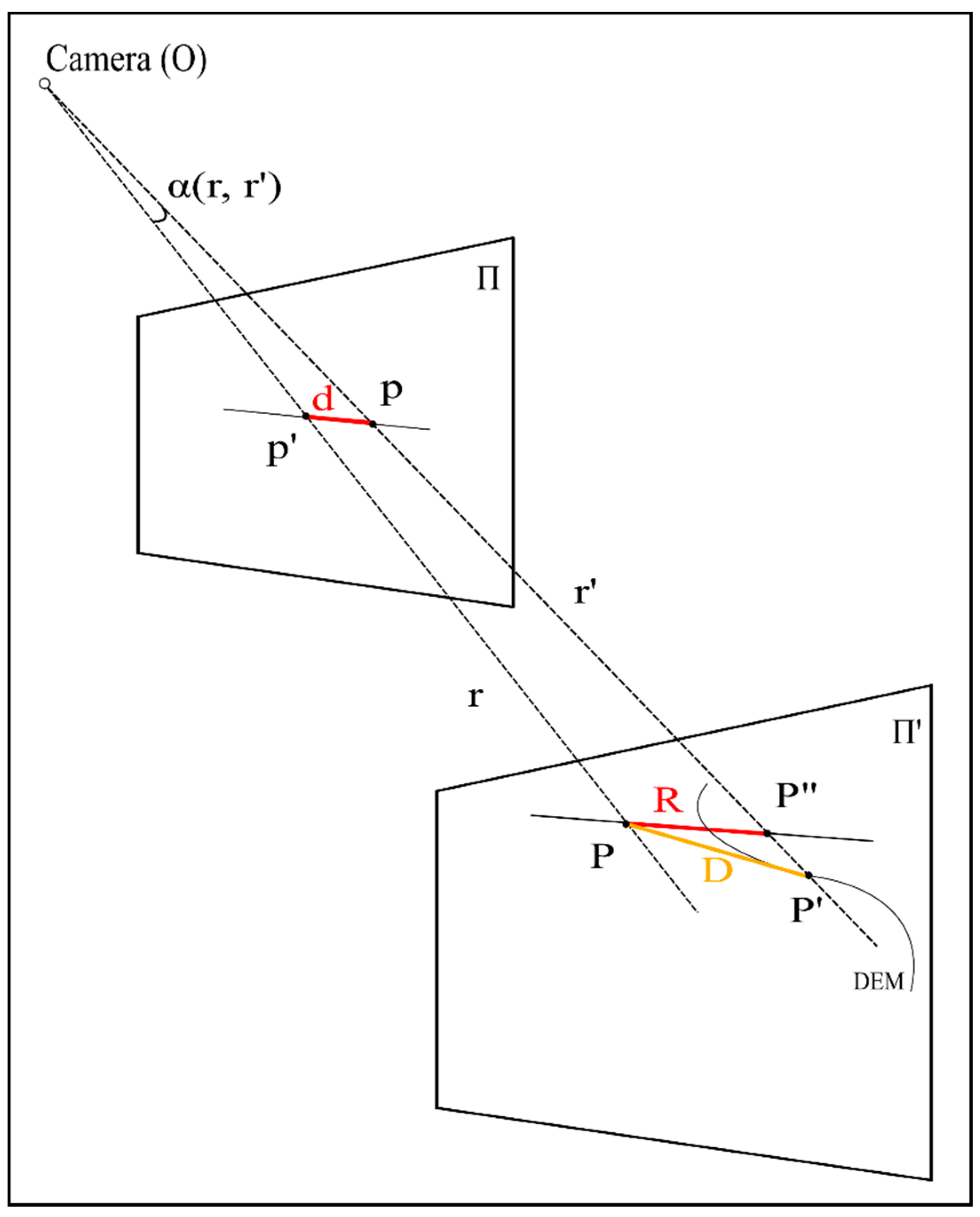






| Error | Unit | Symbol | Description |
|---|---|---|---|
| Pixels | px | d | Distance from user defined image GCP (p) coordinates to MPT calculated image point (p’) coordinates given in pixels |
| Angle | ° | α(r, r’) | The angle between the two light rays (r, r’) |
| Radius | m | R | Distance from MPT calculated ground point (P”) to user defined ground GCP (P) |
| World 3D | m | D | Distance from MPT calculated ground point (P’) to the user defined ground GCP (P) |
| World 2D | m | D2d | Projection of the World 3D error (D) on the horizontal plane |
| Site Number | Landscape Features | Vegetation Type |
|---|---|---|
| 1 | Flat riparian landscape, open areas with shrubs, patchy forest | Engelmann spruce—Subalpine fir forest |
| 2 | Flat landscape, two building structures, open areas with shrubs, forest and agricultural areas | Ponderosa Pine—Douglas-fir |
| 3 | Moderately sloped landscape, open grass field with lone standing trees | Interior grassland, cured |
| 4 | Steeply sloped landscape, two buildings, patchy forested sections with lone standing trees | Grassland—Ponderosa pine forest transition |
| 5 | A: Moderately sloped landscape, many buildings, sports fields, forested areas B: Moderately sloped landscape, two buildings, densely forested with open disturbance patches | Closed Douglas-fir forest |
| Image # | Aerial Image Time Stamp | Mean Angle Error (°) | 3D Error (m) Min. | 3D Error (m) Max. | 3D Error (m) Mean |
|---|---|---|---|---|---|
| 1A | 14:31 | 0.008 | 0.033 | 0.388 | 0.244 |
| 1B | 15:13 | 0.011 | 0.033 | 0.382 | 0.253 |
| 2A | 18:16 | 0.009 | 0.053 | 1.034 | 0.600 |
| 2B | 19:13 | 0.002 | 0.087 | 0.822 | 0.500 |
| 3A | 18:33 | 0.001 | 0.137 | 1.127 | 0.555 |
| 3B | 19:04 | 0.001 | 0.102 | 0.672 | 0.322 |
| 4A | 14:56 | 0.009 | 0.327 | 0.691 | 0.475 |
| 4B | 16:09 | 0.012 | 0.234 | 0.962 | 0.706 |
| 5A | 13:48 | 0.014 | 0.133 | 2.030 | 1.197 |
| 5B | 15:46 | 0.011 | 0.103 | 0.959 | 0.477 |
| Mean or Extreme | NA | 0.008 | 0.033 | 2.030 | 0.533 |
| Image # | Approx. Distance to Fire Front (m) | Elevation above Ground Level (m) | Angle of Incidence (°) | Azimuth (°) |
|---|---|---|---|---|
| 1A | 1040 | 587.63 | −42.02 | 85.44 |
| 1B | 650 | 360.16 | −43.40 | 290.86 |
| 2A | 1725 | 836.29 | −31.95 | 205.09 |
| 2B | 3720 | 1443.46 | −25.67 | 224.78 |
| 3A | 1720 | 794.27 | −36.32 | 114.35 |
| 3B | 2130 | 516.12 | −42.52 | 153.80 |
| 4A | 1275 | 1024.43 | −49.52 | 104.10 |
| 4B | 2420 | 631.57 | −31.54 | 332.08 |
| 5A | 4665 | 810.97 | −18.82 | 11.80 |
| 5B | 1575 | 772.71 | −37.09 | 352.91 |
| Mean | 2092 | 777.76 | −35.89 | NA |
| Site # | Fire Year | Fire Spread Distance (m) | Burning Period (min) | Max Total 3D Error (m) | Max HROS Error (%) | HROS (m·min−1) |
|---|---|---|---|---|---|---|
| 1 | 2013 | 200.63 | 42 | 0.770 | 0.38 | 4.78 |
| 2 | 2009 | 581.13 | 57 | 1.856 | 0.32 | 10.20 a |
| 3 | 2014 | 845.77 | 31 | 1.799 | 0.21 | 27.28 |
| 4 | 2014 | 377.42 | 73 | 1.653 | 0.44 | 5.17 |
| 5 | 2014 | 554.30 | 118 | 2.989 | 0.54 | 4.70 |
| Fire Obs. # | FBP Fuel Type | HROSp (m·min−1) | HROSO (m·min−1) | Difference (m·min−1) | Difference (%) |
|---|---|---|---|---|---|
| 1 | C-2, C-3 | 5.80 | 4.78 | +1.02 | 21.33 |
| 2 | C-7 | 4.10 | 10.20 | −6.10 | −59.80 a |
| 3 | O1-b | 22.0 | 27.28 | −5.28 | −19.35 |
| 4 | C-7 (O1-b) | 3.10 | 5.17 | −2.07 | −40.03 |
| 5 | C-7 | 9.20 | 4.70 | +4.50 | +95.74 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hart, H.; Perrakis, D.D.B.; Taylor, S.W.; Bone, C.; Bozzini, C. Georeferencing Oblique Aerial Wildfire Photographs: An Untapped Source of Fire Behaviour Data. Fire 2021, 4, 81. https://doi.org/10.3390/fire4040081
Hart H, Perrakis DDB, Taylor SW, Bone C, Bozzini C. Georeferencing Oblique Aerial Wildfire Photographs: An Untapped Source of Fire Behaviour Data. Fire. 2021; 4(4):81. https://doi.org/10.3390/fire4040081
Chicago/Turabian StyleHart, Henry, Daniel D. B. Perrakis, Stephen W. Taylor, Christopher Bone, and Claudio Bozzini. 2021. "Georeferencing Oblique Aerial Wildfire Photographs: An Untapped Source of Fire Behaviour Data" Fire 4, no. 4: 81. https://doi.org/10.3390/fire4040081
APA StyleHart, H., Perrakis, D. D. B., Taylor, S. W., Bone, C., & Bozzini, C. (2021). Georeferencing Oblique Aerial Wildfire Photographs: An Untapped Source of Fire Behaviour Data. Fire, 4(4), 81. https://doi.org/10.3390/fire4040081






