Estimation of Byram’s Fire Intensity and Rate of Spread from Spaceborne Remote Sensing Data in a Savanna Landscape
Abstract
:1. Introduction
- FRED-ROS: Fire Radiative Energy Density (FRED)-ROS: this method uses (pixel-wise) fire radiative power integrated over the pixel’s burn time to provide pixel FRE and combines this with a pixel based estimate of rate of spread following [44].
- FRP-FD: Fire Radiative Power (FRPD)-Flame Depth (FD): this approach is based on a different formulation of Byram’s equation conceptualizing ROS as the depth of the flaming zone multiplied by the flame residence time.
2. Materials and Methods
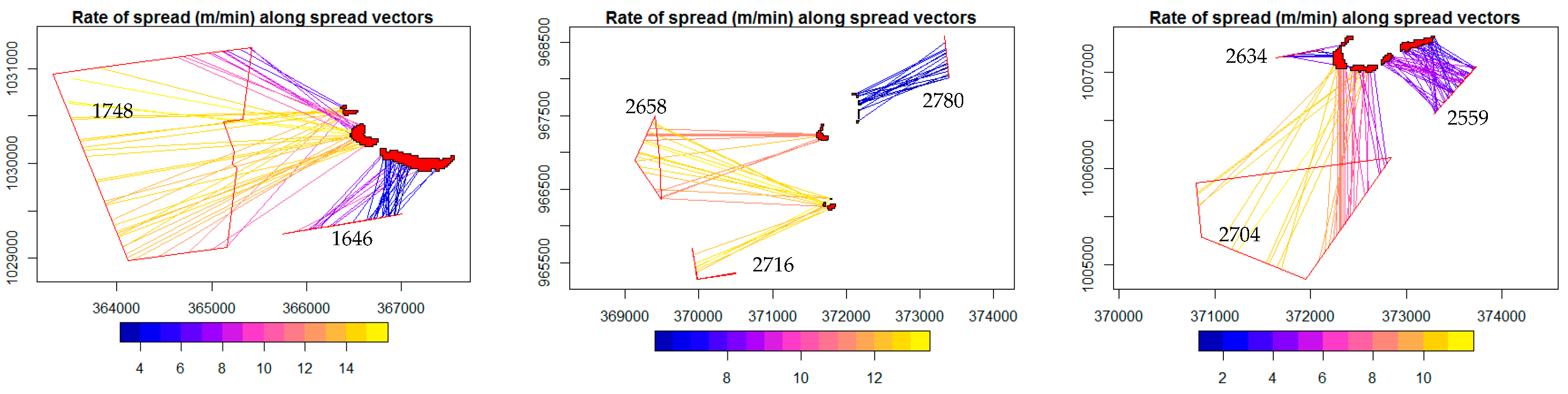
2.1. Identification of fire Fronts and Estimation of Rate of Spread (ROS)
- Exclusion of connectors that are crossing already-burned area as the fire is not expected to travel through already-burned areas.
- Exclusion of connectors that cross S-2 fronts that are closer to the connecting VIIRS fronts than the originating S-2 front, as the connections of the spatially closer S-2 front shall be used for the ROS calculation.
- Exclusion of connectors that go through barriers other than burned area which are not expected to be crossed by a fire.
- Exclusion of connectors which are associated with different ignition events.
2.2. Estimating Fuel Consumption and Byram’s Fireline Intensity
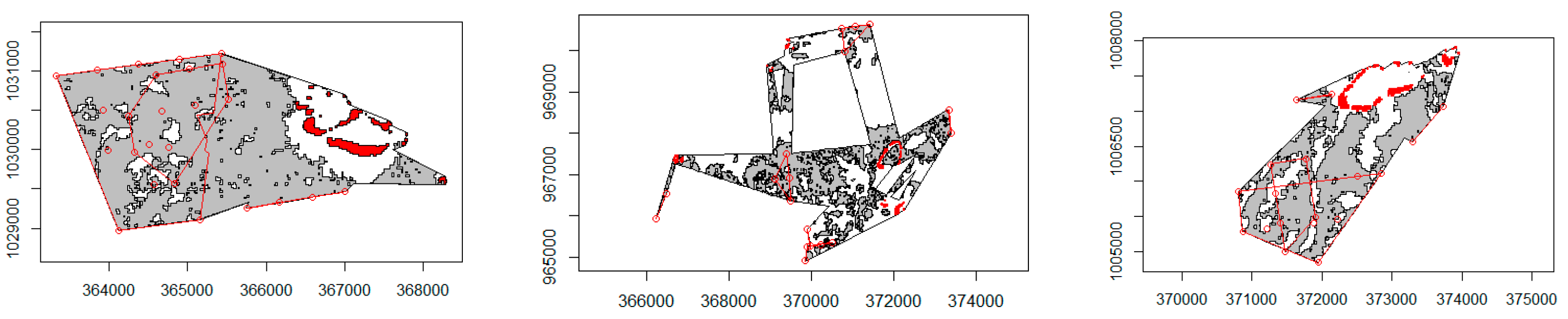
2.3. Study Area
3. Results
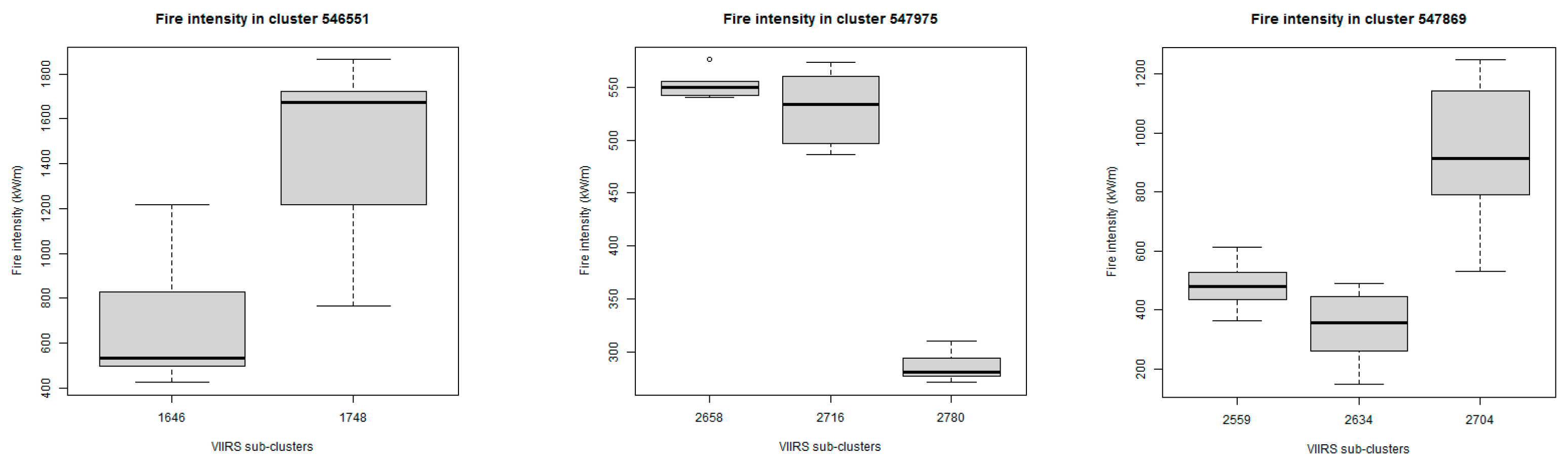
3.1. Illustration of Rate of Spread, Fuel Consumption and Fireline Intensity Retrievals
3.2. Characteristics of the Observed Fire Clusters
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Govender, N.; Trollope, W.S.W.; Van Wilgen, B.W. The effect of fire season, fire frequency, rainfall and management on fire intensity in savanna vegetation in South Africa. J. Appl. Ecol. 2006, 43, 748–758. [Google Scholar] [CrossRef]
- Byram, G.M. Combustion of Forest Fuels. In Forest Fire: Control and Use; McGraw-Hill: New York, NY, USA, 1959; pp. 61–89. [Google Scholar]
- Alexander, M.E. Calculating and interpreting forest fire intensities. Can. J. Bot. 1982, 60, 349–357. [Google Scholar] [CrossRef]
- Wotton, B.M.; Flannigan, M.; Marshall, G.A. Potential climate change impacts on fire intensity and key wildfire suppression thresholds in Canada. Environ. Res. Lett. 2016, 12, 095003. [Google Scholar] [CrossRef]
- Williams, R.J.; Cook, G.D.; Gill, A.M.; Moore, P.H.R. Fire regime, fire intensity and tree survival in a tropical savanna in northern Australia. Austral. Ecol. 1999, 24, 50–59. [Google Scholar] [CrossRef]
- Miranda, A.C.; Miranda, H.; Dias, I.D.F.O.; Dias, B.F.D.S. Soil and air temperatures during prescribed cerated fires in Central Brazil. J. Trop. Ecol. 1993, 9, 313–320. [Google Scholar] [CrossRef]
- Lipsett-Moore, G.J.; Wolff, N.H.; Game, E.T. Emissions mitigation opportunities for savanna countries from early dry season fire management. Nat. Commun. 2018, 9, 2247. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Laris, P. On the problems and promises of savanna fire regime change. Nat. Commun. 2021, 12, 4891. [Google Scholar] [CrossRef] [PubMed]
- Johnston, J.M.; Wooster, M.J.; Paugam, R.; Wang, X.; Lynham, T.J.; Johnston, L.M. Direct estimation of Byram’s fire intensity from infrared remote sensing imagery. Int. J. Wildland Fire 2017, 26, 668. [Google Scholar] [CrossRef] [Green Version]
- Zhukov, B.; Lorenz, E.; Oertel, D.; Wooster, M.; Roberts, G. Spaceborne detection and characterization of fires during the bi-spectral infrared detection (BIRD) experimental small satellite mission (2001–2004). Remote Sens. Environ. 2006, 100, 29–51. [Google Scholar] [CrossRef]
- Kauffman, J.Y.; Justice, C.O.; Flynn, L.P.; Kendall, J.D.; Prins, E.M.; Giglio, L.; Ward, D.E.; Menzel, W.P.; Setzer, A.W. Potential global fire monitoring from EOS-MODIS. J. Geophys. Res. 1998, 103, 32215–32238. [Google Scholar] [CrossRef]
- Justice, C.; Giglio, L.; Korontzi, S.; Owens, J.; Morisette, J.T.; Roy, D.; Descloitres, J.; Alleaume, S.; Petitcolin, F.; Kaufman, Y. The MODIS fire products. Remote Sens. Environ. 2002, 83, 244–262. [Google Scholar] [CrossRef]
- Wooster, M.J.; Zhukov, B.; Oertel, D. Fire radiative energy for quantitative study of biomass burning: Derivation from the BIRD experimental satellite and comparison to MODIS fire products. Remote Sens. Environ. 2003, 86, 83–107. [Google Scholar] [CrossRef]
- Dozier, J. A method for satellite identification of surface temperature fields of subpixel resolution. Remote Sens. Environ. 1981, 11, 221–229. [Google Scholar] [CrossRef]
- Matson, M.; Dozier, J. Identification of subresolution high temperature sources using a thermal IR sensor. Photogramm. Eng. Remote Sens. 1981, 47, 1311–1318. [Google Scholar]
- Wooster, M.J.; Roberts, G.; Perry, G.; Kaufman, Y.J. Retrieval of biomass combustion rates and totals from fire radiative power observations: FRP derivation and calibration relationships between biomass consumption and fire radiative energy release. J. Geophys. Res. Space Phys. 2005, 110. [Google Scholar] [CrossRef]
- Schroeder, W.; Csiszar, I.; Giglio, L.; Schmidt, C.C. On the use of fire radiative power, area, and temperature estimates to characterize biomass burning via moderate to coarse spatial resolution remote sensing data in the Brazilian Amazon. J. Geophys. Res. Space Phys. 2010, 115. [Google Scholar] [CrossRef] [Green Version]
- Roberts, G.J.; Wooster, M.J. Fire Detection and Fire Characterization Over Africa Using Meteosat SEVIRI. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1200–1218. [Google Scholar] [CrossRef] [Green Version]
- Xu, W.; Wooster, M.J.; He, J.; Zhang, T. Improvements in high-temporal resolution active fire detection and FRP retrieval over the Americas using GOES-16 ABI with the geostationary Fire Thermal Anomaly (FTA) algorithm. Sci. Remote Sens. 2021, 3, 100016. [Google Scholar] [CrossRef]
- Xu, W.; Wooster, M.; Roberts, G.; Freeborn, P. New GOES imager algorithms for cloud and active fire detection and fire radiative power assessment across North, South and Central America. Remote Sens. Environ. 2010, 114, 1876–1895. [Google Scholar] [CrossRef]
- Xu, W.; Wooster, M.; Kaneko, T.; He, J.; Zhang, T.; Fisher, D. Major advances in geostationary fire radiative power (FRP) retrieval over Asia and Australia stemming from use of Himarawi-8 AHI. Remote Sens. Environ. 2017, 193, 138–149. [Google Scholar] [CrossRef] [Green Version]
- Schroeder, W. Visible Infrared Imaging Radiometer Suite (VIIRS) 375 m & 750 m Active Fire Detection Data Sets Based on NASA VIIRS Land Science Investigator Processing System (SIPS) Reprocessed Data—Version 1, Product User Guide, NASA. 2017. Available online: https://lpdaac.usgs.gov/documents/132/VNP14_User_Guide_v1.3.pdf (accessed on 27 September 2021).
- Li, F.; Zhang, X.; Kondragunta, S.; Csiszar, I. Comparison of Fire Radiative Power Estimates From VIIRS and MODIS Observations. J. Geophys. Res. Atmos. 2018, 123, 4545–4563. [Google Scholar] [CrossRef]
- Giglio, L.; Schroeder, W.; Justice, C.O. The collection 6 MODIS active fire detection algorithm and fire products. Remote Sens. Environ. 2016, 178, 31–41. [Google Scholar] [CrossRef] [Green Version]
- Wooster, M.; Xu, W.; Nightingale, T. Sentinel-3 SLSTR active fire detection and FRP product: Pre-launch algorithm development and performance evaluation using MODIS and ASTER datasets. Remote Sens. Environ. 2012, 120, 236–254. [Google Scholar] [CrossRef]
- Xu, W.; Wooster, M.J.; He, J.; Zhang, T. First study of Sentinel-3 SLSTR active fire detection and FRP retrieval: Night-time algorithm enhancements and global intercomparison to MODIS and VIIRS AF products. Remote Sens. Environ. 2020, 248, 111947. [Google Scholar] [CrossRef]
- Kaiser, J.W.; Heil, A.; Andreae, M.O.; Benedetti, A.; Chubarova, N.; Jones, L.; Morcrette, J.-J.; Razinger, M.; Schultz, M.G.; Suttie, M.; et al. Biomass burning emissions estimated with a global fire assimilation system based on observed fire radiative power. Biogeosciences 2012, 9, 527–554. [Google Scholar] [CrossRef] [Green Version]
- Andela, N.; van der Werf, G.; Kaiser, J.W.; Van Leeuwen, T.T.; Wooster, M.; Lehmann, C. Biomass burning fuel consumption dynamics in the tropics and subtropics assessed from satellite. Biogeosciences 2016, 13, 3717–3734. [Google Scholar] [CrossRef] [Green Version]
- Roberts, G.; Wooster, M.J.; Xu, W.; He, J. Fire Activity and Fuel Consumption Dynamics in Sub-Saharan Africa. Remote Sens. 2018, 10, 1591. [Google Scholar] [CrossRef] [Green Version]
- Boschetti, L.; Roy, D.P. Strategies for the fusion of satellite fire radiative power with burned area data for fire radiative energy derivation. J. Geophys. Res. Space Phys. 2009, 114. [Google Scholar] [CrossRef] [Green Version]
- Schroeder, W.; Ellicott, E.; Ichoku, C.; Ellison, L.; Dickinson, M.; Ottmar, R.D.; Clements, C.; Hall, D.; Ambrosia, V.; Kremens, R. Integrated active fire retrievals and biomass burning emissions using complementary near-coincident ground, airborne and spaceborne sensor data. Remote Sens. Environ. 2014, 140, 719–730. [Google Scholar] [CrossRef] [Green Version]
- Hudak, A.T.; Dickinson, M.B.; Bright, B.C.; Kremens, R.L.; Loudermilk, E.L.; O’Brien, J.J.; Hornsby, B.S.; Ottmar, R.D. Measurements relating fire radiative energy density and surface fuel consumption—RxCADRE 2011 and 2012. Int. J. Wildland Fire 2016, 25, 25–37. [Google Scholar] [CrossRef] [Green Version]
- Schroeder, W.; Oliva, P.; Giglio, L.; Csiszar, I.A. The New VIIRS 375 m active fire detection data product: Algorithm description and initial assessment. Remote Sens. Environ. 2014, 143, 85–96. [Google Scholar] [CrossRef]
- Lorenz, E.; Mitchell, S.; Säuberlich, T.; Paproth, C.; Halle, W.; Frauenberger, O. Remote Sensing of High Temperature Events by the FireBird Mission. ISPRS—Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, XL-7/W3, 461–467. [Google Scholar] [CrossRef] [Green Version]
- Caseiro, A.; Rücker, G.; Tiemann, J.; Leimbach, D.; Lorenz, E.; Frauenberger, O.; Kaiser, J.W. Persistent Hot Spot Detection and Characterisation Using SLSTR. Remote Sens. 2018, 10, 1118. [Google Scholar] [CrossRef] [Green Version]
- Fisher, D.; Wooster, M.J. Shortwave IR Adaption of the Mid-Infrared Radiance Method of Fire Radiative Power (FRP) Retrieval for Assessing Industrial Gas Flaring Output. Remote Sens. 2018, 10, 305. [Google Scholar] [CrossRef] [Green Version]
- Elvidge, C.D.; Zhizhin, M.; Hsu, F.-C.; Baugh, K.E. VIIRS Nightfire: Satellite Pyrometry at Night. Remote Sens. 2013, 5, 4423–4449. [Google Scholar] [CrossRef] [Green Version]
- Schroeder, W.; Oliva, P.; Giglio, L.; Quayle, B.; Lorenz, E.; Morelli, F. Active fire detection using Landsat-8/OLI data. Remote Sens. Environ. 2016, 185, 210–220. [Google Scholar] [CrossRef] [Green Version]
- Kumar, S.S.; Roy, D.P. Global operational land imager Landsat-8 reflectance-based active fire detection algorithm. Int. J. Digit. Earth 2018, 11, 154–178. [Google Scholar] [CrossRef] [Green Version]
- Sofan, P.; Bruce, D.; Jones, E.; Khomarudin, M.; Roswintiarti, O. Applying the Tropical Peatland Combustion Algorithm to Landsat-8 Operational Land Imager (OLI) and Sentinel-2 Multi Spectral Instrument (MSI) Imagery. Remote Sens. 2020, 12, 3958. [Google Scholar] [CrossRef]
- Wooster, M.J.; Perry, G.L.W.; Zhukov, B.; Oertel, D. Estimation of Energy. In Spatial Modelling of the Terrestrial Environment; Kelly, R., Drake, N., Barr, S., Eds.; John Wiley & Sons: London, UK, 2004. [Google Scholar]
- Wooster, M.J.; Zhang, Y. Boreal forest fires burn less intensely in Russia than in North America. Geophys. Res. Lett. 2004, 31, L20505. [Google Scholar] [CrossRef] [Green Version]
- Smith, A.M.S.; Wooster, M.J. Remote classification of head and backfire types from MODIS fire radiative power and smoke plume observations. Int. J. Wildland Fire 2005, 14, 249. [Google Scholar] [CrossRef] [Green Version]
- Paugam, R.; Wooster, M.; Roberts, G. Use of Handheld Thermal Imager Data for Airborne Mapping of Fire Radiative Power and Energy and Flame Front Rate of Spread. IEEE Trans. Geosci. Remote Sens. 2012, 51, 3385–3399. [Google Scholar] [CrossRef]
- Ononye, A.E.; Vodacek, A.; Saber, E. Automated extraction of fire line parameters from multispectral infrared images. Remote Sens. Environ. 2007, 108, 179–188. [Google Scholar] [CrossRef] [Green Version]
- Hu, X.; Ban, Y.; Nascetti, A. Sentinel-2 MSI data for active fire detection in major fire-prone biomes: A multi-criteria approach. Int. J. Appl. Earth Obs. Geoinf. 2021, 101, 102347. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining (KDD’96), Portland, Oregon, 2–4 August 2016; AAAI Press: Palo Alto, CA, USA, 1996; pp. 226–231. [Google Scholar]
- García, M.J.L.; Caselles, V. Mapping burns and natural reforestation using thematic Mapper data. Geocarto Int. 1991, 6, 31–37. [Google Scholar] [CrossRef]
- Trigg, S.; Flasse, S. An evaluation of different bi-spectral spaces for discriminating burned shrub-savannah. Int. J. Remote Sens. 2001, 22, 2641–2647. [Google Scholar] [CrossRef]
- Zhu, Z.; Wang, S.; Woodcock, C.E. Improvement and expansion of the Fmask algorithm: Cloud, cloud shadow, and snow detection for Landsats 4–7, 8, and Sentinel 2 images. Remote Sens. Environ. 2015, 159, 269–277. [Google Scholar] [CrossRef]
- Goetze, D.; Hörsch, B.; Porembski, S. Dynamics of forest-savanna mosaics in north-eastern Ivory Coast from 1954 to 2002. J. Biogeogr. 2006, 33, 653–664. [Google Scholar] [CrossRef]
- Soro, T.D.; Soro, T.D.; Koné, M.; N’Dri, A.B.; N’Datchoh, E.T. Identified main fire hotspots and seasons in Cote d’lvoire (West Africa) using MODIS fire data. S. Afr. J. Sci. 2021, 117, 1–13. [Google Scholar]
- Hennenberg, K.J.; Fischer, F.; Kouadio, K.; Goetze, D.; Orthmann, B.; Linsenmair, K.E.; Jeltsch, F.; Porembski, S. Phytomass and fire occurrence along forest–savanna transects in the Comoé National Park, Ivory Coast. J. Trop. Ecol. 2006, 22, 303–311. [Google Scholar] [CrossRef]
- Ruecker, G. Suivi des Feux au Parc National de la Comoé et dans Ses Zones Périphériques (Warigué et Mt. Tingui) par Télédétection Pendant la Saison Sèche 2018/2019; Rapport de Projet; GIZ-Profiab II: Munich, Germany, 2019. [Google Scholar]
- Kremens, R.L.; Smith, A.; Dickinson, M. Fire Metrology: Current and Future Directions in Physics-Based Measurements. Fire Ecol. 2010, 6, 13–35. [Google Scholar] [CrossRef]
- N’Dri, A.B.; Soro, T.D.; Gignoux, J.; Dosso, K.; Koné, M.; N’Dri, J.K.; Koné, N.A.; Barot, S. Season affects fire behavior in annually burned humid savanna of West Africa. Fire Ecol. 2018, 14, 5. [Google Scholar] [CrossRef]
- Laris, P.; Jacobs, R.; Koné, M.; Dembélé, F.; Rodrigue, C.M. Determinants of fire intensity in working landscapes of an African savanna. Fire Ecol. 2020, 16, 27. [Google Scholar] [CrossRef]
- Bojinski, S.; Verstraete, M.; Peterson, T.C.; Richter, C.; Simmons, A.; Zemp, M. The Concept of Essential Climate Variables in Support of Climate Research, Applications, and Policy. Bull. Am. Meteorol. Soc. 2014, 95, 1431–1443. [Google Scholar] [CrossRef]
- Johnston, J.M.; Wheatley, M.J.; Wooster, M.J.; Paugam, R.; Davies, G.M.; DeBoer, K.A. Flame-Front Rate of Spread Estimates for Moderate Scale Experimental Fires Are Strongly Influenced by Measurement Approach. Fire 2018, 1, 16. [Google Scholar] [CrossRef] [Green Version]
- Friedl, H.; Stampfer, E. Jackknife resampling. Encycl. Environ. 2002, 2, 1089–1098. [Google Scholar]
- Holmlund, K.; Grandell, J.; Schmetz, J.; Stuhlmann, R.; Bojkov, B.; Munro, R.; Lekouara, M.; Coppens, D.; Viticchie, B.; August, T.; et al. Meteosat Third Generation (MTG): Continuation and Innovation of Observations from Geostationary Orbit. Bull. Am. Meteorol. Soc. 2021, 102, E990–E1015. [Google Scholar] [CrossRef]
- Johnston, J.M.; Jackson, N.; Mcfayden, C.; Phong, L.N.; Lawrence, B.; Davignon, D.; Wooster, M.J.; Van Mierlo, H.; Thompson, D.K.; Cantin, A.S.; et al. Development of the User Requirements for the Canadian WildFireSat Satellite Mission. Sensors 2020, 20, 5081. [Google Scholar] [CrossRef]
- Schultz, J.A.; Hartmann, M.; Heinemann, S.; Janke, J.; Jürgens, C.; Oertel, D.; Rücker, G.; Thonfeld, F.; Rienow, A. DIEGO: A Multispectral Thermal Mission for Earth Observation on the International Space Station. Eur. J. Remote Sens. 2019, 53, 28–38. [Google Scholar] [CrossRef] [Green Version]




| Platform | Sensor | Spatial Resolution 1 | Observation Times | Use in the Study |
|---|---|---|---|---|
| Sentinel 2A and 2B | MSI | 20 m | ~10:40, every five days | ROS, 1st obs.; burned area |
| S-NPP and NOAA 20 | VIIRS | 375 m | ~13:30–15:00 and 01:30–3:00, daily | ROS, 2nd obs. |
| Meteosat | SEVIRI | 3 km | Every 15 min | Fuel consumption |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruecker, G.; Leimbach, D.; Tiemann, J. Estimation of Byram’s Fire Intensity and Rate of Spread from Spaceborne Remote Sensing Data in a Savanna Landscape. Fire 2021, 4, 65. https://doi.org/10.3390/fire4040065
Ruecker G, Leimbach D, Tiemann J. Estimation of Byram’s Fire Intensity and Rate of Spread from Spaceborne Remote Sensing Data in a Savanna Landscape. Fire. 2021; 4(4):65. https://doi.org/10.3390/fire4040065
Chicago/Turabian StyleRuecker, Gernot, David Leimbach, and Joachim Tiemann. 2021. "Estimation of Byram’s Fire Intensity and Rate of Spread from Spaceborne Remote Sensing Data in a Savanna Landscape" Fire 4, no. 4: 65. https://doi.org/10.3390/fire4040065
APA StyleRuecker, G., Leimbach, D., & Tiemann, J. (2021). Estimation of Byram’s Fire Intensity and Rate of Spread from Spaceborne Remote Sensing Data in a Savanna Landscape. Fire, 4(4), 65. https://doi.org/10.3390/fire4040065






