Monopole Contribution to the Stark Width of Hydrogenlike Spectral Lines in Plasmas: Analytical Results

Abstract

One of the most reliable and frequently used methods for diagnosing various laboratory and astrophysical plasmas is based on the Stark broadening of spectral lines. It allows for determining from the experimental line profiles important parameters, such as the electron density and temperature, the ion density, the magnetic field, and the field strength of various types of the electrostatic plasma turbulence. Since, in this method, radiating atoms or ions are used as the sensitive probes of the above parameters, these probes have to be properly calibrated. In other words, an accurate theory of the Stark broadening of spectral lines in plasmas is required. In the present paper, we study, analytically, the monopole contribution to the Stark width of hydrogen-like spectral lines in plasmas. For this purpose, we use the formalism from paper by Mejri, Nguyen, and Ben Lakhdar. We show that the monopole contribution to the width has a non-monotonic dependence on the velocity of perturbing electrons. Namely, at relatively small electron velocities, the width decreases as the velocity increases. Then it reaches a minimum and (at relatively large electron velocities), as the velocity further increases, the width increases. The non-monotonic dependence of the monopole contribution to the width on the electron velocity is a counter-intuitive result. The outcome that at relatively large electron velocities, the monopole contribution to the width increases with the increase in the electron velocity is in a striking distinction to the dipole contribution to the width, which decreases as the electron velocity increases. We show that, in the situation encountered in various areas of plasma research (such as in magnetically-controlled fusion), where there is a relativistic electron beam (REB) in a plasma, the monopole contribution to the width due to the REB exceeds the corresponding dipole contribution by four orders of magnitude and practically determines the entire Stark width of hydrogenic spectral lines due to the REB.

1. Introduction

One of the most reliable and frequently used methods for diagnosing various laboratory and astrophysical plasmas is based on the Stark broadening of spectral lines. It allows determining from the experimental line profiles such important parameters as, for example, the electron density and temperature, the ion density, the magnetic field, and the field strength of various types of the electrostatic plasma turbulence. Since, in this method, radiating atoms or ions are used as the sensitive probes of the above parameters, these probes have to be properly calibrated. In other words, an accurate theory of the Stark broadening of spectral lines in plasmas is required.

In particular, the theory of the Stark broadening of hydrogenlike spectral lines by plasma electrons was initially developed by Griem and Shen [1] (later being presented also in books [2,3]). In the literature it is frequently called the Conventional Theory (hereafter CT), sometimes also referred to as the standard theory. The assumption made in the CT was that the motion of the perturbing electron can be described in frames of a two-body problem—the perturbing electron moves along a hyperbolic trajectory around a “particle” of the charge Z − 1 (in atomic units).

In paper [4], the authors took into account that, actually, it is a three-body problem: the perturbing electron, the nucleus, and the bound electron, so that trajectories of the perturbing electrons are more complicated. They showed analytically by examples of the electron broadening of the Lyman lines of He II that this effect increases with the growth of the electron density N_e, becomes significant already at N_e ~ 10¹⁷ cm⁻³ and very significant at higher densities.

There were analytical advances beyond the CT, including the development of the so-called generalized theory of the Stark broadening of hydrogen-like spectral lines by plasma electrons [5]. Details can be found also in books [6,7] and references therein.

In all of the above works, the authors focused on the dipole interaction of the radiating ion with perturbing electrons. In distinction, in paper [8] the authors analytically studied the shift in hydrogen-like spectral lines due to the monopole interaction with plasma electrons.

In the present paper we use the formalism from paper [8] to analytically study the monopole contribution to the width of hydrogen-like spectral lines. We demonstrate that the monopole contribution to the width has a non-monotonic dependence on the velocity of perturbing electrons. Namely, at relatively small electron velocities, the width decreases as the velocity increases. Then it reaches a minimum and (at relatively large electron velocities), as the velocity further increases, the width increases.

2. Analytical Results

The monopole interaction potential can be represented as follows (Equation (3b) from paper [8])

V⁽⁰⁾(t) = −e²[1/|R(t) − 1/r] E[R(t) < r],

(1)

where R and r are the absolute values of the radii-vectors of the perturbing electron and of the bound electron, respectively; E[…] is the Heaviside function manifesting the fact that the monopole interaction vanishes for R(t) > r.*^/ According to Equation (17) from paper [8], for the Lyman lines, the monopole contribution to the shift, caused by N_e electrons/cm³ of velocity v, is given by

$${\mathrm{d}}_{\mathrm{nl}}{}_{\to 1\mathrm{s}}= 2\mathsf{\pi }{\mathrm{N}}_{\mathrm{e}}\mathrm{v}\underset{{}^0}{\overset{{\mathsf{\rho }}_{\max }}{\int }}\mathsf{\rho } \sin \left[<nl\left|{\mathsf{\Phi }}_0\right|nl> - <1s\left|{\mathsf{\Phi }}_0\right|1s>\right]{ \mathrm{d}\mathsf{\rho },}^{ }$$

(2)

where the matrix elements of the electron broadening operator have the form

<nlm|Φ₀|nl‘m‘> = −[e²/(ħv)](1 + u₀){ln[(1 + x)/(1 − x)] − 2x} E[R(t) < r_nl] δ_ll‘δ_mm‘.

(3)

Here

x = [1 − (u² + u₀²)/(1 + u₀)²]^1/2, u = ρ/r_nl, u₀ = ρ₀/r_nl.

(4)

*^/ The Heaviside function (also known as the step-function) in paper [8] and in the present paper is the mathematical embodiment of the vanishing monopole contribution for R(t) > r. It has been also previously used in other papers for the same purpose. For example, it was also employed in papers [9,10] devoted to the effect of penetrating collisions (corresponding to R(t) < r) on the shift of hydrogenic lines. As a result, the authors of papers [9,10] eliminated a huge discrepancy (up to an order of magnitude) between the theoretical shift and the shift observed from the laboratory and astrophysical sources. This means that the usage of the Heaviside function for this purpose provides a sufficient accuracy of the results.

In Equation (4), ρ is the impact parameter and

ρ₀ = (Z − 1)e²/(m_ev²), r_nl = (<nl|r²|nl>)^1/2 = (a₀n/Z){[5n² + 1 − 3l(l + 1)]/2}^1/2,

(5)

where r_nl is the root-mean-square size of the radiating ion in the state of the quantum numbers n and l, a₀ is the Bohr radius. Here are some useful practical formulas from paper [8]:

e²/(ħv) = [13.605/kT_e(eV)]^1/2, u₀ = [Z(Z − 1)/n²] [13.605/kT_e(eV)].

(6)

As noted in paper [8], from the condition R < r_nl it follows that

u_max = ρ_max/r_nl = (1 + 2u₀)^1/2.

(7)

Equation (7) is equivalent to

ρ_max = (r_nl² + 2 r_nlρ₀)^1/2.

(8)

In paper [8], it was noted that for relatively high temperatures, such that e²/(ħv) << 1, one has |<nlm|Φ₀|nlm>| < 1. In the opposite limit of relatively low temperatures, such that u₀ >> 1, the authors of paper [8] estimated that |<nlm|Φ₀|nlm>| does not exceed (4/3)2^1/2n/[Z(Z − 1)]^1/2. Then, by limiting themselves to the range of parameters where Z is no less than 5 and n is no more than 4, the authors of paper [8] replaced, in Equation (2), sin[…] by its argument.

In the present paper we are interested in the monopole contribution to the width w⁽⁰⁾. For the Lyman lines, it can be represented by Equation (2) with sin[…] replaced by cos[…]:

$${\mathrm{w}}^{\left(0\right)}{{}_{\mathrm{nl}}}_{\to 1\mathrm{s}}= 2\mathsf{\pi }{\mathrm{N}}_{\mathrm{e}}\mathrm{v}\underset{{}^0}{\overset{{\mathsf{\rho }}_{\max }}{\int }}\mathsf{\rho } \cos \left[<nl\left|{\Phi }_0\right|nl> - <1s\left|{\Phi }_0\right|1s>\right] \mathrm{d}\mathsf{\rho },$$

(9)

In distinction to paper [8] we focus on the situation where n >> 1 (or practically n > 4), so that the contribution of the ground level can be disregarded, and Equation (9) simplifies to

$${\mathrm{w}}^{\left(0\right)}{{}_{\mathrm{nl}}}_{\to 1\mathrm{s}}= 2\mathsf{\pi }{\mathrm{N}}_{\mathrm{e}}\mathrm{v}\underset{{}^0}{\overset{{\mathsf{\rho }}_{\max }}{\int }}\mathsf{\rho } \cos \left(<nl\left|{\mathsf{\Phi }}_0\right|nl>\right) \mathrm{d}\mathsf{\rho }.$$

(10)

In a further distinction to paper [8], we do not limit ourselves by the case where |<nlm|Φ₀|nlm>| < 1. Therefore, we keep the corresponding trigonometric function (cos [..]) in the integrand in Equation (10).

By using the relation between x and ρ from Equation (4), we now, in Equation (10), proceed from the integration over ρ to the integration over x:

$${\mathrm{w}}^{\left(0\right)}{{}_{\mathrm{nl}}}_{\to 1\mathrm{s}}= 2\mathsf{\pi }{\mathrm{N}}_{\mathrm{e}}{\mathrm{vr}}_{nl}{}^2{\left({1 + \mathrm{u}}_0\right)}^2\underset{{}^0}{\overset{{}_{\mathrm{y}}}{\int }}{\mathrm{x} \cos \left\{\right[ \mathrm{e}}^2\left({1 + \mathrm{u}}_0\right)/(ħ\mathrm{v}\left)\right][\ln \left(\left(1 + \mathrm{x}\right)/\left(1-\mathrm{x}\right)\right)-2\mathrm{x}\left]\right\},$$

(11)

where

y = (1 +2u₀)^1/2/(1 + u₀).

(12)

We denote

A = (Z − 1)a_B/r_nl, B = ħv/e²,

(13)

B being the scaled dimensionless velocity of the perturbing electrons. Then, the width w⁽⁰⁾_nl→1s can be represented in the following final form

w⁽⁰⁾_nl→1s = (2πN_er_nl²e²/ħ) F[A, B],

(14)

where

$$\mathrm{F}\left[\mathrm{A}, \mathrm{B}\right] = \mathrm{B}{\left({1 + \mathrm{A}/\mathrm{B}}^2\right)}^2\underset{{}^0}{\overset{{}_{\mathrm{y}\left(\mathrm{A}, \mathrm{B}\right)}}{\int }}\mathrm{x} \cos \{\left({1/\mathrm{B} + \mathrm{A}/\mathrm{B}}^3\right)\left[\ln \left(\left(1 + \mathrm{x}\right)/\left(1-\mathrm{x}\right)\right)-2\mathrm{x}\right]\} \mathrm{dx}.$$

(15)

The upper limit of the integration in Equation (15) is

y(A, B) = (1 +2 A/B²)^1/2/(1 + A/B²)

(16)

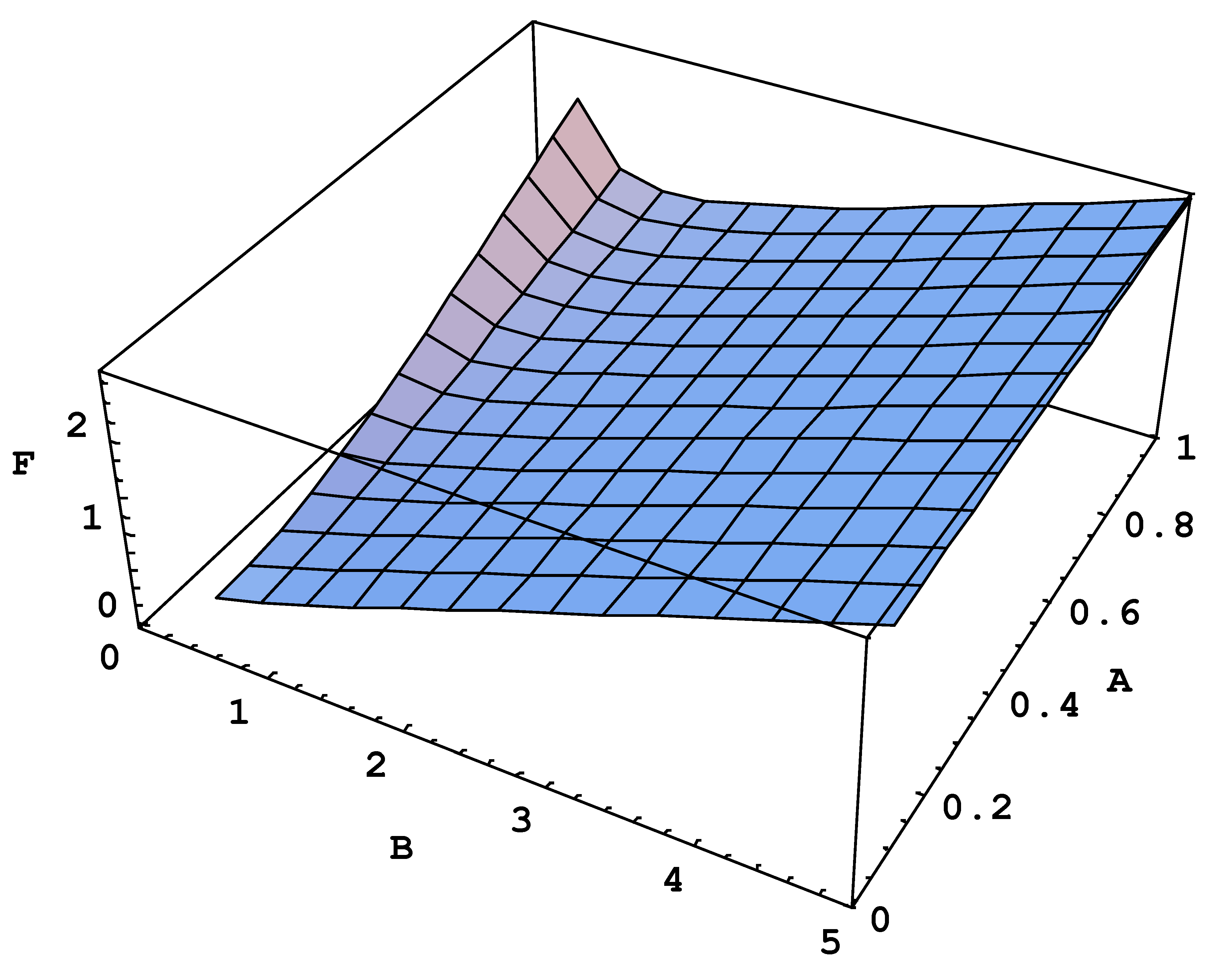
Thus, the dependence of the width w⁽⁰⁾_nl→1s on the scaled dimensionless electron velocity B is given by the function F(A, B). Figure 1 shows a three-dimensional plot of this function.

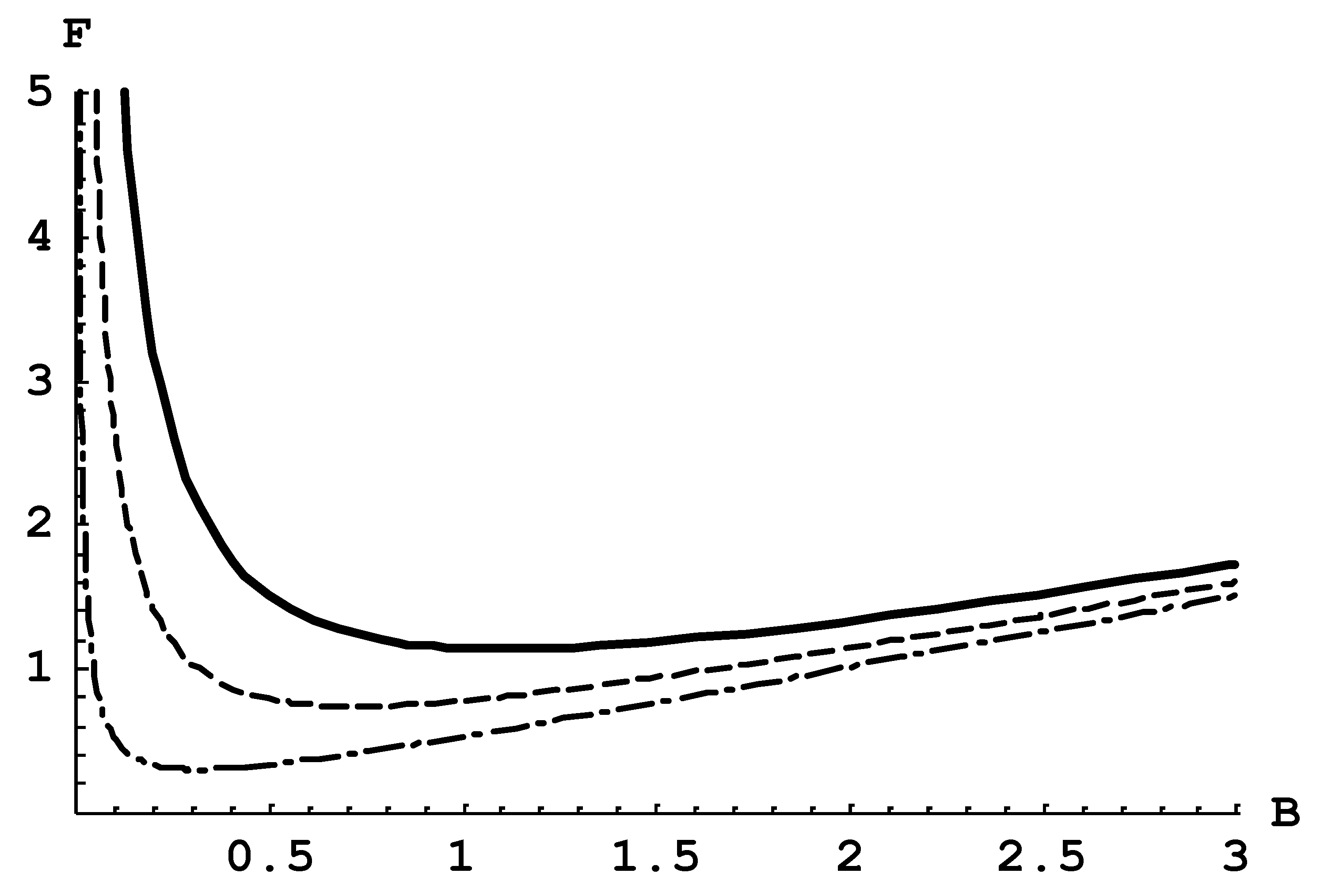
Figure 2 presents the dependence of the function F(A, B) on the scaled dimensionless electron velocity B for three values of the parameter A: A = 1 (solid line), A = 0.6 (dashed line), and A = 0.3 (dash-dotted line). Both from Figure 1 and Figure 2, it is seen that the width w⁽⁰⁾_nl→1s has a non-monotonic dependence on B. Namely, at relatively small electron velocities, as B increases, the width decreases. Then, it reaches a minimum and (at relatively large electron velocities), as B further increases, the width increases. The non-monotonic dependence of the monopole contribution to the width on the electron velocity is a counter-intuitive result.

For relatively large electron velocities—i.e., when B >> max(A, 1), the integration in Equation (15) becomes trivial and we get F(A, B) = B/2, so that

w⁽⁰⁾_nl→1s = πr_nl²N_ev.

(17)

Physically this means that the corresponding optical cross-section—i.e., the cross-section for the line broadening collisions, becomes equal to the “geometrical” cross section πr_nl².

It is remarkable that, at relatively large electron velocities, the monopole contribution to the width increases with increasing velocity. This is in a striking distinction to the dipole contribution to the width, which decreases as the electron velocity increases.

For thermal velocities of plasma electrons, the parameter B (defined in Equation (13)) does not reach the range of B >> 1. However, there are situations where there is a relativistic electron beam (REB) in a plasma. Some examples are inertial fusion, heating of plasmas by a REB, acceleration of charged particles in plasmas, and generation of high-intensity coherent microwave radiation—see papers [11,12,13] and references therein.

Last but not least: in magnetic fusion research, one has sometimes to deal with a REB developing in the plasma. Namely, in some discharges in tokamaks, due to the phenomenon of runaway electrons, there occurs a decay in the plasma current and is partial replacement by runaway electrons that reach relativistic energies. This situation endangers the performance of the next generation tokamak ITER—see papers [14,15,16] and references therein.

In paper [17], the authors calculated, analytically, the dipole contribution w_d to the Stark width of hydrogenic spectral lines due to a REB. Based on the results of paper [17] it can be estimated as follows:

w_d ~ N_beamc(n²/Z)²λ_Comp²/(1 − 1/γ²)^1/2,  λ_Comp = ħ/(m_ec), γ = 1/(1 − v²/c²)^1/2.

(18)

In Equation (18), N_beam is the REB density, λ_Comp is the Compton wavelength, and γ is the relativistic factor. Using Equations (5), (17) and (18), we can estimate the ratio of the corresponding monopole contribution w_mdue to the REB to w_d as follows:

w_m/w_d ~ (a₀/λ_Comp)²/(1 − 1/γ²)^1/2.

(19)

For an ultra-relativistic REB—i.e., for γ >> 1—Equation (19) simplifies to

w_m/w_d ~ (a₀/λ_Comp)² = (ħc/e²)² ~ 10⁴ >> 1.

(20)

It shows that the monopole contribution to the width due to the REB exceeds the corresponding dipole contribution by four orders of magnitude and practically determines the entire Stark width of hydrogenic spectral lines due to the REB.

3. Conclusions

By using the formalism from paper [8], we studied analytically the monopole contribution to the width of hydrogen-like spectral lines. We demonstrated that the monopole contribution to the width has a non-monotonic dependence on the velocity of perturbing electrons. Namely, at relatively small electron velocities, as the velocity increases, the width decreases. Then, it reaches a minimum and (at relatively large electron velocities), as the velocity further increases, the width increases. The non-monotonic dependence of the monopole contribution to the width on the electron velocity is a counter-intuitive result.

We showed, analytically, that at relatively large electron velocities, the so-called optical cross-section—i.e., the cross-section for the line broadening collisions—becomes equal to the “geometrical” cross section. We underscored that at relatively large electron velocities, the monopole contribution to the width increases with increasing velocity. This is in a striking distinction to the dipole contribution to the width, which decreases as the electron velocity increases.

Finally, we studied the situation, encountered in various areas of plasma research, where there is a relativistic electron beam (REB) in a plasma. We showed that the monopole contribution to the Stark width due to the REB exceeds the corresponding dipole contribution by four orders of magnitude and practically determines the entire Stark width of hydrogenic spectral lines due to the REB.