Structural and Dielectric Impedance Studies of Mixed Ionic–Electronic Conduction in SrLaFe1−xMnxTiO6 (x = 0, 0.33, 0.67, and 1.0) Double Perovskites
Abstract
1. Introduction
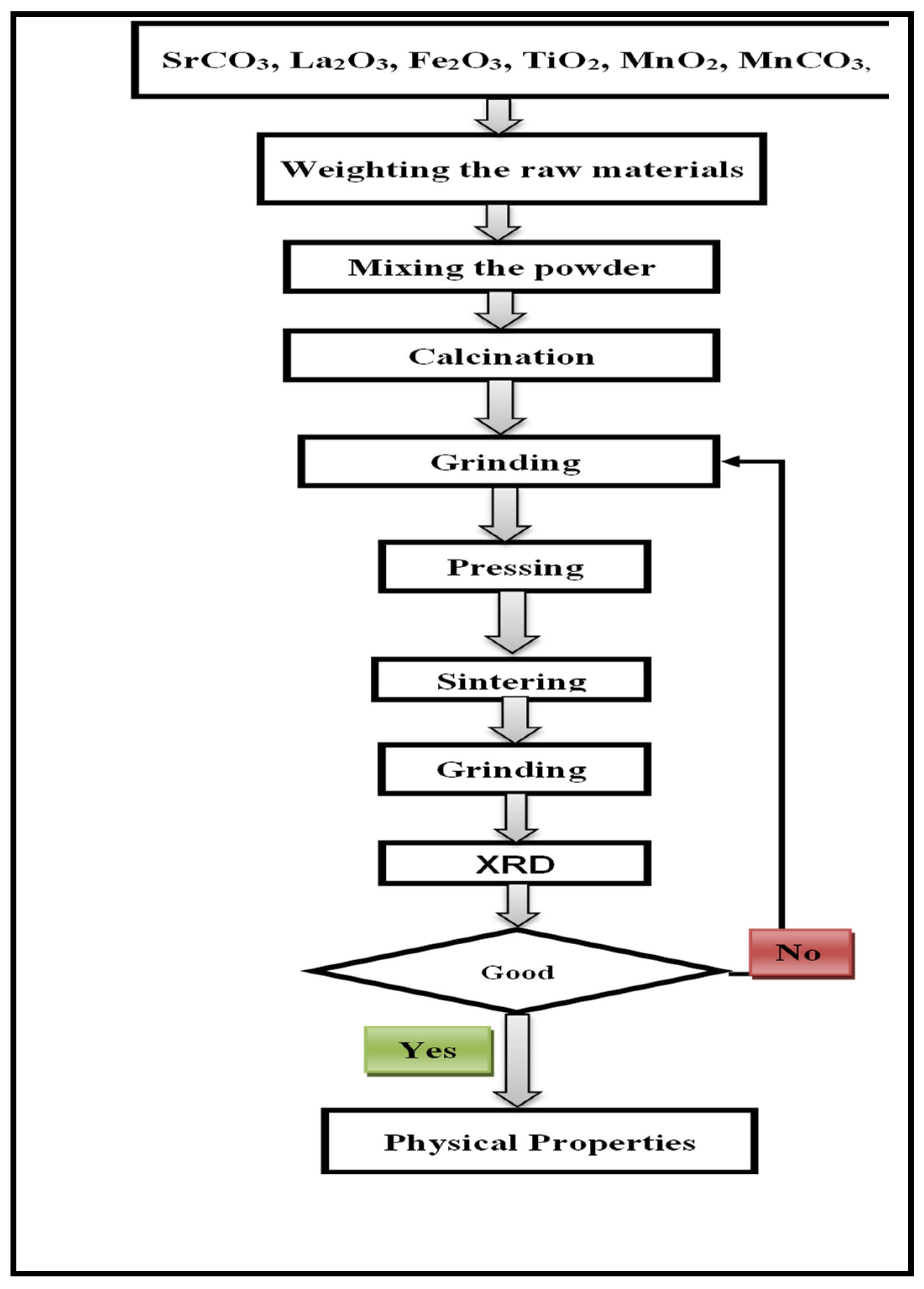
2. Experimental Section
3. Results and Discussion
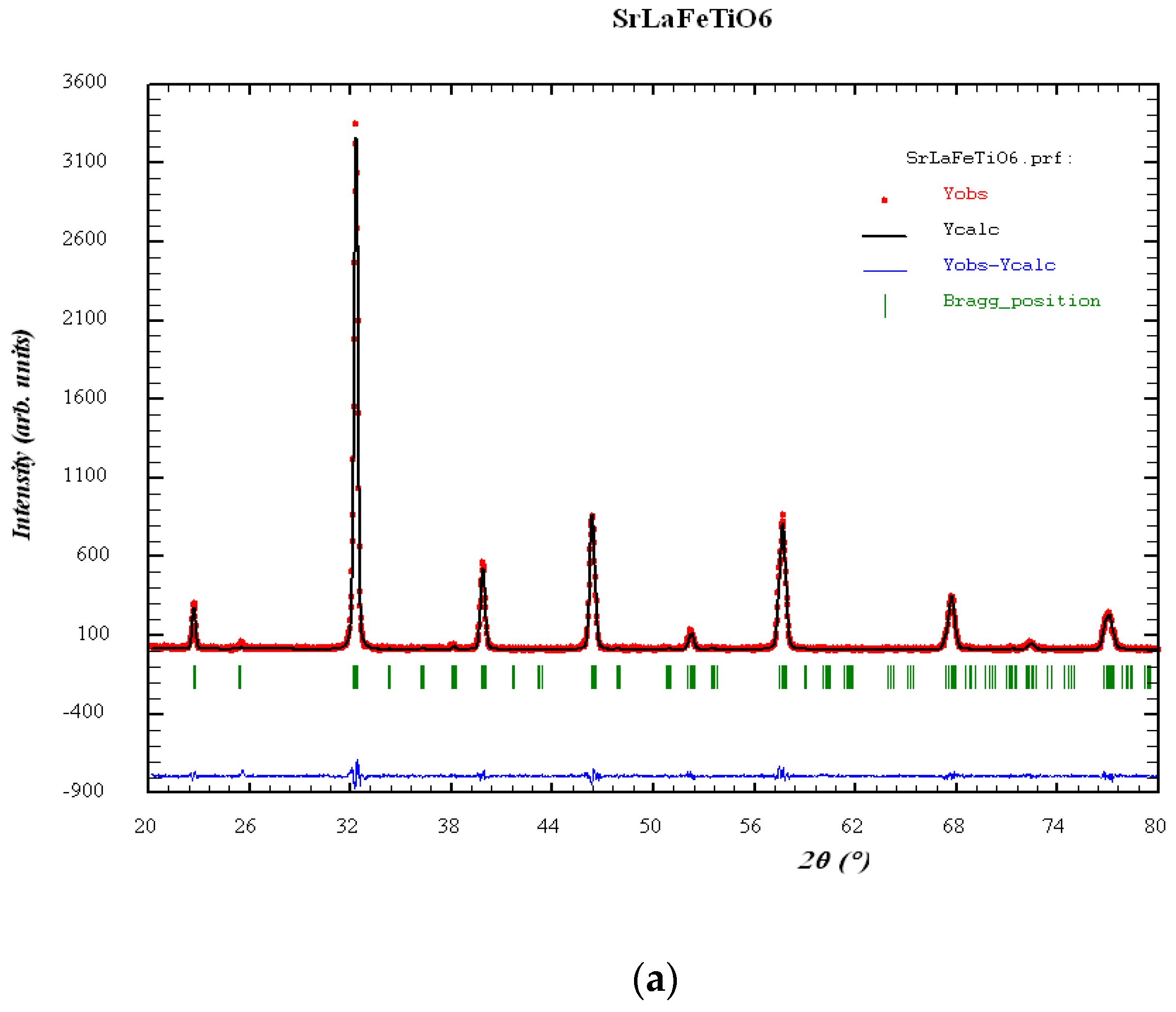
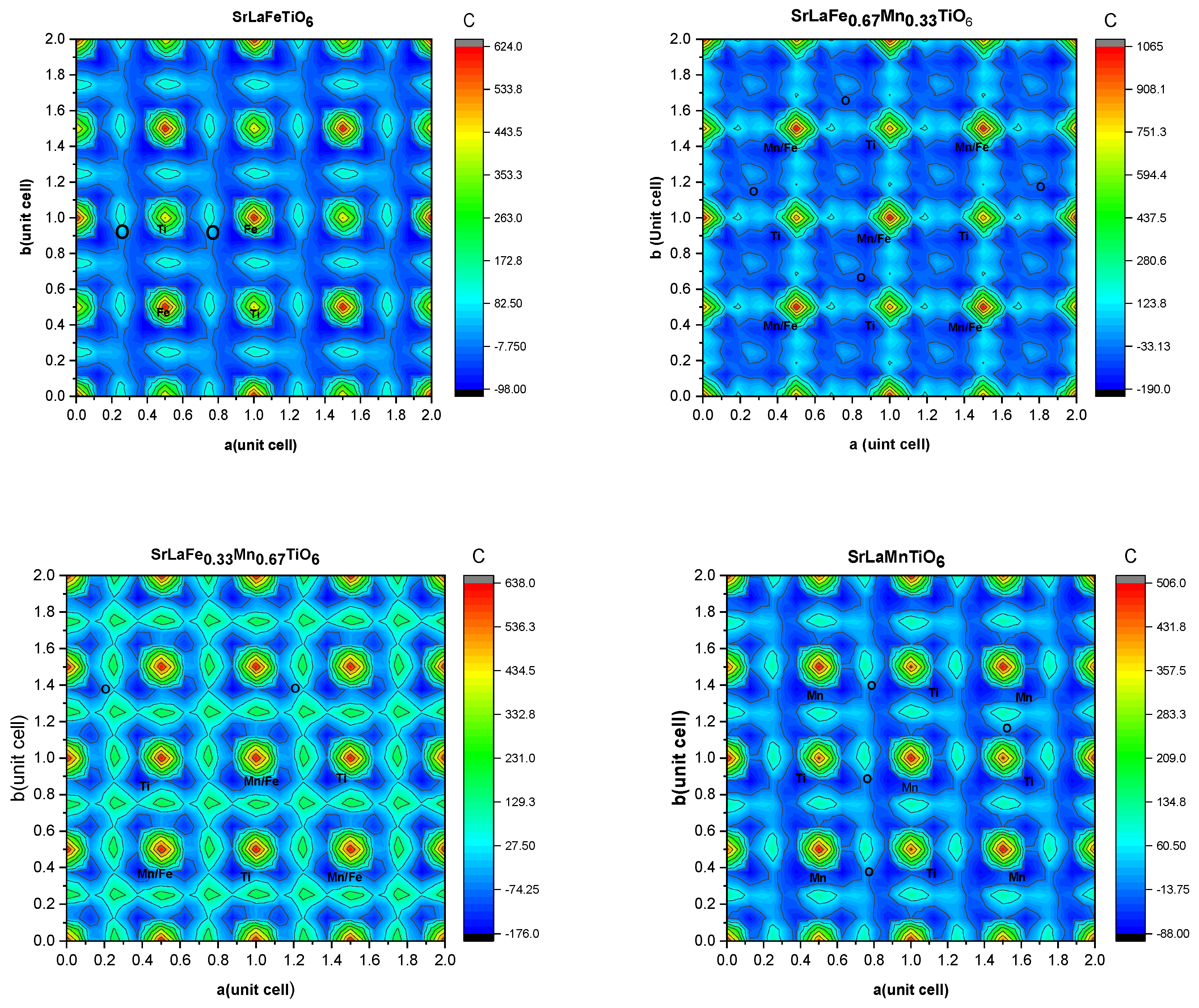
3.1. Structural Characterization and Charge Density Contour Maps
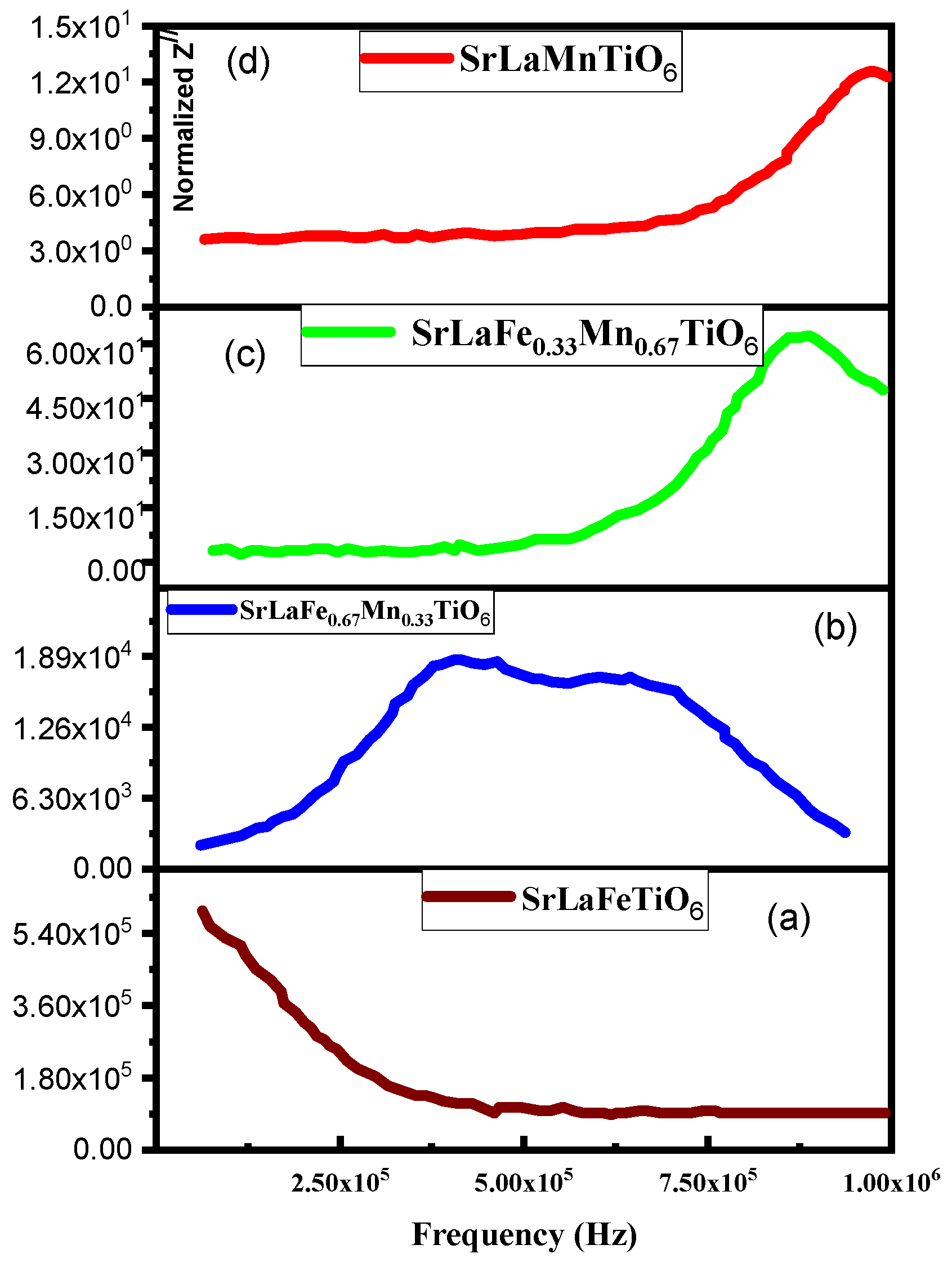
3.2. Frequency Response of Dielectric Impedance
3.3. Equivalent Circuits and Modeling of Impedance Data
3.4. Complex Cole–Cole Representation and Phase Shift
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bibi, B.; Nazar, A.; Zhu, B.; Yang, F.; Yousaf, M.; Raza, R.; Yousaf Shah, M.A.K.; Kim, J.-S.; Afzal, M.; Lei, Y.; et al. Emerging semiconductor ionic materials tailored by mixed ionic-electronic conductors for advanced fuel cells. Adv. Powder Mater. 2024, 3, 100231. [Google Scholar] [CrossRef]
- Mogensen, M.; Lindegaard, T.; Hansen, U.R.; Mogensen, G. Physical properties of mixed conductor solid oxide fuel cell anodes of doped CeO2. J. Electrochem. Soc. 1994, 141, 2122–2128. [Google Scholar] [CrossRef]
- Deronzier, E.; Chartier, T.; Geffroy, P.-M. Oxygen semi-permeation properties of La1−xSrx FeO3−δ perovskite membranes under high oxygen gradient. J. Mater. Res. 2020, 35, 2506–2515. [Google Scholar] [CrossRef]
- Kim, C.S.; Bishop, S.R.; Tuller, H.L. Electro-chemo-mechanical studies of perovskite-structured mixed ionic-electronic conducting SrS1−x FexO3−x/2+δ part II: Electrical conductivity and cathode performance. J. Electroceram. 2018, 40, 57–64. [Google Scholar] [CrossRef]
- Arrive, C.; Delahaye, T.; Joubert, O.; Gauthier, G.H. Study of (La, Sr)(Ti, Ni)O3−δ materials for symmetrical Solid Oxide Cell electrode—Part B: Conditions of Ni exsolution. Ceram. Int. 2020, 46, 5841–5849. [Google Scholar] [CrossRef]
- Liu, S.; Liu, Q.; Luo, J.-L. The excellence of La(Sr)Fe(Ni)O3 as an active and efficient cathode for direct CO2 electrochemical reduction at elevated temperatures. J. Mater. Chem. A 2017, 5, 2673–2680. [Google Scholar] [CrossRef]
- Riess, I. Mixed ionic-electronic conductors-material properties and applications. Solid State Ion. 2003, 157, 1–17. [Google Scholar] [CrossRef]
- Wolf, S.E.; Winterhalder, F.E.; Vibhu, V.; de Haart, L.B.; Guillon, O.; Eichel, R.A.; Menzler, N.H. Solid oxide electrolysis cells—Current material development and industrial application. Matter Chem. A 2023, 11, 17977–18028. [Google Scholar] [CrossRef]
- Pockett, A.; Carnie, M.J. Ionic Influences on Recombination in Perovskite Solar Cells. ACS Energy Lett. 2017, 2, 1683–1689. [Google Scholar] [CrossRef]
- Senocrate, A.; Maier, J. Solid-State Ionics of Hybrid Halide Perovskites. J. Am. Chem. Soc. 2019, 141, 8382–8396. [Google Scholar] [CrossRef]
- Vadhva, P.; Hu, J.; Johnson, M.J.; Stocker, R.; Braglia, M.; Brett, D.J.; Rettie, A.J. Electrochemical Impedance Spectroscopy for All-Solid-State Batteries: Theory, Methods and Future Outlook. ChemElectroChem 2021, 8, 1930–1947. [Google Scholar] [CrossRef]
- Mahato, N.; Banerjee, A.; Gupta, A.; Omar, S.; Balani, K. Progress in material selection for solid oxide fuel cell technology: A review. Prog. Mater. Sci. 2015, 72, 141–337. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Z.; Zhang, L.; Luo, Z.; Shen, J.; Lin, H.; Long, J.; Wu, J.C.; Fu, X.; Wang, X.; et al. Visible-Light Driven Overall Conversion of CO2 and H2O to CH4 and O2 on 3D-SiC@ 2D-MoS2 Heterostructure. J. Am. Chem. Soc. 2018, 140, 14595–14598. [Google Scholar] [CrossRef] [PubMed]
- Hossain, S.; Abdalla, A.M.; Jamain, S.N.B.; Zaini, J.H.; Azad, A.K. A review on proton conducting electrolytes for clean energy and intermediate temperature-solid oxide fuel cells. Renew. Sustain. Energy Rev. 2017, 79, 750–764. [Google Scholar] [CrossRef]
- Jia, H.; Zhou, W.; Duan, S.; Nan, H.; Luo, F.; Zhu, D. DC conductivity and AC impedance of Mn doped magnesia alumina spinel (MgAl2−2xMn2xO4) over a large temperature range. J. Eur. Ceram. Soc. 2018, 39, 1251–1256. [Google Scholar] [CrossRef]
- Satapathy, A.; Sinha, E. A comparative proton conductivity study on Yb-doped BaZrO3 perovskite at intermediate temperatures under wet N2 environment. J. Alloys Compd. 2019, 772, 675–682. [Google Scholar] [CrossRef]
- Jasinski, P.; Petrovsky, V.; Suzuki, T.; Anderson, H.U. Impedance studies of diffusion phenomena and ionic and electronic conductivity of cerium oxide. J. Electrochem. Soc. 2005, 152, J27–J32. [Google Scholar] [CrossRef]
- Bashir, J.; Shaheen, R. Structural and complex AC impedance spectroscopic studies of A2CoNbO6 (A= Sr, Ba) ordered double perovskites. Solid State Sci. 2011, 13, 993–999. [Google Scholar] [CrossRef]
- Xia, T.; Liu, X.; Li, Q.; Meng, J.; Cao, X. Synthesis, structural and electrical characterizations of Sr2Fe1−xMxNbO6 (M = Zn and Cu) with double perovskite structure. J. Alloys Compd. 2006, 422, 264–272. [Google Scholar] [CrossRef]
- Liu, Q.; Dong, X.; Xiao, G.; Zhao, F.; Chen, F. A novel electrode material for symmetrical SOFCs. Adv. Mater. 2010, 22, 5478–5482. [Google Scholar] [CrossRef]
- Marrero-López, D.; Peña-Martínez, J.; Ruiz-Morales, J.; Martín-Sedeño, M.; Núñez, P. High temperature phase transition in SOFC anodes based on Sr2MgMoO6−δ. J. Solid State Chem. 2009, 182, 1027–1034. [Google Scholar] [CrossRef]
- Kalanda, N.; Kim, D.H.; Demyanov, S.; Yu, S.C.; Yarmolich, M.; Petrov, A.; Oh, S.K. Sr2FeMoO6 nanosized compound with dielectric sheaths for magnetically sensitive spintronic devices. Curr. Appl. Phys. 2018, 18, 27–33. [Google Scholar] [CrossRef]
- Jung, W.; Tuller, H.L. Impedance study of SrTi1−xFexO3−δ (x = 0.05 to 0.80) mixed ionic-electronic conducting model cathode. Solid State Ion. 2009, 180, 843–847. [Google Scholar] [CrossRef]
- Álvarez-Serrano, I.; de Larramendi, I.R.; López, M.; Pico, C.; Rojo, T.; Veiga, M. Oriented nanocrystals in SrLaMnTiO6 perovskite thin films grown by pulsed laser deposition. J. Alloys Compd. 2011, 509, 1457–1462. [Google Scholar] [CrossRef]
- Baumann, F.S.; Fleig, J.; Habermeier, H.-U.; Maier, J. Impedance spectroscopic study on well-defined (La, Sr)(Co, Fe)O3−δ model electrodes. Solid State Ion. 2006, 177, 1071–1081. [Google Scholar] [CrossRef]
- El Hachmi, A.; Tamraoui, Y.; Manoun, B.; Haloui, R.; Elaamrani, M.A.; Saadoune, I.; Bih, L.; Lazor, P. Synthesis and Rietveld refinements of new ceramics Sr2CaFe2WO9 and Sr2PbFe2TeO9 perovskites. Powder Diffr. 2018, 33, 134–140. [Google Scholar] [CrossRef]
- Correia, V.; Mitra, K.Y.; Castro, H.; Rocha, J.G.; Sowade, E.; Baumann, R.R.; Lanceros-Méndez, S. Design and fabrication of multilayer inkjet-printed passive components for printed electronics circuit development. J. Manuf. Process. 2018, 31, 364–371. [Google Scholar] [CrossRef]
- Buniatyan, V.; Tsakanov, V.; Martirosyan, N.; Melikyan, G.; Dashtoyan, H. Dielectric Characteristics of Pt/BaxSr1−xTiO3/Pt Thin Film Structure under the Electron Beam Irradiation. Armen. J. Phys. 2016, 9, 138–146. [Google Scholar]
- Ashfaq, A.; Almufarij, R.S.; Ali, M.Y.; Ali, A.; Tahir, S.; Sabugaa, M.M.; Fahmy, M.A.; Shokralla, E.A.; Ragab, A.H.; El-Refaey, D.E.; et al. High thermoelectric power factor of n-type Bi2 (Se, S) via synergetic influence on the charge carrier concentration and energy filtering effect. Int. Commun. Heat Mass Transf. 2023, 146, 106870. [Google Scholar] [CrossRef]
- Bondarenko, A.S. Analysis of large experimental datasets in electrochemical impedance spectroscopy. Anal. Chim. Acta 2012, 743, 41–50. [Google Scholar] [CrossRef]
- Albrecht, E.; Siponkoski, T.; Rautama, E.; Karppinen, M.; Karttunen, A. Centrosymmetric to non-centrosymmetric transition in the Ca2-xMnxTi2O6 double perovskite system studied through structural analysis and dielectric properties. Dalton Trans. 2024, 53, 6282–6288. [Google Scholar] [CrossRef]
- Zaraq, A.; Orayech, B.; Igartua, J.; Bouari, E.; Gregory, D.; Gesing, T. Crystallography at non-ambient conditions and physical properties of the synthesized double perovskites, Sr2(Co1−xFex)TeO6. Dalton Trans. 2023, 52, 4086–4102. [Google Scholar] [CrossRef] [PubMed]
- Haneef, M.; Almufarij, R.S.; Tahir, S.; Gazo-Hanna, E.; Arayro, J.; Shokralla, E.A.; Alrefaee, S.H.; Fahmy, M.A.; Macadangdang, R.R., Jr.; Ashfaq, A. Optimization of a novel lead-free MASiI3 based perovskite solar cell: A comprehensive study on device performance enhancement. Results Eng. 2024, 23, 102809. [Google Scholar] [CrossRef]
- Szczodrowski, K.; Behrendt, M.; Barzowska, J.; Górecka, N.; Majewska, N.; Leśniewski, T.; Łapiński, M.; Mahlik, S. Lanthanide ions (Eu3+, Er3+, Pr3+) as luminescence and charge carrier centers in Sr2TiO4. Dalton Trans. 2023, 52, 4329–4335. [Google Scholar] [CrossRef]
- Song, B.; Shen, J.; Zhao, H.; Kumar, A.; Xu, Q.; Zhai, Y.; Li, Q. A new room-temperature multiferroic material: Y2FeAlO6. Ceram. Int. 2021, 47, 10873–10879. [Google Scholar] [CrossRef]
- Uvarov, V. The influence of X-ray diffraction pattern angular range on Rietveld refinement results used for quantitative analysis, crystallite size calculation and unit-cell parameter refinement. J. Appl. Crystallogr. 2019, 52, 252–261. [Google Scholar] [CrossRef]
- Gómez-Peralta, J.; Bokhimi, X.; Quintana, P. Convolutional Neural Networks to Assist the Assessment of Lattice Parameters from X-ray Powder Diffraction. J. Phys. Chem. A 2023, 127, 7655–7664. [Google Scholar] [CrossRef]
- Sullivan, B.; Archibald, R.; Langan, P.; Dobbek, H.; Bommer, M.; McFeeters, R.; Coates, L.; Wang, X.; Gallmeier, F.; Carpenter, J.; et al. Improving the accuracy and resolution of neutron crystallographic data by three-dimensional profile fitting of Bragg peaks in reciprocal space. Struct. Biol. 2018, 74, 1085–1095. [Google Scholar] [CrossRef]
- Rai, A.; Thakur, A. Co-substitution tailored dielectric relaxation and electrical conduction in lanthanum orthoferrite. Ceram. Int. 2020, 46, 22752–22765. [Google Scholar] [CrossRef]
- Tripathy, A.; Das, S.N.; Bhuyan, S.; Choudhary, R.N.P. Structural and dielectric properties of double perovskite lead free BiGdMnNiO6 electronic system. Mater. Tody Proc. 2021, 35 Pt 2, 109–111. [Google Scholar] [CrossRef]
- Burnat, D.; Nasdaurk, G.; Holzer, L.; Kopecki, M.; Heel, A. Lanthanum doped strontium titanate-ceria anodes: Deconvolution of impedance spectra and relationship with composition and microstructure. J. Power Sources 2018, 385, 62–75. [Google Scholar] [CrossRef]
- Gajula, G.R.; Kumar, K.C.; Buddiga, L.R.; Nethala, G.P. Dielectric and impedance properties of Li0.5Fe2.5O4 doped BaTiO3 composite ceramics. Results Phys. 2018, 11, 899–904. [Google Scholar] [CrossRef]
- Zawar, S.; Atiq, S.; Tabasum, M.; Riaz, S.; Naseem, S. Highly stable dielectric frequency response of chemically synthesized Mn-substituted ZnFe2O4. J. Saudi Chem. Soc. 2019, 23, 417–426. [Google Scholar] [CrossRef]
- Dhahri, A.; Dhahri, E.; Hlil, E.K. Electrical conductivity and dielectric behaviour ofnanocrystalline La0.6Gd0.1Sr0.3Mn0.75Si0.25O3. RSC Adv. 2018, 8, 9103–9111. [Google Scholar] [CrossRef]
- Maity, S.K.; Dutta, A.; Kumar, S.; Sinha, T. Electrical properties of Ba2YbNbO6: An impedance spectroscopy study. Phys. Scr. 2013, 88, 065702. [Google Scholar] [CrossRef]
- Almufarij, R.S.; Jamil, M.; Alsubhe, E.; Alghamdi, S.M.; Shokralla, E.A.; Khan, K.M.; Ashfaq, A.; Ali, A.; Jafri, S.A.A.; Khan, M.S. Enhancing solar cell efficiency through tandem structures utilizing lead-free mixed cation perovskites and CZTSe absorber layers. Chem. Phys. Impact 2024, 8, 100562. [Google Scholar] [CrossRef]
- Feng, W.; Zhao, Y.; Xia, Y. Solid interface of garnet electrolytes. Adv. Mater. 2024, 15, 2306111. [Google Scholar] [CrossRef]
- Jamnik, J.; Maier, J. Generalised equivalent circuits for mass and charge transport: Chemical capacitance and its implications. Phys. Chem. Chem. Phys. 2001, 3, 1668–1678. [Google Scholar] [CrossRef]
- Reddy, M.V.; Julien, C.M.; Mauger, A.; Zaghib, K. Sulfide and oxide inorganic solid electrolytes for all-solid-state li batteries: A review. Nanomaterials 2020, 10, 1606. [Google Scholar] [CrossRef]
- Abitonze, M.; Diko, C.S.; Zhu, Y.; Yang, Y. Recent progress on inorganic composite electrolytes for all-solid-state lithium batteries. MRS Energy Sustain. 2024, 11, 219–266. [Google Scholar] [CrossRef]
- Lasia, A. The Oregine of the CPE. J. Phys. Chem. Lett. 2022, 13, 589. [Google Scholar] [CrossRef]
- Dizon, A.; Orazem, M.E. On the impedance response of interdigitated electrodes. Electrochim. Acta 2019, 327, 135000. [Google Scholar] [CrossRef]
- Yang, E.-H.; Noh, Y.-S.; Ramesh, S.; Lim, S.S.; Moon, D.J. The effect of promoters in La0.9M0.1Ni0.5Fe0.5O3 (M = Sr, Ca) perovskite catalysts on dry reforming of methane. Fuel Process. Technol. 2015, 134, 404–413. [Google Scholar] [CrossRef]
- Wang, C.; Shi, Z.; Wang, Y.; Peng, G.; Luo, W.; Xiao, M.; Xing, W.; Sang, G.; Liu, C. Ruthenium Phosphide Nanoclusters Dispersed on Zeolitic Imidazolate Framework-8 and Encapsulated in N,P-Codoped Carbon as Electrocatalysts for the Hydrogen Evolution Reaction. ACS Appl. Nano Mater. 2024, 7, 25335–25344. [Google Scholar] [CrossRef]
- Huang, V.M.-W.; Vivier, V.; Orazem, M.E.; Pébère, N.; Tribollet, B. The apparent constant-phase-element behavior of an ideally polarized blocking electrode a global and local impedance analysis. J. Electrochem. Soc. 2007, 154, C81–C88. [Google Scholar] [CrossRef]
- Medvedkin, G.A.; Ishibashi, T.; Nishi, T.; Hayata, K.; Hasegawa, Y.; Sato, K. Room temperature ferromagnetism in novel diluted magnetic semiconductor Cd1−xMnxGeP2. Jpn. J. Appl. Phys. 2000, 39, L949. [Google Scholar] [CrossRef]
- Gul, I.; Maqsood, A. Structural, magnetic and electrical properties of cobalt ferrites prepared by the sol-gel route. J. Alloys Compd. 2008, 465, 227–231. [Google Scholar] [CrossRef]
- Shang, P.-P.; Zhang, B.-P.; Liu, Y.; Li, J.-F.; Zhus, H.-M. Preparation and Thermoelectric Properties of La-Doped SrTiO3 Ceramics. J. Electron. Mater. 2011, 40, 926–931. [Google Scholar] [CrossRef]
- Qin, M.; Lou, Z.; Shi, Z.; Zhang, R.; Xu, J.; Gao, F. Enhanced thermoelectric properties of Sr0.9La0.1TiO3 Ceramics fabricated by SPS with nanosized Ti addition. J. Mater. Sci. Mater. Electron. 2020, 31, 6919–6926. [Google Scholar] [CrossRef]
- Wang, H.; Su, W.; Liu, J.; Wang, C. Recent development of n-type perovskite thermoelectrics. J. Mater. 2016, 2, 225e236. [Google Scholar] [CrossRef]



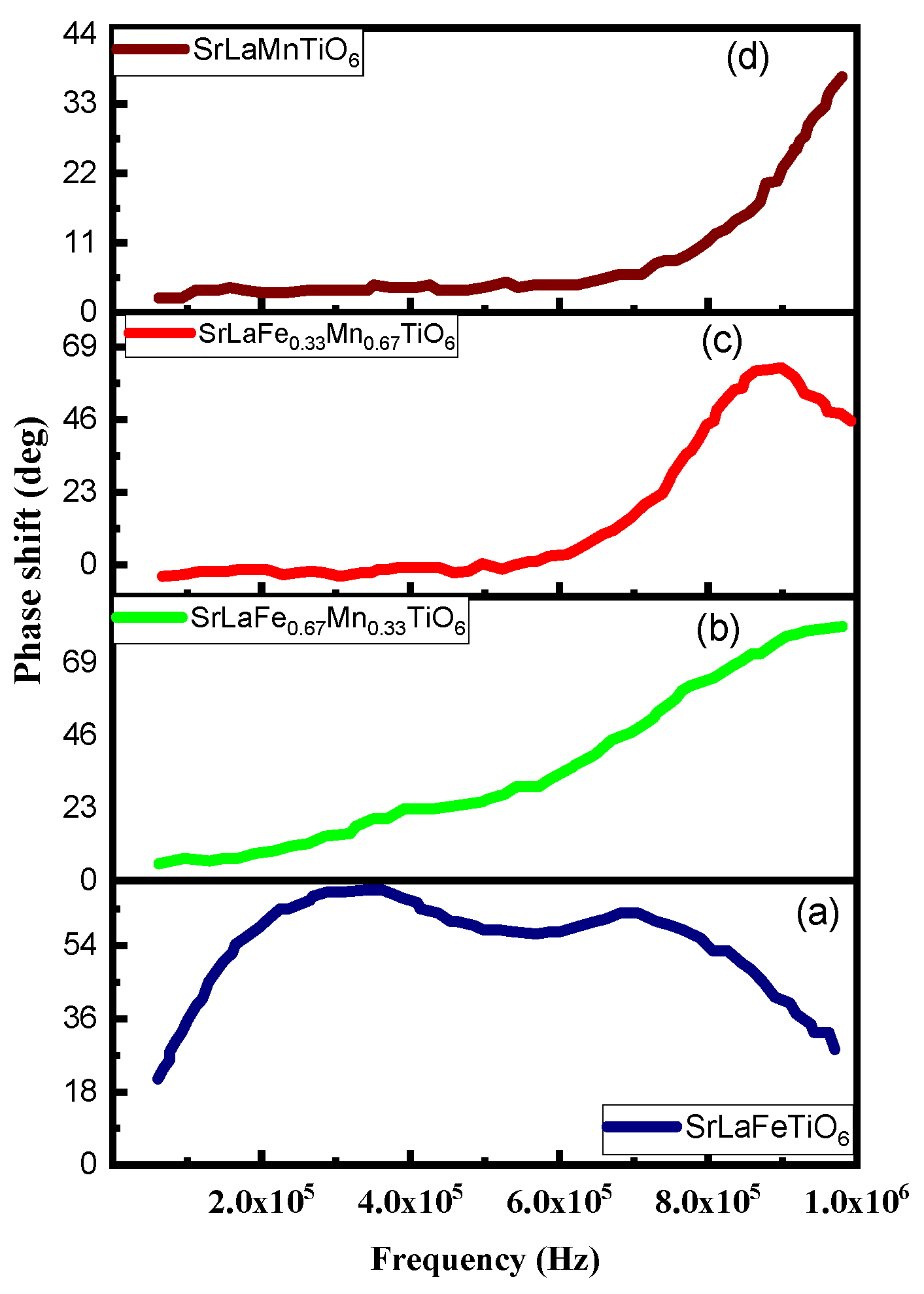


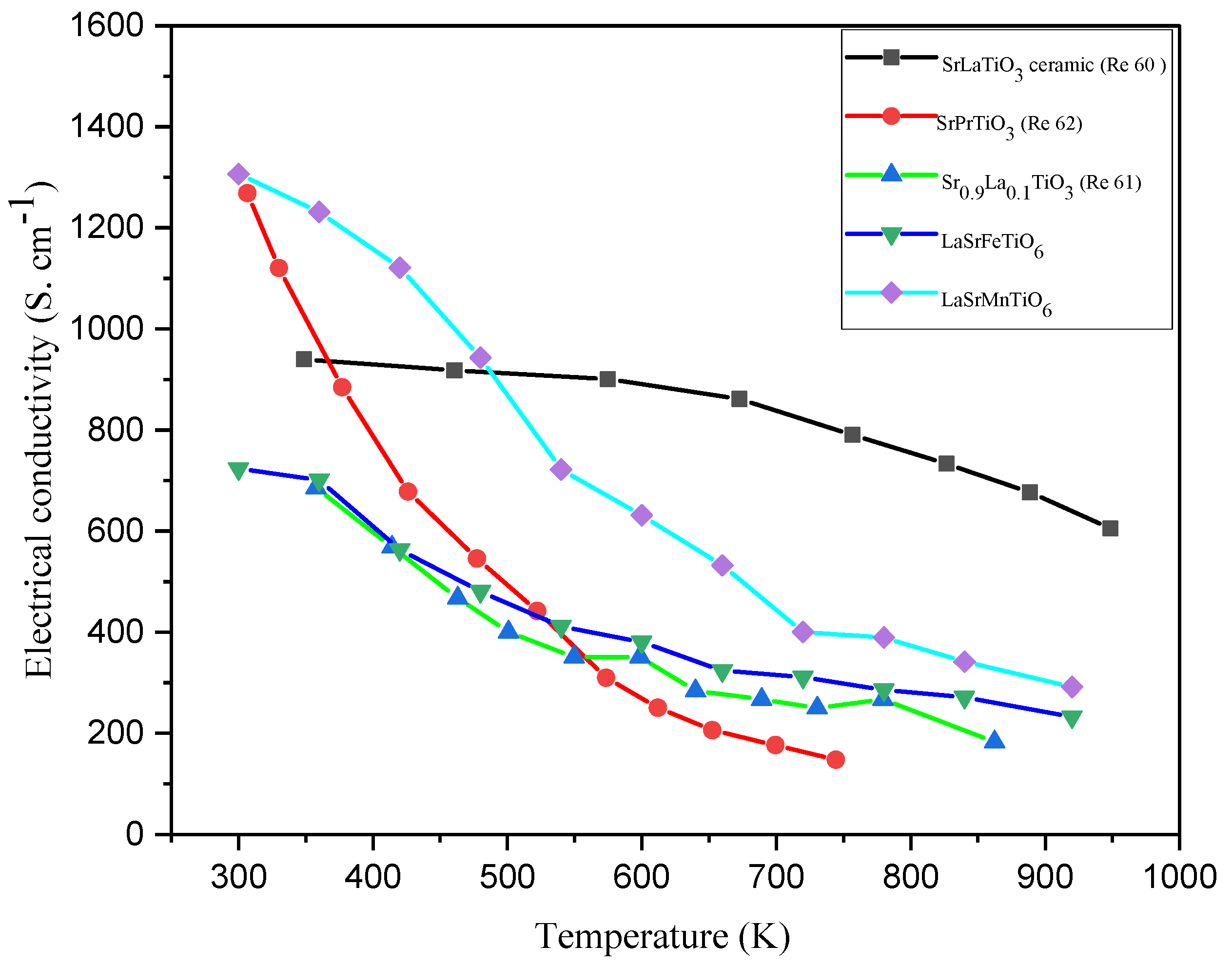
| Powder | LaSrFeTiO6 | LaSrMnTiO6 | LaSrFe0.67 Mn0.33TiO6 | LaSrFe0.33 Mn0.67TiO6 |
|---|---|---|---|---|
| Published density | 6.5 g/cm3. | 6.3 g/cm3 | 5.4 g/cm3 | 5.38g/cm3 |
| Experimental density | 6.4 g/cm3 | 6.1 g/cm3 | 5.64 sg/cm3 | 5.42g/cm3 |
| Elements | Coordinates | SrLaFeTiO6 | SrLaFe0.67Mn0.33TiO6 | SrLaFe0.33Mn0.67TiO6 | SrLaMnTiO6 |
|---|---|---|---|---|---|
| Pnma | Fm3m | Fm3m | I/4m | ||
| Sr/La | X | 0.01016 ± 0.00008 | 0.25000 ± 0.00001 | 0.25000 ± 0.00002 | 0.00000 |
| Y | 0.25000 ± 0.00003 | 0.25000 ± 0.00004 | 0.25000 ± 0.00003 | 0.50000 ± 0.00006 | |
| Z | 0.00795 ± 0.00005 | 0.25000 ± 0.00002 | 0.25000 ± 0.00001 | 0.25000 ± 0.00003 | |
| Fe/Mn | X | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| Y | 0.00000 | 0.00000 | 0.00000 | 0.00000 | |
| Z | 0.50000 ± 0.00004 | 0.00000 | 0.00000 | 0.00000 | |
| Ti | X | 0.00000 | 0.50000 ± 0.00002 | 0.50000 ± 0.00003 | 0.50000 ± 0.00004 |
| Y | 0.00000 | 0.50000 ± 0.00004 | 0.50000 ± 0.00001 | 0.50000 ± 0.00003 | |
| Z | 0.50000 ± 0.00003 | 0.50000 ± 0.00005 | 0.50000 ± 0.00001 | 0.00000 | |
| O1 | X | −0.00176 ± 0.00025 | 0.24900 ± 0.00021 | 0.26846 ± 0.00012 | 0.00000 |
| Y | 0.25000 ± 0.00001 | 0.00000 | 0.00000 | 0.00000 | |
| Z | 0.52003 ± 0.00002 | 0.00000 | 0.00000 | 0.24503 ± 0.00011 | |
| O2 | X | 0.25942 ± 0.00031 | - | - | 0.24174 ± 0.00051 |
| Y | −0.01639 ± 0.00025 | - | - | 0.30077 ± 0.00034 | |
| Z | 0.26433 ± 0.00011 | - | - | 0.00000 | |
| a (Å) | 5.55765 ± 0.00006 | 7.81499 ± 0.00007 | 7.81934 ± 0.00007 | 5.51964 ± 0.00006 | |
| b (Å) | 7.82408 ± 0.00007 | - | - | - | |
| c (Å) | 5.53766 ± 0.00004 | - | - | 7.80438 ± 0.00007 | |
| RWP | 2.4 | 3.52 | 5.08 | 3.83 | |
| RP | 3.61 | 3.15 | 3.71 | 4.9 | |
| Constant Phase Element | Parameters | SrLaFeTiO6 | SrLaFe0.67Mn0.33TiO6 | SrLaFe0.33Mn0.67TiO6 | SrLaMnTiO6 |
|---|---|---|---|---|---|
| Grain (R1 + CPE1) | R1 (Ω) | 3248.900 | 5390.100 | 8.990 | 37.024 |
| P1 × 10−9 | 10.160 | 0.610 | - | - | |
| n1 | 0.950 | 0.940 | - | - | |
| C1 (nF) | 5.90 | 0.270 | - | - | |
| τ1 (Sec) | 19.17 × 10−6 | 14.55 × 10−7 | - | - | |
| Grain boundary (R2 + CPE2) | R2 (Ω) | 1.22 × 106 | 43,055 | 125.700 | - |
| P2 × 10−9 | 9.450 | 17.450 | 1.100 | - | |
| n2 | 0.920 | 0.810 | 0.920 | - | |
| C2 (nF) | 6.410 | 3.230 | 0.250 | - | |
| τ2 (Sec) | 7.82 × 10−3 | 13.91 × 10−5 | 31.43 × 10−9 | - | |
| Electrode (R3 + CPE3) | R3 (Ω) | 95.680 | 26,198 | 138.99 | 456.140 |
| P3 × 10−9 | 0.570 | 0.720 | 0.001 | 0.001 | |
| n3 | 0.960 | 0.910 | 0.087 | 0.158 | |
| C3 (nF) | 0.280 | 0.250 | 0.006 | 190.930 | |
| τ3 (Sec) | 26.79 × 10−9 | 65.50 × 10−7 | 8.33 × 10−10 | 87.09 × 10−6 | |
| Wsr2 | 1.87 × 105 | 2.0 × 10−14 | 2.0 × 10−12 | - | |
| Ws1 | 10.460 | 9.740 | - | - | |
| Celec (nF) | - | - | 1786.2 | 37.020 | |
| Electronic resistance | Re (Ω) | - | - | 6.22 | 5.580 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elbadawi, A.A.; Shokralla, E.A.; Siddig, M.A.; Algethami, O.A.; Alghamdi, A.A.; Idris, H.H.E. Structural and Dielectric Impedance Studies of Mixed Ionic–Electronic Conduction in SrLaFe1−xMnxTiO6 (x = 0, 0.33, 0.67, and 1.0) Double Perovskites. Ceramics 2025, 8, 87. https://doi.org/10.3390/ceramics8030087
Elbadawi AA, Shokralla EA, Siddig MA, Algethami OA, Alghamdi AA, Idris HHE. Structural and Dielectric Impedance Studies of Mixed Ionic–Electronic Conduction in SrLaFe1−xMnxTiO6 (x = 0, 0.33, 0.67, and 1.0) Double Perovskites. Ceramics. 2025; 8(3):87. https://doi.org/10.3390/ceramics8030087
Chicago/Turabian StyleElbadawi, Abdelrahman A., Elsammani A. Shokralla, Mohamed A. Siddig, Obaidallah A. Algethami, Abdullah Ahmed Alghamdi, and Hassan H. E. Idris. 2025. "Structural and Dielectric Impedance Studies of Mixed Ionic–Electronic Conduction in SrLaFe1−xMnxTiO6 (x = 0, 0.33, 0.67, and 1.0) Double Perovskites" Ceramics 8, no. 3: 87. https://doi.org/10.3390/ceramics8030087
APA StyleElbadawi, A. A., Shokralla, E. A., Siddig, M. A., Algethami, O. A., Alghamdi, A. A., & Idris, H. H. E. (2025). Structural and Dielectric Impedance Studies of Mixed Ionic–Electronic Conduction in SrLaFe1−xMnxTiO6 (x = 0, 0.33, 0.67, and 1.0) Double Perovskites. Ceramics, 8(3), 87. https://doi.org/10.3390/ceramics8030087










