Oxygen–Ion Conductivity, Dielectric Properties and Spectroscopic Characterization of “Stuffed” Tm2(Ti2−xTmx)O7−x/2 (x = 0, 0.1, 0.18, 0.28, 0.74) Pyrochlores
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
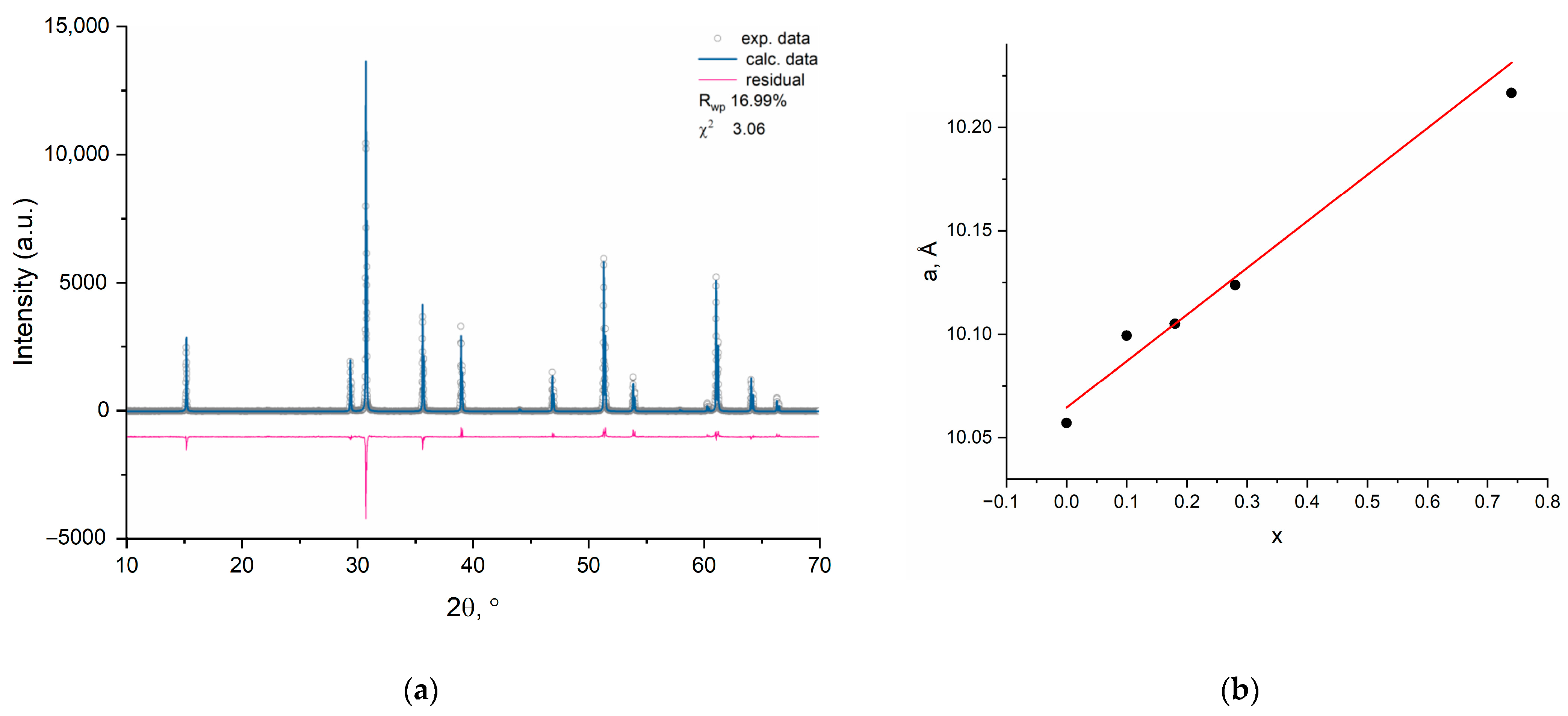
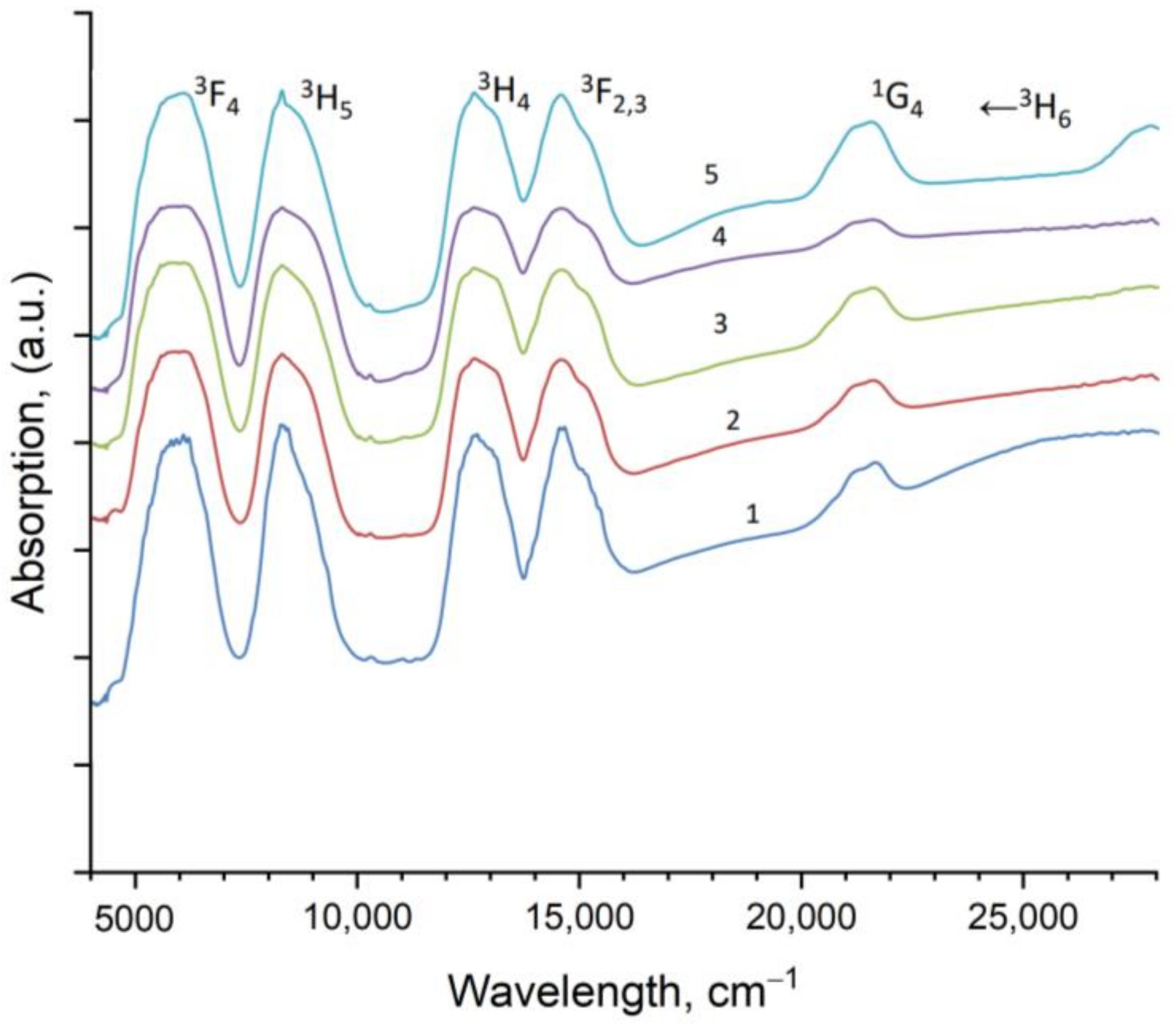
3.1. Structure of the Solid Solutions Studied by XRD and Optical Spectroscopy
- 1.
- Tm2(Ti2−xTmx)O7−x/2 (x = 0.28) as a single-phase titanate pyrochlore and
- 2.
- Tm2(Ti2−xTmx)O7−x/2 (x = 0.28) as a mixture of two (pyrochlore + fluorite) phases.
3.2. Microstructure of the Tm2(Ti2−xTmx)O7−x/2 (x = 0, 0.1, 0.18, 0.28, 0.74) Ceramics
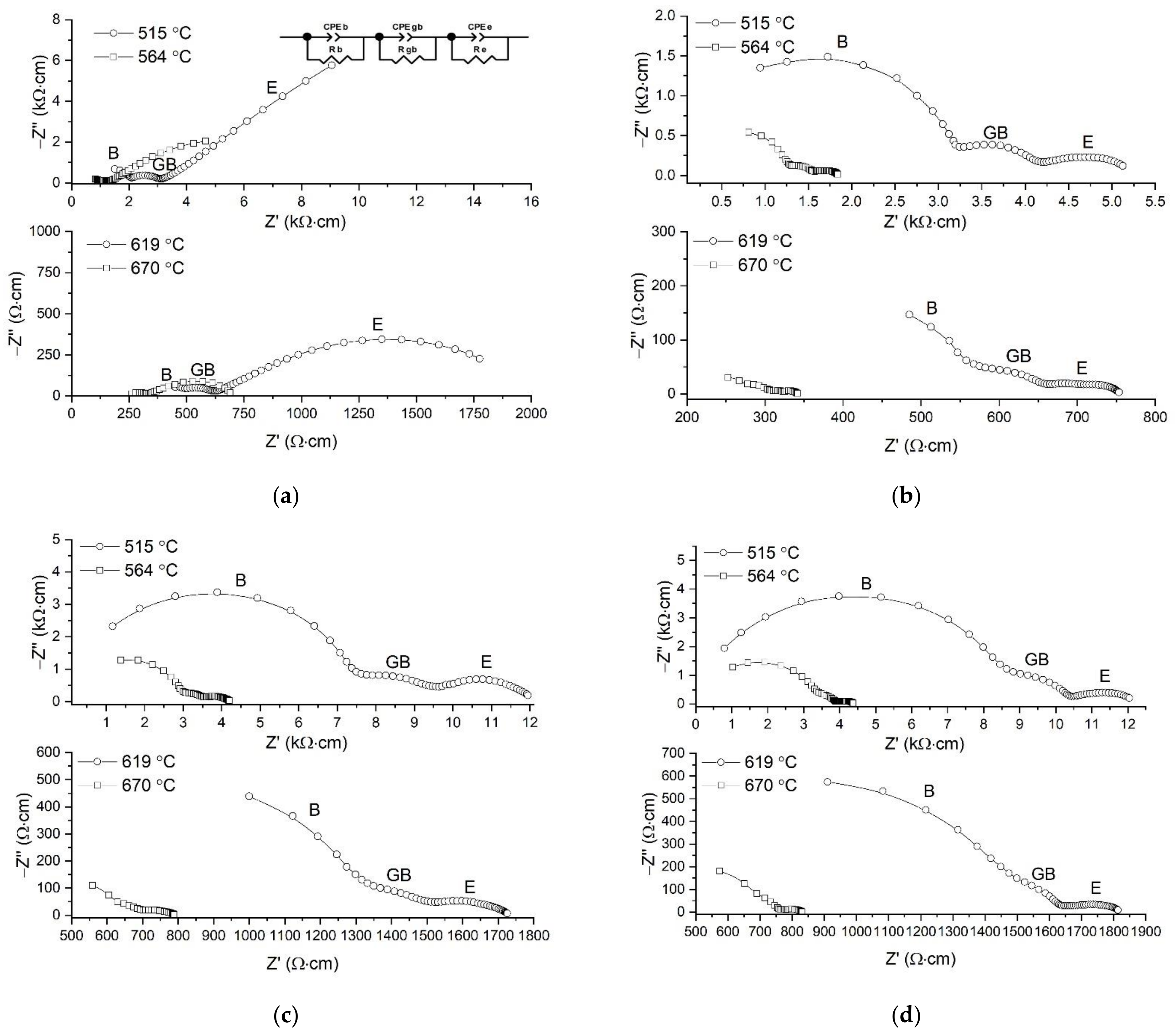
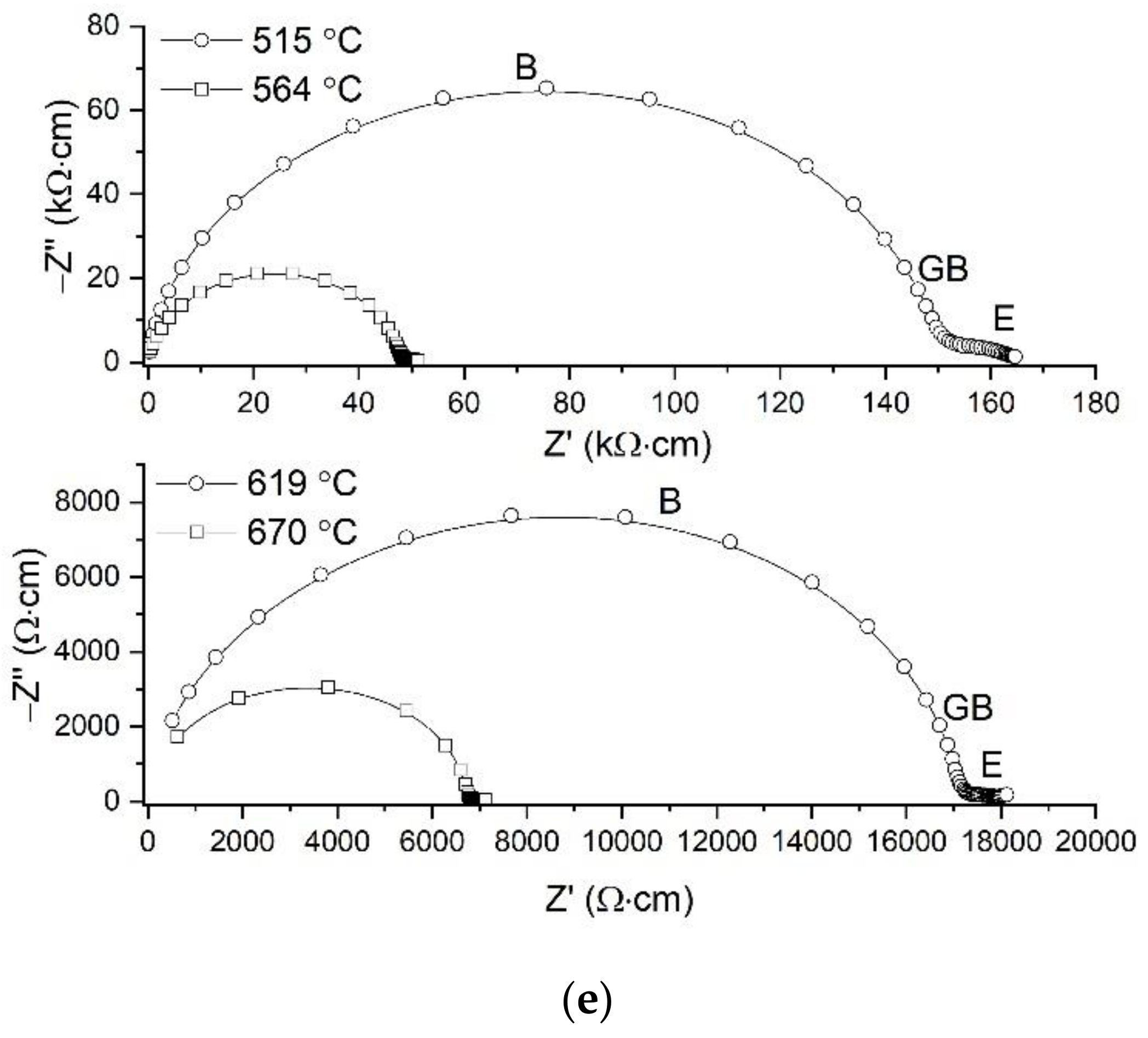
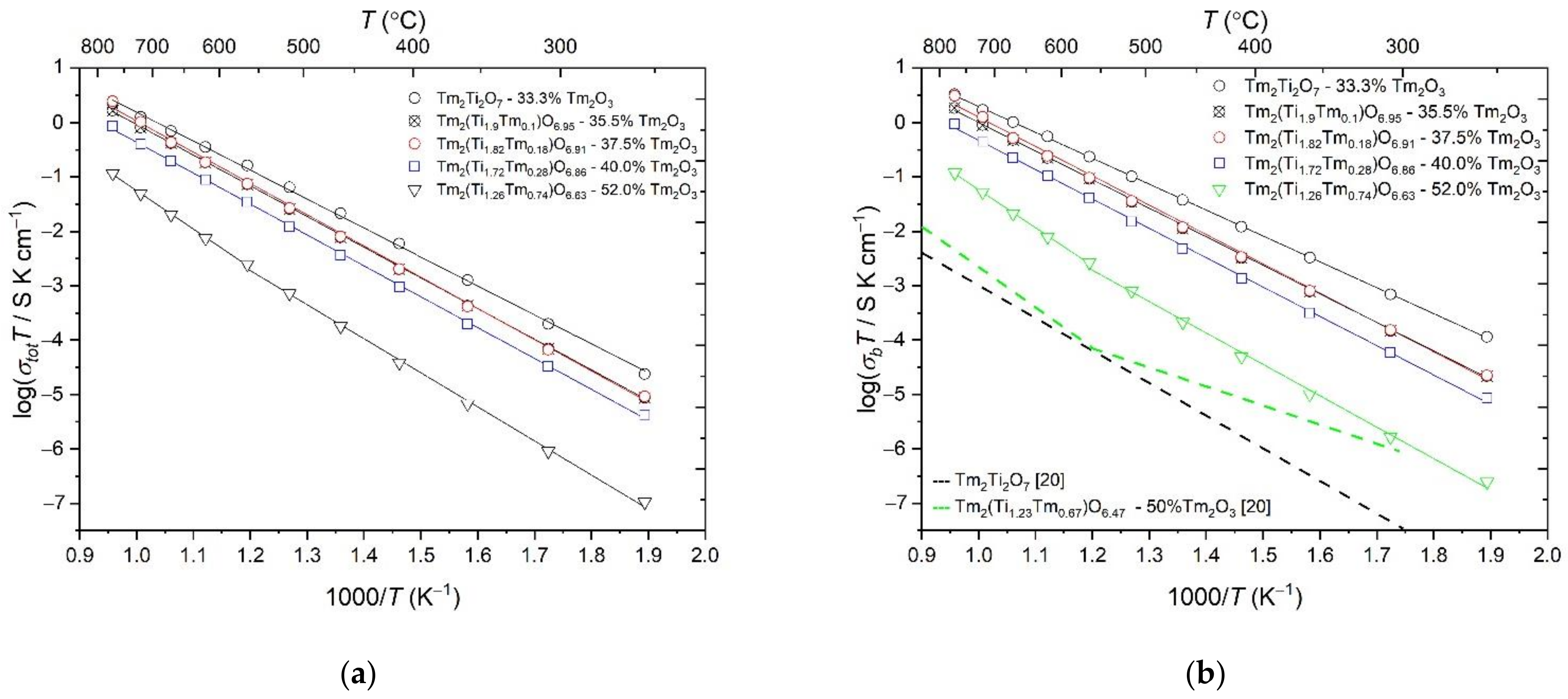
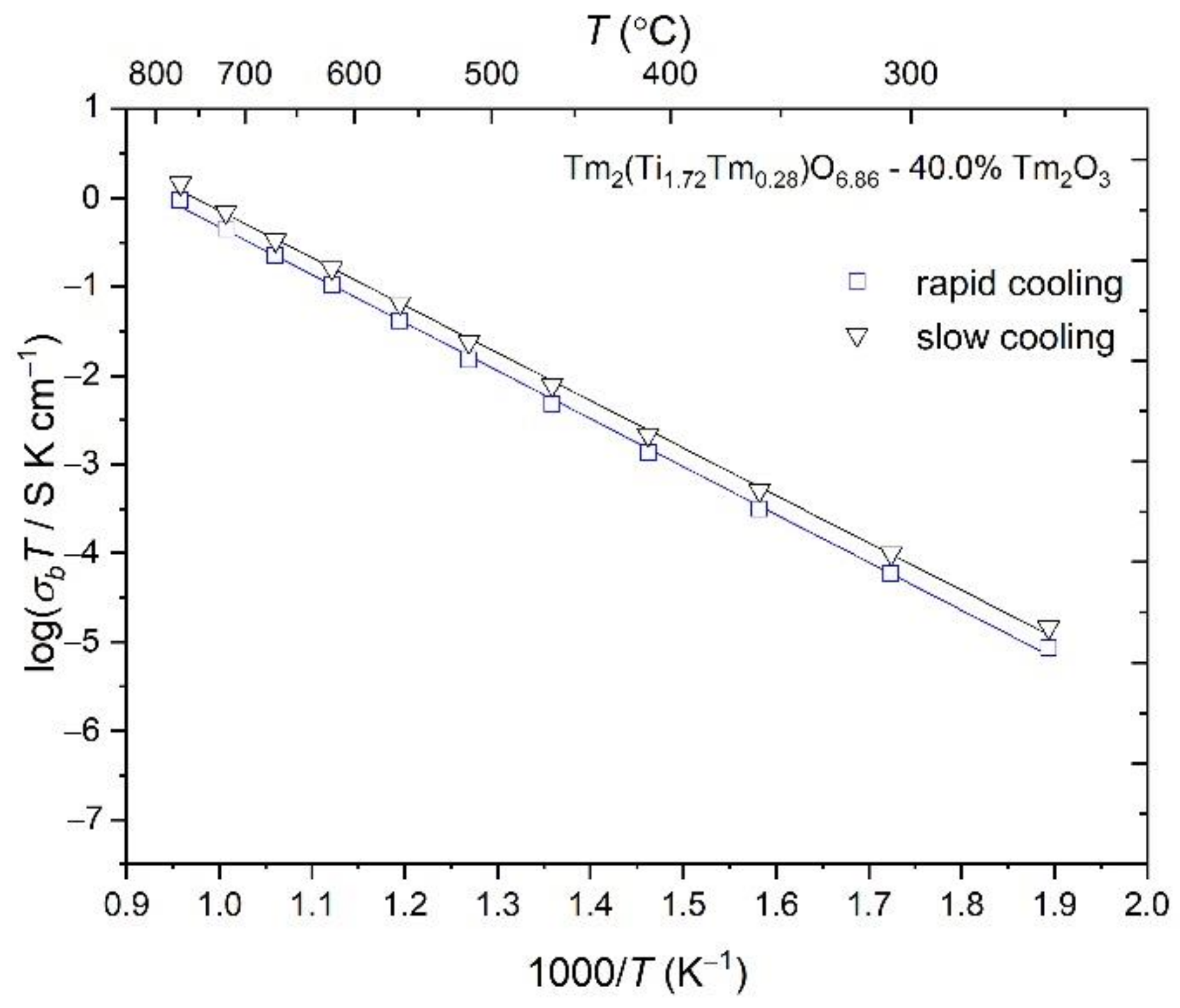
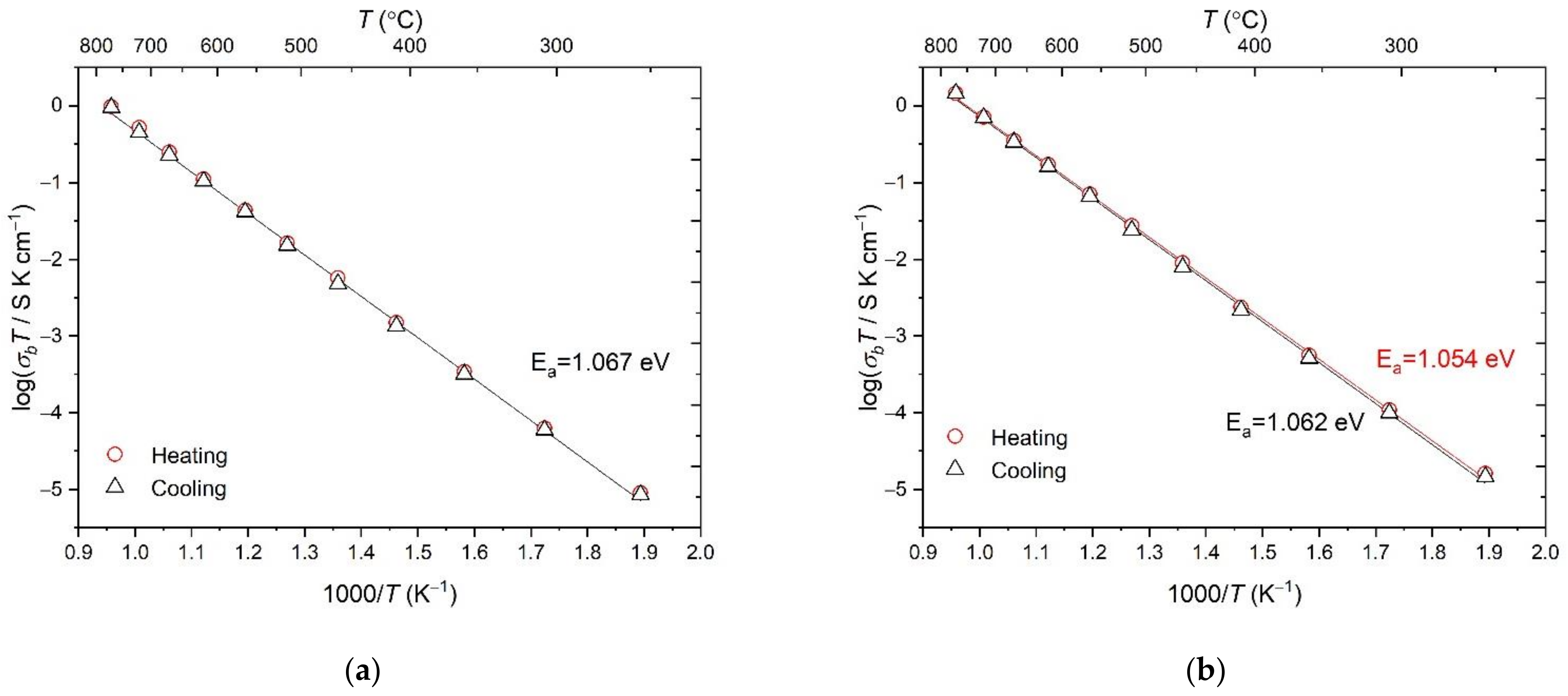
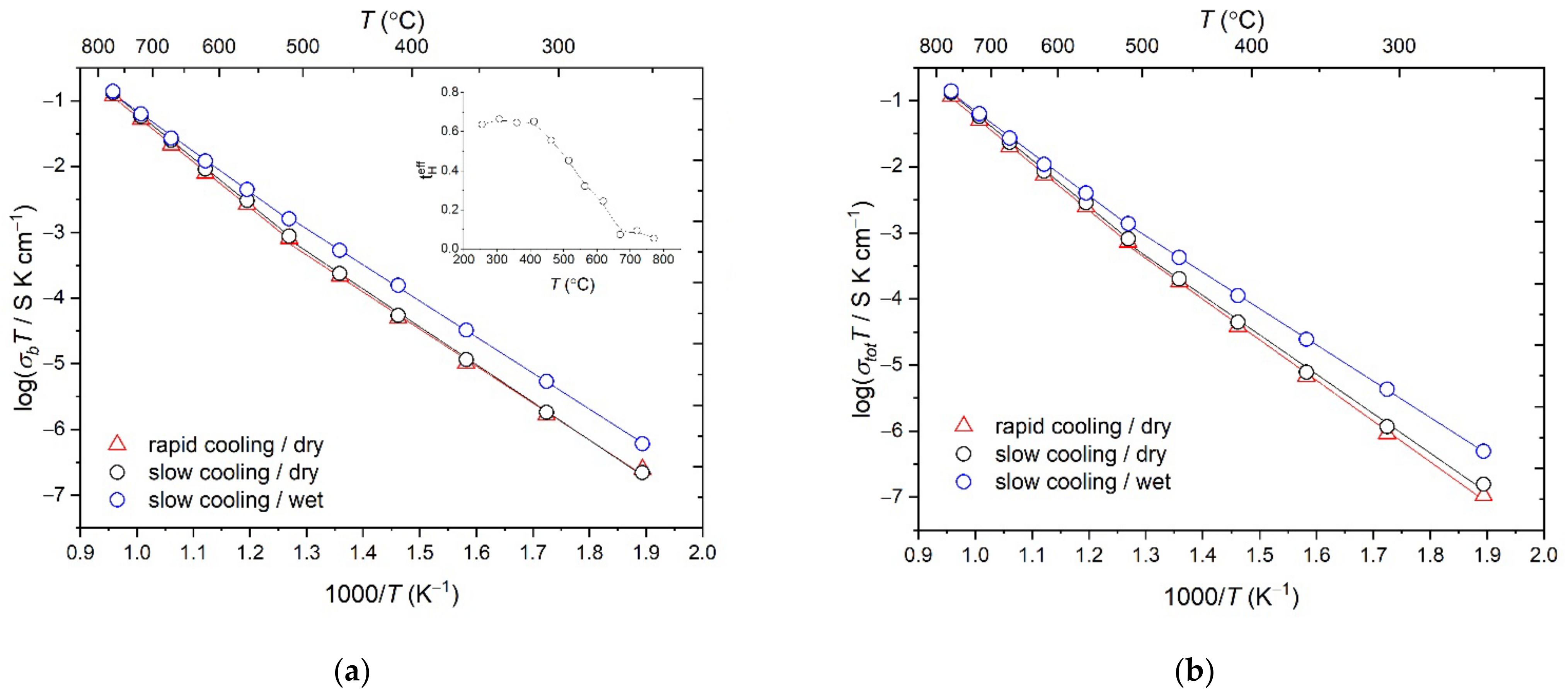
3.3. Conductivity of the Solid Solutions Studied by Impedance Spectroscopy
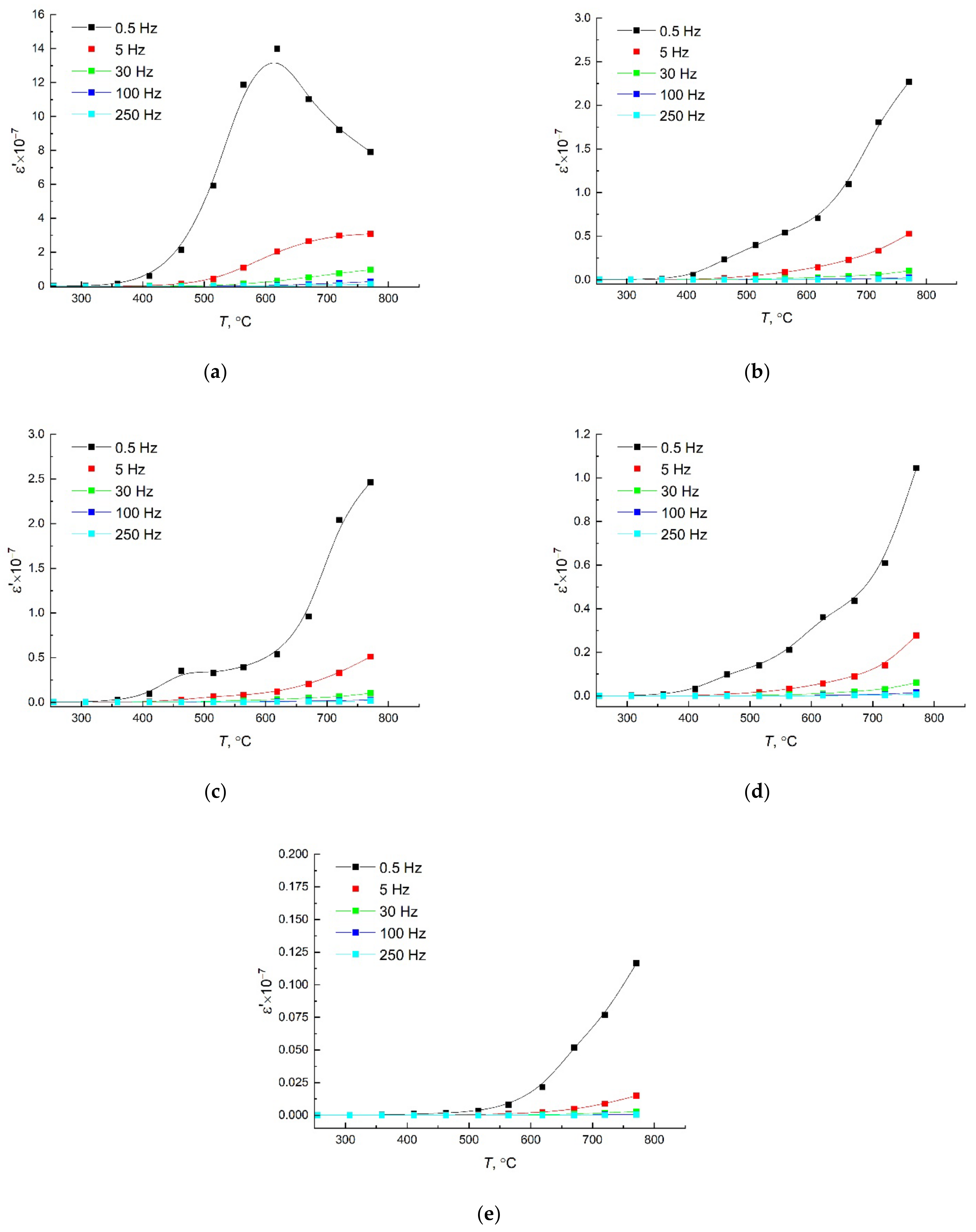
3.4. Dielectric Properties of the Solid Solutions
3.5. Causes of the Difference in Conductivity between the Tm2(Ti2−xTmx)O7−x/2 Ceramics Prepared via Coprecipitation and by Solid-State Reaction and Single Crystals with the Pyrochlore Structure
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mandal, P.; Tyagi, A.K. Ionic conductivity in materials with a pyrochlore structure. In Pyrochlore Ceramics Properties, Processing, and Applications, 1st ed.; Chowdhury, A., Ed.; Elsevier: Amsterdam, The Netherlands, 2022; pp. 277–294. ISBN 978-032-390-483-4. [Google Scholar]
- Anantharaman, A.P.; Dasari, H.P. Potential of pyrochlore structure materials in solid oxide fuel cell applications. Ceram. Int. 2021, 47, 4367–4388. [Google Scholar] [CrossRef]
- Anithakumari, P.; Grover, V.; Nandi, C.; Bhattacharyya, K.; Tyagi, A.K. Utilizing non-stoichiometry in Nd2Zr2O7pyrochlore: Exploring superior ionic conductors. RSC Adv. 2016, 6, 97566–97579. [Google Scholar] [CrossRef]
- Anokhina, I.A.; Animitsa, I.E.; Voronin, V.I.; Vykhodets, V.B.; Kurennykh, T.E.; Molchanova, N.G.; Vylkov, A.I.; Dedyukhin, A.E.; Zaikov, Y.P. The structure and electrical properties of lithium doped pyrochlore Gd2Zr2O7. Ceram. Int. 2021, 47, 1949–1961. [Google Scholar] [CrossRef]
- Lyskov, N.; Shchegolikhin, A.; Stolbov, D.; Kolbanev, I.; Gomes, E.; Abrantes, J.; Shlyakhtina, A. Study of oxygenion conductivity and luminescence in the ZrO2–Nd2O3 system: Impact of local heterogeneity. Electrochim. Acta 2022, 403, 139632. [Google Scholar] [CrossRef]
- Raghuveer, V.; Viswanathan, B. Nanocrystalline pyrochlore bonded to proton exchange membrane electrolyte as electrode material for oxygen reduction. J. Mater. Sci. 2005, 40, 6249–6255. [Google Scholar] [CrossRef]
- Liang, P.; Dong, S.; Zeng, J.; Yuan, J.; Jiang, J.; Deng, L.; Zhou, X.; Cao, X. La2Hf2O7 ceramics as potential top-coat materials for thermal/environmental barrier coatings. Ceram. Int. 2019, 45, 22432–22436. [Google Scholar] [CrossRef]
- Shlyakhtina, A.; Kondrat′eva, O.; Nikiforova, G.; Shchegolikhin, A.; Stolbov, D.; Kolbanev, I.; Liang, W.; Lyskov, N. Study of Nd2 ± Hf2 ± O7 ± δ system: The ionic and thermal transport properties. Mater. Res. Bull. 2022, 155, 111971. [Google Scholar] [CrossRef]
- Korf, S.J.; Koopmans, H.J.A.; Lippens, B.C.; Burggraaf, A.J.; Gellings, P.J. Electrical and catalytic properties of some oxides with the fluorite or pyrochlore structure. CO oxidation on some compounds derived from Gd2Zr2O7. J. Chem. Soc. Faraday Trans. 1 1987, 83, 1485–1491. [Google Scholar] [CrossRef]
- Fang, X.; Zhang, X.; Guo, Y.; Chen, M.; Liu, W.; Xu, X.; Peng, H.; Gao, Z.; Wang, X.; Li, C. Highly active and stable Ni/Y2Zr2O7 catalysts for methane steam reforming: On the nature and effective preparation method of the pyrochlore support. Int. J. Hydrogen Energy 2016, 41, 11141–11153. [Google Scholar] [CrossRef]
- Kumar, B.S.; Perumal, R.N.; Venkateswaran, C. Concurrence of ferroelectric, dielectric and magnetic behaviour in Tb2Ti2O7 pyrochlore. Phys. Lett. A 2021, 389, 127085. [Google Scholar] [CrossRef]
- Zuniga, J.P.; Gupta, S.K.; Abdou, M.; De Santiago, H.A.; Puretzky, A.A.; Thomas, M.P.; Guiton, B.S.; Liu, J.; Mao, Y. Size, structure, and luminescence of Nd2Zr2O7 nanoparticles by molten salt synthesis. J. Mater. Sci. 2019, 54, 12411–12423. [Google Scholar] [CrossRef]
- Patra, A. Effect of crystal structure and concentration on luminescence in Er3+:ZrO2 nanocrystals. Chem. Phys. Lett. 2004, 387, 35–39. [Google Scholar] [CrossRef]
- Lu, X.; Shu, X.; Shao, D.; Chen, S.; Zhang, H.; Yuan, X.; Chi, F. Radiation stability of Gd2Zr2O7 and Nd2Ce2O7 ceramics as nuclear waste forms. Ceram. Int. 2018, 44, 760–765. [Google Scholar] [CrossRef]
- Arsent’ev, P.A.; Glushkova, V.B.; Evdokimov, A.A.; Keler, E.K.; Kravchenko, V.B.; Kravchinskaya, M.V.; Krzhizhanovskaya, V.A.; Kuznetsov, A.K.; Kurbanov, K.M.; Potemkin, A.V.; et al. Rare-Earth Compounds: Zirconates, Hafnates, Niobates, Tantalates, and Antimonates; Nauka: Moscow, Russia, 1985. [Google Scholar]
- Shamblin, J.; Feygenson, M.; Neuefeind, M.F.J.; Tracy, C.; Zhang, F.; Finkeldei, S.; Bosbach, S.F.D.; Zhou, H.; Ewing, C.L.T.R.C.; Lang, J.S.M. Probing disorder in isometric pyrochlore and related complex oxides. Nat. Mater. 2016, 15, 507–511. [Google Scholar] [CrossRef]
- Shamblin, J.; Tracy, C.L.; Palomares, R.I.; O’Quinn, E.C.; Ewing, R.C.; Neuefeind, J.; Feygenson, M.; Behrens, J.; Trautmann, C.; Lang, M. Similar local order in disordered fluorite and aperiodic pyrochlore structures. Acta Mater. 2018, 144, 60–67. [Google Scholar] [CrossRef]
- Lau, G.; McQueen, T.; Huang, Q.; Zandbergen, H.; Cava, R. Long- and short-range order in stuffed titanate pyrochlores. J. Solid State Chem. 2008, 181, 45–50. [Google Scholar] [CrossRef]
- Shlyakhtina, A.; Savvin, S.; Levchenko, A.; Boguslavskii, M.; Shcherbakova, L. Heavily doped oxygen-ion conducting Ln2 + xTi2 − xO7 − δ (Ln = Ho − Lu; x = 0.44 − 0.81) pyrochlores: Crystal structure, microstructure and electrical conductivity. Solid State Ionics 2008, 179, 985–990. [Google Scholar] [CrossRef]
- Mullens, B.G.; Zhang, Z.; Avdeev, M.; Brand, H.E.A.; Cowie, B.C.C.; Múzquiz, M.S.; Kennedy, B.J. Effect of Long- and Short-Range Disorder on the Oxygen Ionic Conductivity of Tm2(Ti2–xTmx)O7–x/2 “Stuffed” Pyrochlores. Inorg. Chem. 2021, 60, 4517–4530. [Google Scholar] [CrossRef]
- Mullens, B.G.; Zhang, Z.; Avdeev, M.; Brand, H.E.; Cowie, B.C.; D’Angelo, A.; Múzquiz, M.S.; Kennedy, B.J. Average and local ordering of Yb2(Ti2-xYbx)O7-x/2 ‘stuffed’ pyrochlores: The development of a robust structural model. J. Solid State Chem. 2021, 302, 122412. [Google Scholar] [CrossRef]
- Marlton, F.P.; Zhang, Z.; Zhang, Y.; Proffen, T.E.; Ling, C.D.; Kennedy, B.J. Lattice Disorder and Oxygen Migration Pathways in Pyrochlore and Defect-Fluorite Oxides. Chem. Mater. 2021, 33, 1407–1415. [Google Scholar] [CrossRef]
- Shlyakhtina, A.V.; Knot’Ko, A.V.; Larina, L.L.; Borichev, S.A.; Shcherbakova, L.G. High-temperature phase transition of Tm2Ti2O7. Inorg. Mater. 2004, 40, 1312–1316. [Google Scholar] [CrossRef]
- Pandit, A.; Wanklyn, B.; Ansari, T.; Singh, R. Electrical conduction in Tm2Ti2O7 single crystal. Solid State Commun. 1992, 84, 469–473. [Google Scholar] [CrossRef]
- Wanklyn, B.M.; Maqsood, A. The flux growth of some rare-earth and iron group complex oxides. J. Mater. Sci. 1979, 14, 1975–1981. [Google Scholar] [CrossRef]
- Ross, K.A.; Proffen, T.; Dabkowska, H.A.; Quilliam, J.A.; Yaraskavitch, L.R.; Kycia, J.B.; Gaulin, B.D. Lightly stuffed pyrochlore structure of single-crystalline Yb2Ti2O7grown by the optical floating zone technique. Phys. Rev. B 2012, 86, 174424. [Google Scholar] [CrossRef]
- Abrantes, J.; Levchenko, A.; Shlyakhtina, A.; Shcherbakova, L.; Horovistiz, A.; Fagg, D.; Frade, J. Ionic and electronic conductivity of Yb2 + xTi2 − xO7 − x/2 materials. Solid State Ion. 2006, 177, 1785–1788. [Google Scholar] [CrossRef]
- Shlyakhtina, A.; Abrantes, J.; Levchenko, A.; Knot’Ko, A.; Karyagina, O.; Shcherbakova, L. Synthesis and electrical transport properties of Lu2 + xTi2 − xO7 − x/2 oxide-ion conductors. Solid State Ion. 2006, 177, 1149–1155. [Google Scholar] [CrossRef]
- Uematsu, K.; Shinozaki, K.; Sakurai, O.; Mizutani, N.; Kato, M. Electrical Conductivity of the System Y2O3-TiO2. J. Am. Ceram. Soc. 1979, 62, 219–221. [Google Scholar] [CrossRef]
- Fuentes, A.F.; Montemayor, S.M.; Maczka, M.; Lang, M.; Ewing, R.C.; Amador, U. A Critical Review of Existing Criteria for the Prediction of Pyrochlore Formation and Stability. Inorg. Chem. 2018, 57, 12093–12105. [Google Scholar] [CrossRef]
- Chambrier, M.-H.; Le Bail, A.; Giovannelli, F.; Redjaïmia, A.; Florian, P.; Massiot, D.; Suard, E.; Goutenoire, F. La10W2O21: An Anion-Deficient Fluorite-Related Superstructure with Oxide Ion Conduction. Inorg. Chem. 2014, 53, 147–159. [Google Scholar] [CrossRef]
- Shlyakhtina, A.V.; Lyskov, N.V.; Kolbanev, I.V.; Vorob’eva, G.A.; Shchegolikhin, A.N.; Voronkova, V.I. Specific Features of Phase Formation and Properties of Compounds La2W1 + xO6 + 3x (x ~ 0; 0.11–0.22). Russ. J. Electrochem. 2023, 59, 60–69. [Google Scholar]
- Aughterson, R.D.; Lumpkin, G.R.; Reyes, M.D.L.; Sharma, N.; Ling, C.D.; Gault, B.; Smith, K.L.; Avdeev, M.; Cairney, J.M. Crystal structures of orthorhombic, hexagonal, and cubic compounds of the Sm(x)Yb(2−x)TiO5 series. J. Solid State Chem. 2014, 213, 182–192. [Google Scholar] [CrossRef]
- Judd, B.R. Optical Absorption Intensities of Rare-Earth Ions. Phys. Rev. 1962, 127, 750–761. [Google Scholar] [CrossRef]
- Tracy, C.L.; Shamblin, J.; Park, S.; Zhang, F.; Trautmann, C.; Lang, M.; Ewing, R.C. Role of composition, bond covalency, and short-range order in the disordering of stannate pyrochlores by swift heavy ion irradiation. Phys. Rev. B 2016, 94, 64102. [Google Scholar] [CrossRef]
- Reutova, O.V.; Red’kin, A.F. Hydrothermal Synthesis and Structural Changes of Ca2-xCdxSb2O7 and Ca2-xCdxSb2O6F Compounds. In Proceedings of the 11th All-Russia Young Scientists Conference on Minerals: Structure, Properties, and Characterization Methods, Ekaterinburg, Russia, 25 May 2020; p. 252. [Google Scholar]
- Wang, H.; Lei, Z.; Jiang, W.; Xu, X.; Jing, J.; Zheng, Z.; Yang, Z.; Peng, S. High-conductivity electrolyte with a low sintering temperature for solid oxide fuel cells. Int. J. Hydrogen Energy 2022, 47, 11279–11287. [Google Scholar] [CrossRef]
- Bonanos, N.; Steele, B.C.H.; Butler, E.P. Impedance Spectroscopy Theory, Experiment, and Applications. In Impedance Spectroscopy, 2nd ed.; Barsoukov, E., MacDonald, J.R., Eds.; Wiley and Sons: New York, NY, USA, 2005; pp. 205–263. ISBN 0-471-64749-7. [Google Scholar]
- Näfe, H. Ionic conductivity of ThO2− and ZrO2−based electrolytes between 300 and 2000 K. Solid State Ion. 1984, 13, 255–263. [Google Scholar] [CrossRef]
- Guo, X.; Yuan, R.-Z. Grain boundary ionic conduction of zirconia-based solid electrolyte: Idea and practice. J. Mater. Sci. Lett. 1995, 14, 499–502. [Google Scholar] [CrossRef]
- Christie, G. Microstructure—Ionic conductivity relationships in ceria-gadolinia electrolytes. Solid State Ion. 1996, 83, 17–27. [Google Scholar] [CrossRef]
- Haile, S.M.; West, D.L.; Campbell, J. The role of microstructure and processing on the proton conducting properties of gadolinium-doped barium cerate. J. Mater. Res. 1998, 13, 1576–1595. [Google Scholar] [CrossRef]
- Sadykov, V.; Shlyakhtina, A.; Lyskov, N.; Sadovskaya, E.; Cherepanova, S.; Eremeev, N.; Skazka, V.; Goncharov, V.; Kharitonova, E. Oxygen diffusion in Mg-doped Sm and Gd zirconates with pyrochlore structure. Ionics 2020, 26, 4621–4633. [Google Scholar] [CrossRef]
- Vorotnikov, V.; Belyakov, S.; Plekhanov, M.; Stroeva, A.Y.; Lesnichyova, A.; Zhigalina, O.; Khmelenin, D.; Atanova, A.; Basu, V.; Kuzmin, A. Proton transfer in La2-xCaxZr2O7-δ pyrochlores: Reasons for limited water uptake and high grain boundary conductivity. Ceram. Int. 2022, 48, 35166–35175. [Google Scholar] [CrossRef]
- Gonzalo-Juan, I.; Riedel, R. Ceramic synthesis from condensed phases. Chemtexts 2016, 2, 6. [Google Scholar] [CrossRef]
- Heremans, C.; Wuensch, B.J.; Stalick, J.K.; Prince, E. Fast-Ion Conducting Y2(ZryTi1-y)2O7 Pyrochlores: Neutron Rietveld Analysis of Disorder Induced by Zr Substitution. J. Solid State Chem. 1995, 117, 108–121. [Google Scholar] [CrossRef]
- Zhang, Z.; Avdeev, M.; Reyes, M.D.L.; Lumpkin, G.R.; Kennedy, B.J.; Blanchard, P.E.R.; Liu, S.; Tadich, A.; Cowie, B.C.C. Probing Long- and Short-Range Disorder in Y2Ti2–xHfxO7 by Diffraction and Spectroscopy Techniques. J. Phys. Chem. C 2016, 120, 26465–26479. [Google Scholar] [CrossRef]
- Putilov, L.; Tsidilkovski, V. Improving the performance of protonic ceramic fuel cells and electrolyzers: The role of acceptor impurities in oxide membranes. Energy Convers. Manag. 2022, 267, 115826. [Google Scholar] [CrossRef]
- Politova, E.D.; Fortal’Nova, E.A.; Kaleva, G.M.; Mosunov, A.V.; Andronova, L.I.; Andropova, S.A.; Safronenko, M.G.; Venskovskiĭ, N.U. Ferroelectric phase transitions in ionic conductors based on bismuth vadanate. Phys. Solid State 2009, 51, 1443–1448. [Google Scholar] [CrossRef]
- Kaleva, G.M.; Mosunov, A.V.; Sadovskaya, N.V.; Politova, E.D.; Stefanovich, S.Y. Phase formation, structure and dielectric properties of ceramics (Na0.5Bi0.5)TiO3–(K0.5Na0.5)NbO3–BiFeO3. J. Adv. Dielectr. 2016, 6, 1650007. [Google Scholar] [CrossRef]
- Politova, E.; Strebkov, D.; Belkova, D.; Kaleva, G.; Golubko, N.; Mosunov, A.; Sadovskaya, N.; Panda, P. Relaxation Effects in Nonstoichiometric NBT-Based Ceramics. Defect Diffus. Forum 2019, 391, 95–100. [Google Scholar] [CrossRef]
- Shlyakhtina, A.; Lyskov, N.; Shchegolikhin, A.; Kolbanev, I.; Chernyak, S.; Konysheva, E.Y. Valence state of europium and samarium in Ln2Hf2O7 (Ln = Eu, Sm) based oxygen ion conductors. Ceram. Int. 2021, 47, 26898–26906. [Google Scholar] [CrossRef]
- Shlyakhtina, A.V.; Vorobieva, G.A.; Leonov, A.V.; Shchegolikhin, A.N.; Chernyak, S.A.; Baldin, E.D.; Streletskii, A.N. Kinetics of Formation and Crystallization of Ln2Ti2O7 (Ln = Gd, Lu) Pyrochlores from Nanoparticulate Precursors. Inorg. Mater. 2022, 58, 964–982. [Google Scholar] [CrossRef]
- Shlyakhtina, A.V.; Vorobieva, G.A.; Shchegolikhin, A.N.; Leonov, A.V.; Kolbanev, I.V.; Streletskii, A.N. Phase Relations and Behavior of Carbon-Containing Impurities in Ceramics Prepared from Mechanically Activated Ln2O3 + 2HfO2 (Ln = Nd, Dy) Mixtures. Inorg. Mater. 2020, 56, 528–542. [Google Scholar] [CrossRef]
- Popov, V.; Menushenkov, A.; Gaynanov, B.; Ivanov, A.; D’Acapito, F.; Puri, A.; Shchetinin, I.; Zheleznyi, M.; Berdnikova, M.; Pisarev, A.; et al. Formation and evolution of crystal and local structures in nanostructured Ln2Ti2O7 (Ln = Gd − Dy). J. Alloy. Compd. 2018, 746, 377–390. [Google Scholar] [CrossRef]
- Sastry, R.; Yoganarasimhan, S.; Mehrotra, P.; Rao, C. Preparation, characterization and thermal decomposition of praseodymium, terbium and neodymium carbonates. J. Inorg. Nucl. Chem. 1966, 28, 1165–1177. [Google Scholar] [CrossRef]
- Caro, P.; Lemaitre-Blase, M. Hydroxycarbonates de terre rare Ln2(CO3)2(OH)2(3−) nH2O. C. R. Acad. Sci. 1969, 269, 687–690. [Google Scholar]
- Samuskevich, V.V.; Prodan, E.A.; Pavlyuchenko, M.M. Effect of the gas phase on the thermal decomposition of lanthanum carbonate. Zhurnal Neorg. Khimii 1972, 17, 2067–2071. [Google Scholar]
- Kokhanovskii, V.V.; Pavlyuchenko, M.M.; Prodan, E.A. Thermal decomposition of yttrium carbonate in vacuum. Izv. Akad. Nauk Bel. SSR Ser. Khim. 1970, 2, 34–41. [Google Scholar]
- Pavlyuchenko, M.M.; Samuskevich, V.V.; Prodan, E.A. Effect of water vapor on lanthanum carbonate octahydrate dehydration. Vestn. Akad. Nauk Bel. SSR Ser. Khim. Nauk 1970, 6, 11–15. [Google Scholar]
- Lacroix, C.; Mendels, P.; Mila, F. Introduction to Frustrated Magnetism: Materials, Experiments, Theory; Springer Series in Sol-id-State Sciences; Springer: Berlin/Heidelberg, Germany, 2011; Volume 164, ISBN 978-3-642-10588-3. [Google Scholar]
- Subramanian, M.; Aravamudan, G.; Rao, G.S. Oxide pyrochlores—A review. Prog. Solid State Chem. 1983, 15, 55–143. [Google Scholar] [CrossRef]
- Gardner, J.S.; Gingras, M.J.P.; Greedan, J.E. Magnetic pyrochlore oxides. Rev. Mod. Phys. 2010, 82, 53–107. [Google Scholar] [CrossRef]
- Dhanaraj, G.; Byrappa, K.; Prasad, V.; Dudley, M. Springer Handbook of Crystal Growth; Springer: Berlin/Heidelberg, Germany, 2010; ISBN 978-3-540-74182-4. [Google Scholar]
- Chang, L.-J.; Onoda, S.; Su, Y.; Kao, Y.-J.; Tsuei, K.-D.; Yasui, Y.; Kakurai, K.; Lees, M.R. Higgs transition from a magnetic Coulomb liquid to a ferromagnet in Yb2Ti2O7. Nat. Commun. 2012, 3, 992. [Google Scholar] [CrossRef]
- Quilliam, J.A.; Meng, S.; Craig, H.A.; Corruccini, L.R.; Balakrishnan, G.; Petrenko, O.A.; Gingras, M.J.P.; Kycia, J.B. Juxtaposition of spin freezing and long range order in a series of geometrically frustrated antiferromagnetic gadolinium garnets. Phys. Rev. B Condens. Mat. 2013, 87, 174421. [Google Scholar] [CrossRef]
- Schiffer, P.; Ramirez, A.P.; Huse, D.A.; Gammel, P.L.; Yaron, U.; Bishop, D.J.; Valentino, A.J. Frustration Induced Spin Freezing in a Site-Ordered Magnet: Gadolinium Gallium Garnet. Phys. Rev. Lett. 1995, 74, 2379–2382. [Google Scholar] [CrossRef] [PubMed]



| Composition, Cooling Mode | Pyrochlore (P) | Pyrochlore + Fluorite (P + F) | Fluorite (F) |
|---|---|---|---|
| Tm2(Ti2−xTmx)O7−x/2 (x = 0.28) Fast cooling | Rwp = 12.62% Rp = 10.10% S = 1.19 χ2 = 1.41 a = 10.1241(9) Å | Rwp = 12.68% Rp = 10.12% S = 1.18 χ2 = 1.39 P = 99.32 wt% F = 0.68 wt% a = 10.1261(8) Å | - |
| Tm2(Ti2−xTmx)O7−x/2 (x = 0.28) Slow cooling | Rwp = 12.00% Rp = 9.40% S = 1.15 χ2 = 1.33 a = 10.1226(2) Å | Rwp = 11.46% Rp = 9.18% S = 1.09 χ2 = 1.20 P = 98.61 wt% F = 1.39 wt% a = 10.1229(7) Å | - |
| Tm2(Ti2−xTmx)O7−x/2 (x = 0.74) Fast cooling | Rwp = 14.27% Rp = 10.36% S = 1.33 χ2 = 1.77 a = 10.2158(11) Å | Rwp = 10.47% Rp = 8.41% S = 0.98 χ2 = 0.95 P = 6.5 wt% F = 93.5 wt% a = 10.215 (4) Å | Rwp = 10.58% Rp = 8.46% S = 0.99 χ2 = 0.97 a = 10.2153(8) Å |
| Tm2(Ti2−xTmx)O7−x/2 (x = 0.74) Slow cooling | Rwp = 13.78% Rp = 10.54% S = 2.29 χ2 = 5.27 a = 10.23738(47) Å | Rwp = 13.06% Rp = 9.51% S = 2.15 χ2 = 4.64 P = 13 wt% F = 87 wt% a = 10.23574(1) Å | Rwp = 13.19% Rp = 9.52% S = 2.21 χ2 = 4.90 a = 10.2494(6) Å |
| Curve No. in Figure 2 | Percent Tm2O3, % | x in Tm2(Ti2−xTmx)O7−x/2 | R2 | First Band | Second Band | ||||
|---|---|---|---|---|---|---|---|---|---|
| Center | Width | Height | Center | Width | Height | ||||
| 1 | 33.3 | 0 | 0.999 | 8146 | 613 | 0.412 | 8808 | 861 | 0.374 |
| 2 | 35 | 0.1 | 0.999 | 8057 | 609 | 0.288 | 8767 | 925 | 0.359 |
| 3 | 37.5 | 0.18 | 0.999 | 8026 | 632 | 0.254 | 8773 | 1067 | 0.362 |
| 4 | 40 | 0.28 | 0.998 | 7977 | 674 | 0.261 | 8811 | 1141 | 0.381 |
| 5 | 52 | 0.74 | 0.999 | 8054 | 714 | 0.290 | 8797 | 1134 | 0.402 |
| Samples No | Composition, %, Cooling Mode | Composition, Tm2(Ti2−xTmx)O7−x/2, Cooling Mode | Bulk Conductivity at 771 °C (S/cm) | Apparent Activation Energy (Ea) of Bulk Conductivity in Dry and Wet Air, eV | Apparent Activation Energy (Ea) of Total Conductivity in Dry and Wet Air, eV | ||
|---|---|---|---|---|---|---|---|
| 1 | 33.3% Tm2O3 + 66.7% TiO2, fast cooling | Tm2(Ti2−xTmx)O7−x/2 (x = 0), fast cooling | 3.16·10−3 | 0.946 | 1.058 | ||
| 2 | 35.5% Tm2O3 + 64.5% TiO2, fast cooling | Tm2(Ti2−xTmx)O7−x/2 (x = 0.1), fast cooling | 1.78·10−3 | 1.043 | 1.121 | ||
| 3 | 37.5% Tm2O3 + 62.5% TiO2, fast cooling | Tm2(Ti2−xTmx)O7−x/2 (x = 0.18), fast cooling | 2.96·10−3 | 1.071 | 1.141 | ||
| 4 | 40.0% Tm2O3 + 60.0% TiO2, fast cooling | Tm2(Ti2−xTmx)O7−x/2 (x = 0.28), fast cooling | 0.91·10−3 | 1.067 | 1.123 | ||
| 4S | 40.0% Tm2O3 + 60.0% TiO2, slow cooling | Tm2(Ti2−xTmx)O7−x/2 (x = 0.28), slow cooling | 1.36·10−3 | 1.062 | 1.096 | ||
| 5 | 52.0% Tm2O3 + 48.0% TiO2, fast cooling | Tm2(Ti2−xTmx)O7−x/2 (x = 0.74), fast cooling | 0.11·10−3 | 771–515 °C | 1.380 | 1.339 | |
| 515–255 °C | 1.119 | 1.222 | |||||
| 5S | 52.0% Tm2O3 + 48.0% TiO2, slow cooling | Dry air | Tm2(Ti2−xTmx)O7−x/2 (x = 0.74), slow cooling | 0.10·10−3 | 771–515 °C | 1.381 | 1.404 |
| 515–255 °C | 1.142 | 1.186 | |||||
| Wet air | 0.13·10−3 | 771–515 °C | 1.228 | 1.276 | |||
| 515–255 °C | 1.091 | 1.092 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gorshkov, N.; Baldin, E.; Stolbov, D.; Rassulov, V.; Karyagina, O.; Shlyakhtina, A. Oxygen–Ion Conductivity, Dielectric Properties and Spectroscopic Characterization of “Stuffed” Tm2(Ti2−xTmx)O7−x/2 (x = 0, 0.1, 0.18, 0.28, 0.74) Pyrochlores. Ceramics 2023, 6, 948-967. https://doi.org/10.3390/ceramics6020056
Gorshkov N, Baldin E, Stolbov D, Rassulov V, Karyagina O, Shlyakhtina A. Oxygen–Ion Conductivity, Dielectric Properties and Spectroscopic Characterization of “Stuffed” Tm2(Ti2−xTmx)O7−x/2 (x = 0, 0.1, 0.18, 0.28, 0.74) Pyrochlores. Ceramics. 2023; 6(2):948-967. https://doi.org/10.3390/ceramics6020056
Chicago/Turabian StyleGorshkov, Nikolay, Egor Baldin, Dmitry Stolbov, Viktor Rassulov, Olga Karyagina, and Anna Shlyakhtina. 2023. "Oxygen–Ion Conductivity, Dielectric Properties and Spectroscopic Characterization of “Stuffed” Tm2(Ti2−xTmx)O7−x/2 (x = 0, 0.1, 0.18, 0.28, 0.74) Pyrochlores" Ceramics 6, no. 2: 948-967. https://doi.org/10.3390/ceramics6020056
APA StyleGorshkov, N., Baldin, E., Stolbov, D., Rassulov, V., Karyagina, O., & Shlyakhtina, A. (2023). Oxygen–Ion Conductivity, Dielectric Properties and Spectroscopic Characterization of “Stuffed” Tm2(Ti2−xTmx)O7−x/2 (x = 0, 0.1, 0.18, 0.28, 0.74) Pyrochlores. Ceramics, 6(2), 948-967. https://doi.org/10.3390/ceramics6020056







