1. Introduction
Ca
12Al
14O
33, the mineral mayenite or C12A7, crystallizes in a clathrate structure where a positively-charged framework is balanced by occluded anionic species. The high interconnectivity of the cages in the clathrate structure leads to high occluded anion mobility. The functionality of the structure is derived from the mobility and diversity of occluded chemical species leading to a wide range of applications [
1,
2]. The C12A7 structure, occluded anion speciation, lattice parameter, and kinetic formation are all heavily correlated to processing conditions [
3,
4,
5]. Current thermodynamic studies of C12A7 present a thermodynamic equilibrium-derived inference on the kinetics of phase formation. With the thermodynamic phase equilibria defined, an in situ kinetic structural investigation of C12A7 is warranted to better understand the proposed kinetic pathways to thermodynamic equilibrium. With this knowledge, careful control of synthesis can lead to optimization of material properties for a wide variety of applications.
C12A7 thermodynamic phase equilibria is well characterized, and through characterization of these end points inferences of the kinetic pathways were made [
6,
7]. Thermodynamic equilibria of calcium aluminate formation via solid state synthesis (SSS) reactants CaCO
3 and Al
2O
3 identify C5A3 (Ca
5Al
6O
14) and C3A (Ca
3Al
2O
6) as the first phases to form, followed by aluminum rich phases—for example CA (CaAl
2O
4)—regardless of starting reactant stoichiometry; this leads to the suggestion that the diffusion of Ca is the kinetic pathway to the equilibrium [
6]. Tian et al. characterized an onion-like microstructure structure where Al
2O
3 particles are at the core and layers of progressively higher Ca containing calcium aluminate phases consecutively surround the core through to the surface [
6]. More specifically, for C12A7 stoichiometry the synthesis pathway is dependent on the heterogeneity of starting reactants and two formation pathways—(1) C5A3 + C3A and (2) C3A + CA—are observed in high homogeneity and low homogeneity cases, respectively [
7]. The C5A3 and C3A pathway is predicted to be the low temperature pathway for C12A7 formation as reactant homogeneity increases via wet chemistry/sol-gel techniques. C12A7 thermodynamic phase equilibria also changes with process environment. C12A7 is precluded from the thermodynamic CaO-Al
2O
3 binary phase diagram under dry atmospheres and only appears when moisture is present, indicating metastability under elevated temperature conditions in inert, dry oxidative, or reducing atmospheres [
2]. Thermodynamic studies have thoroughly characterized the phase equilibria, but a kinetic characterization and confirmation of the proposed kinetic pathway to equilibrium is missing.
The historical characterization of phase equilibria has adopted a thermodynamic approach. The technique dubbed ‘cook and look’ involves heating at a temperature for an extended period of time, quenching to retain the phase assemblage, and then structurally characterizing the results. This characterizes the thermodynamic equilibria well but information on the kinetic pathway is lost. The kinetic transformation can be captured by quenching the sample at various process durations and temperatures to ‘freeze in the evolving phases’; however, this requires Edisonian experimental procedures, and only provides a single snapshot of the behavior. If the sampling rate is not high enough full kinetic pathways could be missed. While quenching works to freeze diffusive transformations, non-diffusive phase transformations behavior may be lost during the quench due to the fast transformation rates.
With the advances in computational modeling and instrumentation software and hardware, the precise and high-resolution structural determination of kinetic pathways is now possible in a laboratory setting. In situ non-ambient high-temperature X-ray diffraction (HTXRD) provides a characterization method that can probe the kinetics of phase transformations in real time by rapidly collecting diffraction patterns during heating. This allows for identification of metastable and non-equilibrium phases and formation pathways. Until recently this type of characterization required travel to a synchrotron X-ray or time-of-flight neutron source to collect diffraction data at the intervals needed to capture fast kinetic transitions. Lab XRD has evolved to where an area detector can continuously monitor a large enough region of °2θ, where several key phase diffraction maxima are located, dynamically replacing point detectors and leading to large increases in measurement of diffracted intensity as a function of °2θ.
The Malvern PANalytical Empyrean diffractometer (PANalytical, Almelo, The Netherlands) equipped with an Anton Paar HTK1200N high temperature furnace and PIXcel3d area detector provides stable controllable sample environmental modification and rapid data collection. Rapid data collection on heating captures dynamic and static phase transformations. A combination of isothermal and non-isothermal data collection, normally acquired through thermal analysis characterization, can be used to derive information about the activation energy, type of kinetic process, limitations in kinetic transformations, and modes of structural transformation.
Specifics of the kinetic transformation can be determined by analyzing the integrated peak area, or phase fraction determined through Rietveld refinement if multiple phases coexist, to track the evolution of crystallization as a function of time or temperature. This parameter, frequently denoted
, is analyzed as a function of time at a constant temperature in an isothermal characterization, or time and temperature in a non-isothermal characterization. To properly identify the limiting kinetics of the phase transformations, the development of a master plot allows for direct comparison of the rate of reaction to various kinetic models [
8].
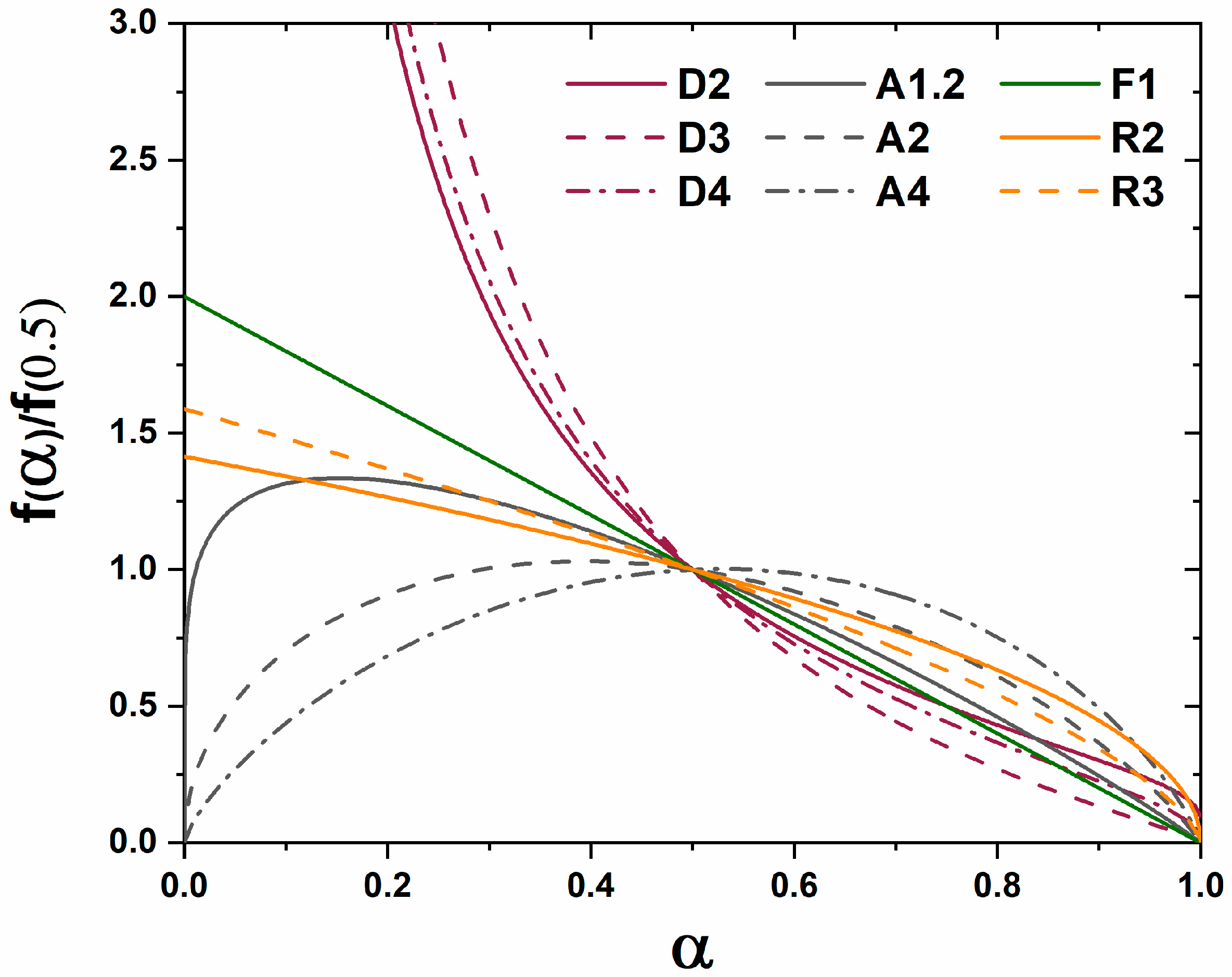
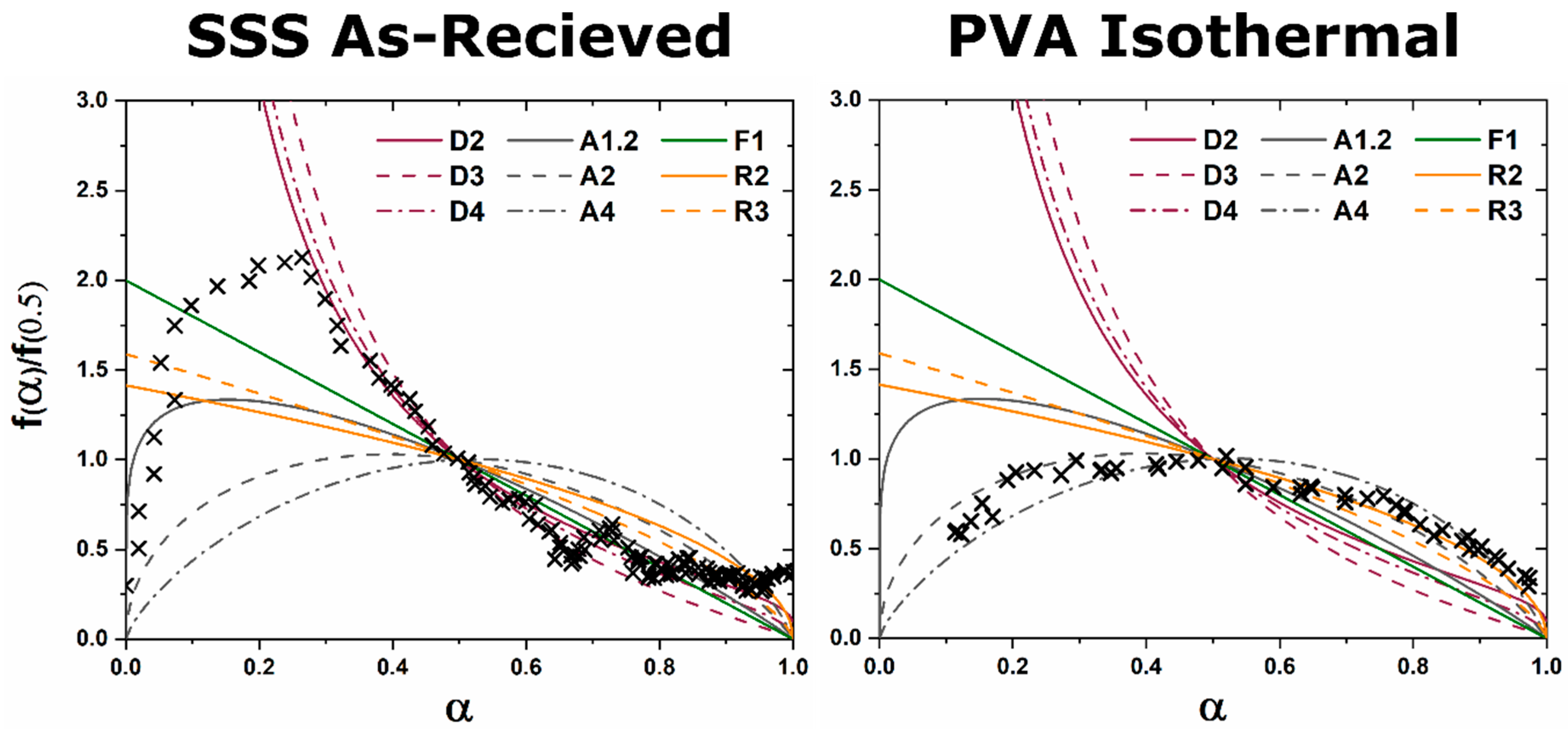
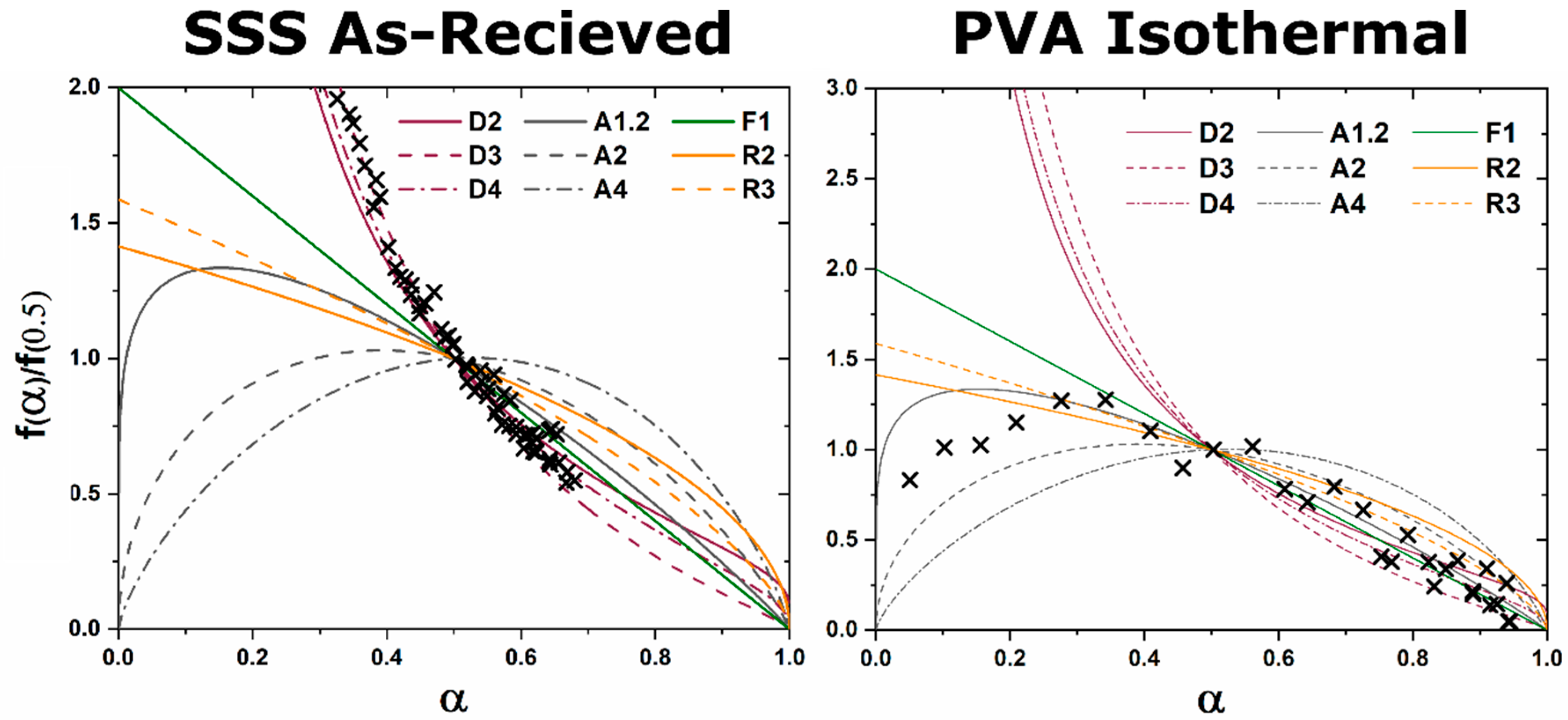
A master plot is a diagram which graphically represents an analytical expression for the rate of transformation vs. transformed fraction for diffusion, phase boundary, and random nucleation and growth kinetic models [
8]. When experimental data are superimposed on the diagram the type of kinetic transformation can be elucidated based on the correlation of experimental data to the analytical expression of the theoretical models. Gotor et al. redefined a method for creating master plots which can be applied universally to the analysis of solid state kinetic transformations regardless of the temperature dependence of the characterization [
8]. The original application was mass loss and controlled rate thermal analysis techniques, but with the advent of kinetic HTXRD analysis the methods can be reinterpreted for X-ray characterization. For isothermal characterization only a single isothermal
vs. time curve is needed to identify the kinetic model which best characterizes the kinetic transformation. For a linear non-isothermal temperature vs. time dependence (isochronal), an
vs. temperature curve and the activation energy of the transition is needed to utilize the master plot. Activation energy can be derived from thermal analysis characterization or through multiple isothermal characterization and implementation of methods such as the Kissinger method [
9]. For a non-linear non-isothermal temperature vs. time dependence the relationship between temperature and time,
α as a function of temperature, and activation energy must be known [
8].
The functions
for diffusion, grain boundary, and homogenous nucleation and growth kinetic transformations are represented in
Table 1. The master plot is created by plotting
and the experimental data
. The master plot of
vs.
is shown
Figure 1.
The homogenous nucleation and growth kinetic model is known as the Johnson-Mehl-Avrami-Kolmogorov (JMAK) model. The kinetics of this transformation have three distinct processes: the first is homogenous random nucleation, followed by nuclei growth, and nuclei impingement. The most widely used form of the model is a special JMAK case which assumes that nucleation occurs randomly and homogeneously and that the growth rate is constant with respect to time and transformed fraction (Equation (1)) [
10].
k, described in Equation (2), represents a temperature-dependent rate constant dependent on the growth mode factor,
m, dimensionality,
d, dimensionality of growth,
fd,
system entropy,
effective attempt frequency,
kb Boltzmann constant, and
particle growth rate.
n, described in Equation (3), represents the JMAK exponent which is dependent on the dimensionality and the growth mode [
11].
Conventional analysis involves determining these two values (
k and
n) through data fitting and deriving information about the kinetic transformation dimensionality, growth mode, and activation energy.
Table 2 demonstrates the analysis of JMAK exponent for different kinetic models.
In the case of heterogeneous kinetic transformations, commonly referred to as diffusion controlled transformations, the mobility of constituents in the system controls the transformation rate. In homogeneous reactions the growth of the new phase is expected to occur non-preferentially, whereas in heterogenous reactions the nucleation and growth occurs at preferred non-homogenous interfaces. In heterogeneous systems the constituents are separated into their own particles, normally individual oxides in solid state synthesis reactions, and long diffusion pathways are required to reach and grow the nucleating phase. The kinetics of these reactions are dependent on constituent mobility; for oxides this include anion and cation mobility, and mobility can be limited by lattice defects and microstructural voids [
12]. As the diffusion-based kinetic reactions continue the growing phase will further separate the two reactant phases leading to a decay of the reaction rate. When the reactant particles are spherical, three-dimensional diffusion will occur;
α, given by Equation (4), is analytically derived from the radius of the reactant particle,
R, and the thickness of the product layer,
x [
12].
Geometric contraction models assume that nucleation of the transformed phase occurs on the surface of the reactant phase and growth is controlled by the consumption of the bulk phase. In general, the reaction rate is governed by Equation (5) where
r is radius at time
t,
r0 is the untransformed particle radius, and
is the reaction rate constant. The reaction rate can be expressed for special cases such as 2D cylinder (contracting area) or 3D spherical (contracting volume) growth [
12]. For the spherical case,
α is given by Equation (6). The particle size is incorporated in the rate constant in both the contracting volume and geometric models (diffusion models) indicating a change in the reactant particle sizes will alter the transformation reaction rate [
12].
A physical representation of the three kinetic models is shown in
Figure 2. With the tool of in situ XRD, this study characterizes the kinetic pathways of a C12A7 stochiometric reactant mixture as a function of reactant homogeneity, atmosphere humidity, and oxidizing/reducing conditions. The kinetic transformations observed with HTXRD are analyzed applying the master plot method. This study aims to determine the effect of reactant heterogeneity on the kinetic formation pathway of C12A7, identify the thermodynamic phase equilibrium as a function of process atmosphere, and elucidate the role of C5A3 in the calcium aluminate phase space.
2. Materials and Methods
Three different reactant mixtures were characterized to identify changes in kinetic formation as a function of reactant homogeneity. Solid state synthesis (SSS) reactants were analyzed both with the reactant materials in the as-received state resulting in a high heterogeneity mixture, and with the as-received reactant subject to ball milling to reduce the particle size resulting in a lower heterogeneity mixture. A polymer assisted sol-gel reactant mixture was used to characterize the case of atomic level homogeneity.
A high heterogeneity reactant mixture was derived from the standard solid-state synthesis precursors of CaCO3 and Al2O3 powders. The powders were dried in a vacuum drying oven at 37 torr and 200 °C for 24 h before being measured into stoichiometric amounts and thoroughly mixed in a vibratory mill. The starting particle size of as-received reactants is in the order of 10 µm for CaCO3 and ≤100 nm for Al2O3.
A lower heterogeneity reactant mixture was prepared by ball milling the as-received CaCO3 to decrease the particle size to ≤200 nm. The reactant powder mix was milled in a Pulversette 7 premium high energy planetary ball mill in an yttria stabilized zirconia (YSZ) bowl with 1 mm YSZ milling media and isopropanol alcohol. Process parameters consisted of a 0.5 h milling step at 900 rpm followed by a 0.5 h hold and repeated six times.
An atomically homogenous reactant mixture was prepared through the polymer assisted (PA) synthesis route utilizing polyvinyl alcohol (PVA) [
13]. A 4:1 cation to PVA ratio was chosen and the appropriate mass of PVA (molecular mass of 20,000–30,000) was dissolved in deionized (DI) water and allowed to age for 24 h. Ca(NO
3)
2·4H
2O and Al(NO
3)
3·9H
2O were used as cation sources and were measured from 1 molar stock solutions whose molarities were determined through inductively coupled plasma spectroscopy (ICP). Stoichiometric amounts of nitrate solutions were extracted and combined with the PVA solution under vigorous stirring. The solution was aged for 1 h before solvent evaporation was performed at a solution temperature of 90 °C. When approximately 15% of the solvent volume remained, the solution exhibited bubbling before returning to a steady state. Powder was continually scraped off the bottom and sides of the beaker after this step until the solution was completely converted to a yellow powder. This powder was then ground in a YSZ mortar and pestle and calcined to 600 °C to remove moisture and organic components. The obtained white powder is the homogenous non-carbonaceous reactant for the kinetic investigations; carbon has been shown to act as a templating anion, and oxidation of residual carbon species removes this possibility in the current investigations [
5,
14,
15].
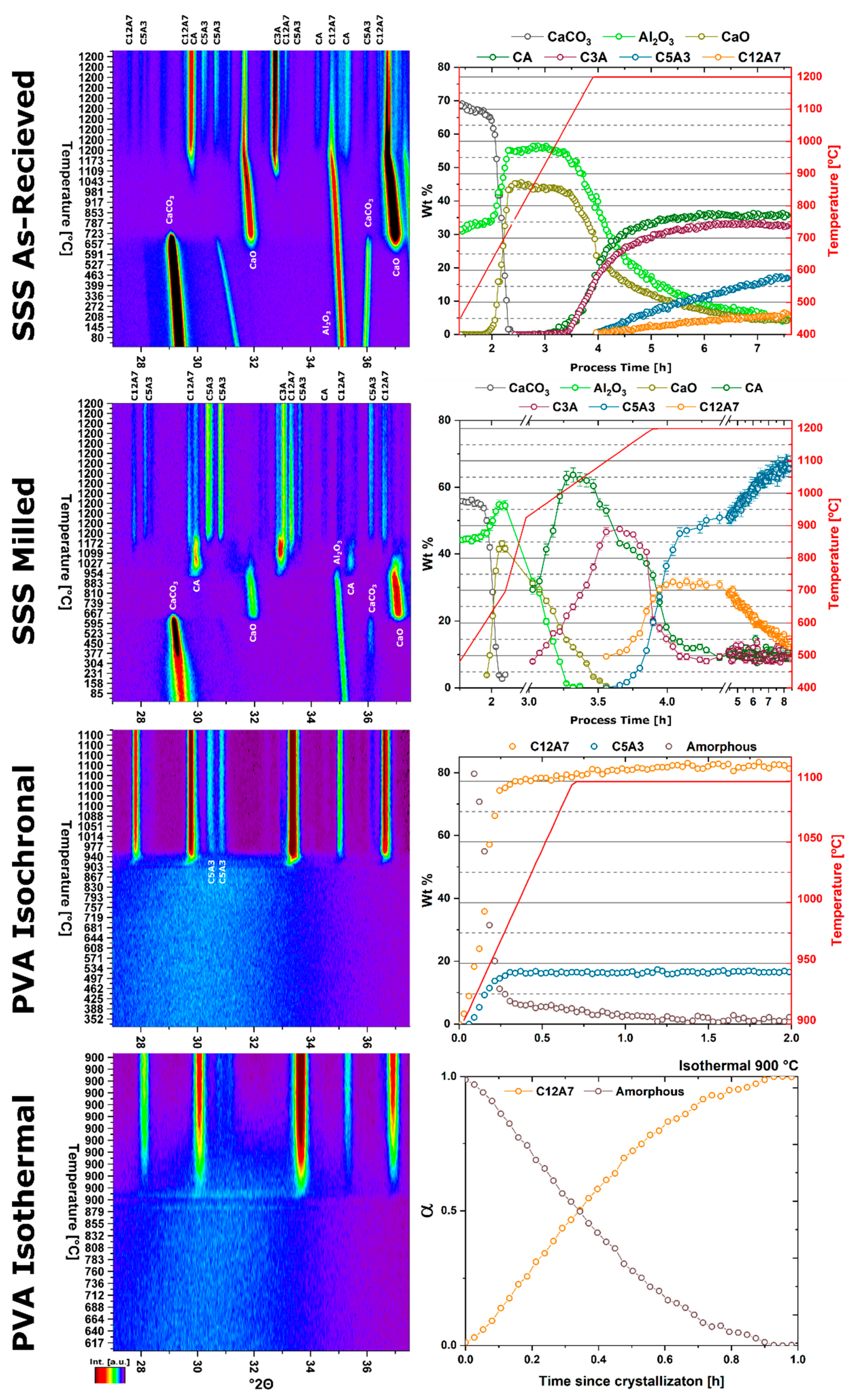
In situ non-ambient high-temperature X-ray diffraction (HTXRD) experiments were performed on a Malvern PANalytical Empyrean diffractometer utilizing an Anton Paar HTK 1200N high temperature furnace sample stage and a PIXcel
3D area detector with 255 active channels and ~3° 2θ of coverage. Samples were heated to either 1100 or 1200 °C with a ramp rate of 300 °C/h under flowing compressed air (~120 ppm H
2O), static ambient atmosphere, or high vacuum (8 × 10
−5 torr); in the case of PA sol-gel reactants, the ramp rate was decreased to ~150 °C/h to yield more transformation resolution due to the rapid kinetics of formation. Data were collected both rapidly (<2 min per pattern) and continuously during the furnace ramp. A small 2θ range of 27.5–37° 2θ captures the amorphous hump of the sol-gel reactant mixture, high-intensity peaks for all phases Ca
5Al
6O
14 (C5A3), C
3Al
2O
6 (C3A), CaAl
2O
4 (CA), CaCO
3, Al
2O
3, and CaO, and five characteristic peaks of C12A7. Reported temperature is the sample temperature, not the set temperature, and was measured by a thermocouple directly below the sample. Instrumental setup and collection specifics are summarized in
supplementary information (Table S1); incident and diffracted beam optics were optimized for intensity over resolution. For data collection, all reactant mixtures were pressed into 13 mm pellets with a thickness of 2 mm and placed in the sample holder. Experimental characterization is summarized in
Table 3.
Following the method previously employed in HTXRD characterization of amorphous citrate sol-gel formation [
16], phase matching was performed utilizing the International Centre for Diffraction Data (ICDD) PDF-4+ 2018 database. Rietveld refinement was performed using the Malvern PANalytical HighScore Plus software package [
17]. Lattice parameters, background, scale factors, surface sample displacement, phase fractions, and profile parameters relevant to crystallite size determination were refined. During the formation of the C12A7 phase from an amorphous reactant mixture, pseudo-Voight peak fitting was used to determine the change in peak area relating to an increase in the concentration of C12A7 relative to the amorphous content. Crystallite size was determined through pseudo-Voigt profile fitting and is documented in the HighScore Plus software package as being calculated using Equations (7) and (8), which describe crystallite size and size variance, respectively [
17].
Wi and
Wstd are coefficients used to describe peak width for a given reflection and the standard, respectively, and
refers to the variance of those values.
Instrumental broadening was characterized with NIST (National Institute of Standards and Technology) standard SRM 640e (Si), and the refined values were used during the HTXRD Rietveld refinements.
4. Discussion
The change in reactant homogeneity has no effect on the thermodynamic equilibrium. Given sufficient time for the kinetics and diffusion to occur, all systems should reach the same final state for a specified temperature. The change produced by altering reactant homogeneity alters the kinetic behavior and pathway to that final state. Characterization of stoichiometrically C12A7 reactant mixtures as a function of reactant homogeneity and processing atmosphere leads to changes in C12A7 formation, elucidates the atmosphere dependent thermodynamic equilibrium and role of C5A3 in the calcium aluminate system, and defines the low temperature kinetic equilibrium of C12A7 regardless of the thermodynamic equilibrium.
4.1. Kinetics Pathways of Formation
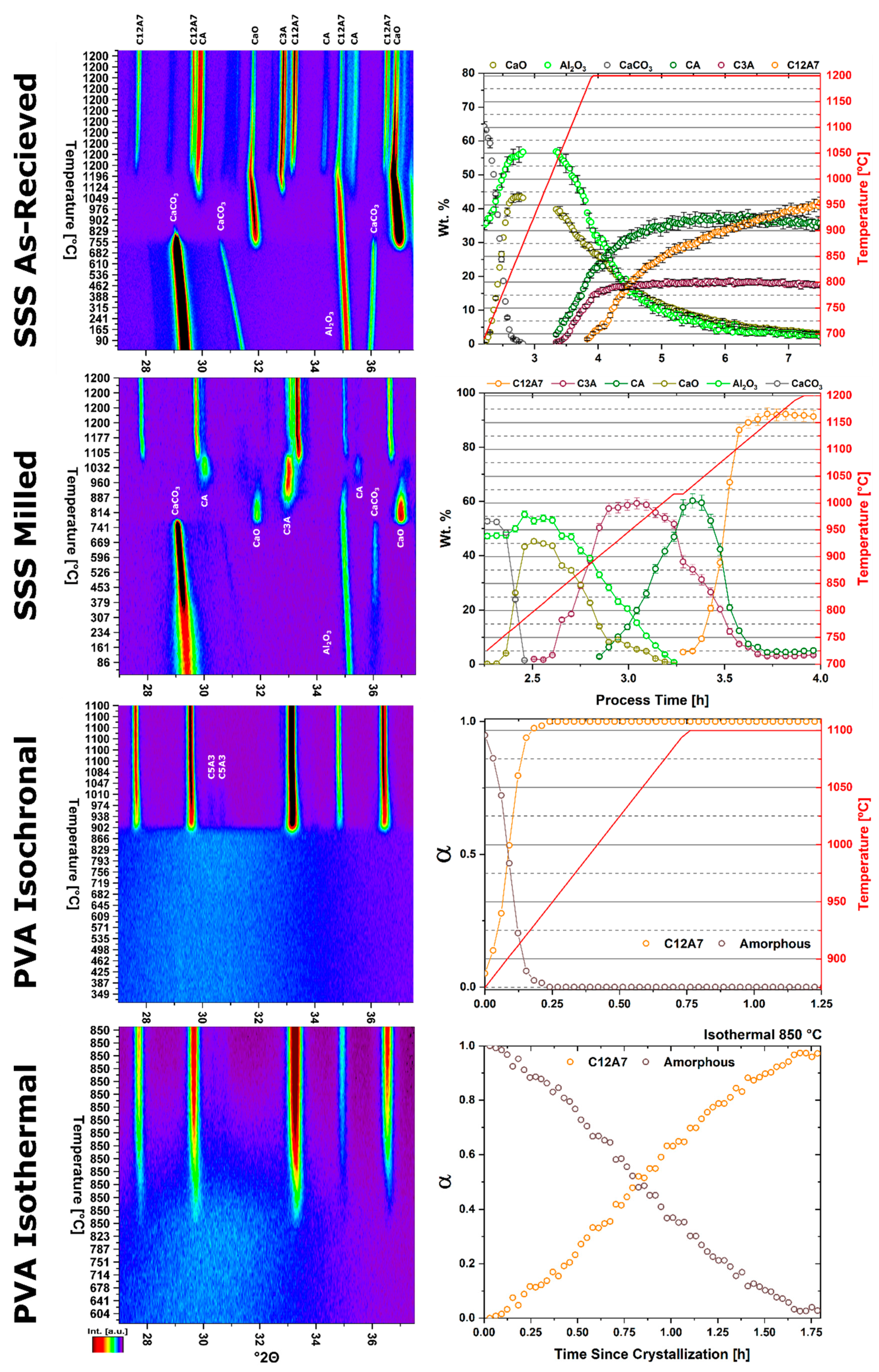
The kinetic pathway toward C12A7 equilibrium displays changes in the rate of reaction and a decrease in temperature; the following discussion pertains to ambient atmosphere characterization. Large reactant heterogeneity exists when the CaCO3 particles are orders of magnitude larger than the Al2O3 particles. In this case, the kinetic pathway demonstrates evolution through off-C12A7 stoichiometry phases C3A and CA with the latter Al-rich phase showing a larger concentration. C12A7 formation is not observed until approximately 1200 °C and the system approaches an equilibrium of C3A, CA, and C12A7. No three-phase region exists in the thermodynamic phase diagram indicating the system is not yet at equilibrium, and, with increased process time, reaction of C3A + CA to C12A7 should occur. The kinetic characterization shows clear diffusion-type behavior as the diffusion pathways are long and grow longer with continued formation of C12A7. This is typical behavior for solid-state reaction synthesis and results in the need of the iterative process of firing, grinding, and pressing usually implemented to disrupt this long diffusion pathway and facilitate reaction of the off-stoichiometry phases.
The alternative to grinding after the initial reaction is milling the initial starting reactants to lower the degree of mixture heterogeneity. In this study the reactants are milled until both CaCO3 and Al2O3 reactants have particle sizes on the order of 100 nm. This reduction in heterogeneity, when compared to the high heterogenous as-received reactants, leads to a reduction in the formation temperature by 15% to approximately 1000 °C with most of the formation occurring above 1050 °C. The kinetic pathway follows the same route through off-stoichiometric C3A and CA phases, however, the rate of formation of these phases and C12A7 is drastically increased. The ultimate C12A7 concentration of >90 wt% is achieved after 0.5 h. A non-equilibrium state of C3A, CA, and C12A7 is observed but the concentration of C12A7 has more than doubled. The type of kinetic transformation cannot be determined as the formation occurs in a non-isothermal region, but under dry conditions a JMAK-type kinetic formation is observed that can be assumed to be the type of kinetic transformation under ambient conditions as well. This indicates that nucleation and growth of the C12A7 phase, rather than long-range diffusion, is the limiting factor in phase formation.
If the highly-heterogenous solid-state reactant mixture represents the extreme of heterogeneity, an amorphous sol-gel reactant represents the opposite extreme, where atomic level homogeneity eliminates reactant heterogeneity. The formation temperature of C12A7 reduces 30% from the heterogeneous extreme to 850 °C with C12A7 being the first and only crystalline phase to form. Previously, thermodynamic studies have proposed the pathway through C5A3 and C3A to be the low temperature formation pathway [
6,
7]. For homogeneous reactants, this pathway is not present. At these low temperatures, diffusion does not readily occur and kinetically favorable phases, which are often disordered, lower-density phases, will form [
18]. In the calcium aluminate system C3A (ρ
theoretical = 3.064 g/cm
3), C5A3 (ρ
theoretical = 3.067 g/cm
3), and CA (ρ
theoretical = 2.94 g/cm
3) are all ordered higher-density phases while C12A7 (ρ
theoretical = 2.68 g/cm
3) forms a disordered clathrate structure with a large amount of crystallographic void space [
19,
20,
21,
22]. Therefore, there is no precursor crystalline phase and C12A7 is the only favorable phase to form at low temperature. The kinetic formation of C12A7 under these conditions exhibits JMAK-type behavior with an
n value approaching 2; however, the existence of a non-uniform growth rate (best observed under dry and vacuum conditions) invalidates physical representation of the
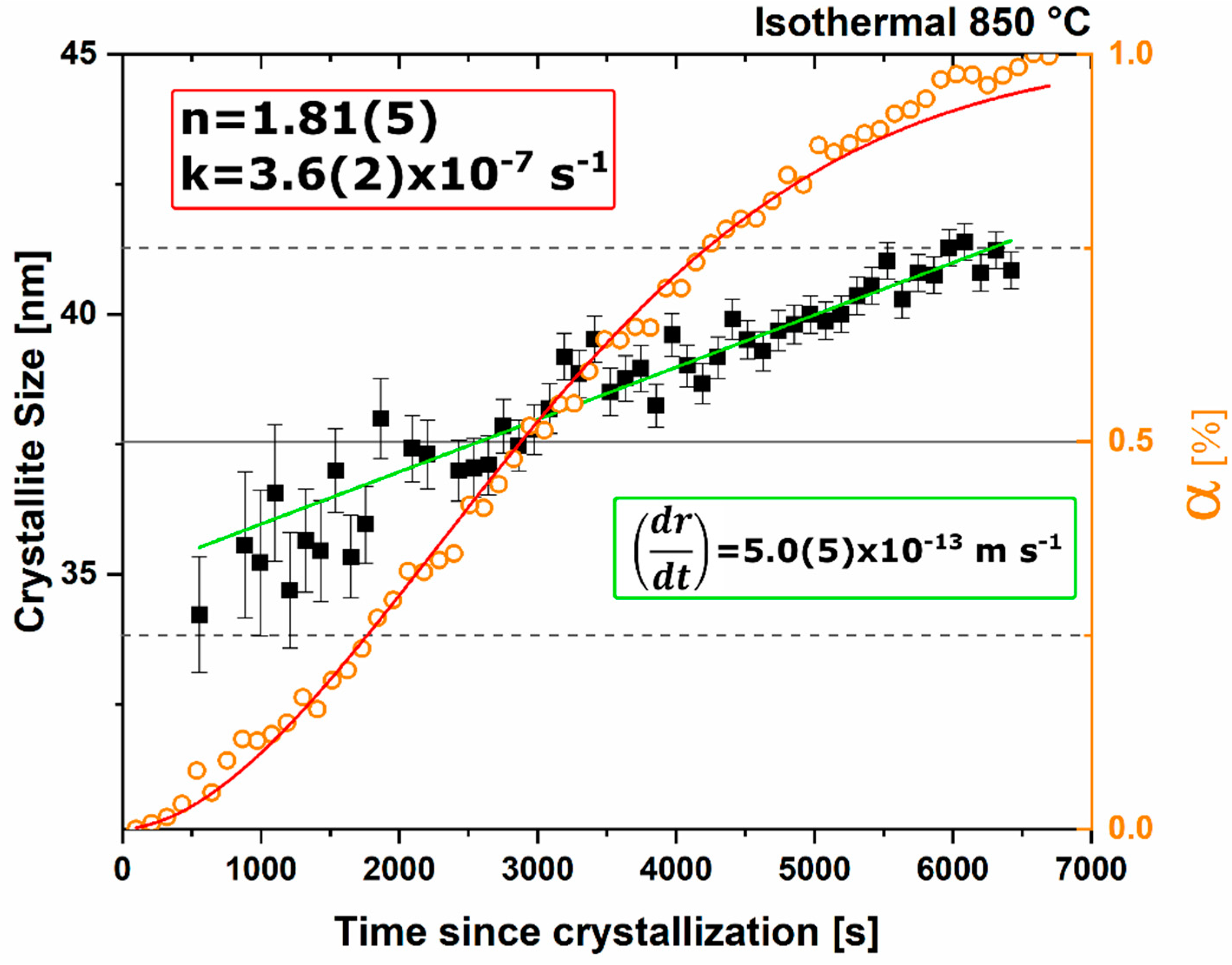
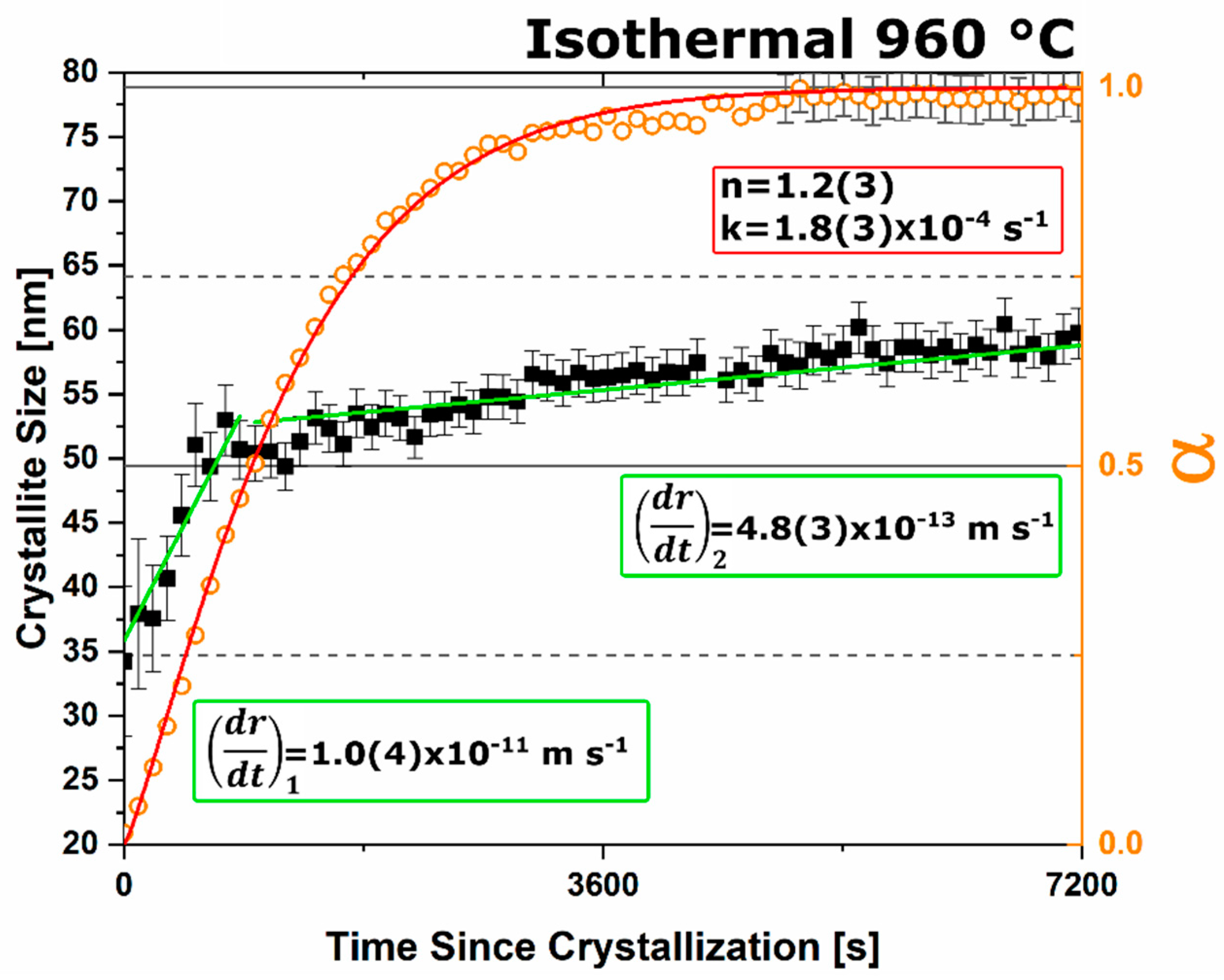
n value. The lack of diffusion-driven thermodynamic behavior leads to a slowly evolving microstructure with crystallite size of ~40 nm.
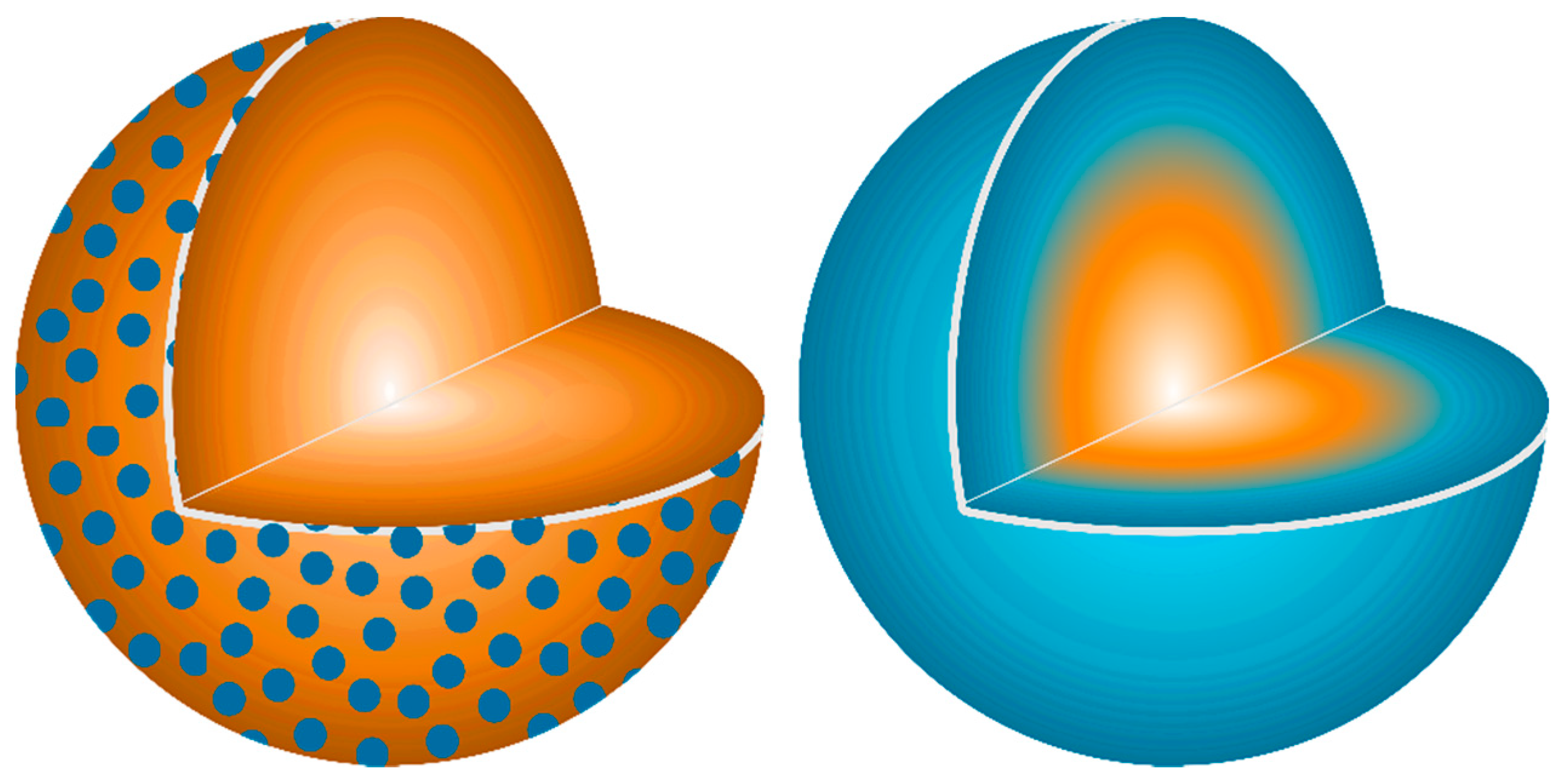
A physical relationship between reactant homogeneity and the observed behavior is shown in
Figure 12. In the heterogenous reactant case (
Figure 12A) a large portion of the Ca stoichiometry is trapped at the center of the large CaCO
3 particles and is essentially blind to the ensuing reactions after decomposition to CaO. This leads to local Al-rich regions and highly reactive Al
2O
3 particles due to their higher surface area explaining the preferential formation of the aluminum-rich CA phase. The long distance to the Ca stoichiometry limits the reaction yielding diffusion-limited kinetic behavior.
When the particle size is reduced as in
Figure 12B, both reactants have equivalent surface area and reactivity leading to high nucleation and growth of the thermodynamically-favored C12A7 phase. The shorter diffusion pathways change the limiting kinetic behavior from the availability of stoichiometry to the nucleation, growth, and impingement of nucleates; this is a process that requires less energy, lowering the formation temperature and accelerating the reaction.
When reactant heterogeneity is removed, and atomic homogeneity is achieved as in
Figure 12C, formation of C12A7 requires the diffusion of atoms on the order of single atomic spacings. The kinetic behavior is also controlled by the nucleation, growth, and impingement of nuclei giving the observed JMAK behavior. The controlling kinetic process in C12A7 formation is dependent on reactant heterogeneity and diffusion of cationic/anionic pairs, indicating a microstructural and processing behavior which varies as the reactant mixture changes. The intrinsic behavior of the system without microstructural influence is revealed if diffusion is not required. Under these conditions, C12A7 is the only phase to form as it is the most disordered and lowest density calcium aluminate phase and kinetically favorable to form at low temperatures.
4.2. C12A7 Atmospheric Effects on Thermodynamic Stability
The role of process atmosphere has a significant, systematic effect on the stability and occluded anion chemistry of the C12A7 structure and, by correlation, its properties and application. C12A7 is the thermodynamically-favorable structure under humid, ambient conditions. Furthermore, the literature thoroughly establishes that the C12A7 structure is thermodynamically unfavored in non-humid atmospheres (e.g., dry or vacuum conditions) at elevated temperatures (>1050 °C). This includes both thermodynamically-calculated phase diagrams and experimental results [
2,
4]. The kinetic characterization for dry (~150 ppm H
2O) and vacuum atmospheres reported herein supports the instability of C12A7 under non-humid atmospheres but details a formation pathway contrary to that reported in thermodynamic studies. Under dry conditions the formation of C12A7 occurs but it is only an intermediary phase en route to the final C5A3 thermodynamic equilibrium. Under vacuum conditions no C12A7 forms and, by correlation, no C5A3 leading to a C3A and CA thermodynamic equilibrium.
With heterogenous reactants under a dry atmosphere the formation pathways remain the same as under ambient conditions, albeit with an additional step in the kinetics related to the decomposition of C12A7 to the thermodynamically-favored phase C5A3. When heterogeneity is high, C12A7 formation and C5A3 formation occurs slowly due to the diffusive nature of the formation process. As the reactants are milled and heterogeneity is decreased, the formation of C12A7 and C5A3 initially occur with JMAK-type kinetic behavior leading to rapid phase formation. The formation of C5A3 follows the formation of C12A7 with an increase in temperature supporting the decomposition of C12A7 to C5A3 formation mechanism. Comparison of the extended behavior at 1200 °C confirms this reaction; a linearly decreasing rate is observed, consistent with a particle conversion process. Initially JMAK-type behavior is observed as C5A3 nucleates on the outside of the C12A7 particles. As the formation process proceeds, the inward conversion of the C12A7 particle leads to a change in the limiting kinetic process,
Figure 13.
With heterogenous reactants under a vacuum atmosphere only the high-heterogeneity characterization was performed to protect vacuum integrity. No C5A3 formation from C12A7 was observed. The combined long-diffusion pathways and lack of atmospheric oxygen further precludes C12A7 formation, with oxygen as the occluded anion, which prevents the kinetic decomposition and transformation to C5A3. C5A3 itself does not appear to form from C3A and CA, indicating it is only favorable to form through the kinetic pathway with C12A7 as an intermediary phase.
This represents a shift in the understanding of the C12A7 phase space where C5A3 and C3A are currently reported as the low temperature formation routes to C12A7 and to calcium aluminates in general [
6,
7]. In these kinetics studies C5A3 was never observed as an intermediary product to C12A7 formation regardless of atmosphere and reactant homogeneity. C5A3 is only a product that is formed through the decomposition of C12A7. This is a discrepancy when considering thermodynamic studies of calcium aluminate formation, however, review of the relevant literature shows that a misclassification of the C12A7 as C5A3 has led to the dialog where C5A3 and C3A are the intermediary phases; this justification is provided in the
supplementary information [
6,
7]. When this correction is made the results from the thermodynamic studies support the observed kinetic behavior and C5A3 should be considered a decomposition product of C12A7 and not an intermediary phase in the formation of calcium aluminates. The presence of C5A3 indicates a lack of sufficient moisture to stabilize the C12A7 structure after formation at elevated temperatures above 1050 °C.
4.3. C12A7 Atmospheric Effects on Kinetic Stability
Thermodynamic equilibrium drives the system kinetics to the lowest free energy phase; however, the process inherently requires the diffusion of cationic and anionic species in ionic materials. When in a temperature regime where this diffusion is sluggish, the thermodynamic equilibrium may not be achieved due to sluggish kinetics and instead a new kinetic equilibrium exists. The kinetic equilibrium is characterized by phases favored by limited diffusion. As the reactant mixture heterogeneity is removed and atomic level homogeneity is achieved diffusion is no longer the limit to formation and C12A7 is observed as the first crystalline phase at a temperature 30% lower than with heterogenous reactants. C12A7 is the kinetically-favored phase to form under ambient conditions and as the atmosphere is changed C12A7 is still the predominant phase to form regardless of the thermodynamic equilibrium characterized at higher temperatures.
Under dry and vacuum environments C12A7 is still the first crystalline phase to form from the amorphous precursor, but the formation temperature is increased from 850 °C under humid environments to 900 and 960 °C for dry conditions and under a vacuum, respectively. This change in temperature also comes with a change in the evolution of the microstructure and fitted JMAK behavior. The change in temperature indicates a change in the activation energy for C12A7 formation indicating a change in the formation process as a function of atmosphere. Initially hydration and the hydroxide occluded anion play a role in the formation kinetics. When this moisture is removed, the increase in temperature indicates that the formation of just oxygen occupied cages has a higher activation energy. The further increase in temperature with the removal of oxygen partial pressure can be characterized by a change in the occluded anion source from the atmosphere to purely the reactant mixture. This process requires solid-state rather than atmosphere-solid interface diffusion leading to the higher observed formation temperature correlated to a higher activation energy.
The change in the source of the anionic species leads to the observed change of the fitted kinetic parameters. A two-stage nuclei-growth behavior is observed under dry and vacuum conditions where rapid growth is observed for the first 50% of the transformation followed by a slower growth rate that is equivalent to the growth rate under ambient humid atmospheric conditions. The change is the removal of moisture and the lack of hydroxide occupied cages. In C12A7 the rate of diffusion for
vs.
is higher allowing for rapid diffusion of oxygen [
4,
23]. The diffusion within ionic materials requires the co-diffusion of cation and anionic species. With this change in occluded anion mobility the extra framework oxygen can quickly diffuse to the growing particle interface, which facilitates the diffusion of only cationic species, rather than the combined diffusion of anionic and cationic species, to lead to further growth. In the presence of rapid diffusion of oxygen to the surface of the C12A7 particle, only the diffusion of cationic species is required. Control over the change in occluded anion through processing conditions will aid in the application of C12A7 where either
or
are desired; this is especially true in catalytic applications where oxygen mobility, and by correlation catalytic efficiency, is limited by the presence of the slow hydroxyl species [
4,
24,
25].
This is the first report of crystallization of C12A7 in a non-carbonaceous vacuum environment and is achieved by limiting the expression of the thermodynamic equilibrium in favor of the kinetic equilibrium; this raises the issue of the source of the occluded anion which has historically been correlated to the atmosphere. The decomposition of PVA results in an amorphous low C content precursor which is white in color after calcining at 600 °C. The PVA reactant consists of Ca-O and Al-O complexes with no long-range order and when viewed stoichiometrically CaO and Al
2O
3 requires no additional oxygen to reach oxy-C12A7 stoichiometry.
When diffusion pathways are short this extra oxygen could be used to template the cages and form C12A7 without the addition of atmospheric oxygen. This observation represents a fundamental shift in the perception that no template anion is present in reducing non-oxidizing atmospheric conditions [
3]. The compromise for sourcing the stabilizing anion from the reactant mixture is the needed increase in energy to promote diffusion which leads to a formation temperature 110 °C higher than under a humid environment; this also enters an energy regime where the thermodynamic equilibrium can be expressed leading to the concurrent formation of C3A and CA. When atomic homogeneity exists, the short diffusion pathways allows for reactant mixture occluded oxygen to template the C12A7 structure under vacuum conditions.
5. Conclusions
In situ rapid XRD data provide insight into the kinetics of solid-state phase transformations and represents a valuable tool to further understand the evolution of materials toward thermodynamic equilibrium. Through this characterization a new understanding of the evolution of phase formation and thermodynamic and kinetic stability of various calcium aluminates, and especially C12A7, formation has been presented.
The kinetics and process variables for calcium aluminate formation are directly related to the physical heterogeneity of the reactant mixture. By decreasing reactant heterogeneity, the rate of reaction and the temperature of phase formation can be controlled. When reactant homogeneity is eliminated, C12A7 no longer requires intermediary crystalline phases and forms directly form the reactant mixture. It was previously understood that C5A3 and C3A, along with C3A and CA, were preferred formation pathways to C12A7 and that C5A3 and C3A are the initial intermediary phases to all calcium aluminates. In situ kinetic studies highlight that this is not the case and that C3A and CA, and direct crystallization to C12A7, are the formation pathways under heterogenous and homogeneous conditions, respectively. C5A3 is a decomposition product of C12A7 and is only observed to form through a kinetic pathway related to a particle conversion transformation.
The thermodynamic equilibrium for a Ca:Al ratio of 12:14, given enough time for all kinetic processes to complete, is as follows:
- (1)
Ambient Conditions: C12A7
- (2)
Dry (≤150 ppm H2O) Conditions: C5A3 through C12A7 particle conversion process
- (3)
Vacuum Conditions: C3A and CA
The thermodynamic equilibrium is contrasted by the kinetic equilibrium observed at temperatures below 1000 °C with a homogeneous reactant mixture. C12A7 is the predominate phase (≥80 wt%) to form under ambient, dry, and vacuum conditions. When the temperature is raised, the thermodynamic equilibrium ultimately results with decomposition of C12A7 to C5A3 under dry and vacuum conditions; the rate of decomposition is higher under vacuum conditions. The presence of C12A7 formation under vacuum conditions demonstrates that the anion source is not solely derived from the process atmosphere but also from the reactant mixtures. This is the first reported formation of C12A7 under vacuum conditions due to the favorable kinetic conditions. With the correlation of reactant heterogeneity and process atmosphere understood, synthesis and processing of calcium aluminates, including the highly functional C12A7, can be better controlled for desired micro- and atomic structured products.