Fracture Toughness Evaluation and Plastic Behavior Law of a Single Crystal Silicon Carbide by Nanoindentation
Abstract
:1. Introduction
1.1. Silicon Carbide
1.2. Fracture Toughness Measurement Using Nanoindentation
1.3. Estimation of Flow Properties Using Nanoindentation Experiments
2. Materials and Methods
3. Results and Discussion
3.1. Berkovich Indentation on SiC-6H Single Crystal
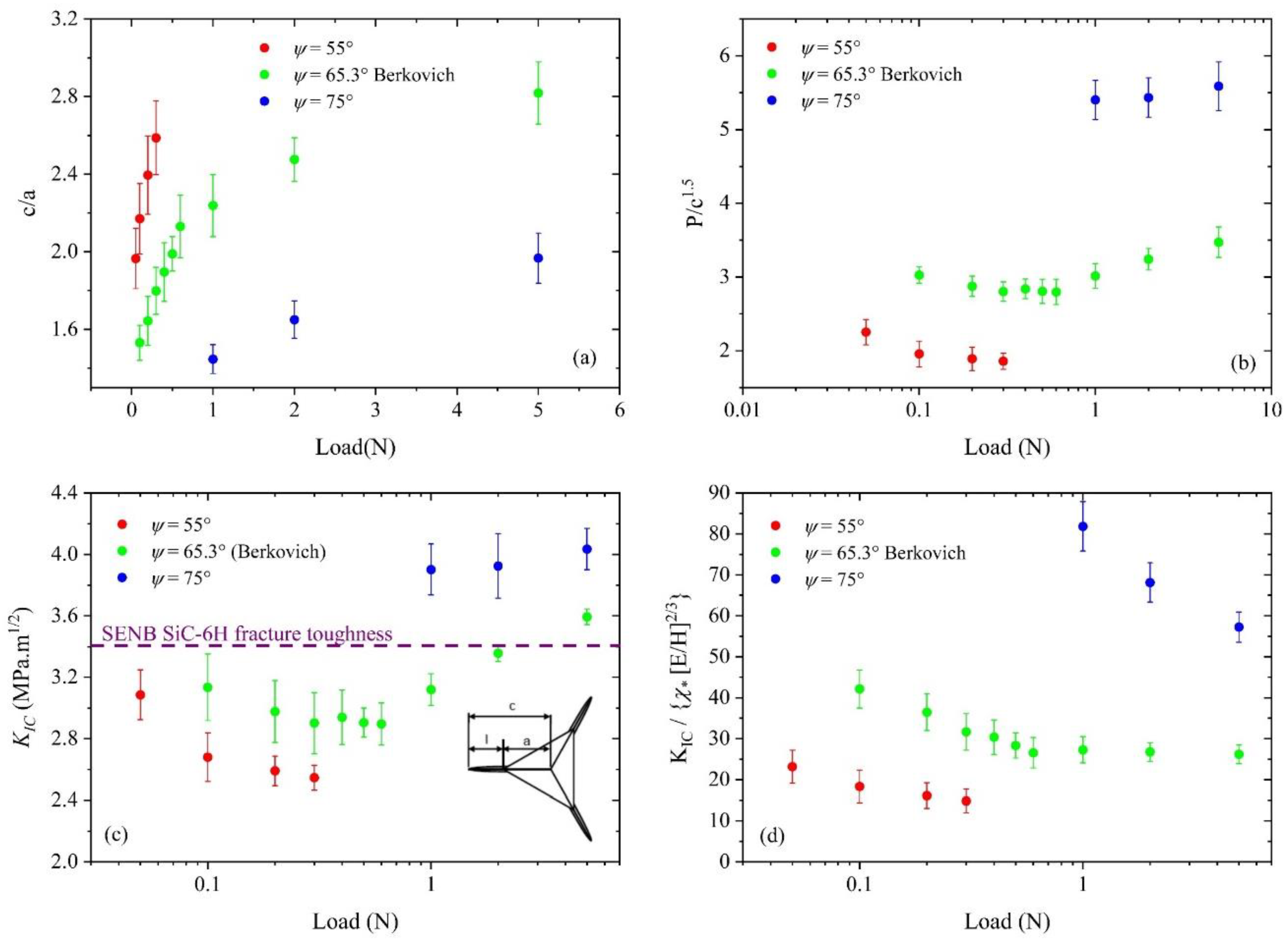
3.2. Indentation Cracking in SiC-6H
3.2.1. Orientation Effects in SiC-6H Single Crystals during Indentation in the <0001> Direction
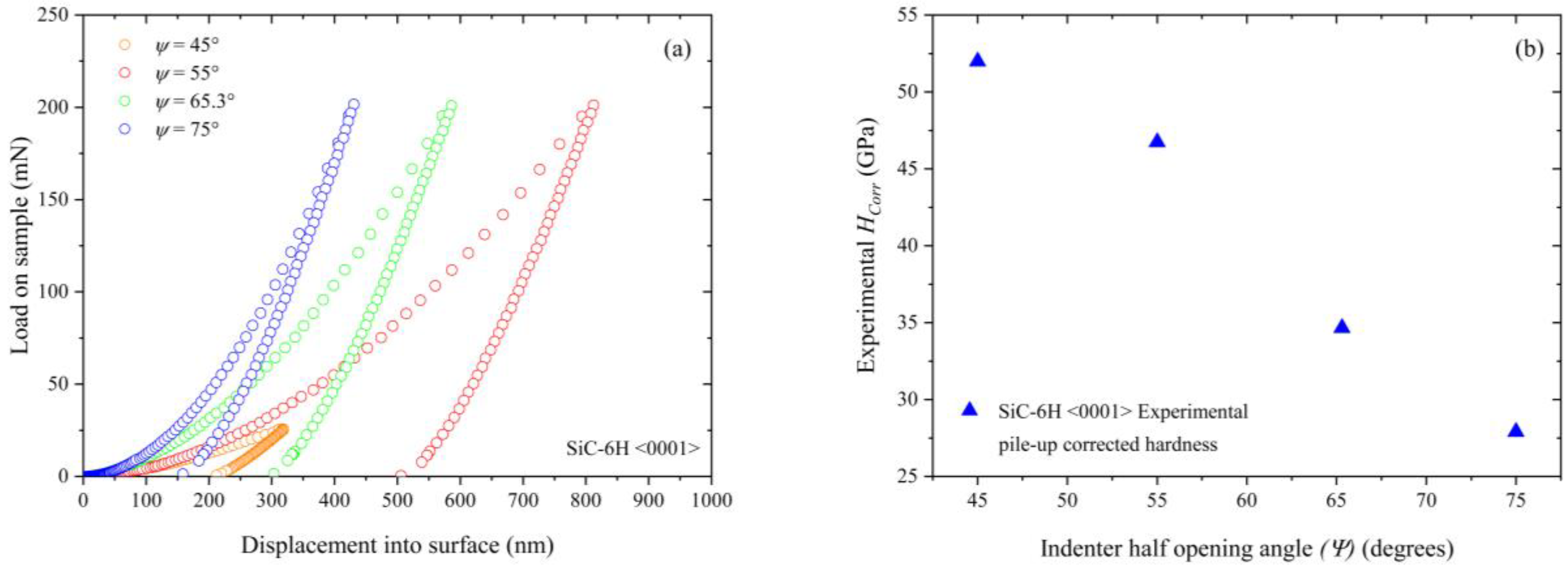
3.2.2. Influence of Indenter Angle (Centerline-to-Face) on Cracking in SiC-6H(0001)
3.3. Fracture Toughness Measurement in SiC-6H(0001)
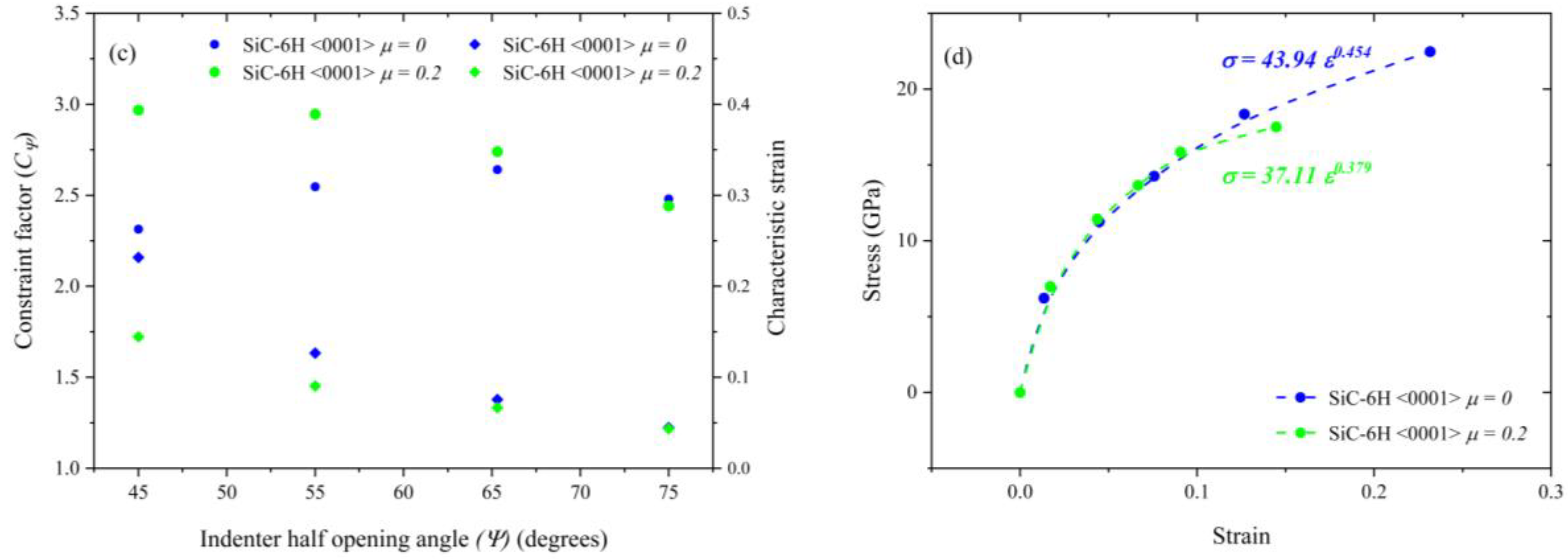
3.4. Extraction of Flow Properties
4. Conclusions
- There is no significant indenter orientation dependence when indented in the <0001> direction using a Berkovich indenter, indicating that SiC-6H is a transversely isotropic material.
- It was found as expected that the sharper indenters produce more strains in the material and longer cracks for a given peak load. The surface cracking patterns are similar for all pyramidal indenters used in this research. This does not consider any subsurface cracking that might occur due to different pyramidal indenters. It is also possible that there might be lateral subsurface cracking at higher loads along with possible phase transformation in the material at higher loads for a particular indenter. Further careful study of the subsurface cracking needs to be done for a better understanding of the effects of cracking on fracture toughness.
- Fracture toughness measurements were carried out, and the Jang and Pharr model based on the Lawn model and the Laugier models were evaluated for different pyramidal indenters. It was found that within the range of our testing loads, the Jang and Pharr model for the fracture toughness measurement works better for estimating the fracture toughness of SiC-6H in the <0001> direction. It was also found that for a Berkovich indenter, the Lawn model, which is for medial radial cracking modes, gives approximately constant values at low loads (<1 N). It was also found that for a Berkovich indentation experiments in SiC-6H in the <0001> direction, at higher loads (>1 N), the Laugier model gives constant fracture toughness values. It is conceivable that there is a change in the cracking modes in this range of loads. Since most indentation fracture toughness models are developed using assumptions based on the top view of residual impressions, it becomes apparent based on the experimental results that careful consideration and attention must be given to possible changes in cracking, phase transitions and other mechanisms with increasing loads along with the indenter geometry.
- Finite element analysis using equivalent cones was used along with measured hardness values to estimate the yield strength, the work hardening exponents and the stress–strain curve for single crystal SiC-6H in the <0001> direction. It was found that it is possible to estimate the stress–strain curve, the yield strength of a material and the Holloman fit constants for a brittle material like SiC-6H, provided accurate information about friction coefficients is available. Verification of the stress–strain curve is not possible due to the non-availability of room temperature uniaxial stress–strain curves. The results obtained in this study show good agreement with previous researchers.
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Fisher, G.R.; Barnes, P. Towards a unified view of polytypism in silicon carbide. Philos. Mag. Part B 1990, 61, 217–236. [Google Scholar] [CrossRef]
- Bechstedt, F.; Käckell, P.; Zywietz, A.; Karch, K.; Adolph, B.; Tenelsen, K.; Furthmüller, J. Polytypism and Properties of Silicon Carbide. Phys. Status Solidi B 1997, 202, 35–62. [Google Scholar] [CrossRef]
- Shaffer, P. A review of the structure of silicon carbide. Acta Crystallogr. Sect. B 1969, 25, 477–488. [Google Scholar] [CrossRef] [Green Version]
- Page, T.F.; Oliver, W.C.; McHargue, C.J. The deformation behavior of ceramic crystals subjected to very low load (nano)indentations. J. Mater. Res. 1992, 7, 450–473. [Google Scholar] [CrossRef]
- Pierson, H.O. Handbook of Refractory Carbides & Nitrides; William Andrew: Norwich, NY, USA, 1996. [Google Scholar]
- Snead, L.L.; Nozawa, T.; Katoh, Y.; Byun, T.-S.; Kondo, S.; Petti, D.A. Handbook of SiC properties for fuel performance modeling. J. Nucl. Mater. 2007, 371, 329–377. [Google Scholar] [CrossRef]
- Powell, A.R.; Rowland, L.B. SiC materials-progress, status, and potential roadblocks. Proc. IEEE 2002, 90, 942–955. [Google Scholar] [CrossRef]
- Korsunsky, A.M.; McGurk, M.R.; Bull, S.J.; Page, T.F. On the hardness of coated systems. Surf. Coat. Technol. 1998, 99, 171–183. [Google Scholar] [CrossRef]
- Herbert, E.G.; Tenhaeff, W.E.; Dudney, N.J.; Pharr, G.M. Mechanical characterization of LiPON films using nanoindentation. Thin Solid Films 2011, 520, 413–418. [Google Scholar] [CrossRef]
- Borrero-López, O.; Hoffman, M.; Bendavid, A.; Martin, P.J. A simple nanoindentation-based methodology to assess the strength of brittle thin films. Acta Mater. 2008, 56, 1633–1641. [Google Scholar] [CrossRef]
- Hainsworth, S.V.; McGurk, M.R.; Page, T.F. The effect of coating cracking on the indentation response of thin hard-coated systems. Surf. Coat. Technol. 1998, 102, 97–107. [Google Scholar] [CrossRef]
- Nair, A.K.; Cordill, M.J.; Farkas, D.; Gerberich, W.W. Nanoindentation of thin films: Simulations and experiments. J. Mater. Res. 2009, 24, 1135–1141. [Google Scholar] [CrossRef] [Green Version]
- Nix, W.D.; Gao, H. Indentation size effects in crystalline materials: A law for strain gradient plasticity. J. Mech. Phys. Solids 1998, 46, 411–425. [Google Scholar] [CrossRef]
- Ma, Q.; Clarke, D.R. Size dependent hardness of silver single crystals. J. Mater. Res. 1995, 10, 853–863. [Google Scholar] [CrossRef]
- Beake, B.D.; Goodes, S.R.; Smith, J.F. Nanoscale materials testing under industrially relevant conditions: High-temperature nanoindentation testing. Z. Met. 2003, 94, 798–801. [Google Scholar] [CrossRef]
- Constantinides, G.; Tweedie, C.A.; Holbrook, D.M.; Barragan, P.; Smith, J.F.; van Vliet, K.J. Quantifying deformation and energy dissipation of polymeric surfaces under localized impact. Mater. Sci. Eng. A 2008, 489, 403–412. [Google Scholar] [CrossRef]
- Wright, W.J.; Nix, W.D. Storage and loss stiffnesses and moduli as determined by dynamic nanoindentation. J. Mater. Res. 2009, 24, 863–871. [Google Scholar] [CrossRef]
- Lucas, B.N.; Oliver, W.C. Indentation power-law creep of high-purity indium. Metall. Mater. Trans. A 1999, 30, 601–610. [Google Scholar] [CrossRef]
- Su, C.; Herbert, E.G.; Sohn, S.; LaManna, J.A.; Oliver, W.C.; Pharr, G.M. Measurement of power-law creep parameters by instrumented indentation methods. J. Mech. Phys. Solids 2013, 61, 517–536. [Google Scholar] [CrossRef]
- Mann, A.B.; Pethica, J.B. Nanoindentation Studies in a Liquid Environment. Langmuir 1996, 12, 4583–4586. [Google Scholar] [CrossRef]
- Sharpe, W.N.; Beheim, G.M.; Evans, L.J.; Nemeth, N.N.; Jadaan, O.M. Fracture Strength of Single-Crystal Silicon Carbide Microspecimens at 24 °C and 1000 °C. J. Microelectromech. Syst. 2008, 17, 244–254. [Google Scholar] [CrossRef]
- Sharpe, W.N., Jr.; Jadaan, O.; Beheim, G.M.; Quinn, G.D.; Nemeth, N.N. Fracture strength of silicon carbide microspecimens. J. Microelectromech. Syst. 2005, 14, 903–913. [Google Scholar] [CrossRef]
- Nakao, S.; Ando, T.; Chen, L.; Mehregany, M.; Sato, K. Mechanical characterization of SiC film at high temperatures by tensile test. In Proceedings of the 2008 IEEE 21st International Conference on Micro Electro Mechanical Systems, Wuhan, China, 13–17 January 2008; pp. 447–450. [Google Scholar]
- Henshall, J.L.; Rowcliffe, D.J.; Edington, J.W. Fracture Toughness of Single-Crystal Silicon Carbide. J. Am. Ceram. Soc. 1977, 60, 373–375. [Google Scholar] [CrossRef]
- Liang, K.M.; Orange, G.; Fantozzi, G. Evaluation by indentation of fracture toughness of ceramic materials. J. Mater. Sci. 1990, 25, 207–214. [Google Scholar] [CrossRef]
- Niihara, K. Slip systems and plastic deformation of silicon carbide single crystals at high temperatures. J. Less Common Met. 1979, 65, 155–166. [Google Scholar] [CrossRef]
- Sawyer, G.R.; Sargent, P.M.; Page, T.F. Microhardness anisotropy of silicon carbide. J. Mater. Sci. 1980, 15, 1001–1013. [Google Scholar] [CrossRef]
- Henshall, J.L.; Brookes, C.A. The Measurement of Kic in Single-Crystal Sic Using the Indentation Method. J. Mater. Sci. Lett. 1985, 4, 783–786. [Google Scholar] [CrossRef]
- Miyoshi, K.; Buckley, D.H. Friction and Deformation Behavior of Single-Crystal Silicon Carbide; NASA-TP-1053; NASA Lewis Research Center: Cleveland, OH, USA, 1977. [Google Scholar]
- Qian, J.; Daemen, L.L.; Zhao, Y. Hardness and fracture toughness of moissanite. Diam. Relat. Mater. 2005, 14, 1669–1672. [Google Scholar] [CrossRef]
- Page, T.F.; Riester, L.; Hainsworth, S.V. The Plasticity Response of 6H-Sic and Related Isostructural Materials to Nanoindentation: Slip vs Densification. MRS Online Proc. Libr. 1998, 522. [Google Scholar] [CrossRef]
- Kitahara, H.; Noda, Y.; Yoshida, F.; Nakashima, H.; Shinohara, N.; Abe, H. Mechanical behavior of single crystalline and polycrystalline silicon carbides evaluated by Vickers indentation. J. Ceram. Soc. Jpn. 2001, 109, 602–606. [Google Scholar] [CrossRef]
- Yan, J.; Gai, X.; Harada, H. Subsurface damage of single crystalline silicon carbide in nanoindentation tests. J. Nanosci. Nanotechnol. 2010, 10, 7808–7811. [Google Scholar] [CrossRef] [PubMed]
- Datye, A.; Li, L.; Zhang, W.; Wei, Y.J.; Gao, Y.F.; Pharr, G.M. Extraction of Anisotropic Mechanical Properties From Nanoindentation of SiC-6H Single Crystals. J. Appl. Mech. 2016, 83, 091003. [Google Scholar] [CrossRef] [Green Version]
- Lawn, B.R.; Evans, A.G.; Marshall, D.B. Elastic/Plastic Indentation Damage in Ceramics: The Median/Radial Crack System. J. Am. Ceram. Soc. 1980, 63, 574–581. [Google Scholar] [CrossRef]
- Anstis, G.R.; Chantikul, P.; Lawn, B.R.; Marshall, D.B. A Critical Evaluation of Indentation Techniques for Measuring Fracture Toughness: I, Direct Crack Measurements. J. Am. Ceram. Soc. 1981, 64, 533–538. [Google Scholar] [CrossRef]
- Laugier, M.T. Palmqvist indentation toughness in WC-Co composites. J. Mater. Sci. Lett. 1987, 6, 897–900. [Google Scholar] [CrossRef]
- Jang, J.-I.; Pharr, G.M. Influence of indenter angle on cracking in Si and Ge during nanoindentation. Acta Mater. 2008, 56, 4458–4469. [Google Scholar] [CrossRef]
- Gong, J.; Wang, J.; Guan, Z. Indentation toughness of ceramics: A modified approach. J. Mater. Sci. 2002, 37, 865–869. [Google Scholar] [CrossRef]
- Dukino, R.D.; Swain, M.V. Comparative Measurement of Indentation Fracture Toughness with Berkovich and Vickers Indenters. J. Am. Ceram. Soc. 1992, 75, 3299–3304. [Google Scholar] [CrossRef]
- Shim, S.; Jang, J.-I.; Pharr, G.M. Extraction of flow properties of single-crystal silicon carbide by nanoindentation and finite-element simulation. Acta Mater. 2008, 56, 3824–3832. [Google Scholar] [CrossRef]
- Berkovich, E.S. Three-faceted diamond pyramid for micro-hardness testing. Ind. Diam. Rev. 1951, 11, 129–133. [Google Scholar]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Shim, S.; Bei, H.; George, E.P.; Pharr, G.M. A different type of indentation size effect. Scr. Mater. 2008, 59, 1095–1098. [Google Scholar] [CrossRef]
- Shaffer, P.T.B. Effect of Crystal Orientation on Hardness of Silicon Carbide. J. Am. Ceram. Soc. 1964, 47, 466. [Google Scholar] [CrossRef]
- Li, C.; Zhang, F.H.; Meng, B.B.; Ma, Z.K. Simulation and Experiment on Surface Morphology and Mechanical Properties Response in Nano-Indentation of 6H-SiC. J. Mater. Eng. Perform. 2017, 26, 1000–1009. [Google Scholar] [CrossRef]
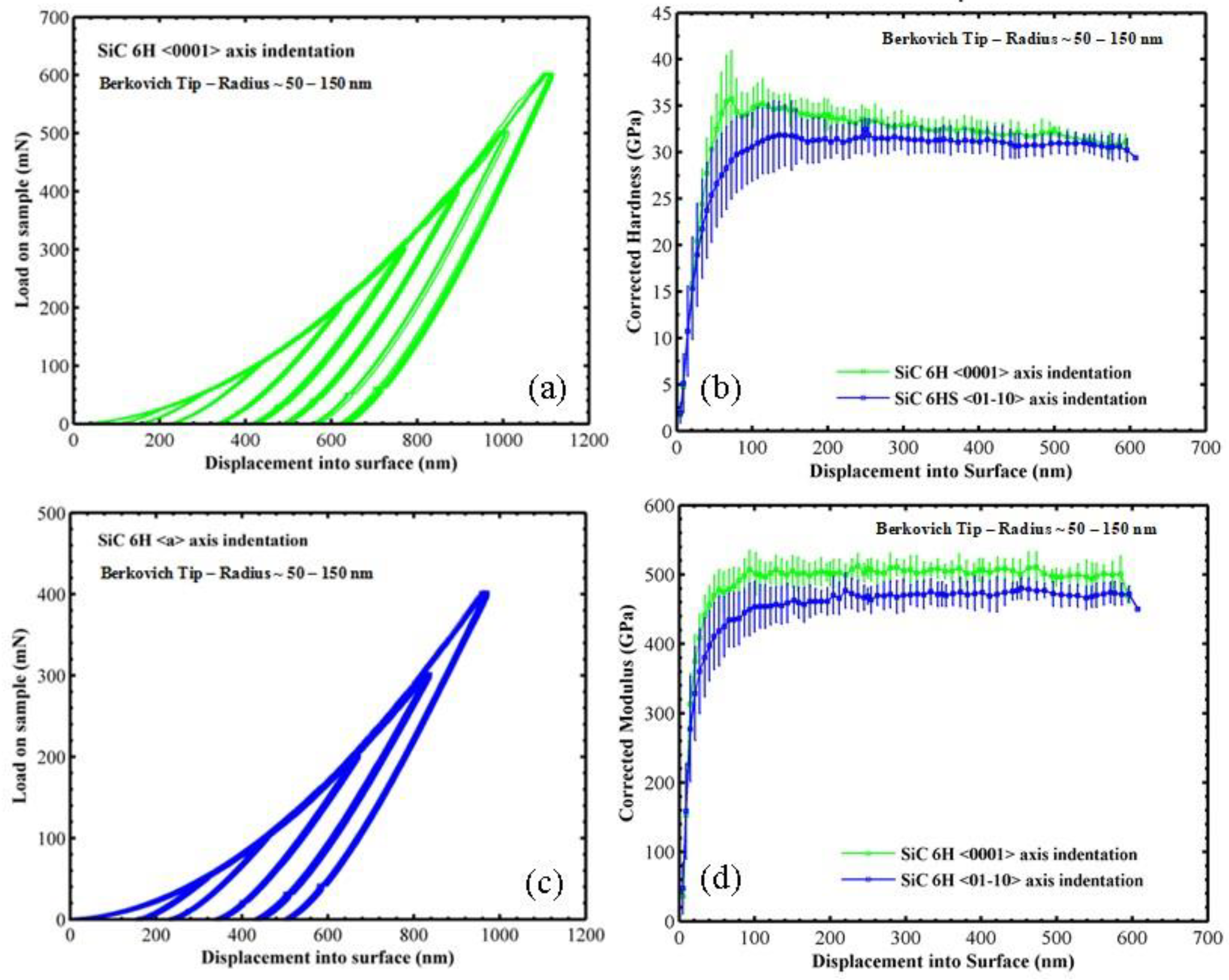



| SiC-6H—Indentation Direction | Berkovich Indentation | |||
|---|---|---|---|---|
| EOP | HOP | ECorr | HCorr | |
| (GPa) | (GPa) | (GPa) | (GPa) | |
| <0001> | 549.66 ± 20.63 | 40.97 ± 1.21 | 503.13 ± 28.19 | 32.26 ± 5.01 |
| <01-10> | 513.71 ± 19.84 | 39.13 ± 0.79 | 461.94 ± 22.49 | 30.81 ± 2.1 |
 | EOP | HOP | c/a |
|---|---|---|---|
| (GPa) | (GPa) | @ 500 mN | |
| R1 (θ ≈ 19°) | 543.81 ± 27.13 | 49.70 ± 3.67 | 1.97 ± 0.06 |
| R2 (θ ≈ 12°) | 546.58 ± 29.29 | 49.64 ± 3.14 | 1.96 ± 0.09 |
| R3 (θ ≈ 5°) | 545.64 ± 24.46 | 49.08 ± 2.75 | 2.03 ± 0.07 |
| R4 (θ ≈ 7°) | 542.77 ± 21.44 | 48.85 ± 2.49 | 1.98 ± 0.13 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Datye, A.; Schwarz, U.D.; Lin, H.-T. Fracture Toughness Evaluation and Plastic Behavior Law of a Single Crystal Silicon Carbide by Nanoindentation. Ceramics 2018, 1, 198-210. https://doi.org/10.3390/ceramics1010017
Datye A, Schwarz UD, Lin H-T. Fracture Toughness Evaluation and Plastic Behavior Law of a Single Crystal Silicon Carbide by Nanoindentation. Ceramics. 2018; 1(1):198-210. https://doi.org/10.3390/ceramics1010017
Chicago/Turabian StyleDatye, Amit, Udo D. Schwarz, and Hua-Tay Lin. 2018. "Fracture Toughness Evaluation and Plastic Behavior Law of a Single Crystal Silicon Carbide by Nanoindentation" Ceramics 1, no. 1: 198-210. https://doi.org/10.3390/ceramics1010017
APA StyleDatye, A., Schwarz, U. D., & Lin, H.-T. (2018). Fracture Toughness Evaluation and Plastic Behavior Law of a Single Crystal Silicon Carbide by Nanoindentation. Ceramics, 1(1), 198-210. https://doi.org/10.3390/ceramics1010017





