Tantalum Arsenide-Based One-Dimensional Photonic Structures
Abstract
1. Introduction
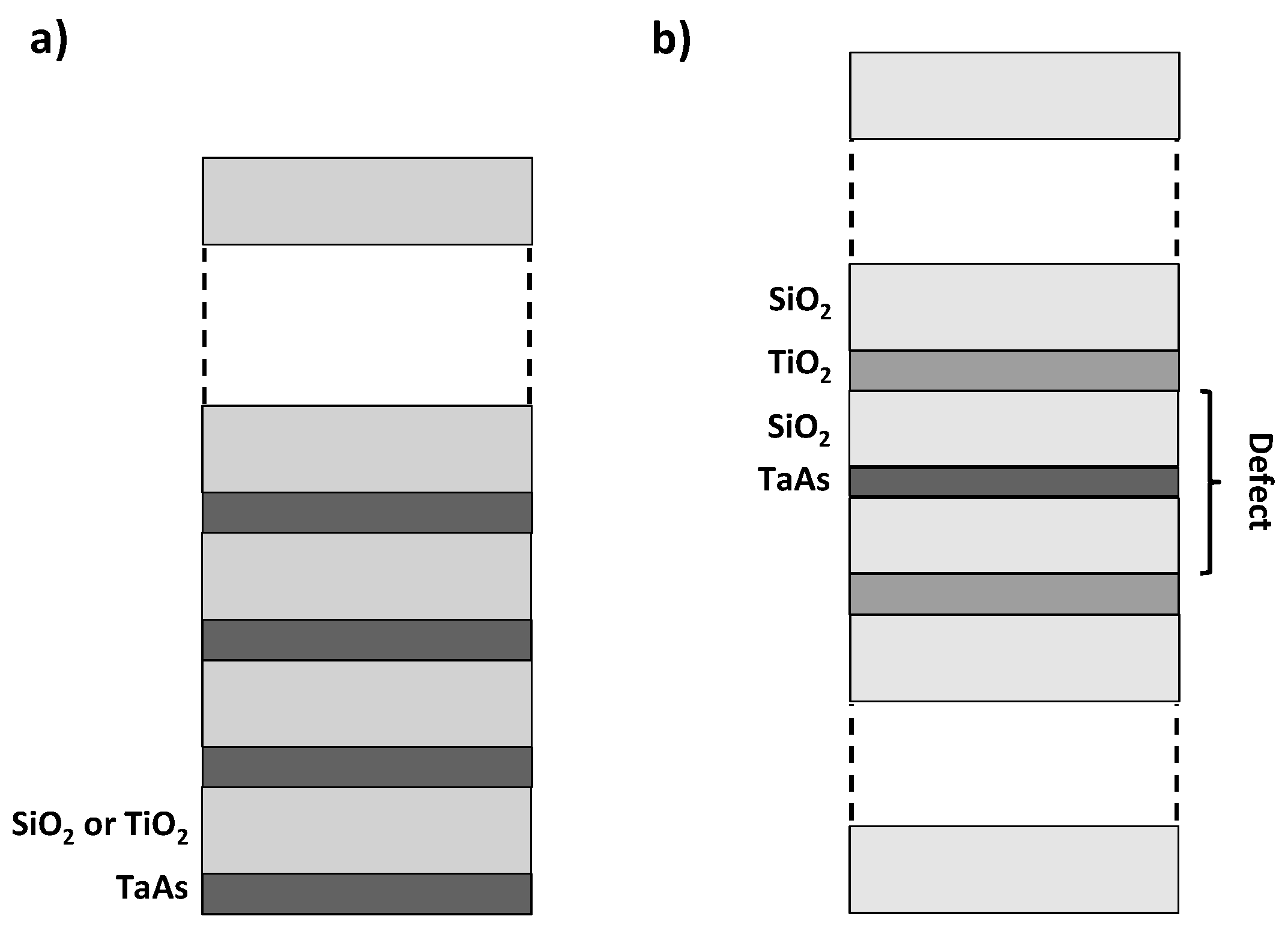
2. Methods
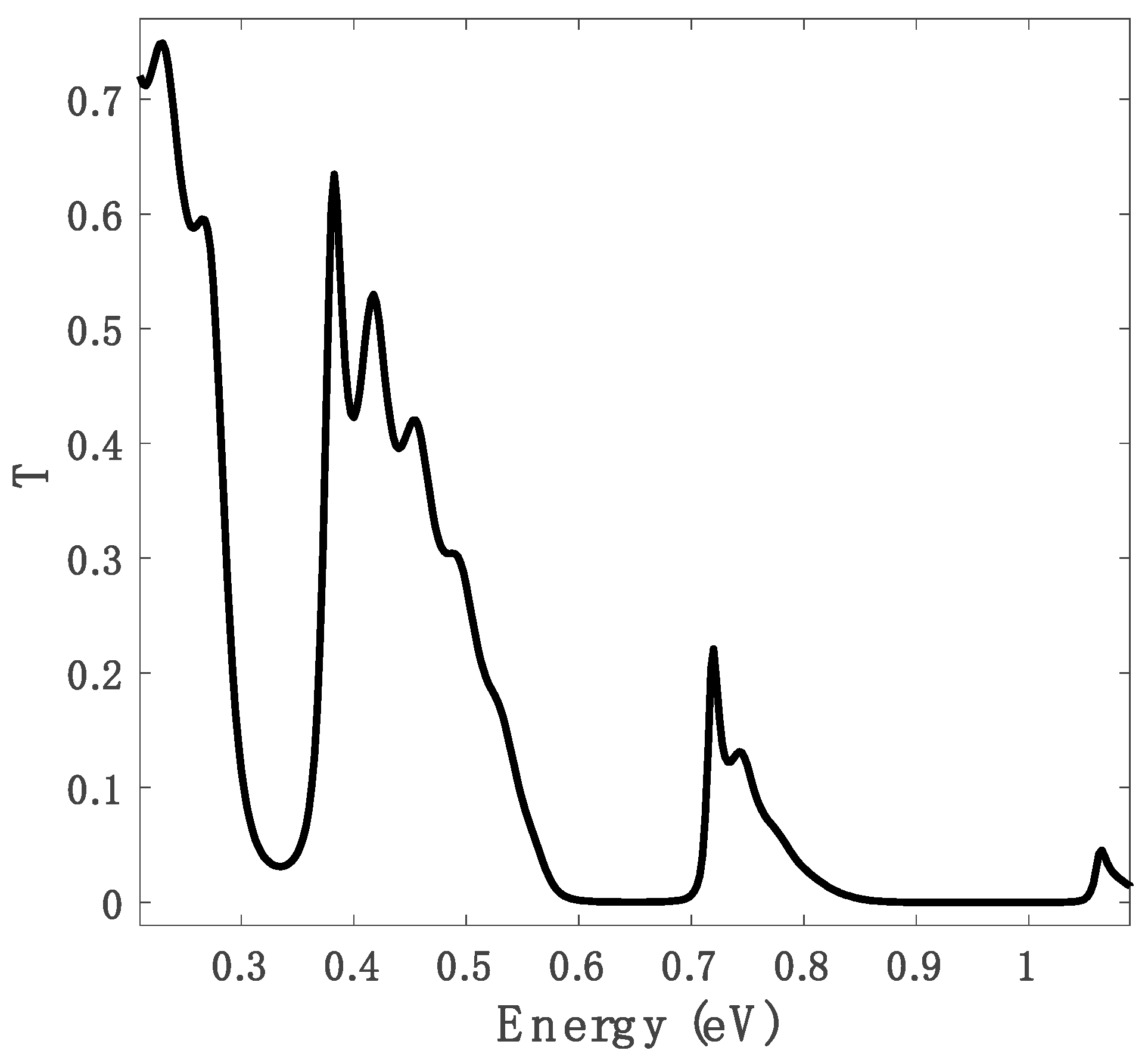
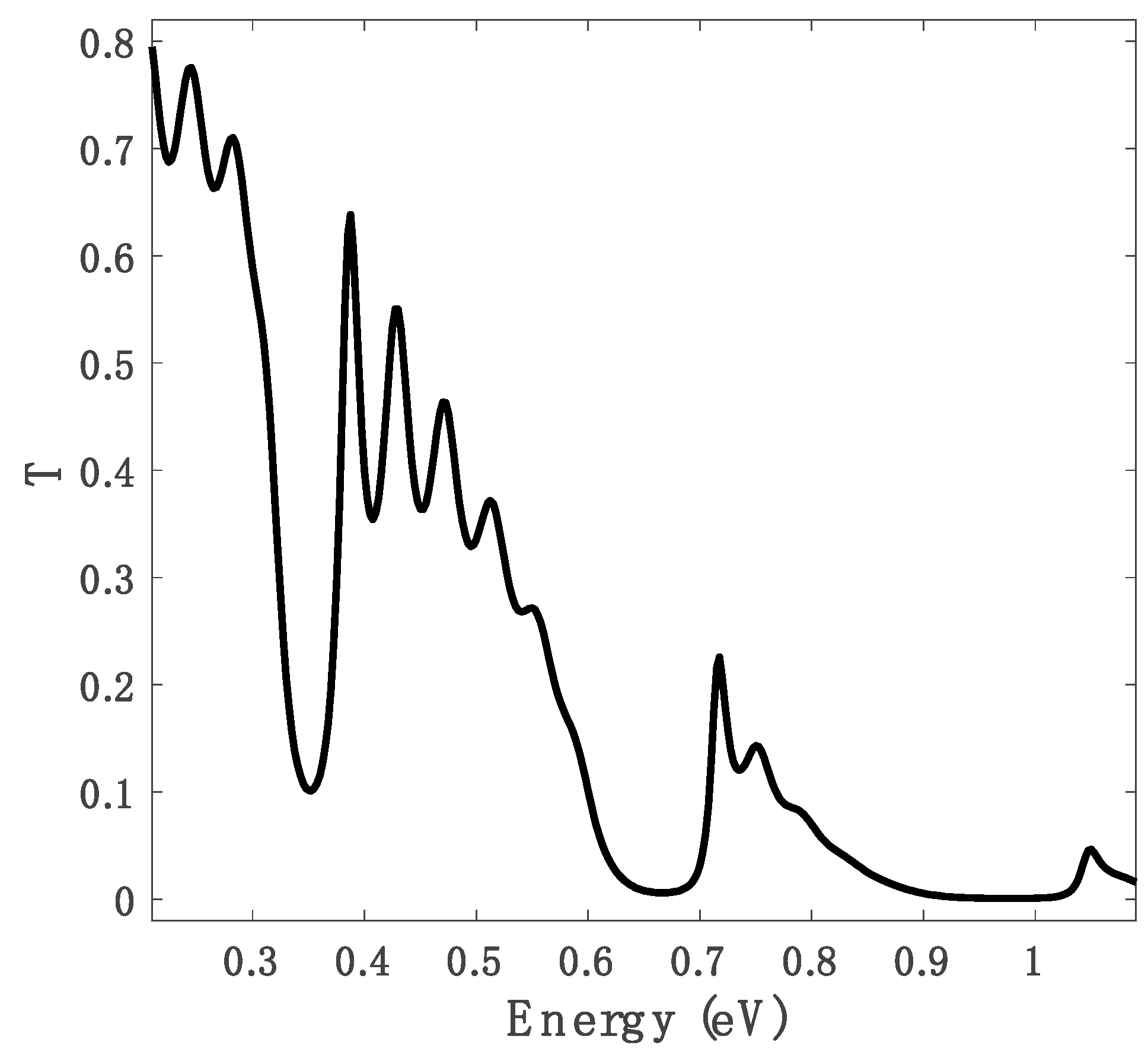
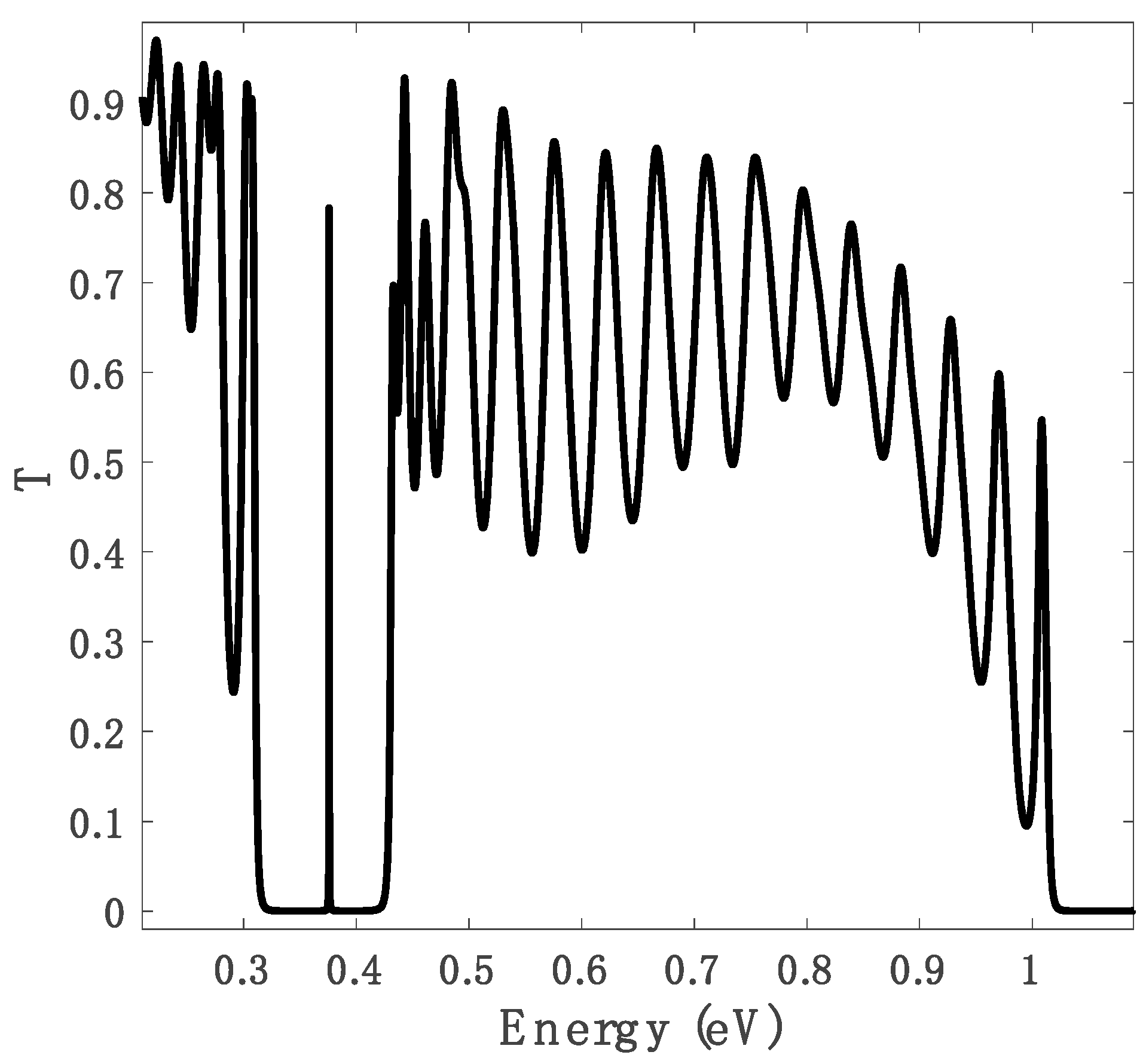
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yan, B.; Felser, C. Topological Materials: Weyl Semimetals. Annu. Rev. Condens. Matter Phys. 2017, 8, 337–354. [Google Scholar] [CrossRef]
- Xu, S.-Y.; Belopolski, I.; Alidoust, N.; Neupane, M.; Bian, G.; Zhang, C.; Sankar, R.; Chang, G.; Yuan, Z.; Lee, C.-C.; et al. Discovery of a Weyl fermion semimetal and topological Fermi arcs. Science 2015, 349, 613–617. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.X.; Liu, Z.K.; Sun, Y.; Peng, H.; Yang, H.F.; Zhang, T.; Zhou, B.; Zhang, Y.; Guo, Y.F.; Rahn, M.; et al. Weyl semimetal phase in the non-centrosymmetric compound TaAs. Nat. Phys. 2015, 11, 728–732. [Google Scholar] [CrossRef]
- Lv, B.Q.; Weng, H.M.; Fu, B.B.; Wang, X.P.; Miao, H.; Ma, J.; Richard, P.; Huang, X.C.; Zhao, L.X.; Chen, G.F.; et al. Experimental Discovery of Weyl Semimetal TaAs. Phys. Rev. X 2015, 5. [Google Scholar] [CrossRef]
- Lv, B.Q.; Xu, N.; Weng, H.M.; Ma, J.Z.; Richard, P.; Huang, X.C.; Zhao, L.X.; Chen, G.F.; Matt, C.E.; Bisti, F.; et al. Observation of Weyl nodes in TaAs. Nat. Phys. 2015, 11, 724–727. [Google Scholar] [CrossRef]
- Lv, B.Q.; Muff, S.; Qian, T.; Song, Z.D.; Nie, S.M.; Xu, N.; Richard, P.; Matt, C.E.; Plumb, N.C.; Zhao, L.X.; et al. Observation of Fermi-Arc Spin Texture in TaAs. Phys. Rev. Lett. 2015, 115. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Patankar, S.; Morimoto, T.; Nair, N.L.; Thewalt, E.; Little, A.; Analytis, J.G.; Moore, J.E.; Orenstein, J. Giant anisotropic nonlinear optical response in transition metal monopnictide Weyl semimetals. Nat. Phys. 2017, 13, 350–355. [Google Scholar] [CrossRef]
- Weber, C.P.; Berggren, B.S.; Masten, M.G.; Ogloza, T.C.; Deckoff-Jones, S.; Madéo, J.; Man, M.K.L.; Dani, K.M.; Zhao, L.; Chen, G.; et al. Similar ultrafast dynamics of several dissimilar Dirac and Weyl semimetals. J. Appl. Phys. 2017, 122, 223102. [Google Scholar] [CrossRef]
- Buckeridge, J.; Jevdokimovs, D.; Catlow, C.R.A.; Sokol, A.A. Bulk electronic, elastic, structural, and dielectric properties of the Weyl semimetal TaAs. Phys. Rev. B 2016, 93. [Google Scholar] [CrossRef]
- Sakoda, K. Optical Properties of Photonic Crystals; Springer Science & Business Media: Berlin, Germany, 2004; ISBN 978-3-540-20682-8. [Google Scholar]
- Joannopoulos, J.D. Photonic Crystals: Molding the Flow of Light; Princeton University Press: Princeton, NJ, USA, 2008; ISBN 978-0-691-12456-8. [Google Scholar]
- Yablonovitch, E. Inhibited Spontaneous Emission in Solid-State Physics and Electronics. Phys. Rev. Lett. 1987, 58, 2059–2062. [Google Scholar] [CrossRef] [PubMed]
- John, S. Strong localization of photons in certain disordered dielectric superlattices. Phys. Rev. Lett. 1987, 58, 2486–2489. [Google Scholar] [CrossRef] [PubMed]
- Bonifacio, L.D.; Lotsch, B.V.; Puzzo, D.P.; Scotognella, F.; Ozin, G.A. Stacking the Nanochemistry Deck: Structural and Compositional Diversity in One-Dimensional Photonic Crystals. Adv. Mater. 2009, 21, 1641–1646. [Google Scholar] [CrossRef]
- Scotognella, F.; Puzzo, D.P.; Zavelani-Rossi, M.; Clark, J.; Sebastian, M.; Ozin, G.A.; Lanzani, G. Two-Photon Poly(phenylenevinylene) DFB Laser. Chem. Mater. 2011, 23, 805–809. [Google Scholar] [CrossRef]
- Von Freymann, G.; Kitaev, V.; Lotsch, B.V.; Ozin, G.A. Bottom-up assembly of photonic crystals. Chem. Soc. Rev. 2013, 42, 2528–2554. [Google Scholar] [CrossRef] [PubMed]
- Chiasera, A.; Scotognella, F.; Criante, L.; Varas, S.; Valle, G.D.; Ramponi, R.; Ferrari, M. Disorder in Photonic Structures Induced by Random Layer Thickness. Sci. Adv. Mater. 2015, 7, 1207–1212. [Google Scholar] [CrossRef]
- Bellingeri, M.; Chiasera, A.; Kriegel, I.; Scotognella, F. Optical properties of periodic, quasi-periodic, and disordered one-dimensional photonic structures. Opt. Mater. 2017, 72, 403–421. [Google Scholar] [CrossRef]
- Manfredi, G.; Lova, P.; Di Stasio, F.; Rastogi, P.; Krahne, R.; Comoretto, D. Lasing from dot-in-rod nanocrystals in planar polymer microcavities. RSC Adv. 2018, 8, 13026–13033. [Google Scholar] [CrossRef]
- Criante, L.; Scotognella, F. Low-Voltage Tuning in a Nanoparticle/Liquid Crystal Photonic Structure. J. Phys. Chem. C 2012, 116, 21572–21576. [Google Scholar] [CrossRef]
- Lova, P.; Grande, V.; Manfredi, G.; Patrini, M.; Herbst, S.; Würthner, F.; Comoretto, D. All-Polymer Photonic Microcavities Doped with Perylene Bisimide J-Aggregates. Adv. Opt. Mater. 2017, 5, 1700523. [Google Scholar] [CrossRef]
- Lova, P.; Cortecchia, D.; Krishnamoorthy, H.N.S.; Giusto, P.; Bastianini, C.; Bruno, A.; Comoretto, D.; Soci, C. Engineering the Emission of Broadband 2D Perovskites by Polymer Distributed Bragg Reflectors. ACS Photonics 2018, 5, 867–874. [Google Scholar] [CrossRef]
- Park, C.; Yoon, J.; Thomas, E.L. Enabling nanotechnology with self assembled block copolymer patterns. Polymer 2003, 44, 6725–6760. [Google Scholar] [CrossRef]
- Szendrei, K.; Jiménez-Solano, A.; Lozano, G.; Lotsch, B.V.; Míguez, H. Fluorescent Humidity Sensors Based on Photonic Resonators. Adv. Opt. Mater. 2017, 5, 1700663. [Google Scholar] [CrossRef]
- Giusto, P.; Lova, P.; Manfredi, G.; Gazzo, S.; Srinivasan, P.; Radice, S.; Comoretto, D. Colorimetric Detection of Perfluorinated Compounds by All-Polymer Photonic Transducers. ACS Omega 2018, 3, 7517–7522. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light; Cambridge University Press: Cambridge, UK, 2000; ISBN 978-0-521-78449-8. [Google Scholar]
- Xiao, X.; Wenjun, W.; Shuhong, L.; Wanquan, Z.; Dong, Z.; Qianqian, D.; Xuexi, G.; Bingyuan, Z. Investigation of defect modes with Al2O3 and TiO2 in one-dimensional photonic crystals. Opt. Int. J. Light Electron Opt. 2016, 127, 135–138. [Google Scholar] [CrossRef]
- Malitson, I.H. Interspecimen Comparison of the Refractive Index of Fused Silica. J. Opt. Soc. Am. 1965, 55, 1205–1208. [Google Scholar] [CrossRef]
- Siefke, T.; Kroker, S.; Pfeiffer, K.; Puffky, O.; Dietrich, K.; Franta, D.; Ohlídal, I.; Szeghalmi, A.; Kley, E.-B.; Tünnermann, A. Materials Pushing the Application Limits of Wire Grid Polarizers further into the Deep Ultraviolet Spectral Range. Adv. Opt. Mater. 2016, 4, 1780–1786. [Google Scholar] [CrossRef]
- Polyanskiy, M.N. Refractive Index Database. Available online: http://refractiveindex.info (accessed on 11 August 2018).
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kriegel, I.; Guizzardi, M.; Scotognella, F. Tantalum Arsenide-Based One-Dimensional Photonic Structures. Ceramics 2018, 1, 139-144. https://doi.org/10.3390/ceramics1010012
Kriegel I, Guizzardi M, Scotognella F. Tantalum Arsenide-Based One-Dimensional Photonic Structures. Ceramics. 2018; 1(1):139-144. https://doi.org/10.3390/ceramics1010012
Chicago/Turabian StyleKriegel, Ilka, Michele Guizzardi, and Francesco Scotognella. 2018. "Tantalum Arsenide-Based One-Dimensional Photonic Structures" Ceramics 1, no. 1: 139-144. https://doi.org/10.3390/ceramics1010012
APA StyleKriegel, I., Guizzardi, M., & Scotognella, F. (2018). Tantalum Arsenide-Based One-Dimensional Photonic Structures. Ceramics, 1(1), 139-144. https://doi.org/10.3390/ceramics1010012




