Numerical Solution of the Direct and Inverse Problems in the Gas Lift Process of Oil Production Using the Conjugate Equations Method

Abstract

This article considers the numerical solution of the direct and inverse problems of the gas lift process in oil production, described by a system of hyperbolic equations. The inverse problem is reduced to an optimal control problem, where the control is the initial velocity of the gas. To minimize the quadratic objective functional, the gradient method is used, in which the gradient is determined using the conjugate equation method. The latter involves constructing a conjugate problem based on the Lagrange identity and the duality principle. Solving the conjugate problem allows us to obtain an analytical expression for the gradient of the functional and effectively implements the Landweber iterative method. A numerical experiment was carried out that confirmed the effectiveness of the proposed method in optimizing the parameters of the gas lift process.

1. Introduction

The gas lift process is one of the most widely used methods of mechanized oil production, in which compressed gas is pumped into the annular space of a well to reduce the density of the gas–liquid mixture (GLM), reduce hydrostatic pressure, and, as a result, facilitate the lifting of production to the surface. The gas lift system includes two key areas: the annular space between the casing and the tubing through which the gas moves and the lift, an internal well through which a mixture of oil, gas, and water is lifted to the surface.

The dynamics of gas and gas–liquid mixture movement in a well can be described by a system of hyperbolic partial differential equations, in which pressure $P$ and volumetric gas flow rate $Q$ are the main variables. These models take into account the spatio-temporal distribution of parameters and allow for the analysis of processes under different boundary and initial conditions [1].

One of the urgent tasks in the context of gas lift process management is the determination of the optimal initial conditions (for example, gas velocity distribution) that ensure the required oil production with a minimum volume of injected gas. This problem is framed as an optimal control problem, where the functionality reflecting the well production indicators is optimized. The use of numerical optimization methods based on models obtained from simulators such as PIPESIM is found, for example, in [2], and the problems related to distributing gas injection between wells are solved using mathematical programming methods and evolutionary algorithms [3].

Modern methods for solving inverse problems arising in mathematical physics involve reducing them to optimal control problems with partial differential equations as constraints. The classical theory of such problems was developed by J.L. Lions [4,5], and the method of conjugate equations, based on the Lagrange identity and the duality principle, was studied in detail in the works of Agashkov [6], Marchuk [7] and other authors. The conjugate problem method allows us to effectively calculate the gradient of the objective functional, which makes it possible to apply gradient optimization methods [8,9].

Additional interest in the application of the conjugate equation method is due to its successful use in various fields—from string vibration control [8] to numerical solutions of acoustic problems and problems involving regularization methods [10,11,12,13,14,15,16]. An example of this work is study [17], which deals with the modeling and optimization of an industrial rotary kiln (RHF) used for processing solid metallurgical waste. In the study, a numerical model is built based on heat transfer and gas dynamics equations, and then a surrogate model is built using machine learning methods. Optimization is performed using industrial data to minimize energy costs. This methodology, which combines direct modeling and numerical optimization methods integrated with real data, is of great interest and can be adapted for gas lift process problems, where it is also necessary to determine the optimal initial pressure distribution or gas flow rate.

A number of papers have proposed effective numerical methods for solving applied problems in mathematical physics. In [18], an algorithm was developed for solving the inverse problem for the acoustics equation using the gradient method, which ensures high accuracy of reconstruction of unknown parameters. In [19], an approach to numerical modeling of the transport of pollutants in the atmosphere is presented, which makes it possible to increase the accuracy of the forecast in an industrial environment. Both works demonstrate the importance of using modern computational methods to solve inverse and predictive problems in various fields.

Despite the simplicity of the mathematical model used, the novelty of this work lies in the formalization and numerical solution of the inverse problem of determining the initial gas velocity function, $G^0\left(x\right)\in H^1\left(\mathrm{0,2}l\right)$, for a given flow rate distribution, $Q^1\left(x\right)$, at time $t=T$. Such a formulation is rarely considered in relation to gas lift processes. In this work, a numerical algorithm is developed based on the method of conjugate equations, the duality principle, and the Landweber method, which allows for the effective solution of such problems while taking into account the design features of the well (two zones with different characteristics and transition conditions at the point $x=l$).

The aim of this work is to reconstruct the initial distribution of gas velocity in a system described by hyperbolic equations using additional information about the state of the system at the final moment in time. This task arises when it is necessary to clarify the initial conditions for modeling the gas lift process, particularly when direct measurements at the depth of the well are difficult or impossible.

Unlike existing methods, this paper uses the conjugate equation method, which allows us to effectively find the gradient of the target functional and implement an iterative optimization procedure. This approach ensures high accuracy in solving the inverse problem with minimal computational costs. The obtained results confirm the applicability of the developed numerical method for restoring hidden parameters and optimizing the operating conditions of gas lift wells.

2. Materials and Methods

2.1. Statement of Direct and Inverse Problems

The mathematical model of the gas lift well operation is described using the following linear system of differential equations [1]:

$$\frac{\partial P}{\partial t}=-\frac{c^2}{\overline{F}}\cdot \frac{\partial Q}{\partial x}, t\ge 0, x\in \left(0; 2l\right),$$

(1)

$$\frac{\partial Q}{\partial t}=-\overline{F}\cdot \frac{\partial P}{\partial x}-2a\cdot Q, t\ge 0,x\in \left(0; 2l\right),$$

(2)

where $t$ is time; $x$ is a coordinate along the well depth; $P$ is the pressure; $Q$ is the volume flow rate of gas; $\overline{F}$ is the cross-sectional area of the well; c is the speed of sound in liquid; l is the well depth; and a is a coefficient that depends on the input parameters.

$$c=\left\{\begin{array}{ll}{c}_1,& x\in \left(0; l\right)\\ c_2,& x\in \left(l; 2l\right)\end{array}\right., \overline{ F}=\left\{\begin{array}{ll}{\overline{F}}_1,& x\in \left(0; l\right)\\ {\overline{F}}_2,& x\in \left(l; 2l\right)\end{array}\right., a=\left\{\begin{array}{ll}{a}_1,& x\in \left(0; l\right)\\ a_2,& x\in \left(l; 2l\right)\end{array}\right.,$$

Parameters $a_1$ and $a_2$ characterize the combined effect of gravitational acceleration and hydraulic resistance on gas movement in the annular space and lift, respectively. These coefficients reflect energy losses due to friction and lifting along the well.

Variables $c_c$ and $c_2$ denote the speed of sound in a gas–liquid medium in different zones of the well: $c_1$—in the annular space, where gas predominantly moves, and $c_c$—inside the lifting pipe, where a mixture of gas and oil moves. The difference between $c_1$ and $c_2$ is due to differences in the composition and density of the media, which is critical for the correct modeling of wave processes.

The initial conditions are as follows:

$$P\left(0,x\right)=P^0\left(x\right), Q\left(0,x\right)=Q^0\left(x\right),$$

(3)

and the boundary conditions are as follows:

$$P\left(t,0\right)=P_0\left(t\right), Q\left(t,0\right)=Q_0\left(t\right), for x=0,$$

(4)

$$\begin{array}{ll}P\left(t,l+0\right)=P\left(t,l-0\right)+P_{pl}\left(t\right),Q\left(t,l+0\right)=Q_0\left(t,l-0\right)+Q_{pl}\left(t\right),& \end{array}$$

(5)

$$for x=l,$$

$$\begin{array}{ll}P\left(t,2l\right)=P_{out}\left(t\right), P\left(t,2l\right)=Q_{out}\left(t\right),& x=2l.\end{array}$$

(6)

where $Q_{pl}$ is the volumetric flow rate from the reservoir; $P_{pl}$ is the reservoir pressure; $P^0\left(x\right)$ is the initial gas pressure; $Q^0\left(x\right)$ is the initial gas volume; $P_{out}\left(t\right)$ is the discharge pressure; and $Q_{out}\left(t\right)$ is the discharge volume.

We will reduce the system of hyperbolic Equations (1) and (2) to one second-order equation. To accomplish this, we must find the derivative with respect to x from Equation (1).

$$\frac{{\partial }^{2}P}{\partial t\partial x}=\frac{\partial }{\partial x}\left(\frac{\partial P}{\partial t}\right)=\frac{\partial }{\partial x}\left(-\frac{c^2}{\overline{F}}\cdot \frac{\partial Q}{\partial x}\right)=-\frac{c^2}{\overline{F}}\cdot \frac{{\partial }^{2}Q}{\partial x^2}.$$

(7)

Using Equation (2), we can determine the derivative with respect to $t$.

$$\frac{{\partial }^{2}Q}{\partial t^2}=-\overline{F}\cdot \frac{{\partial }^{2}P}{\partial t\partial x}-2a\cdot \frac{\partial Q}{\partial t}.$$

(8)

Let us substitute (7) into Equation (8). Then, Equation (8) assumes the following form:

$$\frac{{\partial }^{2}Q}{\partial t^2}+2a\frac{\partial Q}{\partial t}=c^2\frac{{\partial }^{2}Q}{\partial x^2}, x\in \left(\mathrm{0,2}l\right), t\in \left(0,T\right),$$

(9)

The initial conditions are as follows:

$$Q\left(0,x\right)=Q^0\left(x\right), \frac{\partial Q}{\partial t}\left(0,x\right)=G^0\left(x\right), x\in \left[\mathrm{0,2}l\right],$$

(10)

and the boundary conditions are as follows:

$$Q\left(t,0\right)=Q_0\left(t\right), Q\left(t,2l\right)=Q_{out}\left(t\right), t\in \left[0,T\right],$$

(11)

$$Q\left(t,l+0\right)=Q\left(t,l-0\right)+Q_{pl}\left(t\right), t\in \left[0,T\right],$$

(12)

where $G^0\left(x\right)=-\overline{F}\cdot \frac{\partial P^0\left(x\right)}{\partial x}-2a{Q}^0\left(x\right)$ is the initial rate of gas displacement.

In the direct problem, it is necessary to find $\mathrm{Q}\left(t,x\right)$ based on the given functions $Q^0\left(x\right)$, $G^0\left(x\right),$ ${\mathrm{Q}}_0\left(t\right)$, ${\mathrm{Q}}_{pl}\left(t\right)$, and $Q_{out}\left(t\right)$.

The inverse problem is formulated as follows:

$$\begin{array}{ll}Q\left(T,x\right)=Q^1\left(x\right)& when t=T, x\in \left[\mathrm{0,2}l\right].\end{array}$$

(13)

The main issue with the inverse problem deriving $G^0\left(x\right)$ from Equations (9)–(12) with additional conditions (13).

The transformation of the system of hyperbolic equations into one second-order equation allows us to move from the description of the interacting quantities, $P$ and $Q$, to focusing on one objective function—the volumetric gas flow rate, $\mathrm{Q}\left(t,x\right)$. This significantly simplifies both the numerical implementation of the direct problem and the formulation of the inverse problem, in which the behavior of the function, $Q$, at the final moment of time is used as the observed data.

In addition, the use of one second-order equation allows us to explicitly formulate the conjugate problem and calculate the gradient of the target functional, which forms the basis of the conjugate equation method.

2.2. Statement of the Variational Problem

One of the most widely used methods for solving inverse problems of mathematical physics is reducing Equations (9)–(12) and (13) to an optimal control problem.

The aim of the problem is to find the initial values of $G^0\left(x\right)ϵW_2^2\left(\mathrm{0,2}l\right)$ so that the corresponding solution to Equation (9) approaches the specified desired value of $Q^1\left(x\right)$.

More precisely, our problem is to minimize the objective functional, as follows:

$$cJ\left(G^0\right)=\underset{0}{\overset{2l}{\int }} {\left[Q\left(T,x;G^0\left(x\right)\right)-Q^1\left(x\right)\right]}^{2}dx\to min.$$

(14)

on the admissible control set, $G^0\left(x\right)\subset W_2^2\left(\mathrm{0,2}l\right)$.

Here, $Q\left(T,x;G^0\left(x\right)\right)$ represents the solution’s, $Q\left(T,x\right)$, dependence on Equations (9)–(12) and (13) using the initial conditions.

Minimize the functional using the gradient method as follows [20]:

$$G_{n+1}=G_n-\alpha \cdot J^{\prime }{G}_n, n=0,1,2,\dots ,$$

(15)

where $\alpha$ is a relaxation parameter.

The choice of relaxation parameter determines the gradient method, which plays an important role. The relaxation parameter α determines the length of the gradient descent step and has a direct impact on the convergence rate of the iteration process. A value of α that is too large can lead to divergence of the method, while a value that is too small can lead to slow convergence.

In practice, the choice of $\alpha$ is made either empirically (based on preliminary tests) or using adaptive strategies such as the steepest descent method, where $\alpha$ is selected at each iteration to minimize the functional along the current direction. In this study, α was taken as constant and selected in such a way as to ensure a stable monotonic decrease in the values of the functional $J\left(G_n^0\right)$ with an acceptable number of iterations.

The procedure for obtaining the variational and conjugate problems is as follows:

• Let us consider the variation of the functional, $\delta J\left(G^0\right)$, under the perturbation, $\delta G^0$.
• We introduce the perturbed solution, $\tilde{Q}\left(t,x\right)$, and define $\delta Q\left(t,x\right)=\tilde{Q}\left(t,x\right)-Q\left(t,x\right).$
• We perform a convolution of the variation through the unknown function, $Q^{*}\left(t,x\right),$ satisfying the following conjugate equation:

$$A^{*}{Q}^{*}=\frac{{\partial }^2{Q}^{*}}{\partial t^2}-2a\frac{\partial Q^{*}}{\partial t}-c^2\frac{{\partial }^2{Q}^{*}}{\partial x^2}=0,$$

(16)

with the following boundary conditions:

$$Q^{*}\left(T,x\right)=0, \frac{\partial Q^{*}}{\partial t}\left(T,x\right)=2\left[Q\left(T,x;G^0\right)-Q^1\left(x\right)\right],$$

(17)

$$Q^{*}\left(t,0\right)=0, Q^{*}\left(t,2l\right)=0.$$

(18)

4.

Then, the Frechet derivative of the functional takes the following the form:

$$J^{\prime }{(G}_n^0)=-Q^{*}\left(0,x\right),$$

All intermediate calculations, including integration by parts and proof of the identity, are given in Appendix A.

2.3. Landweber Algorithm (Simple Iteration Method)

• We set the initial approximation, $G^0$.
• Suppose that $G_n^0$ is already known; then, we solve the direct problem (9)–(12).
• Calculate the value of the following functional:

  $$J\left(G_n^0\right)=\underset{0}{\overset{2l}{\int }} {\left[Q\left(T,x;G_n^0\right)-Q^1\left(x\right)\right]}^{2}dx.$$
• If the current value of the functional, $J\left(G_n^0\right)$, is not small enough, solve the conjugate problem (16)–(18).
• Calculate the gradient of the following functional:

  $$J^{\prime }{(G}_n^0)=-Q^{*}\left(0,x\right).$$
• Calculate the following approximation:

$$G_{n+1}^0=G_n^0-\alpha \cdot J^{\prime }{G}_n^0$$

and proceed to point 2.

2.4. Numerical Solutions for the Direct and Conjugate Problem

Here, we present a method for numerically solving both direct and conjugate problems using the finite difference method [21]. To achieve this, the solution area is divided into a uniform grid, and the initial differential equations are approximated by difference schemes. The first part describes the process of solving a direct problem, including building a grid, approximating equations, and implementing boundary conditions. In the second part, the solution of the conjugate problem is considered in detail. A similar difference technique considers the specifics of the boundary and initial conditions. The numerical schemes obtained make it possible to efficiently solve both problems in a discrete formulation.

2.4.1. Scheme for Solving a Direct Problem

Let us approximate the direct problem in (9)–(12). Let $N_t$ be the number of nodes in the uniform grid on the interval $\left[0, T\right]$ and let $N_x$ be the number of nodes in the uniform grid on the interval $\left[0, 2l\right]$.

Construct a grid, ${\omega }_h$, with a step of $h=2l/N_x$, $\tau =T/N_t$, where $N_x$ and $N_t$ are positive integers in the domain of $\mathsf{\Omega }$ = ($\left(\mathrm{0,2}l\right)\times \left(0,T\right)$).

Then, in the grid, ${\omega }_h=\left\{x=ih, t=k\tau , i=\overline{1, N_x-1}, k=\overline{1, N_t-1},\right\}$, we can write the following difference direct problem. Thus, problems (9)–(12) assume the following form:

$$\frac{Q_i^{k+1}-2Q_i^k+Q_i^{k-1}}{{\tau }^2}+2a\cdot \frac{Q_i^k-Q_i^{k-1}}{\tau }=c^2\cdot \frac{Q_{i+1}^k-2Q_i^k+Q_{i-1}^k}{h^2},$$

(19)

$$Q_i^0=Q^0, \frac{Q_i^1-Q_i^0}{\tau }=G_i^0,$$

(20)

$$Q_0^k=Q_0, Q_{N_x}^k=Q_{out},$$

(21)

$$Q_{\frac{N_x}{2}}^k=Q_{\frac{N_x}{2}-1}^k+Q_{pl}.$$

(22)

From Equations (19)–(22) we obtain the following equations:

$$Q_i^{k+1}=2Q_i^k-Q_i^{k-1}+{\tau }^2\left(c^2\frac{Q_{i+1}^k-2Q_i^k+Q_{i-1}^k}{h^2}-2a\frac{Q_i^k-Q_i^{k-1}}{\tau }\right),$$

(23)

$$Q_i^0=Q^0, Q_i^1=Q_i^0+\tau G_i^0,$$

(24)

$$Q_0^k=Q_0, Q_{N_x}^k=Q_{out},$$

(25)

$$Q_{\frac{N_x}{2}}^k=Q_{\frac{N_x}{2}-1}^k+Q_{pl}.$$

(26)

Solving the problem, we obtain a trace of the solution $Q^1$ as follows:

$$Q_i^{N_t}=Q^1.$$

2.4.2. A Scheme for Solving the Conjugate Problem

For the conjugate problem, we use the same grid as that of the direct problem. Thus, the problem in (16)–(18) takes the following form:

$$\frac{Q_i^{*k+1}-2Q_i^{*k}+Q_i^{*k-1}}{{\tau }^2}-2a\frac{Q_i^{*k+1}-Q_i^{*k}}{\tau }=c^2\frac{Q_{i+1}^{*k}-2Q_i^{*k}+Q_{i-1}^{*k}}{h^2},$$

(27)

$$Q_i^{*N_t}=0, \frac{Q_i^{*N_t-1}-Q_i^{*N_t}}{\tau }=2\left[Q_i^{N_t}-Q^1\left(x\right)\right],$$

(28)

$$Q_0^{*k}=Q_{N_x}^{*k}=0.$$

(29)

From Equations (27)–(29) we derive the following equations:

$$Q_i^{*k-1}=2Q_i^{*k}-Q_i^{*k+1}+{\tau }^2\left(c^2\frac{Q_{i+1}^{*k}-2Q_i^{*k}+Q_{i-1}^{*k}}{h^2}+2a\frac{Q_i^{*k+1}-Q_i^{*k}}{\tau }\right),$$

(30)

$$Q_i^{*N_t}=0,$$

(31)

$$Q_0^{*k}=Q_{N_x}^{*k}=0,$$

(32)

$$Q_i^{*N_t-1}=2\tau \left[Q_i^{N_t}-Q^1\right].$$

(33)

2.5. Study of the Approximation and Stability of a Family of Difference Schemes

The mathematical model of the gas lift well operation is described using the following linear system of differential equations:

$$\frac{\partial P}{\partial t}=-\frac{c^2}{\overline{F}}\cdot \frac{\partial Q}{\partial x}, t\ge 0, x\in \left(0; 2l\right),$$

(34)

$$\frac{\partial Q}{\partial t}=-\overline{F}\cdot \frac{\partial P}{\partial x}-2a\cdot Q, t\ge 0, x\in \left(0; 2l\right).$$

(35)

The implicit difference scheme for Equations (1) and (2) is as follows:

$$\frac{P_i^{n+1}-P_i^n}{\tau }=-\frac{c^2}{\overline{F}}\cdot \frac{Q_i^{n+1}-Q_{i-1}^{n+1}}{h},$$

(36)

$$\frac{Q_i^{n+1}-Q_i^n}{\tau }=-\overline{F}\cdot \frac{P_i^{n+1}-P_{i-1}^{n+1}}{h}-2a\cdot Q_i^{n+1},$$

(37)

that is

$$P_t^n+\frac{c^2}{\overline{F}}\cdot Q_{\overline{x}}^{n+1}=0,$$

$$Q_t^n+\overline{F}\cdot P_{\overline{x}}^{n+1}+2a\cdot Q_i^{n+1}=0.$$

Here, $P_t^n$ and $Q_t^n$ are the values of the functions $P$ and $Q$ at the point $x_i$ on the time layer $t_n$, with the following initial conditions:

$$P_i^0=P^0\left(x_i\right), Q_i^0=Q^0\left(x_i\right), i=\overline{0, N_x}$$

(38)

and boundary conditions, respectively

$$P_0^j=P_0\left(t_j\right), Q_0^j=Q_0\left(t_j\right), i=0,1,\dots ,N_x,$$

(39)

$$P_{\frac{N_x}{2}}^j=P_{\frac{N_x}{2}-1}^j+P_{pl}, Q_{\frac{N_x}{2}}^j=Q_{\frac{N_x}{2}-1}^j+Q_{pl},$$

(40)

$$P_{N_x}^j=P_1\left(t_j\right), Q_{N_x}^j=Q_1\left(t_j\right).$$

(41)

Let us rewrite (36)–(37) in the following form:

$$P_i^{j+1}=P_i^j-{\gamma }_1\cdot \left(Q_i^{j+1}-Q_{i-1}^{j+1}\right),$$

(42)

$$Q_i^{j+1}=\frac{\left[Q_i^j-{\gamma }_2\cdot \left(P_i^{j+1}-P_{i-1}^{j+1}\right)\right]}{\left(1+2a\tau \right)},$$

(43)

where ${\gamma }_1=\frac{\tau c^2}{\overline{F}\cdot h},{\gamma }_1=\frac{\tau \cdot \overline{F}}{h}.$

It can be seen that the count can be started from the point $i=1, j=0$. Then, we obtain the following equations:

$$P_1^1=P_1^0-{\gamma }_1\cdot \left(Q_1^1-Q_0^1\right),$$

(44)

$$Q_1^1=\frac{\left[Q_1^0-{\gamma }_2\cdot \left(P_1^1-P_0^1\right)\right]}{\left(1+2a\tau \right)}.$$

(45)

by multiplying Equation (45) by ${\gamma }_1$ and summing it with the first one, we obtain the following equation:

$$P_1^1=P_1^0+{\gamma }_1\cdot Q_0^1-\frac{{\gamma }_1}{1+2a\tau }\cdot Q_1^0+\frac{{\gamma }_1{\gamma }_2}{1+2a\tau }\cdot P_1^1-\frac{{\gamma }_1{\gamma }_2}{1+2a\tau }\cdot P_0^1.$$

Using this formula, we derive $P_1^1$ as follows:

$$P_1^1=\frac{1+2a\tau }{1+2a\tau -{\gamma }_1{\gamma }_2}\cdot \left[P_1^0+{\gamma }_1\cdot Q_0^1-\frac{{\gamma }_1}{1+2a\tau }\cdot Q_1^0-\frac{{\gamma }_1{\gamma }_2}{1+2a\tau }\cdot P_0^1\right].$$

(46)

Substituting $P_1^1$ in (45), we obtain $Q_1^1$.

With $P_1^1$ and $Q_1^1$, it is possible to calculate all values of $P_1^j$ and $Q_1^j$ up to some $j=j_0$ and taking $i=2$; find $P_2^j$ and $Q_2^j$ for $0\le j\le j_0$, etc.

In the general case, to determine $P_i^{j+1}$ we obtain the following formula:

$$P_i^{j+1}=\frac{1+2a\tau }{1+2a\tau -{\gamma }_1{\gamma }_2}\cdot \left[P_i^j+{\gamma }_1\cdot Q_{i-1}^{j+1}-\frac{{\gamma }_1}{1+2a\tau }\cdot Q_i^j-\frac{{\gamma }_1{\gamma }_2}{1+2a\tau }\cdot P_{i-1}^{j+1}\right].$$

(47)

Let us consider the following family of schemes defined on a four-point template:

$$P_t^n+\frac{c^2}{\overline{F}}\left(\sigma \cdot Q_{\overline{x}}^{n+1}+\left(1-\sigma \right)Q_{\overline{x}}^n\right)=0, x\in {\omega }_h, t\in {\omega }_{\tau },$$

(48)

$$Q_t^n+\overline{F}\left(\sigma \cdot P_{\overline{x}}^{n+1}+\left(1-\sigma \right)P_{\overline{x}}^n+2a{Q}_i^{n+1}\right)=0, x\in {\omega }_h, t\in {\omega }_{\tau },$$

(49)

with the following initial conditions:

$$P\left(0, x_j\right)=P_0\left(x_j\right), Q\left(0, x_j\right)=Q_0\left(x_j\right), x_j\in {\omega }_h,$$

(50)

and the following boundary conditions:

$$P\left(t_j, 0\right)=P_0\left(t_j\right), Q\left(t_j, 0\right)=Q_0\left(t_j\right), t_j\in {\omega }_{\tau },$$

(51)

$$P\left(t_j, x_{\frac{N_x}{2}}\right)=P\left(t_j, x_{\frac{N_x}{2}-1}\right)+P_{pl},$$

(52)

$$Q\left(t_j, x_{\frac{N_x}{2}}\right)=Q\left(t_j, x_{\frac{N_x}{2}-1}\right)+Q_{pl},$$

(53)

$$P\left(t_j, x_{N_x}\right)=P_1\left(t_j\right), Q\left(t_j, x_{N_x}\right)=Q_1\left(t_j\right).$$

(54)

Schemes (36) and (37) belong to this family and correspond to $\sigma =1$.

Let us calculate the residual for this system of difference equations.

$${\psi }_1=P_t^n+\frac{c^2}{\overline{F}}\left(\sigma \cdot Q_{\overline{x}}^{n+1}+\left(1-\sigma \right)Q_{\overline{x}}^n\right),$$

(55)

$${\psi }_2=Q_t^n+\overline{F}\left(\sigma \cdot P_{\overline{x}}^{n+1}+\left(1-\sigma \right)P_{\overline{x}}^n+2a{Q}_{\overline{x}}^{n+1}\right).$$

(56)

Let us use the Taylor series expansion as follows:

$$\begin{gathered} P\left(t_{n+1}, x_i\right)=P\left(t_{n+\frac{1}{2}}, x_i\right)+\frac{\tau }{2}\cdot \left(\frac{\partial P}{\partial t}\right)\left(t_{n+\frac{1}{2}}, x_i\right)+\frac{{\tau }^2}{8}\cdot \left(\frac{{\partial }^{2}P}{\partial t^2}\right)\left(t_{n+\frac{1}{2}}, x_i\right)+ \\ +\frac{{\tau }^3}{48}\cdot \left(\frac{{\partial }^{3}P}{\partial t^3}\right)\left(t_{n+\frac{1}{2}}, x_i\right)+\frac{{\tau }^4}{384}\cdot \left(\frac{{\partial }^{4}P}{\partial t^4}\right)\left(t_{n+\frac{1}{2}}, x_i\right)+O\left({\tau }^5\right), \end{gathered}$$

$$\begin{gathered} P\left(t_n, x_i\right)=P\left(t_{n+\frac{1}{2}}, x_i\right)-\frac{\tau }{2}\cdot \left(\frac{\partial P}{\partial t}\right)\left(t_{n+\frac{1}{2}}, x_i\right)+\frac{{\tau }^2}{8}\cdot \left(\frac{{\partial }^{2}P}{\partial t^2}\right)\left(t_{n+\frac{1}{2}}, x_i\right)- \\ -\frac{{\tau }^3}{48}\cdot \left(\frac{{\partial }^{3}P}{\partial t^3}\right)\left(t_{n+\frac{1}{2}}, x_i\right)+\frac{{\tau }^4}{384}\cdot \left(\frac{{\partial }^{4}P}{\partial t^4}\right)\left(t_{n+\frac{1}{2}}, x_i\right)+O\left({\tau }^5\right). \end{gathered}$$

Substituting these expansions into $\frac{\left(P_i^{n+1}-P_i^n\right)}{\tau }$, we obtain the following equation:

$$P_t^n=\left(\frac{\partial P}{\partial t}\right)\left(t_{n+\frac{1}{2}}, x_i\right)+O\left({\tau }^2\right).$$

(57)

Similarly, we obtain the following equation:

$$Q_t^n=\left(\frac{\partial Q}{\partial t}\right)\left(t_{n+\frac{1}{2}}, x_i\right)+O\left({\tau }^2\right).$$

(58)

Let us expand functions $P$ and $Q$ with respect to the variable $x$ as follows:

$$Q_{i-1}^n=Q_i^n-h{\left(\frac{\partial Q}{\partial x}\right)}_i^n+\frac{h^2}{2}{\left(\frac{{\partial }^{2}Q}{\partial x^2}\right)}_i^n+O\left(h^3\right).$$

Find the backward difference derivative as follows:

$$\frac{Q_i^n-Q_{i-1}^n}{h}={\left(\frac{\partial Q}{\partial x}\right)}_i^n-\frac{h^2}{2}{\left(\frac{{\partial }^{2}Q}{\partial x^2}\right)}_i^n+O\left(h^2\right).$$

(59)

Similarly, we obtain the following equation:

$$\frac{P_i^n-P_{i-1}^n}{h}={\left(\frac{\partial P}{\partial x}\right)}_i^n-\frac{h^2}{2}{\left(\frac{{\partial }^{2}P}{\partial x^2}\right)}_i^n+O\left(h^2\right).$$

(60)

By substituting (37)–(40) into (55) and (56), we obtain the following equations:

$$\begin{gathered} {\psi }_1={\left(\frac{\partial P}{\partial t}\right)}_i^{n+\frac{1}{2}}+\frac{c^2}{\overline{F}}\left\{\sigma \cdot \left[{\left(\frac{\partial Q}{\partial x}\right)}_i^{n+1}-\frac{h}{2}{\left(\frac{{\partial }^{2}Q}{\partial x^2}\right)}_i^{n+1}+O\left(h^2\right)\right]+\right. \\ \left.+\left(1-\sigma \right)\left[{\left(\frac{\partial Q}{\partial x}\right)}_i^{n+1}-\frac{h}{2}{\left(\frac{{\partial }^{2}Q}{\partial x^2}\right)}_i^{n+1}+O\left(h^2\right)\right]\right\}+O\left({\tau }^2\right), \end{gathered}$$

(61)

$$\begin{gathered} {\psi }_2={\left(\frac{\partial Q}{\partial t}\right)}_i^{n+\frac{1}{2}}+\overline{F}\left\{\sigma \cdot \left[{\left(\frac{\partial P}{\partial x}\right)}_i^{n+1}-\frac{h}{2}{\left(\frac{{\partial }^{2}P}{\partial x^2}\right)}_i^{n+1}+O\left(h^2\right)\right]+\right. \\ \left.+\left(1-\sigma \right)\left[{\left(\frac{\partial P}{\partial x}\right)}_i^{n+1}-\frac{h}{2}{\left(\frac{{\partial }^{2}P}{\partial x^2}\right)}_i^{n+1}+O\left(h^2\right)\right]+2a{Q}_i^{n+1}\right\}+O\left({\tau }^2\right). \end{gathered}$$

(62)

To make further calculations for residuals ${\psi }_1$ and ${\psi }_2$ more convenient, we assume the following equalities:

$$\frac{c^2}{\overline{F}}=1, \overline{F}=1.$$

(63)

Let us expand the terms ${\left(\frac{\partial Q}{\partial x}\right)}_i^{n+1},{\left(\frac{\partial Q}{\partial x}\right)}_i^n,{\left(\frac{\partial P}{\partial x}\right)}_i^{n+1},\mathrm{and}{\left(\frac{\partial P}{\partial x}\right)}_i^n$ in a Taylor series with respect to $t$ in the vicinity of the point $t=t_{n+\frac{1}{2}}$.

$${\left(\frac{\partial Q}{\partial x}\right)}_i^{n+1}={\left(\frac{\partial Q}{\partial x}\right)}_i^{n+\frac{1}{2}}+0.5\tau {\left(\frac{{\partial }^{2}Q}{\partial x\partial t}\right)}_i^{n+\frac{1}{2}}+O\left({\tau }^2\right),$$

(64)

$${\left(\frac{\partial Q}{\partial x}\right)}_i^n={\left(\frac{\partial Q}{\partial x}\right)}_i^{n+\frac{1}{2}}-0.5\tau {\left(\frac{{\partial }^{2}Q}{\partial x\partial t}\right)}_i^{n+\frac{1}{2}}+O\left({\tau }^2\right),$$

(65)

$${\left(\frac{\partial P}{\partial x}\right)}_i^{n+1}={\left(\frac{\partial P}{\partial x}\right)}_i^{n+\frac{1}{2}}+0.5\tau {\left(\frac{{\partial }^{2}P}{\partial x\partial t}\right)}_i^{n+\frac{1}{2}}+O\left({\tau }^2\right),$$

(66)

$${\left(\frac{\partial P}{\partial x}\right)}_i^n={\left(\frac{\partial P}{\partial x}\right)}_i^{n+\frac{1}{2}}-0.5\tau {\left(\frac{{\partial }^{2}P}{\partial x\partial t}\right)}_i^{n+\frac{1}{2}}+O\left({\tau }^2\right).$$

(67)

Then, from (61)–(62), taking assumption (63) into account, we obtain the following equations:

$$\begin{gathered} {\psi }_1={\left(\frac{\partial P}{\partial t}\right)}_i^{n+\frac{1}{2}}+\sigma \cdot \left[{\left(\frac{\partial Q}{\partial x}\right)}_i^{n+\frac{1}{2}}+0.5\tau {\left(\frac{{\partial }^{2}Q}{\partial x\partial t}\right)}_i^{n+\frac{1}{2}}+O\left({\tau }^2\right)-\frac{h}{2}{\left(\frac{{\partial }^{2}Q}{\partial x^2}\right)}_i^{n+1}+O\left(h^2\right)\right]+ \\ +\left(1-\sigma \right)\cdot \left[{\left(\frac{\partial Q}{\partial x}\right)}_i^{n+\frac{1}{2}}-0.5\tau {\left(\frac{{\partial }^{2}Q}{\partial x\partial t}\right)}_i^{n+\frac{1}{2}}+O\left({\tau }^2\right)-\frac{h}{2}{\left(\frac{{\partial }^{2}Q}{\partial x^2}\right)}_i^n+O\left(h^2\right)\right], \end{gathered}$$

(68)

$$\begin{gathered} {\psi }_2={\left(\frac{\partial Q}{\partial t}\right)}_i^{n+\frac{1}{2}}+\sigma \cdot \left[{\left(\frac{\partial P}{\partial x}\right)}_i^{n+\frac{1}{2}}+0.5\tau {\left(\frac{{\partial }^{2}P}{\partial x\partial t}\right)}_i^{n+\frac{1}{2}}+O\left({\tau }^2\right)-\frac{h}{2}{\left(\frac{{\partial }^{2}P}{\partial x^2}\right)}_i^{n+1}+O\left(h^2\right)\right]+ \\ +\left(1-\sigma \right)\cdot \left[{\left(\frac{\partial P}{\partial x}\right)}_i^{n+\frac{1}{2}}-0.5\tau {\left(\frac{{\partial }^{2}P}{\partial x\partial t}\right)}_i^{n+\frac{1}{2}}+O\left({\tau }^2\right)-\frac{h}{2}{\left(\frac{{\partial }^{2}P}{\partial x^2}\right)}_i^n+O\left(h^2\right)+2a{Q}_i^{n+1}\right]. \end{gathered}$$

(69)

From the main, Equations (34) and (35), we derive the following equations:

$${\left(\frac{\partial Q}{\partial x}\right)}_i^{n+\frac{1}{2}}=-{\left(\frac{\partial P}{\partial t}\right)}_i^{n+\frac{1}{2}},$$

$${\left(\frac{\partial P}{\partial x}\right)}_i^{n+\frac{1}{2}}=-{\left(\frac{\partial Q}{\partial t}\right)}_i^{n+\frac{1}{2}}-2a{Q}_i^{n+\frac{1}{2}}.$$

Substituting these expressions into (69), we obtain the following expressions:

$$\begin{gathered} {\psi }_1={\left(\frac{\partial P}{\partial t}\right)}_i^{n+\frac{1}{2}}-\sigma \cdot {\left(\frac{\partial P}{\partial t}\right)}_i^{n+\frac{1}{2}}-\left(1-\sigma \right)\cdot {\left(\frac{\partial P}{\partial t}\right)}_i^{n+\frac{1}{2}}+0.5\left(2\sigma -1\right){\left(\frac{{\partial }^{2}Q}{\partial x\partial t}\right)}_i^{n+\frac{1}{2}}- \\ -\frac{\sigma h}{2}\cdot {\left(\frac{{\partial }^{2}Q}{\partial x^2}\right)}_i^{n+1}-\frac{\left(1-\sigma \right)h}{2}\cdot {\left(\frac{{\partial }^{2}Q}{\partial x^2}\right)}_i^n+O\left({\tau }^2+h^2\right), \end{gathered}$$

$$\begin{gathered} {\psi }_2={\left(\frac{\partial Q}{\partial t}\right)}_i^{n+\frac{1}{2}}-\sigma \cdot {\left(\frac{\partial Q}{\partial t}\right)}_i^{n+\frac{1}{2}}-\left(1-\sigma \right)\cdot \left[-{\left(\frac{\partial Q}{\partial t}\right)}_i^{n+\frac{1}{2}}-2a{Q}_i^{n+\frac{1}{2}}\right]+ \\ +0.5\tau \cdot \left(2\sigma -1\right){\left(\frac{{\partial }^{2}P}{\partial x\partial t}\right)}_i^{n+\frac{1}{2}}-\frac{\left(1-\sigma \right)h}{2}\cdot {\left(\frac{{\partial }^{2}P}{\partial x^2}\right)}_i^{n+1}-\frac{\left(1-\sigma \right)h}{2}\cdot {\left(\frac{{\partial }^{2}P}{\partial x^2}\right)}_i^n+ \\ +\left(1-\sigma \right)2a{Q}_i^{n+\frac{1}{2}}+O\left({\tau }^2+h^2\right). \end{gathered}$$

It is clear that the terms containing ${\left(\frac{\partial P}{\partial t}\right)}_i^{n+\frac{1}{2}} and {\left(\frac{\partial Q}{\partial t}\right)}_i^{n+\frac{1}{2}}$ cancel each other out and we obtain the following equations:

$${\psi }_1=0.5\tau \left(2\sigma -1\right){\left(\frac{{\partial }^{2}Q}{\partial x\partial t}\right)}_i^{n+\frac{1}{2}}-\frac{\sigma h}{2}\cdot {\left(\frac{{\partial }^{2}Q}{\partial x^2}\right)}_i^{n+1}-\frac{\left(1-\sigma \right)h}{2}\cdot {\left(\frac{{\partial }^{2}Q}{\partial x^2}\right)}_i^n+O\left({\tau }^2+h^2\right),$$

(70)

$$\begin{gathered} {\psi }_2=0.5\tau \left(2\sigma -1\right){\left(\frac{{\partial }^{2}P}{\partial x\partial t}\right)}_i^{n+\frac{1}{2}}-\frac{\sigma h}{2}\cdot {\left(\frac{{\partial }^{2}P}{\partial x^2}\right)}_i^{n+1}-\frac{\left(1-\sigma \right)h}{2}\cdot {\left(\frac{{\partial }^{2}P}{\partial x^2}\right)}_i^n+ \\ +2a\left(1-\sigma \right)\cdot \left(Q_i^{n+1}-Q_i^{n+\frac{1}{2}}\right)+O\left({\tau }^2+h^2\right). \end{gathered}$$

(71)

Let us expand the second derivatives in a Taylor series with respect to t in the vicinity of the point $t=t_{n+\frac{1}{2}}$.

$$\begin{array}{l}{\left(\frac{{\partial }^{2}Q}{\partial x^2}\right)}_i^{n+1}={\left(\frac{{\partial }^{2}Q}{\partial x^2}\right)}_i^{n+\frac{1}{2}}+O\left(\tau \right),\\ {\left(\frac{{\partial }^{2}Q}{\partial x^2}\right)}_i^n={\left(\frac{{\partial }^{2}Q}{\partial x^2}\right)}_i^{n+\frac{1}{2}}+O\left(\tau \right),\\ {\left(\frac{{\partial }^{2}P}{\partial x^2}\right)}_i^{n+1}={\left(\frac{{\partial }^{2}P}{\partial x^2}\right)}_i^{n+\frac{1}{2}}+O\left(\tau \right),\\ {\left(\frac{{\partial }^{2}P}{\partial x^2}\right)}_i^n={\left(\frac{{\partial }^{2}P}{\partial x^2}\right)}_i^{n+\frac{1}{2}}+O\left(\tau \right).\end{array}$$

(72)

Suppose that $Q_i^{n+1}=Q_i^{n+\frac{1}{2}}+O\left({\tau }^2\right)$.

Taking into account (72) from (70) and (71), we obtain the following equations:

$${\psi }_1=0.5\tau \left(2\sigma -1\right){\left(\frac{{\partial }^{2}Q}{\partial x\partial t}\right)}_i^{n+\frac{1}{2}}-0.5h\cdot {\left(\frac{{\partial }^{2}Q}{\partial x^2}\right)}_i^{n+\frac{1}{2}}+O\left({\tau }^2+h^2\right),$$

$${\psi }_2=0.5\tau \left(2\sigma -1\right){\left(\frac{{\partial }^{2}P}{\partial x\partial t}\right)}_i^{n+\frac{1}{2}}-0.5h\cdot {\left(\frac{{\partial }^{2}P}{\partial x^2}\right)}_i^{n+\frac{1}{2}}+O\left({\tau }^2+h^2\right).$$

From the system of Equations (34) and (35), we obtain the following equation:

$$\frac{{\partial }^{2}Q}{\partial x^2}=-\frac{{\partial }^{2}P}{\partial t\partial x}, \frac{{\partial }^{2}Q}{\partial x\partial t}=-\frac{{\partial }^{2}P}{\partial x^2}-2a\frac{\partial Q}{\partial x}.$$

Consider the following equations:

$$\begin{gathered} {\psi }_1+{\psi }_2=0.5\tau \left(2\sigma -1\right){\left(\frac{{\partial }^{2}Q}{\partial x\partial t}\right)}_i^{n+\frac{1}{2}}-0.5h\cdot {\left(\frac{{\partial }^{2}P}{\partial x^2}\right)}_i^{n+\frac{1}{2}}+ \\ +0.5\tau \left(2\sigma -1\right){\left(\frac{{\partial }^{2}P}{\partial x\partial t}\right)}_i^{n+\frac{1}{2}}-0.5h\cdot {\left(\frac{{\partial }^{2}Q}{\partial x^2}\right)}_i^{n+\frac{1}{2}}+O\left({\tau }^2+h^2\right). \end{gathered}$$

As well as the following equations:

$$\begin{gathered} {\left(\frac{{\partial }^{2}P}{\partial x^2}\right)}_i^{n+\frac{1}{2}}=-{\left(\frac{{\partial }^{2}Q}{\partial x\partial t}\right)}_i^{n+\frac{1}{2}}-2a{\left(\frac{\partial Q}{\partial x}\right)}_i^{n+\frac{1}{2}}, \\ {\left(\frac{{\partial }^{2}Q}{\partial x^2}\right)}_i^{n+\frac{1}{2}}=-{\left(\frac{{\partial }^{2}P}{\partial x\partial t}\right)}_i^{n+\frac{1}{2}} \end{gathered}$$

We obtain the following equations:

$$\begin{gathered} \psi ={\psi }_1+{\psi }_2=0.5\tau \left(2\sigma \tau -\tau +h\right)\cdot {\left(\frac{{\partial }^{2}Q}{\partial x\partial t}\right)}_i^{n+\frac{1}{2}}-ah\cdot {\left(\frac{\partial Q}{\partial x}\right)}_i^{n+\frac{1}{2}}+ \\ +0.5\tau \left(2\sigma \tau -\tau +h\right)\cdot {\left(\frac{{\partial }^{2}P}{\partial x\partial t}\right)}_i^{n+\frac{1}{2}}+O\left({\tau }^2+h^2\right). \end{gathered}$$

It can be seen that the scheme with weights has a second-order approximation.

$$\psi =O\left({\tau }^2+h^2\right),$$

if the following equality holds:

$$\sigma =\frac{1}{2}-\frac{h}{2\tau }={\sigma }_0,$$

(73)

and $\sigma \ne {\sigma }_0$—the first order, $\psi =O\left(\tau +h\right)$.

Stability is based on the initial data.

Let us now show that the scheme of the family of schemes with weights (48)–(54) is stable with respect to the initial data when the following condition is met:

$$\sigma \ge \frac{1}{2}-\frac{h}{2\tau }.$$

Using the method of energy inequalities, we obtain the following equation:

$$u_t^n+\sigma v_{\overline{x}}^{n+1}+\left(1-\sigma \right)v_{\overline{x}}^n=0,$$

(74)

We can consider the sum $w=u+v$ as follows:

$$w_t^n+\sigma w_{\overline{x}}^{n+1}+\left(1-\sigma \right)w_{\overline{x}}^n=0$$

(75)

We will introduce the grid, ${\overline{\omega }}_h=\left\{x_i=ih, i=0,1,\dots ,N,\mathrm{N}h=1\right\}$, in the segment $0\le x\le 1$.

The scalar product and norm are defined as follows:

$$\left(y, z\right]=\sum _{i=1}^N y_i\cdot z_i\cdot h, ‖y‖=\sqrt{\left(y, z\right]}.$$

taking the following equations into account:

$$y^{n+1}=0.5\left(y^{n+1}+y^n\right)+0.5\left(y^{n+1}-y^n\right),$$

$$y^n=0.5\left(y^{n+1}+y^n\right)-0.5\left(y^{n+1}-y^n\right),$$

and assuming that $y=w_{\overline{x}}$.

We can rewrite the scheme (75) in the following form:

$$w_t+\sigma \left(0.5\left(w_{\overline{x}}^{n+1}+w_{\overline{x}}^n\right)+0.5\mathsf{\tau }\cdot w_{\overline{x}t}^n\right)+0.5\cdot \left(1-\sigma \right)\left[\left(w_{\overline{x}}^{n+1}+w_{\overline{x}}^n\right)-\tau w_{\overline{x}t}^n\right]=0,$$

$$w_t^n+\left(\sigma -0.5\right)\tau \cdot w_{\overline{x}t}^n+0.5\left(w_{\overline{x}}^{n+1}+w_{\overline{x}}^n\right)=0.$$

(76)

Multiply this equation by $2\tau w_{\overline{x}t}^n=2\left(w_{\overline{x}}^{n+1}-w_{\overline{x}}^n\right)$ as follows:

$$2\tau w_t^n\cdot w_{\overline{x}t}^n+2{\tau }^2\left(\sigma -0.5\right){\left(w_{\overline{x}t}^n\right)}^2+{\left(w_{\overline{x}}^{n+1}\right)}^2-{\left(w_{\overline{x}}^n\right)}^2=0$$

We transform the first term as follows:

$$2w_t^n\cdot w_{\overline{x}t}^n=\left(w_{\overline{x}t}^2\right)+h{\left(w_{\overline{x}t}^n\right)}^2.$$

Then, we obtain the following equation:

$$\tau \cdot \left(w_{\overline{x}t}^2\right)+h\tau {\left(w_{\overline{x}t}^n\right)}^2+2{\tau }^2\left(\sigma -0.5\right){\left(w_{\overline{x}t}^n\right)}^2+{\left(w_{\overline{x}}^{n+1}\right)}^2-{\left(w_{\overline{x}}^n\right)}^2=0$$

If we combine the second and third terms, we obtain the following equation:

$$\tau \cdot \left(w_{\overline{x}t}^2\right)+2{\tau }^2\left(\left(\sigma -0.5\right)\tau +0.5h\right){\left(w_{\overline{x}t}^n\right)}^2+{\left(w_{\overline{x}}^{n+1}\right)}^2-{\left(w_{\overline{x}}^n\right)}^2=0.$$

Multiplying by $h$ and summing up over all grid nodes, $x_i=ih, i=0,1,\dots ,N,$ we obtain the following equation:

$$\tau \sum _{i=1}^N {\left(w_t^2\right)}_{\overline{x},i}h+2{\tau }^2\left(\left(\sigma -0.5\right)\tau +0.5h\right)\cdot {‖w_{\overline{x}t}^n‖}^2+{‖w_{\overline{x}}^{n+1}‖}^2={‖w_{\overline{x}}^n‖}^2.$$

We write out the difference derivative with respect to x in the first term and then obtain the following equation:

$$\tau \sum _{i=1}^N \left[{\left(w_t^n\right)}_i^2-{\left(w_t^n\right)}_{i-1}^2\right]+2\tau \left(\left(\sigma -0.5\right)\tau +0.5h\right)\cdot {‖w_{\overline{x}t}^n‖}^2+{‖w_{\overline{x}}^{n+1}‖}^2={‖w_{\overline{x}}^n‖}^2.$$

We expand the sum, cancel the terms, and derive the following equation:

$$\tau \sum _{i=1}^N \left[{\left(w_t^n\right)}_N^2-{\left(w_t^n\right)}_0^2\right]+2\tau \left(\left(\sigma -0.5\right)\tau +0.5h\right)\cdot {‖w_{\overline{x}t}^n‖}^2+{‖w_{\overline{x}}^{n+1}‖}^2={‖w_{\overline{x}}^n‖}^2,$$

Here, $w_{t,0}^n=w_t\left(t, 0\right)=0$ because $w_t\left(t, 0\right)\equiv 0$.

Finally, we obtain the following identity:

$$\tau \cdot {\left({\mathrm{w}}_{\mathrm{t}}^{\mathrm{n}}\right)}_{\mathrm{N}}^2+2\tau \left(\left(\sigma -0.5\right)\tau +0.5h\right)\cdot {‖w_{\overline{x}t}^n‖}^2+{‖w_{\overline{x}}^{n+1}‖}^2={‖w_{\overline{x}}^n‖}^2.$$

(77)

From identity (77), it can be seen that if the following condition is met:

$$\left(\sigma -0.5\right)\tau +0.5h\ge 0,$$

i.e., $\sigma =\frac{1}{2}-\frac{h}{2\tau }={\sigma }_0,$ then we obtain the following equation:

$$‖w_{\overline{x}}^{j+1}‖\le ‖w_{\overline{x}}^j‖\le \dots \le ‖w_{\overline{x}}^0‖.$$

(78)

Scheme (75) is stable in the following energy norm:

$${‖w‖}_{\left(1\right)}=‖w_{\overline{x}}‖.$$

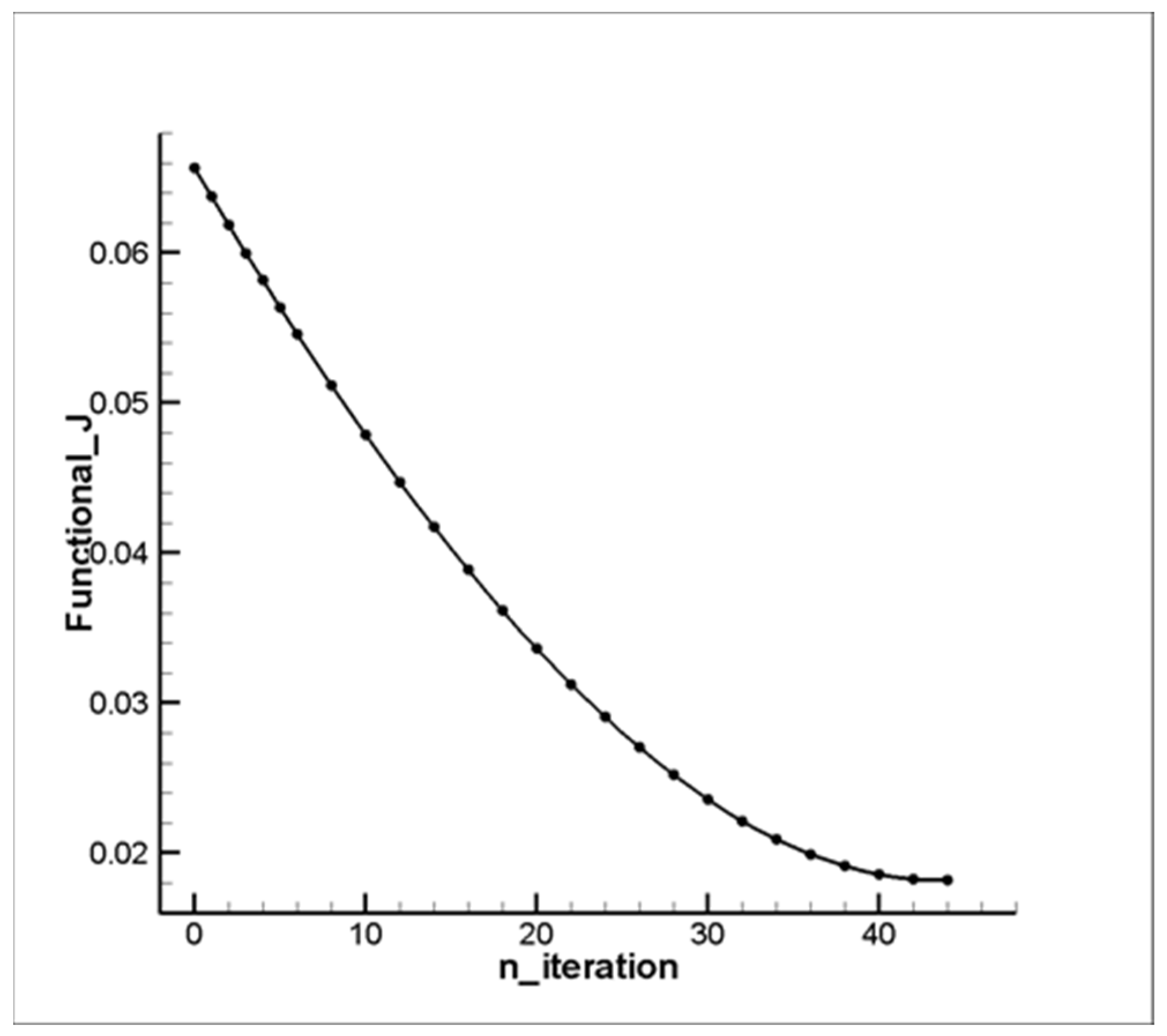
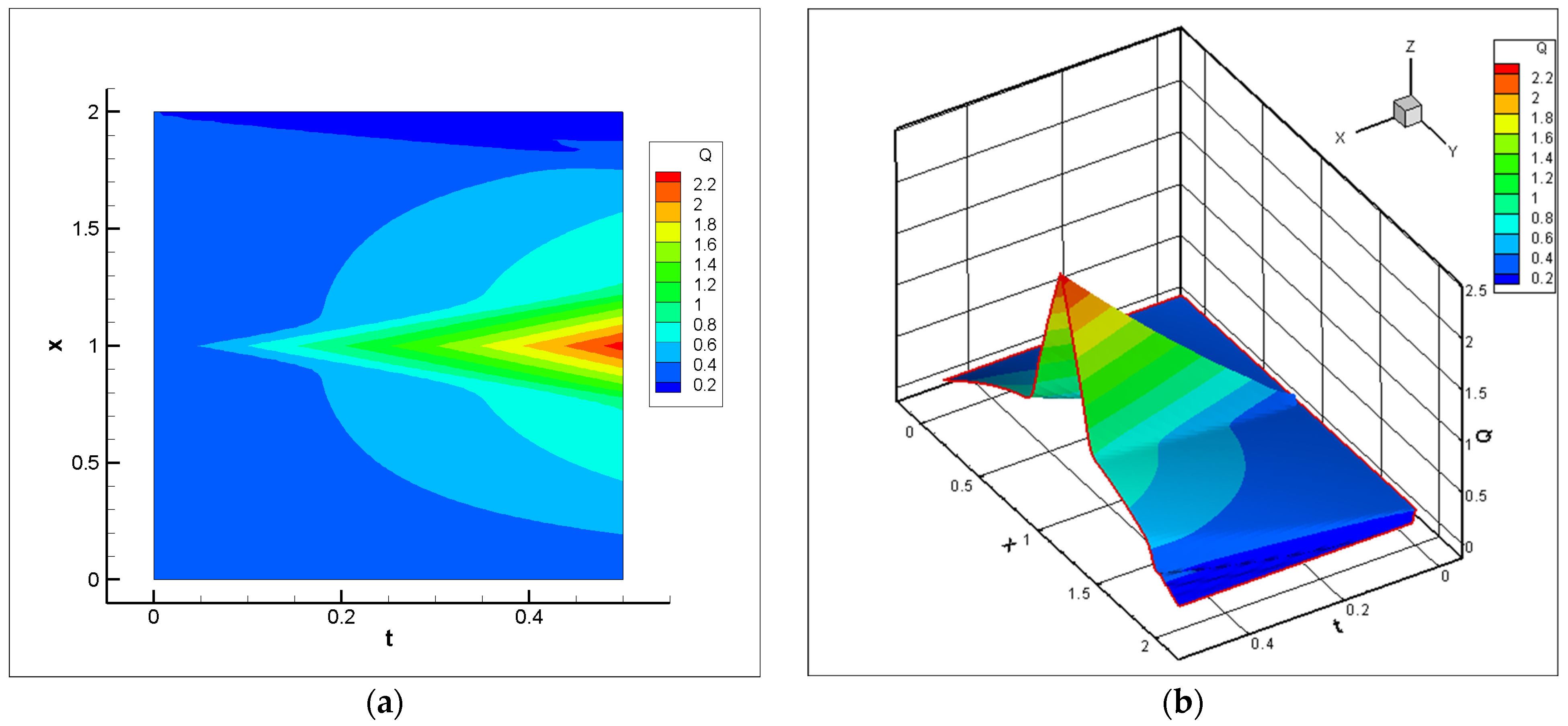
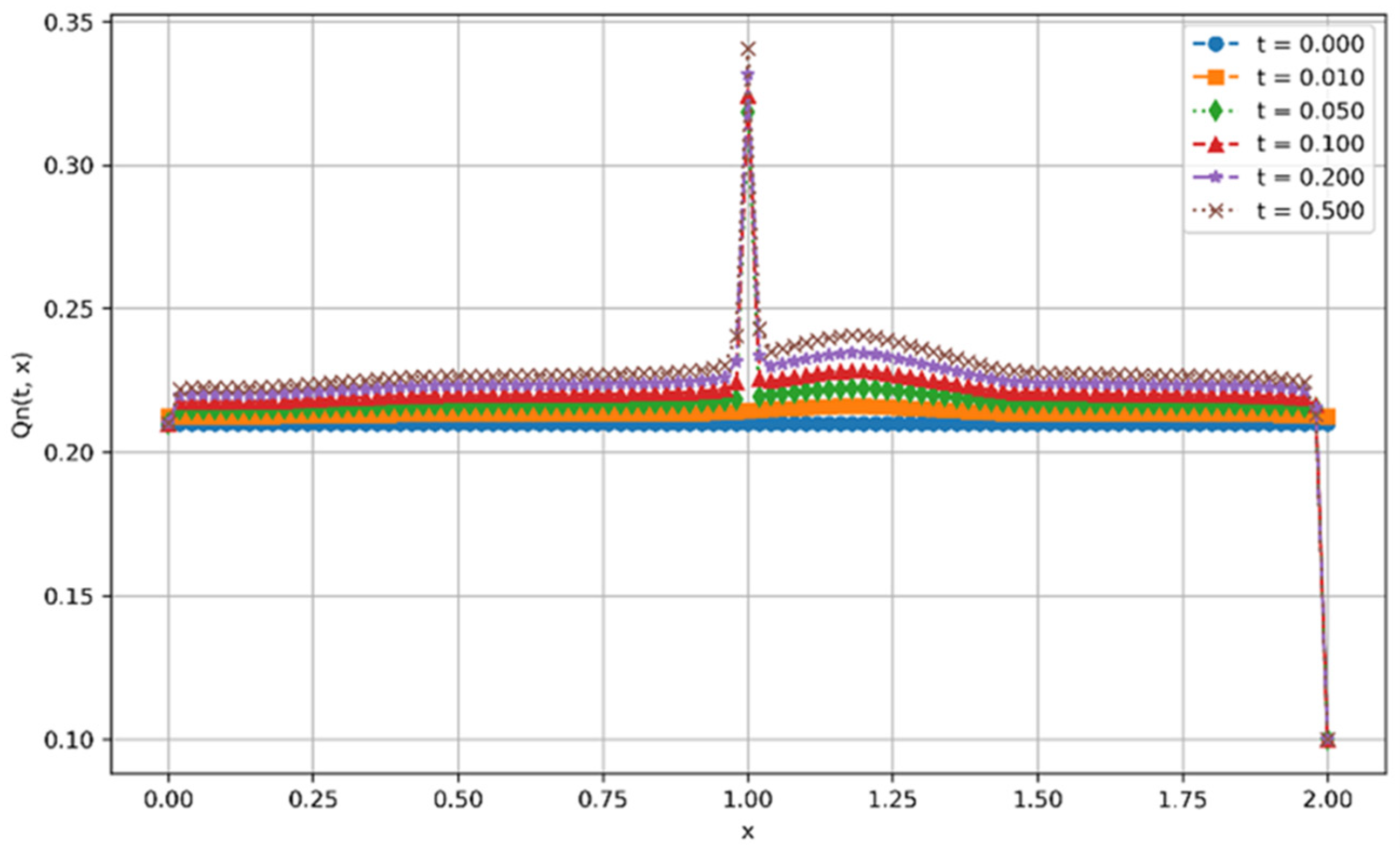
3. Results and Discussion

Numerical Solution for the Problem

Computational Experiment

The initial data for the computational experiment are as follows: $Q^0=0.21$ is the volumetric flow rate of injected gas (${\mathrm{m}}^3/\mathrm{s}$); $P^0=5177500$ is the initial pressure distribution ($\mathrm{P}\mathrm{a}$); $l=1485$ is the well depth (m); ${\lambda }_1=0.01$ is the hydraulic resistance in the ring; ${\lambda }_2=0.23$ is the hydraulic resistance in the pipe; $d_1\approx 0.1353$ is the effective diameter of the well annular space (m); and $d_2=0.073$ is the internal diameter of the well (m).

${\rho }_1=0.75$ is the gas density ($\mathrm{k}\mathrm{g}/{\mathrm{m}}^3$); ${\rho }_2=700$ is the oil density ($\mathrm{k}\mathrm{g}/{\mathrm{m}}^3$); g = 9.8 is the gravity acceleration ($\mathrm{m}/{\mathrm{s}}^2$); $c_1=331$ is the speed of sound in the annular space (m/s); $c_2=850$ is the speed of sound in the pipe (m/s); ${\mathrm{r}}_1=\frac{{\mathrm{d}}_1}{2}$ is the radius of the annular space (m); $r_2=\frac{d_2}{2}$ is the radius of the inner pipe (m); $F_1=\pi r_1^2$ is the cross-sectional area of the pipe of the well’s annular space (${\mathrm{m}}^2$); $F_2=\pi r_2^2$ is the cross-sectional area of the inner pipe of the well (${\mathrm{m}}^2$); $w_1=\frac{Q_0}{F_1{\rho }_1}$ is averaged over the cross-section speed of the mixture in the ring (m/s); and $w_2=\frac{Q_0}{F_2{\rho }_2}$ is the average cross-sectional speed of the mixture in the pipe (m/s).

The coefficients in the ring and pipe are described as follows:

$$a_1=\frac{g}{2w_1}+\frac{{\lambda }_1{w}_1}{4d_1}, a_2=\frac{g}{2w_2}+\frac{{\lambda }_2{w}_2}{4d_2}$$

Calculations of the test problem were performed for the parameters $T=0.5$, $l=1$, $N_x=100,$ $N_t=100$, $h=\raisebox{1ex}{$2l$}\!\left/ \!\raisebox{-1ex}{$N_x$}\right.$, and $\tau =\raisebox{1ex}{$T$}\!\left/ \!\raisebox{-1ex}{$N_t$}\right.$. The step of gradient descent is $\alpha =0.01$, the exact solution of which is known, as follows:

$$G^0\left(x\right)=sin\left[\right(\pi x/2l\left)\right]$$

The initial approximation is as follows:

$$G_0^0\left(x\right)=0.1.$$

Figure 1 shows a graph of change in the functional $J\left(G_n^0\right)$ during the numerical solution process of the inverse problem. The graph demonstrates a monotonic decrease in functional values during the iteration process.

To quantitatively assess the accuracy of the numerical method, an error analysis was performed between the approximate and exact solution of the function $Q(T,x)$. The Euclidean (discrete $L_2$) error norm was used as a measure as follows:

$$\epsilon ={\left({\sum }_{i=1}^{N_x} {\left[Q_i^{N_t}-Q^1\left(x_i\right)\right]}^{2}h\right)}^{1/2}.$$

When using the gradient descent step, $\alpha =0.01$, and 46 iterations, the error value was $\mathsf{\epsilon }\approx 0.018$. This confirms the good accuracy of the approximation, especially in the central part of the region, while the main discrepancies are concentrated in the interval $x\in (0.8, 1.6)$, where high gradients of the function are observed.

The convergence analysis of the functional $J\left(G_n^0\right)$ showed its monotonous decrease from the initial value to the level of $\approx 0.02$ over 46 iterations. Further increases in the number of iterations did not provide significant improvement, which indicates the achievement of the optimum and the stability of the method. Thus, the proposed numerical method provides a reliable approximation of the desired function and demonstrates stable behavior with respect to computational costs.

Figure 2 shows (a) a two-dimensional and (b) a three-dimensional picture of the smooth distribution of the function $Q(t,x)$, reflecting correct wave and symmetry development. The range of changes in the function is wider, and the changes in gradient are smoother.

Figure 3 shows (a) two-dimensional and (b) three-dimensional solutions, which diverge for an approximate value of the initial condition, $G_n^0\left(x\right)$, in areas close to $x=l$ and $t\approx 0.4$. A distortion in the shape and a narrowing in the range of maximum values of the function $Q(t,x)$ indicate incomplete convergence of the iterative process.

The main discrepancies between the exact and approximate solutions are in the region of $x\in (0.8,1.6)$, where the values of $Q\left(t,x\right)$ on the right graph are smaller than the exact solution. This discrepancy is caused by insufficient correction of the initial condition in the Landweber method at this stage. The exact solution reflects the correct distribution of wave processes, while the approximate solution shows minor deviations in areas with high gradients. Additional iterations of the Landweber method can improve convergence and reduce discrepancies between the numerical and exact solutions. The graphs clearly show the importance of accurately approximating the initial condition, $G^0\left(x\right)$, to achieve high accuracy in modeling gas lift wells.

Both graphs (Figure 4 and Figure 5) show a smooth change in the function along the x-axis for small values of time intervals, t. As the time increases, an increase in the amplitude is observed in the central part of the graph, near $x\approx 1$. This increase indicates the formation of a localized maximum, which is typical for solutions of the considered system of equations. The function $Q_{fix}(t,x)$ demonstrates a more pronounced symmetry with respect to the center than the function $Q_n(t,x)$, indicating the high accuracy of the exact solution.

In both cases, a distinct peak is visible in the vicinity of $x\approx 1.2.$ With increasing time, this peak becomes stronger and reaches its maximum values at $t=0.5$. However, in the right graph, which represents an approximate solution, the central peak shows a slight shift and fluctuation, which may indicate the approximation’s inaccuracy.

At the initial time intervals, the values of the function $Q(t,x)$ at the boundaries $x=0$ and $x=2$ remain practically unchanged. However, with an increase in the time parameter, t, a decrease in the values of the function at the boundaries is observed. This phenomenon is consistent with the physical interpretation of the boundary conditions and reflects the expected behavior of the solution for the system.

The proposed method has important practical applications, as it helps optimize the parameters of the gas lift process and minimizes gas consumption for maximum oil production. This optimization leads to a significant reduction in operating costs during oil production, which is especially important for aging fields with low flow rates.

4. Conclusions

In this paper, a numerical method for solving the direct and inverse problems of the gas lift process in oil production, based on the method of conjugate equations, is developed and implemented. The key novelty of the method lies in the application of a variational formulation and the construction of a conjugate problem for calculating the gradient of the functional, which allows us to effectively solve the inverse problem of restoring the initial distribution of gas velocity for a given final state.

Unlike traditional empirical or heuristic methods for optimizing gas lift processes, the proposed method is based on a rigorous mathematical framework and ensures controlled convergence. This allows us not only to increase the accuracy of calculations but also to reduce the volume of injected gas while maintaining the level of oil production, which is of great practical importance.

The conducted numerical experiments confirmed the effectiveness of the method: high accuracy in approximating the target function was achieved in a limited number of iterations, while stable and reproducible results were obtained. The method can be used to optimize the operating parameters of gas lift wells and can also be adapted to more complex models, including multidimensional and nonlinear settings.

The practical significance of the proposed method lies in its potential integration into software packages for managing oil production at gas lift wells. By restoring the optimal initial distribution of gas velocity, a more precise adjustment of the injection mode is ensured, which allows for the following benefits:

-

Reduce the volume of gas consumed while maintaining the production level.

-

Adapt control to changing reservoir and well characteristics.

-

Increase operating efficiency without the need to install additional sensors.

-

Predict and minimize the risks of underloading or the over-consumption of gas.

Thus, this study represents a significant contribution to the development of optimal control methods for problems described by hyperbolic equations and opens up opportunities for further applied developments in modeling oil and gas processes. The method can also serve as a decision support tool in intelligent oil field management systems, especially when implementing automation and digitalization in oil production.