Identification, Control, and Characterization of Peristaltic Pumps in Hemodialysis Machines
Abstract
1. Introduction
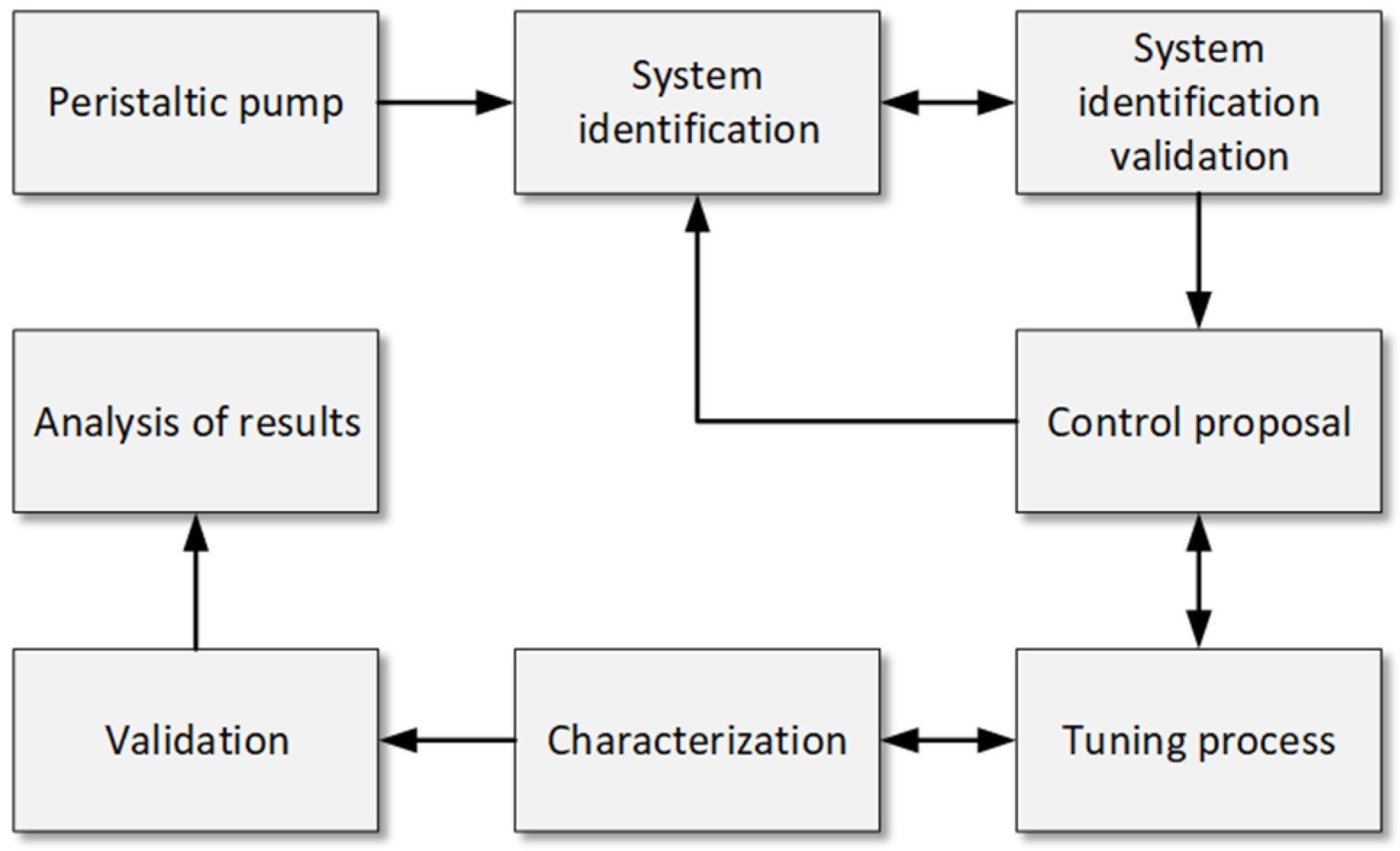
2. Methodology
2.1. Peristaltic Pump
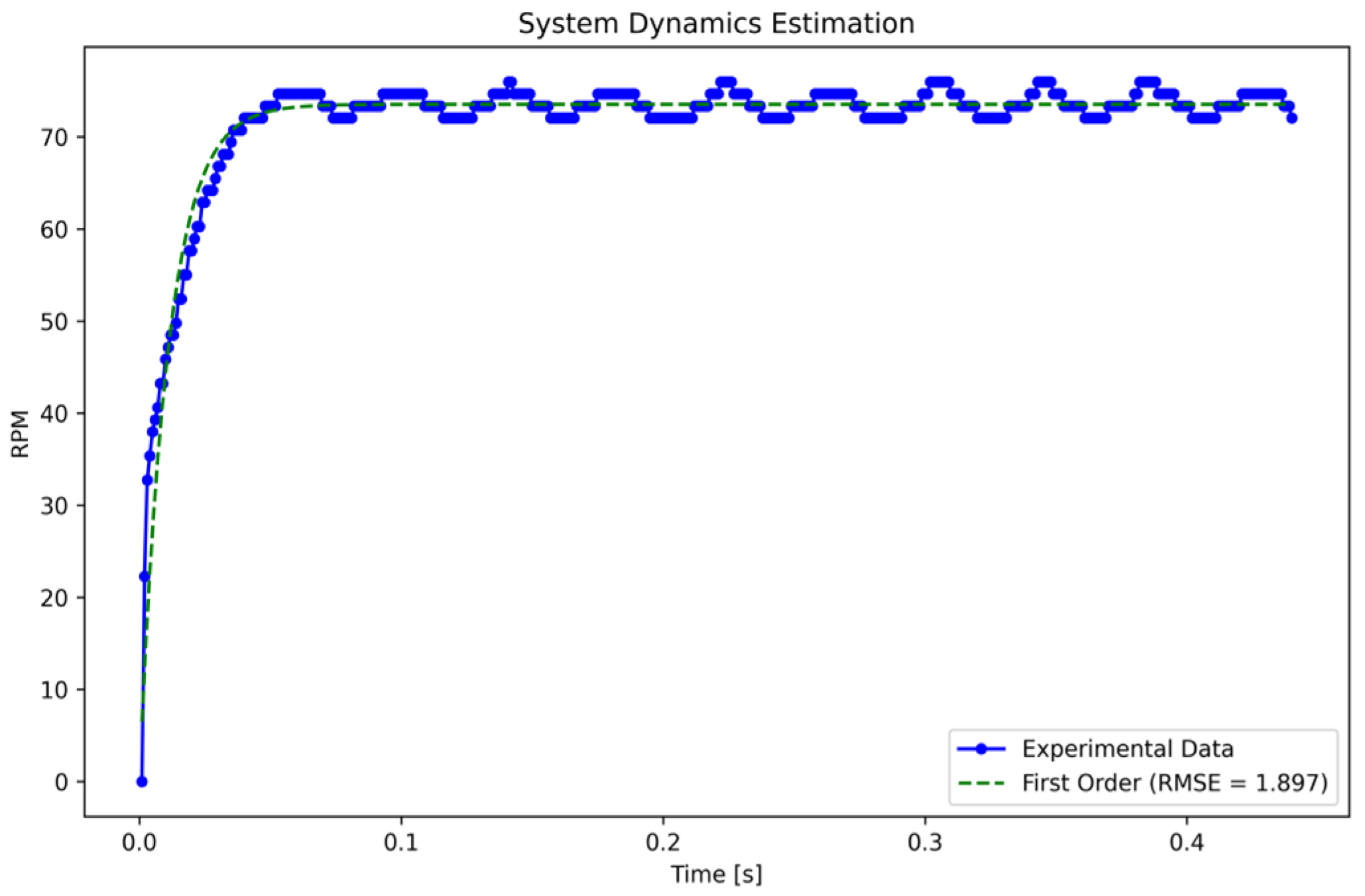
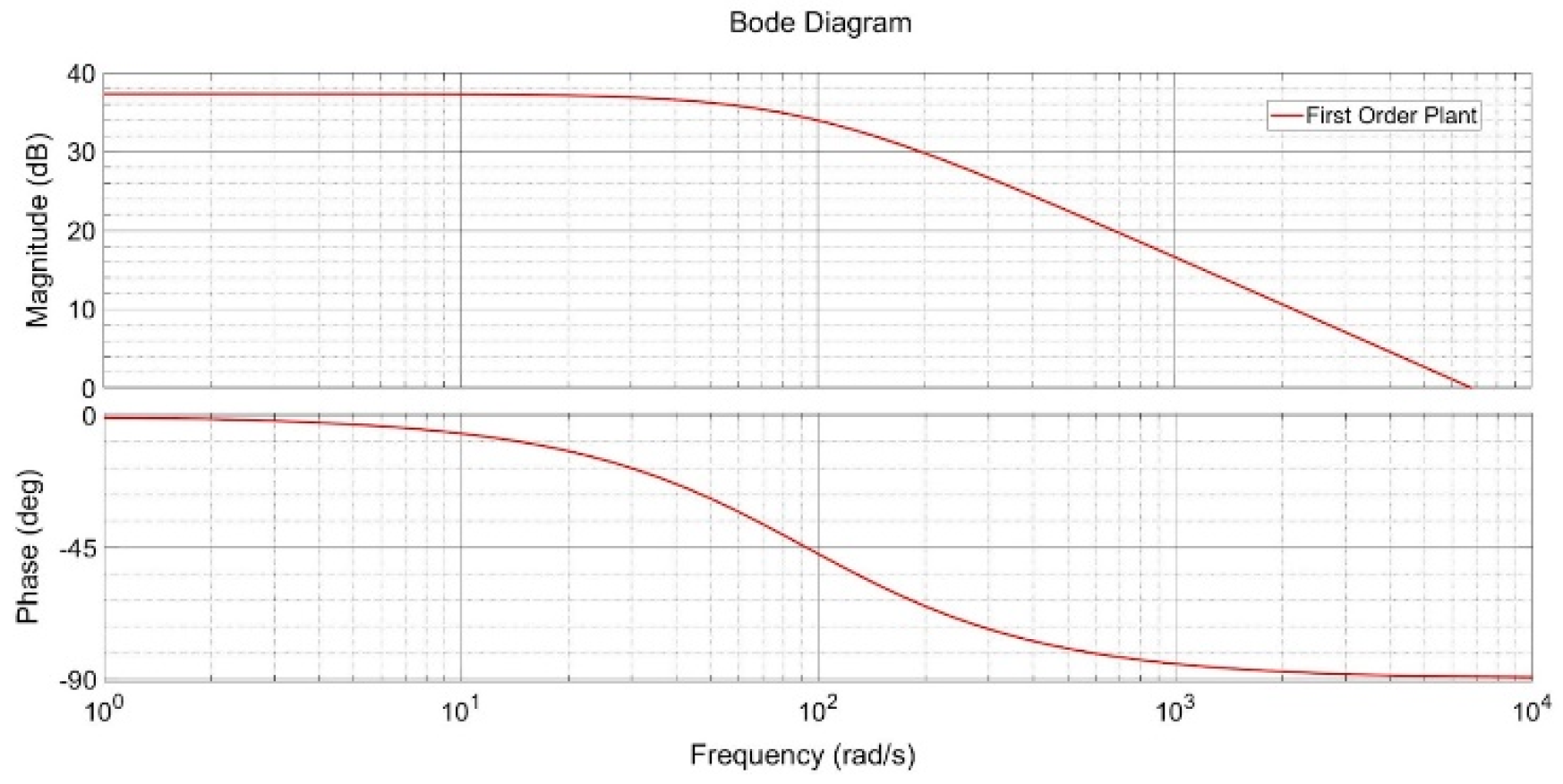
2.2. System Identification
2.3. Auxiliary Methodologies for System Approximation Verification
2.4. Controller Design
2.5. Gain Estimation
- System modeling: The application can accept a transfer function as an input or estimate it. The previously estimated transfer function (see Equation (5)) was input in the present case;
- The initial parameters of the PID controller are calculated by MATLAB using frequency-based techniques based on the principles set forth by the Frequency Response Theorem and Ziegler-Nichols. This approach permits the identification of an initial configuration that offers an optimal equilibrium between stability, response speed, and damping;
- The objective of performance-based optimization is to achieve optimal performance. Once the initial PID parameter values have been obtained, the PID Tuner employs optimization algorithms to fine-tune the Kp, Ki, and Kd parameters;
- The following performance criteria will be considered: In the preceding step of the optimization process, the application also considers performance criteria, including minimizing overshoot, settling time, response speed, and steady-state error;
- Controller validation: The tuned controller is subsequently validated through simulations to guarantee that it fulfills the design specifications, including stability and the desired performance regarding response time and frequency analysis.
2.6. Statistical Analysis and Validation of Results
3. Analysis of Results
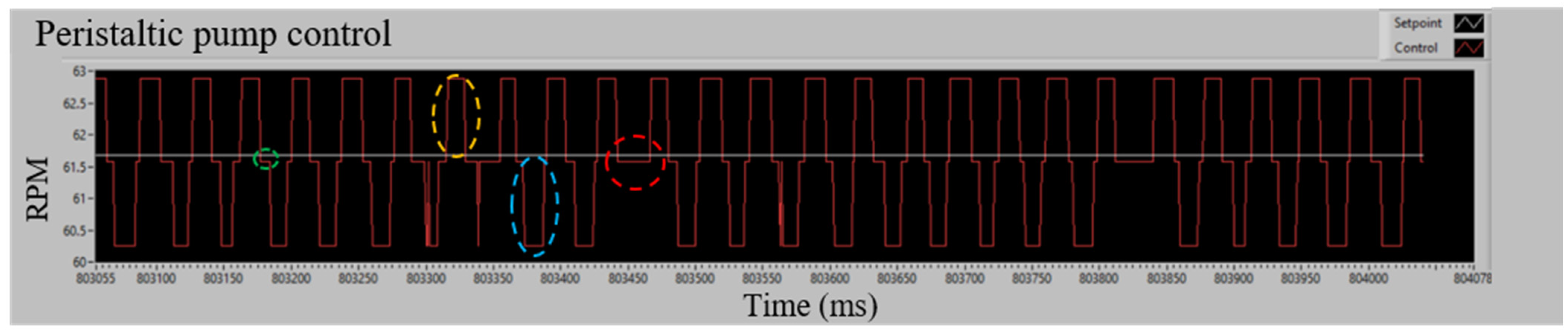
3.1. Control System
3.2. Characterization
3.3. Validation
3.4. Statistical Analysis Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Park, S.H. Modality Selection. In The Essentials of Clinical Dialysis; Kim, Y.L., Kawanishi, H., Eds.; Springer: Singapore, 2018. [Google Scholar] [CrossRef]
- Azar, A.T.; Canaud, B. Hemodialysis System. In Modelling and Control of Dialysis Systems; Azar, A., Ed.; Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2013; Volume 404. [Google Scholar] [CrossRef]
- Brophy, P.D.; Yap, H.K.; Alexander, S.R. Acute Kidney Injury: Diagnosis and Treatment with Peritoneal Dialysis, Hemodialysis, and CRRT. In Pediatric Dialysis; Springer: Cham, Switzerland, 2012. [Google Scholar] [CrossRef]
- Klespitz, J.; Kovács, L. Identification and control of peristaltic pumps in hemodialysis machines. In Proceedings of the 2013 IEEE 14th International Symposium on Computational Intelligence and Informatics (CINTI), Budapest, Hungary, 19–21 November 2013; pp. 83–87. [Google Scholar] [CrossRef]
- Klespitz, J.; Takacs, M.; Rudas, I.; Kovacs, L. Adaptive soft computing methods for control of hemodialysis machines. In Proceedings of the 2014 International Conference on Fuzzy Theory and Its Applications (iFUZZY2014), Kaohsiung, Taiwan, 26–28 November 2014; pp. 47–50. [Google Scholar] [CrossRef]
- Klespitz, J.; Takács, M.; Kovács, L. Application of fuzzy logic in hemodialysis equipment. In Proceedings of the IEEE 18th International Conference on Intelligent Engineering Systems INES 2014, Tihany, Hungary, 3–5 July 2014; pp. 169–173. [Google Scholar] [CrossRef]
- Busono, P.; Iswahyudi, A.; Rahman, M.A.A.; Fitrianto, A. Design of Embedded Microcontroller for Controlling and Monitoring Blood Pump. Procedia Comput. Sci. 2015, 72, 217–224. [Google Scholar] [CrossRef]
- Samuel, G.; Arifin, A.; Fatoni, M.H.; Setiawan, R. Design and Implementation Control of PID Controller of Dialysate Pump of Hemodialysis Machine. In Proceedings of the 2020 International Conference on Computer Engineering, Network, and Intelligent Multimedia (CENIM), Surabaya, Indonesia, 17–18 November 2020; pp. 287–291. [Google Scholar] [CrossRef]
- Andras Szolga, L.; Heredea, P.C.; Potarniche, I.A. Low-Cost Peristaltic Pump for Laboratory Applications. In Proceedings of the 2021 IEEE 27th International Symposium for Design and Technology in Electronic Packaging (SIITME), Timisoara, Romania, 27–30 October 2021; pp. 322–325. [Google Scholar] [CrossRef]
- Sadhana, T.K.; Sardjono, T.A.; Fatoni, M.H. Mechanism Development of Blood Pump and Syringe Pump in Hemodialysis Machine. In Proceedings of the 2022 International Conference on Computer Engineering, Network, and Intelligent Multimedia (CENIM), Surabaya, Indonesia, 22–23 November 2022; pp. 157–161. [Google Scholar] [CrossRef]
- Klesnitz, J.; Felde, I.; Kovács, L.; Pintér, G.; Nádai, L. Systemic Fluid Balance Control in Hemodialysis Machines with ANFIS. In Proceedings of the 2019 IEEE-RIVF International Conference on Computing and Communication Technologies (RIVF), Danang, Vietnam, 20–22 March 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Arifin, B.; Nugroho, A.A.; Suprapto, B.; Prasetyowati, S.A.D.; Nawawi, Z. Review of Method for System Identification on Motors. In Proceedings of the 2021 8th International Conference on Electrical Engineering, Computer Science and Informatics (EECSI), Semarang, Indonesia, 20–21 October 2021. [Google Scholar] [CrossRef]
- Naajihah Ab Rahman, N.; Yahya, N.M. System Identification for a Mathematical Model of DC Motor System. In Proceedings of the 2022 IEEE International Conference on Automatic Control and Intelligent Systems (I2CACIS), Shah Alam, Malaysia, 25 June 2022; pp. 30–35. [Google Scholar] [CrossRef]
- Leylaz, G.; Wang, S.; Sun, J.Q. Identification of nonlinear dynamical systems with time delay. Int. J. Dyn. Control 2022, 10, 13–24. [Google Scholar] [CrossRef]
- Yunus, R.B.; Zainuddin, N.; Daud, H.; Kannan, R.; Abdul Karim, S.A.; Yahaya, M.M. A Modified Structured Spectral HS Method for Nonlinear Least Squares Problems and Applications in Robot Arm Control. Mathematics 2023, 11, 3215. [Google Scholar] [CrossRef]
- Grisetti, G.; Guadagnino, T.; Aloise, I.; Colosi, M.; Della Corte, B.; Schlegel, D. Least Squares Optimization: From Theory to Practice. Robotics 2020, 9, 51. [Google Scholar] [CrossRef]
- Moré, J.J. The Levenberg-Marquardt algorithm: Implementation and theory. In Numerical Analysis; Watson, G.A., Ed.; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 1978; Volume 630. [Google Scholar] [CrossRef]
- Johnson, M.A.; Moradi, M.H. (Eds.) PID Control; Springer-Verlag: Berlin/Heidelberg, Germany, 2005. [Google Scholar] [CrossRef]
- Abbas, I.A.; Mustafa, M.K. A review of adaptive tuning of PID-controller: Optimization techniques and applications. Int. J. Nonlinear Anal. Appl. 2024, 15, 29–37. [Google Scholar] [CrossRef]
- Mousakazemi, S.M.H. Comparison of the error-integral performance indexes in a GA-tuned PID controlling system of a PWR-type nuclear reactor point-kinetics model. Prog. Nucl. Energy 2021, 132, 103604. [Google Scholar] [CrossRef]
- Tavakoli, S.; Tavakoli, M. Optimal Tuning of PID Controllers for First Order Plus Time Delay Models Using Dimensional Analysis. In Proceedings of the 2003 4th International Conference on Control and Automation Proceedings, Montreal, QC, Canada, 12 June 2003; pp. 942–946. [Google Scholar] [CrossRef]
- Visioli, A. Practical PID Control; Springer: London, UK, 2006. [Google Scholar] [CrossRef]
- Astrom, J.K.; Hagglund, T. Control PID Avanzado, 1st ed.; Pearson Prentice Hall: Madrid, Spain, 2009; Volume 1. [Google Scholar]
- PID Control System Design and Automatic Tuning Using MATLAB/Simulink, Wiley. Available online: https://www.wiley.com/en-us/PID+Control+System+Design+and+Automatic+Tuning+using+MATLAB+Simulink-p-9781119469346 (accessed on 10 October 2024).
- Böhme, G.; Müller, A. Analysis of non-Newtonian effects in peristaltic pumping. J. Non-Newton. Fluid Mech. 2013, 201, 107–119. [Google Scholar] [CrossRef]
- Fresenius Medical Care. 2000. Available online: https://freseniusmedicalcare.com/content/dam/fmcna/live/support/documents/operator%27s-manuals---hemodialysis-(hd)/2008k-operator%27s-manuals/490042_Rev_P.pdf (accessed on 1 July 2024).
- Ramírez-Carvajal, L.; Puerto-López, K.; López-Barrera, G.L. Nonlinear regression for the characterization of peristaltic pumps, an alternative in the control of biological fluids. Ingeniería y Competitividad 2024, 26, e-21113256. [Google Scholar] [CrossRef]
- Camargo, C.; García, C.; Duarte, J.; Rincón, A. Modelo estadístico para la caracterización y optimización en bombas periféricas. Ingeniería y Desarrollo 2018, 36, 18–39. [Google Scholar] [CrossRef]
- Hostettler, M.; Grüter, R.; Stingelin, S.; De Lorenzi, F.; Fuechslin, R.M.; Jacomet, C.; Koll, S.; Wilhelm, D.; Boiger, G.K. Modelling of Peristaltic Pumps with Respect to Viscoelastic Tube Material Properties and Fatigue Effects. Fluids 2023, 8, 254. [Google Scholar] [CrossRef]
- Ferretti, P.; Pagliari, C.; Montalti, A.; Liverani, A. Design and development of a peristaltic pump for constant flow applications. Front. Mech. Eng. 2023, 9, 1207464. [Google Scholar] [CrossRef]
- Walker, S.W.; Shelley, M.J. Shape optimization of peristaltic pumping. J. Comput. Phys. 2010, 229, 1260–1291. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design and Analysis of Experiments, 9th ed.; EMEA Edition; John Wiley & Sons: Hoboken, NJ, USA, 2020; ISBN 978-1-119-63842-1. [Google Scholar]
- Voelkel, J.G. Design and Analysis of Gauge R&R Studies: Making Decisions with Confidence Intervals in Random and Mixed ANOVA Models. J. Qual. Technol. 2006, 38, 193–195. [Google Scholar] [CrossRef]



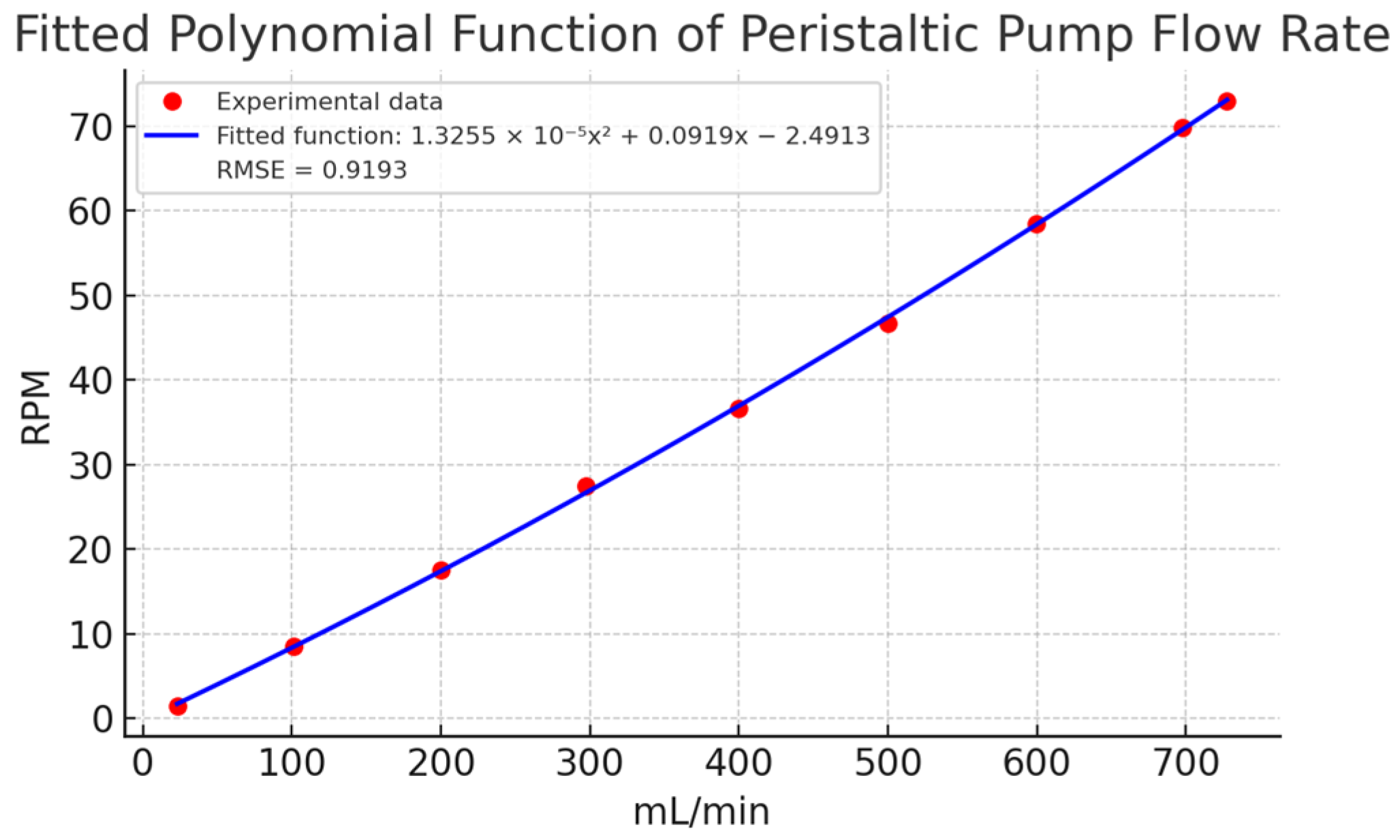
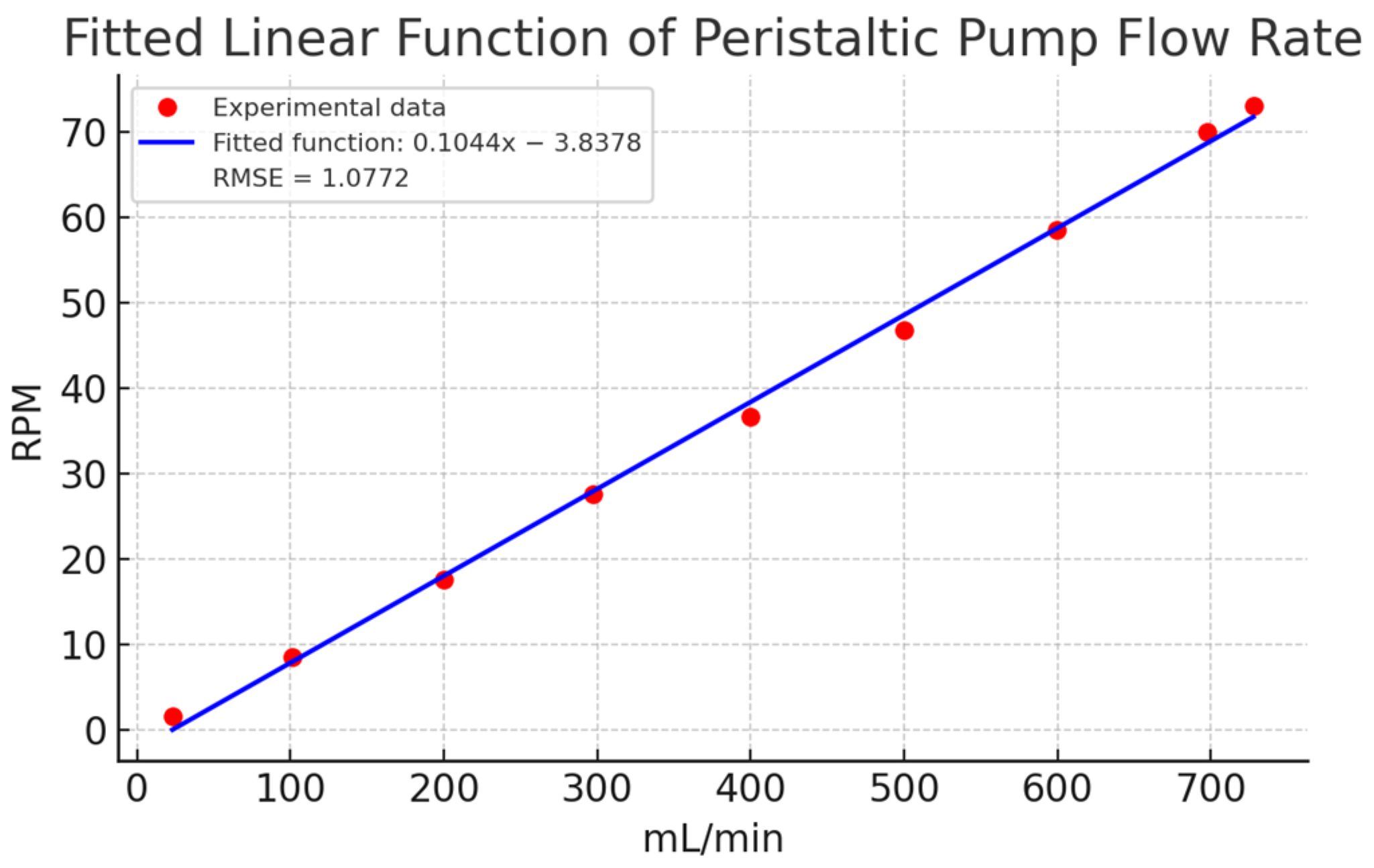


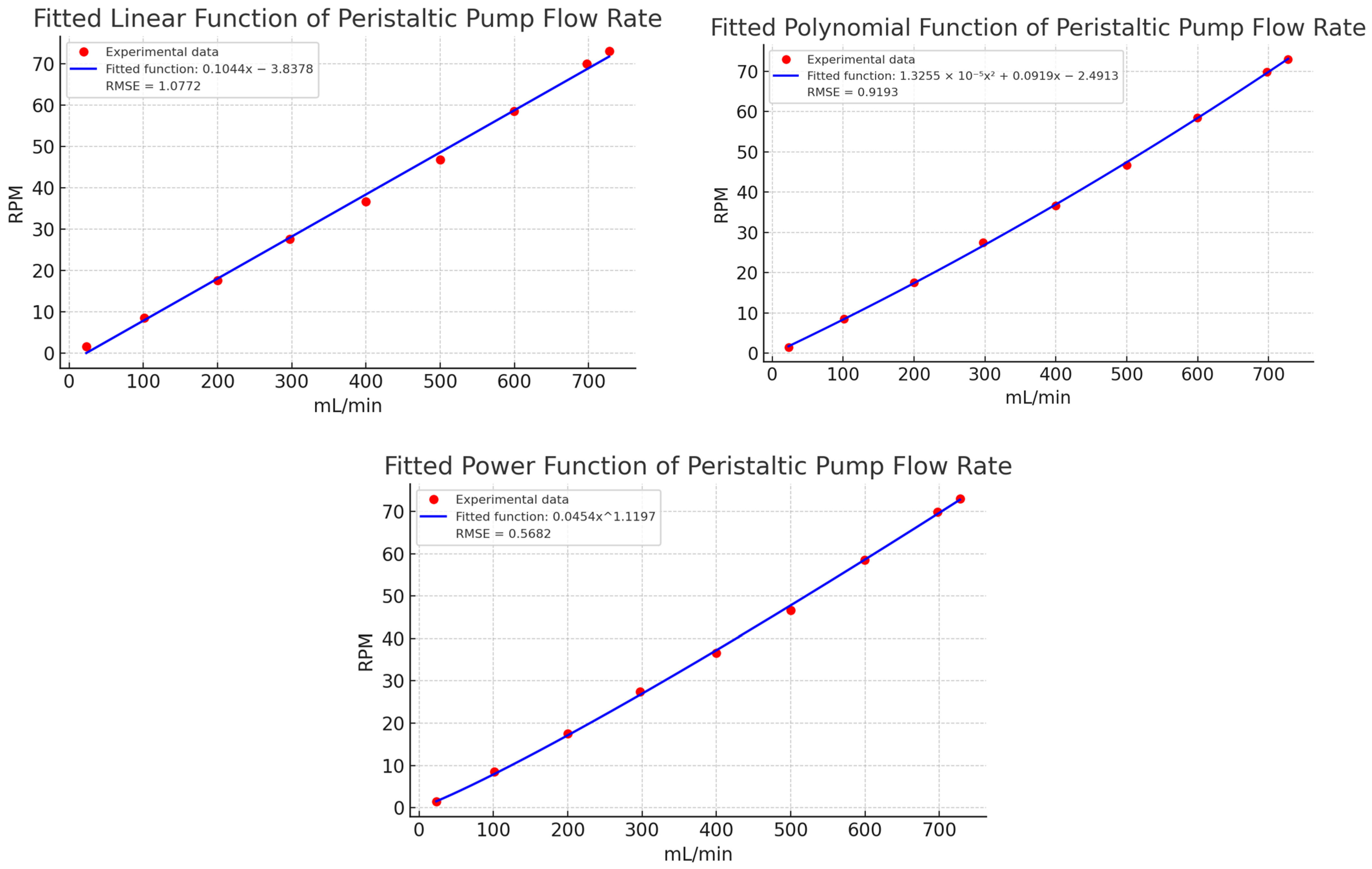
| Methodology for Absolute Error Calculation | Data | First Order | Error | %Approximation Error of the System |
|---|---|---|---|---|
| Integral Absolute Error IAE | 2383 | 2394 | −10.9300 | 0.4586% |
| Integral Square Error ISE | 7.706 × 104 | 7.973 × 104 | −2671 | 3.4670% |
| Integral Time Absolute Error ITAE | 286.2 | 286.4 | −0.1534 | 0.0536% |
| Integral Time Square Error ITSE | 7740 | 7722 | 18.16 | 0.2345% |
| Sample | Target Flow (mL/min) | RPM | Average Flow (mL/min) | Standard Deviation | RMSE |
|---|---|---|---|---|---|
| 1 | 20 | 1.50 | 23.06 | 0.18 | 0.97 |
| 2 | 100 | 8.50 | 101.35 | 0.45 | 0.45 |
| 3 | 200 | 17.50 | 200.00 | 0.00 | 0.00 |
| 4 | 300 | 27.49 | 297.55 | 1.03 | 0.84 |
| 5 | 400 | 36.60 | 400.00 | 0.00 | 0.00 |
| 6 | 500 | 46.70 | 500.00 | 0.00 | 0.00 |
| 7 | 600 | 58.50 | 599.80 | 0.60 | 0.20 |
| 8 | 700 | 69.90 | 697.40 | 0.18 | 0.97 |
| 9 | 730 | 73.00 | 727.60 | 0.45 | 0.45 |
| Range | g/min (Scale Weight) | Setpoint (mL/min) | Error (Set Point vs. Scale Weight) | mL/min (Graduated Cylinder) | Error (Set Point vs. Graduated Cylinder) | Ratio (g/min) | Ratio (mL/min) |
|---|---|---|---|---|---|---|---|
| 20–100 | 54.4 | 55 | 0.6 | 55 | 0 | 1.0110 | 1 |
| 85.7 | 87 | 1.3 | 86 | 1 | 1.0090 | 0.9942 | |
| 93.6 | 95 | 1.4 | 94 | 1 | 1.0090 | 0.9947 | |
| 98.1 | 99 | 0.9 | 98 | 1 | 1.0090 | 1.0050 | |
| 100–200 | 108.5 | 109 | 0.5 | 110 | 1 | 1.0140 | 1.0090 |
| 136.4 | 137 | 0.6 | 138 | 1 | 1.0120 | 1.0070 | |
| 185.5 | 185 | 0.5 | 185 | 0 | 1.0000 | 1.0030 | |
| 194.5 | 195 | 0.5 | 194 | 1 | 1.0120 | 1.0263 | |
| 200–300 | 218.1 | 217 | 1.1 | 218 | 1 | 1.0000 | 1.0050 |
| 263.5 | 263 | 0.5 | 262 | 1 | 1.0000 | 1.0020 | |
| 290.1 | 289 | 1.1 | 290 | 1 | 1.0000 | 1.0030 | |
| 277.8 | 277 | 0.8 | 277 | 0 | 0.9970 | 1.0000 | |
| 300–400 | 301 | 301 | 0 | 301 | 0 | 1.0000 | 1.0000 |
| 324.4 | 325 | 0.6 | 324 | 1 | 0.9990 | 0.9970 | |
| 347.8 | 347 | 0.8 | 348 | 1 | 1.0010 | 1.0030 | |
| 380.4 | 379 | 1.4 | 380 | 1 | 0.9990 | 1.0030 | |
| 400–500 | 411.7 | 411 | 0.7 | 411 | 0 | 0.9980 | 1.0000 |
| 442.2 | 441 | 1.2 | 441 | 0 | 0.9980 | 1.0010 | |
| 464.3 | 463 | 1.3 | 463 | 0 | 0.9970 | 1.0000 | |
| 479.8 | 477 | 2.8 | 480 | 3 | 1.0000 | 1.0060 | |
| 500–600 | 505 | 503 | 2 | 502 | 1 | 0.9940 | 0.9980 |
| 528.1 | 527 | 1.1 | 528 | 1 | 1.0000 | 1.0020 | |
| 567.8 | 565 | 2.8 | 567 | 2 | 0.9990 | 1.0040 | |
| 591.7 | 591 | 0.7 | 591 | 0 | 0.9990 | 1.0000 | |
| 600–700 | 615.8 | 615 | 0.8 | 615 | 0 | 0.9990 | 1.0000 |
| 641.2 | 641 | 0.2 | 641 | 0 | 1.0000 | 1.0000 | |
| 677.4 | 679 | 1.6 | 678 | 1 | 1.0010 | 0.9990 | |
| 691.6 | 695 | 3.4 | 691 | 4 | 0.9990 | 0.9940 | |
| 700–730 | 708 | 713 | 5 | 710 | 3 | 1.0030 | 0.9960 |
| 727.5 | 731 | 3.5 | 729 | 2 | 1.0020 | 0.9970 | |
| Average | 1.7867 | 1.3833 | 1.0013 | 0.9999 | |||
| Complement of a ratio | 0.1314% | 0.0010% |
| Range | Setpoint (mL/min) | Lineal Estimation Flow Rate | Potential Estimation Flow Rate | Polynomial Estimation Flow Rate | Error (Lineal Estimation) | Error (Potential Estimation) | Error Polynomial Estimation) | Ratio (Lineal Estimation) | Ratio (Potential Estimation) | Ratio (Polynomial Estimation) |
|---|---|---|---|---|---|---|---|---|---|---|
| 20–100 | 55 | 35 | 46 | 55 | 20 | 9 | 0 | 1.5865 | 1.1786 | 1.0000 |
| 87 | 74 | 79 | 86 | 13 | 8 | 1 | 1.1678 | 1.1013 | 0.9667 | |
| 95 | 78 | 84 | 94 | 17 | 10 | 1 | 1.2102 | 1.1243 | 1.0000 | |
| 99 | 90 | 90 | 98 | 9 | 9 | 1 | 1.1000 | 1.1000 | 1.0102 | |
| 100–200 | 109 | 100 | 100 | 110 | 9 | 9 | 1 | 1.0900 | 1.0900 | 1.0283 |
| 137 | 135 | 125 | 138 | 2 | 12 | 1 | 1.0148 | 1.0960 | 1.0074 | |
| 185 | 187 | 175 | 185 | 2 | 10 | 0 | 0.9867 | 1.0571 | 1.0054 | |
| 195 | 196 | 185 | 194 | 1 | 10 | 1 | 0.9949 | 1.0541 | 1.0263 | |
| 200–300 | 217 | 217 | 205 | 218 | 0 | 12 | 1 | 1.0000 | 1.0585 | 1.0236 |
| 263 | 260 | 245 | 262 | 3 | 18 | 1 | 1.0115 | 1.0735 | 1.0194 | |
| 277 | 277 | 265 | 290 | 0 | 12 | 1 | 1.0000 | 1.0453 | 1.0109 | |
| 289 | 287 | 275 | 277 | 2 | 14 | 0 | 1.0052 | 1.0509 | 1.0176 | |
| 300–400 | 301 | 295 | 299 | 301 | 6 | 2 | 0 | 1.0203 | 1.0067 | 1.0033 |
| 325 | 325 | 329 | 324 | 0 | 4 | 1 | 1.0000 | 0.9878 | 1.0156 | |
| 347 | 347 | 349 | 348 | 0 | 2 | 1 | 1.0000 | 0.9943 | 1.0087 | |
| 379 | 379 | 379 | 380 | 0 | 0 | 1 | 1.0000 | 1.0000 | 1.0080 | |
| 400–500 | 411 | 413 | 409 | 411 | 2 | 2 | 0 | 0.9952 | 1.0049 | 1.0123 |
| 441 | 440 | 445 | 441 | 1 | 4 | 0 | 1.0023 | 0.9910 | 1.0115 | |
| 463 | 461 | 462 | 463 | 2 | 1 | 0 | 1.0043 | 1.0022 | 1.0109 | |
| 477 | 479 | 478 | 480 | 2 | 1 | 3 | 0.9958 | 0.9979 | 1.0106 | |
| 500–600 | 503 | 500 | 499 | 502 | 3 | 4 | 1 | 1.0060 | 1.0080 | 1.0060 |
| 527 | 525 | 520 | 528 | 2 | 7 | 1 | 1.0038 | 1.0135 | 1.0135 | |
| 565 | 559 | 559 | 567 | 6 | 6 | 2 | 1.0107 | 1.0107 | 1.0125 | |
| 591 | 568 | 579 | 591 | 23 | 12 | 0 | 1.0405 | 1.0207 | 1.0103 | |
| 600–700 | 615 | 590 | 605 | 615 | 25 | 10 | 0 | 1.0424 | 1.0165 | 1.0082 |
| 641 | 613 | 623 | 641 | 28 | 18 | 0 | 1.0457 | 1.0289 | 1.0079 | |
| 679 | 643 | 669 | 678 | 36 | 10 | 1 | 1.0560 | 1.0149 | 1.0074 | |
| 695 | 658 | 671 | 691 | 37 | 24 | 4 | 1.0562 | 1.0358 | 1.0131 | |
| 700–730 | 713 | 679 | 689 | 710 | 34 | 24 | 3 | 1.0501 | 1.0348 | 1.0113 |
| 731 | 695 | 705 | 729 | 36 | 26 | 2 | 1.0518 | 1.0369 | 1.0097 | |
| Average | 10.7000 | 9.6666 | 1.3833 | 1.0516 | 1.0411 | 0.9999 | ||||
| Complement of a ratio | 5.1623% | 4.1170% | 0.9887% |
| Range | Setpoint (mL/min) | Commercial Hemodialysis Machine Flow Rate | Our Control Flow Rate | Error (Commercial Hemodialysis Machine) | Error (Our Control) | Ratio (Commercial Hemodialysis Machine) | Ratio (Our Control, mL/min) |
|---|---|---|---|---|---|---|---|
| 20–100 | 55 | 59 | 55 | 4.33 | 0 | 0.9270 | 1.0000 |
| 90 | 96.00 | 90 | 6.00 | 0 | 0.9375 | 1.0000 | |
| 95 | 101.00 | 94 | 6.00 | 1 | 0.9406 | 1.0106 | |
| 100 | 106.00 | 100 | 6.00 | 0 | 0.9434 | 1.0000 | |
| 100–200 | 110 | 117.00 | 112 | 7.00 | 2 | 0.9402 | 0.9821 |
| 140 | 150.00 | 138 | 10.00 | 2 | 0.9333 | 1.0145 | |
| 185 | 195.00 | 182 | 10.00 | 3 | 0.9487 | 1.0165 | |
| 195 | 205.00 | 195 | 10.00 | 0 | 0.9512 | 1.0000 | |
| 200–300 | 220 | 231.00 | 214 | 11.00 | 6 | 0.9524 | 1.0280 |
| 265 | 275.00 | 268 | 10.00 | 2 | 0.9636 | 0.9888 | |
| 280 | 290.00 | 280 | 10.00 | 0 | 0.9655 | 1.0000 | |
| 290 | 300 | 290 | 10.50 | 0 | 0.9651 | 1.0000 | |
| 300–400 | 300 | 290.00 | 300 | 10.00 | 0 | 1.0345 | 1.0000 |
| 325 | 320 | 325 | 5.00 | 0 | 1.0140 | 1.0000 | |
| 350 | 350.00 | 355 | 0.00 | 5 | 1.0000 | 0.9859 | |
| 380 | 385.00 | 385 | 5.00 | 5 | 0.9870 | 0.9870 | |
| 400–500 | 410 | 425.00 | 420 | 15.00 | 10 | 0.9647 | 0.9762 |
| 440 | 455.00 | 450 | 15.00 | 10 | 0.9670 | 0.9778 | |
| 460 | 475.00 | 470 | 15.00 | 10 | 0.9684 | 0.9787 | |
| 480 | 490.00 | 490 | 10.00 | 10 | 0.9796 | 0.9796 | |
| 500–600 | 505 | 510.00 | 510 | 5.00 | 5 | 0.9902 | 0.9902 |
| 530 | 530.00 | 535 | 0.00 | 5 | 1.0000 | 0.9907 | |
| 565 | 550.00 | 575 | 15.00 | 10 | 1.0273 | 0.9826 | |
| 600 | 580.00 | 610 | 20.00 | 10 | 1.0172 | 0.9836 | |
| Average | 8.9929 | 4.0000 | 0.9723 | 0.9947 | |||
| Complement of a ratio | 2.6582% | 0.5296 |
| Metric | Commercial System | Our System | Interpretation |
|---|---|---|---|
| RMSE (mL/min) | 10.25 | 4.75 | Lower error in the developed system |
| Mean Error (mL/min) | 10.25 | 4.75 | Slightly improved accuracy in the developed system |
| Standard Deviation (mL/min) | 7.15 | 2.60 | Greater stability in the developed system |
| t-value | 2.96 | N/A | Confirms that errors are lower |
| p-value | 0.021 | N/A | Statistically significant difference (p < 0.05) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Institute of Knowledge Innovation and Invention. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sánchez-Saquín, C.H.; Soto-Cajiga, J.A.; Barrera-Fernández, J.M.; Gómez-Hernández, A.; Rodríguez-Olivares, N.A. Identification, Control, and Characterization of Peristaltic Pumps in Hemodialysis Machines. Appl. Syst. Innov. 2025, 8, 44. https://doi.org/10.3390/asi8020044
Sánchez-Saquín CH, Soto-Cajiga JA, Barrera-Fernández JM, Gómez-Hernández A, Rodríguez-Olivares NA. Identification, Control, and Characterization of Peristaltic Pumps in Hemodialysis Machines. Applied System Innovation. 2025; 8(2):44. https://doi.org/10.3390/asi8020044
Chicago/Turabian StyleSánchez-Saquín, Cristian H., Jorge A. Soto-Cajiga, Juan M. Barrera-Fernández, Alejandro Gómez-Hernández, and Noé A. Rodríguez-Olivares. 2025. "Identification, Control, and Characterization of Peristaltic Pumps in Hemodialysis Machines" Applied System Innovation 8, no. 2: 44. https://doi.org/10.3390/asi8020044
APA StyleSánchez-Saquín, C. H., Soto-Cajiga, J. A., Barrera-Fernández, J. M., Gómez-Hernández, A., & Rodríguez-Olivares, N. A. (2025). Identification, Control, and Characterization of Peristaltic Pumps in Hemodialysis Machines. Applied System Innovation, 8(2), 44. https://doi.org/10.3390/asi8020044






