Numerical Investigations and Artificial Neural Network-Based Performance Prediction of a Centrifugal Fan Having Innovative Hub Geometry Designs
Abstract
:1. Introduction
2. CFD Modelling
2.1. Geometrical Specifics
2.2. Mesh Creation and Sensitivity Testing
2.3. Numerical Model Boundary Conditions
2.4. Overview of the Output Parameters Used in the CFD Study
2.5. Validation of the Numerical Analysis
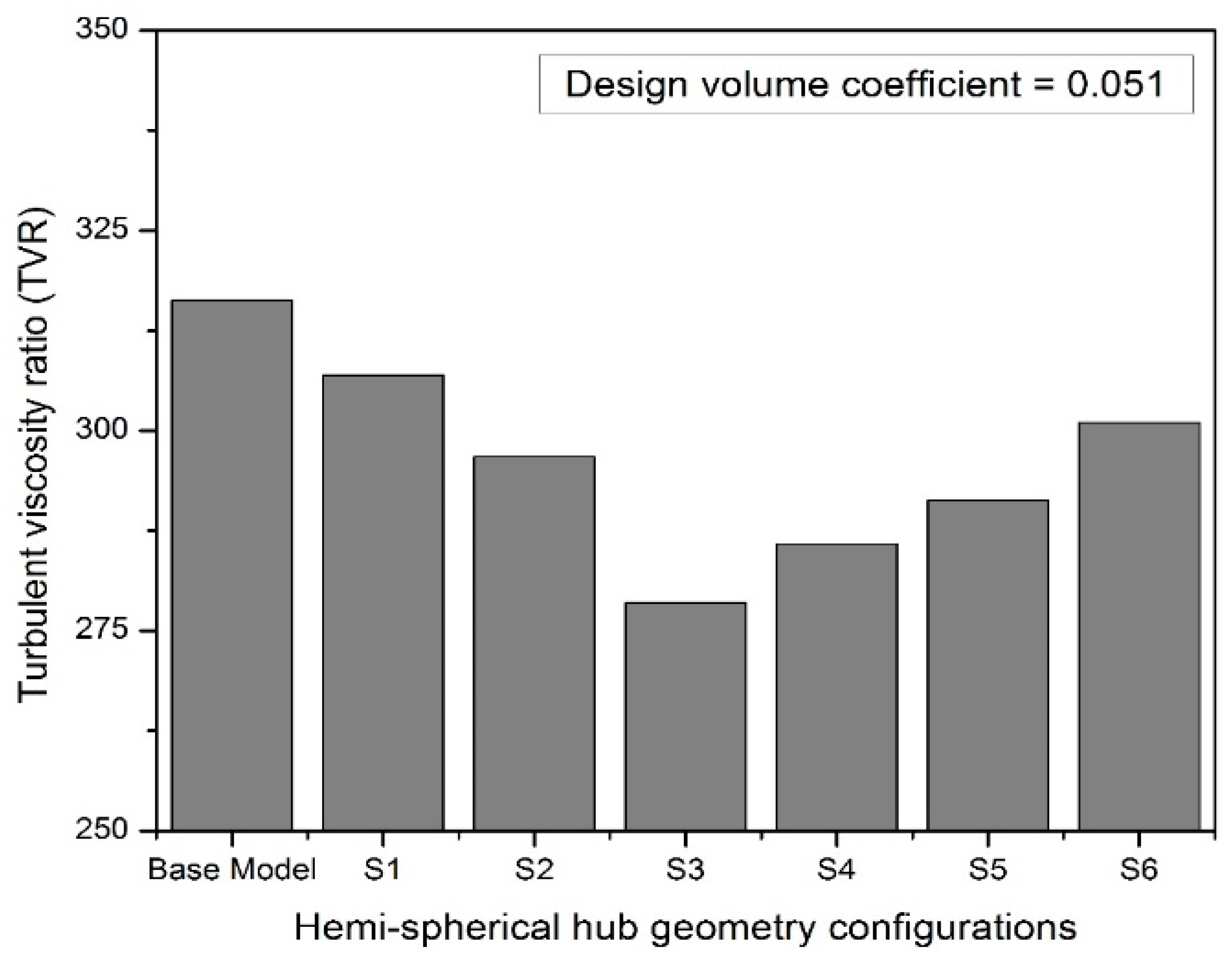
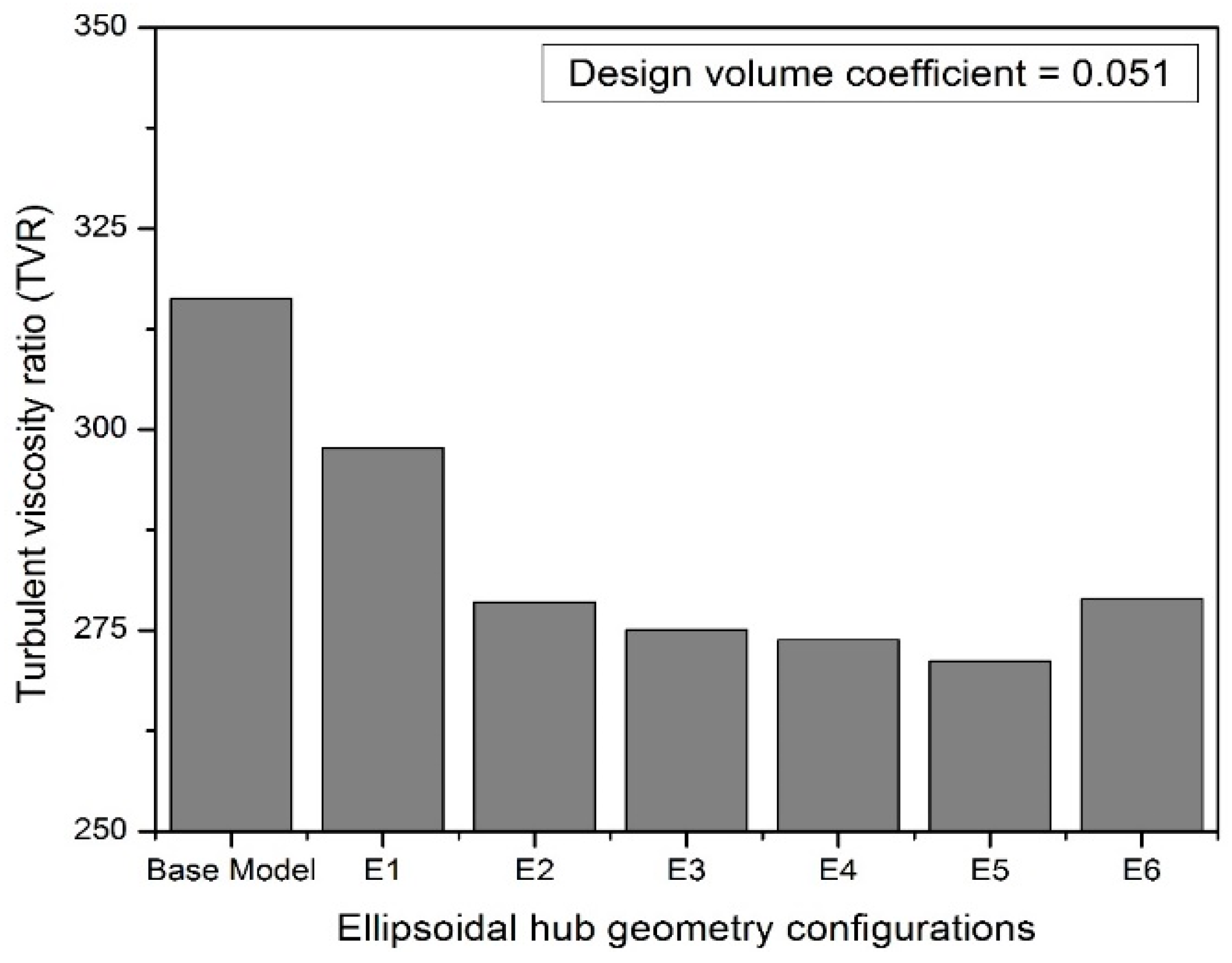
2.6. Different Hub Geometries Used in the Numerical Analysis
3. Results and Discussion
3.1. CFD Analysis
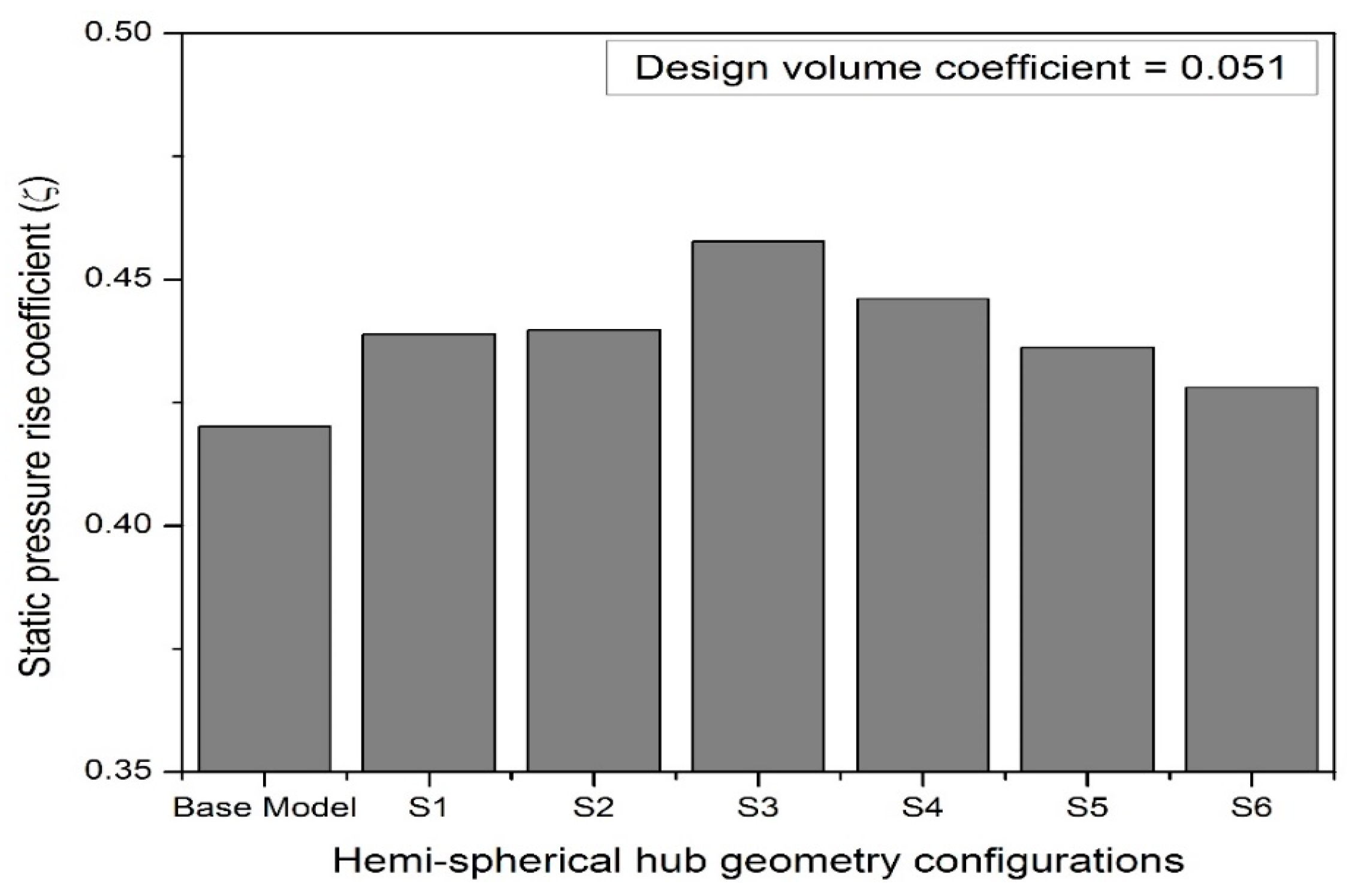
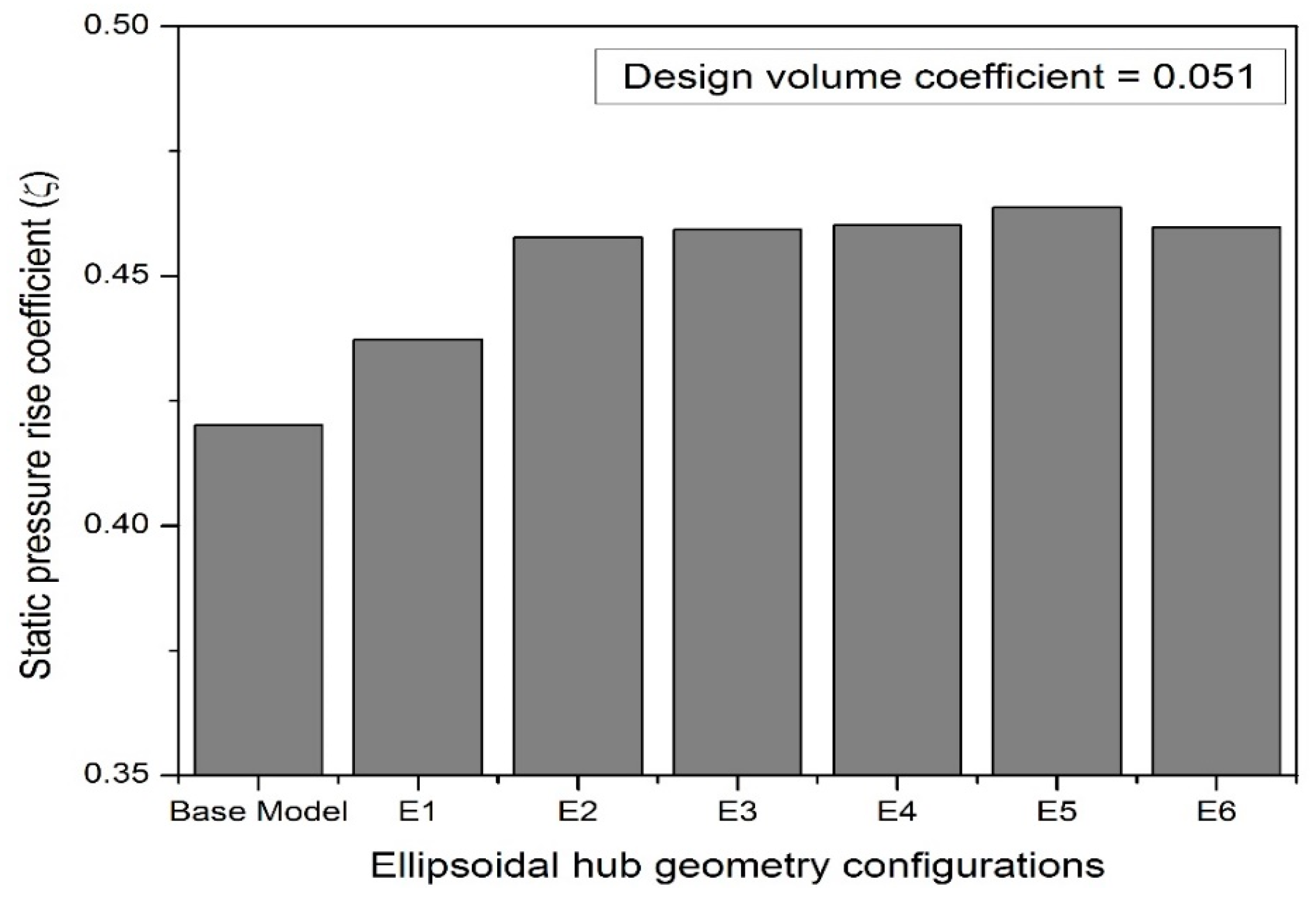
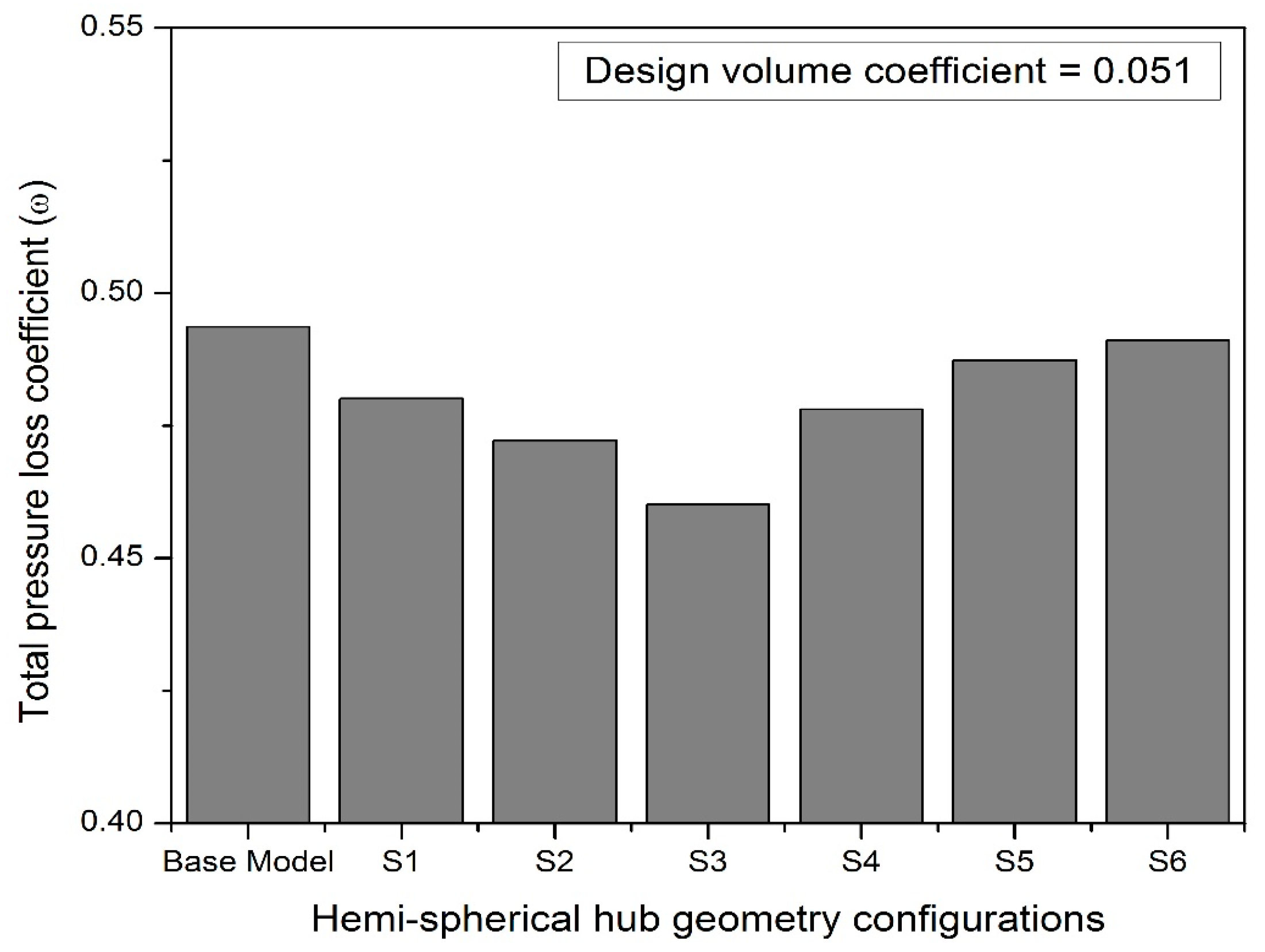
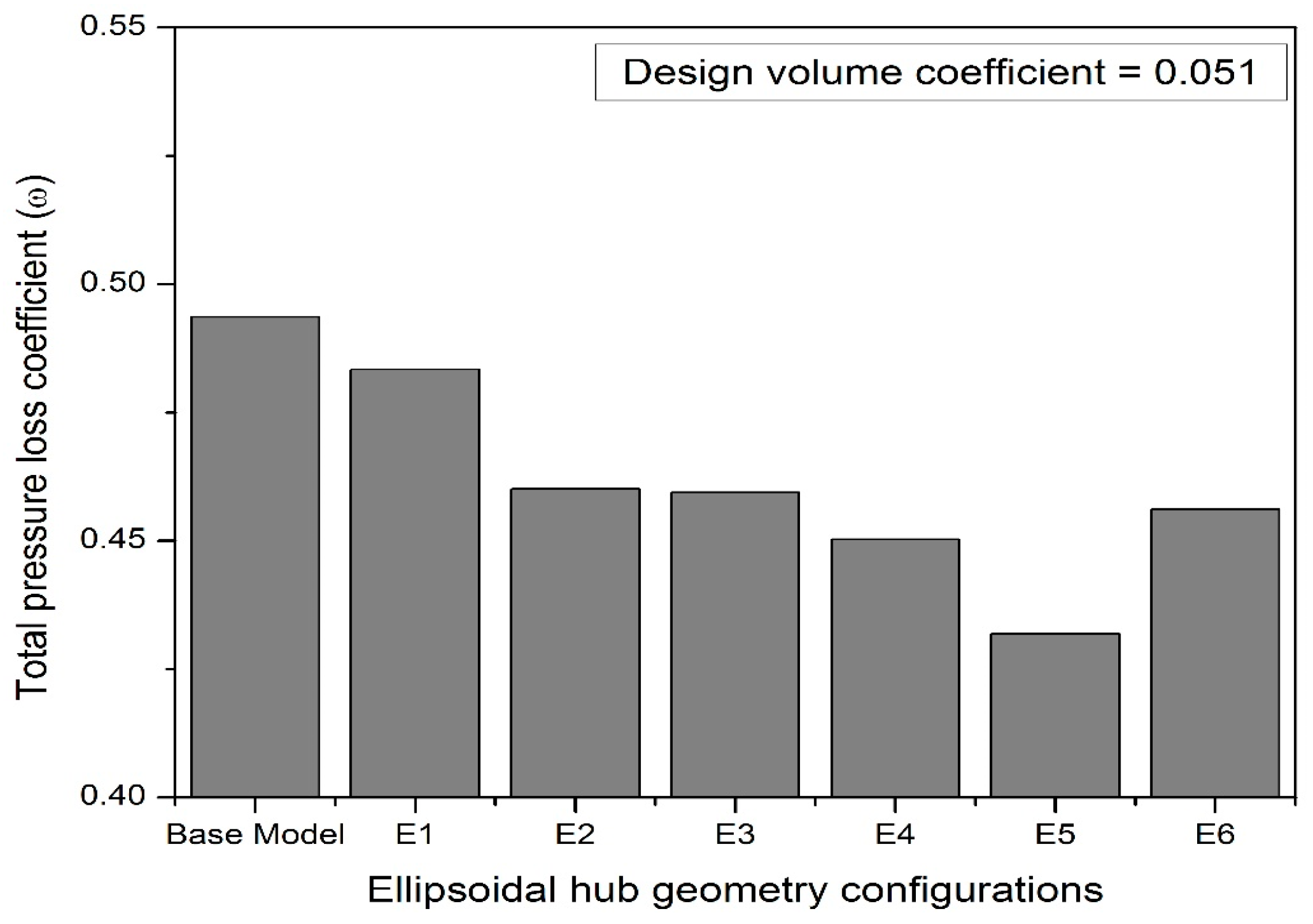
3.1.1. Performance Augmentation of the Fan Due to Hub Geometry Treatment at Design Mass Flow Rate
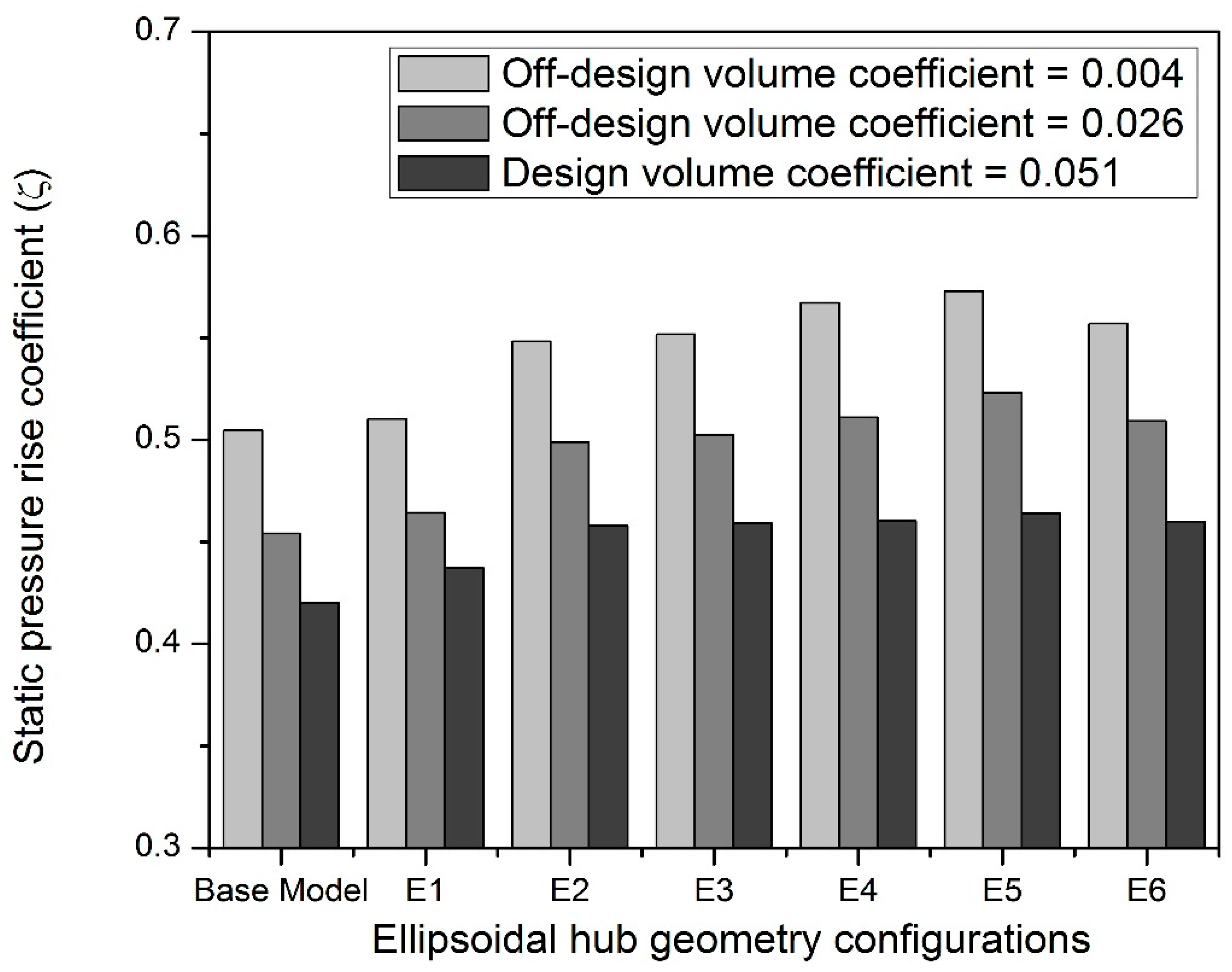
3.1.2. Effect of Hub Geometry Treatment on Performance for Off-Design Conditions
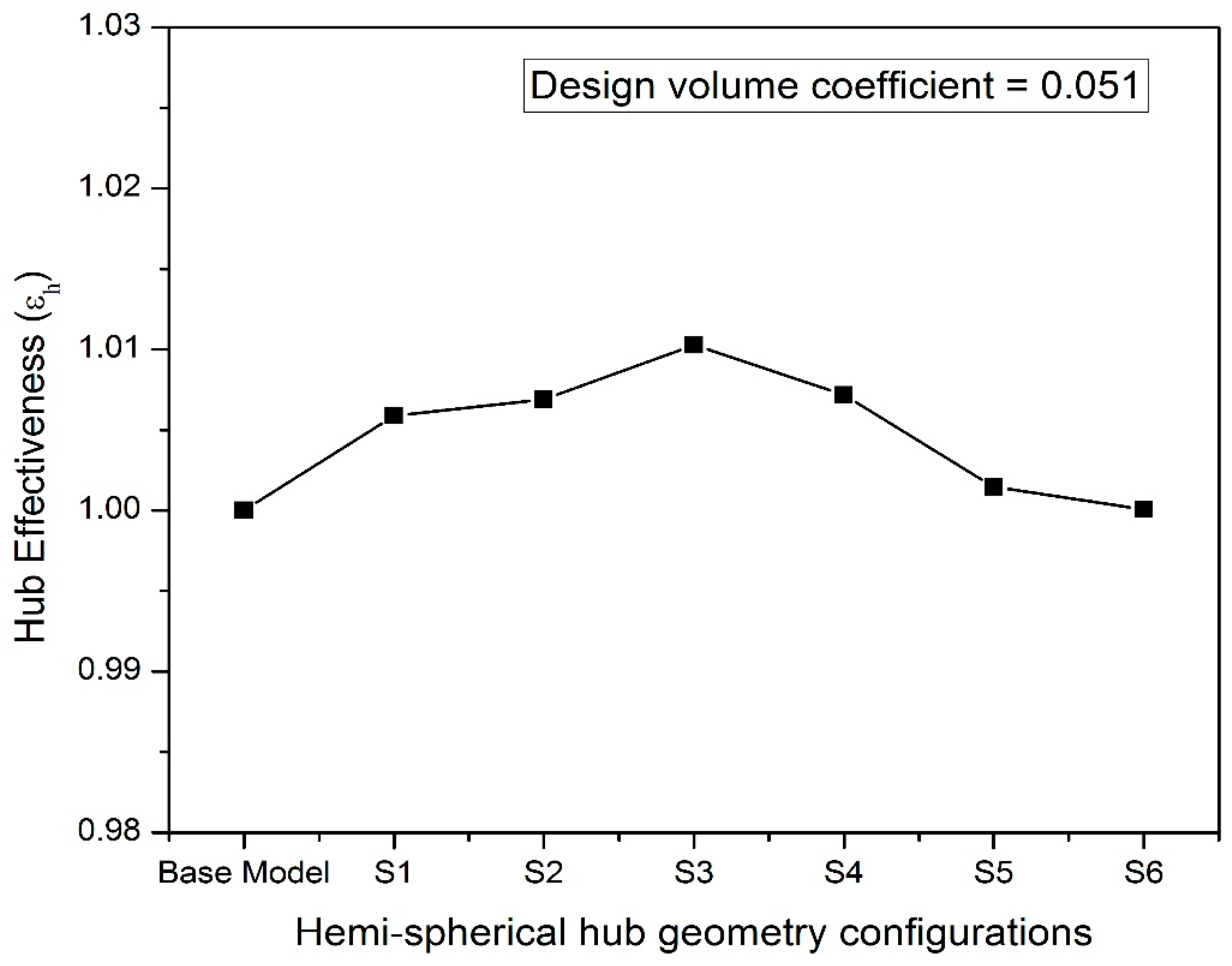
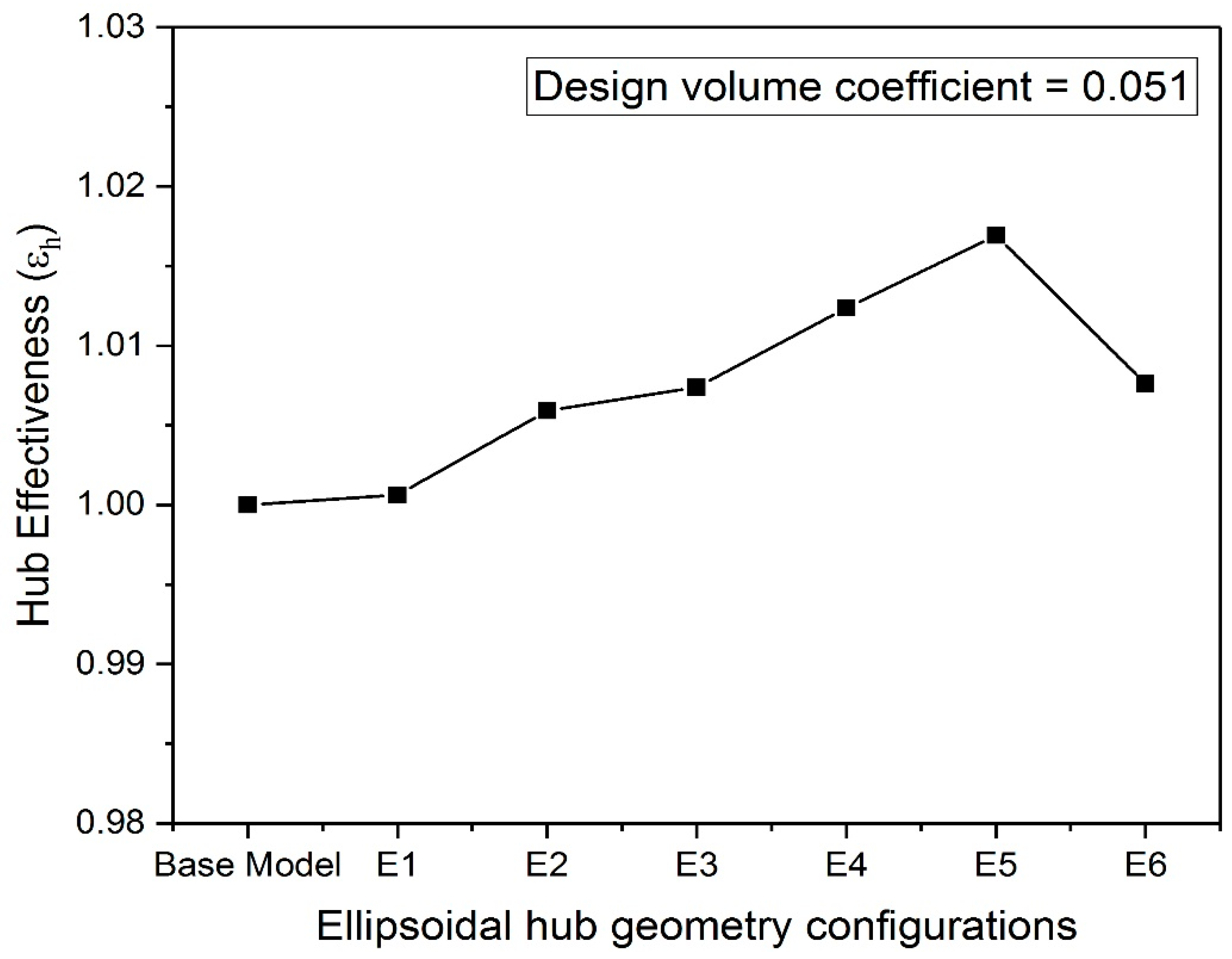
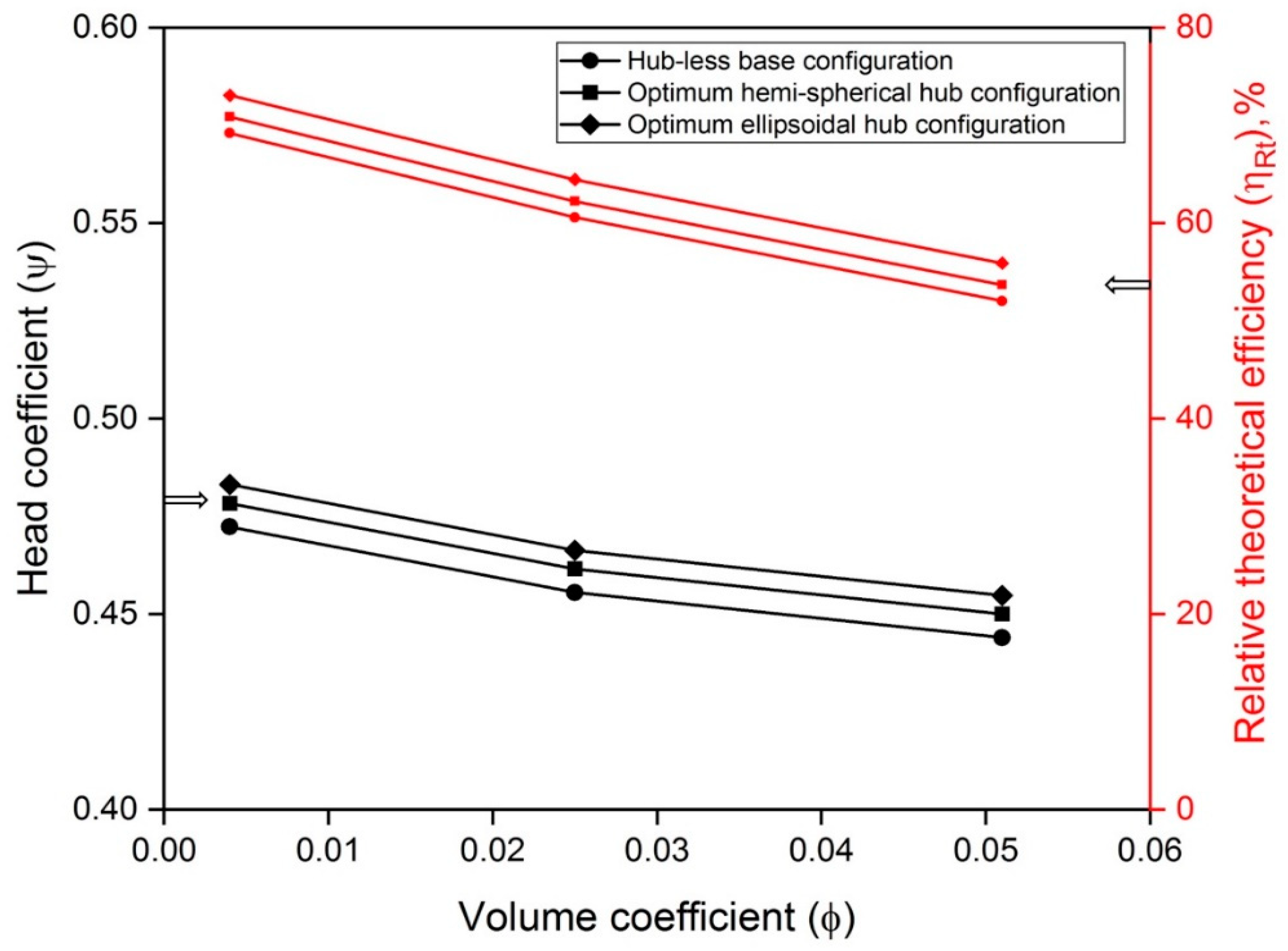
3.1.3. Optimal Hemispherical and Ellipsoidal Hub Arrangement Comparison
3.2. Artificial Neural Network Prediction Analysis
3.2.1. Background of ANN Model
3.2.2. Proposed ANN Model
3.2.3. Key Performance Indices for ANN Study
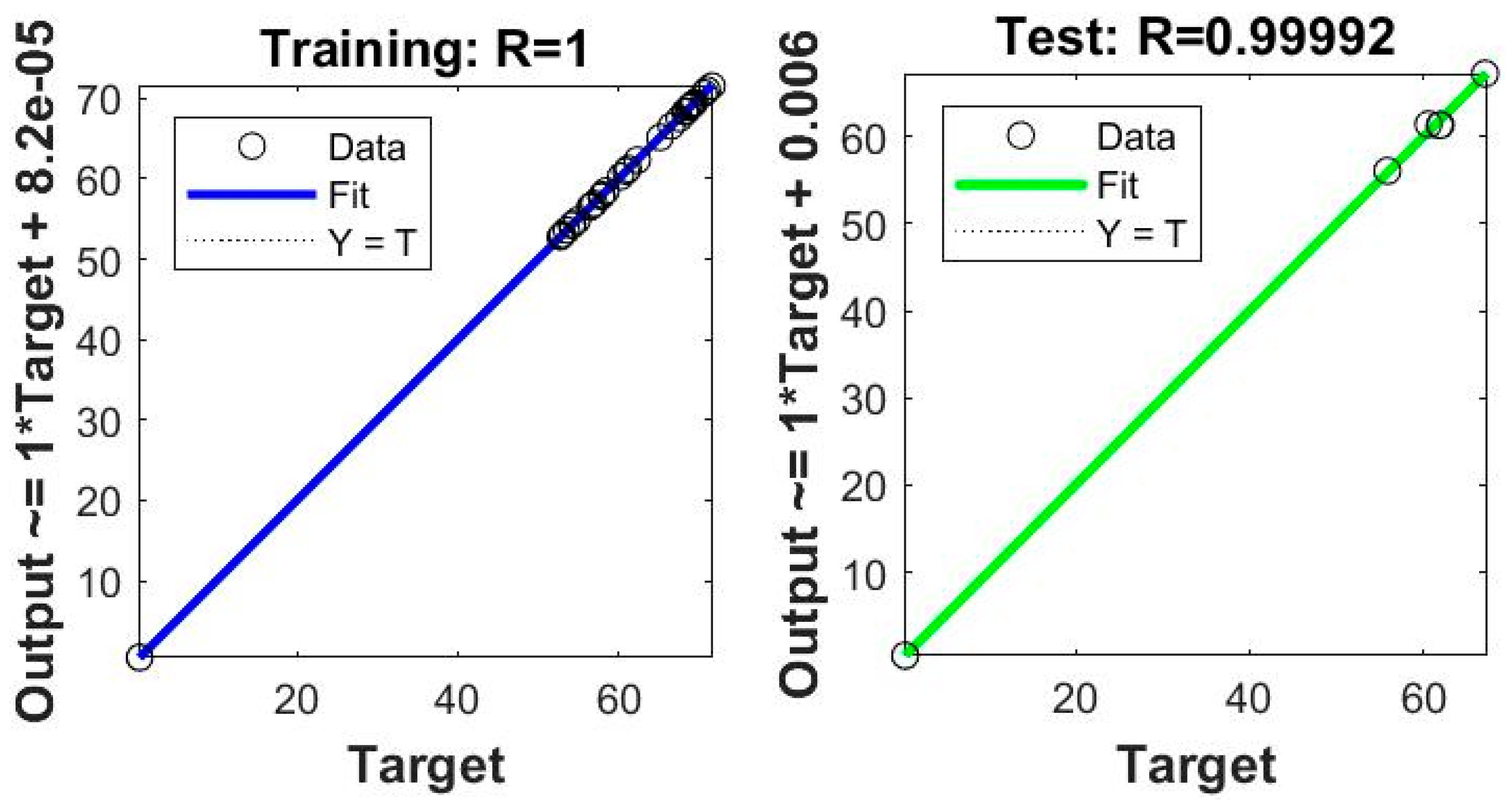
3.2.4. ANN Model Training and Simulation
Selection of Training Algorithm
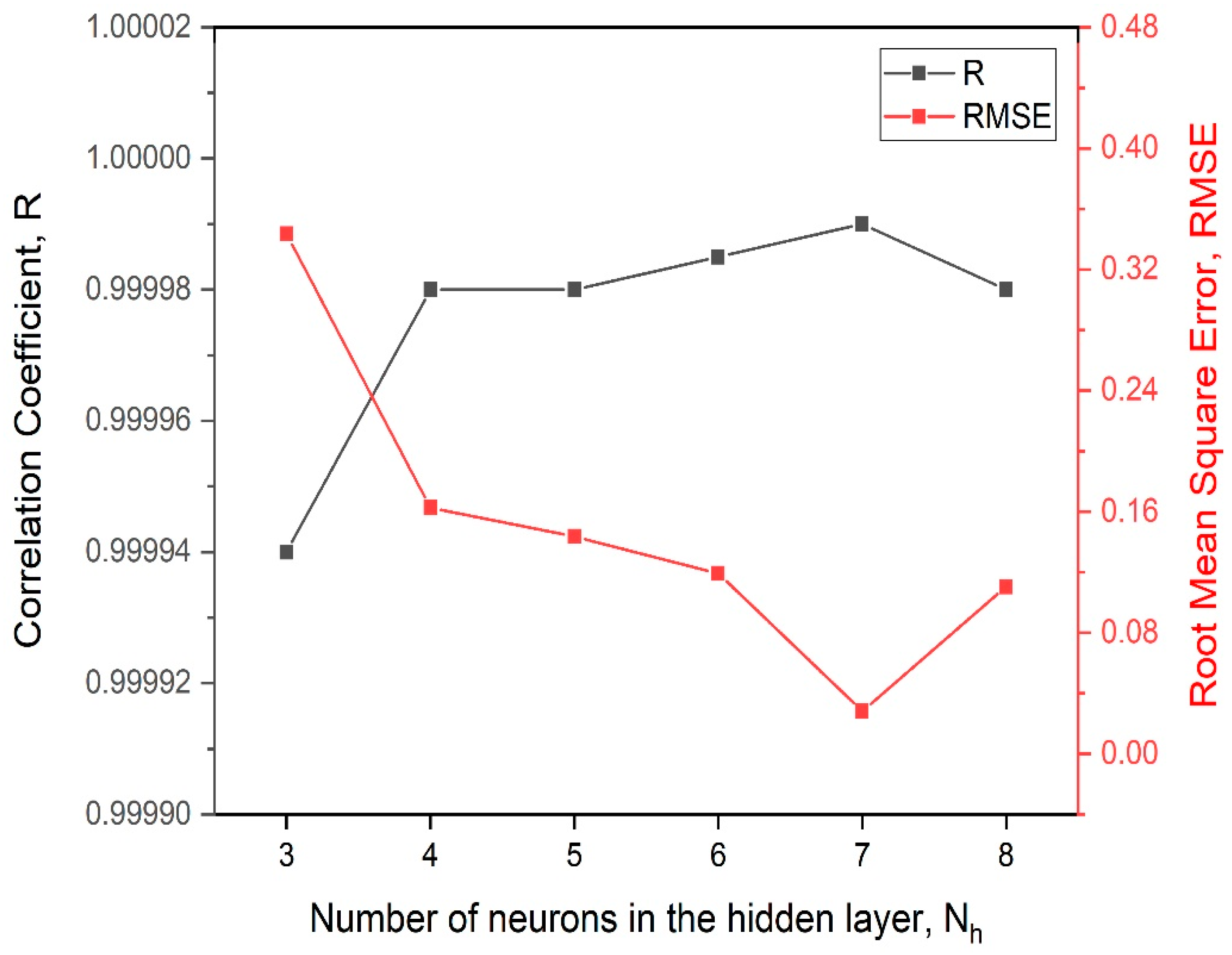
Selection of the Number of Neurons in the Hidden Layer
Results of the Training Process
4. Conclusions
- It is found that, compared to the hub-less base model, both hemispherical and ellipsoidal hub geometry model configurations lead to relatively better overall efficiency at all volume coefficients considered in the analysis.
- An ellipsoidal hub design with an ellipsoidal hub ratio of 1.10 improved head coefficient by about 8.4% and relative theoretical efficiency by about 8.6% when compared with those of a hub-less base model for the operating range of volume coefficients employed in the current numerical studies.
- In comparison with the hub-less base model configuration, a hemispherical hub design with a spheroidal hub ratio of 0.50 produced a higher head coefficient of around 2.3% and a greater relative theoretical efficiency of about 3.2% at all the values of volume coefficients.
- The performance characteristics of the fan only slightly improved for hub designs with ellipsoidal hub ratios above 1.1 and spheroidal hub ratios over 0.5.
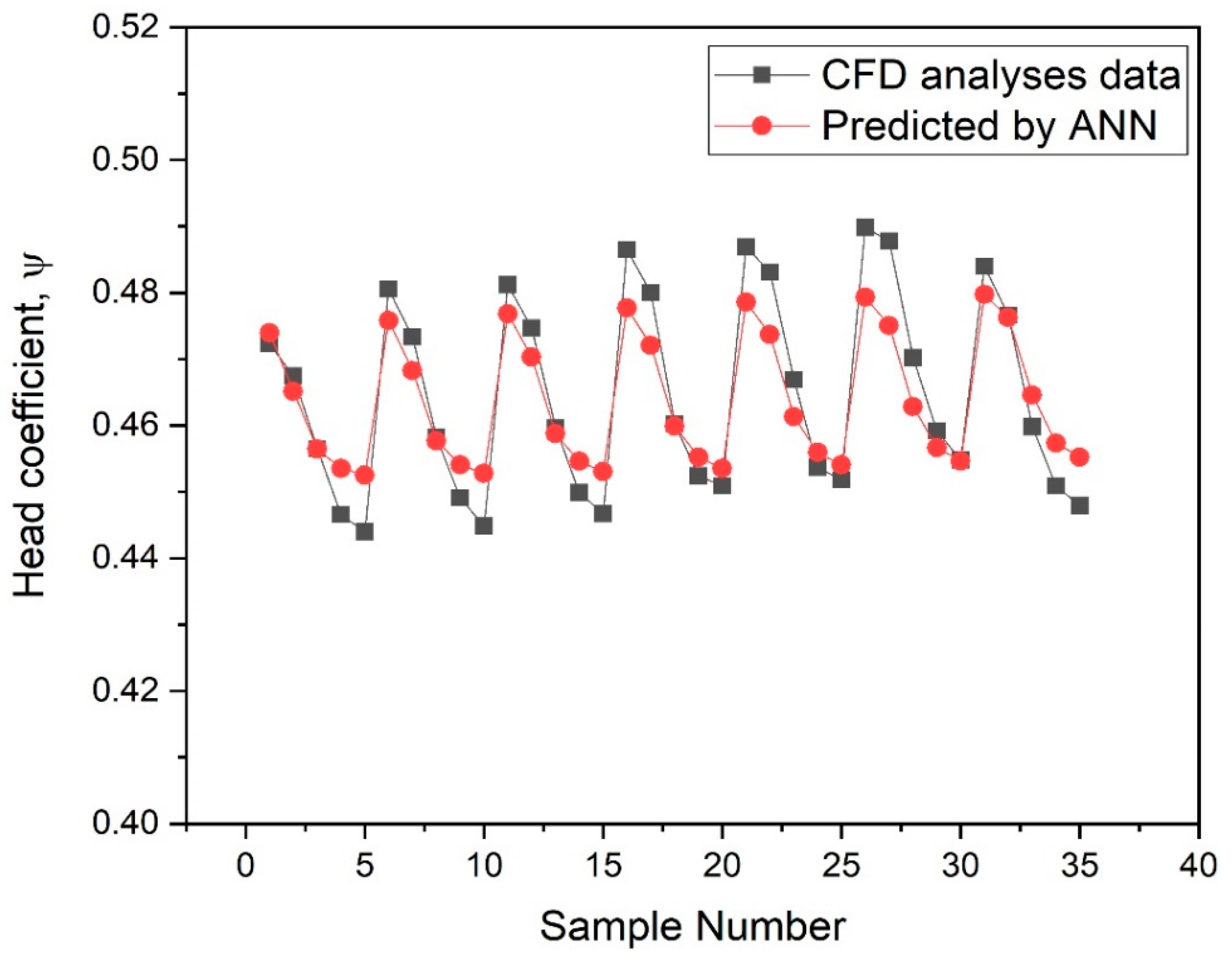
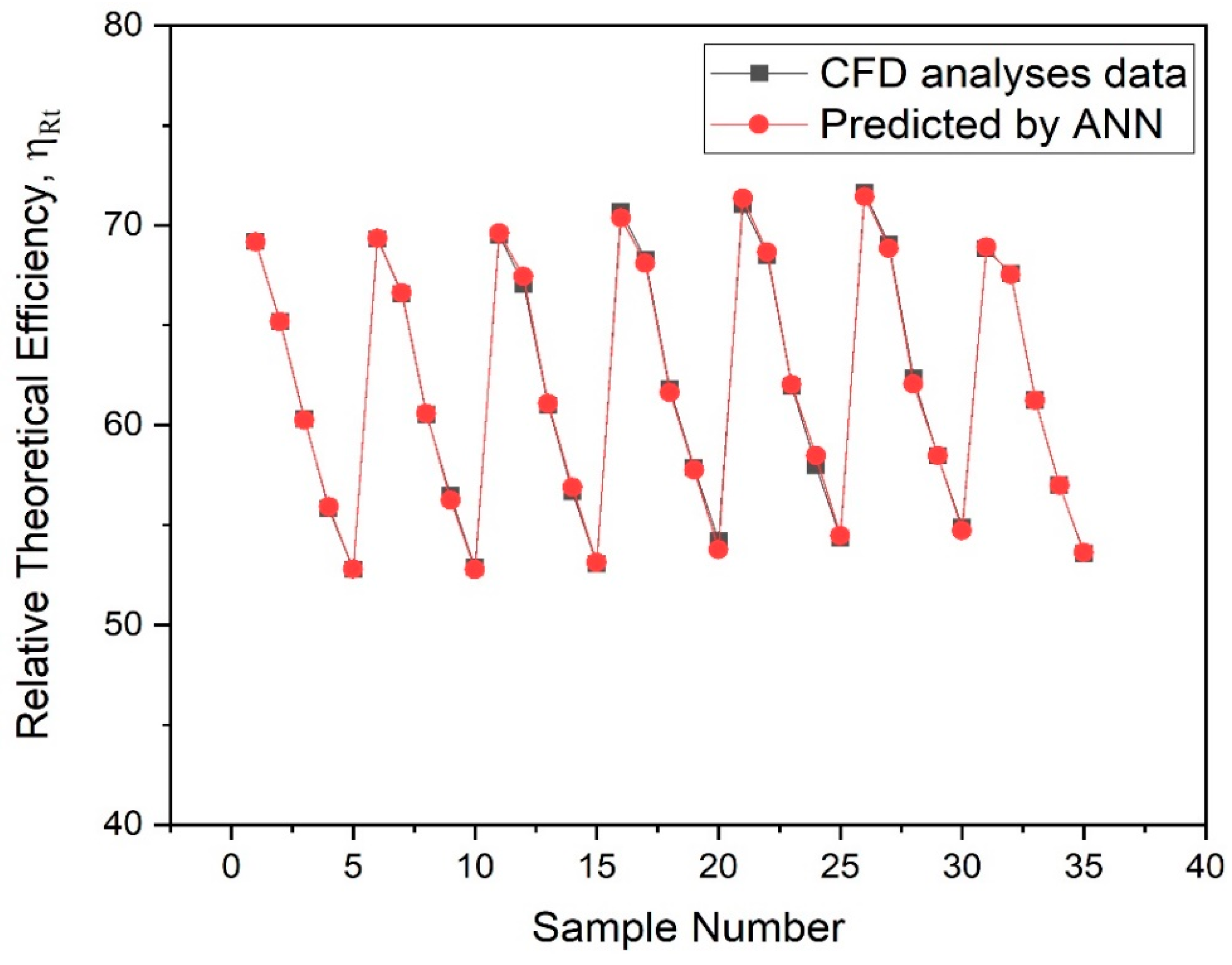
- The values of average error between CFD and ANN results for head coefficient and relative theoretical efficiency are found to be 0.0008% and 0.0002%, respectively, and are well within the range of acceptable limits.
- The significant improvement in performance indicators primarily targets energy efficiency, thereby ensuring access to affordable, reliable energy for all as per one of the sustainable development goals, SDG 7.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| d | Radial height of an ellipsoidal hub (mm) | r: | Duct radius at the entrance (mm) |
| U | Blade speed (m/s) | Air density (kg/m3) | |
| pt | Stagnation pressure (Pa) | rh | Hub radius (mm) |
| R0 | Exit radius of the impeller (mm) | p | Static pressure (Pa) |
| Energy obtainable from Euler’s equation (kJ/kg) | lh | Hub length in the axial direction (mm) | |
| Q | Volume flow rate of air (m3/s) | TVR | Turbulent viscosity ratio |
| HCFD | Energy transfer obtained from CFD analysis (kJ/kg) = | TR | No. of training data sets |
| I | No. of input variables | O | No. of output variables |
| Subscripts | |||
| 1 | Fan inlet | 3 | Diffuser exit |
| 2 | Impeller exit | 4 | Volute exit |
References
- Jung, J.H.; Joo, W.-G. The Effect of the Entrance Hub Geometry on the Efficiency in an Axial Flow Fan. Int. J. Refrig. 2019, 101, 90–97. [Google Scholar] [CrossRef]
- Vagnoli, S.; Verstraete, T. URANS analysis of the effect of realistic inlet distortions on the stall inception of a centrifugal compressor. Comput. Fluids 2015, 116, 192–204. [Google Scholar] [CrossRef]
- Wang, Y.; Dong, Q.; Wang, P. Numerical investigation on fluid flow in a 90-degree curved pipe with large curvature ratio. Math. Probl. Eng. 2015, 2015, 548262. [Google Scholar] [CrossRef]
- Gholamian, M.; Rao, G.K.M.; Panitapu, B. Effect of axial gap between inlet nozzle and impeller on efficiency and flow pattern in centrifugal fans, numerical and experimental analysis. Case Stud. Therm. Eng. 2013, 1, 26–37. [Google Scholar] [CrossRef]
- Son, P.N.; Kim, J.; Ahn, E.Y. Effects of bell mouth geometries on the flow rate of centrifugal blowers. J. Mech. Sci. Technol. 2011, 25, 2267–2276. [Google Scholar] [CrossRef]
- Ce, Y.; Shan, C.; Du, L.; Changmao, Y.; Yidi, W. Inlet Recirculation Influence to the Flow Structure of Centrifugal Impeller. Chin. J. Mech. Eng. 2010, 23, 647. [Google Scholar] [CrossRef]
- Cai, R. The Influence of Shrouded Stator Cavity Flows on Multistage Compressor Performance. ASME J. Turbomach. 1999, 121, 497. [Google Scholar] [CrossRef]
- Tiwari, R.; Bordoloi, D.; Dewangan, A. Blockage and cavitation detection in centrifugal pumps from dynamic pressure signal using deep learning algorithm. Measurement 2020, 173, 108676. [Google Scholar] [CrossRef]
- Ping, X.; Yang, F.; Zhang, H.; Zhang, J.; Zhang, W.; Song, G. Introducing machine learning and hybrid algorithm for prediction and optimization of multistage centrifugal pump in an ORC system. Energy 2021, 222, 120007. [Google Scholar] [CrossRef]
- Pei, J.; Wang, W.; Osman, M.K.; Gan, X. Multiparameter optimization for the nonlinear performance improvement of centrifugal pumps using a multilayer neural network. J. Mech. Sci. Technol. 2019, 33, 2681–2691. [Google Scholar] [CrossRef]
- Oro, J.F.; García, B.P.; González, J.; Díaz, K.A.; Velarde-Suárez, S. Numerical methodology for the assessment of relative and absolute deterministic flow structures in the analysis of impeller–tongue interactions for centrifugal fans. Comput. Fluids 2013, 86, 310–325. [Google Scholar] [CrossRef]
- Sanjose, M.; Moreau, S. Direct noise prediction and control of an installed large low-speed radial fan. Eur. J. Mech.—B/Fluids 2017, 61, 235–243. [Google Scholar] [CrossRef]
- Yang, X.; Tang, M.; Li, S.; Li, W. Design of a high-performance centrifugal compressor impeller and an investigation on the linear effects of the hub. AIP Adv. 2022, 12, 025322. [Google Scholar] [CrossRef]
- Kuang, R.; Zhang, Z.; Wang, S.; Chen, X. Effect of hub inclination angle on internal and external characteristics of centrifugal pump impellers. AIP Adv. 2021, 11, 025043. [Google Scholar] [CrossRef]
- Pakle, S.; Jiang, K. Design of a high-performance centrifugal compressor with new surge margin improvement technique for high speed turbomachinery. Propuls. Power Res. 2018, 7, 19–29. [Google Scholar] [CrossRef]
- Meakhail, T.; Park, S.O. A Study of Impeller-Diffuser-Volute Interaction in a Centrifugal Fan. J. Turbomach. 2005, 127, 687–695. [Google Scholar] [CrossRef]
- Madhwesh, N.; Karanth, K.V.; Sharma, N.Y. Experimental investigations and empirical relationship on the influence of innovative hub geometry in a centrifugal fan for performance augmentation. Int. J. Mech. Mater. Eng. 2021, 16, 5. [Google Scholar] [CrossRef]
- Madhwesh, N.; Karanth, K.V.; Sharma, N.Y. Investigations into the Flow Behavior in a Nonparallel Shrouded Diffuser of a Centrifugal Fan for Augmented Performance. J. Fluids Eng. 2018, 140, 081103. [Google Scholar] [CrossRef]
- Som, S.K.; Sharma, N.Y. Energy and Exergy Balance in the Process of Spray Combustion in a Gas Turbine Combustor. J. Heat Transf. 2002, 124, 828–836. [Google Scholar] [CrossRef]
- Karanth, K.V.; Sharma, N.Y. Numerical analysis of a centrifugal fan for performance enhancement using boundary layer suction slots. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2010, 224, 1665–1678. [Google Scholar] [CrossRef]
- Ghritlahre, H.; Prasad, R. Prediction of exergetic efficiency of arc shaped wire roughened solar air heater using ANN model. Int. J. Heat Technol. 2018, 36, 1107–1115. [Google Scholar] [CrossRef]
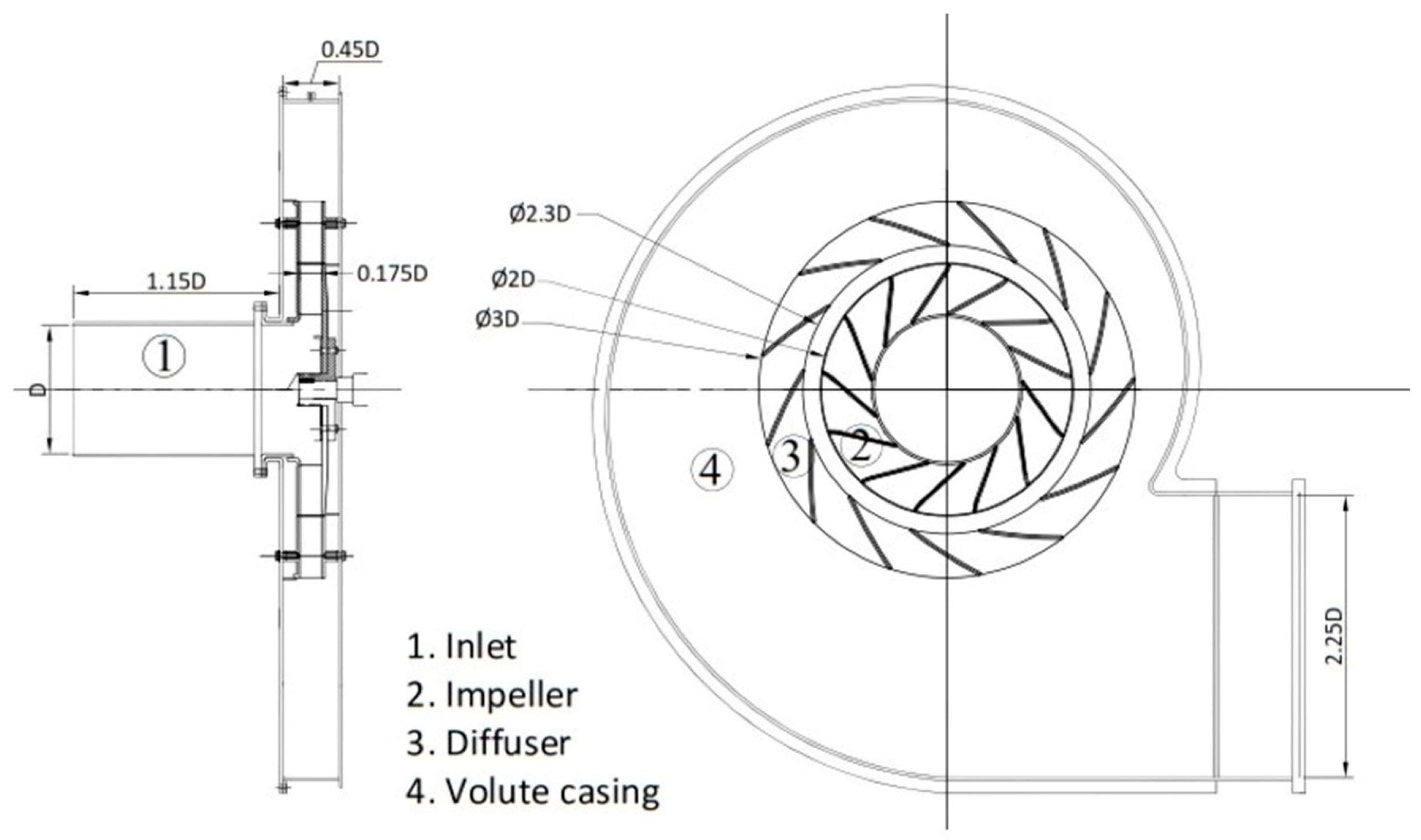


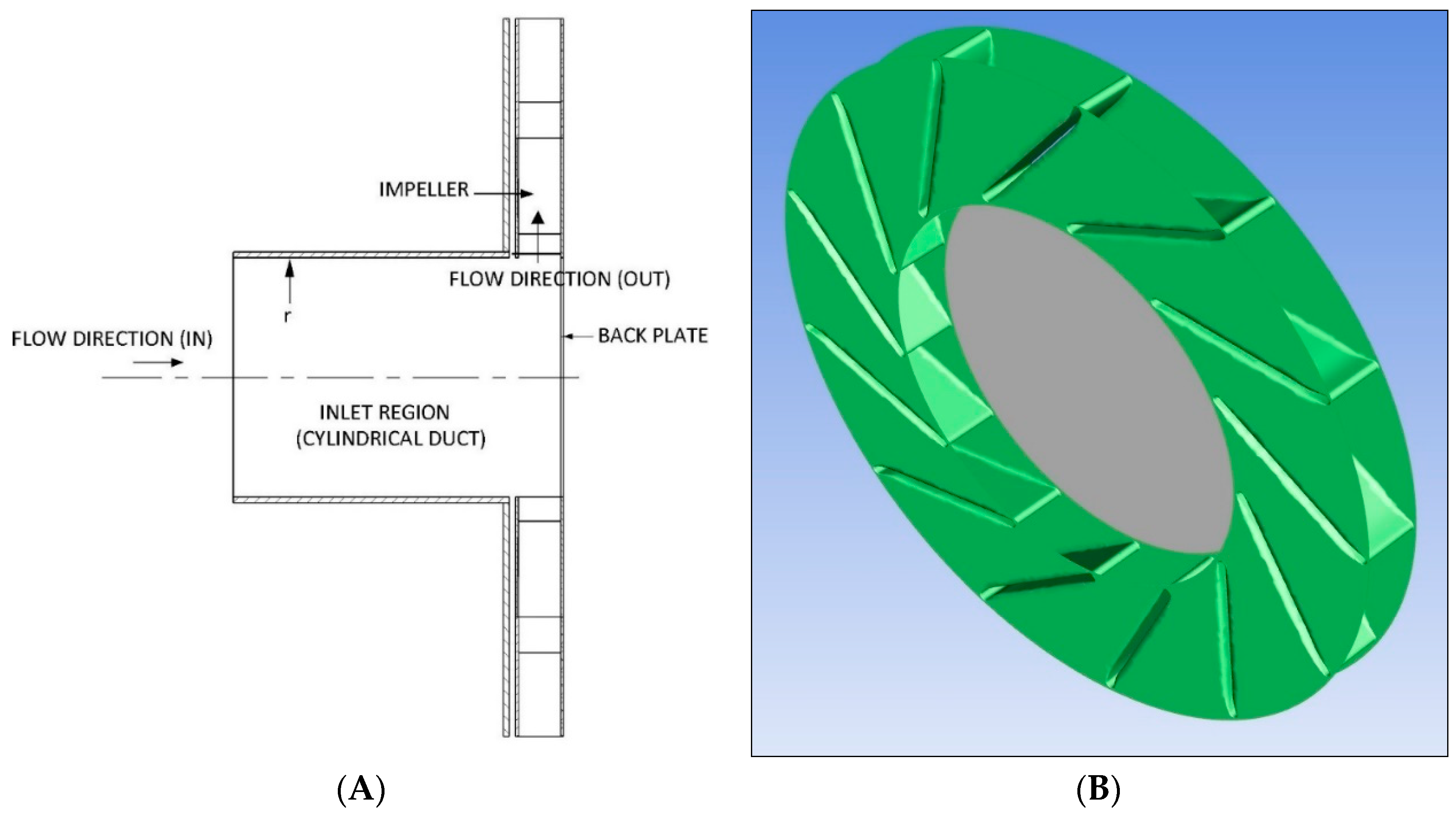











| Impeller: | |
| Radius at the inlet | : 0.6 D |
| Radius at the exit | : D |
| Inlet blade angle | : 30° |
| Exit blade angle | : 76° |
| Number of blades | : 13 |
| Diffuser: | |
| Diameter of the inlet | : 2.3 D |
| Diameter of the exit | : 3 D |
| Blade angle at the inlet | : 23 deg |
| Blade angle at the outlet | : 38 deg |
| Number of diffuser vanes | : 13 |
| Volute casing: | |
| Height of the channel | : 0.45 D |
| Flange width | : 2.25 D |
| Blade thickness | : 0.025 D |
| Impeller and diffuser passage width | : 0.175 D |
| The meridional gap between the diffuser and impeller | : 0.15 D |
| Rated RPM of the fan | : 1500 |
| Zones | Inlet | Impeller | Diffuser | Volute Casing |
|---|---|---|---|---|
| Total number of control cells (in lakh) | 13.6 | 13.8 | 21.7 | 19.8 |
| Hemispherical Hub | Ellipsoidal Hub | ||
|---|---|---|---|
| Model | Spheroidal Hub Ratio | Model | Ellipsoidal Hub Ratio |
| Hub-less base | 0.00 | Hub-less base | 0.00 |
| S1 | 0.30 | E1 | 0.30 |
| S2 | 0.40 | E2 | 0.50 |
| S3 | 0.50 | E3 | 0.70 |
| S4 | 0.60 | E4 | 0.90 |
| S5 | 0.70 | E5 | 1.10 |
| S6 | 0.80 | E6 | 1.30 |
| Parameters | Range |
|---|---|
| Input parameters | |
| Volume coefficient | 0.004–0.051 |
| Ellipsoidal Ratio | 0–1.3 |
| Output parameters | |
| Head Coefficient (Ellipsoidal) | 0.4440–0.4898 |
| Relative Theoretical Efficiency (Ellipsoidal) in percentage | 52.79–71.65 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nagaraj, M.; Karanth, K.V. Numerical Investigations and Artificial Neural Network-Based Performance Prediction of a Centrifugal Fan Having Innovative Hub Geometry Designs. Appl. Syst. Innov. 2023, 6, 104. https://doi.org/10.3390/asi6060104
Nagaraj M, Karanth KV. Numerical Investigations and Artificial Neural Network-Based Performance Prediction of a Centrifugal Fan Having Innovative Hub Geometry Designs. Applied System Innovation. 2023; 6(6):104. https://doi.org/10.3390/asi6060104
Chicago/Turabian StyleNagaraj, Madhwesh, and Kota Vasudeva Karanth. 2023. "Numerical Investigations and Artificial Neural Network-Based Performance Prediction of a Centrifugal Fan Having Innovative Hub Geometry Designs" Applied System Innovation 6, no. 6: 104. https://doi.org/10.3390/asi6060104
APA StyleNagaraj, M., & Karanth, K. V. (2023). Numerical Investigations and Artificial Neural Network-Based Performance Prediction of a Centrifugal Fan Having Innovative Hub Geometry Designs. Applied System Innovation, 6(6), 104. https://doi.org/10.3390/asi6060104






