Abstract
A scheme for solving the problem of determining the probability of failure and probabilistic (statistical) characteristics of the failure loading magnitude of a composite material plate is considered. The plate structure is a flat homogeneous matrix with stochastically distributed rigid rod inclusions. The geometric parameters of inclusions are considered independent random variables with given probability distribution laws. The expressions for the failure loading distribution function, the probability of failure, the mean value, and the dispersion of the failure loading were received and presented. Their dependence on the type of stress state, the inclusion number, and matrix Poisson’s ratio were studied graphically.
1. Introduction
Studying the stress state and failure of composite materials, in particular those reinforced with random rigid linear inclusions, is an urgent task. Probability assessment of the failure state under a given loading is an important stage in calculations of the strength and reliability of machine parts and structural elements. The strength and reliability of the material depend on structural defects and are always some random value. Therefore, when solving the problems of predicting the limited state of structural materials, the complex application of probabilistic statistical methods and deterministic solutions in fracture mechanics is relevant. These methods, applied to the study of the strength of materials with structural defects, in particular to composites, have been developed recently. The paper [1] presents a simulation of the damage growth in open-hole laminates under compression. It used the developed numerical scheme with discontinuous elements of the hard shell and enriched connected elements. The authors hypothesized that due to localized bending damage, compressive loading could lead to the formation of oblique cracks in the matrix. According to the modeling technology, an assumed vertical connected fracture was formulated with a coordinate system of an inclined fracture. Representation of damage in the form of discrete cracks makes it possible to more accurately predict models of brittle failure of composite materials. In article [2], an assessment of the fatigue reliability of welded joints in orthotropic steel bridge decks was carried out, taking into account the effects of loading sequences. The effect of initial damage and traffic growth on fatigue reliability was studied. It was concluded that while evaluating the fatigue life of orthotropic steel decks equipped with long-term deformation control systems, initial damage reduces the fatigue life of orthotropic steel decks significantly, and the importance of considering load sequence effects is also shown. The study [3] proposed a model of a symmetrical multilayer plate, which contains elliptical cutouts, under conditions of a flat tensile loading. An analysis of stress change and progressive failure was carried out. The failure of the first and last layers of the composite depends on various parameters. The influence of the parameters was analyzed too. Using the complex variable of Muskhelishvili’s formula enables one to write analytical representations of layer-by-layer stresses around elliptical cuts. Progressive fracture prediction is based on the Tsai–Hill and Tsai–Wu strength criteria. Accordingly, before the studies were carried out, the most significant influence on the tensile strength of the laminate under a given loading was exerted by the stacking sequence of the fibers and their orientation. Conclusions were drawn about the effectiveness of using the method of complex variables and conformal mapping to study the failure of a composite plate with an elliptical cut. The article [4] shows the importance of joint use of the deterministic approach and taking into account stochastic effects in the design of structures made of composite materials. All geometric and material parameters of the investigated composite layered plates were supposed to be stochastic. To study the stochastic effect of material properties, orientation, and layer thickness on the failure of multilayer composite plates under the action of static loadings, Monte Carlo simulation was used. A classical lamination theory was proposed to calculate strength factors using maximum stress, Tsai–Wu, and Tsai–Hill strength criteria for plates of three different materials in different stacking sequences. It was shown that an increase in the variation coefficient of the input variables leads to an increase in the variation in the distribution of failure layers. Conclusions were drawn about a significant degree of dependence between the distribution of failure layers and the probability of failure from a combination of laminate laying sequences. The empirical probability of failure of multilayer materials with transverse layers was the highest for the layer predicted by the deterministic analysis. With an increase in the input parameters’ variation, a rapid decrease was observed. The general significance of considering the tensile strength and thickness of the composite material layer as random variables was shown. The significance of randomness in the orientation of layers for laminates with balanced and corner layers was analyzed. In [5], bistable composite laminates are considered. They can be used in the design of engineering structures because of their low density and deformation properties. An analysis of their reliability was carried out via the Monte Carlo simulation method. Several types of uncertain parameters, geometry, and material properties were considered random variables. It was shown that the thickness and thermal expansion coefficient of the studied composite material mostly affect the bistability behavior compared to the other input parameters. The research results were validated by comparing them with the results obtained by the finite element method. Paper [6] proposed a method for studying the crack resistance of composite materials. The structure of the composite was represented by an embedded cell near the crack tip. The rest of the composite under study was modeled as an anisotropic elastic body. Experimental data on transverse cracking of the matrix as a result of tests for three-point bending with one notch were used. The effectiveness of the microstructure in increasing the fracture toughness due to the disruption of the bond between the fiber and the matrix, fiber rupture, and crack deflection was shown. An increase in fracture toughness due to the disruption of the bond between the fiber and the matrix, fiber rupture, and crack deflection has been studied. It was shown that the research results are an important aspect of the development of composites with high crack resistance. Paper [7] investigated the reliability of composite plates made using the process of vacuum transfer casting resin based on carbon fiber/epoxy resin. An assessment was made of the change in the volume fraction of fibers in different parts of a plate made of a composite material. The effective orthotropic properties of the composite are numerically calculated for the various volume fractions of fibers by the homogenization method using periodic boundary conditions. The problem of predicting the failure probability of a composite beam with a double cantilever was considered. The accuracy and efficiency of the proposed approach are demonstrated by the study of meta-model stability. In [8], adaptive multipoint modeling with actively damaged areas of composite materials using high-precision 3D brick elements and discrete cracks, while dormant and inactive areas are considered with lower values, is proposed. The criteria for the transition between the two levels of modeling were studied to ensure the efficiency of calculations. The obtained results were compared to the experimental data known in the scientific literature on the tension of transverse-layer and quasi-isotropic composite materials and the results of a high-precision simulation.
The article is another variation on the strength of composite materials with internal type inclusions/holes which has been studied since 1950-60. It must be agreed that there has been no significant progress in this area since the indicated data. Mathematical ideas (G. Papanicolaou and co-authors [9,10], M. Kozlov and co-authors [11]) have not yet been implemented. V. Mityushev and co-authors [12,13] have made some progress in calculating random compositions with rigorous mathematical methods, but not exactly of the class considered in this article.
In contrast to the specified publications, the main content of this study is the construction and numerical and graphic analysis of expressions of the limit (failure) loading distribution function and the probability of failure of plates reinforced with random rigid rectilinear inclusions under different types of loading, different numbers of inclusions (structural heterogeneity) and the Poisson’s ratio of the matrix.
Taking defectiveness and randomness into account as interrelated phenomena makes it possible to qualitatively build a theory of the structural material’s strength. Thus, the relevance of the work is determined by the importance of taking into account the stochasticity of the structure of the material when evaluating their strength properties.
2. Materials and Methods
The failure of the composites with rigid inclusion under conditions of a complex stress state was extensively studied recently. In papers [14,15], various methods for solving the inverse problem of determining a rigid inclusion in linear elastic bodies are considered. The optimal inequality of three spheres was presented as a mathematical apparatus for solving the inverse problem of determining a rigid inclusion in a thin plate [16,17]. The article [18] considers the problem of separating a rigid inclusion from an infinite elastic plate. Many results have been obtained to determine the limiting state of such materials depending on their physical and mechanical properties, loading conditions, plate geometry, and parameters of individual defects in them. In this case, these factors are considered given (deterministic), although they can be arbitrary. In particular, in [19], an experimental and numerical analysis of the short fiber-reinforced composite material’s behavior during failure was carried out. We will utilize a technique that provides for joint consideration of defectiveness and stochastic of the composite materials structure.
We study an elastic rectangular plate made of a brittle material reinforced with rigid linear (rod) inclusions of random size and placement which do not interact with each other. The strength of the contact layer between the inclusions and the matrix (base material) is higher than the strength of the matrix. The plate is considered in conditions of comprehensive tension compression under the action of uniform loading and (Figure 1), where is the loading biaxial coefficient. The values and are introduced as the principal stresses in the plane stress state. The geometric parameters of the inclusions are the next: is the length and is the angle between the direction of the inclusion and the action of the loading , . They are defined as independent random variables. The laws of the probability distribution for these random variables because of certain physical reasons would be formulated assuming that the material of the plate is isotropic.
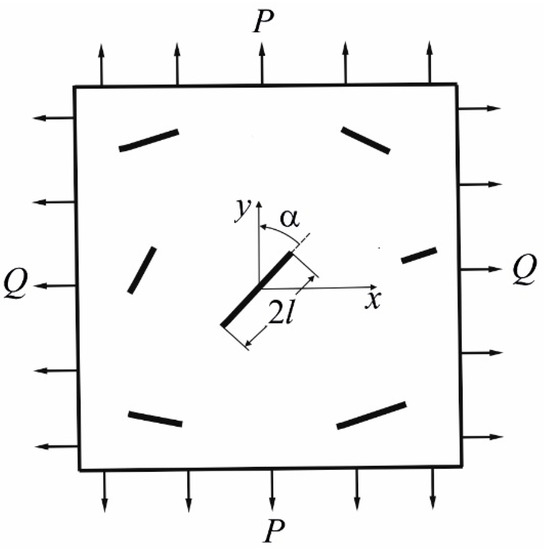
Figure 1.
Model of a plate reinforced with random rigid linear inclusions.
In the case of a surface crack that is larger, the thickness of the plate should also be taken into account. Similarly, in the case of through cracks in limited (small) plates, the magnitude of the failure loading will be influenced by the linear dimensions of the plate.
This algorithm can be applied to the study of fiber concrete failure with metal reinforcing fibers as one of the components. The introduction of such fibers with arbitrary orientation into the concrete composition helps to increase its tensile and compressive strength, increase crack resistance, impact toughness, and wear resistance.
It was shown in the paper [20] that in the small vicinity of the inclusion ends, which is not restrained from turning under the action of external loading, the components of the stress tensor in the local polar coordinate system are written as follows:
where the value is analytically represented:
are polar coordinates centered at the crack tip ( is the radial coordinate, is the polar angle), is the elastic constant (the case of plane stress state), and is the Poisson’s ratio of the plate material.
It follows from Expressions (1) and (2) that the inequality is true in the vicinity of the inclusion vertex. Therefore, in [21], stress is assumed to be responsible for the occurrence of brittle fracture. It is also hypothesized that the strength of the contact layer between the inclusion and the matrix is higher than the strength of the matrix. Similarly to the cracks theory, the next condition is proposed for the failure criterion
where , the constant characterizes the material’s resistance to local failure. This characteristic is determined from the experiment (or expressed in terms of the energy density of a given material failure). It is taken into consideration that the matrix material is assumed to be homogeneous, isotropic, and does not have the property of strength anisotropy.
According to Expressions (1)–(3), the formulas for calculating the failure loading (a crack forms in the vicinity of a rigid rectilinear inclusion) of the plate under the conditions of plane stress state are presented in the following general form [22]:
where the analytical form of the function is:
where
Expressions (4)–(7) and relations [22] allow us to write the formulas for calculating the failure loading .
For the case (biaxial tension, or tension–compression)
For the case (biaxial compression)
The angle value is determined as follows:
We assume that the random half-length of inclusions can be of arbitrary values . This assumption simplifies mathematical calculations and the material model and is adopted in several papers as well. In addition, the values of the failure loading are also possible. The minimum value of the failure loading is (the strength threshold value). This means that even with arbitrarily small loading and , there exists a non-zero probability of failure.
3. Failure Loading Probability Distribution Function
The probability distribution density of the random variable was chosen in accordance with the results of the development of the statistical theory of strength [23], in the exponential law form
Here, is a distribution parameter with the dimension of the random variable . The physical content of (13) consists of reducing the probability of the quantity presence in case of its increase. In articles [24,25], the study was based on the laws of size distribution of defects during the failure of materials.
The integral probability distribution function depending on the parameter can be defined as follows:
The failure loading distribution function of a plate element with one crack can be determined by applying formula [22]
According to Expressions (8)–(12), from (15), one can obtain
is a set of the parameter possible values in the case when the condition is satisfied under the given loading and
For the distribution of inclusion half-lengths in the form of an exponential law (13), according to Formulas (14) and (16), we obtain
Since we suppose the material of the plate to be isotropic, we set the probability distribution density of the random variable by the uniform law . We substitute this expression into Formula (17) and the relation for the function (5)–(7); according to Formulas (8)–(12), we obtain the following expressions.
For the case (biaxial tension, or tension–compression):
- at
- at
For the case (biaxial compression):
- at
- at we obtain the Expression (20) with a replacement in its left part by .
If , then Expressions (18) and (20) are appreciably simplified. From Formulas (6) and (7) one can obtain .
In accordance:
- at (biaxial symmetric tension)
- at (biaxial symmetric compression)
Using the obtained relations for the distribution function (18)–(22), it is possible to determine the statistical characteristics of the strength of the plate with randomly distributed rigid linear inclusions under the different types of stress state: the probability of failure, the most probable and mean value, the dispersion and the coefficient of variation of the failure loading, etc.
For a plate with defects, can be applied to the next relation to determine the failure loading distribution function [22]
The ratio
enables us to find the most probable value of the failure loading. This value corresponds to the loading level when the probability distribution density achieves its maximum value.
The mean value of the failure loading can be represented as:
The dispersion of the failure loading is determined by the formula
4. The Probability of Failure of the Reinforced Plates
The distribution function (23) at fixed values and determines the failure probability of a plate reinforced with random rigid linear inclusions
We introduce dimensionless loading . Then, the probability of failure according to (19), (21), (23), and (24) is recorded for the following individual cases:
under symmetric biaxial tension
under uniaxial tension
under biaxial symmetric compression
According to Expressions (25) and (26), in Figure 2 and Figure 3, diagrams of the probability of failure under different types of stress states are shown. Graphs were plotted using the Maple 7 computer mathematics package.
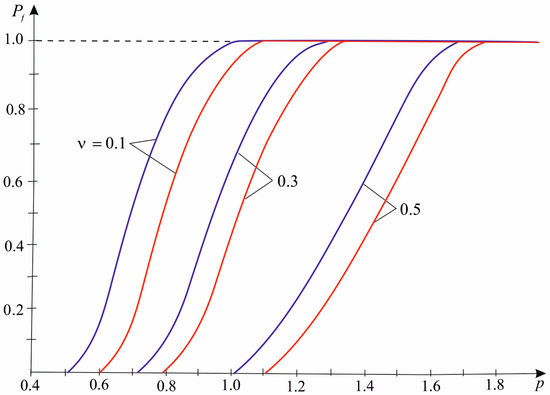
Figure 2.
Probability of failure under biaxial symmetric tension ( for blue line, for red line).
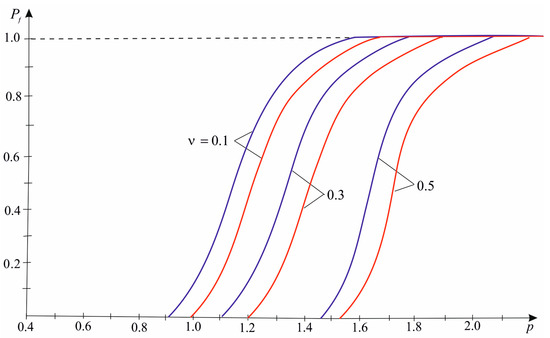
Figure 3.
Probability of failure under uniaxial tension ( for blue line, for red line).
According to Expression (27), Figure 4 demonstrates diagrams of the failure probability under biaxial symmetric compression at a fixed value of Poisson’s ratio for different numbers of inclusions.
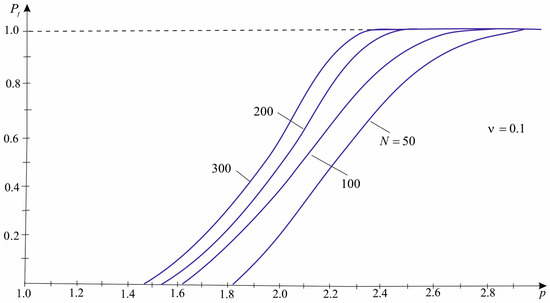
Figure 4.
Probability of failure under biaxial symmetrical compression.
5. Mean Value and Dispersion of Failure Loading
Let us substitute expressions for the distribution function in Formulas (24) and (25) and introduce dimensionless loading . We will obtain statistical characteristics of strength for the following individual cases:
under biaxial symmetric tension
under uniaxial tension
under biaxial symmetric compression
In Figure 5, the effect of the applied loading ratio, the number of inclusions, and the Poisson’s ratio of the matrix on the mean values of failure loading calculated according to Formulas (30), (32), and (34) are shown.
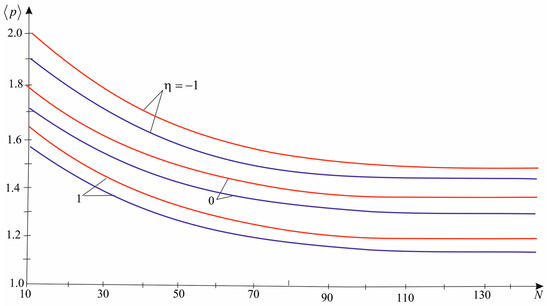
Figure 5.
Mean value of failure loading (blue lines for , red for ).
Figure 6 shows the dependence of the failure loading dispersion calculated according to Formulas (31), (33), and (35) on the applied loading ratio, the number of inclusions, and the matrix Poisson’s ratio.
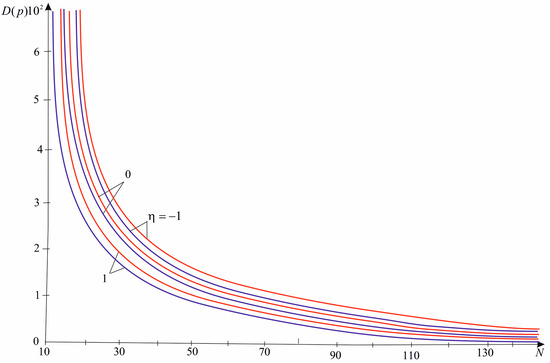
Figure 6.
Dispersion of failure loading (blue lines for , red for ).
In article [26], a probabilistic description of experimental statistical regularities and strength characteristics of stochastically defective isotropic materials was carried out. It is shown that the method considered in this article allows the selection of parameters to match the theory well with the experimental data. The considered method of researching composite material failure is consistent with the results of the work [26].
6. Discussion
Several statistical approaches for the construction of the strength theory do not take into account the defectiveness and heterogeneity of composite materials in an obvious way; that is, their geometric parameters and mechanical properties. The disadvantages of such approaches are the veiled role of the defect in the elementary act of failure, and the reduction of the composite element strength. Our proposed approach of explicit introduction into the material model of structural defects with the laws of their geometric parameter’s distribution allows for eliminating the specified shortcomings. It opens up the possibility of calculating the statistical characteristics of the structural material’s strength and failure based on data on their defect structure and resistance to the initiation and cracks development.
In contrast to the previously applicable laws of distribution of cracks random half-length (power-law distribution and beta distribution), in our work we propose an exponential distribution law which simplifies the material model and mathematical calculations, but nevertheless makes it possible to relatively easily obtain several results that adequately reflect reality.
Analyzing the constructed curves, we can see that at a given loading level, the probability of composite failure increases with a decrease in the Poisson’s ratio of the matrix. On the other hand, an increase in the value leads to an increase in the loading, which corresponds to a fixed probability of failure. Similar regularities were observed in the paper [22] when choosing the probability distribution density of the half-length of inclusions in the form of a power law. With an increase in the number of inclusions, the probability of material failure increases. A certain loading level corresponds to a very low probability of failure, . There exists a certain range of plate sizes (number of inclusions) when the probability of failure increases rapidly. The nature of this growth is invariant to the Poisson’s ratio of the plate material. It is possible to assert a certain scale threshold for the value of .
With biaxial symmetric compression, we observe a significant increase in the value of failure loading compared to the cases of biaxial symmetric tension and uniaxial tension. This feature can be explained by the presence of compressive stress components.
At the same level of loading, for plates with the same dimensions and the value of the coefficient , the value for biaxial symmetric tension compression is greater than for uniaxial tension (Figure 2 and Figure 3). It will be the largest under biaxial symmetrical compression (Figure 4). With the increase in the number of plate inclusions (increase in its size), we observe an increase in the failure probability. It should be noted that their nature is almost independent of the type of loading (from ). The revealed regularities were also observed for stochastically defective isotropic plates [22] and orthotropic composite materials [27].
An increase of the inclusions number leads to a decrease in strength (Figure 5). The lowest strength of the composite is obtained under biaxial symmetric tension. For different types of stress states, we observe that an increase in the value causes an increase in the mean value of failure loading.
The strength dispersion is a decreasing function of the inclusions number in the plate (Figure 6). Within a certain interval of the value change, we observe a rapid decrease in the value . Decreasing nature does not depend on the type of stress state and Poisson’s ratio as well. With the change of , the dispersion of the failure loading changes by a value that is almost independent of the applied loading type. As in the case of the mean value of the failure loading, an increase in the value causes an increase in the dispersion value.
7. Conclusions
- In this paper, a new class of problems for the study of composite material failure is considered, taking into account the stochasticity of their structure.
- According to the obtained results, it is stated that the dependence of the probability of failure of the plate on the loading and the number of rigid linear inclusions have the same features as for a plate with cracks, while the dependence on the type of loading (from ) will be different.
- Further research directions could examine inclusions and their spatial placement in three-dimensional bodies.
- According to (18)–(20), in future studies, the criteria for failure under plane stress will be analyzed. In particular, the limit state curves expressed in failure loading mean values, taking into account that and the limit state curves corresponding to the given probability of failure .
- Similar probabilistic studies of strength also can be applied to structural fiberglass since reinforced fiberglass is used as a load-bearing support element for mining and construction equipment.
Author Contributions
Conceptualization, R.K. and P.P.; methodology R.K., M.V., and T.S.; software, T.S.; validation, M.V. and T.S.; investigation, P.P. and M.V.; writing—original draft preparation, M.V. and T.S.; writing—review and editing, R.K. and P.P.; visualization, M.V. and T.S.; project administration, R.K. and P.P.; funding acquisition, P.P. and M.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhi, J.; Tay, T.E. Interrogating failure mechanisms of notched composites through a discrete crack modeling approach. Compos. Sci. Technol. 2020, 196, 108203. [Google Scholar] [CrossRef]
- Xu, J.-H.; Zhou, G.-D.; Zhu, T.-Y. Fatigue reliability assessment for orthotropic steel bridge decks considering load sequence effects. Front. Mater. 2021, 8, 678855. [Google Scholar] [CrossRef]
- Magar, A.; Lal, A. Progressive failure analysis of laminated plate containing elliptical cutout. Int. J. Struct. Integr. 2021, 12, 569–588. [Google Scholar] [CrossRef]
- Martinez, J.; Bishay, P. On the stochastic first-ply failure analysis of laminated composite plates under in-plane tensile loading. Compos. Part C Open Access 2021, 4, 100102. [Google Scholar] [CrossRef]
- Saberi, S.; Abdollahi, A.; Inam, F. Reliability analysis of bistable composite laminates. AIMS Mater. Sci. 2021, 8, 29–41. [Google Scholar] [CrossRef]
- Tan, W.; Martínez-Pañeda, E. Phase-field fracture predictions of microscopic bridging behavior of composite materials. Compos. Struct. 2022, 286, 115242. [Google Scholar] [CrossRef]
- Rakesh, P.; More, A.; Kumar, M.; Muthu, N. Probabilistic failure prediction in a double composite cantilever beam with single and double source uncertainty. Compos. Struct. 2022, 279, 114870. [Google Scholar] [CrossRef]
- Leong, K.H.; Zhi, J.; Lee, H.P.; Tan, V.B.C.; Tay, T.E. Adaptive multi-fidelity (AMF) modeling of progressive damage in notched composite laminates. Compos. Part A Appl. Sci. Manuf. 2022, 154, 106790. [Google Scholar] [CrossRef]
- Papanicolaou, G.; Bakos, D. Effect of treatment conditions on the mode delamination fracture toughness of sandwich structures. J. Compos. Mater. 1995, 29, 2295–2316. [Google Scholar] [CrossRef]
- Kontaxis, L.; Kozaniti, F.; Papanicolaou, G. Mechanical behavior modelling and filler geometry effect of glass filler reinforced starch-epoxy hybrid matrix composites. Materials 2021, 14, 6587. [Google Scholar] [CrossRef]
- Kozlov, M.; Sheshenin, S. Modeling the progressive failure of laminated composites. Mech. Compos. Mater. 2016, 51, 695–706. [Google Scholar] [CrossRef]
- Drygaś, P.; Mityushev, V. Effective elastic properties of random two-dimensional composites. Int. J. Solids Struct. 2016, 97–98, 543–553. [Google Scholar] [CrossRef]
- Drygaś, P.; Gluzman, S.; Mityushev, V.; Nawalaniec, W. Applied Analysis of Composite Media: Analytical and Computational Results for Materials Scientists and Engineers; Woodhead Publishing: Sawston, UK, 2019; ISBN 9780081027325. [Google Scholar]
- Morassi, A.; Rosset, E.; Vessella, S. Stable determination of a rigid inclusion in an anisotropic elastic plate. SIAM J. Math. Anal. 2012, 44, 2204–2235. [Google Scholar] [CrossRef][Green Version]
- Alessandrini, G.; Di Cristo, M.; Morassi, A.; Rosset, E. Stable determination of an inclusion in an elastic body by boundary measurements. SIAM J. Math. Anal. 2014, 46, 2692–2729. [Google Scholar] [CrossRef]
- Morassi, A.; Rosset, E.; Vessella, S. Optimal stability in the identification of a rigid inclusion in an isotropic Kirchhoff–Love plate. SIAM J. Math. Anal. 2019, 51, 731–747. [Google Scholar] [CrossRef]
- Alessandrini, G.; Rosset, E.; Vessella, S. Optimal three spheres inequality at the boundary for the Kirchhoff-Love plate’s equations with Dirichlet conditions. Arch. Ration. Mech. Anal. 2019, 231, 1455–1486. [Google Scholar] [CrossRef]
- Salasiya, P.; Sundaram, K. Receding contact between an inclusion of generalized shape and a remotely-stressed plate. Int. J. Solids Struct. 2022, 252, 111826. [Google Scholar] [CrossRef]
- Carpinteri, A.; Fernandez-Canteli, A.; Fortese, G.; Muñiz-Calvente, M.; Ronchei, C.; Scorza, D.; Vantadori, S. Probabilistic failure assessment of fiberglass composites. Compos. Struct. 2017, 160, 1163–1170. [Google Scholar] [CrossRef]
- Panasyuk, V.; Berezhnytskyi, L.; Trush, I. Stress distribution about defects such as rigid sharp-angled inclusions. Strength Mater. 1972, 4, 771–777. [Google Scholar] [CrossRef]
- Berezhnytskyi, L.; Panasyuk, V.; Trush, I. Local failure of a brittle body with a sharp-ended rigid inclusion. Strength Mater. 1973, 5, 1166–1170. [Google Scholar] [CrossRef]
- Vytvytskyi, P.; Popina, S. Strength and Criteria of Brittle Fracture of Stochastically Defective Bodies; Naukova Dumka: Kyiv, Ukraine, 1980. (In Ukrainian) [Google Scholar]
- Kvit, R. Investigation of probabilistic aspects reliability of isotropic bodies with internal defects. J. Appl. Math. Comput. Mech. 2022, 21, 73–84. [Google Scholar] [CrossRef]
- Petersen, T. The laws of defect-size distribution in the failure of materials. Dokl. Phys. 2001, 46, 369–372. [Google Scholar] [CrossRef]
- Ignatovich, S.; Bouraou, N. Power law of crack length distribution in the multiple damage process. Strength Mater. 2019, 51, 735–745. [Google Scholar] [CrossRef]
- Vitvitskiy, P.; Kvit, R. Probabilistic description of experimental statistical strength characteristics. Mater. Sci. 1992, 28, 83–86. [Google Scholar] [CrossRef]
- Kvit, R. Development of orthotropic composite materials statistical model failure. J. Appl. Math. Comput. Mech. 2023, 22, 26–35. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).