Abstract
The purpose of this paper is to assess how three shaking procedures affect the performance of a metaheuristic GVNS algorithm. The first shaking procedure is generally known in the literature as intensified shaking method. The second is a quantum-inspired perturbation method, and the third is a shuffle method. The GVNS schemes are evaluated using a search strategy for both First and Best improvement and a time limit of one and two minutes. The formed GVNS schemes were applied on Traveling Salesman Problem (sTSP, nTSP) benchmark instances from the well-known TSPLib. To examine the potential advantage of any of the three metaheuristic schemes, extensive statistical analysis was performed on the reported results. The experimental data shows that for aTSP instances the first two methods perform roughly equivalently and, in any case, much better than the shuffle approach. In addition, the first method performs better than the other two when using the First Improvement strategy, while the second method gives results quite similar to the third. However, no significant deviations were observed when different methods of perturbation were used for Symmetric TSP instances (sTSP, nTSP).
1. Introduction
Variable Neighborhood Search (VNS) is a metaheuristic approach proposed by Mladenovic and Hansen to solve combinatorial and global optimization problems [1,2]. This framework is primarily designed to systematically modify the neighborhood structure, to reach an optimal (or near-optimal) solution [3]. VNS and its extensions have demonstrated their effectiveness in solving many problems in the combinatorial and global optimization field [4,5].
Each VNS heuristic consists of three parts. The first is a process of shaking (phase of diversification) used to escape from local optimal solutions. The next one is changing the neighborhood, where the next neighborhood structure to be searched will be determined; an approval or rejection criterion will also be applied to the last solution found during this part. The third part is the phase of improvement (intensification) achieved by exploring neighborhood structures by applying various local search moves. This exploration is carried out primarily through one of the following steps to change the neighborhood:
- Cyclic neighborhood change step: Whether there is an improvement in some neighborhood or not, the search continues in the next neighborhood structure in the list.
- Pipe neighborhood change step: If the current solution is improved in some neighborhood, exploration in that neighborhood will continue.
- Skewed neighborhood change step: Accept as new incumbent alternatives that not only improve solutions, but also some that are worse than the current incumbent solution. Such a neighborhood change step is intended to allow valley exploration away from the incumbent solution. A trial solution is evaluated taking into consideration not only the trial’s objective values and the incumbent solution, but also their distance.
Variable neighborhood search variants. Many VNS variants have already been developed and used to solve hard optimization problems [6,7]. The most commonly used variants are the Basic VNS (BVNS), the Variable Neighborhood Descent (VND), and the General VNS (GVNS) and the Reduced VNS (RVNS). In the BVNS a method of diversification is alternated with a local search operator. VND consists of an improvement procedure in which neighborhood structures are systematically explored and a neighborhood change step. According to their neighborhood change step, there are different variants of VND. The pipe-VND, which uses the pipe neighborhood change step, appears to be the most efficient way to solve computational problems [6]. General Variable Neighborhood Search (GVNS) is a VNS variant that uses a VND method to improve. In many applications, GVNS has been successfully tested, as several recent works have shown [8,9].
The efficiency of metaheuristics depends on the efficiency of their components. Performance studies are a prerequisite for evaluating different metaheuristics [10] or different components of a metaheuristic algorithm [11]. In this direction and based on the VNS, Huber and Geiger (2017) [12] examined the impact of different order of local search operators in the improvement component of a VNS algorithm. There are similar studies for the impact of the initial solution [13] or the use of different neighborhood change strategies [2] to the overall performance of a VNS algorithm. However, there is a lack of contributions on studying the impact of the shaking components to the overall performance of a VNS algorithm. Papalitsas et al. (2019) [14] attempted an initial study on the impact of diversification methods on the performance of GVNS by focusing on asymmetric TSP instances.
This work is a substantial extension of our recent conference paper [14] in which we investigated the impact of three shaking methods on a GVNS metaheuristic, applied on asymmetric Traveling Salesman Problem (TSP) instances from the TSPLib. In an effort to build a comprehensive view related to that potential impact of diversification methods, the findings of the previous work are integrated with further analysis on the obtained solutions of symmetric and world TSP instances from TSPLib. To examine this potential impact of the different perturbation strategies, the three shaking methods were examined within the same improvement step. Moreover, the resulting GVNS schemes were executed both with First and Best improvement search strategies, and two different time limits were used as the main stopping criteria: 60 s and 120 s. The obtained experimental results were analyzed statistically to establish whether the use of different perturbation methods affects the performance of the GVNS algorithm. Our findings demonstrate that the use of different perturbation strategies clearly affect the solution quality in aTSP instances, while no significant differences were observed for the case of sTSP instances, with the exception of the experiments conducted using Best Improvement and 120 s run time limit. Moreover, to examine the efficiency of the formed methods, a comparison is performed between the obtained results and other recent metaheuristic solution approaches for the TSP in the literature. As it can be confirmed by our experimental results, the proposed GVNS schemes produce better solutions than the other metaheuristics.
Organization
This paper is organized as follows. In Section 2 the proposed GVNS solution methods and their technical components are explained. Section 3 contains the experimental results of our performance analysis, while the statistical tests applied to our numerical results are presented in Section 4. Section 5 provides a comparative study between our algorithms and other metaheuristic solution approaches in the recent literature. Finally, conclusions and ideas for future work are given in Section 6.
2. GVNS Heuristics
The formed GVNS methods use the pipe-VND scheme, which means that the search is taking place in the same neighborhood where the improvement occurs, as their improvement phase.
2.1. Neighborhood Structures
Three local search operators are considered for exploring different solutions:
- 1-0 Relocate. This move removes node i from its current position in the route and re-inserts it after a selected node b.
- 2-Opt. The 2-Opt move breaks two arcs in the current solution and reconnects them in a different way.
- 1-1 Exchange. This move swaps two nodes in the current route.
All three neighborhood structures are incorporated in a pipe-VND scheme, as illustrated in Algorithm 1, where denotes the number of neighborhood structures.
| Algorithm 1 pipe-VND. |
|
2.2. Shaking Methods
To avoid local optimum traps, three different shaking procedures are examined. These perturbation methods are the following:
Shake_1. This diversification method randomly selects one of the predefined neighborhood structures and applies it k times (, where is the maximum number of shaking iterations) in the current solution. The method is summarized in Algorithm 2.
Shake_2 [15]. The scientific community seems to tend to revolve around new unconventional computing methods. Overall, unconventional computing is a wide range of proposed new or unusual computing models. Part of these computing models is natural computing [16]. Nature-inspired computing has emerged as an efficient paradigm for designing and simulating innovative computational models inspired by natural phenomena to solve complex nonlinear, dynamic specific problems. Some of the well-known nature-inspired computational systems and algorithms are [17]:
- Evolutionary, biological-inspired algorithms.
- Swarm intelligence algorithms inspired by swarm/agent group behavior.
- Social and cultural algorithms inspired by society’s interactions and beliefs.
- Inspired by quantum physics, Quantum-inspired algorithms.
| Algorithm 2 Shake_1. |
|
Quantum Computing Principles
Quantum inspired methods imitate the fundamental principles of quantum computing. Quantum computing, a natural computing subsection and a field recently introduced by Feynman (1980s). Feynman realized that an effective simulation of an actual quantum system using a standard computer is not possible because the simulation of actual quantum processes would be exponentially slowed down [18,19]. Quantum computing is an important addition to the existing standard computing models. A general concept which considers the process as a quantum phenomenon. Quantum computing combines, apart from computer science, definitions, mathematical abstractions, and physics. Mathematics, such as linear algebra, and physics, such as quantum mechanics, are mainly involved.
The qubit is the quantum analogue of the classical bit. Similarly, the quantum register, which is a collection of qubits, is the quantum analogue of the classical processor register. In each call of this shaking method, a simulated quantum n-qubit register generates a normalized complex n-dimensional unit vector. In this context, normalized means that if is the complex vector, then . The dimension n of the complex unit vector is greater than or equal to the dimension of the problem. The complex n-dimensional vector is converted into a real n-dimensional vector, the components of which are real numbers in the interval . If and are the ith components of the complex and real vectors respectively, then , i.e., is equal to the modulus squared of . Moreover, each of the real vector’s selected components corresponds to a current solution node. For each node of the incumbent solution, the components are used as a flag. Sorting the first vector affects the order in the solution vector due to the correspondence between components and nodes in a tour and thus drives the exploration effort to another point in the search space. This shaking procedure’s pseudocode is given in Algorithm 3.
| Algorithm 3 Shake_2. |
|
Shake_3. This shaking method is a shuffle method, where in each iteration the customers are placed in a random order. The method is shown in Algorithm 4.
| Algorithm 4 Shake_3. |
|
2.3. GVNS Schemes
For each perturbation method a GVNS scheme is formed. Specifically, the GVNS_1 contains Shake_1 as its shaking method, GVNS_2 uses Shake_2 to diversify solutions, and GVNS_3 adopts the Shake_3 perturbation method. The initial solution is produced by the Nearest Neighbor heuristic in all GVNS schemes. The pseudocode for three GVNS approaches is given in Algorithms 5–7, respectively.
| Algorithm 5 GVNS_1. |
|
| Algorithm 6 GVNS_2. |
|
| Algorithm 7 GVNS_3. |
|
It should be mentioned that in all three GVNS methods the neighborhoods are searched with both the First and Best improvement search strategy.
3. Computational Analysis
3.1. Computing Environment & Parameter Settings
The aforementioned methods were implemented in Fortran and were executed in a PC running Windows 64-bit on an Intel Core i7-6700 CPU at 2.6 GHz with 16 GB RAM. The compilation of the code was done using the Intel Fortran 64 compiler XE with the optimization option /O3. The maximum execution time limit was set to s and s and the maximum number of shaking iterations in the Shake_1 was experimentally set to .
3.2. Computational Results
This section presents the computational results of the different perturbation strategies for each class of experiments. The GVNS schemes with the different shaking methods were applied on TSPLIB instances. The TSP is one of the most famous NP-hard combinatorial optimization problems. Solving the TSP means finding the minimum cost route so that the salesman starts from a particular node and returns to that node after passing from all the other nodes once.
All experiments were executed 5 times and the average value of all runs was computed. Table 1 and Table 2 contain the aggregated experimental results. Specifically, they show the benchmark name, the optimal value (zOpt), the cost of the three GVNS schemes (GVNS_1, GVNS_2 and GVNS_3) and their corresponding gaps from the optimal value. The results depicted in Table 1 were obtained using the First Improvement search strategy and an execution time limit of 1 min, whereas the results in Table 2 were obtained using the Best Improvement search strategy and the same execution time of 1 min. As mentioned earlier, the cost of each GVNS scheme is the average of 5 runs for each problem. The reported gap is computed as follows: given the outcome x, its gap from the optimal value is given by the formula .

Table 1.
The results shown here were obtained using the First Improvement search strategy and an execution time limit of 1 min [14].

Table 2.
The results depicted here were obtained using the Best Improvement search strategy and an execution time limit of 1 min [14].
The results in Table 1 indicate a definite pattern, namely that both GVNS_1 and GVNS_2 outperform GVNS_3 in most cases. Recall that GVNS_3 is a shuffle perturbation strategy. For example, consider benchmark ftv47; we can see that the cost of GVNS_1 is 1821, the cost of GVNS_2 is 1992 and of GVNS_3 is 2101. GVNS_1 and GVNS_2 both outperform GVNS_3 and are also relatively close to the optimal value (1778).
In addition, the provided results in Table 2 lead to the same statement that both GVNS_1 and GVNS_2 produce better results than GVNS_3 in most cases. Table 3 shows the results of the GVNS schemes within a 2 min run time limit and the First Improvement as search strategy. The results of Table 3 mention that GVNS_1 outperform GVNS_2 and GVNS_3 in most cases. However, the main difference from the results of Table 1 and Table 2 is that now the behavior of GVNS_2 is closer to that of GVNS_3 solution approach. Table 4 shows the results achieved by the GVNS schemes within a 2 min run time limit and the Best Improvement search strategy. The results of Table 4 corroborate the conclusion of Table 1 and Table 2 that both GVNS_1 and GVNS_2 outperform GVNS_3 in most cases.

Table 3.
Results using the First Improvement search strategy and an execution time limit of 2 min [14].

Table 4.
Results using the Best Improvement search strategy and an execution time limit of 2 min [14].
Table 5, Table 6, Table 7 and Table 8 contain the aggregated experimental results for Symmetric TSP instances. Specifically, they contain the benchmark name, the optimal value (zOpt), the cost of the three GVNS variations (GVNS_1, GVNS_2 and GVNS_3) and their corresponding gaps from the optimal value. Table 5 depicts GVNS using the First Improvement search strategy and an execution time limit of 1 min. Table 6 shows GVNS using the Best Improvement as search strategy and an execution time of 1 min. Table 7 and Table 8 are executed for 120 s within First and Best improvement search strategy respectively. The reported results show that the GVNS_3 produce better solutions than the other two algorithms, and that GVNS_1 and GVNS_2 do not have significant differences.

Table 5.
Results using the First Improvement search strategy and an execution time limit of 1 min.

Table 6.
Results using the Best Improvement search strategy and an execution time limit of 1 min.

Table 7.
Results using the First Improvement search strategy and an execution time limit of 2 min.

Table 8.
Results using the Best Improvement search strategy and an execution time limit of 2 min.
In some cases, GVNS_3 with a time limit of 1 min produced better results than using the 2 min time limit in solving sTSP instances. This might be happened due to the use of pure random diversification method such as the shuffle operator. More precisely, by executing more times GVNS_3, the shuffle operator is also executed more times and consequently it can shift the search into not so promising areas. Thus, the search may be trapped into low quality local optima.
Table 9, Table 10, Table 11 and Table 12 contain the aggregated experimental results for the National TSP instances. They contain the benchmark name, the optimal value (zOpt), the cost of the three GVNS algorithms (GVNS_1, GVNS_2 and GVNS_3) and the solution gaps from the optimal value for each method. Table 9 depicts GVNS using the First Improvement search strategy and an execution time limit of 1 min. Table 10 shows GVNS using the Best Improvement search strategy and an execution time limit of 1 min. Table 11 and Table 12 provide the results achieved by the developed GVNS algorithms with a 2 min time limit within the First and Best improvement search strategy respectively. A notable observation is that in general there are not any significant differences between different methods. However, we notice that on First Improvement for both 1 and 2 min GVNS_3 outperforms GVNS_1 and GVNS_2 implementations. Contrariwise, on Best Improvement all three methods perform better in general than on First Improvement. However, there is no significant difference between them.

Table 9.
Results using the First Improvement search strategy and an execution time limit of 1 min.

Table 10.
Results using the Best Improvement search strategy and an execution time limit of 1 min.

Table 11.
Results using the First Improvement search strategy and an execution time limit of 2 min.

Table 12.
Results using the Best Improvement search strategy and an execution time limit of 2 min.
4. Statistical Analysis on Computational Results
This section presents the statistical tests which were performed on the computational results, to evaluate the performance of the three different GVNS methods. Different statistical tests are applied to different data structures. In particular, statistical analysis methods can be divided on parametric and non-parametric tests. The first category examines normal variables whereas the other methods concern non-normal variables [20].
Initially, the application of a normality test showed that the numerical data does not follow the normal distribution. Consequently, we applied the Kruskal–Wallis test for checking the existence of a statistically significant difference between the methods. In this test receiving a p-value less than 0.05 means that there is a statistically significant difference.
At the present point, it should be mentioned that the statistical analysis was performed on median values to eliminate potential extreme deviation on the average values based on extreme values. Also, the related to the aTSP analysis is taken from our previous work [14] and it is presented here for building a more comprehensive view.
4.1. Statistical Analysis on aTSP Results
In Table 13 we can see that for all cases p-value is less than 0.05, which means that there is a statistically significant difference between the three methods in all cases. For further examination, pairwise Wilcoxon tests were performed.

Table 13.
Kruskal–Wallis rank sum test.
In accordance with the pairwise tests which are summarized in Table 14, it is clear that the GVNS_1 has significant differences with the other two schemes in all cases. Both GVNS_2 and GVNS_3 perform equivalently using the First Improvement search strategy independently of the execution time limit, while using the Best Improvement strategy they have significant reported differences with both time limits [14].

Table 14.
KPairwise comparisons using Wilcoxon signed rank test.
In respect to this Kruskal–Wallis statistical analysis, we have four box-plots illustrated in Figure 1a,b and Figure 2a,b four box plots. Each one depicts either First Improvement or Best Improvement for one minute, as well as for two minutes runs.
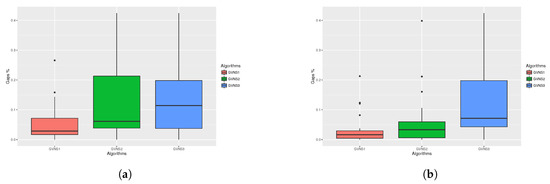
Figure 1.
Statistical test for aTSP (1/2). (a) Statistical test box plots for aTSP 1min FI; (b) Statistical test box plots for aTSP 1min BI.
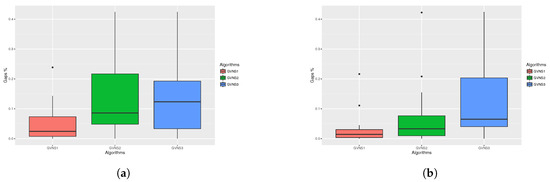
Figure 2.
Statistical test for aTSP (2/2). (a) Statistical test box plots for aTSP 2mins FI; (b) Statistical test box plots for aTSP 2mins BI.
Moreover, based on the corresponding of the previous statistical summary, box plots, it is confirmed that the GVNS_1 produces much better results than the other two algorithms in all cases for the aTSP, while the GVNS_2 outperform the GVNS_3 in also all cases. Also, by checking the medians at the box plots it can be seen that the GVNS_2 performs significantly better on Best Improvement, as it produces results that are “close" to the results of GVNS_1.
4.2. Statistical Analysis on sTSP
In this subsection the statistical analysis on the results achieved by the three GVNS schemes on sTSP instances is provided.
According to the values in Table 15 we can see that only using the Best Improvement search strategy within a 2 min execution time limit, there are statistically significant differences.

Table 15.
Kruskal–Wallis rank sum test.
More specifically, the values in Table 16 highlights that there is a difference between the GVNS_1 and the other two GVNS algorithms. In particular, based on the following box plots, the GVNS_1 is slightly better than the GVNS_2 and GVNS_3, which they perform almost equivalently.

Table 16.
KPairwise comparisons using Wilcoxon signed rank test.
Subsequently of this Kruskal–Wallis statistical analysis, we have four box-plots illustrated in Figure 3a,b and Figure 4a,b four box plots. Each one depicts either First Improvement or Best Improvement for one minute, as well as for two minutes runs.
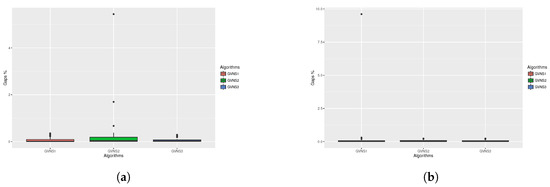
Figure 3.
Statistical test for sTSP (1/2). (a) Statistical test box plots for sTSP 1min FI; (b) Statistical test box plots for sTSP 1min BI.
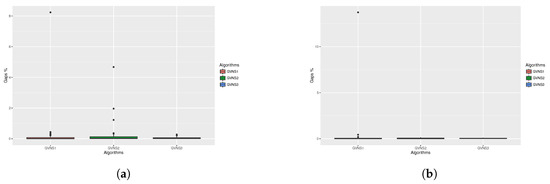
Figure 4.
Statistical test for sTSP (2/2). (a) Statistical test box plots for sTSP 2min FI; (b) Statistical test box plots for sTSP 2min BI.
4.3. Statistical Analysis on nTSP
In the case of the National TSP instances and based on the values given in Table 17 we can see that there is no significant statistical difference between the three methods.

Table 17.
Kruskal–Wallis rank sum test.
As a result of this Kruskal–Wallis statistical analysis, we have four box-plots illustrated in Figure 5a,b and Figure 6a,b four box plots. Each one depicts either First Improvement or Best Improvement for one minute, as well as for two minutes runs. By checking the median value of each method, it is clear that the three algorithms perform equivalently.
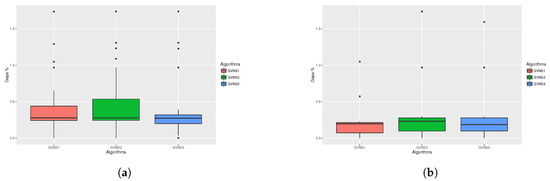
Figure 5.
Statistical test for nTSP (1/2). (a) Statistical test box plots for nTSP 1min FI; (b) Statistical test box plots for nTSP 1min BI.
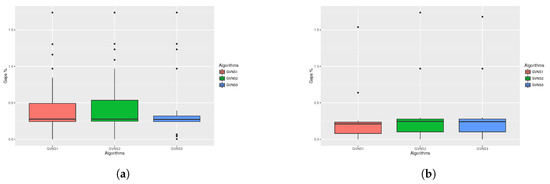
Figure 6.
Statistical test for nTSP (2/2). (a) Statistical test box plots for nTSP 2min FI; (b) Statistical test box plots for nTSP 2min BI
5. Comparison with Recent Similar Works
In their recent work, Halim et al. have presented an extensive analysis over the performance of different heuristic and metaheuristic algorithms on some TSPLib instances [21]. In addition, Hore et al. [22] proposed an improved hybrid VNS algorithm for solving TSP instances. In this section, a comparison between our proposed GVNS schemes (GVNS_1 and GVNS_2) and those algorithms presented on papers [21,22] is performed.
Table 18 shows the comparison between our GVNS_1 and GVNS_2, within the Best Improvement search strategy and a time limit of 120 s, with all metaheuristic solution approaches presented in the work of Halim et al. [21]. The results show that our methods produce better results than the previously mentioned metaheuristics, except the case of instance rat195.tsp in which the GA and the TS perform better than GVNS_2.

Table 18.
Comparisons between GVNS_1 and GVNS_2 with BI for 2mins with the recent work of Halim et al.
Table 19 shows the comparison between our GVNS_1 and GVNS_2, within the Best Improvement search strategy and a time limit of 120 s with the results obtained by a hybrid VNS in the second mentioned work [22]. It is clearly observed that our methods outperform the hybrid VNS. More specifically, the GVNS_1 outperforms the hybrid VNS algorithm in all tested instances, while the GNVS_2 produce better results than those achieved by Hore et al. approach in seven out of 10 problem instances.

Table 19.
Comparisons between GVNS_1 and GVNS_2 with BI for 2 mins with the recent VNS work of Hore et al.
Table 20 shows the abbreviations regarding the metaheuristic algorithms presented in [21].

Table 20.
Abbreviations.
6. Conclusions and Future Work
A thorough and comprehensive performance analysis on the efficiency of three GVNS algorithms has been presented in this work. The main difference lies on the perturbation strategy used. Our comparative performance analysis involves problems that are modelled as asymmetric and Symmetric TSP instances that are resolved using GVNS. The well-known TSP benchmarks from the TSPLIB are used for extensive experimental testing. We believe that the experimental results are quite conclusive, as they confirm that for asymmetric TSP instances GVNS_1 outperforms the other two methods and GVNS_2 consistently provides better solutions in all cases compared to GVNS_3. Simultaneously, the perturbation strategy does not seem to critically affect the solutions of Symmetric TSP instances.
It is also worth emphasizing that even though the improvement stage of the GVNS schemes has been given limited attention, the present paper shows that the tested approaches to the solution, can be quite promising. This is justified by the solutions produced, which are significantly better than other metaheuristic approaches in recent literature.
The investigation of alternative neighborhood structures and neighborhood change movements in VND under the GVNS framework could be a possible direction for future work. In the same vein, one might potentially study modifications or specific combinations with more than one perturbation strategy during the perturbation phase in an effort to determine whether optimal solutions can be achieved even closer, especially on large asymmetric benchmarks.
Author Contributions
All of the authors have contributed extensively to this work. C.P. and P.K. conceived the initial algorithm and worked on the first prototypes. P.K. and C.P. thoroughly analyzed the current literature gathering all the necessary material. T.A. assisted C.P. in designing the methods used in the main part. T.A. was responsible for supervising the construction of this work. C.P. was responsible for the interlinking between the theoretic model and the actual application. C.P. contributed to the appropriate typing of the formal definitions and the math used in the paper.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| TSP | Traveling Salesman Problem |
| VNS | Variable Neighborhood Search |
| GVNS | General Variable Neighborhood Search |
| GA | Genetic Algorithm |
| SA | Simulated Annealing |
| TS | Tabu Search |
| ACO | Ant Colony Optimization |
| TPO | Tree Physiology Optimization |
References
- Mladenovic, N.; Hansen, P. Variable neighborhood search. Comput. Oper. Res. 1997, 24, 1097–1100. [Google Scholar] [CrossRef]
- Hansen, P.; Mladenovic, N.; Todosijevic, R.; Hanafi, S. Variable neighborhood search: Basics and variants. EURO J. Comput. Optim. 2017, 5, 423–454. [Google Scholar] [CrossRef]
- Mladenovic, N.; Todosijevic, R.; Uroševic, D. Less is more: Basic variable neighborhood search for minimum differential dispersion problem. Inf. Sci. 2016, 326, 160–171. [Google Scholar] [CrossRef]
- Mladenović, N.; Sifaleras, A.; Sörensen, K. Editorial to the Special Cluster on Variable Neighborhood Search, Variants and Recent Applications. Int. Trans. Oper. Res. 2017, 24, 507–508. [Google Scholar] [CrossRef]
- Karakostas, P.; Sifaleras, A.; Georgiadis, C. Basic VNS algorithms for solving the pollution location inventory routing problem. In Proceedings of the LNCS Proc. of the 6th International Conference on Variable Neighborhood Search (ICVNS 2018), Sithonia, Greece, 4–7 October 2018; Sifaleras, A., Salhi, S., Brimberg, J., Eds.; Springer: Berlin, Germany, 2019; Volume 11328. [Google Scholar]
- Karakostas, P.; Sifaleras, A.; Georgiadis, C. A general variable neighborhood search-based solution approach for the location-inventory-routing problem with distribution outsourcing. Comput. Chem. Eng. 2019, 126, 263–279. [Google Scholar] [CrossRef]
- Papalitsas, C.; Karakostas, P.; Andronikos, T.; Sioutas, S.; Giannakis, K. Combinatorial GVNS (General Variable Neighborhood Search) Optimization for Dynamic Garbage Collection. Algorithms 2018, 11, 38. [Google Scholar] [CrossRef]
- Sifaleras, A.; Konstantaras, I. General variable neighborhood search for the multi-product dynamic lot sizing problem in closed-loop supply chain. Electron. Notes Discret. Math. 2015, 47, 69–76. [Google Scholar] [CrossRef]
- Sifaleras, A.; Konstantaras, I. Variable neighborhood descent heuristic for solving reverse logistics multi-item dynamic lot-sizing problems. Comput. Oper. Res. 2017, 78, 385–392. [Google Scholar] [CrossRef]
- Silva, M.A.; Souza, S.R.; Souza, M.J.; Filho, M.F.F. Hybrid metaheuristics and multi-agent systems for solving optimization problems A review of frameworks and a comparative analysis. Appl. Soft Comput. 2018, 71, 433–459. [Google Scholar] [CrossRef]
- Duan, Q.; Liao, T.; Yi, H. A comparative study of different local search application strategies in hybrid metaheuristics. Appl. Soft Comput. 2013, 13, 1464–1477. [Google Scholar] [CrossRef]
- Huber, S.; Geiger, M.J. Order matters–A Variable Neighborhood Search for the Swap-Body Vehicle Routing Problem. Eur. J. Oper. Res. 2017, 263, 419–445. [Google Scholar] [CrossRef]
- Papalitsas, C.; Giannakis, K.; Andronikos, T.; Theotokis, D.; Sifaleras, A. Initialization methods for the TSP with Time Windows using Variable Neighborhood Search. In Proceedings of the IEEE Proc. of the 6th International Conference on Information, Intelligence, Systems and Applications (IISA 2015), Corfu, Greece, 6–8 July 2015. [Google Scholar]
- Papalitsas, C.; Karakostas, P.; Andronikos, T. Studying the impact of perturbation methods on the efficiency of GVNS for the ATSP. In LNCS Proc. of the 6th International Conference on Variable Neighborhood Search (ICVNS 2018), Sithonia, Greece, 4–7 October 2018; Sifaleras, A., Salhi, S., Brimberg, J., Eds.; Springer: Berlin, Germany, 2019; Volume 11328. [Google Scholar]
- Papalitsas, C.; Karakostas, P.; Kastampolidou, K. A Quantum Inspired GVNS: Some Preliminary Results; Vlamos, P., Ed.; GeNeDis 2016; Springer International Publishing: Cham, Switzerland, 2017; pp. 281–289. [Google Scholar]
- Nunes, D.C.L. Fundamentals of Natural Computing: Basic Concepts, Algorithms, and Applications; Chapman & Hall/CRC: Boca Raton, FL, USA, 2006. [Google Scholar]
- Dey, S.; Bhattacharyya, S.; Maulik, U. New quantum inspired meta-heuristic techniques for multi-level colour image thresholding. Appl. Soft Comput. 2016, 46, 677–702. [Google Scholar] [CrossRef]
- Feynman, R.P. Simulating physics with computers. Int. J. Theor. Phys. 1982, 21, 467–488. [Google Scholar] [CrossRef]
- Feynman, R.P.; Hey, J.; Allen, R.W. Feynman Lectures on Computation; Longman Publishing Co., Inc.: Cambridge, MA, USA, 1998. [Google Scholar]
- Coffin, M.; Saltzman, M.J. Statistical Analysis of Computational Tests of Algorithms and Heuristics. INFORMS J. Comput. 2000, 12, 24–44. [Google Scholar] [CrossRef]
- Halim, A.H.; Ismail, I. Combinatorial optimization: Comparison of heuristic algorithms in travelling salesman problem. Arch. Comput. Methods Eng. 2019, 26, 367–380. [Google Scholar] [CrossRef]
- Hore, S.; Chatterjee, A.; Dewanji, A. Improving variable neighborhood search to solve the traveling salesman problem. Appl. Soft Comput. 2018, 68, 83–91. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).