Model-Free Robotic Architecture with Task-Multiplexer and Discrete-Time Adaptive Control
Abstract
:1. Introduction
- The design of the controller requires only the relation between the input and output of robotic systems within the format of IF-THEN rules, according to basic human knowledge. Unlike the model-free approaches in [10,24], the covariance matrix and the qualitative dynamic system are not required in this work.
2. Problem Formulation
3. Identification of an Equivalent Model
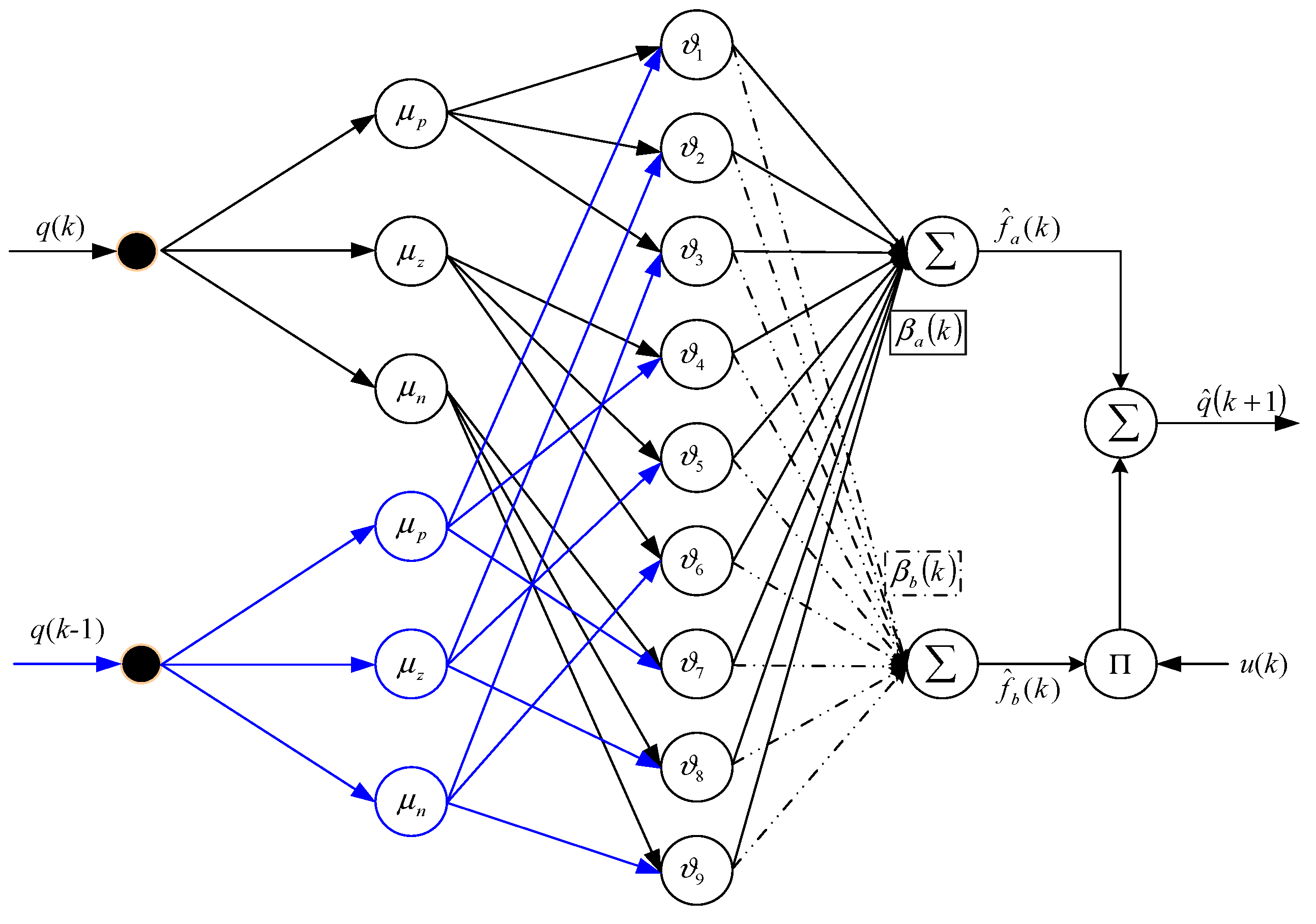
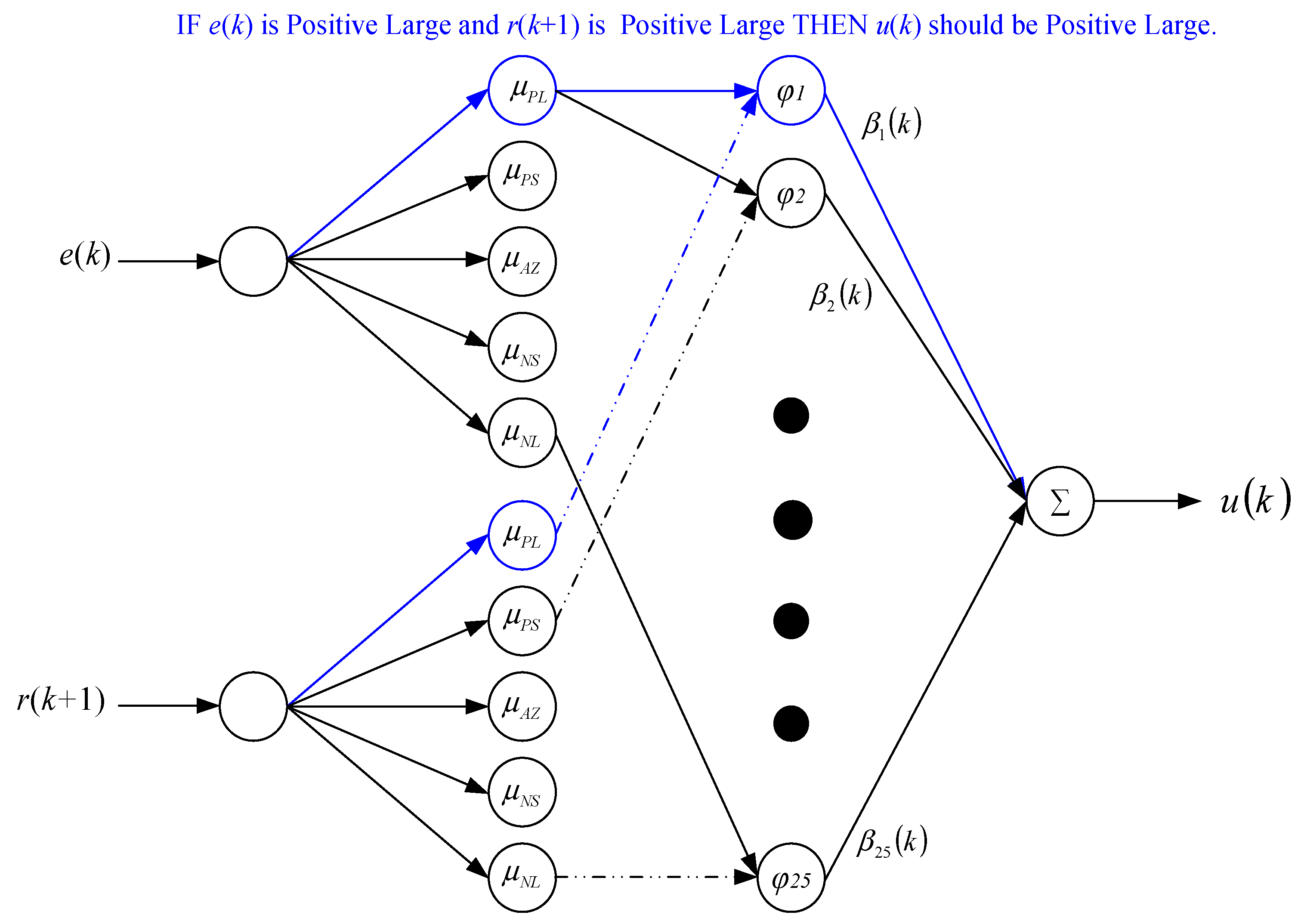
4. MiFREN Adaptive Control and Closed-Loop Analysis
4.1. MiFREN Adaptive Controller
4.2. Adaptive Algorithm and Closed Loop Analysis
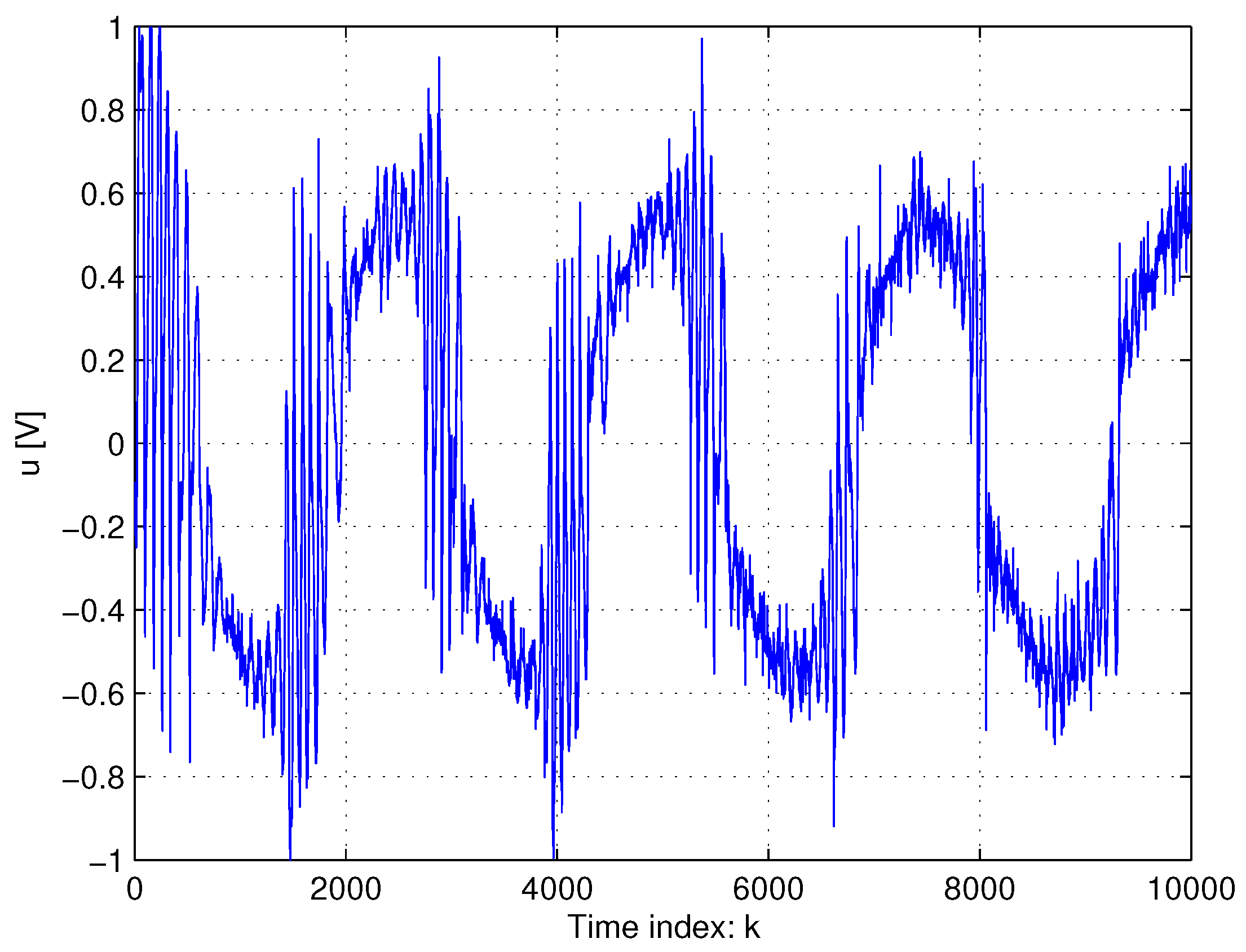
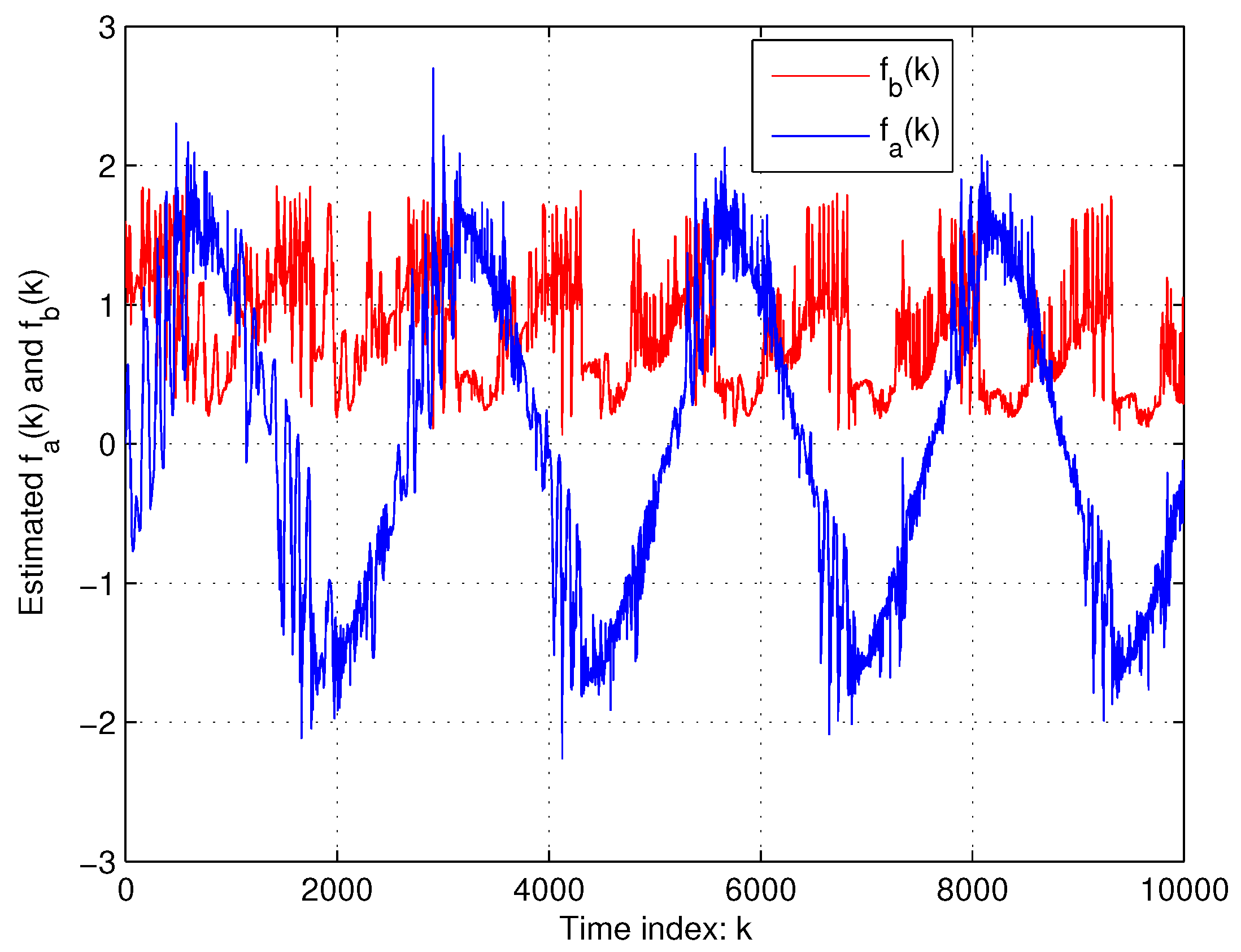
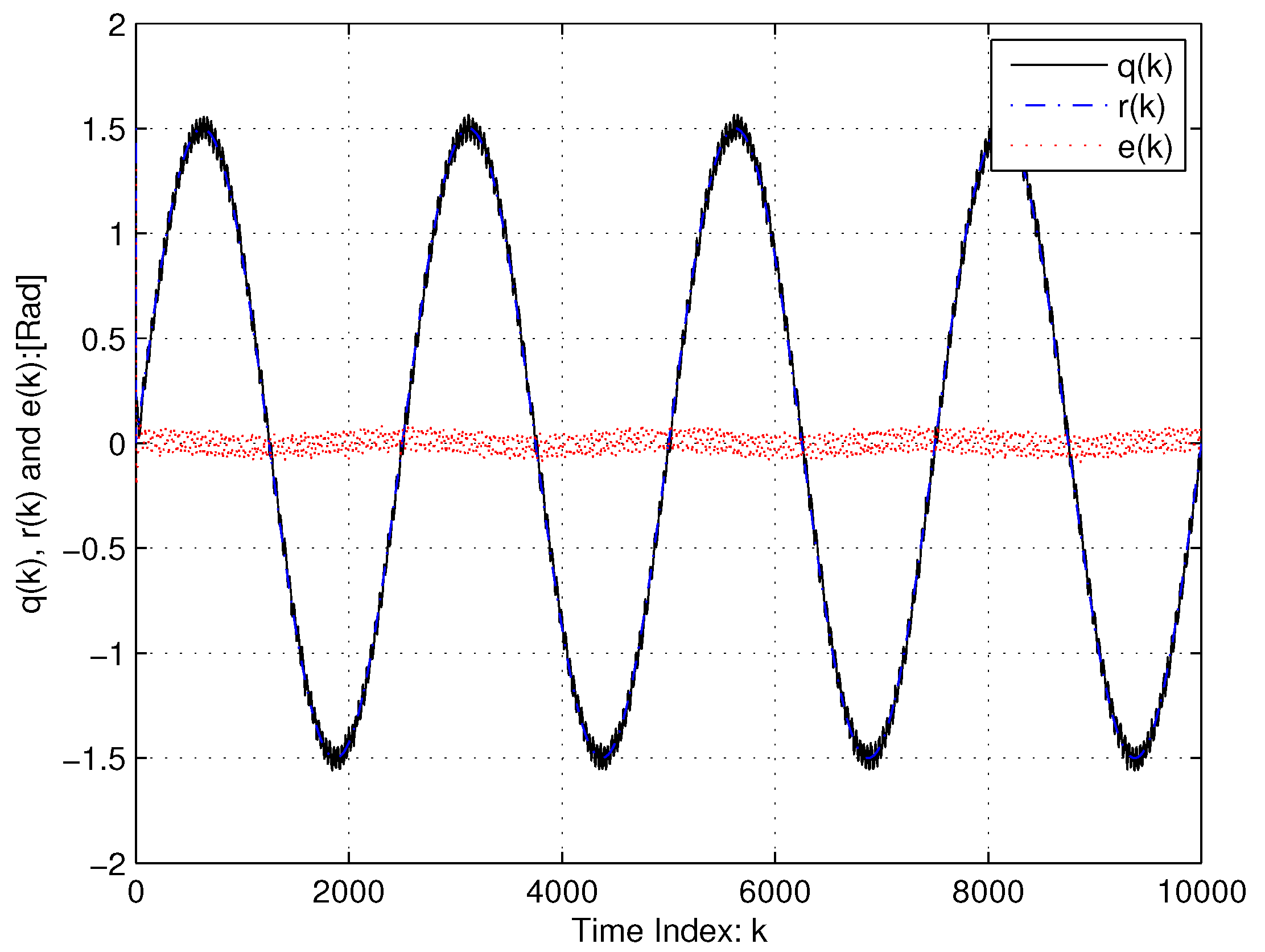
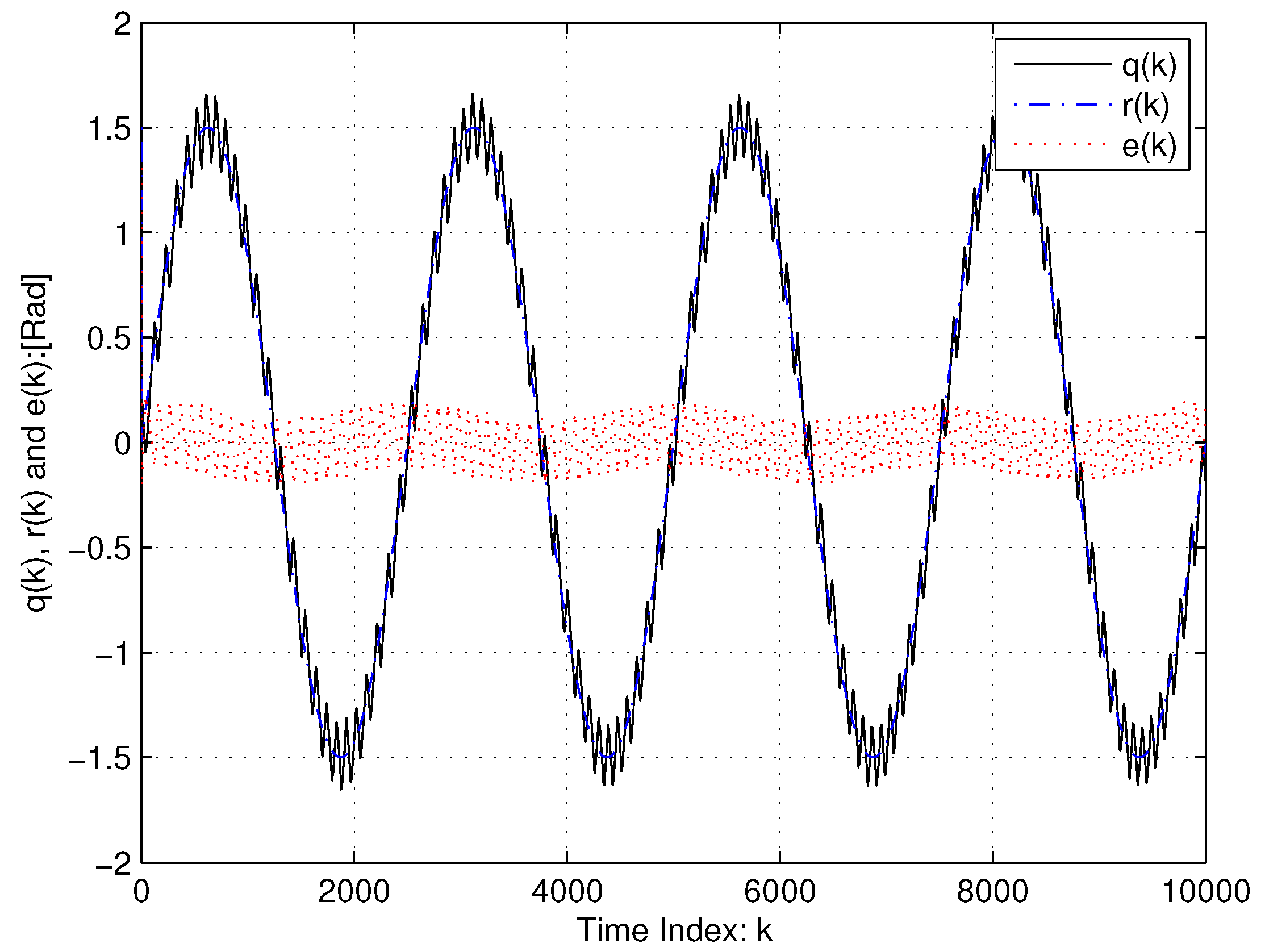
5. Experimental Results
6. Conclusions
Funding
Conflicts of Interest
References
- Mohammad, A.-E.K.; Hong, J.; Wang, D. Design of a force-controlled end-effector with low-inertia effect for robotic polishing using macro-mini robot approach. Robot. Comput. Integr. Manuf. 2018, 49, 54–65. [Google Scholar] [CrossRef]
- Zheng, M. Control Framework for a Macro/Mini Manipulator. Ph.D. Thesis, National University of Singapore, Singapore, 2018. [Google Scholar]
- Wang, H.; Jiang, N.; Liu, T.; Cao, Y. Adaptive stable control of manipulator system based on immersion and invariance. Math. Model. Anal. 2018, 23, 379–389. [Google Scholar] [CrossRef]
- Markus, E.D.; Agee, J.T.; Jimoh, A.A. Flat control of industrial robotic manipulators. Robot. Auton. Syst. 2017, 87, 226–236. [Google Scholar] [CrossRef]
- Sankar, S.; Tsai, C.Y. ROS-based human detection and tracking from a wireless controlled mobile robot using kinect. Appl. Syst. Innov. 2019, 2, 5. [Google Scholar] [CrossRef]
- Martinez-Prado, M.A.; Resendiz, J.R.; Gomez-Loenzo, R.A.; Herrera-Ruiz, G.; Franco-Gasca, L.A. An FPGA-Based open architecture industrial robot controller. IEEE Access 2018, 6, 13407–13417. [Google Scholar] [CrossRef]
- Alabdo, A.; Javier, P.; Garcia, G.J.; Pomares, J.; Torres, F. FPGA-based architecture for direct visual control robotic systems. Mechatronics 2016, 39, 204–216. [Google Scholar] [CrossRef]
- Treesatayapun, C. A data-driven adaptive controller for a class of unknown nonlinear discrete-time systems with estimated PPD. Eng. Sci. Technol. Int. J. 2015, 18, 218–228. [Google Scholar] [CrossRef]
- Zhu, Y.; Hou, Z.S. Data-driven MFAC for a class of discrete-time nonlinear systems with RBFNN. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 1013–1020. [Google Scholar] [PubMed]
- Minhan, L.; Rongjie, K.; Branson, D.T.; Dai, J.S. Model-free control for continuum robots based on an adaptive Kalman filter. IEEE/ASME Trans. Mechatron. 2018, 23, 286–297. [Google Scholar]
- Chi, R.; Hou, Z.; Jin, S. A data-driven adaptive ILC for a class of nonlinear discrete-time systems with random initial states and iteration-varying target trajectory. J. Frankl. Inst. 2015, 352, 2407–2424. [Google Scholar] [CrossRef]
- Bu, X.; Qiao, Y.; Hou, Z.; Yang, J. Model free adaptive control for a class of nonlinear systems using quantized information. Asian J. Control 2018, 20, 1–7. [Google Scholar] [CrossRef]
- Treesatayapun, C. Data input-output adaptive controller based on IF-THEN rules for a class of non-affine discrete-time systems: The robotic plant. J. Intell. Fuzzy Syst. 2015, 28, 661–668. [Google Scholar]
- Treesatayapun, C. Adaptive control based on IF-THEN rules for grasping force regulation with unknown contact mechanism. Robot. Comput. Integr. Manuf. 2014, 30, 11–18. [Google Scholar] [CrossRef]
- Chen, C.; Wen, C.; Liu, Z.; Xie, K.; Zhang, Y.; Philip-Chen, C.L. Adaptive consensus of nonlinear multi-agent systems with non-identical partially unknown control directions and bounded Modelling errors. IEEE Trans. Autom. Control 2017, 62, 4654–4659. [Google Scholar] [CrossRef]
- Sarangapani, J. Neural Network Control of Nonlinear Discrete-Time Systems; CRC Press: New York, NY, USA, 2006. [Google Scholar]
- Hosseinzadeh, S.; Larijani, H.; Curtis, K.; Wixted, A. An adaptive neuro-fuzzy propagation model for LoRaWAN. Appl. Syst. Innov. 2019, 2, 10. [Google Scholar] [CrossRef]
- Treesatayapun, C.; Uatrongjit, S. Adaptive controller with Fuzzy rules emulated structure and its applications. Eng. Appl. Artif. Intell. 2005, 18, 603–615. [Google Scholar] [CrossRef]
- Beechner, T.L.; Carpenter, A.L. A >98% efficient >150 kRPM high-temperature liquid-cooled SiC VFD for hybrid-electric turbochargers. In Proceedings of the 2017 IEEE Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA, 26–30 March 2017; pp. 3674–3680. [Google Scholar]
- Shenoy, P.; Solis, O.; Zheng, L. Commereializing medium voltage VFD that utilizes high voltage SiC technology. In Proceedings of the 2017 IEEE International Workshop on Integrated Power Packaging (IWIPP), Delft, The Netherlands, 5–7 April 2017. [Google Scholar]
- Guo, C.; Zhang, A.; Zhang, H.; Zhang, L. Adaptive backstepping control with online parameter estimator for a plug-and-play parallel converter system in a power switcher. Energies 2018, 11, 3528. [Google Scholar] [CrossRef]
- Das, K.; Srinivas, M.N.; Madhusudanan, V.; Pinelas, S. Mathematical analysis of a prey–predator system: An adaptive back-stepping control and stochastic approach. Math. Comput. Appl. 2019, 24, 22. [Google Scholar] [CrossRef]
- Rodriguez, M.D.; Valera, A.; Mata, V.; Valles, M. Model-based control of a 3-DOF parallel robot based on identified relevant parameters. IEEE/ASME Trans. Mechatron. 2013, 18, 1737–1744. [Google Scholar] [CrossRef]
- Yang, X.; Ge, S.S.; Liu, J. Dynamics and noncollocated model-free position control for a space robot with multi-link flexible manipulators. Asian J. Control 2019, 21, 1–11. [Google Scholar] [CrossRef]




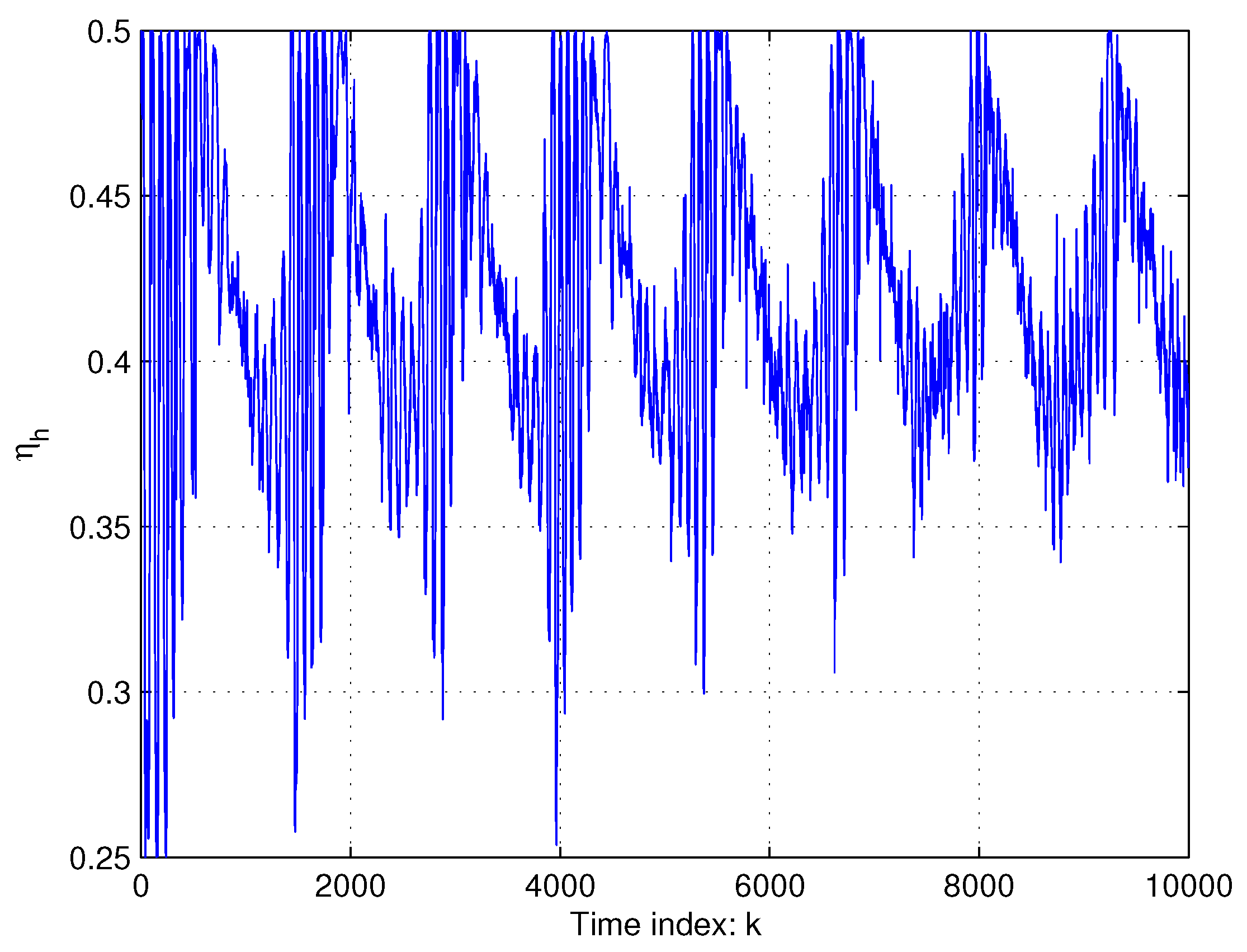
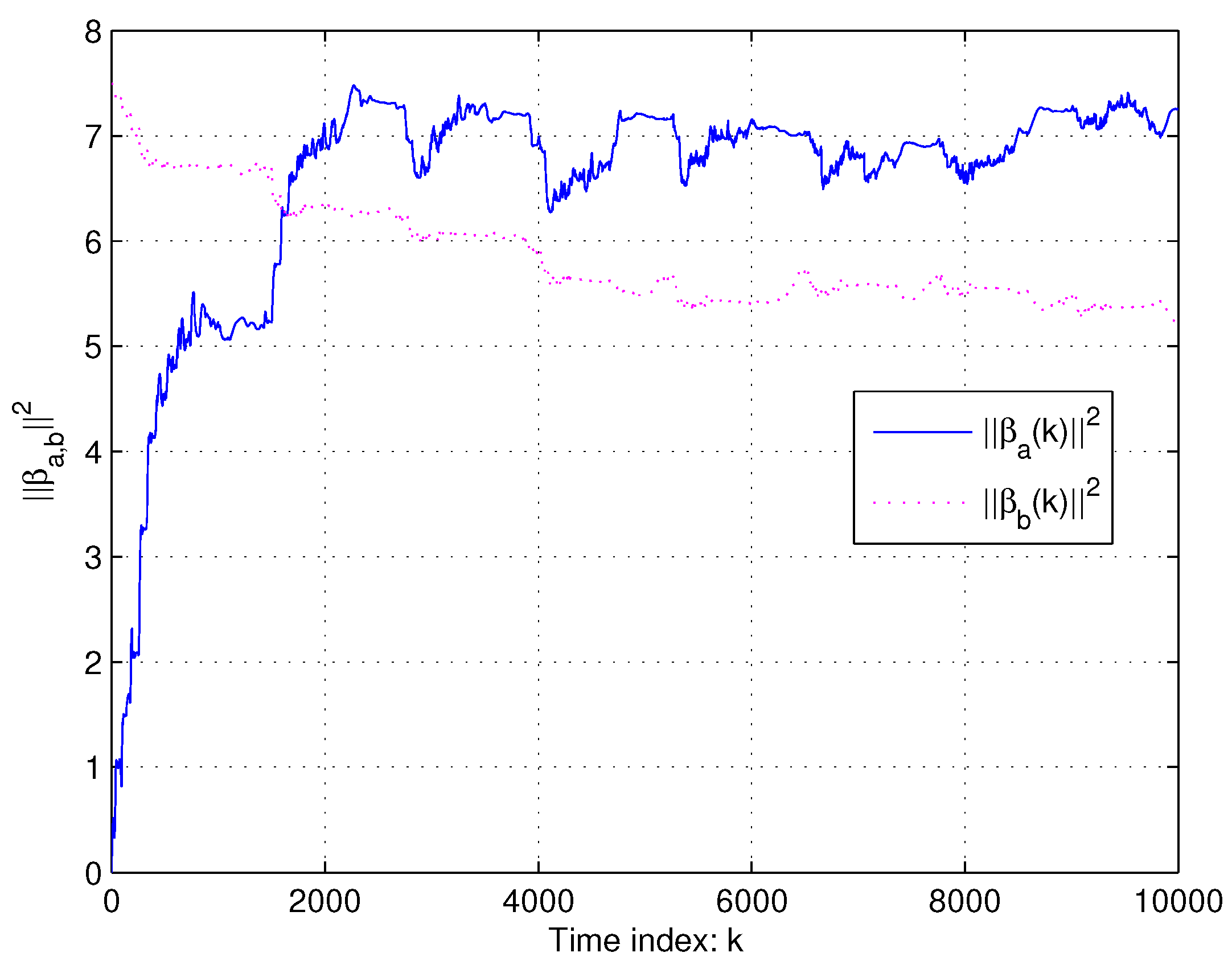
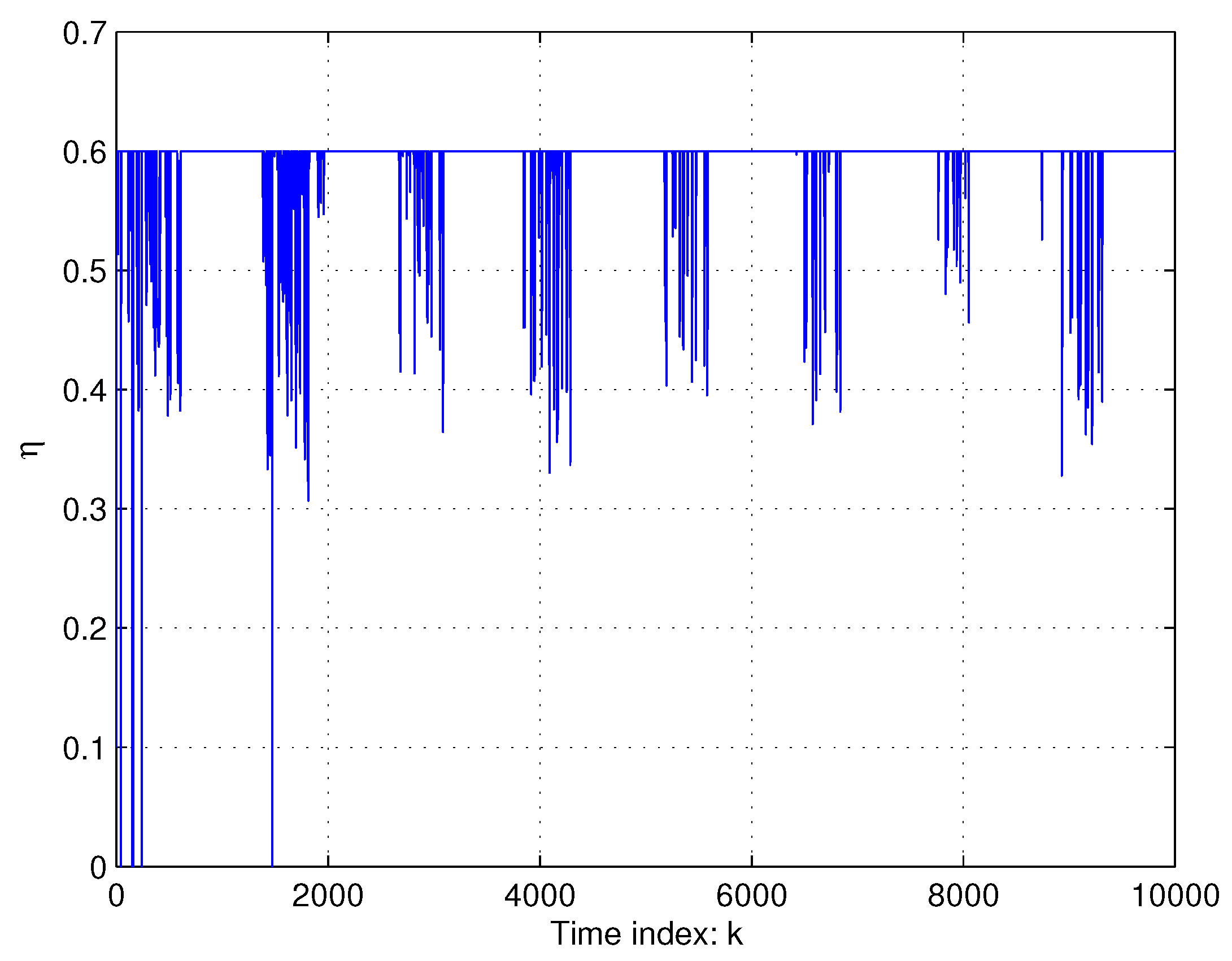

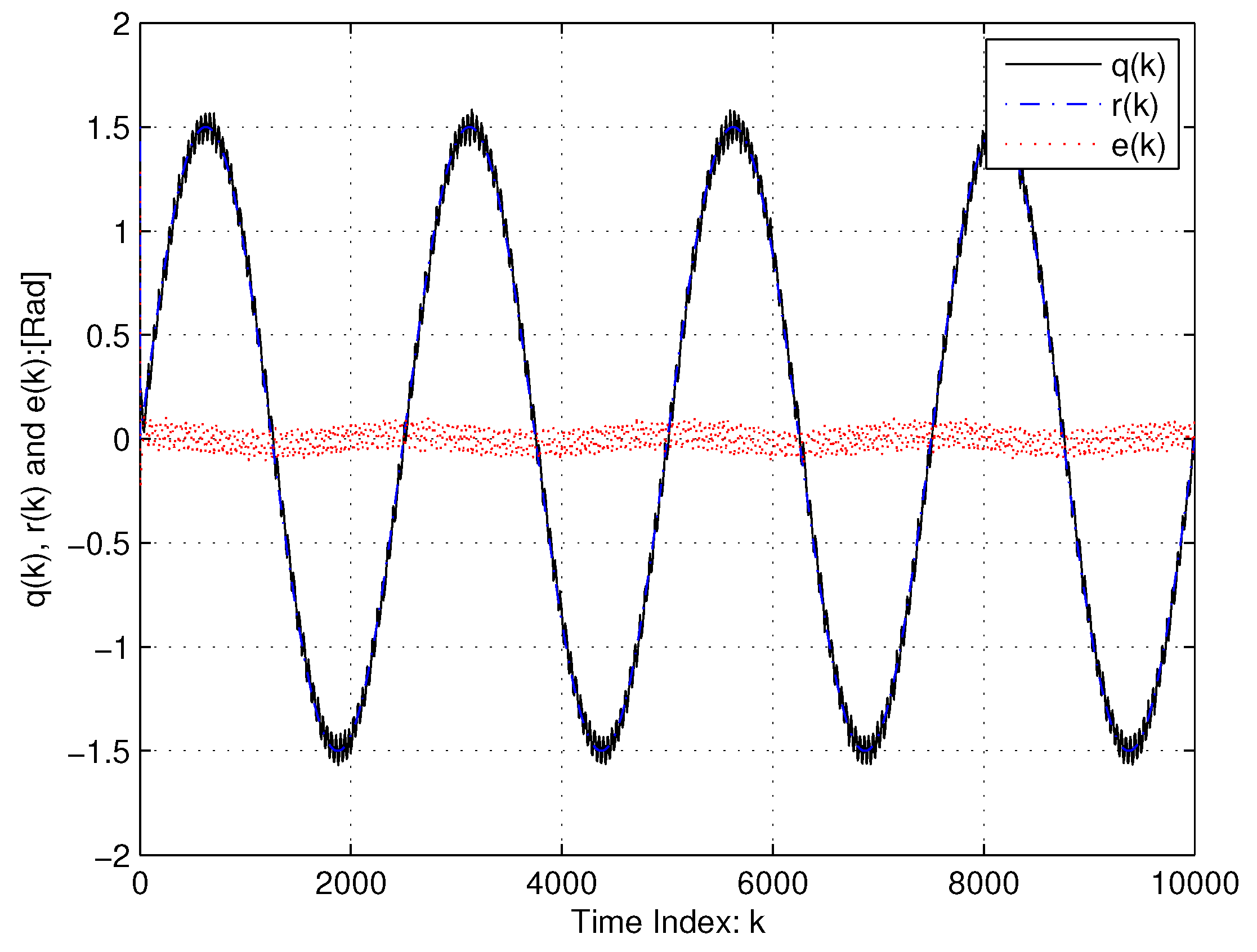
| Joint | |||
|---|---|---|---|
| 1 | 5.26 | 0.36 | 0.11 |
| 2 | 8.74 | 0.27 | 0.11 |
| 3 | 13.91 | 0.21 | 0.17 |
| 4 | 2.72 | 0.11 | 0.14 |
| 5 | 6.83 | 0.13 | 0.12 |
| 6 | 4.85 | 0.07 | 0.12 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Treesatayapun, C. Model-Free Robotic Architecture with Task-Multiplexer and Discrete-Time Adaptive Control. Appl. Syst. Innov. 2019, 2, 12. https://doi.org/10.3390/asi2020012
Treesatayapun C. Model-Free Robotic Architecture with Task-Multiplexer and Discrete-Time Adaptive Control. Applied System Innovation. 2019; 2(2):12. https://doi.org/10.3390/asi2020012
Chicago/Turabian StyleTreesatayapun, Chidentree. 2019. "Model-Free Robotic Architecture with Task-Multiplexer and Discrete-Time Adaptive Control" Applied System Innovation 2, no. 2: 12. https://doi.org/10.3390/asi2020012
APA StyleTreesatayapun, C. (2019). Model-Free Robotic Architecture with Task-Multiplexer and Discrete-Time Adaptive Control. Applied System Innovation, 2(2), 12. https://doi.org/10.3390/asi2020012





