2.1. Multipath System-Level Models
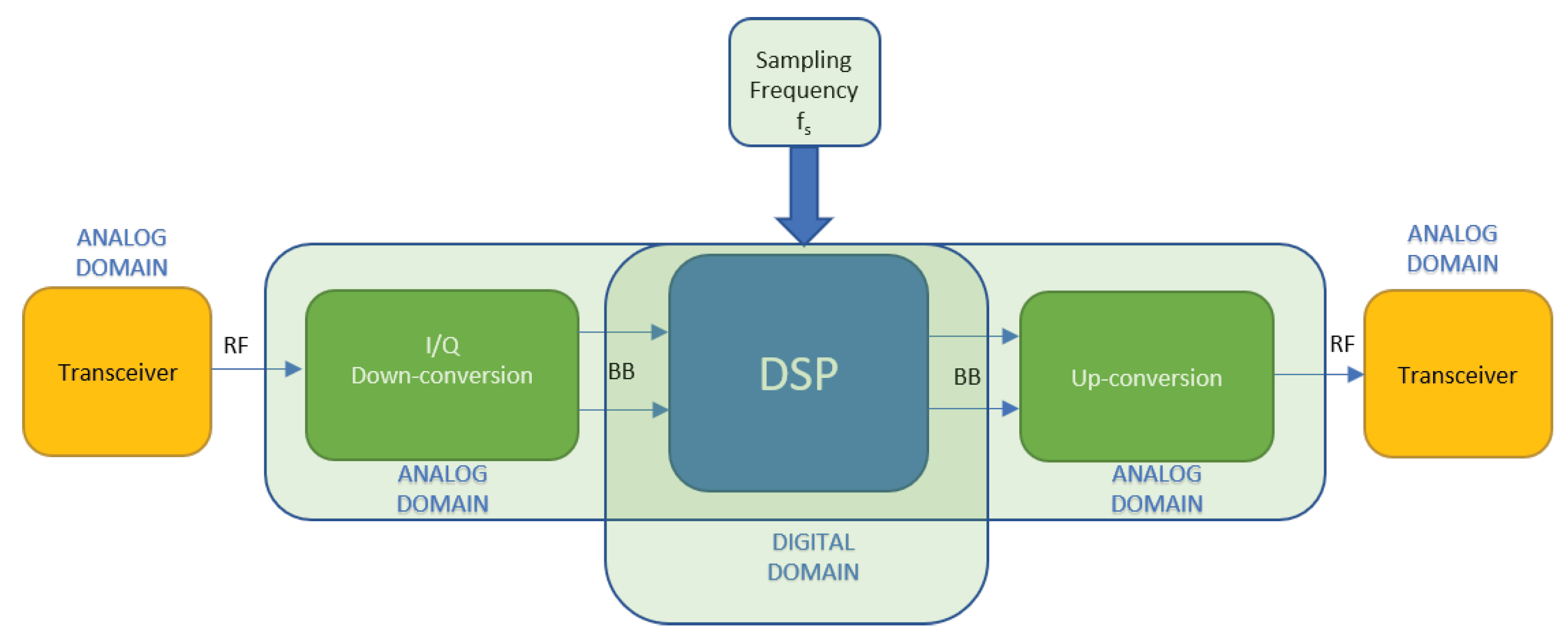
A general system-level schematic for a RF channel emulator can be synthesized as in
Figure 1.
The system consists of a transmitter under test, a receiver and a channel emulation block having a number of key tasks to perform. The RF analog signal undergoes a down-conversion with the extraction of the in phase and quadrature components. The subsequent band-limited analog signal is sampled and processed in a specialized Digital Signal Processing unit (DSP) in order to introduce all the impairments typically present in a real propagation channel. These phenomena include the time-dependent attenuation, additive gaussian noise, jammers, Doppler spread and many others. The modified signal undergoes a digital-to-analog conversion and an up-conversion to be injected into the receiver. It has been investigated here with particular emphasis on the presence of time-variant delays due to a multipath propagation. Bearing in mind this aspect, with reference to
Figure 1, the generic RF signal coming from the transceiver under test can be written as [
2]
in which appear the envelope module
, the instantaneous phase
(t) of the modulating signal and the carrier angular frequency
. The transit of the signal in Equation (
1) through a delay line of
seconds generates a new signal
y(t) of the type:
The complex envelope of the signal in Equation (
2), with respect to the angular frequency
is equal to:
Equation (
3) allows the processing of the signal in Equation (
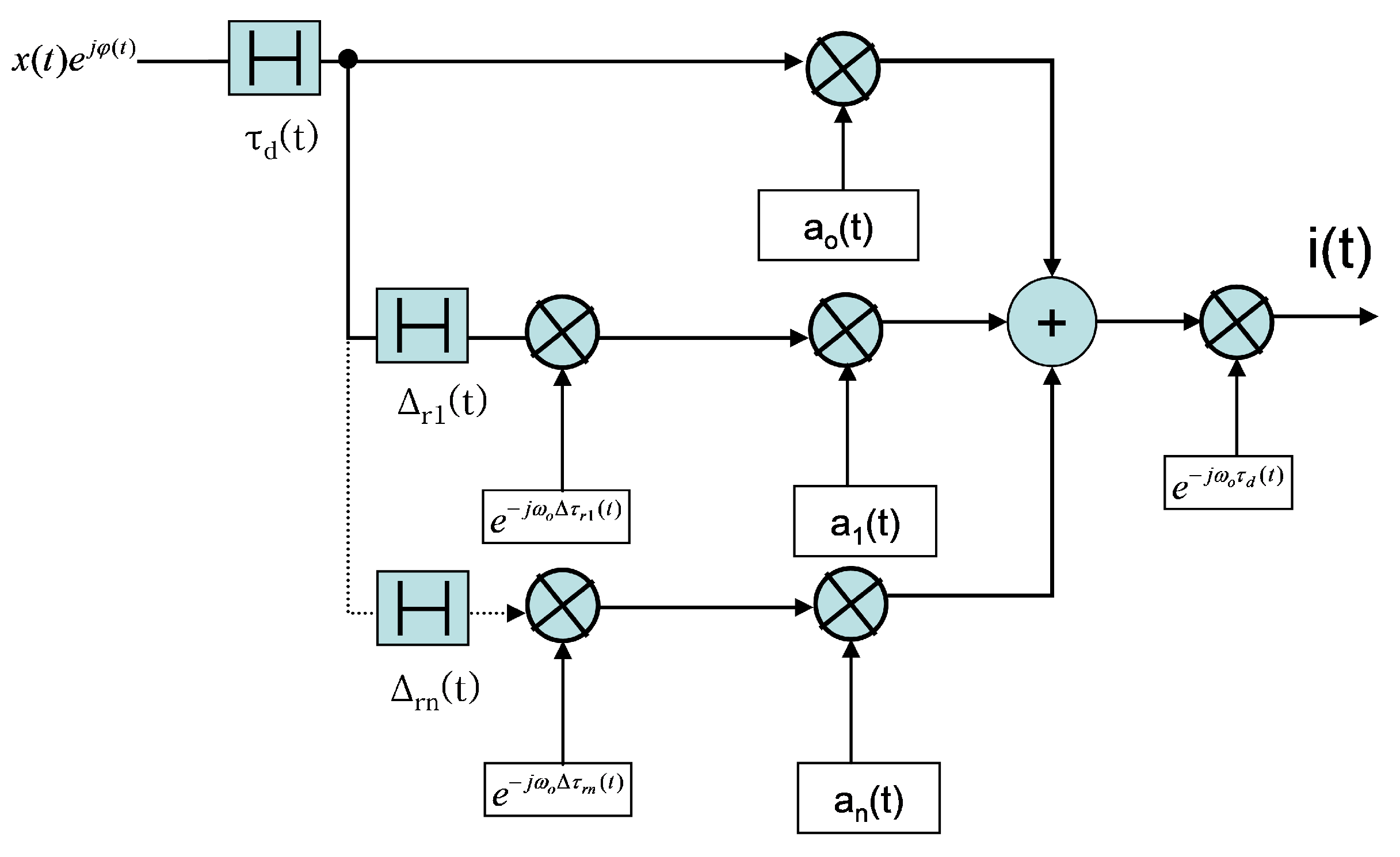
1) using directly its equivalent low frequency representation. When multipath is present, it can be correctly represented at complex envelope level as in
Figure 2, where the complex envelope of the signal affected by multipath propagation is seen as the sum of the contributions coming from
n discrete independent paths, each affected by a time-dependent delay and a time-dependent attenuation. The direct path is characterized by an absolute delay starting from the initial observation time. The remaining paths are affected not only by the main delay, but also by differential delays (small) with respect to the latter:
with
equal to the distance (instantaneous) travelled by the direct path between transmitter and receiver;
m/s equal to the speed of light;
equal to the difference between the k-th path and the direct path.
By correctly emulating the behavior of the attenuations and the delays over time, the diagram in
Figure 2 is able to correctly reproduce both fading and Doppler shift over the entire signal band, assuming the existence of a
discrete number of independent paths [
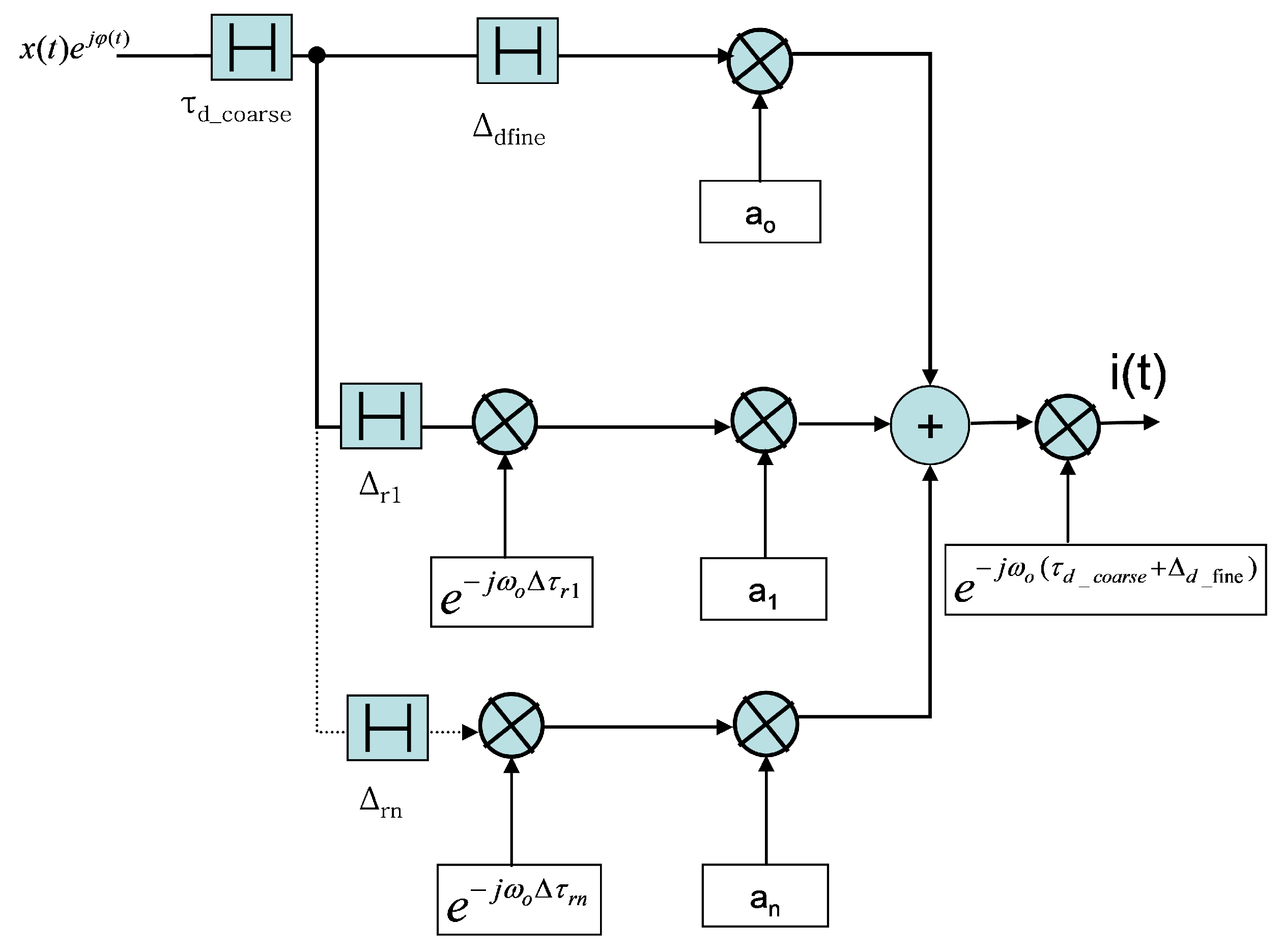
3]. In the perspective of a discrete-time realization, the scheme in
Figure 3 considers the amplitudes and delays of each path as constants for sufficiently representative time intervals [
4].
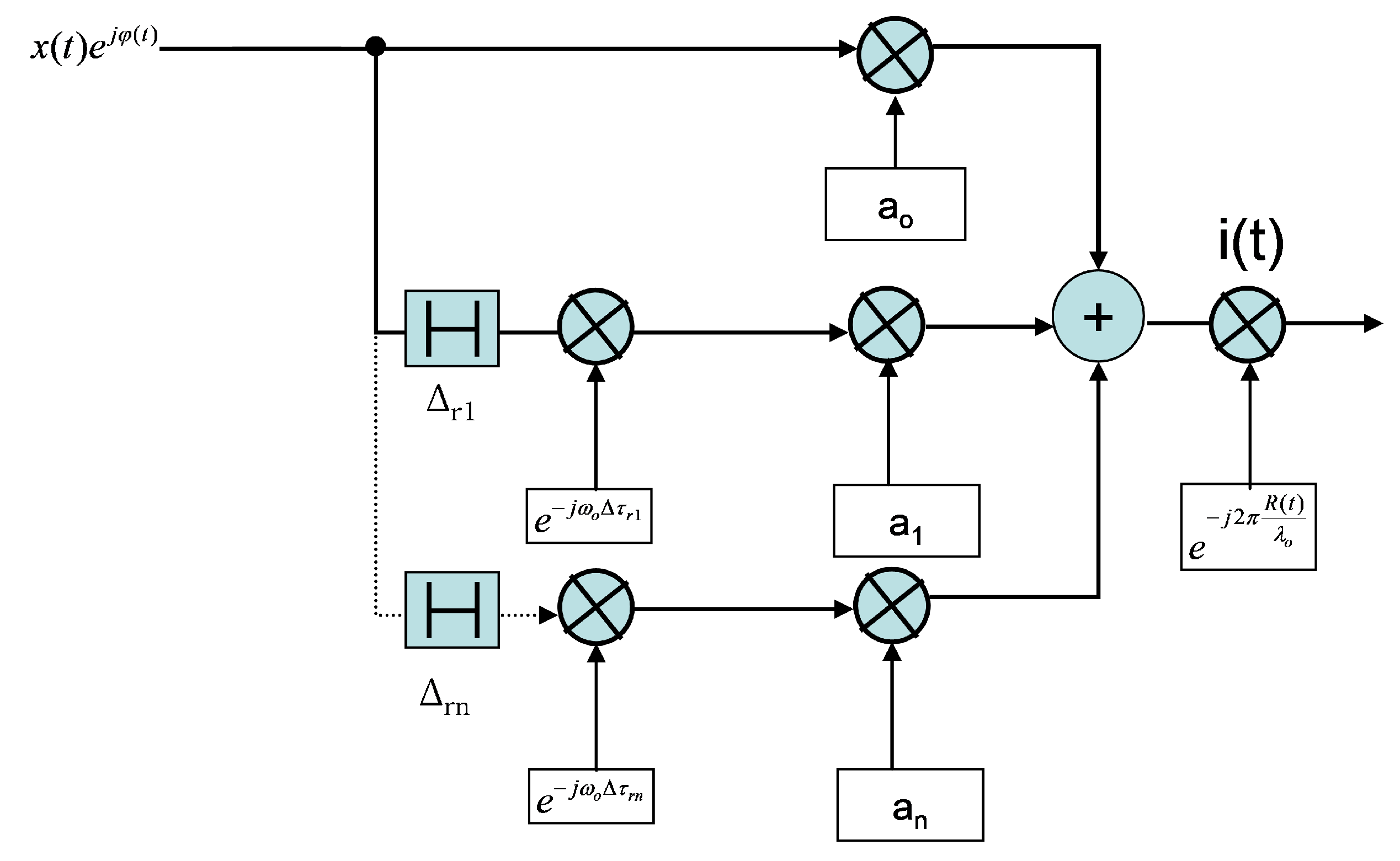
If we renounce to the complete emulation of the time-dependant delay of the direct path, losing therefore the absolute Doppler information, we arrive at the scheme in
Figure 4.
In this last scheme, the Doppler shift is the one related to the frequency and depends directly on the law of variation of the direct path, with the addition of the spreading due to the variations of the delays of the reflected paths.
RF propagation in mobile channels is a very complex matter and several channel models have been developed, based on a statistical approach [
5]. Narrowband channel emulators implementation have been proposed [
6] and low-complexity architectures have been developed dealing with delays that are not integer multiples of the sampling rate [
7] or solutions where massive calculations are demanded to a GPU (Graphical Processing Unit) using native highly parallelized architecture [
8].
2.2. Required Sampling Step Size for the Emulation of the Effects of the Electromagnetic Propagation
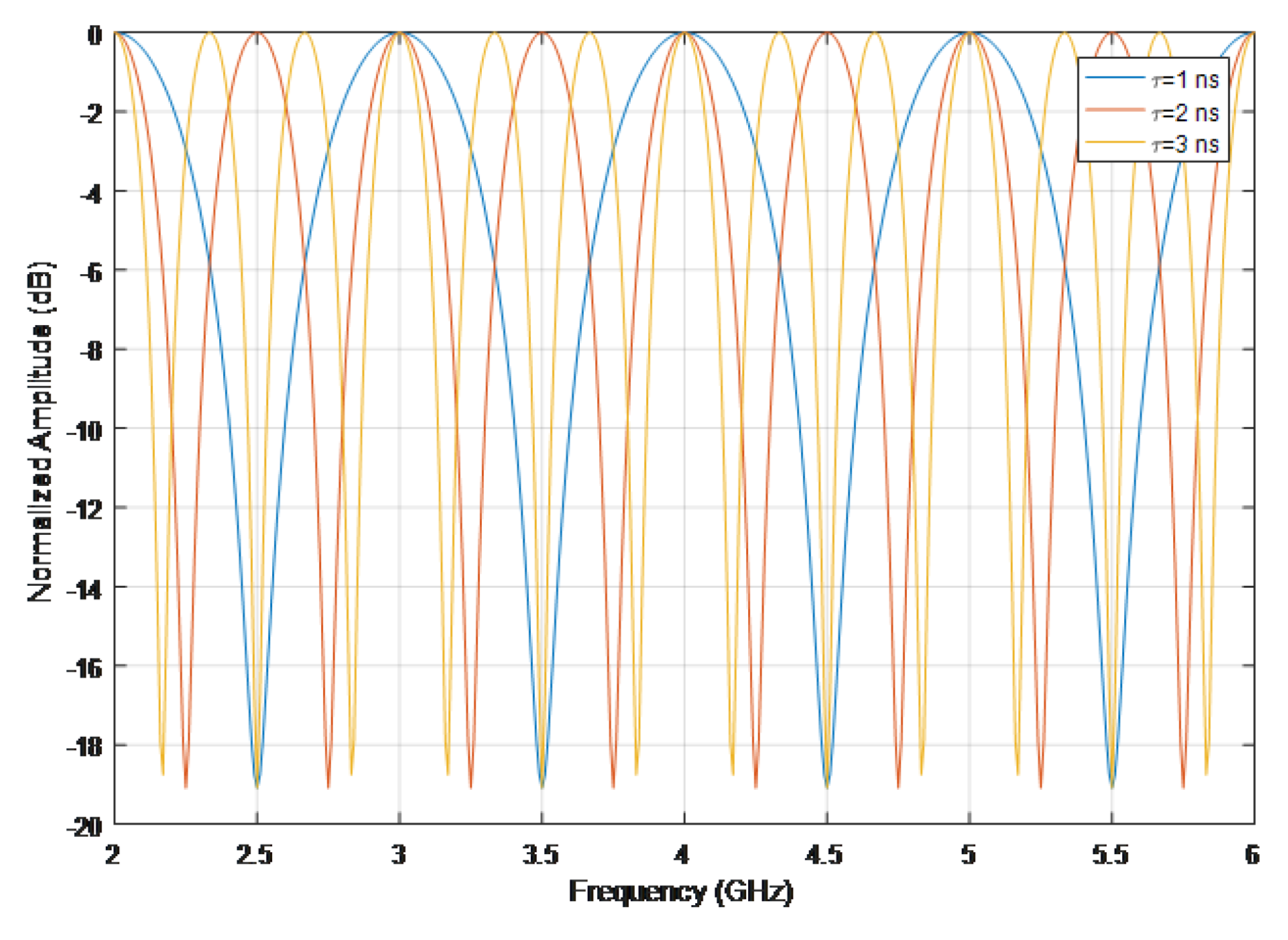
Taking into account typical high speed vehicle dynamics and carrier frequencies (around few GHz), even with a simple two-rays model, the maximum expected Doppler shift is usually below few KHz. With reference to
Figure 1, a correct emulation of the phenomenon performed by a DSP section requires a sampling step size of tens of microseconds (typically, ≤30 us). This is largely guaranteed by the sampling frequencies of the DSP sections that can run up to few GHz. To correctly emulate the multipath phenomenon, it is instead necessary that, during the minimum value of the differential delay of a path, the signal of the generic ray covers a space less than a fraction of the wavelength. The simple two-rays model allows some basic evaluations: for each differential delay
, the spectral distance between two contiguous minima of the time-varying transfer function is approximately
Hz. If the system bandwidth is
B MHz, and the differential delay
is expressed in
, the number of in-band minima is therefore about equal to
. The bandwidth of each minimum, evaluated at −10 dB compared to the maximum, is equal approximately to
Hz.
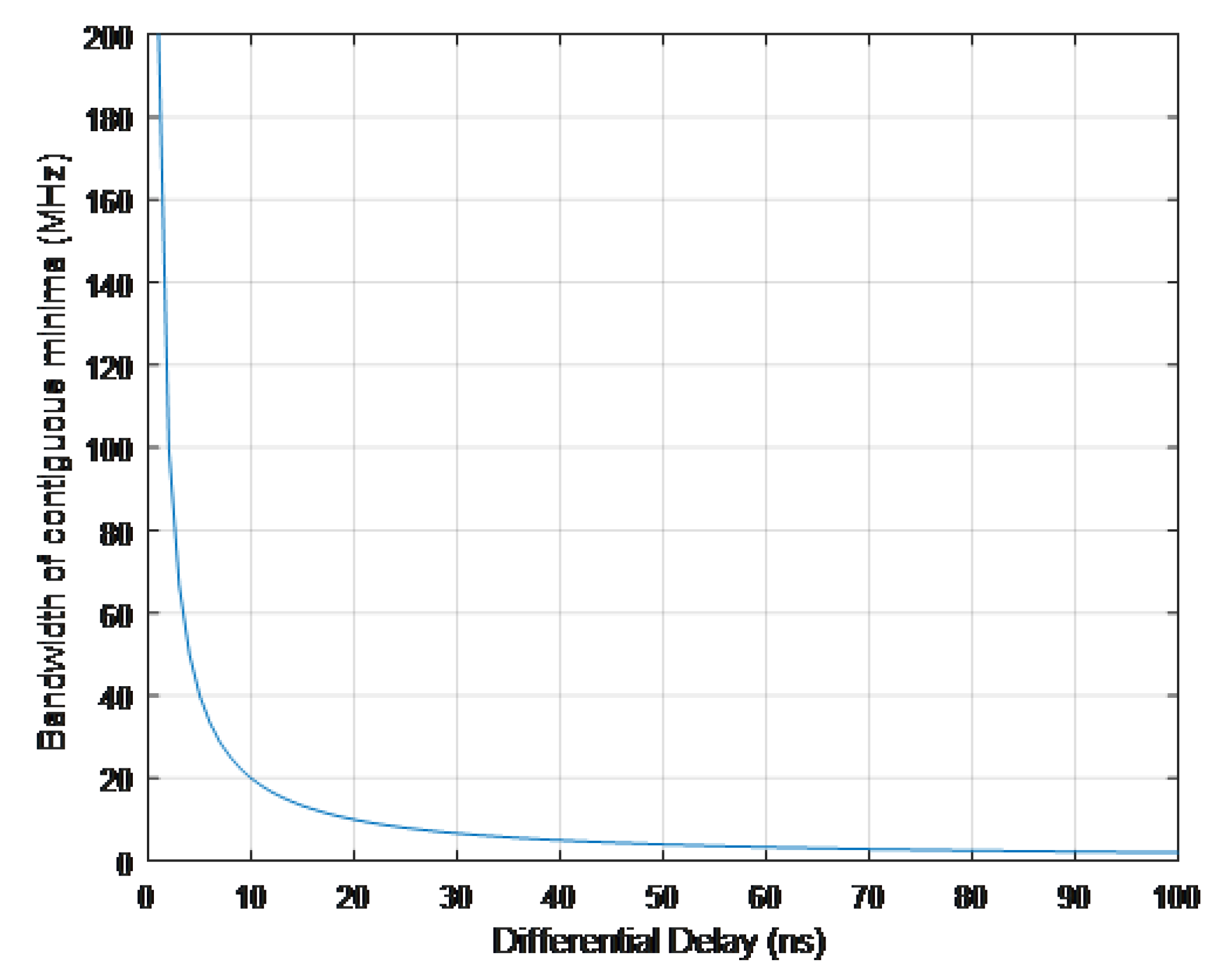
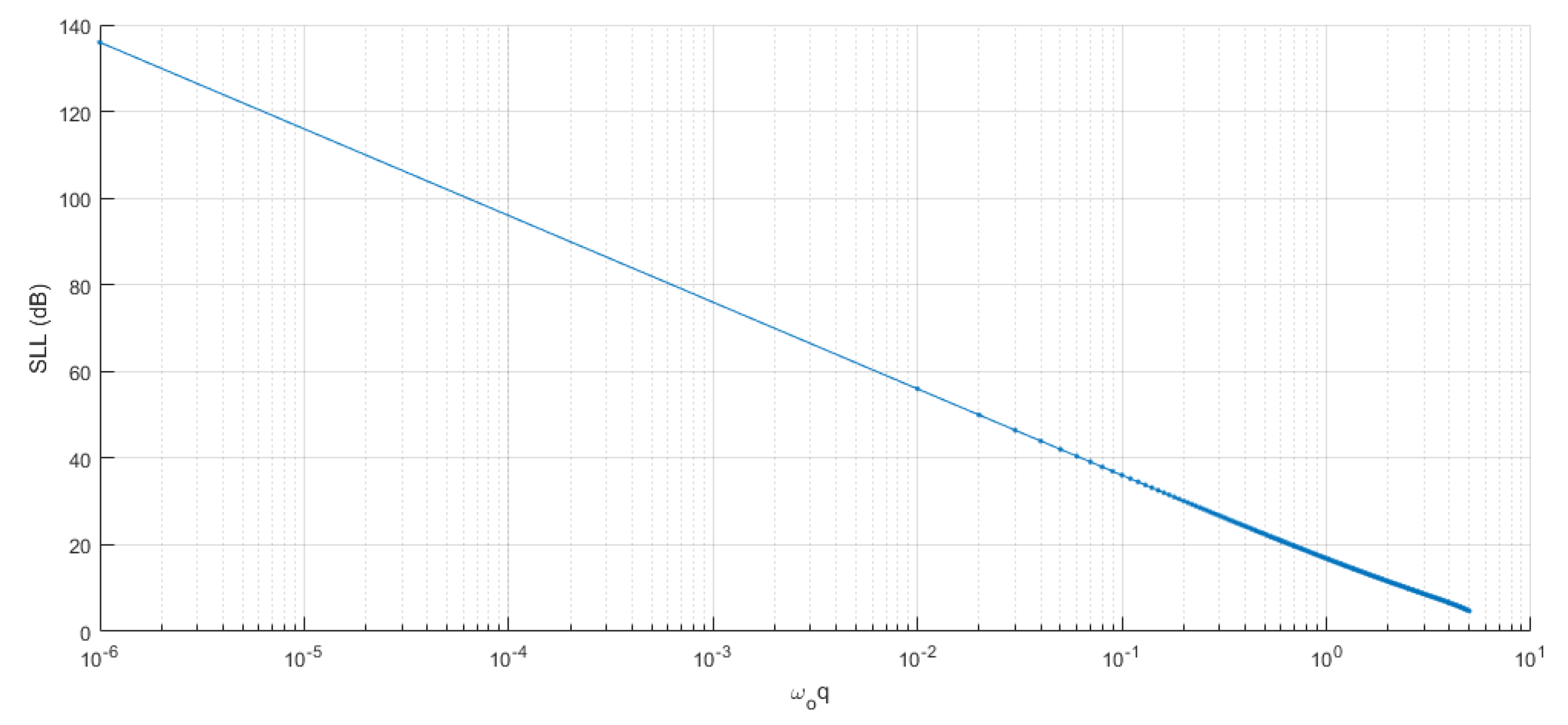
The bandwidth associated to the minima of the transfer function, for some values of
, is visible in
Figure 5 and
Figure 6.
Assuming a sampling frequency of 2 GHz for the DSP section and a corresponding sampling interval of 0.5 ns, in this interval the kth path covers about 0.15 m or up to 3 , for a RF spectrum from 2 to 6 GHz. Considering the phenomenon only in terms of RF propagation, it can be considered sufficient to limit the sampling frequency in order to have at least two samples per period or better.
2.3. Required Sampling Step Size for the Emulation of the Time Expansion
The emulation of the Doppler effect according to the principle of time expansion, performed digitally, implies a continuous discrete rotation of the signal phases in the different paths (see
Figure 3) according to the time evolution of the respective delays. This entails an in-depth examination of what has already been discussed. To try to quantify the phenomenon, take into consideration the operation of quantization of the delay
using a quantum equal to
seconds:
The previous operation performs a uniform quantization of the original signal. For simplicity, we can imagine the following scenario: a fixed source transmits a pure tone at frequency
f, a receiver moving at constant speed
with a null initial distance, receives this signal with a variable delay
:
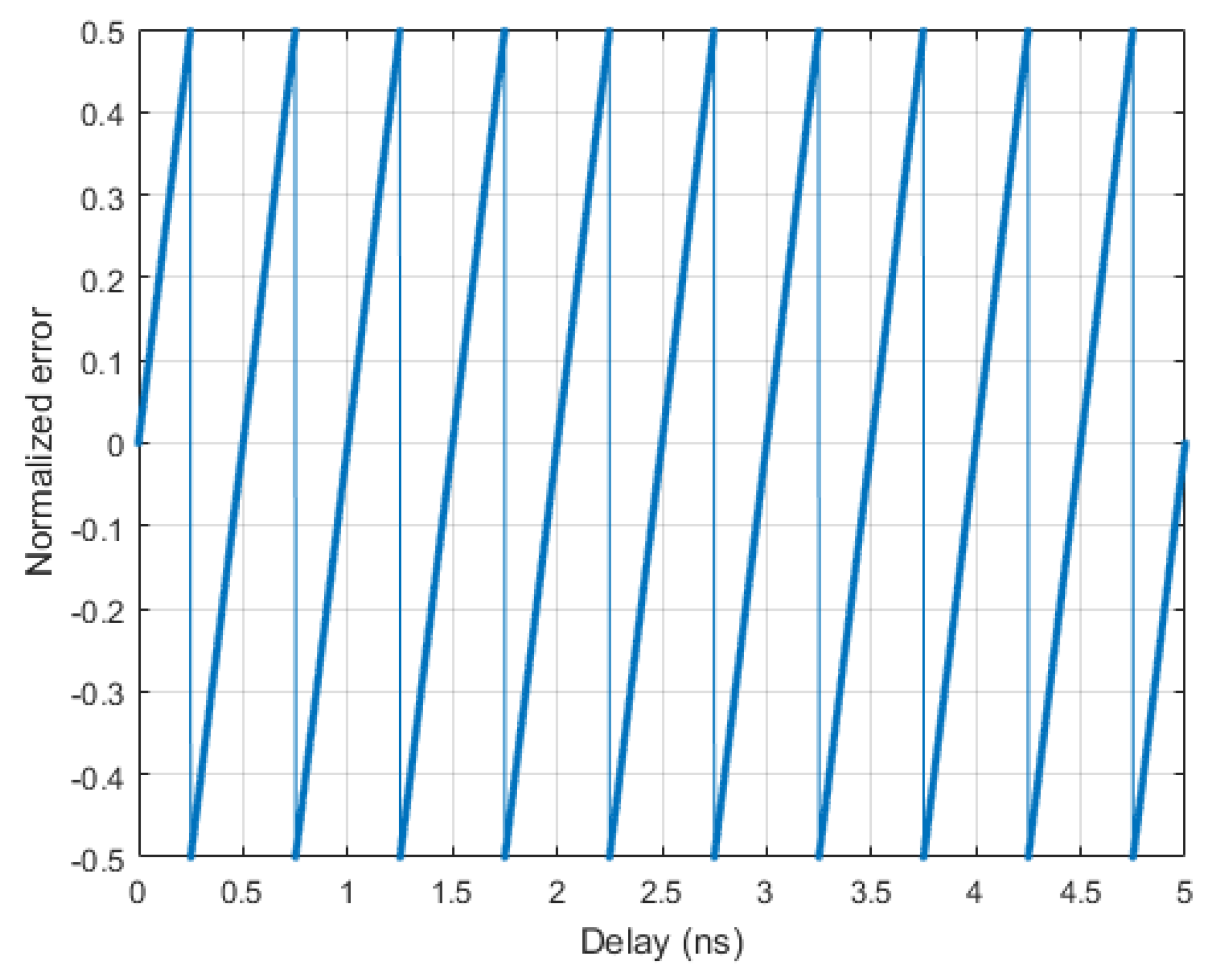
The quantization of the delay generates a discrete signal so that the error
i.e., the difference between the original and the quantized one, normalized to
, is limited to
. The error pattern is a sawtooth signal with a period
(see
Figure 7).
The complex envelope of the received analog signal, with respect to the angular frequency
, is:
Considering therefore the quantized delay, equal to
, it is possible to calculate the complex envelope of the actual received signal obtaining:
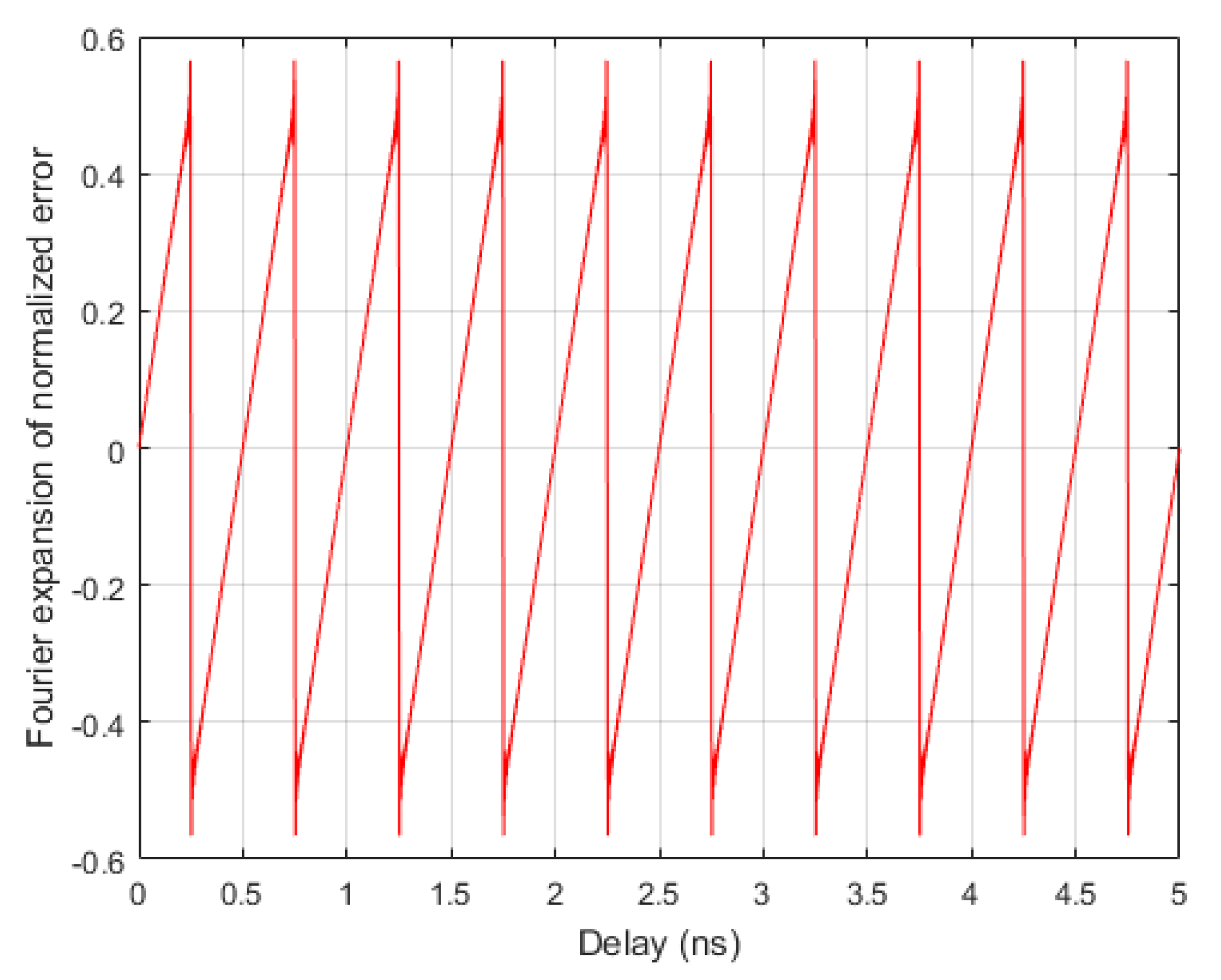
The error signal is periodic, therefore it is possible to write it as a Fourier series expansion:
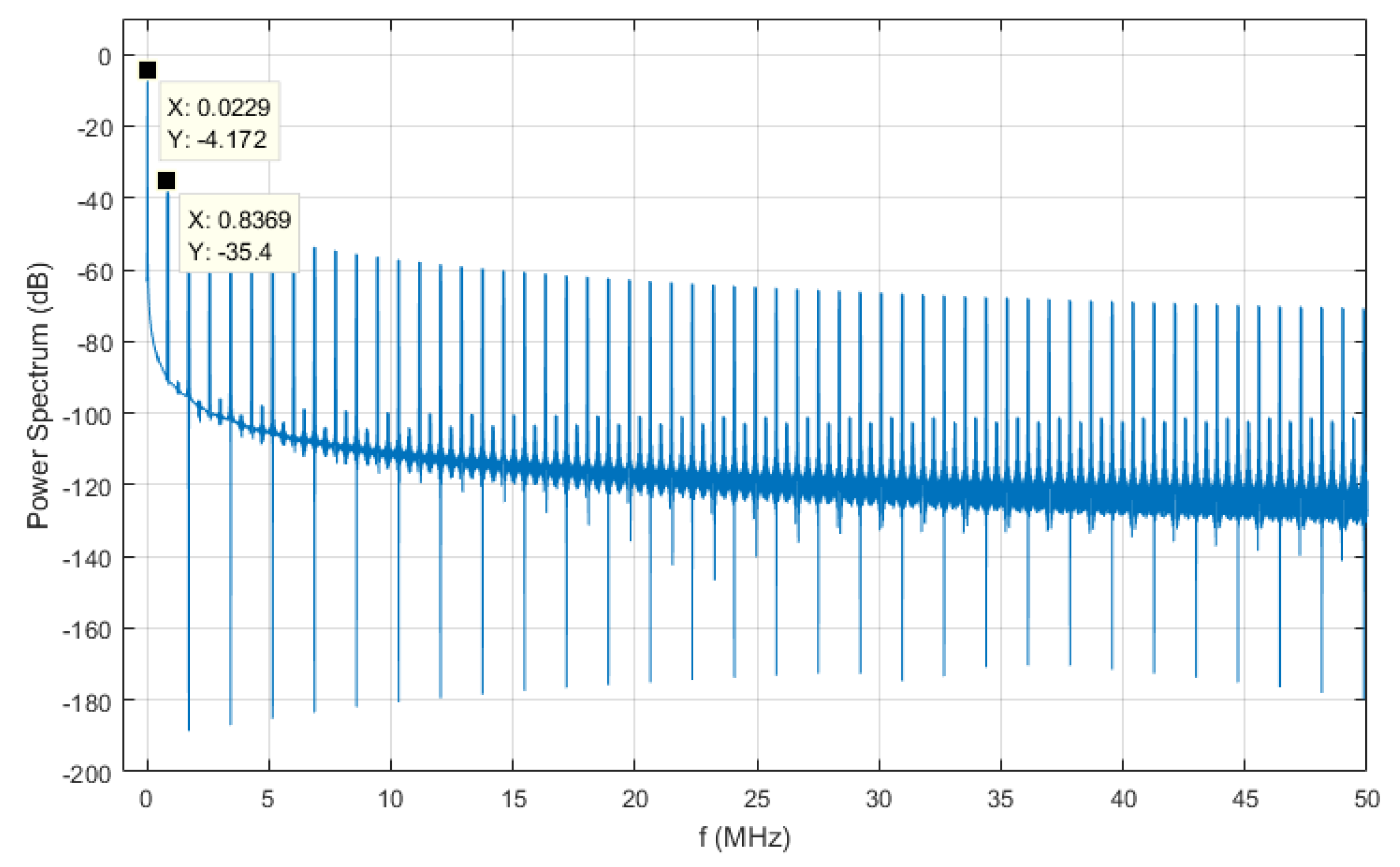
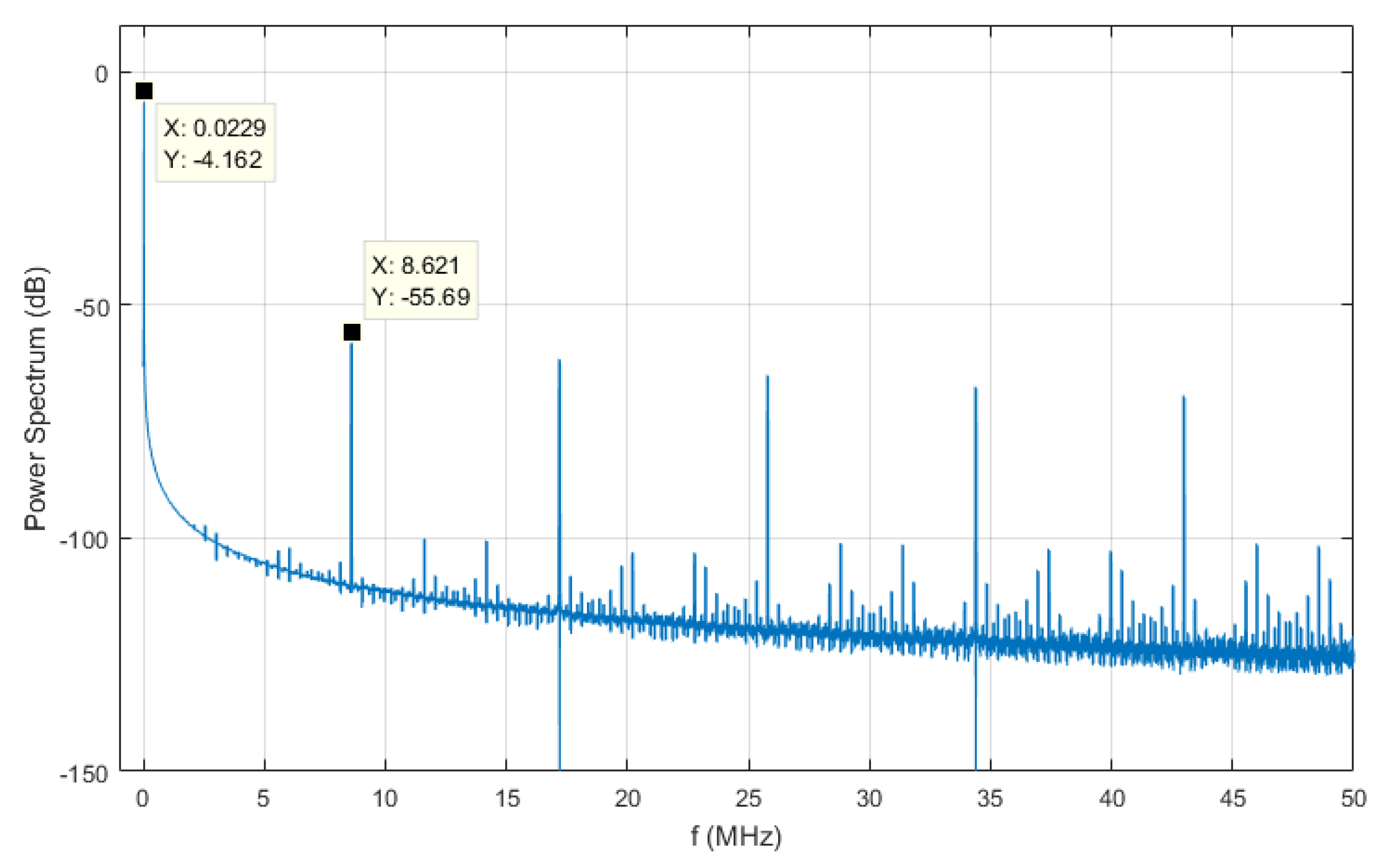
Figure 8 shows Equation (
10) limiting the series to the 100th order.
The complex envelope of the received signal thus results:
From Equation (
11) it is evident how the quantization of the delay involves the generation of a non-linear phase modulation of the received signal. The associated real signal results:
The spurious phase modulation introduced may be neglected if
. The time-dependent delay time, provided as input to the channel emulator, is still sampled at frequency
even if no longer quantized. The signal received is therefore also sampled at this frequency. For a given platform speed, it is theoretically possible to eliminate unwanted components by imposing
, resulting in a sampling of the sinusoidal component at integer multiples of the period. The complex envelope of the quantized signal can be placed in the form:
with a theoretically infinite number of products. Each complex exponential, with sinusoidal argument, can be placed in the form:
with
equal to the Bessel function of order
n of first kind. In first approximation, it can be sufficient to stop the series in Equation (
12) considering only the orders
and remembering that
. Each summation in Equation (
14) can then be put as follows:
thus obtaining:
by stopping the products at the third order, it is possible to write, for the real signal:
In addition to the expected tone, affected by a Doppler shift at frequency with an amplitude equal to , there are also spurious tones arranged symmetrically with respect to the central one. These components are separated by multiple integers of the frequency of the sawtooth wave with decreasing amplitudes.