Enhanced Gradient-Based Local Feature Descriptors by Saliency Map for Egocentric Action Recognition
Abstract
:1. Introduction
2. Related Work
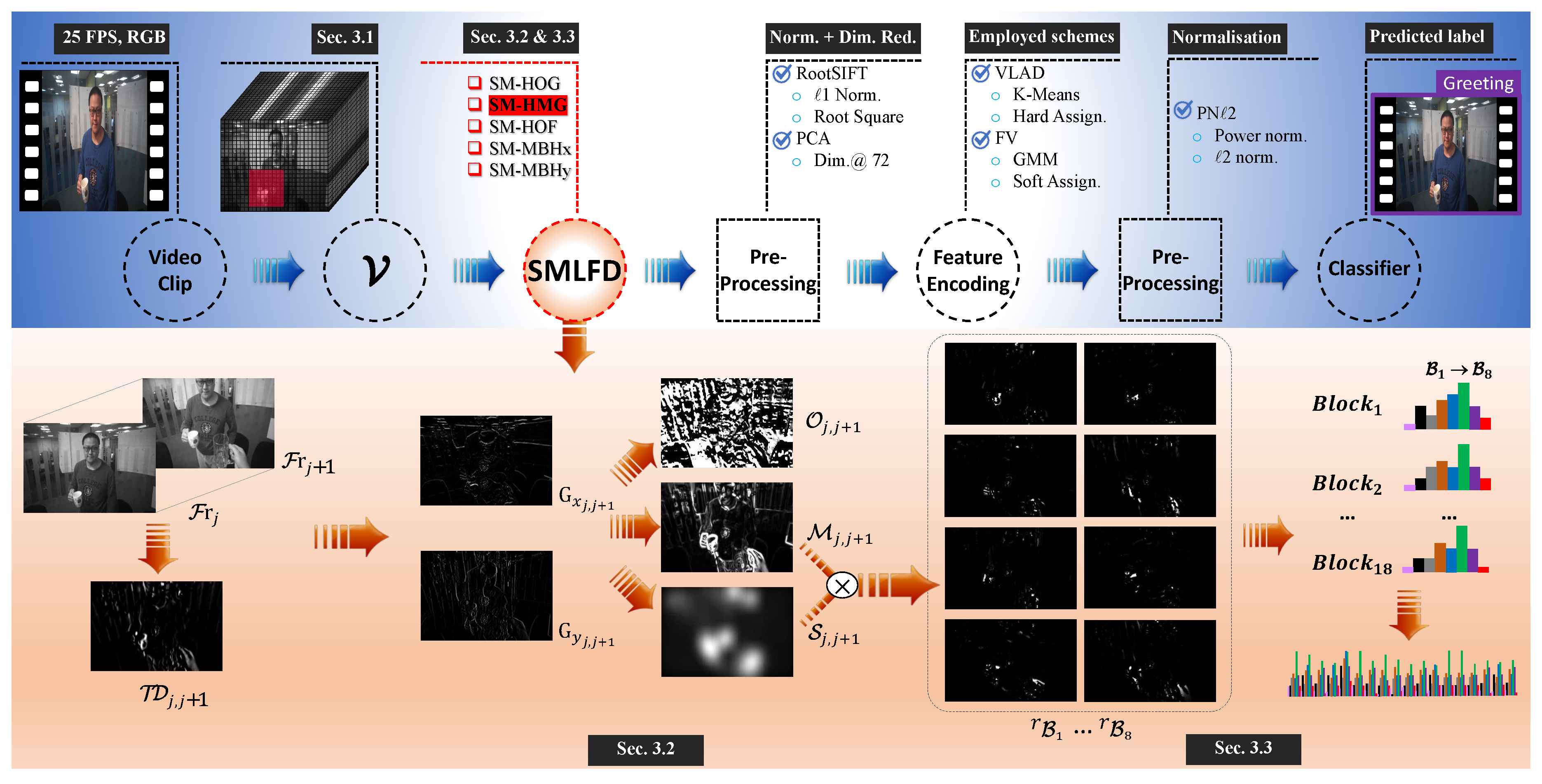
3. Saliency Map-Based Local Feature Descriptors for Egocentric Action Recognition
3.1. Video Representation
3.2. Local Spatial and Temporal Information Calculation
3.3. Saliency Map-Informed Bin Response Generation
| Algorithm 1: Saliency Membership Calculation Procedure. |
| Input: : the ith 2D video frame, Output: S: saliency membership of the ith frame Procedure getSaliencyMap
|
4. Experiments and Results
4.1. Experimental Setup
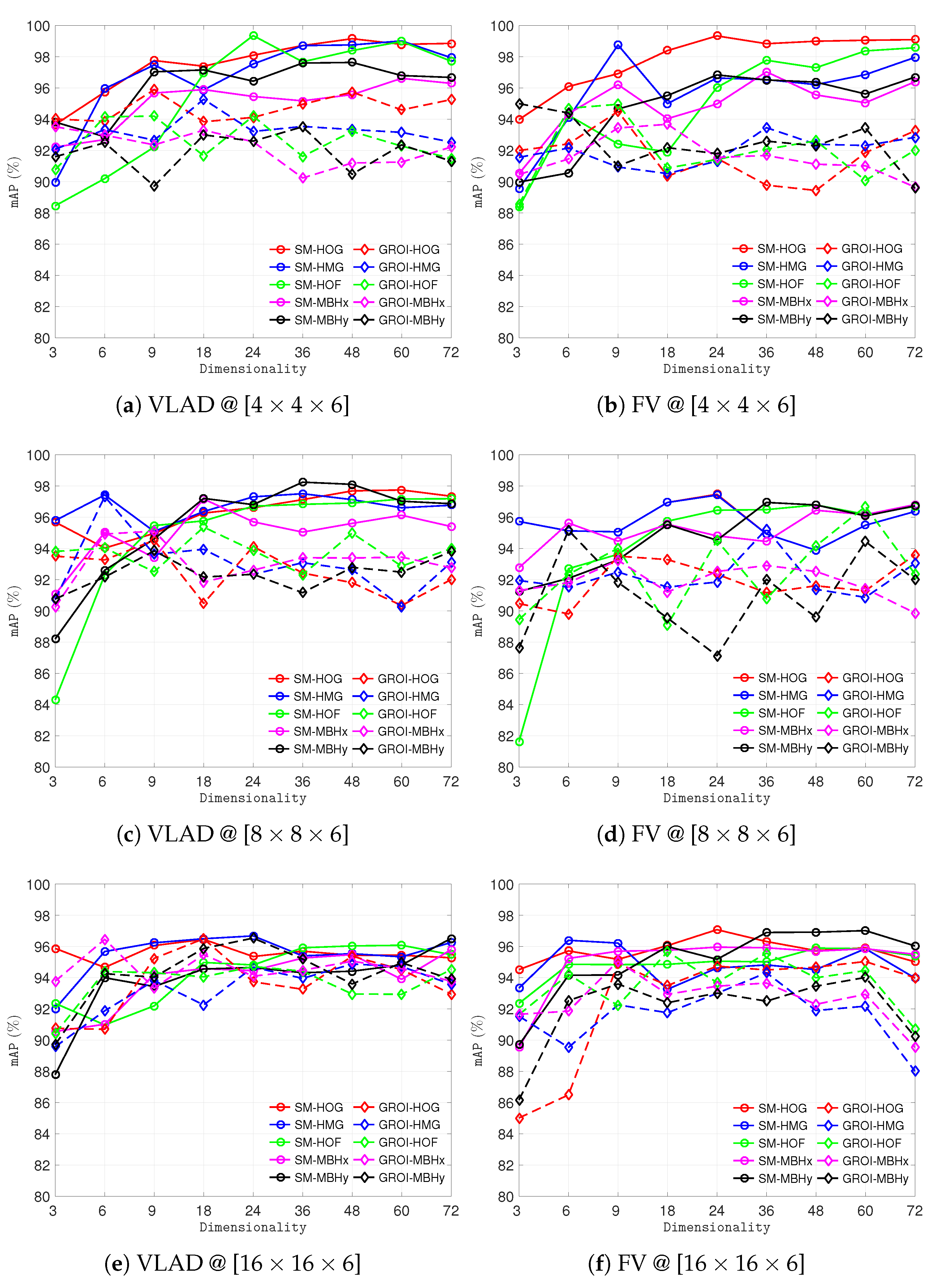
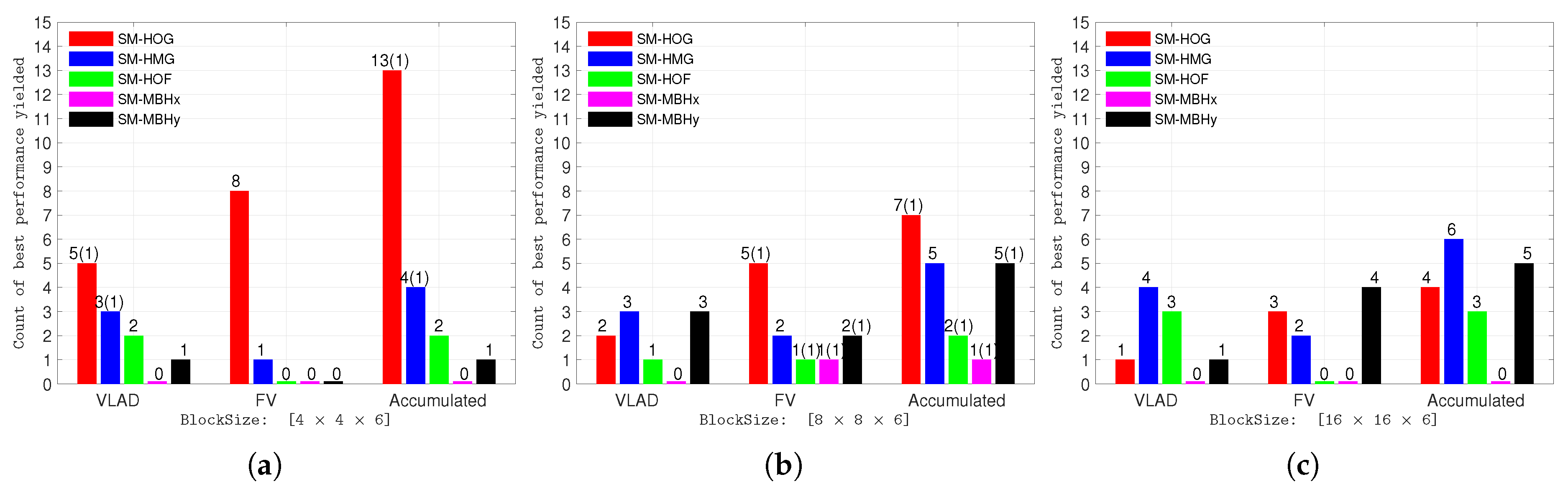
4.2. Experiments with Different Resolutions, Block Sizes, and Feature Encoding Methods
4.3. Experiments with Varying Number of Visual Words for Encoding
4.4. Experiment Using the Memory Aid Dataset
4.5. Comparison with Original Resolution
4.6. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| BoVW | Bag of Visual Words |
| LFD | Local Feature Descriptors |
| SMLFD | Saliency Membership based Local Feature Descriptors |
| SM-HOG | Saliency Membership based Histogram of Oriented Gradients |
| SM-HMG | Saliency Membership based Histogram of Motion Gradients |
| SM-HOF | Saliency Membership based Histogram of Optical Flow |
| SM-MBHx | Saliency Membership based Motion Boundary Histogram (in x direction) |
| SM-MBHy | Saliency Membership based Motion Boundary Histogram (in y direction) |
| GROILFD | Gaze Region of Interest based Local Feature Descriptors |
| GROI-HOG | Gaze Region of Interest based Histogram of Oriented Gradients |
| GROI-HMG | Gaze Region of Interest based Histogram of Motion Gradients |
| GROI-HOF | Gaze Region of Interest based Histogram of Optical Flow |
| GROI-MBHx | Gaze Region of Interest based Motion Boundary Histogram (in x direction) |
| GROI-MBHy | Gaze Region of Interest based Motion Boundary Histogram (in y direction) |
References
- Betancourt, A.; Morerio, P.; Regazzoni, C.S.; Rauterberg, M. The Evolution of First Person Vision Methods: A Survey. IEEE Trans. Circ. Syst. Video Technol. 2015, 25, 744–760. [Google Scholar] [CrossRef]
- Nguyen, T.H.C.; Nebel, J.C.; Florez-Revuelta, F. Recognition of activities of daily living with egocentric vision: A review. Sensors 2016, 16, 72. [Google Scholar] [CrossRef] [PubMed]
- Zaki, H.F.M.; Shafait, F.; Mian, A. Modeling Sub-Event Dynamics in First-Person Action Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2017), Honolulu, HI, USA, 21–26 July 2017; pp. 1619–1628. [Google Scholar]
- Fan, C.; Lee, J.; Xu, M.; Singh, K.K.; Lee, Y.J.; Crandall, D.J.; Ryoo, M.S. Identifying First-Person Camera Wearers in Third-Person Videos. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2017), Honolulu, HI, USA, 21–26 July 2017; pp. 4734–4742. [Google Scholar]
- Zuo, Z.; Yang, L.; Peng, Y.; Chao, F.; Qu, Y. Gaze-Informed Egocentric Action Recognition for Memory Aid Systems. IEEE Access 2018, 6, 12894–12904. [Google Scholar] [CrossRef]
- Zuo, Z.; Organisciak, D.; Shum, H.P.H.; Yang, L. Saliency-Informed Spatio-Temporal Vector of Locally Aggregated Descriptors and Fisher Vectors for Visual Action Recognition. In Proceedings of the British Machine Vision Conference (BMVC 2018), Newcastle, UK, 2–6 September 2018; p. 321. [Google Scholar]
- Jegou, H.; Perronnin, F.; Douze, M.; Sánchez, J.; Pérez, P.; Schmid, C. Aggregating local image descriptors into compact codes. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 1704–1716. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Schmid, C. Action recognition with improved trajectories. In Proceedings of the IEEE International Conference on Computer Vision (ICCV 2013), Sydney, NSW, Australia, 1–8 December 2013; pp. 3551–3558. [Google Scholar]
- Cameron, R.; Zuo, Z.; Sexton, G.; Yang, L. A Fall Detection/Recognition System and an Empirical Study of Gradient-Based Feature Extraction Approaches. In UKCI 2017: Advances in Computational Intelligence Systems; Chao, F., Schockaert, S., Zhang, Q., Eds.; Advances in Intelligent Systems and Computing; Springer: Cham, Switzerland, 2017; Volume 650, pp. 276–289. [Google Scholar]
- Sivic, J.; Zisserman, A. Video Google: A text retrieval approach to object matching in videos. In Proceedings of the IEEE International Conference on Computer Vision (ICCV 2003), Nice, France, 13–16 October 2003; pp. 1470–1477. [Google Scholar]
- Dalal, N.; Triggs, B. Histograms of oriented gradients for human detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2005), San Diego, CA, USA, 20–25 June 2005; pp. 886–893. [Google Scholar] [CrossRef]
- Laptev, I.; Marszalek, M.; Schmid, C.; Rozenfeld, B. Learning realistic human actions from movies. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Anchorage, AK, USA, 23–28 June 2008. [Google Scholar] [CrossRef]
- Dalal, N.; Triggs, B.; Schmid, C. Human Detection Using Oriented Histograms of Flow and Appearance. In Proceedings of the European Conference on Computer Vision (ECCV 2006), Graz, Austria, 7–13 May 2006; pp. 428–441. [Google Scholar]
- Duta, I.C.; Uijlings, J.R.R.; Nguyen, T.A.; Aizawa, K.; Hauptmann, A.G.; Ionescu, B.; Sebe, N. Histograms of motion gradients for real-time video classification. In Proceedings of the IEEE International Workshop on Content-Based Multimedia Indexing (CBMI 2016), Bucharest, Romania, 15–17 June 2016. [Google Scholar] [CrossRef]
- Hou, X.; Harel, J.; Koch, C. Image signature: Highlighting sparse salient regions. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 194–201. [Google Scholar]
- Liu, B.; Ju, Z.; Liu, H. A structured multi-feature representation for recognizing human action and interaction. Neurocomputing 2018, 318, 287–296. [Google Scholar] [CrossRef]
- Laptev, I. On Space-Time Interest Points. Int. J. Comput. Vision (IJCV) 2005, 64, 107–123. [Google Scholar] [CrossRef]
- Dollar, P.; Rabaud, V.; Cottrell, G.; Belongie, S. Behavior recognition via sparse spatio-temporal features. In Proceedings of the 2005 IEEE International Workshop on Visual Surveillance and Performance Evaluation of Tracking and Surveillance (VS-PETS), Beijing, China, 15–16 October 2005; pp. 65–72. [Google Scholar]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vision (IJCV) 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Mikolajczyk, K.; Schmid, C. A performance evaluation of local descriptors. IEEE Trans. Pattern Anal. Mach. Intell. (TPAMI) 2005, 27, 1615–1630. [Google Scholar] [CrossRef] [PubMed]
- Bay, H.; Tuytelaars, T.; Van Gool, L. Surf: Speeded up robust features. In Proceedings of the European Conference on Computer Vision (ECCV 2006), Graz, Austria, 7–13 May 2006; pp. 404–417. [Google Scholar]
- Scovanner, P.; Ali, S.; Shah, M. A 3-dimensional sift descriptor and its application to action recognition. In Proceedings of the ACM International Conference on Multimedia (ACMMM), Augsburg, Germany, 24–29 September 2007; pp. 357–360. [Google Scholar]
- Bay, H.; Ess, A.; Tuytelaars, T.; Van Gool, L. Speeded-up robust features (SURF). Comput. Vis. Image Und. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Fathi, A.; Mori, G. Action recognition by learning mid-level motion features. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2008), Anchorage, AK, USA, 23–28 June 2008. [Google Scholar] [CrossRef]
- Sadanand, S.; Corso, J.J. Action bank: A high-level representation of activity in video. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2012), Providence, RI, USA, 16–21 June 2012; pp. 1234–1241. [Google Scholar]
- Wang, S.; Hou, Y.; Li, Z.; Dong, J.; Tang, C. Combining convnets with hand-crafted features for action recognition based on an HMM-SVM classifier. Multimed. Tools Appl. 2016, 77, 18983–18998. [Google Scholar] [CrossRef]
- Hassner, T. A critical review of action recognition benchmarks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW 2013), Portland, OR, USA, 23–28 June 2013; pp. 245–250. [Google Scholar]
- Borji, A.; Cheng, M.M.; Jiang, H.; Li, J. Salient Object Detection: A Benchmark. IEEE Trans. Image Process. 2015, 24, 5706–5722. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.V.; Song, Z.; Yan, S. STAP: Spatial-Temporal Attention-Aware Pooling for Action Recognition. IEEE Trans. Circ. Syst. Video Technol. 2015, 25, 77–86. [Google Scholar] [CrossRef]
- Huang, Y.; Huang, K.; Yu, Y.; Tan, T. Salient coding for image classification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2011), Colorado Springs, CO, USA, 20–25 June 2011; pp. 1753–1760. [Google Scholar]
- Wang, J.; Yang, J.; Yu, K.; Lv, F.; Huang, T.; Gong, Y. Locality-constrained linear coding for image classification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2010), San Francisco, CA, USA, 13–18 June 2010; pp. 3360–3367. [Google Scholar]
- Perronnin, F.; Sánchez, J.; Mensink, T. Improving the Fisher Kernel for Large-scale Image Classification. In Proceedings of the European Conference on Computer Vision (ECCV 2010), Crete, Greece, 5–11 September 2010; pp. 143–156. [Google Scholar]
- Van Der Maaten, L.; Postma, E.; Van den Herik, J. Dimensionality reduction: a comparative. J. Mach. Learn. Res. 2009, 10, 66–71. [Google Scholar]
- Zuo, Z.; Li, J.; Anderson, P.; Yang, L.; Naik, N. Grooming detection using fuzzy-rough feature selection and text classification. In Proceedings of the 2018 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Rio de Janeiro, Brazil, 8–13 July 2018. [Google Scholar]
- Uijlings, J.; Duta, I.C.; Sangineto, E.; Sebe, N. Video classification with Densely extracted HOG/HOF/MBH features: An evaluation of the accuracy/computational efficiency trade-off. Int. J. Multimed. Inf. Retr. 2015, 4, 33–44. [Google Scholar] [CrossRef]
- Iosifidis, A.; Tefas, A.; Pitas, I. View-Invariant Action Recognition Based on Artificial Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 412–424. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Yu, H.; Wang, S. Feature sampling strategies for action recognition. In Proceedings of the IEEE International Conference on Image Processing (ICIP 2017), Beijing, China, 17–20 September 2017; pp. 3968–3972. [Google Scholar]
- Lazebnik, S.; Schmid, C.; Ponce, J. Beyond bags of features: Spatial pyramid matching for recognizing natural scene categories. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR’06), New York, NY, USA, 17–22 June 2006; Volume 2, pp. 2169–2178. [Google Scholar]
- Peng, X.; Wang, L.; Wang, X.; Qiao, Y. Bag of visual words and fusion methods for action recognition: Comprehensive study and good practice. Comput. Vis. Image Und. 2016, 150, 109–125. [Google Scholar] [CrossRef]
- Horn, B.K.; Schunck, B.G. Determining optical flow. Artif. Intell. 1981, 17, 185–203. [Google Scholar] [CrossRef]
- Viola, P.; Jones, M. Rapid object detection using a boosted cascade of simple features. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2001), Kauai, HI, USA, 8–14 December 2001; Volume 1, pp. 511–518. [Google Scholar]
- Zhang, X.; Wandell, B.A. A spatial extension of CIELAB for digital color-image reproduction. J. Soc. Inf. Display 1997, 5, 61–63. [Google Scholar] [CrossRef]
- Kawalec, A.; Rapacki, T.; Wnuczek, S.; Dudczyk, J.; Owczarek, R. Mixed method based on intrapulse data and radiated emission to emitter sources recognition. In Proceedings of the IEEE International Conference on Microwave Radar and Wireless Communications (MIKON 2006), Krakow, Poland, 22–24 May 2006; pp. 487–490. [Google Scholar]
- Matuszewski, J. The radar signature in recognition system database. In Proceedings of the IEEE International Conference on Microwave Radar and Wireless Communications (MIKON 2012), Warsaw, Poland, 21–23 May 2012; Volume 2, pp. 617–622. [Google Scholar]
- Matuszewski, J.; Sikorska-Łukasiewicz, K. Neural network application for emitter identification. In Proceedings of the IEEE International Radar Symposium (IRS 2017), Prague, Czech Republic, 28–30 June 2017. [Google Scholar] [CrossRef]
| Greeting |  |
| Passing a Ball |  |
| Paying |  |
| Shaking Hands |  |
| Talking |  |
| FeatDesc | UNN-GazeEAR @ | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [4 × 4 × 6] | [8 × 8 × 6] | [16 × 16 × 6] | [32 × 32 × 6] | |||||||||||||||||
| T | T | T | VLAD | FV | T | T | T | VLAD | FV | T | T | T | VLAD | FV | T | T | T | VLAD | FV | |
| GROI-HOG [5] | 22 | 83 | 78 | 96.34 | 96.48 | 18 | 34 | 22 | 94.62 | 94.56 | 17 | 6 | 6 | 95.00 | 93.96 | 16 | 2 | 2 | 94.50 | 93.80 |
| SM-HOG | 76 | 112 | 148 | 98.46 | 99.80 | 96 | 25 | 51 | 96.44 | 97.58 | 91 | 9 | 9 | 95.38 | 95.34 | 91 | 2 | 2 | 95.38 | 95.34 |
| GROI-HMG [5] | 22 | 96 | 81 | 95.40 | 96.08 | 18 | 22 | 24 | 93.82 | 92.60 | 17 | 6 | 6 | 94.28 | 92.28 | 16 | 2 | 2 | 95.74 | – |
| SM-HMG | 70 | 111 | 91 | 98.32 | 98.74 | 89 | 23 | 20 | 96.66 | 97.06 | 86 | 7 | 7 | 96.22 | 95.86 | 83 | 2 | 2 | 94.50 | 95.16 |
| GROI-HOF [5] | 26 | 116 | 118 | 93.94 | 91.22 | 22 | 25 | 24 | 93.90 | 92.94 | 21 | 5 | 6 | 95.62 | 91.98 | 20 | 2 | 2 | 92.88 | – |
| SM-HOF | 77 | 91 | 112 | 99.28 | 99.20 | 92 | 20 | 37 | 97.16 | 95.54 | 90 | 6 | 9 | 95.50 | 95.34 | 84 | 2 | 2 | 93.38 | 93.32 |
| GROI-MBHx [5] | 41 | 96 | 89 | 90.72 | 91.80 | 33 | 31 | 30 | 93.14 | 92.48 | 32 | 7 | 7 | 95.88 | 92.12 | 30 | 2 | 2 | 94.34 | – |
| SM-MBHx | 134 | 113 | 86 | 97.22 | 96.06 | 166 | 20 | 28 | 96.58 | 97.46 | 163 | 8 | 7 | 94.82 | 96.24 | 156 | 2 | 2 | 91.78 | 95.70 |
| GROI-MBHy [5] | 41 | 120 | 58 | 93.74 | 91.46 | 33 | 31 | 41 | 94.66 | 91.20 | 32 | 7 | 6 | 95.78 | 93.54 | 30 | 2 | 2 | 95.20 | – |
| SM-MBHy | 134 | 125 | 130 | 98.98 | 96.68 | 166 | 23 | 17 | 97.30 | 96.50 | 163 | 6 | 5 | 94.42 | 96.26 | 156 | 2 | 2 | 95.22 | 92.86 |
| BlockSize | FeatEnc | UNN-GazeEAR with SMLFD @ | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 6 | 9 | 18 | 24 | 36 | 48 | 60 | 72 | ||
| VLAD | 93.82 | 95.96 | 97.76 | 97.40 | 99.36 | 98.72 | 99.16 | 99.02 | 98.86 | |
| FV | 93.98 | 96.10 | 98.76 | 98.40 | 99.34 | 98.84 | 99.00 | 99.06 | 99.10 | |
| VLAD | 95.78 | 97.42 | 95.46 | 97.20 | 97.30 | 98.24 | 98.10 | 97.74 | 97.34 | |
| FV | 95.72 | 96.08 | 98.22 | 97.28 | 97.46 | 96.94 | 96.78 | 97.06 | 96.80 | |
| VLAD | 95.88 | 95.68 | 96.24 | 96.50 | 96.68 | 95.92 | 96.04 | 96.08 | 96.52 | |
| FV | 94.52 | 96.40 | 96.22 | 96.06 | 97.08 | 96.90 | 96.92 | 97.02 | 96.04 | |
| FeatEnc | FeatDesc | TopAcc | BlockSize | FeatDim | FeatDesc | TopAcc | BlockSize | FeatDim |
|---|---|---|---|---|---|---|---|---|
| VLAD | SM-HOG | 99.16 | [4 × 4 × 6] | 48 | GROI-HOG [5] | 96.50 | [16 × 16 × 6] | 18 |
| SM-HMG | 99.02 | [4 × 4 × 6] | 60 | GROI-HMG [5] | 97.32 | [8 × 8 × 6] | 6 | |
| SM-HOF | 99.36 | [4 × 4 × 6] | 24 | GROI-HOF [5] | 95.36 | [8 × 8 × 6] | 18 | |
| SM-MBHx | 97.16 | [8 × 8 × 6] | 18 | GROI-MBHx [5] | 96.46 | [16 × 16 × 6] | 6 | |
| SM-MBHy | 98.24 | [8 × 8 × 6] | 36 | GROI-MBHy [5] | 96.54 | [16 × 16 × 6] | 24 | |
| FV | SM-HOG | 99.34 | [4 × 4 × 6] | 24 | GROI-HOG [5] | 95.04 | [16 × 16 × 6] | 60 |
| SM-HMG | 98.76 | [4 × 4 × 6] | 9 | GROI-HMG [5] | 95.24 | [8 × 8 × 6] | 36 | |
| SM-HOF | 98.58 | [4 × 4 × 6] | 72 | GROI-HOF [5] | 96.68 | [8 × 8 × 6] | 60 | |
| SM-MBHx | 97.04 | [4 × 4 × 6] | 36 | GROI-MBHx [5] | 95.06 | [16 × 16 × 6] | 9 | |
| SM-MBHy | 97.02 | [16 × 16 × 6] | 60 | GROI-MBHy [5] | 95.16 | [8 × 8 × 6] | 6 |
| FeatDesc | FeatEnc |  | ||||
|---|---|---|---|---|---|---|
| ‘Passing a Ball’ | ‘Shaking Hands’ | ‘Talking’ | ‘Paying’ | ‘Greeting’ | ||
| GROI-HOG [5] | VLAD | ✓ | ✗ | ✓ | ✓ | ✓ |
| SM-HOG | VLAD | ✓ | ✗ | ✓ | ✓ | ✗ |
| GROI-HOG [5] | FV | ✓ | ✓ | ✓ | ✓ | ✓ |
| SM-HOG | FV | ✓ | ✓ | ✓ | ✓ | ✓ |
| GROI-HMG [5] | VLAD | ✓ | ✗ | ✓ | ✗ | ✓ |
| SM-HMG | VLAD | ✓ | ✓ | ✓ | ✓ | ✗ |
| GROI-HMG [5] | FV | ✓ | ✓ | ✓ | ✗ | ✓ |
| SM-HMG | FV | ✓ | ✓ | ✓ | ✓ | ✗ |
| GROI-HOF [5] | VLAD | ✓ | ✗ | ✓ | ✗ | ✓ |
| SM-HOF | VLAD | ✓ | ✓ | ✓ | ✗ | ✓ |
| GROI-HOF [5] | FV | ✓ | ✓ | ✓ | ✗ | ✓ |
| SM-HOF | FV | ✓ | ✓ | ✓ | ✓ | ✗ |
| GROI-MBHx [5] | VLAD | ✓ | ✓ | ✓ | ✗ | ✓ |
| SM-MBHx | VLAD | ✓ | ✓ | ✓ | ✗ | ✗ |
| GROI-MBHx [5] | FV | ✓ | ✗ | ✓ | ✓ | ✗ |
| SM-MBHx | FV | ✓ | ✓ | ✓ | ✗ | ✓ |
| GROI-MBHy [5] | VLAD | ✓ | ✓ | ✓ | ✗ | ✓ |
| SM-MBHy | VLAD | ✓ | ✓ | ✓ | ✗ | ✗ |
| GROI-MBHy [5] | FV | ✓ | ✓ | ✓ | ✗ | ✓ |
| SM-MBHy | FV | ✓ | ✓ | ✓ | ✗ | ✓ |
| FeatDesc | FeatType | UNN-GazeEAR @ | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| [16 × 16 × 6] | [32 × 32 × 6] | [64 × 64 × 6] | ||||||||
| T | VLAD | FV | T | VLAD | FV | T | VLAD | FV | ||
| GROI-HOG [5] | 865 | 95.60 | 97.28 | 817 | 94.40 | 95.18 | 802 | 93.94 | 93.74 | |
| SM-HOG | 3611 | 87.24 | 82.92 | 3724 | 88.84 | 84.46 | 3716 | 87.32 | 84.78 | |
| GROI-HMG [5] | 859 | 95.94 | 95.82 | 815 | 94.68 | 92.52 | 802 | 93.64 | 93.62 | |
| SM-HMG | 3541 | 88.84 | 84.22 | 3537 | 87.52 | 84.28 | 3542 | 87.54 | 85.64 | |
| GROI-HOF [5] | 1077 | 94.58 | 95.30 | 1021 | 96.00 | 94.28 | 1011 | 95.02 | 93.64 | |
| SM-HOF | 3878 | 88.06 | 86.68 | 3744 | 87.10 | 83.70 | 3675 | 86.74 | 85.60 | |
| GROI-MBHx [5] | 1767 | 92.78 | 95.82 | 1579 | 93.20 | 95.28 | 1559 | 94.50 | 95.08 | |
| SM-MBHx | 6688 | 83.68 | 83.00 | 6647 | 85.40 | 82.94 | 6643 | 85.60 | 86.16 | |
| GROI-MBHy [5] | 1764 | 97.44 | 94.72 | 1575 | 94.92 | 93.28 | 1558 | 94.10 | 93.98 | |
| SM-MBHy | 6678 | 83.26 | 84.20 | 6647 | 85.64 | 83.20 | 6640 | 85.92 | 84.44 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zuo, Z.; Wei, B.; Chao, F.; Qu, Y.; Peng, Y.; Yang, L. Enhanced Gradient-Based Local Feature Descriptors by Saliency Map for Egocentric Action Recognition. Appl. Syst. Innov. 2019, 2, 7. https://doi.org/10.3390/asi2010007
Zuo Z, Wei B, Chao F, Qu Y, Peng Y, Yang L. Enhanced Gradient-Based Local Feature Descriptors by Saliency Map for Egocentric Action Recognition. Applied System Innovation. 2019; 2(1):7. https://doi.org/10.3390/asi2010007
Chicago/Turabian StyleZuo, Zheming, Bo Wei, Fei Chao, Yanpeng Qu, Yonghong Peng, and Longzhi Yang. 2019. "Enhanced Gradient-Based Local Feature Descriptors by Saliency Map for Egocentric Action Recognition" Applied System Innovation 2, no. 1: 7. https://doi.org/10.3390/asi2010007
APA StyleZuo, Z., Wei, B., Chao, F., Qu, Y., Peng, Y., & Yang, L. (2019). Enhanced Gradient-Based Local Feature Descriptors by Saliency Map for Egocentric Action Recognition. Applied System Innovation, 2(1), 7. https://doi.org/10.3390/asi2010007








